Algoritmo de optimización de neuroboides — Neuroboids Optimization Algorithm (NOA)

Contenido

1. Introducción
2. Implementación del algoritmo
3. Resultados de las pruebas

Introducción

Al investigar algoritmos de optimización, siempre me ha atraído la idea de crear soluciones lo más sencillas y eficientes posible. Observando cómo la naturaleza resuelve problemas complejos a través de las interacciones de organismos más simples, hemos desarrollado un nuevo algoritmo de optimización, el Algoritmo de Optimización de Neuroboides (NOA).

El algoritmo se basa en el concepto de agentes neuronales minimalistas: los neuroboides. Cada neuroboide es una red neuronal rudimentaria con dos capas de neuronas que se entrena usando el algoritmo Adam. La singularidad del planteamiento reside en que, a pesar de la extrema simplicidad de los agentes individuales, su comportamiento colectivo debería explorar eficazmente el espacio de soluciones de problemas de optimización complejos.

El NOA se inspira en los procesos de autoorganización de los sistemas naturales, en los que unidades simples, siguiendo reglas básicas, forman estructuras adaptativas complejas. En este artículo, presentaremos la justificación teórica del algoritmo, su modelo matemático y los resultados de un estudio experimental de su eficacia en funciones de prueba de optimización estándar.

Implementación del algoritmo

Imagine que pasea por un jardín después de una tormenta. Las lombrices de tierra se pueden encontrar por todas partes: criaturas simples con sistemas nerviosos primitivos. No son capaces de pensar como nosotros, pero de algún modo encuentran su camino en terrenos difíciles, evitan los peligros, encuentran comida y compañeros. Sus diminutos cerebros solo tienen unos pocos miles de neuronas y, sin embargo, existen desde hace millones de años. Así nació la idea de los neuroboides.

¿Y si combinamos la sencillez de un gusano con el poder de la inteligencia colectiva? En la naturaleza, los organismos más simples logran resultados increíbles cuando actúan juntos: las hormigas construyen colonias complejas, las abejas resuelven problemas de optimización al recolectar néctar y las bandadas de pájaros forman estructuras dinámicas complejas sin control centralizado.

Mis neuroboides serían como estas lombrices. Todo el mundo tiene su propia red neuronal, no una arquitectura masiva con millones de parámetros, sino unas pocas neuronas de entrada y salida. No conocen todo el espacio de búsqueda, sino que solo ven su entorno local. Cuando una lombriz encuentra un terreno fértil y rico en nutrientes, las demás acuden ahí. Pero estas no se limitan a seguirlos ciegamente: cada una mantiene su propia individualidad, su propia estrategia para viajar. Mis neuroboides no necesitan conocer las matemáticas de la optimización al completo. Aprenden solos, por ensayo y error. Cuando uno encuentra una buena solución, los demás no se limitan a copiar sus coordenadas, sino que aprenden a entender por qué esa solución es positiva y cómo llegar a ella a su manera.

¿Recuerda las puestas de sol en el mar? El sol se refleja en millones de destellos sobre las olas, y cada uno es su propia pequeña historia de luz interactuando con el agua. Lo mismo ocurre con mis neuroboides: cada uno refleja una pieza de la solución, y juntos crean una imagen completa. De lejos, sus movimientos pueden parecer caóticos, pero dentro de este caos aparente, nace el orden: un sistema autoorganizado para encontrar soluciones óptimas.

Los neuroboides tampoco tienen un comandante central. En su lugar, cada uno usa su pequeña red neuronal para decidir si sigue la mejor solución conocida o explora nuevos territorios, copia la estrategia exitosa de su compañero o se aventura a crear la suya propia. 

En un mundo obsesionado con la complejidad y la escala, los neuroboides nos recuerdan que los mejores sistemas suelen construirse partiendo de los elementos más simples. Igual que los granos de arena forman playas y montañas, igual que las gotas forman océanos, así mis pequeños gusanos digitales, cada uno con su diminuta red neuronal, trabajan juntos para resolver problemas que los gigantescos algoritmos monolíticos no logran resolver.

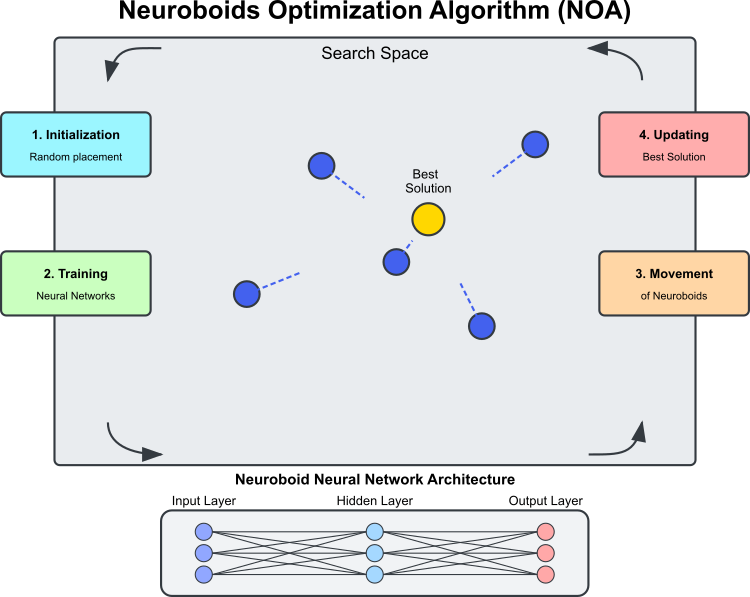
Figura 1. Esquema de funcionamiento del algoritmo NOA

La ilustración (figura 1) muestra los principales componentes y el principio de funcionamiento del algoritmo NOA. El espacio de búsqueda es la región en la que los neuroboides (círculos azules) buscan la solución óptima; los neuroboides son los agentes de optimización, cada cual con su propia red neuronal. La mejor solución será la mejor solución actual encontrada (el círculo dorado) hacia la que tienden los neuroboides. En cuanto a la arquitectura de red neuronal, cada neuroboide utiliza su propia red neuronal para determinar la dirección del movimiento. El proceso cíclico del algoritmo, consta de varias etapas: la inicialización, es decir, la colocación aleatoria de los neuroboides; el entrenamiento de las redes neuronales, a saber, el entrenamiento basado en la mejor solución encontrada; el desplazamiento de los neuroboides bajo el control de las redes neuronales entrenadas y la actualización de la mejor solución si se encuentra una solución mejor que la actual. Las líneas de puntos muestran la dirección de movimiento de los neuroboides, que vienen determinadas por las salidas de sus redes neuronales y tienden hacia la mejor solución con un elemento de aleatoriedad.

El término "neuroboide" combina los conceptos de red neuronal y boid (del inglés "boid", "pájaro" artificial en los modelos de comportamiento colectivo). Cada agente neuroboide es una combinación de: posición en el espacio de soluciones
y una red neuronal personal que determina la estrategia de movimiento.

A diferencia de los algoritmos metaheurísticos tradicionales (como los algoritmos genéticos o los métodos de enjambre), en los que el comportamiento de los agentes viene determinado por reglas fijas, en el NOA, cada neuroboide tiene su propia red neuronal que se entrena durante el proceso de optimización; las redes neuronales aprenden gradualmente a identificar las direcciones de búsqueda más prometedoras y el aprendizaje se produce según la mejor solución encontrada (vector objetivo). Resulta que el algoritmo de optimización implica dos estrategias de búsqueda: la primera es el NOA propiamente dicho y la segunda es el ADAM integrado en la red neuronal. El mecanismo de propagación inversa del error permite utilizar el ADAM en el contexto del algoritmo NOA como una herramienta independiente para sintonizar los pesos de la red neuronal de cada boide; en consecuencia, el número total de pesos de todos los neuroboides puede ser mucho mayor que la dimensionalidad del problema: no hay necesidad de optimizar los pesos de las redes neuronales de toda la población, esto ocurre de forma natural y automática.

El comportamiento de los neuroboides tiene algunos paralelismos con: el aprendizaje social en la naturaleza (observación de individuos exitosos), la neuroplasticidad (capacidad del sistema nervioso para adaptarse a condiciones cambiantes) y la inteligencia colectiva (optimización emergente mediante la interacción de muchos agentes simples).

Entre las principales características técnicas del algoritmo NOA, cabe destacar:

• la propagación directa e inversa del error dentro del proceso de optimización,
• el entrenamiento distribuido de múltiples redes neuronales, cada una de las cuales forma su propia estrategia,
• la corrección adaptativa del comportamiento según el estado actual de la búsqueda,
• el uso de funciones de activación de redes neuronales para crear dinámicas de búsqueda no lineales.

Esta combinación convierte al NOA en un interesante enfoque híbrido que combina los paradigmas del aprendizaje automático y la optimización. En lugar de usar redes neuronales para aproximar la función objetivo (como en los modelos sustitutos), el NOA las utiliza para controlar indirectamente el propio proceso de búsqueda, creando una especie de "metaaprendizaje" para resolver problemas de optimización.

Ahora podemos componer el pseudocódigo del algoritmo NOA:

Inicialización:

1. Creamos una población de N redes neuronales (neuroboides)
2. Cada red neuronal tiene una estructura con un número de entradas y salidas igual a la dimensionalidad del problema de optimización
3. Establecemos los parámetros:
   • popSize (tamaño de la población)
   • actFunc (función de activación neuronal)
   • dispScale (escala de desplazamiento)
   • eliteProb (probabilidad de copiar las coordenadas de élite)

Algoritmo:

1. Si se trata de la primera iteración (revision = false):
   • Por cada neuroboide de la población:
     • Inicializamos aleatoriamente las coordenadas en el espacio de búsqueda
     • Llevamos las coordenadas a valores discretos admisibles
   • Establecemos revision = true y finalizamos la iteración actual
2. Para iteraciones posteriores:
   • Para la mayoría de los neuroboides (todos menos los 5 últimos):
     • Para cada coordenada:
       • Con una probabilidad eliteProb sustituimos el valor de la coordenada por el valor de la mejor solución encontrada (cB)
   • Por cada neuroboide de la población:
     • Escalamos la mejor solución encontrada (cB) y la posición actual del neuroboide al rango [-1, 1].
     • Efectuamos la propagación directa a través de la red neuronal del neuroboide actual.
     • Calculamos el error entre el valor objetivo (cB escalado) y la salida de la red neuronal.
     • Realizamos la propagación inversa del error para entrenar la red neuronal
     • Actualizamos las coordenadas del neuroboide desplazándolas en la dirección determinada por la salida de la red neuronal.
     • Llevamos las coordenadas a valores discretos admisibles
3. Evaluación y actualización:
   • Por cada neuroboide de la población:
     • Calculamos el valor de la función objetivo para las coordenadas actuales
     • Si el valor es mejor que el mejor valor encontrado (fB):
       • Actualizamos el mejor valor encontrado (fB)
       • Guardamos las coordenadas actuales como mejores coordenadas (cB)

Vamos a escribir el código del algoritmo. Primero definimos la clase "C_AO_NOA", que deriva de la clase "C_AO". Esto significa que heredará las propiedades y métodos de "C_AO" y añadirá los suyos propios. Los principales elementos de la clase son:

El destructor ~C_AO_NOA (): borra los objetos de función de activación asignados dinámicamente para cada elemento del array "nn", una red neuronal individual de neuroboides. Esto ayuda a evitar fugas de memoria.

El constructor C_AO_NOA ():

• Inicializa los parámetros del algoritmo de optimización.
• Establece los valores iniciales de los parámetros: "popSize" - tamaño de la población, "actFunc" - función de activación de las neuronas, "dispScale" - escala de desplazamiento, probabilidad de copiar las coordenadas de élite.
• Reserva un array "params" para almacenar parámetros.

El método SetParams (): establece los parámetros basándose en los valores almacenados en el array "params".

El método Init (): se define para inicializar una clase con los rangos de valores rangeMinP, rangeMaxP, rangeStepP y el número de épocas "epochsP". 

Moving () и Revision (): estos métodos se utilizan para desplazar individuos en la población y tomar decisiones de evaluación y actualización.

El array nn: array de instancias de la clase de red neuronal de cada neuroboide.

Métodos cerrados: ScaleInp () y ScaleOut () son métodos para escalar los datos de entrada y salida, respectivamente.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_NOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_NOA ()
  {
    for (int i = 0; i < ArraySize (nn); i++) if (CheckPointer (nn [i].actFunc)) delete nn [i].actFunc;
  }
  C_AO_NOA ()
  {
    ao_name = "NOA";
    ao_desc = "Neuroboids Optimization Algorithm (joo)";
    ao_link = "https://www.mql5.com/es/articles/16992";

    popSize   = 50;   // размер популяции
    actFunc   = 0;    // функция активации нейрона
    dispScale = 0.01; // масштаб перемещений
    eliteProb = 0.1;  // вероятность копирования элитных координат

    ArrayResize (params, 4);
    params [0].name = "popSize";   params [0].val  = popSize;
    params [1].name = "actFunc";   params [1].val  = actFunc;
    params [2].name = "dispScale"; params [2].val  = dispScale;
    params [3].name = "eliteProb"; params [3].val  = eliteProb;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    actFunc   = (int)params [1].val;
    dispScale = params      [2].val;
    eliteProb = params      [3].val;
  }

  bool Init (const double &rangeMinP  [],  // минимальные значения
             const double &rangeMaxP  [],  // максимальные значения
             const double &rangeStepP [],  // шаг изменения
             const int     epochsP = 0);   // количество эпох

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    actFunc;   // функция активации нейрона
  double dispScale; // масштаб перемещений
  double eliteProb; // вероятность копирования элитных координат

  private: //-------------------------------------------------------------------
  C_MLPa nn [];

  void ScaleInp (double &inp [], double &out []);
  void ScaleOut (double &inp [], double &out []);
};
//——————————————————————————————————————————————————————————————————————————————

El método "Init" se usa para inicializar una instancia de la clase "C_AO_NOA". Toma una serie de parámetros que indican el rango de valores y el número de épocas, y realiza las operaciones necesarias para configurar el algoritmo.

Firma del método: indica el éxito de la inicialización. Parámetros:

• MinP [] - valores mínimos de los parámetros.
• MaxP [] - valores máximos de los parámetros.
• PasoP [] - paso de cambio de los parámetros.
• epochsP - número de épocas.

Inicialización estándar: la primera línea del método llama a la función "StandardInit" con los rangos transmitidos.

Ajuste de la configuración de la red neuronal:

• Creamos un array "nnConf" que contiene las dimensiones de las capas de entrada y salida de la red neuronal.
• Llamamos a "ArrayResize" para redimensionar el array "nnConf" a 2 (capa de entrada y salida).
• Ambos elementos del array se inicializan con el valor "coords", que se corresponde con la dimensionalidad de los datos de entrada.

Declaramos una enumeración E_Act: creamos una enumeración que define las diferentes funciones de activación neuronal (eActTanh, eActAlgSigm, eActRatSigm, etc.).

Redundancia del array de neuronas: el tamaño del array "nn" (array de neuronas) se cambia a "popSize", que antes se fijaba en el constructor.

Inicialización de las neuronas:

• La variable "cnt" se inicializa a partir de cero y se usa para pasar un único grano (seed) aleatorio para inicializar cada neurona, garantizando que la inicialización de los pesos en cada una de las redes neuronales sea única.
• En el ciclo for, se inicializa cada neurona. Luego se llama al método "nn[i].Init ()" con la configuración "nnConf", la función de activación "actFunc" y un grano basado en el valor actual de "cnt" y el número de milisegundos transcurridos desde que se inició el sistema.
• El valor de "cnt" aumenta con cada pasada del ciclo, lo cual permite crear granos únicos para cada inicialización de neuronas.

Resultado retornado: si todas las operaciones se realizan correctamente, el método retornará "true", es decir, la inicialización se habrá realizado correctamente.

El método "Init" de la clase "C_AO_NOA" resulta clave para configurar el algoritmo de optimización, posibilitando la inicialización de la red neuronal y los parámetros asociados. 

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_NOA::Init (const double &rangeMinP  [], // минимальные значения
                     const double &rangeMaxP  [], // максимальные значения
                     const double &rangeStepP [], // шаг изменения
                     const int     epochsP = 0)   // количество эпох
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  int nnConf [];
  ArrayResize (nnConf, 2);
  nnConf [0] = coords;
  nnConf [1] = coords;

  enum E_Act
  {
    eActTanh,      //0
    eActAlgSigm,   //1
    eActRatSigm,   //2

    eActSoftPlus,  //3
    eActBentIdent, //4
    eActSiLU,      //5

    eActACON,      //6
    eActSERF,      //7
    eActSnake      //8
  };

  ArrayResize (nn, popSize);
  int cnt = 0;
  for (int i = 0; i < popSize; i++)
  {
    nn [i].Init (nnConf, actFunc, (int)GetTickCount64 () + cnt);
    cnt++;
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

El método "Moving ()" implementa el proceso de desplazamiento de individuos en una población dentro de un algoritmo de optimización neuroboide. Veámoslo paso a paso:

Inicialización de los valores iniciales: si "revision" es "false", el método realizará la primera inicialización. Para cada elemento de la población "popSize" y para cada dimensión "coords", el método establece valores iniciales en el array "a[i].c[c]" que representa a los agentes de búsqueda:

• u.RNDfromCI () - genera un valor aleatorio en el rango "rangoMin[c]" y "rangoMax[c]".
• u.SeInDiSp() - función que utiliza un paso de cambio para ajustar el valor de "a [i].c [c]" dentro de un rango válido.
• Una vez finalizada la inicialización, "revision" se establecerá en "true" y se retornará el control del método. 

Actualización de coordenadas: las coordenadas de los individuos se actualizan según la probabilidad de elitismo. Luego se realiza una comprobación aleatoria de los primeros elementos "popSize - 5" de la población, y si el número aleatorio es menor que "eliteProb", las coordenadas "a [i].c [c]" se establecerán iguales a las coordenadas de élite "cB [c]".

Procesamiento de datos de la red neuronal: se crean los arrays para los datos de entrada y salida, los valores objetivo y los errores, y se preparan con el tamaño "coords". Para cada elemento de la población:

• ScaleInp () - escala las coordenadas objetivo "cB" y las guarda en "targVal".
• ScaleInp () - escala la coordenada actual de la población y la guarda en "inpData".
• nn[i].ForwProp () - realiza la propagación directa en la red neuronal para obtener los datos de salida.
• Después se calcula el error (diferencia entre el valor objetivo y el valor recibido) de cada coordenada.
• nn [i].BackProp (err) - realiza la propagación inversa del error para corregir los pesos.
• Las coordenadas de "a [i].c [c]" se actualizan considerando la salida de la red neuronal, el escalado y un elemento de muestreo aleatorio.
• Al final, el valor de "a[i].c[c] se normaliza usando la función "u.SeInDiSp".

Así, el método "Moving ()" se encarga de desplazar a los individuos en el modelo, inicializándolos al principio y actualizando sus posiciones en función de las salidas de las redes neuronales y la selección probabilística. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    // Инициализация начальных значений якорей во всех параллельных вселенных
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd  = 0.0;
  double val  = 0.0;
  int    pair = 0.0;

  for (int i = 0; i < popSize - 5; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < eliteProb)
      {
        a [i].c [c] = cB [c];
      }
    }
  }

  double inpData []; ArrayResize (inpData, coords);
  double outData []; ArrayResize (outData, coords);
  double targVal []; ArrayResize (targVal, coords);
  double err     []; ArrayResize (err,     coords);

  for (int i = 0; i < popSize; i++)
  {
    ScaleInp (cB,      targVal);
    ScaleInp (a [i].c, inpData);

    nn [i].ForwProp (inpData, outData);

    for (int c = 0; c < coords; c++) err [c] = targVal [c] - outData [c];

    nn [i].BackProp (err);

    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] += outData [c] * (rangeMax [c] - rangeMin [c]) * dispScale * u.RNDprobab ();
      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Vamos a analizar el método "Revision", que realiza una evaluación y actualización de la "mejor" solución actual de la población. Este compara los valores de la función objetivo de cada individuo con el "mejor" valor actual y lo actualiza si encuentra uno mejor. Así, el método garantiza que la mejor solución actual se mantenga en la población. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::Revision ()
{
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "ScaleInp" se encarga de escalar los datos de entrada desde el rango indicado por "rangeMin" y "rangeMax" al rango de -1 a 1. Cada valor "inp[c]" se escala usando la función "u.Scale", que realiza un escalado lineal para situarlo en el intervalo de -1 a 1. El método "ScaleInp" prepara los datos para los cálculos posteriores, asegurándose de que están normalizados en el rango necesario.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::ScaleInp (double &inp [], double &out [])
{
  for (int c = 0; c < coords; c++) out [c] = u.Scale (inp [c], rangeMin [c], rangeMax [c], -1, 1);
}
//——————————————————————————————————————————————————————————————————————————————

El método "ScaleInp" funciona de forma similar al método "ScaleOut", que realiza un escalado inverso del intervalo -1 a 1 al intervalo "rangeMin" y "rangeMax".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::ScaleOut (double &inp [], double &out [])
{
  for (int c = 0; c < coords; c++) out [c] = u.Scale (inp [c], -1, 1, rangeMin [c], rangeMax [c]);
}
//——————————————————————————————————————————————————————————————————————————————

Resultados de las pruebas

El algoritmo muestra resultados interesantes en funciones con dimensionalidad pequeña y moderada. Cuando la dimensionalidad del problema aumenta hasta 1000 variables, el tiempo de cálculo se vuelve inaceptablemente grande, así que no hemos presentado dichas pruebas. El rendimiento alcanza aproximadamente el 45% (en 6 de 9 pruebas) del valor óptimo en las pruebas.

NOA|Neuroboids Optimization Algorithm (joo)|50.0|0.0|0.01|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.7013521128826248
25 Hilly's; Func runs: 10000; result: 0.40128968110640306
=============================
5 Forest's; Func runs: 10000; result: 0.6222984295200933
25 Forest's; Func runs: 10000; result: 0.30830340651626337
=============================
5 Megacity's; Func runs: 10000; result: 0.4523076923076924
25 Megacity's; Func runs: 10000; result: 0.20892307692307693
=============================
All score: 2.69447 (44.91%)

Me gustaría decir unas palabras sobre la visualización del NOA. Como podemos ver, el algoritmo forma interesantes estructuras en forma de abanico. Estas estructuras suponen esencialmente visualizaciones de los resultados de las redes neuronales en neuroboides. 

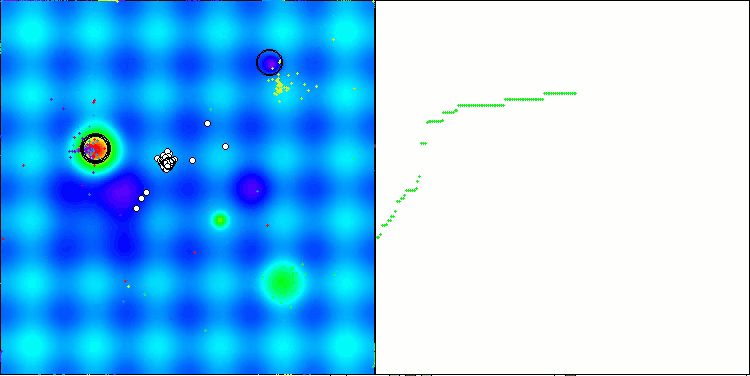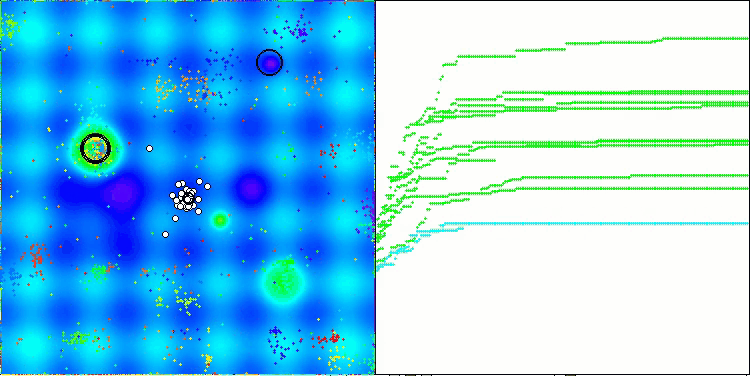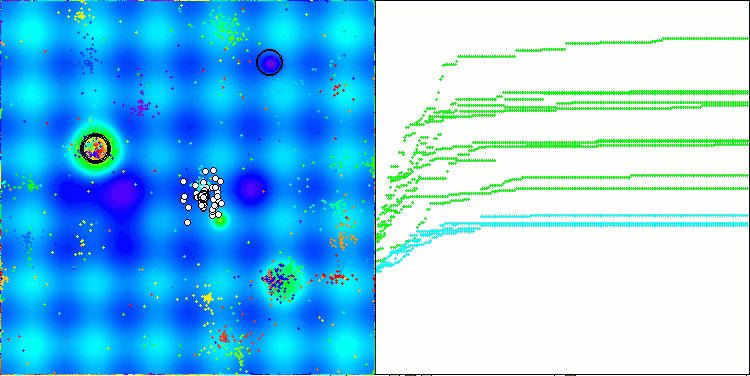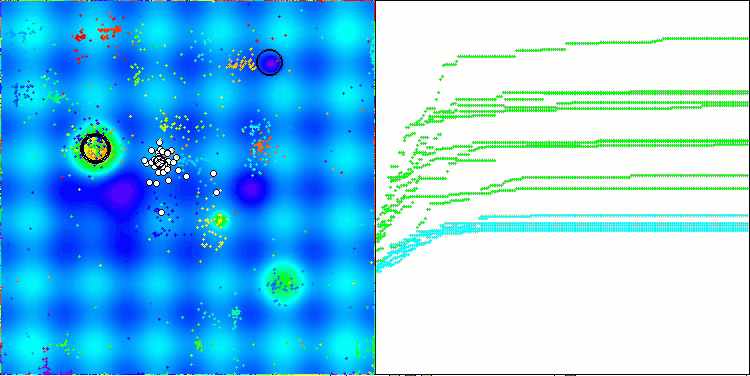
NOA en la función de prueba Hilly

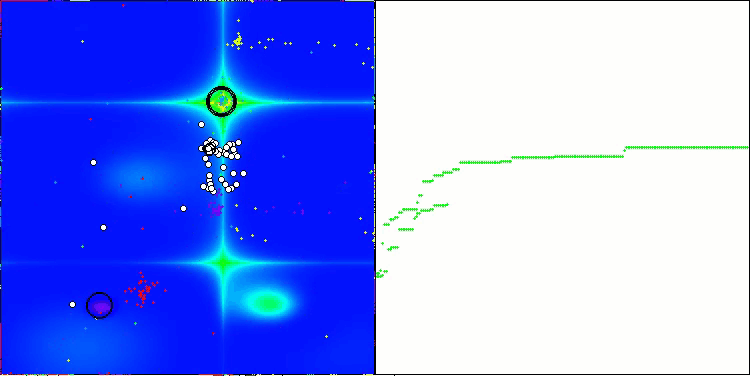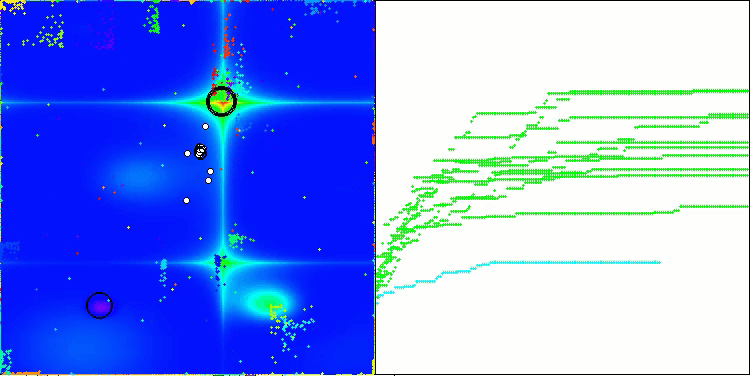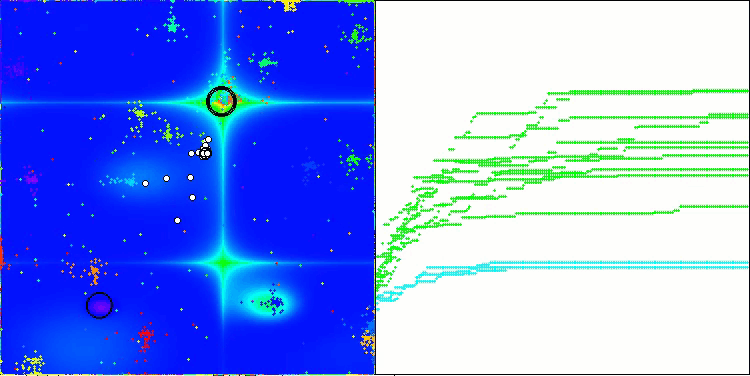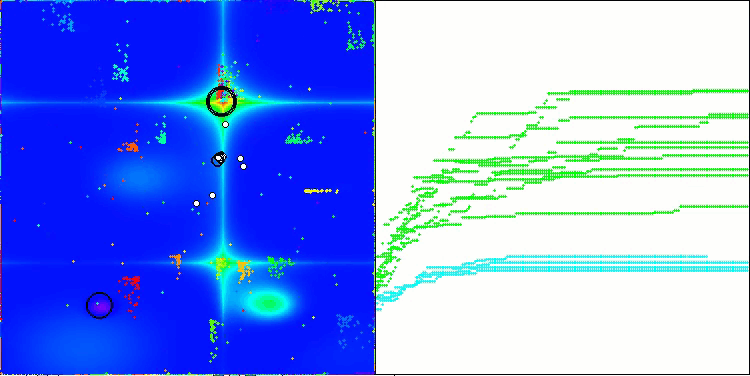
NOA en la función de prueba Forest

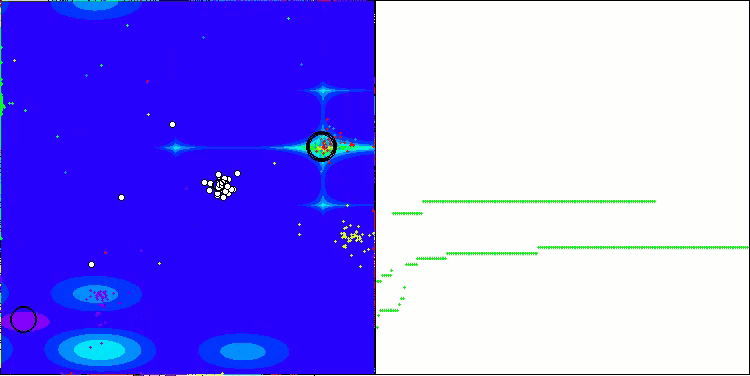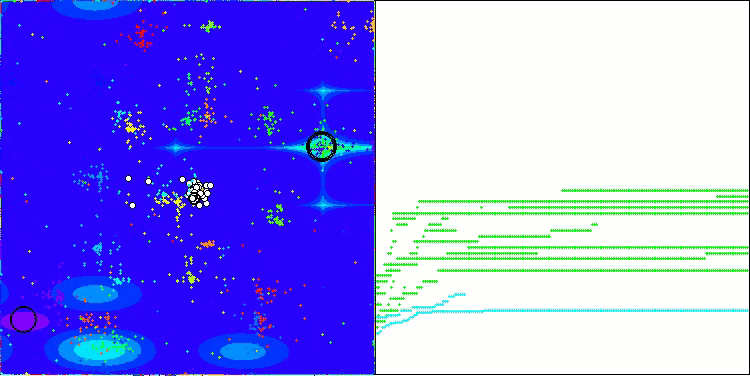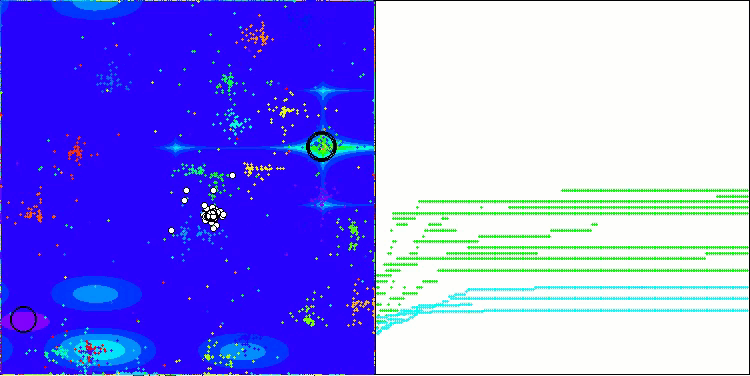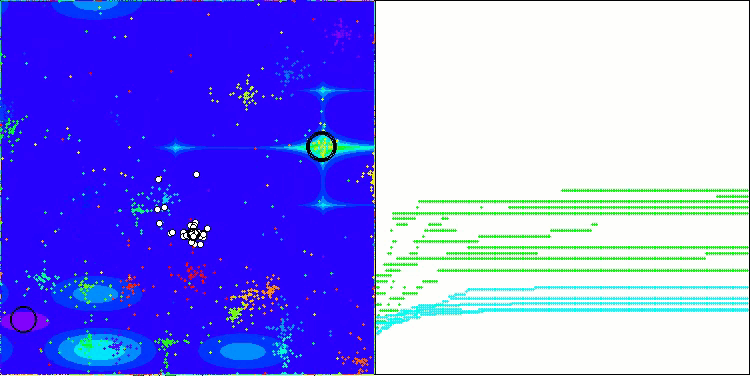
NOA en la función de prueba de Megacity

Tras las pruebas, el algoritmo NOA se coloca en una línea aparte (no tiene número ordinal), porque no se han obtenido los resultados de las pruebas en funciones de alta dimensionalidad. Las siguientes tablas se muestran para el análisis comparativo de los resultados con el resto de algoritmos presentes en la tabla de clasificación.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% de MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm (joo)	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	AMOm	animal migration optimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
4	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
5	CTA	comet tail algorithm (joo)	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
6	TETA	time evolution travel algorithm (joo)	0,91362	0,82349	0,31990	2,05701	0,97096	0,89532	0,29324	2,15952	0,73462	0,68569	0,16021	1,58052	5,797	64,41
7	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
8	BOAm	billiards optimization algorithm M	0,95757	0,82599	0,25235	2,03590	1,00000	0,90036	0,30502	2,20538	0,73538	0,52523	0,09563	1,35625	5,598	62,19
9	AAm	archery algorithm M	0,91744	0,70876	0,42160	2,04780	0,92527	0,75802	0,35328	2,03657	0,67385	0,55200	0,23738	1,46323	5,548	61,64
10	ESG	evolution of social groups (joo)	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
11	SIA	simulated isotropic annealing (joo)	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
12	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
13	DA	dialectical algorithm	0,86183	0,70033	0,33724	1,89940	0,98163	0,72772	0,28718	1,99653	0,70308	0,45292	0,16367	1,31967	5,216	57,95
14	BHAm	black hole algorithm M	0,75236	0,76675	0.34583	1,86493	0.93593	0.80152	0,27177	2,00923	0.65077	0.51646	0,15472	1,32195	5.196	57.73
15	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
16	RFO	royal flush optimization (joo)	0,83361	0,73742	0,34629	1,91733	0,89424	0,73824	0,24098	1,87346	0,63154	0,50292	0,16421	1,29867	5,089	56,55
17	AOSm	búsqueda de orbitales atómicos M	0,80232	0,70449	0,31021	1,81702	0,85660	0,69451	0,21996	1,77107	0,74615	0,52862	0,14358	1,41835	5,006	55,63
18	TSEA	turtle shell evolution algorithm (joo)	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
19	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
20	SRA	successful restaurateur algorithm (joo)	0,96883	0,63455	0,29217	1,89555	0,94637	0,55506	0,19124	1,69267	0,74923	0,44031	0,12526	1,31480	4,903	54,48
21	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
22	BIO	blood inheritance optimization (joo)	0,81568	0,65336	0,30877	1,77781	0,89937	0,65319	0,21760	1,77016	0,67846	0,47631	0,13902	1,29378	4,842	53,80
23	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
24	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
25	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
26	BCOm	bacterial chemotaxis optimization M	0,75953	0,62268	0,31483	1,69704	0,89378	0,61339	0,22542	1,73259	0,65385	0,42092	0,14435	1,21912	4,649	51,65
27	ABO	african buffalo optimization	0,83337	0,62247	0,29964	1,75548	0,92170	0,58618	0,19723	1,70511	0,61000	0,43154	0,13225	1,17378	4,634	51,49
28	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
29	TSm	tabu search M	0,87795	0,61431	0,29104	1,78330	0,92885	0,51844	0,19054	1,63783	0,61077	0,38215	0,12157	1,11449	4,536	50,40
30	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
31	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
32	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
33	AEO	artificial ecosystem-based optimization algorithm	0,91380	0,46713	0,26470	1,64563	0,90223	0,43705	0,21400	1,55327	0,66154	0,30800	0,28563	1,25517	4,454	49,49
34	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
35	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
36	SOA	simple optimization algorithm	0.91520	0.46976	0.27089	1,65585	0.89675	0.37401	0.16984	1,44060	0.69538	0.28031	0.10852	1,08422	4.181	46,45
37	ABH	artificial bee hive algorithm	0,84131	0,54227	0,26304	1,64663	0,87858	0,47779	0,17181	1,52818	0,50923	0,33877	0,10397	0,95197	4.127	45,85
38	ACMO	atmospheric cloud model optimization	0,90321	0,48546	0,30403	1,69270	0,80268	0,37857	0,19178	1,37303	0,62308	0,24400	0,10795	0,97503	4,041	44,90
39	ADAMm	adaptive moment estimation M	0.88635	0.44766	0,26613	1.60014	0.84497	0.38493	0.16889	1,39880	0,66154	0.27046	0.10594	1,03794	4.037	44.85
40	CGO	chaos game optimization	0,57256	0,37158	0,32018	1,26432	0,61176	0,61931	0,62161	1,85267	0,37538	0,21923	0,19028	0,78490	3,902	43,35
41	ATAm	artificial tribe algorithm M	0.71771	0.55304	0,25235	1,52310	0.82491	0.55904	0,20473	1,58867	0,44000	0,18615	0.09411	0.72026	3.832	42.58
42	ASHA	artificial showering algorithm	0,89686	0,40433	0,25617	1,55737	0,80360	0,35526	0,19160	1,35046	0,47692	0,18123	0,09774	0,75589	3,664	40,71
43	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3.657	40,63
44	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
45	CSA	circle search algorithm	0,66560	0,45317	0,29126	1,41003	0,68797	0,41397	0,20525	1,30719	0,37538	0,23631	0,10646	0,71815	3,435	38,17
	NOA	neuroboids optimization algorithm (joo)	0,70135	0,40129	0,00000	1,10264	0,62230	0,30830	0,00000	0,93060	0,45231	0,20892	0,00000	0,66123	2,694	29,94
	R.W.	random walk	0.48754	0.32159	0.25781	1,06694	0.37554	0,21944	0,15877	0,75375	0.27969	0,14917	0.09847	0.52734	2.348	26.09

 

Conclusiones

Al crear NOA, nos proponíamos combinar dos mundos: las redes neuronales y los algoritmos de optimización. El resultado fue tan previsible como inesperado.

Lo que más inspira de este algoritmo es su plausibilidad biológica. A menudo tratamos de crear modelos complejos, al tiempo que la naturaleza ya ha demostrado soluciones eficaces a través de la inteligencia colectiva de organismos simples durante millones de años. Los neuroboides suponen un intento de traducir esta sabiduría natural en forma algorítmica.

Las pruebas realizadas en diversas funciones han demostrado resultados prometedores. Alrededor de un 45% de eficiencia supone un inicio considerable para un enfoque conceptualmente nuevo. Podemos ver que el algoritmo funciona bien en tareas de complejidad media. Sin embargo, existen importantes limitaciones. Los problemas de escalabilidad se vuelven críticos cuando la dimensionalidad del problema es alta. A partir de 1.000 variables, la carga computacional se vuelve inviable: esto se relaciona con el entrenamiento de múltiples redes neuronales, un proceso que en sí mismo exige muchos recursos.

Lo que resulta especialmente atractivo del NOA es su capacidad para el autoaprendizaje de estrategias de búsqueda. A diferencia de las metaheurísticas clásicas con reglas fijas, los neuroboides adaptan su comportamiento usando el aprendizaje.

La variabilidad de los resultados entre las series que hemos observado es de doble naturaleza. Por un lado, falta previsibilidad. Por otro, supone un signo de diversidad en las estrategias de investigación, lo que puede ser una ventaja en los complejos paisajes de optimización.

A nuestro juicio, existen varias direcciones para el desarrollo del algoritmo NOA:

1. La optimización de la arquitectura de redes neuronales para reducir la carga computacional
2. La aplicación de mecanismos de transferencia de conocimientos entre neuroboides

En definitiva, el NOA no es un método de optimización más: se trata de un paso hacia la comprensión de cómo sistemas simples pueden dar lugar a comportamientos complejos. Representa una exploración de la frontera entre el aprendizaje automático y la optimización metaheurística, entre la inteligencia individual y la colectiva.

Creo que este enfoque tiene futuro no solo en la optimización de características, sino también en ámbitos más amplios que van desde la modelización del comportamiento adaptativo hasta la búsqueda de arquitecturas de inteligencia artificial esencialmente nuevas. En un mundo en el que la complejidad se está convirtiendo en la norma, a veces la sencillez con la organización adecuada puede generar soluciones inesperadamente interesantes.

En general, el algoritmo NOA no debe percibirse como una solución completa para los problemas de optimización, sino como una plataforma básica y un punto de partida para muchas direcciones en la investigación y la creación de soluciones prometedoras en el campo de la optimización en general, y del aprendizaje automático en particular.

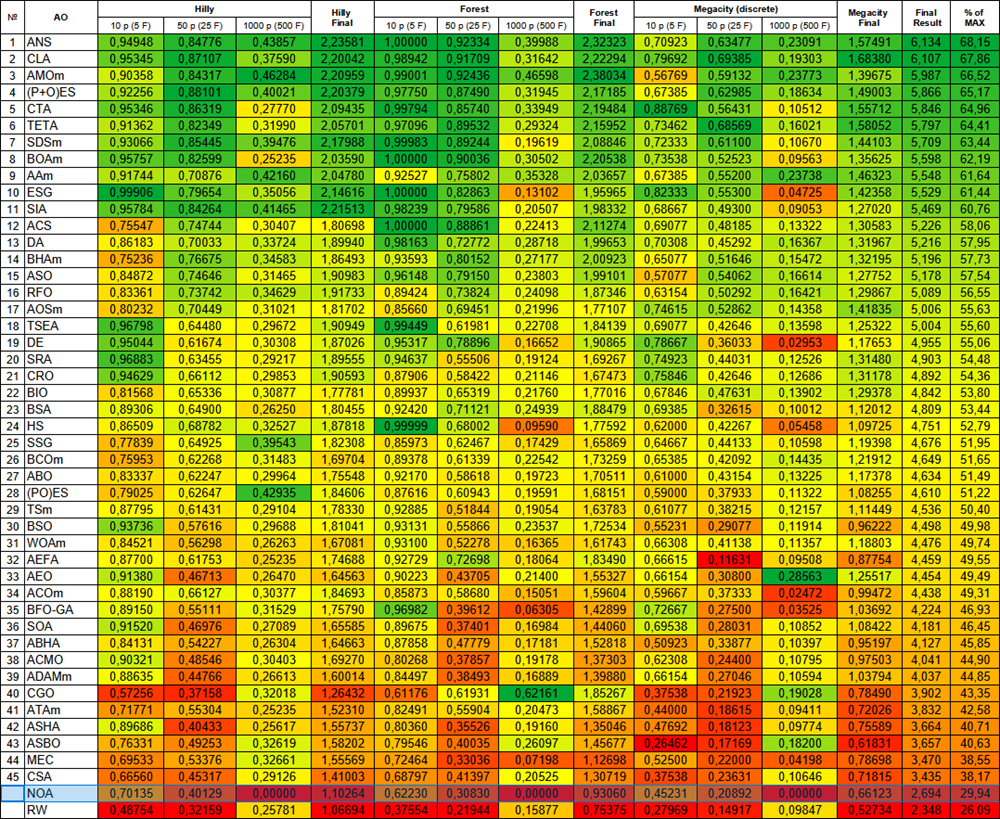
Figura 2. Clasificación por colores de los algoritmos según las pruebas respectivas

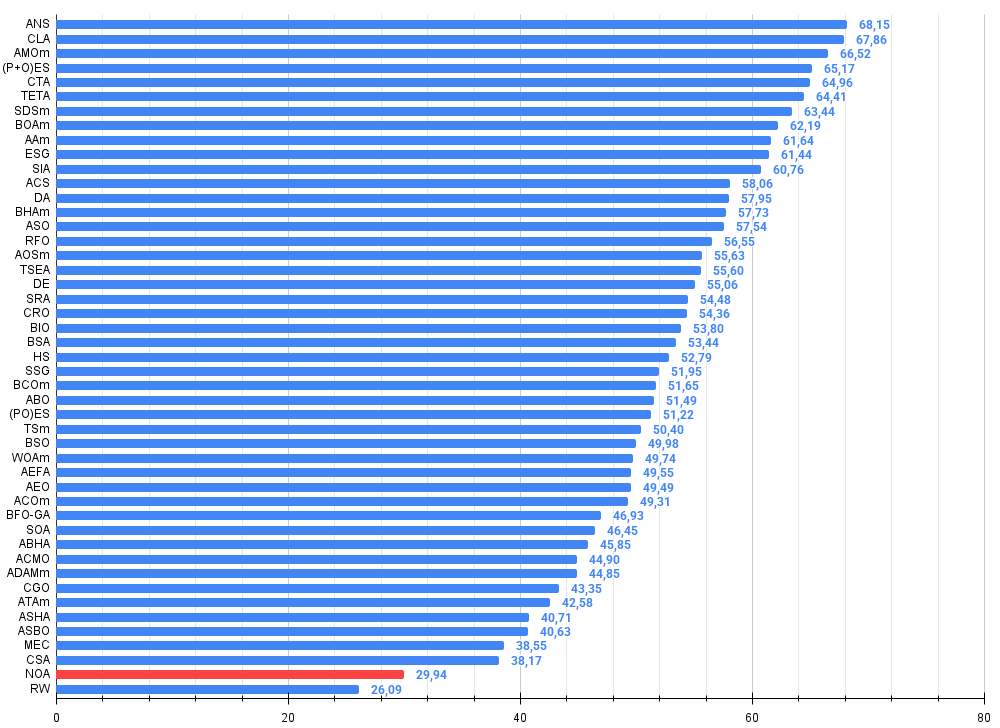
Figura 3. Histograma de los resultados de las pruebas de algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)

Ventajas e inconvenientes del algoritmo NOA:

Ventajas:

1. Implementación sencilla.
   
2. Resultados interesantes.

Desventajas:

1. Debido al largo tiempo de ejecución, no se obtienen resultados para espacios multidimensionales.
   

Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	#C_AO.mqh	Archivo de inclusión	Clase padre de algoritmos de población optimizaciones
2	#C_AO_enum.mqh	Archivo de inclusión	Enumeración de los algoritmos de optimización basados en la población
3	MLPa.mqh	Archivo de inclusión	Red neuronal MLP con ADAM
4	TestFunctions.mqh	Archivo de inclusión	Biblioteca de funciones de prueba
5	TestStandFunctions.mqh	Archivo de inclusión	Biblioteca de funciones del banco de pruebas
6	Utilities.mqh	Archivo de inclusión	Biblioteca de funciones auxiliares
7	CalculationTestResults.mqh	Archivo de inclusión	Script para calcular los resultados en una tabla comparativa
8	Testing AOs.mq5	Script	Banco de pruebas único para todos los algoritmos de optimización basados en la población
9	Simple use of population optimization algorithms.mq5	Script	Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización
10	Test_AO_NOA.mq5	Script	Banco de pruebas para NOA