MetaTrader 5 / 测试者
English Русский Español Português
preview
神经类群优化算法 (NOA)

神经类群优化算法 (NOA)

MetaTrader 5 — 测试者 |
18 0
Andrey Dik
Andrey Dik

内容

  1. 引言
  2. 算法的实现
  3. 测试结果


引言

在研究优化算法的过程中，我始终被创造尽可能简单且高效解决方案的想法所吸引。观察到自然界如何通过简单生物的相互作用来解决复杂问题，我开发了一种新的优化算法——神经类群优化算法（NOA）。

该算法基于极简神经代理（neuroboids）的概念。每个神经类群是一个简单的双层神经网络，使用Adam算法进行训练。这种方法的独特之处在于，尽管单个代理极其简单，但它们的集体行为必须能够有效地探索复杂优化问题的解空间。

NOA的灵感来自于自然系统中的自组织过程，其中简单的单元遵循基本规则，形成复杂的适应性结构。在本文中，我介绍了算法的理论依据、数学模型以及在标准优化测试函数上对其效率的实验研究结果。


算法的实现

想象一下，雨后你在花园里散步。蚯蚓无处不在——这是一种具有简单神经系统的简单生物。它们不具备我们意义上的“思考”能力，但却能以某种方式穿越复杂地形，躲避危险，寻找食物和伴侣。它们微小的大脑只包含几千个神经元，却已生存了数百万年。神经类群的想法正是这样诞生的。

如果我们把蚯蚓的简单性与集体智能的力量结合起来会怎样？在自然界中，简单生物共同努力时能取得令人难以置信的成果——蚂蚁建造复杂的巢穴，蜜蜂在采集花蜜时解决优化问题，鸟群在没有中央控制的情况下形成复杂的动态结构。

我的神经类群就像这些蚯蚓。每个都有自己的小型神经网络——不是具有数百万参数的庞大架构，而只是在输入和输出端有几个神经元。它们不了解整个搜索空间，只看到自己的局部环境。当一条蚯蚓找到一块富含养分的肥沃土壤时，其他的会逐渐向那个地点聚集。但它们并非盲目跟随——每个都保持自己的个性，自己的移动策略。神经类群不需要了解优化背后的所有数学原理。它们通过试错来独自学习。当其中一个找到好的解决方案时，其他的不只是复制其坐标，而是学习理解为什么这个解决方案好以及如何自己到达那里。

还记得海边的日落吗？太阳反射在波浪的数百万道闪光上，每一道闪光都是光与水相互作用的独特故事。我的神经类群也是如此——每个都反映了解决方案的一部分，共同构成了完整的图景。从远处看，它们的移动可能显得混乱。但在这种表面的混乱中，秩序诞生了——一个寻找最优解的自组织系统。

神经类群也没有中央指挥官。相反，每个都使用自己的小型神经网络来决定是遵循已知的最佳解决方案还是探索新领域，复制邻居的成功策略还是冒险创造自己的策略。 

在这个痴迷于复杂性和规模的世界里，神经类群提醒我们，最伟大的系统往往由最简单的元素构建而成。就像沙粒形成沙滩和山脉，水滴形成海洋，我的这些数字小虫，每一个都有自己的微小神经网络，一起工作来解决那些巨大、单体算法无法解决的问题。

noa-algorithm-diagram

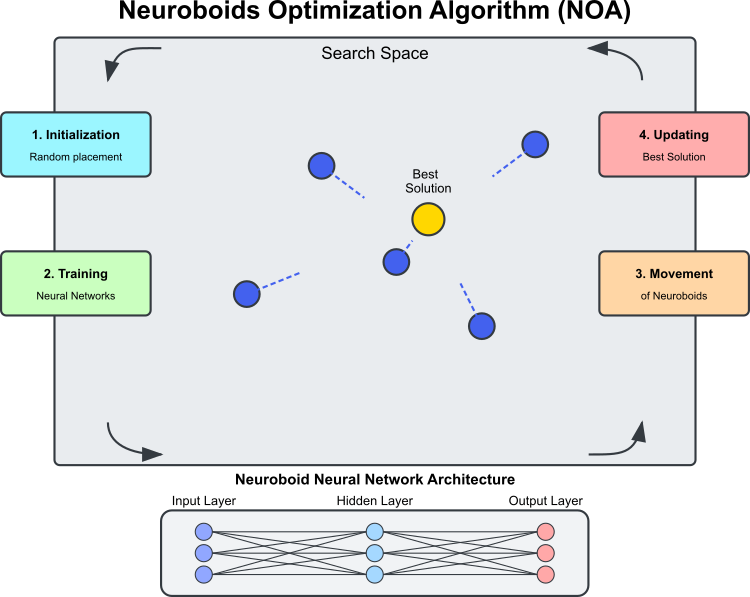
图例 1. NOA算法工作原理

图1展示了NOA算法的主要组成部分和工作原理搜索空间：神经类群（蓝色圆圈）在其中搜索最优解的域。神经类群：优化代理，每个都有自己的神经网络。最佳解决方案：当前找到的最佳解决方案（金色圆圈），神经类群趋向于它。神经网络架构：每个神经类群使用自己的神经网络来确定移动方向。算法的循环过程由以下阶段组成：初始化（随机放置神经类群）；神经网络训练（基于找到的最佳解决方案进行学习）；神经类群在训练后的神经网络控制下移动；如果找到更好的解决方案，则更新最佳解决方案。虚线显示了神经类群的移动方向，这些方向由其神经网络的输出以及趋向最佳解决方案的随机元素确定。

“神经类群”一词结合了神经网络和boid（集体行为模型中的人工“鸟”）的概念。每个神经类群代理是解空间中的一个位置
和一个决定移动策略的个人神经网络的组合。

与传统的元启发式算法（如遗传算法或群体方法）不同，后者的代理行为由固定规则决定，而在NOA中，每个神经类群都有自己的神经网络，该网络在优化过程中进行训练，神经网络逐渐学会确定最有希望的搜索方向，训练是基于找到的最佳解决方案（目标向量）进行的。结果是，优化算法包含两种搜索策略：第一种是NOA本身，第二种是嵌入在神经网络中的ADAM。反向传播机制使得ADAM能够作为独立工具在NOA算法的背景下用于调整每个神经类的神经网络权重。因此，所有神经类群的总权重数量可以远大于问题的维度——无需优化整个种群的神经网络权重；这自然且自动地发生。

神经类群的行为与以下方面有某些相似之处：自然界中的社会学习（观察成功的个体） ，神经可塑性（神经系统适应不断变化条件的能力），集体智能（通过许多简单代理的相互作用涌现出优化）。

NOA算法的主要技术特征可以确定如下：

  • 优化过程中的前向和后向误差传播，
  • 分布式训练多个神经网络，每个形成自己的策略，
  • 基于当前搜索状态的自适应行为调整，
  • 使用神经网络的激活函数来创建非线性搜索动力学。

这种组合使NOA成为一种有趣的混合方法，结合了机器学习和优化范式。NOA不是使用神经网络来近似目标函数（如代理模型），而是使用它们来间接引导搜索本身，创建一种用于解决优化问题的“元学习”。

现在我们可以编写NOA算法的伪代码：

初始化：

  1. 创建一个由N个神经网络（神经类群）组成的群体。
  2. 每个神经网络的结构具有等于优化问题维度的输入和输出数量。
  3. 设置参数：
    • popSize（种群规模）
    • actFunc（神经元激活函数）
    • dispScale（位移尺度）
    • eliteProb（复制精英坐标的概率）

算法：

  1. 如果这是第一次迭代（revision = false）：
    • 对于群体中的每个神经类群：
      • 在搜索空间中随机初始化坐标
      • 将坐标转换为可接受的离散值
    • 设置 revision = true 并终止当前迭代
  2. 对于后续迭代：
    • 对于大多数神经类群（除最后5个之外的所有类群）：
      • 对于每个坐标：
        • 以 eliteProb 的概率，将坐标值替换为从找到的最佳解决方案（cB）中获取的值
    • 对于群体中的每个神经类群：
      • 将找到的最佳解决方案（cB）和神经类群的当前位置缩放到[-1, 1]范围内
      • 通过当前神经类群的神经网络执行前向传播
      • 计算目标值（按cB缩放）与神经网络输出之间的误差
      • 执行反向传播以训练神经网络
      • 通过沿神经网络输出确定的方向移动来更新神经类群的坐标
      • 将坐标转换为可接受的离散值
  3. 评估与更新：
    • 对于群体中的每个神经类群：
      • 计算当前坐标的目标函数值
      • 如果该值优于找到的最佳值（fB）：
        • 更新找到的最佳值（fB）
        • 将当前坐标保存为最佳坐标（cB）

让我们开始编写算法代码。定义 C_AO_NOA 类，它派生自 C_AO 类。这意味着它继承了 C_AO 的属性和方法，并添加了自己的属性和方法。类的主要元素：

~C_AO_NOA () 析构函数：删除为“nn”数组的每个元素动态分配的激活函数对象——神经类群的个人神经网络。这有助于防止内存泄漏。

C_AO_NOA () 构造函数：

  • 初始化优化算法参数。
  • 为参数设置初始值：popSize（群体大小）、actFunc（神经元激活函数）、dispScale（移动尺度）、复制精英坐标的概率。
  • 为“params”数组保留空间以存储参数。

SetParams：根据“params”数组中存储的值设置参数。

Init () 方法：使用 rangeMinP、rangeMaxP 和 rangeStepP 范围值以及 epochsP 来初始化类。 

Moving () 和 Revision () 方法：这些方法用于在群体中移动个体并执行决策的评估和更新。

    nn 数组：神经类群每个神经网络的神经网络类实例的数组。

    封闭方法：ScaleInp () 和 ScaleOut () - 分别用于缩放输入和输出数据的方法。

    //——————————————————————————————————————————————————————————————————————————————
class C_AO_NOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_NOA ()
  {
    for (int i = 0; i < ArraySize (nn); i++) if (CheckPointer (nn [i].actFunc)) delete nn [i].actFunc;
  }
  C_AO_NOA ()
  {
    ao_name = "NOA";
    ao_desc = "Neuroboids Optimization Algorithm (joo)";
    ao_link = "https://www.mql5.com/en/articles/16992";

    popSize   = 50;   // population size
    actFunc   = 0;    // neuron activation function
    dispScale = 0.01; // scale of movements
    eliteProb = 0.1;  // probability of copying elite coordinates

    ArrayResize (params, 4);
    params [0].name = "popSize";   params [0].val  = popSize;
    params [1].name = "actFunc";   params [1].val  = actFunc;
    params [2].name = "dispScale"; params [2].val  = dispScale;
    params [3].name = "eliteProb"; params [3].val  = eliteProb;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    actFunc   = (int)params [1].val;
    dispScale = params      [2].val;
    eliteProb = params      [3].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum values
             const double &rangeMaxP  [],  // maximum values
             const double &rangeStepP [],  // step change
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    actFunc;   // neuron activation function
  double dispScale; // scale of movements
  double eliteProb; // probability of copying elite coordinates

  private: //-------------------------------------------------------------------
  C_MLPa nn [];

  void ScaleInp (double &inp [], double &out []);
  void ScaleOut (double &inp [], double &out []);
};
//——————————————————————————————————————————————————————————————————————————————

    Init 方法旨在初始化 C_AO_NOA 类的实例。该方法接收若干参数，用于指定数值范围和周期数，并执行必要的操作来调整算法。

    方法签名：表示初始化成功。参数：

    • MinP [] - 参数的最小值。
    • MaxP [] - 参数的最大值。
    • StepP [] - 参数变化的步长。
    • epochsP - 周期数（迭代次数）。

    标准初始化：方法的第一行调用 StandardInit 函数，并传入指定的范围。

    设置神经网络配置：

    • 创建 nnConf 数组，其中包含神经网络输入层和输出层的大小。
    • 调用 ArrayResize 将 nnConf 数组的大小调整为 2（输入层和输出层）。
    • 数组的两个元素均使用 “coords” 值进行初始化，该值对应于输入数据的维度。

    E_Act 枚举声明：创建一个枚举，定义了不同的神经元激活函数（如 eActTanh、eActAlgSigm、eActRatSigm 等）。

    调整神经元数组大小：将 “nn” 数组（神经元数组）的大小调整为 popSize，该值先前已在构造函数中设置。

    神经元初始化：

    • 变量 cnt 初始化为零，用于传递唯一的随机种子以初始化每个神经元，确保每个神经网络中的权重都是唯一初始化的。
    • 每个神经元在 “for” 循环中进行初始化。调用 nn[i].Init() 方法，传入 nnConf 配置、actFunc 激活函数，以及基于当前 cnt 值和系统启动后经过的毫秒数的种子。
    • cnt 值在每次循环迭代时递增，从而能够为每个神经元的初始化生成唯一的种子。

    返回结果：如果所有操作均成功，该方法返回 “true”，表示初始化成功。

    С_AO_NOA 类的 Init 方法是设置优化算法的关键，它提供了神经网络及相关参数的初始化。 

    //——————————————————————————————————————————————————————————————————————————————
bool C_AO_NOA::Init (const double &rangeMinP  [], // minimum values
                     const double &rangeMaxP  [], // maximum values
                     const double &rangeStepP [], // step change
                     const int     epochsP = 0)   // number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  int nnConf [];
  ArrayResize (nnConf, 2);
  nnConf [0] = coords;
  nnConf [1] = coords;

  enum E_Act
  {
    eActTanh,      //0
    eActAlgSigm,   //1
    eActRatSigm,   //2

    eActSoftPlus,  //3
    eActBentIdent, //4
    eActSiLU,      //5

    eActACON,      //6
    eActSERF,      //7
    eActSnake      //8
  };

  ArrayResize (nn, popSize);
  int cnt = 0;
  for (int i = 0; i < popSize; i++)
  {
    nn [i].Init (nnConf, actFunc, (int)GetTickCount64 () + cnt);
    cnt++;
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

    Moving() 方法实现了在类神经优化算法框架下种群中个体的移动。让我们逐步拆解这个过程：

    初始值的初始化：如果 revision 为 false，该方法将执行首次初始化。对于种群中 popSize 的每个元素以及 coords 的每个维度，该方法会在代表搜索代理的 a[i].c[c] 数组中设置初始值：

    • u.RNDfromCI() 在 rangeMin[c] 和 rangeMax[c] 范围内生成一个随机值。
    • u.SeInDiSp() 是一个利用步长变化来调整 a[i].c[c] 值，使其处于有效范围内的函数。
    • 初始化完成后，revision 被设置为 true，控制权从该方法返回。 

    更新坐标：个体的坐标基于精英概率进行更新。对于种群中前 popSize - 5 个元素，执行随机检查，如果随机数小于 eliteProb，则将 a[i].c[c] 坐标设置为等于 “cB[c]” 精英的坐标。

    处理神经网络数据：创建输入数据、输出数据、目标值和误差的数组，并调整其大小至 coords 维度。对于种群中的每个元素：

    • ScaleInp() 对 cB 目标坐标进行缩放，并将其存储在 targVal 中。
    • ScaleInp() 对种群中的当前坐标进行缩放，并将其存储在 inpData 中。
    • nn[i].ForwProp() 对神经网络执行前向传播以产生输出。
    • 计算每个坐标的误差（目标值与获得值之间的差值）。
    • nn[i].BackProp(err) 执行误差反向传播以调整权重。
    • 结合神经网络的输出、缩放和随机采样元素，更新 a[i].c[c] 坐标。
    • 最后，通过 u.SeInDiSp 函数对 a[i].c[c] 的值进行归一化处理。

    因此，Moving() 方法负责模型中个体的移动，在开始时对其进行初始化，并根据神经网络的输出和概率选择更新它们的位置。 

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    // Initialize the initial values of anchors in all parallel universes
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd  = 0.0;
  double val  = 0.0;
  int    pair = 0.0;

  for (int i = 0; i < popSize - 5; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < eliteProb)
      {
        a [i].c [c] = cB [c];
      }
    }
  }

  double inpData []; ArrayResize (inpData, coords);
  double outData []; ArrayResize (outData, coords);
  double targVal []; ArrayResize (targVal, coords);
  double err     []; ArrayResize (err,     coords);

  for (int i = 0; i < popSize; i++)
  {
    ScaleInp (cB,      targVal);
    ScaleInp (a [i].c, inpData);

    nn [i].ForwProp (inpData, outData);

    for (int c = 0; c < coords; c++) err [c] = targVal [c] - outData [c];

    nn [i].BackProp (err);

    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] += outData [c] * (rangeMax [c] - rangeMin [c]) * dispScale * u.RNDprobab ();
      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    接下来，让我们看看 Revision 方法，该方法评估并更新种群中当前的“最佳”解。它将每个个体的目标函数值与当前的“最佳”值进行比较，如果发现更好的解，则更新最佳值。因此，该方法确保了在种群中维持当前的最佳解。 

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::Revision ()
{
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    ScaleInp 方法负责将输入数据从 rangeMin 和 rangeMax 指定的范围缩放到 -1 到 1 的区间内。inp[c] 的每个值都使用 u.Scale 函数进行缩放，该函数执行线性缩放以将其转换到 -1 到 1 的范围内。ScaleInp 方法为后续计算准备数据，确保其归一化到所需的范围。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::ScaleInp (double &inp [], double &out [])
{
  for (int c = 0; c < coords; c++) out [c] = u.Scale (inp [c], rangeMin [c], rangeMax [c], -1, 1);
}
//——————————————————————————————————————————————————————————————————————————————

    ScaleOut 方法的工作原理与 ScaleInp 类似，它执行从 -1 到 1 的范围到 rangeMin 和 rangeMax 区间的反向缩放。 

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::ScaleOut (double &inp [], double &out [])
{
  for (int c = 0; c < coords; c++) out [c] = u.Scale (inp [c], -1, 1, rangeMin [c], rangeMax [c]);
}
//——————————————————————————————————————————————————————————————————————————————


    测试结果

    该算法在小维度和中等维度的函数上显示出有趣的结果。当问题规模增加到 1000 个变量时，计算时间变得难以接受地长，因此未展示这些测试结果。 根据测试，性能达到了最优值的约 45%（在 9 次测试中的 6 次）。

    NOA|Neuroboids Optimization Algorithm (joo)|50.0|0.0|0.01|0.1|
    =============================
    5 Hilly's; Func runs: 10000; result: 0.7013521128826248
    25 Hilly's; Func runs: 10000; result: 0.40128968110640306
    =============================
    5 Forest's; Func runs: 10000; result: 0.6222984295200933
    25 Forest's; Func runs: 10000; result: 0.30830340651626337
    =============================
    5 Megacity's; Func runs: 10000; result: 0.4523076923076924
    25 Megacity's; Func runs: 10000; result: 0.20892307692307693
    =============================
    总得分： 2.69447 (44.91%)

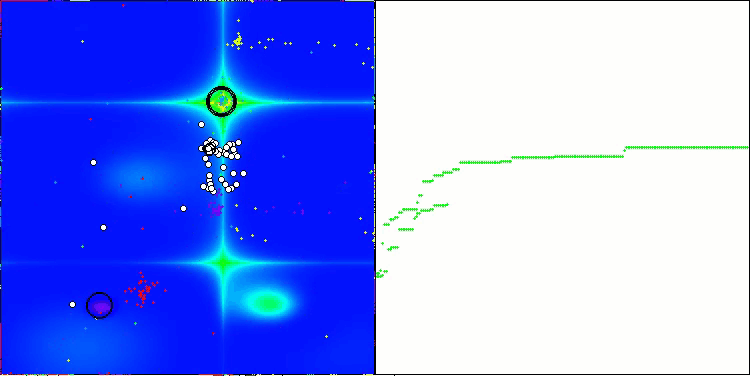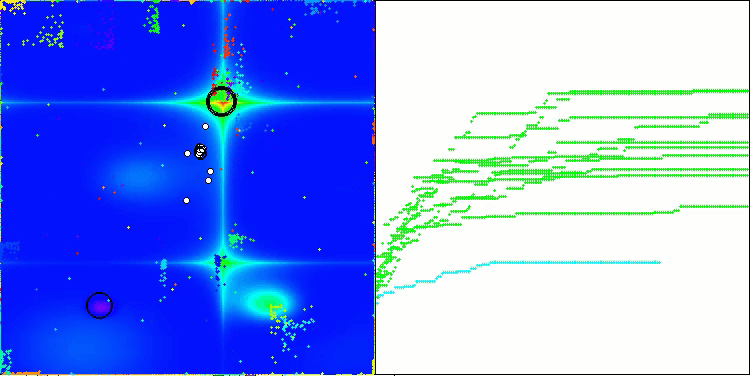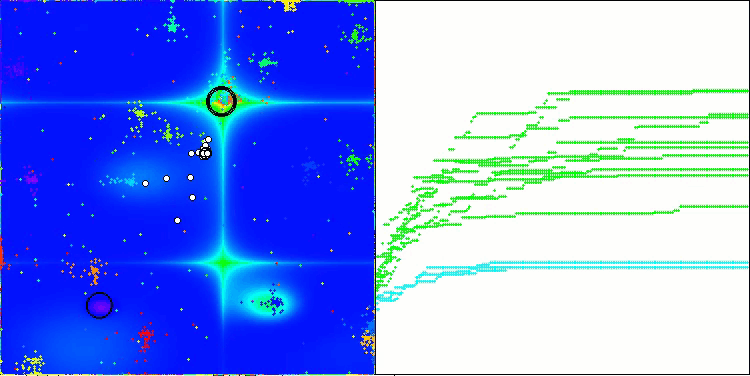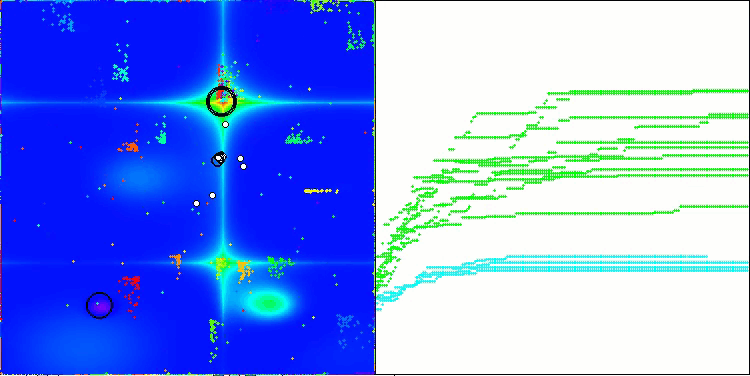
    我想就 NOA 算法的可视化多说几句。正如你所见，该算法形成了有趣的扇形结构。本质上，这些结构是神经类群中神经网络结果的可视化呈现。 

    Hilly

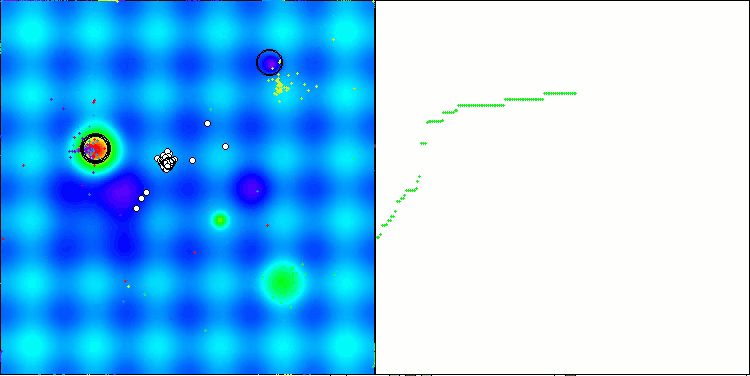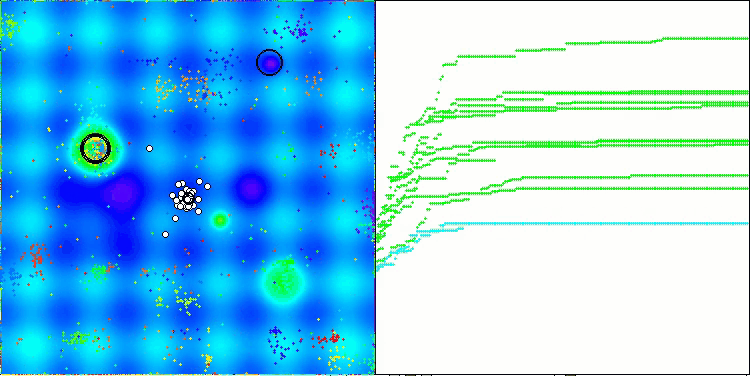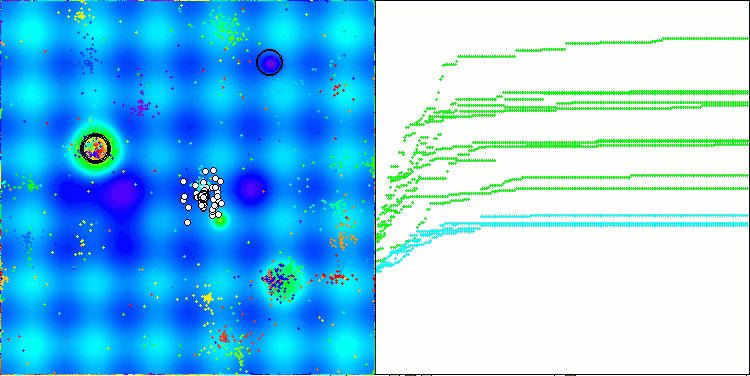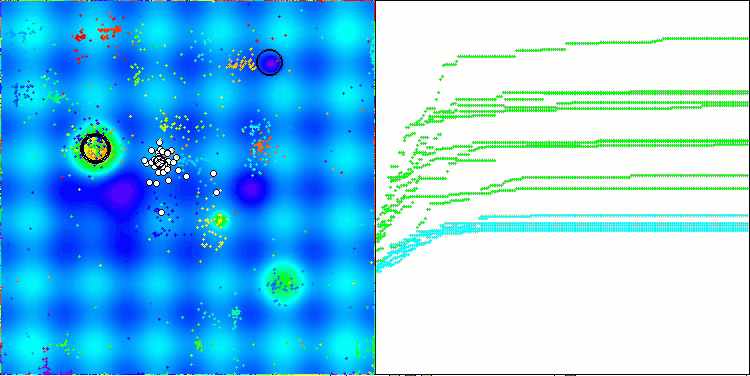
    NOA在Hilly测试函数上

    Forest

    NOA在Forest测试函数上

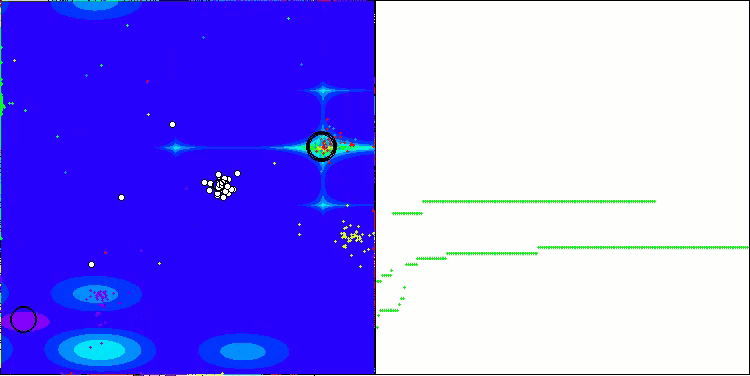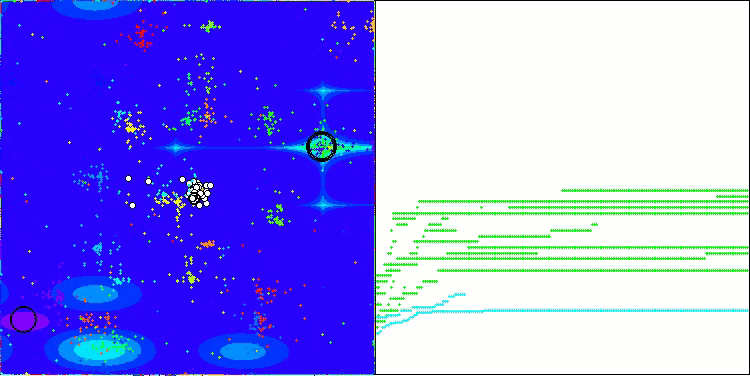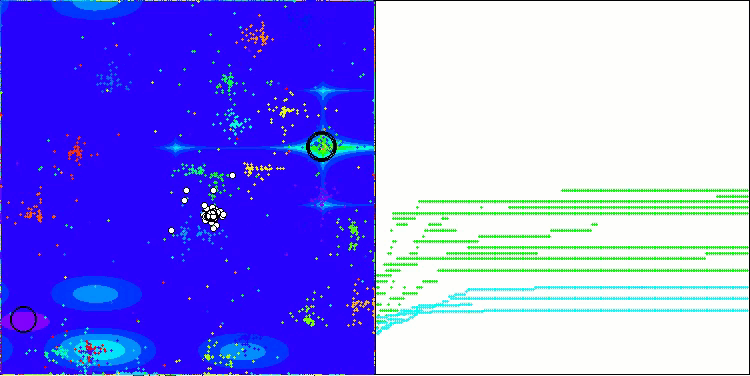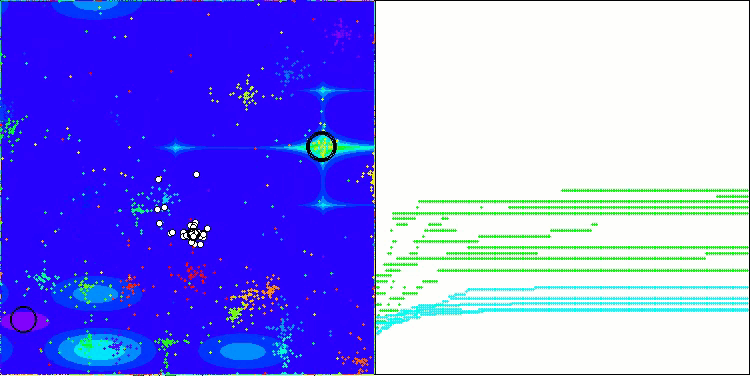
    NOA在Megacity测试函数上

    经过测试后，NOA 算法被单独列在一行（没有序号），因为未获得高维函数上的测试结果。下表用于与评分表中的其他算法进行结果对比分析。

    # 算法 说明 Hilly Hilly 最终结果 Forest Forest 最终结果 Megacity (离散) Megacity 最终结果 最终结果 最大 %
    10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
    1 ANS 交叉邻近搜索 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
    2 CLA 代码锁定算法（JOO） 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
    3 AMOm 动物迁徙优化M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
    4 (P+O)ES (P+O) 进化策略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
    5 CTA 彗尾算法（JOO） 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
    6 TETA 时间演化旅行算法（JOO） 0.91362 0.82349 0.31990 2.05701 0.97096 0.89532 0.29324 2.15952 0.73462 0.68569 0.16021 1.58052 5.797 64.41
    7 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
    8 BOAm 台球优化算法 M 0.95757 0.82599 0.25235 2.03590 1.00000 0.90036 0.30502 2.20538 0.73538 0.52523 0.09563 1.35625 5.598 62.19
    9 AAm 射箭算法 M 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
    10 ESG 社会群体的进化（JOO） 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
    11 SIA 模拟各向同性退火（JOO） 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
    12 ACS 人工协同搜索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
    13 DA 辩证算法 0.86183 0.70033 0.33724 1.89940 0.98163 0.72772 0.28718 1.99653 0.70308 0.45292 0.16367 1.31967 5.216 57.95
    14 BHAm 黑洞算法 M 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
    15 ASO 无政府社会优化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
    16 RFO 皇家同花顺优化算法 (JOO) 0.83361 0.73742 0.34629 1.91733 0.89424 0.73824 0.24098 1.87346 0.63154 0.50292 0.16421 1.29867 5.089 56.55
    17 AOSm 原子环路搜索 M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
    18 TSEA 龟壳进化算法（JOO） 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
    19 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
    20 SRA 成功餐饮经营者算法（joo） 0.96883 0.63455 0.29217 1.89555 0.94637 0.55506 0.19124 1.69267 0.74923 0.44031 0.12526 1.31480 4.903 54.48
    21 CRO 化学反应优化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
    22 BIO 血缘遗传优化算法 (JOO) 0.81568 0.65336 0.30877 1.77781 0.89937 0.65319 0.21760 1.77016 0.67846 0.47631 0.13902 1.29378 4.842 53.80
    23 BSA 鸟群算法 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
    24 HS 和声搜索算法 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
    25 SSG 树苗播种和生长算法 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
    26 BCOm 细菌趋化优化算法M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
    27 ABO 非洲水牛优化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
    28 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
    29 TSm 禁忌搜索优化算法 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
    30 BSO 头脑风暴优化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
    31 WOAm 鲸鱼优化算法M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
    32 AEFA 人工电场算法 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
    33 AEO 基于人工生态系统的优化算法 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
    34 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
    35 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
    36 SOA 简单优化算法 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
    37 ABHA 人工蜂巢算法 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
    38 ACMO 大气云层模型优化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
    39 ADAMm 自适应动量评估 M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
    40 CGO 混沌博弈优化算法 0.57256 0.37158 0.32018 1.26432 0.61176 0.61931 0.62161 1.85267 0.37538 0.21923 0.19028 0.78490 3.902 43.35
    41 ATAm 人工部落算法 M 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
    42 ASHA 人工淋浴算法 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
    43 ASBO 适应性社会行为优化 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
    44 MEC 思维进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
    45 CSA 圆搜索算法 0.66560 0.45317 0.29126 1.41003 0.68797 0.41397 0.20525 1.30719 0.37538 0.23631 0.10646 0.71815 3.435 38.17
    NOA 神经类群优化算法 (joo) 0.70135 0.40129 0.00000 1.10264 0.62230 0.30830 0.00000 0.93060 0.45231 0.20892 0.00000 0.66123 2.694 29.94
    RW 随机游走 0.48754 0.32159 0.25781 1.06694 0.37554 0.21944 0.15877 0.75375 0.27969 0.14917 0.09847 0.52734 2.348 26.09

     

    总结

    在创建 NOA 时，我的目标是将两个领域结合起来：神经网络和优化算法。结果既在预料之中，又出人意料。

    关于这个算法，最让我受到启发的是其生物合理性。我们往往试图创建复杂的模型，而大自然却通过简单生物的集体智能，数百万年来一直在展示高效的解决方案。神经类群正是试图将这种自然智慧以算法形式体现出来的一种尝试。

    在各种函数上的测试显示了令人鼓舞的结果。约 45% 的效率对于一个概念全新的方法来说，是一个不错的开端。我可以看到该算法在中等复杂度的任务中表现良好。然而，也存在显著的局限性。当问题规模较大时，可扩展性问题变得至关重要。在 1000 个变量的情况下，由于需要训练多个神经网络——这一过程本身非常消耗资源——计算负荷变得不切实际。

    NOA 特别吸引我的一点是它能够自主学习搜索策略。与具有固定规则的传统元启发式算法不同，神经类群通过学习来调整其行为。

    我观察到的各次运行结果之间的变化具有两面性。一方面，这是缺乏可预测性的表现。另一方面，这是探索策略多样性的标志，这在复杂的优化景观中可能是一个优势。

    我认为 NOA 算法有几个发展方向：

    1. 优化神经网络架构以减少计算负荷
    2. 实现神经类群之间的知识转移机制

    归根结底，NOA 不仅仅又是一种优化方法。这是向理解简单系统如何产生复杂行为迈出的一步。这是对机器学习与元启发式优化之间、个体与集体智能之间边界的一次探索。

    我相信这种方法不仅在函数优化领域拥有未来，而且在更广泛的领域——从建模自适应行为到寻找根本性的人工智能新架构——也是如此。在复杂性日益成为常态的世界里，有时经过恰当组织后的简洁模式也能产生出人意料的有趣解决方案。

    总的来说，不应将 NOA 算法视为优化问题的完整解决方案，而应将其视为一个基础平台和出发点，适用于许多研究领域，以及在一般优化和特别是机器学习领域创建有前景的解决方案。

    TAB

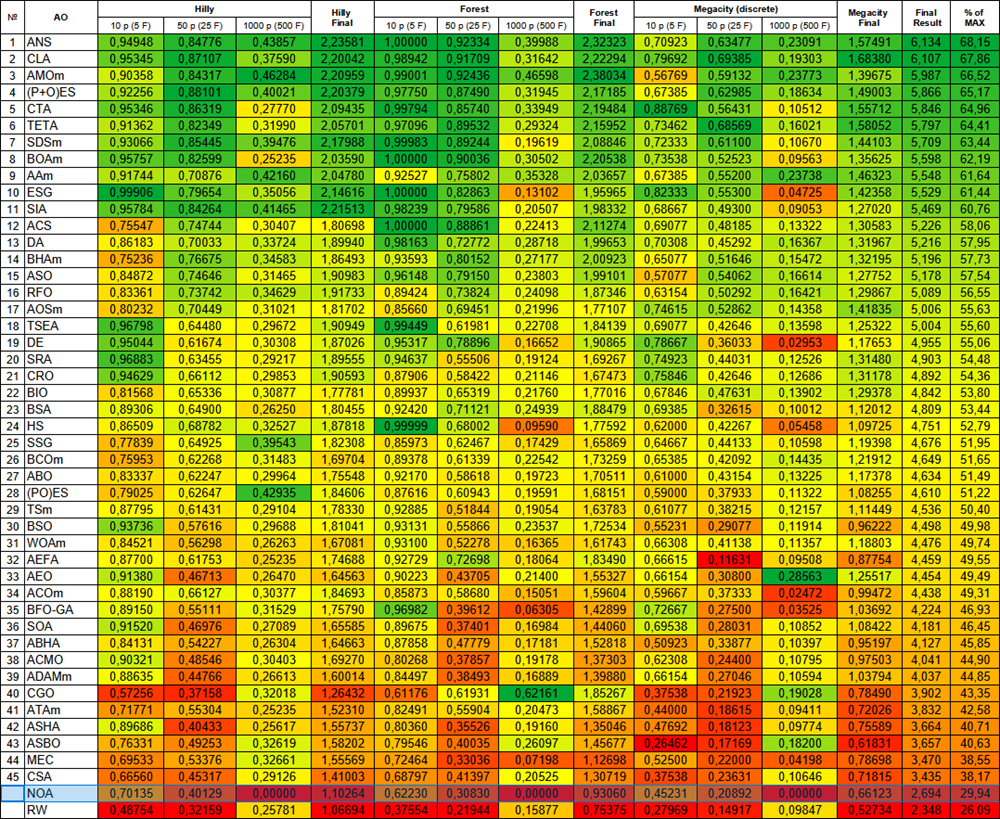
    图例 2. 根据相应测试结果的算法颜色分级

    Chart

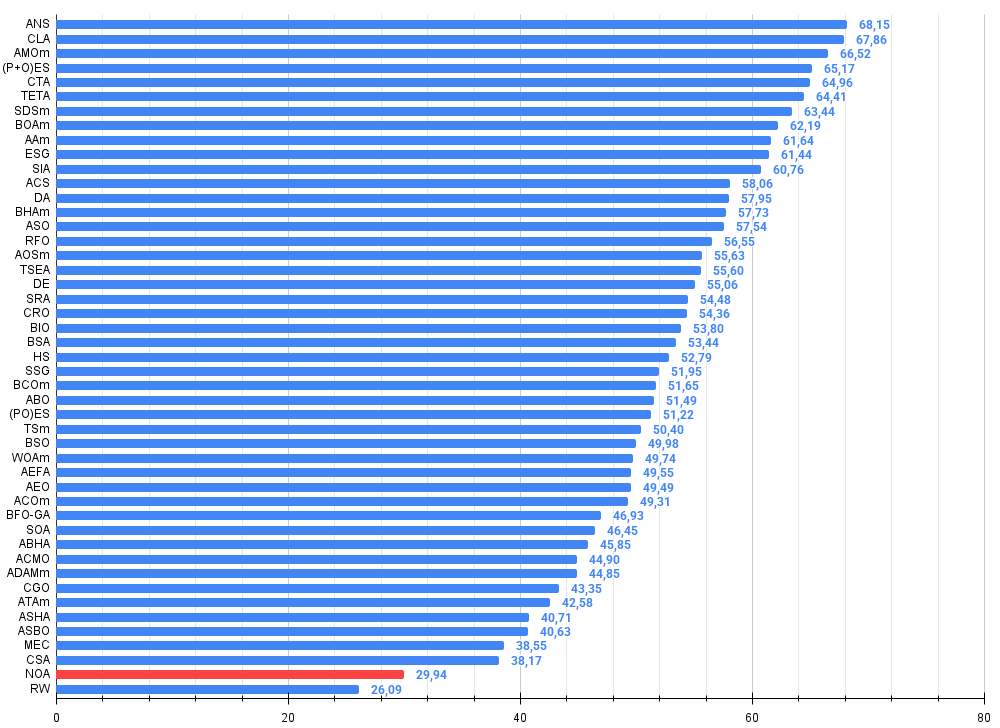
    图例 3. 算法测试结果直方图（比例从 0 到 100，越高越好，其中 100 是最大可能的理论结果，存档中有一个用于计算评级表的脚本）

    NOA的优缺点：

    优点：

    1. 实现简单。
    2. 有趣的结果。

    缺点：

    1. 由于执行时间过长，未能获得多维空间的结果。

    本文附带了一个文档，其中包含了算法代码的当前版本。文章作者不对典型算法描述的绝对准确性负责。对其中进行了多处修改，从而提升搜索能力。文章中表述的结论和论断是基于实验的结果。


    文中所用程序

    # 名称 类型 说明
    1 #C_AO.mqh
    		 库
    		 Parent class of population optimization
    算法
    2 #C_AO_enum.mqh
    		 库
    		 群体优化算法枚举
    3
    		MLPa.mqh 库 带有 ADAM 的 MLP 神经网络
    4
    		 TestFunctions.mqh
    		 库
    		 测试函数函数库
    5
    		 TestStandFunctions.mqh
    		 库
    		 测试台函数库
    6
    		 Utilities.mqh
    		 库
    		 辅助函数库
    7
    		 CalculationTestResults.mqh
    		 库
    		 用于计算对比表中结果的脚本
    8
    		 Testing AOs.mq5
    		 脚本 所有种群优化算法的统一测试平台
    9
    		 Simple use of population optimization algorithms.mq5
    		 脚本
    		 一个不包含可视化功能的种群优化算法使用示例
    10
    		 Test_AO_NOA.mq5
    		 脚本 NOA测试

    本文由MetaQuotes Ltd译自俄文
    原文地址： https://www.mql5.com/ru/articles/16992

    附加的文件 |
    下载ZIP
    NOA.zip (181.52 KB)

    注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

    本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

    该作者的其他文章

    前往讨论
    外汇套利交易：一款轻松上手的简单合成做市商机器人 外汇套利交易：一款轻松上手的简单合成做市商机器人
    今天，来了解一下我的首个套利机器人——一款针对合成资产的流动性提供者（如果这么称呼它也算恰当的话）。目前，该机器人作为一个模块，在一套大型机器学习系统中成功运行，但我从云端调出了一个旧版的外汇套利EA，让我们一起来看一下，并思考如今能用它做些什么。
    从新手到专家：使用 MQL5 制作动画新闻标题 (三) — 指标洞察 从新手到专家：使用 MQL5 制作动画新闻标题 (三) — 指标洞察
    在本文中，我们将通过引入专门的指标洞察通道来推进新闻标题EA —— 一个紧凑的图表显示，显示由RSI、MACD、随机震荡指标和 CCI 等流行指标生成的关键技术信号。这种方法消除了 MetaTrader 5 终端上多个指标子窗口的需要，使您的工作空间保持干净高效。通过利用 MQL5 API 在后台访问指标数据，我们可以使用自定义逻辑实时处理和可视化市场洞察。加入我们，探索如何在 MQL5 中操纵指标数据，以创建一个智能且节省空间的滚动洞察系统，所有这些都在您的交易图表上的一个水平通道内。
    从新手到专家：使用 MQL5 制作动画新闻标题（四） — 本地托管 AI 模型市场洞察 从新手到专家：使用 MQL5 制作动画新闻标题（四） — 本地托管 AI 模型市场洞察
    在今天的讨论中，我们将探讨如何自行托管开源 AI 模型，并使用它们来生成市场洞察。这是我们持续扩展 News Headline EA 的一部分努力，引入了 AI 洞察通道，将其转变为多集成辅助工具。升级后的 EA 旨在通过日历事件、财经突发新闻、技术指标以及现在的 AI 生成的市场观点，让交易者随时了解最新动态，从而为交易决策提供及时、多样化和智能的支持。加入我们的讨论，我们将探讨实用的集成策略，以及 MQL5 如何与外部资源协作，构建强大而智能的交易工作终端。
    数据科学和机器学习（第 34 部分）：时间序列分解，剖析股票市场的核心 数据科学和机器学习（第 34 部分）：时间序列分解，剖析股票市场的核心
    在一个充斥着杂乱且不可预测数据的世界里，识别有意义的形态可能颇具挑战性。在本文中，我们将探讨季节性分解，这是一种强力分析技术，有助于把数据拆分为关键成分：趋势、季节性形态、和噪声。以该途径拆解数据，我们能够揭示隐藏的洞见，并配以更清晰、更易解读的信息工作。