
Оптимизация нейробоидами — Neuroboids Optimization Algorithm (NOA)
Содержание
Введение
В процессе исследования алгоритмов оптимизации меня всегда привлекала идея создания максимально простых, но эффективных решений. Наблюдая за тем, как природа решает сложные задачи через взаимодействие простейших организмов, я разработал новый алгоритм оптимизации — Neuroboids Optimization Algorithm (NOA).
В основе алгоритма лежит концепция минималистичных нейронных агентов — нейробоидов. Каждый нейробоид представляет собой простейшую нейронную сеть с двумя слоями нейронов, которая обучается с помощью алгоритма Adam. Уникальность подхода заключается в том, что, несмотря на предельную простоту отдельных агентов, их коллективное поведение должно эффективно исследовать пространство решений сложных оптимизационных задач.
Вдохновением для создания NOA послужили процессы самоорганизации в природных системах, где простые единицы, следуя базовым правилам, формируют сложные адаптивные структуры. В данной статье я представляю теоретическое обоснование алгоритма, его математическую модель и результаты экспериментального исследования его эффективности на стандартных тестовых функциях оптимизации.
Реализация алгоритма
Представьте, что вы гуляете по саду после дождя. Повсюду дождевые черви — простейшие существа с примитивной нервной системой. Они не умеют думать в нашем понимании, но каким-то образом находят путь в сложной почве, избегают опасности, находят пищу и партнеров. Их крошечный мозг — всего несколько тысяч нейронов, и, тем не менее, они существуют миллионы лет. Так родилась идея нейробоидов.
Что если объединить простоту червячка с мощью коллективного интеллекта? В природе простейшие организмы достигают невероятных результатов, когда действуют сообща — муравьи строят сложные колонии, пчелы решают оптимизационные задачи при сборе нектара, стаи птиц формируют сложные динамические структуры без централизованного управления.
Мои нейробоиды подобны этим дождевым червям. У каждого своя небольшая нейронная сеть — не какая-то массивная архитектура с миллионами параметров, а всего несколько нейронов на входе и выходе. Они не знают всего пространства поиска, видят только своё локальное окружение. Когда один червячок находит плодородный участок почвы, богатый питательными веществами, другие постепенно стягиваются к этому месту. Но они не просто слепо следуют — каждый сохраняет свою индивидуальность, свою стратегию передвижения. Моим нейробоидам не нужно знать всю математику оптимизации. Они учатся самостоятельно, методом проб и ошибок. Когда один находит хорошее решение, остальные не просто копируют его координаты, а учатся понимать, почему это решение хорошее, и как туда добраться своим путём.
Помните закаты на море? Солнце отражается миллионами бликов на волнах, и каждый блик — своя маленькая история взаимодействия света с водой. Так и мои нейробоиды — каждый отражает частицу решения, а вместе они создают полную картину. Издалека их движение может показаться хаотичным. Но внутри этого кажущегося хаоса рождается порядок — самоорганизующаяся система поиска оптимальных решений.
У нейробоидов тоже нет центрального командира. Вместо этого, каждый использует свою маленькую нейросеть, чтобы решить: следовать ли к лучшему известному решению или исследовать новую территорию, копировать успешную стратегию соседа или рискнуть создать свою.
В мире, одержимом сложностью и масштабом, нейробоиды напоминают, что величайшие системы часто построены из простейших элементов. Как песчинки формируют пляжи и горы, как капли образуют океаны — так и мои маленькие цифровые червячки, каждый со своей крошечной нейросетью, вместе решают задачи, перед которыми пасуют гигантские монолитные алгоритмы.
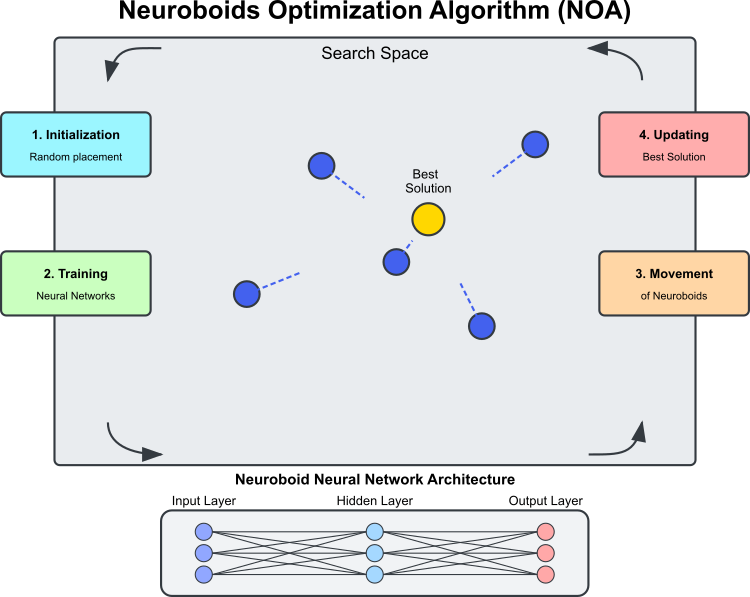
Рисунок 1. Схема работы алгоритма NOA
Иллюстрация (рисунок 1) показывает основные компоненты и принцип работы алгоритма NOA. Пространство поиска — это область, в которой нейробоиды (синие круги) ищут оптимальное решение, нейробоиды — агенты оптимизации, каждый из которых имеет свою нейронную сеть. Лучшим решением является текущее наилучшее найденное решение (золотой круг), к которому стремятся нейробоиды, архитектура нейросети: каждый нейробоид использует собственную нейронную сеть для определения направления движения. Циклический процесс алгоритма, состоит из этапов: инициализация — случайное размещение нейробоидов, обучение нейросетей — обучение на основе лучшего найденного решения, перемещение нейробоидов под управлением обученных нейросетей и обновление лучшего решения, если найдено решение лучше текущего. Пунктирные линии показывают направления движения нейробоидов, которые определяются выходами их нейросетей и стремятся к лучшему решению с элементом случайности.
Термин "нейробоид" объединяет понятия нейронной сети и боида (от английского "boid" — искусственная "птица" в моделях коллективного поведения). Каждый агент-нейробоид представляет собой сочетание: позиции в пространстве решения
и персональной нейронной сети, определяющей стратегию перемещения.
В отличие от традиционных метаэвристических алгоритмов (как генетические алгоритмы или роевые методы), где поведение агентов определяется фиксированными правилами, в NOA: каждый нейробоид имеет собственную нейросеть, которая обучается в процессе оптимизации, нейросети постепенно учатся определять наиболее перспективные направления поиска и обучение происходит на основе лучшего найденного решения (целевой вектор). Получается, что алгоритм оптимизации включает в себя две стратегии поиска: первая — это собственно NOA, а вторая — это встроенный в нейросеть ADAM. Механизм обратного распространения ошибки позволяет использовать ADAM в контексте алгоритма NOA как независимый инструмент настройки весов нейронной сети каждого боида, соответственно общее количество весов всех нейробоидов может быть гораздо больше размерности задачи — не нужно оптимизировать веса нейронных сетей всей популяции, это происходит естественно и автоматически.
Поведение нейробоидов имеет определенные параллели с: социальным обучением в природе (наблюдение за успешными особями), нейропластичностью (способность нервной системы адаптироваться к изменяющимся условиям) и коллективным разумом (эмерджентная оптимизация через взаимодействие множества простых агентов).
Можно выделить основные технические особенности алгоритма NOA:
- прямое и обратное распространение ошибки внутри оптимизационного процесса,
- распределенное обучение множества нейросетей, каждая из которых формирует свою стратегию,
- адаптивная корректировка поведения на основе текущего состояния поиска,
- использование активационных функций нейросетей для создания нелинейной динамики поиска.
Эта комбинация делает NOA интересным гибридным подходом, объединяющим парадигмы машинного обучения и оптимизации. Вместо того чтобы использовать нейросети для аппроксимации целевой функции (как в суррогатных моделях), NOA использует их для косвенного управления самим процессом поиска, создавая своего рода "метаобучение" для решения задач оптимизации.
Теперь можем составить псевдокод алгоритма NOA:
Инициализация:
- Создать популяцию из N нейросетей (нейробоидов)
- Каждая нейросеть имеет структуру с количеством входов и выходов, равным размерности задачи оптимизации
- Установить параметры:
- popSize (размер популяции)
- actFunc (функция активации нейронов)
- dispScale (масштаб перемещений)
- eliteProb (вероятность копирования элитных координат)
Алгоритм:
- Если это первая итерация (revision = false):
- Для каждого нейробоида в популяции:
- Случайно инициализировать координаты в пространстве поиска
- Привести координаты к допустимым дискретным значениям
- Установить revision = true и завершить текущую итерацию
- Для каждого нейробоида в популяции:
- Для последующих итераций:
- Для большинства нейробоидов (все кроме 5 последних):
- Для каждой координаты:
- С вероятностью eliteProb заменить значение координаты на значение из лучшего найденного решения (cB)
- Для каждой координаты:
- Для каждого нейробоида в популяции:
- Масштабировать лучшее найденное решение (cB) и текущее положение нейробоида в диапазон [-1, 1]
- Выполнить прямое распространение через нейросеть текущего нейробоида
- Вычислить ошибку между целевым значением (масштабированным cB) и выходом нейросети
- Выполнить обратное распространение ошибки для обучения нейросети
- Обновить координаты нейробоида, смещая их в направлении, определяемом выходом нейросети
- Привести координаты к допустимым дискретным значениям
- Для большинства нейробоидов (все кроме 5 последних):
- Оценка и обновление:
- Для каждого нейробоида в популяции:
- Вычислить значение целевой функции для текущих координат
- Если значение лучше, чем лучшее найденное (fB):
- Обновить лучшее найденное значение (fB)
- Сохранить текущие координаты как лучшие (cB)
- Для каждого нейробоида в популяции:
Приступим к написанию кода алгоритма. Определим класс "C_AO_NOA", который является производным от класса "C_AO". Это означает, что он наследует свойства и методы "C_AO", а также добавляет свои собственные. Основные элементы класса:
Деструктор ~C_AO_NOA (): удаляет динамически выделенные объекты функции активации для каждого элемента массива "nn" - индивидуальной нейросети нейробоидов. Это помогает предотвратить утечки памяти.
Конструктор C_AO_NOA ():
- Инициализирует параметры алгоритма оптимизации.
- Устанавливает начальные значения для параметров: "popSize" - размер популяции, "actFunc" - функция активации нейрона, "dispScale" - масштаб перемещений, вероятность копирования элитных координат.
- Резервирует массив "params" для хранения параметров.
Метод SetParams (): устанавливает параметры на основе значений, хранящихся в массиве "params".
Метод Init (): определен для инициализации класса с диапазонами значений rangeMinP, rangeMaxP, rangeStepP и количеством эпох "epochsP".
Moving () и Revision (): эти методы служат для перемещения особей в популяции и выполняют оценку и обновление решений.
Массив nn: представляет собой массив экземпляров класса нейронной сети каждого нейробоида.
Закрытые методы: ScaleInp () и ScaleOut () - методы для масштабирования входных и выходных данных, соответственно.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_NOA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_NOA () { for (int i = 0; i < ArraySize (nn); i++) if (CheckPointer (nn [i].actFunc)) delete nn [i].actFunc; } C_AO_NOA () { ao_name = "NOA"; ao_desc = "Neuroboids Optimization Algorithm (joo)"; ao_link = "https://www.mql5.com/ru/articles/16992"; popSize = 50; // размер популяции actFunc = 0; // функция активации нейрона dispScale = 0.01; // масштаб перемещений eliteProb = 0.1; // вероятность копирования элитных координат ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "actFunc"; params [1].val = actFunc; params [2].name = "dispScale"; params [2].val = dispScale; params [3].name = "eliteProb"; params [3].val = eliteProb; } void SetParams () { popSize = (int)params [0].val; actFunc = (int)params [1].val; dispScale = params [2].val; eliteProb = params [3].val; } bool Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0); // количество эпох void Moving (); void Revision (); //---------------------------------------------------------------------------- int actFunc; // функция активации нейрона double dispScale; // масштаб перемещений double eliteProb; // вероятность копирования элитных координат private: //------------------------------------------------------------------- C_MLPa nn []; void ScaleInp (double &inp [], double &out []); void ScaleOut (double &inp [], double &out []); }; //——————————————————————————————————————————————————————————————————————————————
Метод "Init" предназначен для инициализации экземпляра класса "C_AO_NOA". Он принимает ряд параметров, которые задают диапазон значений и количество эпох, и выполняет необходимые операции для настройки алгоритма.
Сигнатура метода: указывает на успешность выполнения инициализации. Параметры:
- MinP [] - минимальные значения для параметров.
- MaxP [] - максимальные значения для параметров.
- StepP [] - шаг изменения параметров.
- epochsP - количество эпох.
Стандартная инициализация: первая строка метода вызывает функцию "StandardInit" с переданными диапазонами.
Настройка конфигурации нейронной сети:
- Создается массив "nnConf", который содержит размеры входного и выходного слоев нейронной сети.
- Вызывается "ArrayResize", чтобы изменить размер массива "nnConf" до 2 (входной и выходной слой).
- Оба элемента массива инициализируются значением "coords", что соответствует размерности входных данных.
Объявление перечисления E_Act: создается перечисление, которое определяет разные функции активации нейронов (eActTanh, eActAlgSigm, eActRatSigm и т.д.).
Резервирование массива нейронов: изменяется размер массива "nn" (массив нейронов) до "popSize", который был ранее установлен в конструкторе.
Инициализация нейронов:
- Переменная "cnt" инициализируется с нуля и используется для передачи уникального случайного зерна (seed) для инициализации каждого нейрона, гарантируя уникальность инициализации весов в каждой из нейронных сетей.
- В цикле "for" происходит инициализация каждого нейрона. Метод "nn [i].Init ()" вызывается с конфигурацией "nnConf", функцией активации "actFunc" и зерном, основанным на текущем значении "cnt" и количества миллисекунд, прошедших с момента старта системы.
- Значение "cnt" увеличивается с каждым проходом цикла, что позволяет создавать уникальные зерна для каждой инициализации нейрона.
Возврат результата: если все операции выполнены успешно, метод возвращает "true", инициализация была выполнена успешно.
Метод "Init" класса "С_AO_NOA" является ключевым для настройки алгоритма оптимизации, обеспечивая инициализацию нейронной сети и связанных параметров.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_NOA::Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0) // количество эпох { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- int nnConf []; ArrayResize (nnConf, 2); nnConf [0] = coords; nnConf [1] = coords; enum E_Act { eActTanh, //0 eActAlgSigm, //1 eActRatSigm, //2 eActSoftPlus, //3 eActBentIdent, //4 eActSiLU, //5 eActACON, //6 eActSERF, //7 eActSnake //8 }; ArrayResize (nn, popSize); int cnt = 0; for (int i = 0; i < popSize; i++) { nn [i].Init (nnConf, actFunc, (int)GetTickCount64 () + cnt); cnt++; } return true; } //——————————————————————————————————————————————————————————————————————————————
Метод "Moving ()" реализует процесс перемещения особей в популяции в рамках нейробоидного алгоритма оптимизации. Давайте разберем его по этапам:
Инициализация начальных значений: если "revision" равно "false", метод выполняет первую инициализацию. Для каждого элемента в популяции "popSize" и для каждого измерения "coords", метод устанавливает начальные значения в массиве "a [i].c [c]", представляющего поисковых агентов:
- u.RNDfromCI () - генерирует случайное значение в диапазоне "rangeMin[c]" и "rangeMax[c]".
- u.SeInDiSp() - функция, использующая шаг изменения, чтобы скорректировать значение "a [i].c [c]" внутри допустимого диапазона.
- После завершения инициализации "revision" устанавливается в "true", и управление возвращается из метода.
Обновление координат: происходит обновление координат особей на основе вероятности элитности. Для первых "popSize - 5" элементов популяции выполняется случайная проверка, и если случайное число оказалось меньше "eliteProb", координаты "a [i].c [c]" устанавливаются равными координатам элиты "cB [c]".
Обработка данных нейронной сети:создаются массивы для входных и выходных данных, целевых значений и ошибок и подготавливаются к размеру "coords". Для каждого элемента популяции:
- ScaleInp () - масштабирует координаты цели "cB" и сохраняет их в "targVal".
- ScaleInp () - масштабирует текущую координату из популяции и сохраняет ее в "inpData".
- nn [i].ForwProp () - выполняет прямое распространение на нейронной сети для получения выходных данных.
- Считается ошибка (разница между целевым и полученным значением) для каждой координаты.
- nn [i].BackProp (err) - выполняет обратное распространение ошибки для корректировки весов.
- Обновление координат "a [i].c [c]" происходит с учетом выхода нейронной сети, масштабирования и рандомного элемента выборки.
- В конце значение "a [i].c [c] нормализуется функцией "u.SeInDiSp".
Таким образом, метод "Moving ()" отвечает за перемещение особей в модели, инициализируя их в начале и обновляя их положения на основе выходов нейронных сетей и вероятностного выбора.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NOA::Moving () { //---------------------------------------------------------------------------- if (!revision) { // Инициализация начальных значений якорей во всех параллельных вселенных for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double rnd = 0.0; double val = 0.0; int pair = 0.0; for (int i = 0; i < popSize - 5; i++) { for (int c = 0; c < coords; c++) { if (u.RNDprobab () < eliteProb) { a [i].c [c] = cB [c]; } } } double inpData []; ArrayResize (inpData, coords); double outData []; ArrayResize (outData, coords); double targVal []; ArrayResize (targVal, coords); double err []; ArrayResize (err, coords); for (int i = 0; i < popSize; i++) { ScaleInp (cB, targVal); ScaleInp (a [i].c, inpData); nn [i].ForwProp (inpData, outData); for (int c = 0; c < coords; c++) err [c] = targVal [c] - outData [c]; nn [i].BackProp (err); for (int c = 0; c < coords; c++) { a [i].c [c] += outData [c] * (rangeMax [c] - rangeMin [c]) * dispScale * u.RNDprobab (); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Давайте разберем далее метод "Revision", который выполняет оценку и обновление текущего "лучшего" решения в популяции. Он сравнивает значения целевой функции для каждой особи с текущим "лучшим" значением и обновляет его, если находит лучшее. Таким образом, метод обеспечивает поддержание актуального наилучшего решения в популяции.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NOA::Revision () { for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c); } } } //——————————————————————————————————————————————————————————————————————————————
Метод "ScaleInp" отвечает за масштабирование входных данных из диапазона, заданного "rangeMin" и "rangeMax", в интервал от -1 до 1. Каждое значение "inp [c]" масштабируется с использованием функции "u.Scale", которая выполняет линейное масштабирование, чтобы привести его в диапазон от -1 до 1. Метод "ScaleInp" подготавливает данные для дальнейших вычислений, обеспечивая их нормализацию в нужный диапазон.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NOA::ScaleInp (double &inp [], double &out []) { for (int c = 0; c < coords; c++) out [c] = u.Scale (inp [c], rangeMin [c], rangeMax [c], -1, 1); } //——————————————————————————————————————————————————————————————————————————————
Аналогично "ScaleInp" работает и метод "ScaleOut", который производит обратное масштабирование из диапазона от -1 до 1 в интервал "rangeMin" и "rangeMax".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NOA::ScaleOut (double &inp [], double &out []) { for (int c = 0; c < coords; c++) out [c] = u.Scale (inp [c], -1, 1, rangeMin [c], rangeMax [c]); } //——————————————————————————————————————————————————————————————————————————————
Результаты тестов
Алгоритм показывает интересные результаты на функциях с малой и умеренной размерностью. При увеличении размерности задачи до 1000 переменных время вычислений становится неприемлемо большим, в следствие чего данные тесты не представлены. Производительность достигает около 45% (для 6-ти тестов из 9-ти) от оптимального значения по тестам.
NOA|Neuroboids Optimization Algorithm (joo)|50.0|0.0|0.01|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.7013521128826248
25 Hilly's; Func runs: 10000; result: 0.40128968110640306
=============================
5 Forest's; Func runs: 10000; result: 0.6222984295200933
25 Forest's; Func runs: 10000; result: 0.30830340651626337
=============================
5 Megacity's; Func runs: 10000; result: 0.4523076923076924
25 Megacity's; Func runs: 10000; result: 0.20892307692307693
=============================
All score: 2.69447 (44.91%)
Хотелось бы сказать несколько слов про визуализацию работы алгоритма NOA. Как можно заметить алгоритм формирует интересные веерообразные структуры. По сути эти структуры являются визуализацией результатов работы нейросетей в нейробоидах.
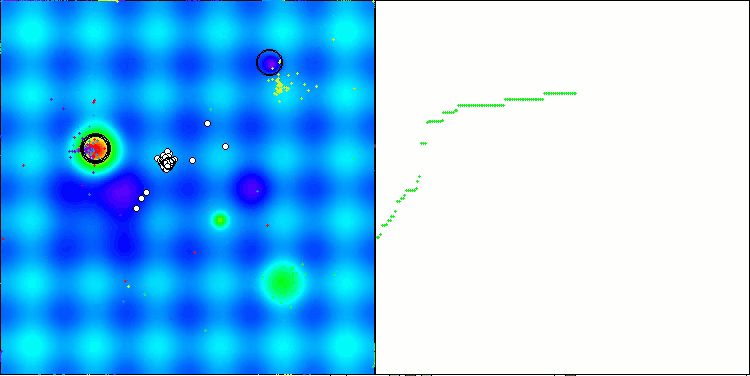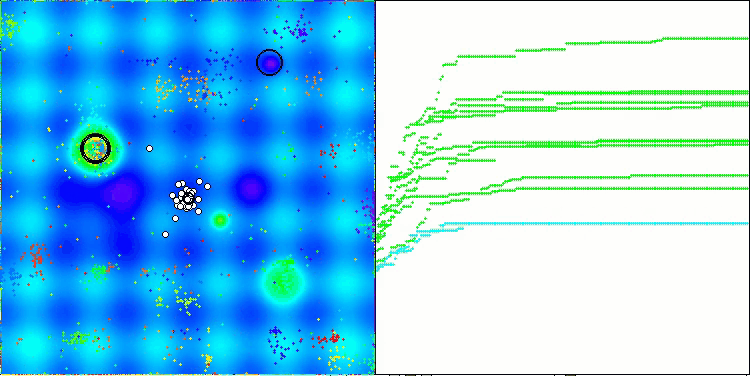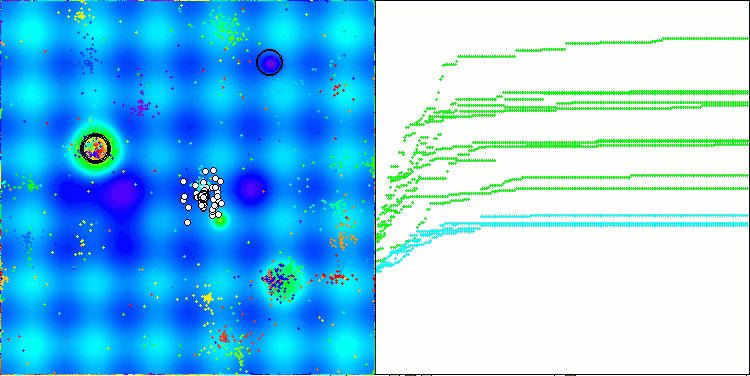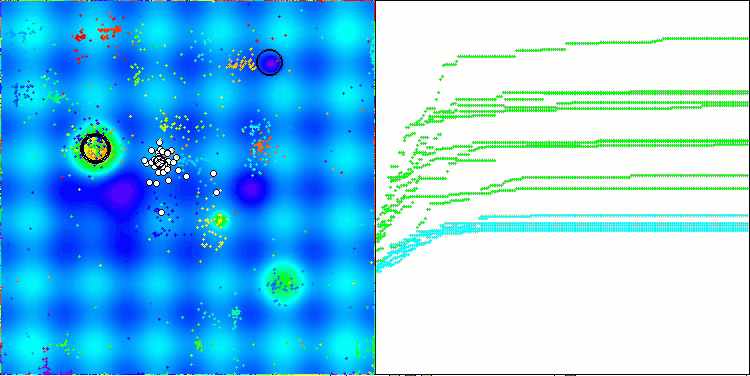
NOA на тестовой функции Hilly
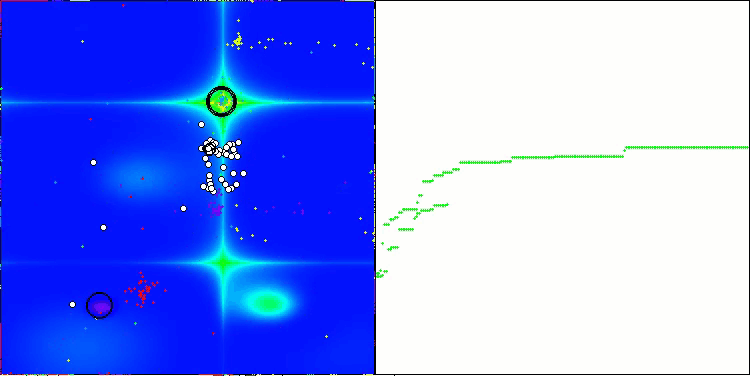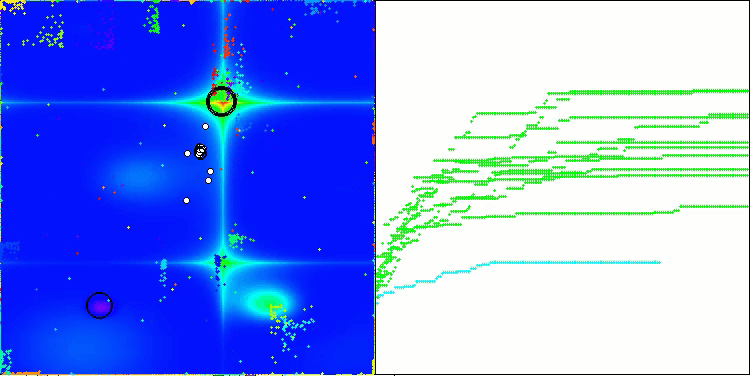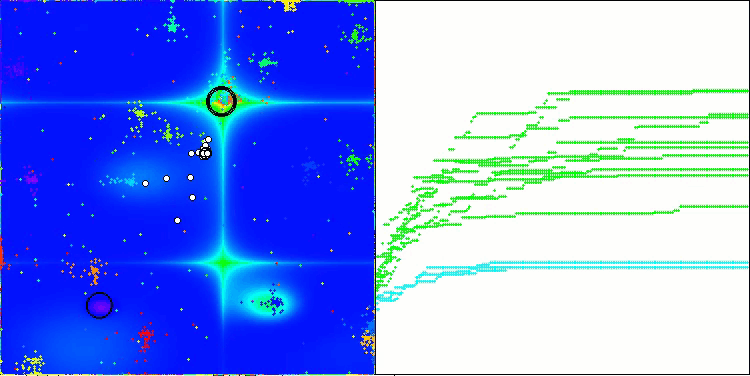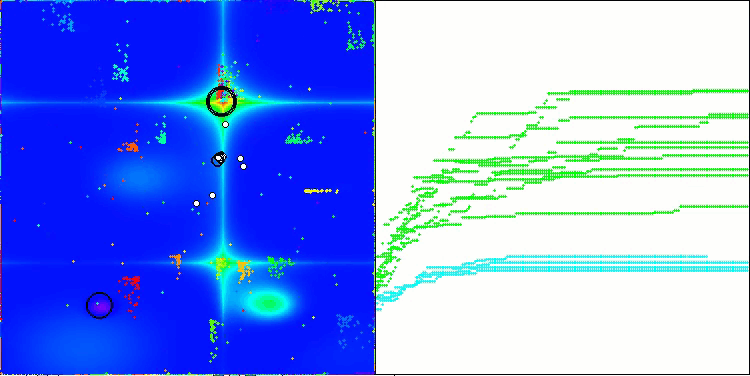
NOA на тестовой функции Forest
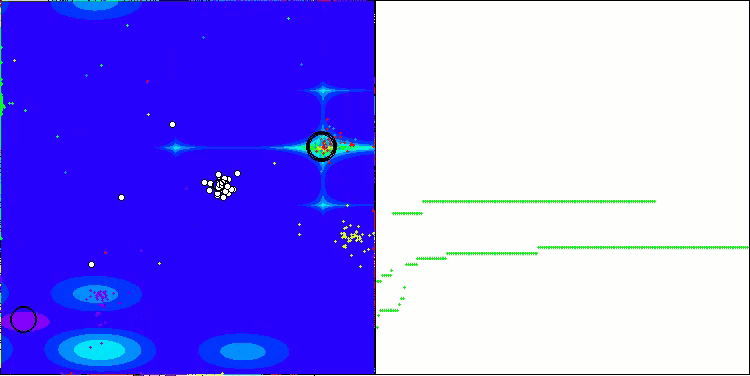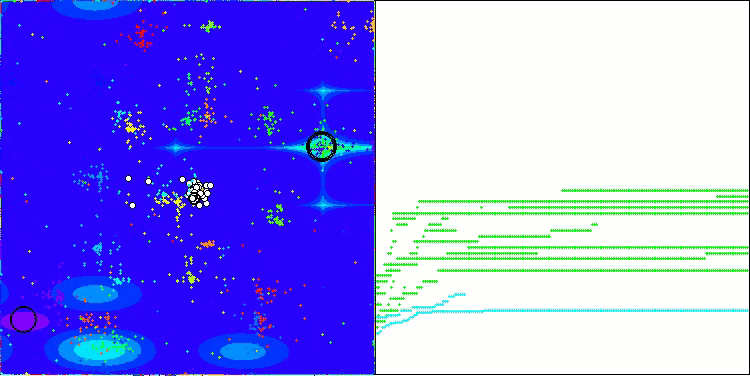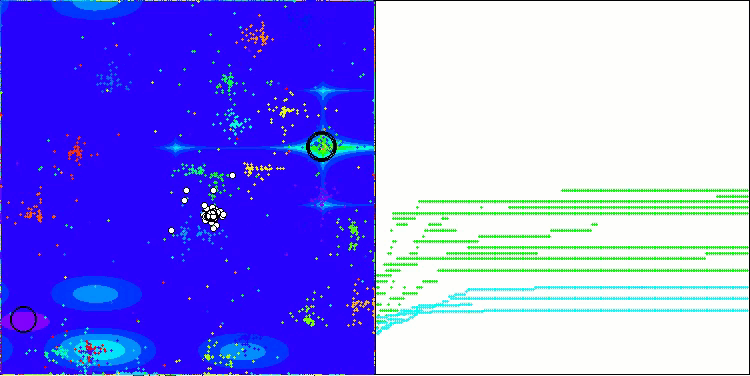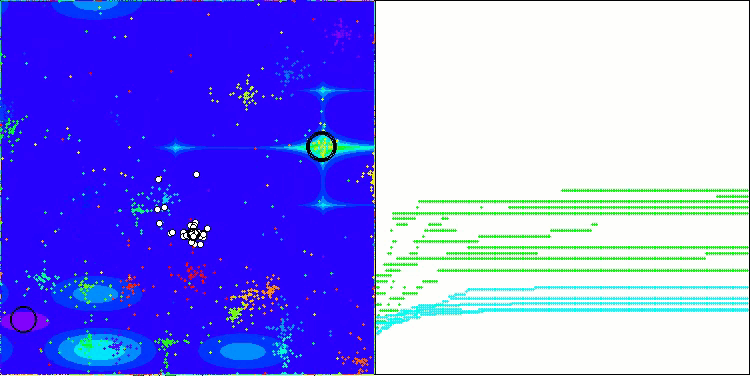
NOA на тестовой функции Megacity
Алгоритм NOA после проведенных тестов помещен в отдельную строку (не имеет порядкового номера), так как не получены результаты тестирования на функциях высокой размерности. Таблицы ниже представлены для сравнительного анализа результатов с остальными алгоритмами - участниками рейтинговой таблицы.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 13 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 14 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 15 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 16 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 17 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 18 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 19 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 20 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 21 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 22 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 23 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 24 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 25 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 26 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 27 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 28 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 29 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 30 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 31 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 32 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 33 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 34 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 35 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 36 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 37 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 38 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 39 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 40 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 41 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 42 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 43 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 44 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 45 | CSA | circle search algorithm | 0,66560 | 0,45317 | 0,29126 | 1,41003 | 0,68797 | 0,41397 | 0,20525 | 1,30719 | 0,37538 | 0,23631 | 0,10646 | 0,71815 | 3,435 | 38,17 |
| NOA | neuroboids optimization algorithm (joo) | 0,70135 | 0,40129 | 0,00000 | 1,10264 | 0,62230 | 0,30830 | 0,00000 | 0,93060 | 0,45231 | 0,20892 | 0,00000 | 0,66123 | 2,694 | 29,94 | |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Создавая NOA, я стремился объединить два мира: нейронные сети и оптимизационные алгоритмы. Результат оказался одновременно и предсказуемым, и неожиданным.
Главное, что меня вдохновляет в этом алгоритме — его биологическая правдоподобность. Мы часто пытаемся создать сложные модели, когда природа уже миллионы лет демонстрирует эффективные решения через коллективный интеллект простых организмов. Нейробоиды — это попытка воплотить эту естественную мудрость в алгоритмической форме.
Тестирование на различных функциях показало многообещающие результаты. Около 45% эффективности — это достойный старт для концептуально нового подхода. Я вижу, что алгоритм хорошо проявляет себя в задачах средней сложности. Однако, есть и существенные ограничения. Проблемы масштабируемости становятся критическими при высокой размерности задачи. При 1000 переменных вычислительная нагрузка становится непрактичной, это связано с обучением множества нейронных сетей — процесс, который сам по себе требователен к ресурсам.
Что особенно привлекает меня в NOA — это его способность к самообучению стратегиям поиска. В отличие от классических метаэвристик с фиксированными правилами, нейробоиды адаптируют своё поведение через обучение.
Вариативность результатов между запусками, которую я наблюдал, имеет двоякую природу. С одной стороны, это недостаток предсказуемости. С другой – это признак разнообразия стратегий исследования, что может быть преимуществом в сложных ландшафтах оптимизации.
Я вижу несколько направлений для развития алгоритма NOA:
- Оптимизация архитектуры нейросетей для снижения вычислительной нагрузки
- Внедрение механизмов переноса знаний между нейробоидами
В конечном счёте, NOA — это не просто ещё один оптимизационный метод. Это шаг к пониманию, как простые системы могут порождать сложное поведение. Это исследование грани между машинным обучением и метаэвристической оптимизацией, между индивидуальным и коллективным интеллектом.
Я верю, что этот подход имеет будущее не только в оптимизации функций, но и в более широких областях – от моделирования адаптивного поведения до поиска принципиально новых архитектур искусственного интеллекта. В мире, где сложность становится нормой, иногда простота с правильной организацией может дать неожиданно интересные решения.
В целом, алгоритм NOA следует воспринимать не как законченное решение для задач оптимизации, а как базовую платформу и отправную точку для множества направлений в исследовании и создания перспективных решений в области оптимизации вообще и машинного обучения в частности.
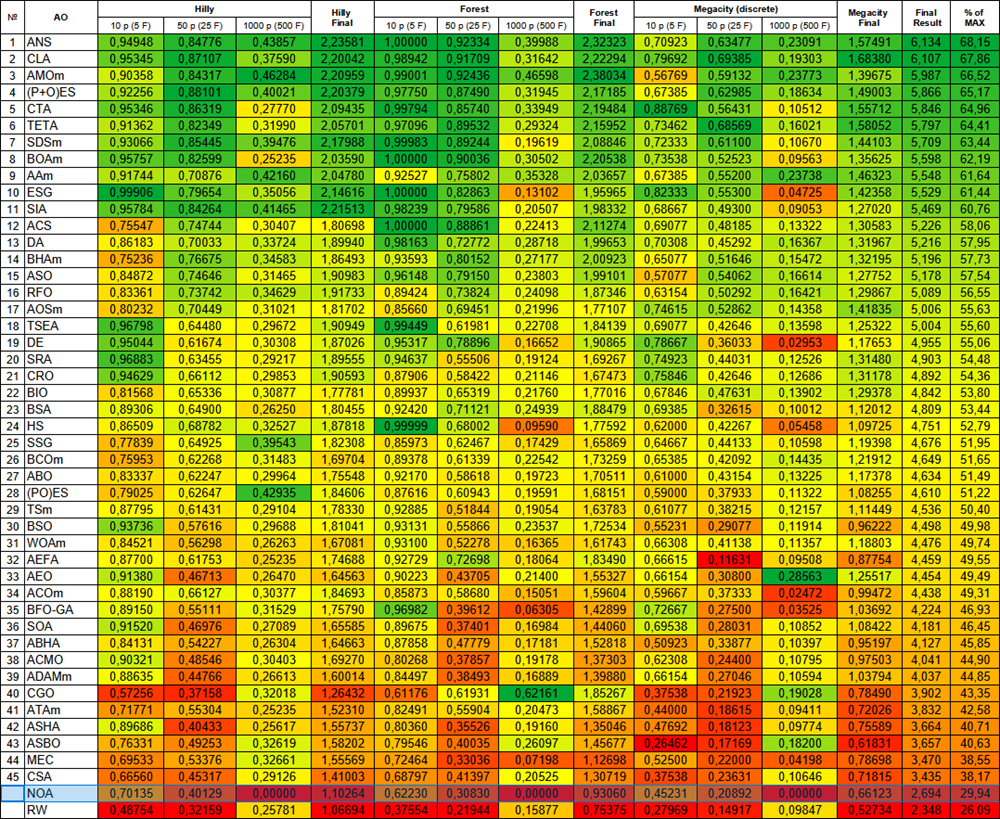
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
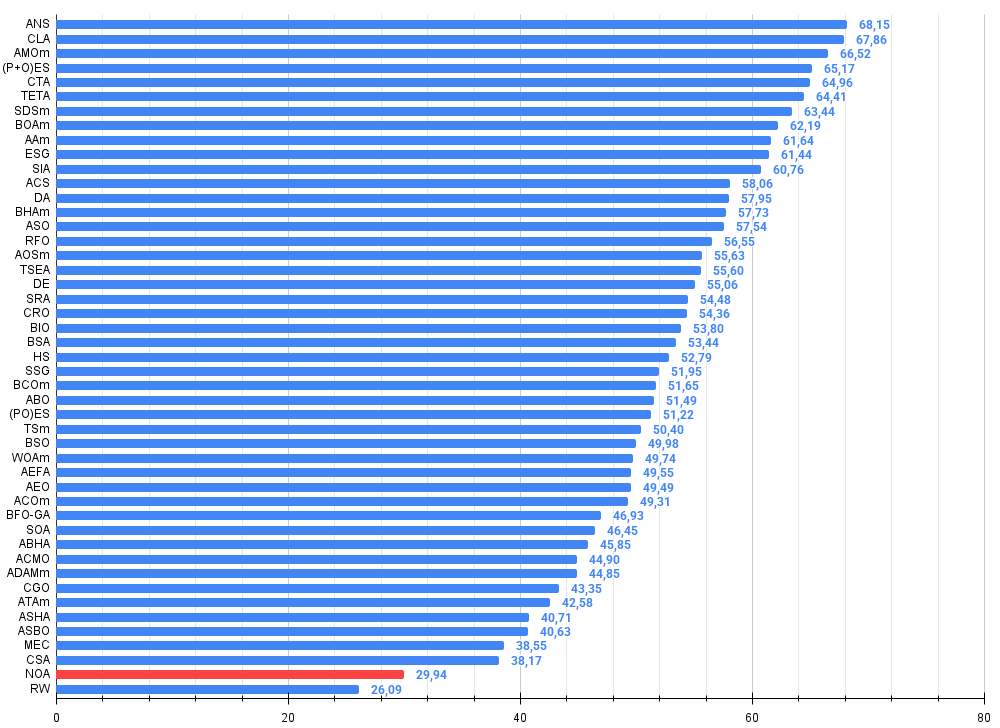
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма NOA:
Плюсы:
- Простая реализация.
- Интересные результаты.
Минусы:
- В виду длительного выполнения не получены результаты для многомерных пространств.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | MLPa.mqh | Включаемый файл | Нейронная сеть MLP с ADAM |
| 4 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 5 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 6 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 7 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 8 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 9 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 10 | Test_AO_NOA.mq5 | Скрипт | Испытательный стенд для NOA |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Построение модели для ограничения диапазона сигналов по тренду (Часть 8): Разработка советника (II)
Построение модели для ограничения диапазона сигналов по тренду (Часть 8): Разработка советника (II)
 Разработка системы репликации (Часть 70): Настройка времени (III)
Разработка системы репликации (Часть 70): Настройка времени (III)
 Разработка системы репликации (Часть 71): Настройка времени (IV)
Разработка системы репликации (Часть 71): Настройка времени (IV)
 Арбитражный трейдинг Forex: Простой бот-маркетмейкер синтетиков для старта
Арбитражный трейдинг Forex: Простой бот-маркетмейкер синтетиков для старта
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования