
Neuroboids Optimierungsalgorithmus (NOA)
Inhalt
Einführung
Bei der Erforschung von Optimierungsalgorithmen fühlte ich mich immer von der Idee angezogen, möglichst einfache und dennoch effiziente Lösungen zu entwickeln. Indem ich beobachtete, wie die Natur komplexe Probleme durch die Interaktion einfacher Organismen löst, entwickelte ich einen neuen Optimierungsalgorithmus – den Neuroboids Optimization Algorithm (NOA).
Der Algorithmus basiert auf dem Konzept der minimalistischen neuronalen Agenten – Neuroboids. Jedes Neuroboid ist ein einfaches neuronales Netz mit zwei Schichten von Neuronen, das mit dem Adam-Algorithmus trainiert wird. Die Einzigartigkeit dieses Ansatzes liegt in der Tatsache, dass trotz der extremen Einfachheit der einzelnen Agenten ihr kollektives Verhalten den Lösungsraum komplexer Optimierungsprobleme effektiv erkunden muss.
Die Inspiration für NOA kam von den Prozessen der Selbstorganisation in natürlichen Systemen, wo einfache Einheiten, die grundlegenden Regeln folgen, komplexe adaptive Strukturen bilden. In diesem Artikel stelle ich die theoretische Begründung des Algorithmus, sein mathematisches Modell und die Ergebnisse einer experimentellen Studie über seine Effizienz bei Standard-Optimierungs-Testfunktionen vor.
Implementierung des Algorithmus
Stellen Sie sich vor, Sie gehen nach dem Regen durch den Garten. Regenwürmer gibt es überall – einfache Lebewesen mit einem primitiven Nervensystem. Sie haben nicht die Fähigkeit, in unserem Sinne zu „denken“, aber irgendwie finden sie ihren Weg durch schwieriges Terrain, vermeiden Gefahren, finden Nahrung und Partner. Ihre winzigen Gehirne enthalten nur ein paar tausend Neuronen, aber sie existieren seit Millionen von Jahren. So wurde die Idee der Neuroboide geboren.
Wie wäre es, wenn wir die Einfachheit eines Wurms mit der Kraft der kollektiven Intelligenz kombinieren würden? In der Natur erzielen einfache Organismen unglaubliche Ergebnisse, wenn sie zusammenarbeiten – Ameisen bilden komplexe Kolonien, Bienen lösen Optimierungsprobleme beim Nektarsammeln, und Vogelschwärme bilden komplexe dynamische Strukturen ohne zentrale Steuerung.
Meine Neuroboide sind wie diese Regenwürmer. Jeder hat sein eigenes kleines neuronales Netz – keine riesige Architektur mit Millionen von Parametern, sondern nur ein paar Neuronen am Eingang und Ausgang. Sie kennen nicht den gesamten Suchraum, sie sehen nur ihre lokale Umgebung. Wenn ein Wurm einen fruchtbaren, nährstoffreichen Fleck Erde findet, zieht es nach und nach andere dorthin. Aber sie folgen nicht einfach blindlings – jeder behält seine eigene Individualität, seine eigene Bewegungsstrategie bei. Die Neuroboiden müssen nicht alle mathematischen Aspekte der Optimierung kennen. Sie lernen selbständig, durch Versuch und Irrtum. Wenn einer von ihnen eine gute Lösung findet, kopieren die anderen nicht einfach seine Koordinaten, sondern lernen zu verstehen, warum diese Lösung gut ist und wie sie selbst dorthin gelangen können.
Erinnern Sie sich an Sonnenuntergänge auf dem Meer? Die Sonne spiegelt sich in Millionen von Lichtreflexen auf den Wellen, und jeder Lichtreflex ist eine eigene kleine Geschichte über die Wechselwirkung von Licht und Wasser. Das Gleiche gilt für meine Neuroboide – jedes einzelne spiegelt einen Teil der Lösung wider, und zusammen ergeben sie ein vollständiges Bild. Aus der Ferne mag ihre Bewegung chaotisch erscheinen. Doch in diesem scheinbaren Chaos entsteht eine Ordnung – ein sich selbst organisierendes System, das optimale Lösungen findet.
Auch die Neuroboiden haben keinen zentralen Kommandanten. Stattdessen nutzt jedes sein eigenes kleines neuronales Netz, um zu entscheiden, ob es der besten bekannten Lösung folgt oder neues Terrain erkundet, die erfolgreiche Strategie eines Nachbarn kopiert oder eine eigene Strategie riskiert.
In einer Welt, die von Komplexität und Größe besessen ist, erinnern Neuroboids daran, dass die größten Systeme oft aus den einfachsten Elementen aufgebaut sind. So wie Sandkörner Strände und Berge bilden und Tröpfchen Ozeane, so arbeiten auch meine kleinen digitalen Würmer, jeder mit seinem eigenen winzigen neuronalen Netzwerk, zusammen, um Probleme zu lösen, die riesige, monolithische Algorithmen nicht lösen können.
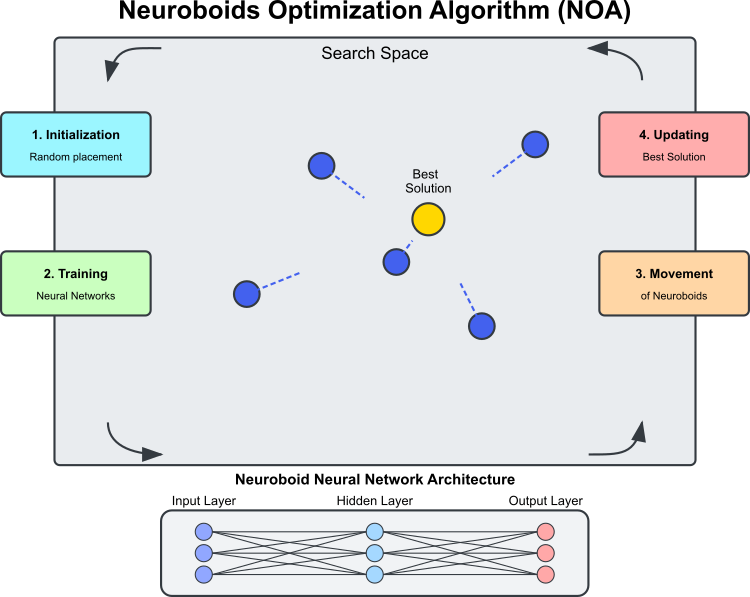
Abbildung 1. Betrieb des NOA-Algorithmus
Abbildung 1 zeigt die Hauptkomponenten und das Funktionsprinzip des NOA-Algorithmus. Der Suchraum ist der Bereich, in dem Neuroboids (blaue Kreise) nach der optimalen Lösung suchen. Neuroboids sind Optimierungsagenten, jeder mit seinem eigenen neuronalen Netz. Die beste Lösung ist die aktuell beste gefundene Lösung (der goldene Kreis), nach der die Neuroboiden streben. Die Architektur des neuronalen Netzes ist wie folgt: Jedes Neuroboid verwendet sein eigenes neuronales Netz, um die Bewegungsrichtung zu bestimmen. Der zyklische Prozess des Algorithmus besteht aus den folgenden Phasen: Initialisierung – zufällige Platzierung der Neuroboids; Training des neuronalen Netzes – Lernen auf der Grundlage der besten gefundenen Lösung; die Neuroboids bewegen sich unter der Kontrolle der trainierten neuronalen Netze; die beste Lösung wird aktualisiert, wenn eine bessere gefunden wird. Die gestrichelten Linien zeigen die Bewegungsrichtungen der Neuroboiden, die durch die Ausgaben ihrer neuronalen Netze bestimmt werden und nach der besten Lösung mit einem Element des Zufalls streben.
Der Begriff „Neuroboid“ kombiniert die Konzepte eines neuronalen Netzes und eines Boids (eines künstlichen „Vogels“ in Modellen des kollektiven Verhaltens). Jeder Neuroboid-Agent ist eine Kombination aus einer Position im Lösungsraum
und ein persönliches neuronales Netz, das die Bewegungsstrategie bestimmt.
Im Gegensatz zu traditionellen metaheuristischen Algorithmen (wie genetische Algorithmen oder Schwarmmethoden), bei denen das Verhalten der Agenten durch feste Regeln bestimmt wird, verfügt bei NOA jeder Neuronenknoten über ein eigenes neuronales Netz, das während der Optimierung trainiert wird; die neuronalen Netze lernen allmählich, die vielversprechendsten Suchrichtungen zu bestimmen, und das Training erfolgt auf der Grundlage der gefundenen besten Lösung (Zielvektor). Es stellt sich heraus, dass der Optimierungsalgorithmus zwei Suchstrategien umfasst: die erste ist NOA selbst und die zweite ist ADAM, die in das neuronale Netz integriert ist. Durch den Backpropagation-Mechanismus kann ADAM im Zusammenhang mit dem NOA-Algorithmus als unabhängiges Werkzeug zur Anpassung der Gewichte der einzelnen Neuronen des neuronalen Netzes verwendet werden. Folglich kann die Gesamtzahl der Gewichte aller Neuronenkörper viel größer sein als die Problemdimension – es besteht keine Notwendigkeit, die Gewichte des neuronalen Netzes der gesamten Population zu optimieren; dies geschieht auf natürliche und automatische Weise.
Das Verhalten von Neuroboiden weist gewisse Parallelen auf zu: sozialem Lernen in der Natur (Beobachtung erfolgreicher Individuen), Neuroplastizität (die Fähigkeit des Nervensystems, sich an veränderte Bedingungen anzupassen) und kollektiver Intelligenz (emergente Optimierung durch die Interaktion vieler einfacher Agenten).
Die wichtigsten technischen Merkmale des NOA-Algorithmus können identifiziert werden:
- Vorwärts- und Rückwärtsfortpflanzung von Fehlern im Rahmen der Optimierung.
- Verteiltes Training mehrerer neuronaler Netze, von denen jedes seine eigene Strategie bildet.
- Adaptive Verhaltensanpassung auf der Grundlage des aktuellen Suchstatus.
- Verwendung von Aktivierungsfunktionen neuronaler Netze, um eine nichtlineare Suchdynamik zu erzeugen.
Diese Kombination macht NOA zu einem interessanten hybriden Ansatz, der maschinelles Lernen und Optimierungsparadigmen kombiniert. Anstatt neuronale Netze zur Annäherung an die Zielfunktion zu verwenden (wie bei Surrogatmodellen), nutzt NOA sie, um die Suche selbst indirekt zu leiten, wodurch eine Art „Meta-Lernen“ für die Lösung von Optimierungsproblemen entsteht.
Jetzt können wir den Pseudocode für den NOA-Algorithmus schreiben:
Initialisierung:
- Erstellen einer Population von N neuronalen Netzen (Neuroboids)
- Jedes neuronale Netz hat eine Struktur mit einer Anzahl von Eingängen und Ausgängen, die der Dimension des Optimierungsproblems entspricht
- Festlegen der Parameter:
- popSize (Größe der Population)
- actFunc (Neuronen-Aktivierungsfunktion)
- dispScale (Verschiebungsskala)
- eliteProb (Wahrscheinlichkeit des Kopierens von Elite-Koordinaten)
Algorithmus:
- Wenn dies die erste Iteration ist (Revision = false):
- Für jedes Neuroboid in der Population:
- Zufällige Initialisierung der Koordinaten im Suchraum
- Koordinaten in akzeptable diskrete Werte umwandeln
- Revision = true setzen und die aktuelle Iteration beenden
- Für jedes Neuroboid in der Population:
- Für nachfolgende Iterationen:
- Für die meisten Neuroboide (alle bis auf die letzten 5):
- Für jede Koordinate:
- Mit der eliteProb-Wahrscheinlichkeit den Koordinatenwert durch den Wert der besten gefundenen Lösung ersetzen (cB)
- Für jede Koordinate:
- Für jedes Neuroboid in der Population:
- Skalierung der besten gefundenen Lösung (cB) und der aktuellen Position des Neuroboids auf den Bereich [-1, 1]
- Vorwärtspropagation durch das neuronale Netz des aktuellen Neuroboids durchführen
- Berechnung des Fehlers zwischen dem Zielwert (skaliert mit cB) und dem Ausgang des neuronalen Netzes
- Backpropagation durchführen, um das neuronale Netz zu trainieren
- Aktualisieren der Koordinaten des Neuroboids durch Verschieben in die Richtung, die durch die Ausgabe des neuronalen Netzes bestimmt wird
- Koordinaten in akzeptable diskrete Werte umwandeln
- Für die meisten Neuroboide (alle bis auf die letzten 5):
- Bewertung und Aktualisierung:
- Für jedes Neuroboid in der Population:
- Berechne den Wert der Zielfunktion für die aktuellen Koordinaten
- Wenn der Wert besser ist als der beste gefundene (fB):
- Aktualisieren des besten gefundenen Wertes (fB)
- Speichern der aktuellen Koordinaten als beste (cB)
- Für jedes Neuroboid in der Population:
Beginnen wir mit dem Schreiben des Algorithmus-Codes. Definieren wir die Klasse C_AO_NOA, die von der Klasse C_AO abgeleitet ist. Das bedeutet, dass es die Eigenschaften und Methoden von C_AO erbt und auch seine eigenen hinzufügt. Hauptelemente des Kurses:
Destruktor ~C_AO_NOA() : Entfernt dynamisch zugewiesene Aktivierungsfunktionsobjekte für jedes Element des Arrays „nn“ – das individuelle neuronale Netz der Neuroboids. Dies hilft, Speicherlecks zu vermeiden.
Konstruktor C_AO_NOA ():
- Initialisiert die Parameter des Optimierungsalgorithmus.
- Setzt Anfangswerte für die Parameter: popSize – Populationsgröße, actFunc – Neuronenaktivierungsfunktion, dispScale – Bewegungsskala, Wahrscheinlichkeit des Kopierens von Elitekoordinaten.
- Reserviert das Arrays „params“ zum Speichern von Parametern.
Methode SetParams (): setzt die Parameter auf der Grundlage der im Array „params“ gespeicherten Werte.
Methode Init (): definiert, um die Klasse mit den Wertebereichen rangeMinP, rangeMaxP und rangeStepP sowie der EpochsP Anzahl der Epochen zu initialisieren.
Moving () und Revision (): Diese Methoden dienen dazu, Individuen in der Population zu verschieben und die Bewertung und Aktualisierung von Entscheidungen durchzuführen.
nn-Array: ein Array mit Instanzen der Klasse des neuronalen Netzes für jedes Neuroboid.
Geschlossene Methoden: ScaleInp () und ScaleOut () – Methoden zur Skalierung von Eingangs- bzw. Ausgangsdaten.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_NOA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_NOA () { for (int i = 0; i < ArraySize (nn); i++) if (CheckPointer (nn [i].actFunc)) delete nn [i].actFunc; } C_AO_NOA () { ao_name = "NOA"; ao_desc = "Neuroboids Optimization Algorithm (joo)"; ao_link = "https://www.mql5.com/en/articles/16992"; popSize = 50; // population size actFunc = 0; // neuron activation function dispScale = 0.01; // scale of movements eliteProb = 0.1; // probability of copying elite coordinates ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "actFunc"; params [1].val = actFunc; params [2].name = "dispScale"; params [2].val = dispScale; params [3].name = "eliteProb"; params [3].val = eliteProb; } void SetParams () { popSize = (int)params [0].val; actFunc = (int)params [1].val; dispScale = params [2].val; eliteProb = params [3].val; } bool Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0); // number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- int actFunc; // neuron activation function double dispScale; // scale of movements double eliteProb; // probability of copying elite coordinates private: //------------------------------------------------------------------- C_MLPa nn []; void ScaleInp (double &inp [], double &out []); void ScaleOut (double &inp [], double &out []); }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Init dient der Initialisierung einer Instanz der Klasse C_AO_NOA. Es nimmt eine Reihe von Parametern entgegen, die den Wertebereich und die Anzahl der Epochen angeben, und führt die notwendigen Operationen zur Abstimmung des Algorithmus durch.
Methodensignatur: zeigt an, dass die Initialisierung erfolgreich war. Parameter:
- MinP [] – Mindestwerte der Parameter.
- MaxP [] – Höchstwerte der Parameter.
- StepP [] – Änderungsschritt der Parameter.
- epochsP – Anzahl der Epochen.
Standardinitialisierung: Die erste Zeile der Methode ruft die Funktion StandardInit mit den übergebenen Bereichen auf.
Einrichten der Konfiguration des neuronalen Netzes:
- Das Array nnConf wird erstellt, das die Größen der Eingabe- und Ausgabeschichten des neuronalen Netzes enthält.
- Die Funktion ArrayResize wird aufgerufen, um die Größe des Arrays nnConf auf 2 (Eingabe- und Ausgabeschicht) zu ändern.
- Beide Array-Elemente werden mit dem Wert „coords“ initialisiert, der den Abmessungen der Eingabedaten entspricht.
Deklaration der Enumeration E_Act: Es wird eine Enumeration erstellt, die verschiedene Neuronenaktivierungsfunktionen definiert (eActTanh, eActAlgSigm, eActRatSigm usw.).
Sichern des Neuronen-Arrays: Ändert die Größe des Arrays „nn“ (das Array der Neuronen) auf popSize, das zuvor im Konstruktor festgelegt wurde.
Initialisierung der Neuronen:
- Die cnt-Variable wird von Null an initialisiert und dient dazu, einen eindeutigen Zufallswert zur Initialisierung jedes Neurons zu übergeben, um sicherzustellen, dass die Gewichte in jedem neuronalen Netz eindeutig initialisiert sind.
- Jedes Neuron wird in der „for“-Schleife initialisiert. Die Methode nn[i].Init() wird mit der Konfiguration nnConf, der Aktivierungsfunktion actFunc und einem Seed aufgerufen, der auf dem aktuellen cnt-Wert und der Anzahl der seit dem Systemstart verstrichenen Millisekunden basiert.
- Der cnt-Wert wird bei jeder Schleifeniteration inkrementiert, sodass für jede Neuroneninitialisierung eindeutige Seeds erzeugt werden können.
Rückgabe des Ergebnisses: Wenn alle Operationen erfolgreich waren, gibt die Methode „true“ zurück, die Initialisierung war erfolgreich.
Die Init-Methode der Klasse С_AO_NOA ist der Schlüssel zum Aufbau des Optimierungsalgorithmus, indem sie die Initialisierung des neuronalen Netzes und der zugehörigen Parameter ermöglicht.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_NOA::Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0) // number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- int nnConf []; ArrayResize (nnConf, 2); nnConf [0] = coords; nnConf [1] = coords; enum E_Act { eActTanh, //0 eActAlgSigm, //1 eActRatSigm, //2 eActSoftPlus, //3 eActBentIdent, //4 eActSiLU, //5 eActACON, //6 eActSERF, //7 eActSnake //8 }; ArrayResize (nn, popSize); int cnt = 0; for (int i = 0; i < popSize; i++) { nn [i].Init (nnConf, actFunc, (int)GetTickCount64 () + cnt); cnt++; } return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving() implementiert das Verschieben von Individuen in einer Population im Rahmen eines neuronenartigen Optimierungsalgorithmus. Lassen Sie uns Schritt für Schritt vorgehen:
Initialisierung der Anfangswerte: Wenn „revision“ „false“ ist, führt die Methode die erste Initialisierung durch. Für jedes Element in der Population popSize und für jede Dimension coords setzt die Methode die Anfangswerte in das Array a[i].c[c], das die Suchagenten darstellt:
- u.RNDfromCI () erzeugt einen Zufallswert im Bereich von rangeMin[c] und rangeMax[c].
- u.SeInDiSp() ist eine Funktion, die eine schrittweise Änderung verwendet, um den Wert von a [i].c [c] innerhalb eines gültigen Bereichs anzupassen.
- Nach Abschluss der Initialisierung wird „revision“ auf „true“ gesetzt, und die Methode wird verlassen.
Aktualisierung der Koordinaten: Die Koordinaten der Individuen werden auf der Grundlage der Wahrscheinlichkeit der Auserwähltheit aktualisiert. Für die ersten popSize – 5 Elemente der Population wird eine Zufallsüberprüfung durchgeführt, und wenn die Zufallszahl kleiner als eliteProb ist, werden die Koordinaten von a [i].c [c] gleich den Koordinaten von Elite „cB [c]“ gesetzt.
Handhabung von Daten des neuronalen Netzes: Arrays für Eingabe- und Ausgabedaten, Zielwerte und Fehler werden erstellt und auf die Größe „coords“ vorbereitet. Für jedes Element der Grundgesamtheit:
- ScaleInp () skaliert die cB-Zielkoordinaten und speichert sie in targVal.
- ScaleInp () skaliert die aktuelle Koordinate der Grundgesamtheit und speichert sie in inpData.
- nn [i].ForwProp () führt eine Vorwärtspropagation des neuronalen Netzes durch, um eine Ausgabe zu erzeugen.
- Der Fehler (die Differenz zwischen dem Soll- und dem Ist-Wert) wird für jede Koordinate berechnet.
- nn [i].BackProp (err) führt eine Backpropagation des Fehlers durch, um die Gewichte anzupassen.
- Die Koordinaten a [i].c [c] werden unter Berücksichtigung der Ausgabe des neuronalen Netzes, der Skalierung und eines Zufallselements aktualisiert.
- Am Ende wird der Wert von a[i].c[c] durch die Funktion u.SeInDiSp normalisiert.
So ist die Methode Moving() für die Bewegung von Individuen im Modell verantwortlich, wobei sie zu Beginn initialisiert und ihre Positionen auf der Grundlage der Ergebnisse neuronaler Netze und probabilistischer Entscheidungen aktualisiert werden.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NOA::Moving () { //---------------------------------------------------------------------------- if (!revision) { // Initialize the initial values of anchors in all parallel universes for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double rnd = 0.0; double val = 0.0; int pair = 0.0; for (int i = 0; i < popSize - 5; i++) { for (int c = 0; c < coords; c++) { if (u.RNDprobab () < eliteProb) { a [i].c [c] = cB [c]; } } } double inpData []; ArrayResize (inpData, coords); double outData []; ArrayResize (outData, coords); double targVal []; ArrayResize (targVal, coords); double err []; ArrayResize (err, coords); for (int i = 0; i < popSize; i++) { ScaleInp (cB, targVal); ScaleInp (a [i].c, inpData); nn [i].ForwProp (inpData, outData); for (int c = 0; c < coords; c++) err [c] = targVal [c] - outData [c]; nn [i].BackProp (err); for (int c = 0; c < coords; c++) { a [i].c [c] += outData [c] * (rangeMax [c] - rangeMin [c]) * dispScale * u.RNDprobab (); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Als Nächstes betrachten wir die Methode der Revision, bei der die aktuell „beste“ Lösung in der Population bewertet und aktualisiert wird. Sie vergleicht die Zielfunktionswerte für jedes Individuum mit dem aktuellen „besten“ Wert und aktualisiert ihn, wenn er einen besseren Wert findet. Auf diese Weise stellt die Methode sicher, dass die derzeit beste Lösung in der Population erhalten bleibt.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NOA::Revision () { for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c); } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode ScaleInp ist für die Skalierung der Eingabedaten von dem durch rangeMin und rangeMax angegebenen Bereich auf das Intervall von -1 bis 1 zuständig. Jeder Wert von inp[c] wird mit der Funktion u.Scale skaliert, die eine lineare Skalierung vornimmt, um ihn in den Bereich von -1 bis 1 zu bringen. Die ScaleInp-Methode bereitet die Daten für weitere Berechnungen vor und sorgt für ihre Normalisierung auf den gewünschten Bereich.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NOA::ScaleInp (double &inp [], double &out []) { for (int c = 0; c < coords; c++) out [c] = u.Scale (inp [c], rangeMin [c], rangeMax [c], -1, 1); } //——————————————————————————————————————————————————————————————————————————————
Die Methode ScaleOut funktioniert ähnlich wie ScaleInp, die eine inverse Skalierung vom Bereich -1 bis 1 in das Intervall rangeMin und rangeMax vornimmt.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_NOA::ScaleOut (double &inp [], double &out []) { for (int c = 0; c < coords; c++) out [c] = u.Scale (inp [c], -1, 1, rangeMin [c], rangeMax [c]); } //——————————————————————————————————————————————————————————————————————————————
Testergebnisse
Der Algorithmus zeigt interessante Ergebnisse bei Funktionen mit kleinen und mittleren Dimensionen. Wenn die Problemgröße auf 1000 Variablen ansteigt, wird die Rechenzeit inakzeptabel groß, sodass diese Tests nicht vorgestellt werden. Die Leistung erreicht etwa 45 % (bei 6 von 9 Tests) des optimalen Wertes gemäß den Tests.
NOA|Neuroboids Optimization Algorithm (joo)|50.0|0.0|0.01|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.7013521128826248
25 Hilly's; Func runs: 10000; result: 0.40128968110640306
=============================
5 Forest's; Func runs: 10000; result: 0.6222984295200933
25 Forest's; Func runs: 10000; result: 0.30830340651626337
=============================
5 Megacity's; Func runs: 10000; result: 0.4523076923076924
25 Megacity's; Func runs: 10000; result: 0.20892307692307693
=============================
All score: 2.69447 (44.91%)
Ich möchte ein paar Worte über die Visualisierung des NOA-Algorithmus sagen. Wie Sie sehen können, bildet der Algorithmus interessante fächerförmige Strukturen. Im Wesentlichen sind diese Strukturen eine Visualisierung der Ergebnisse der neuronalen Netze in Neuroboids.
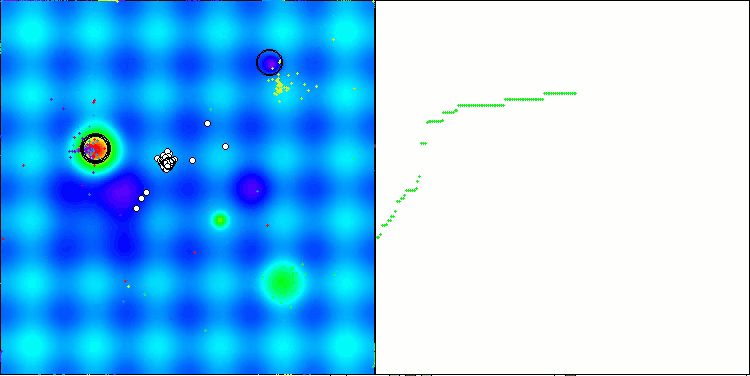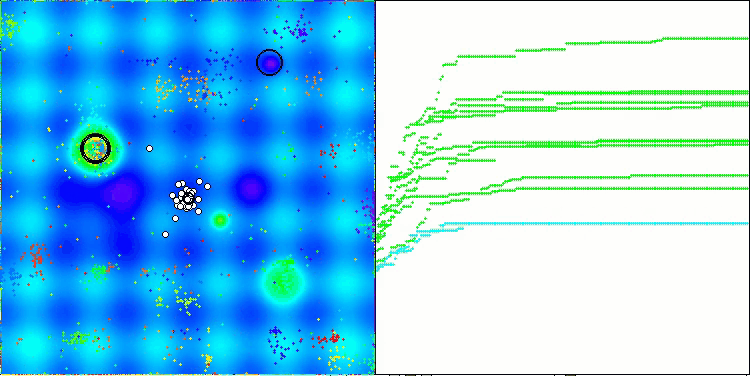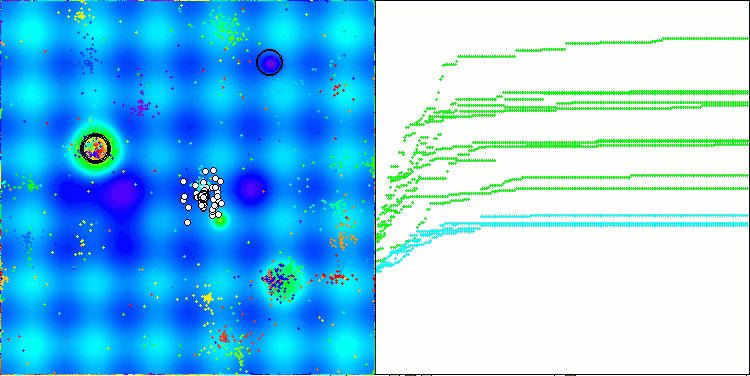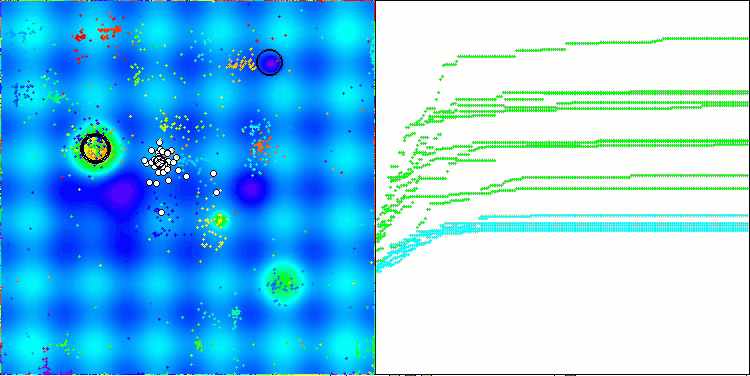
NOA mit der Testfunktion Hilly
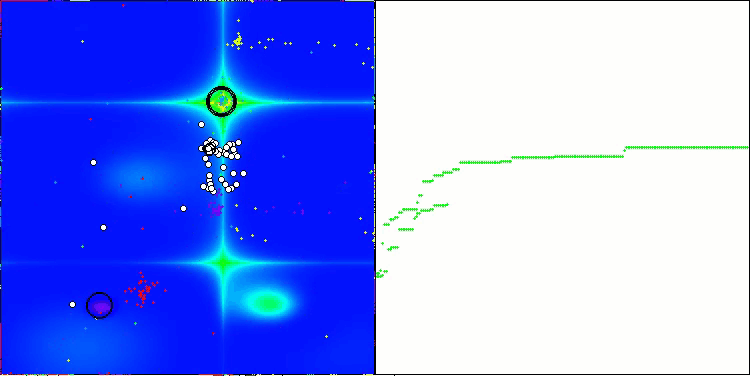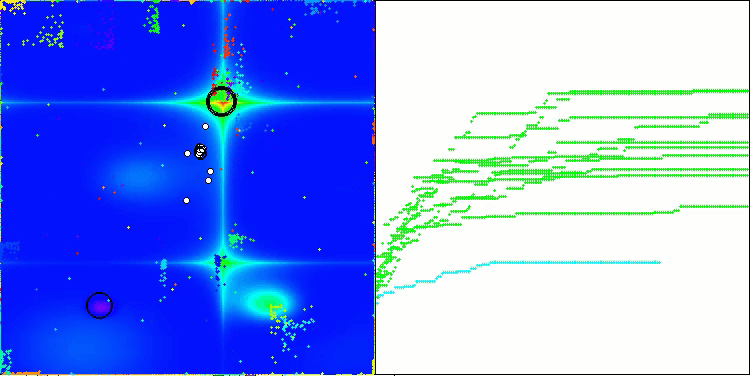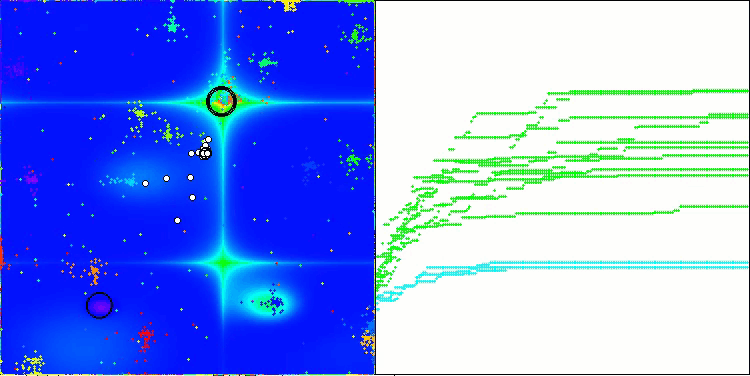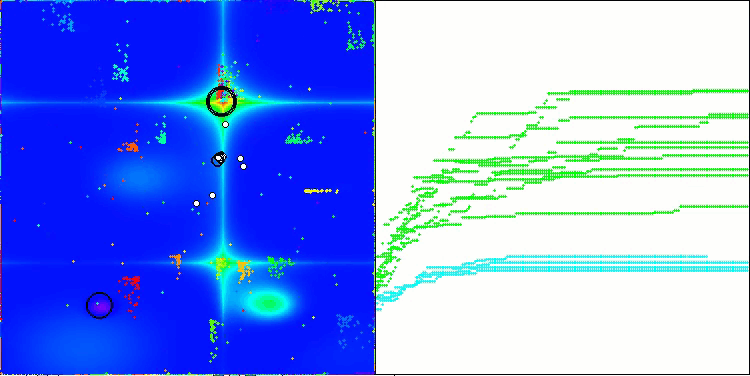
NOA mit der Testfunktion Forest
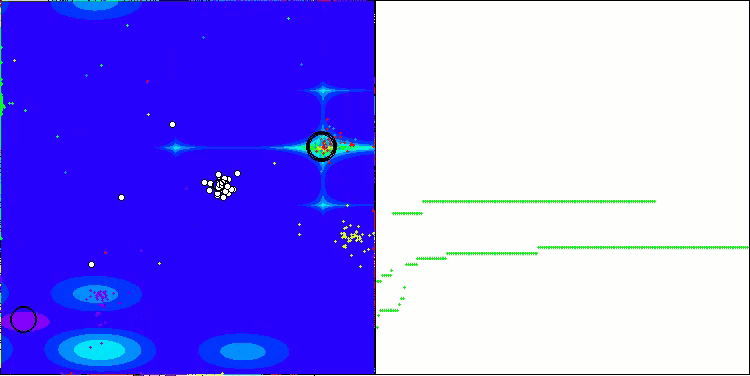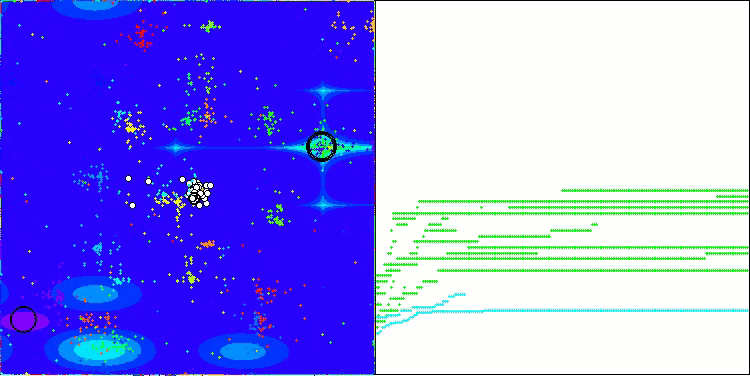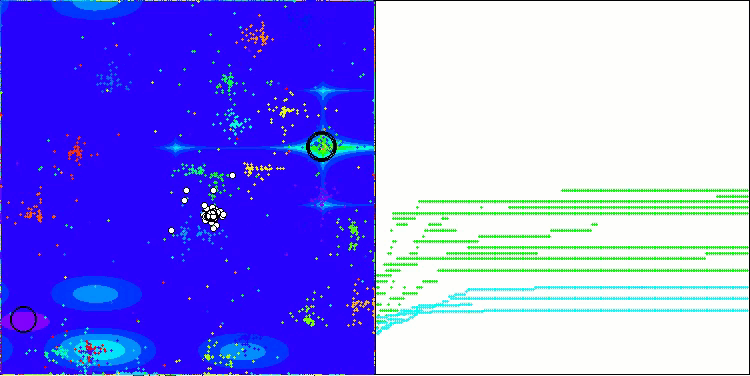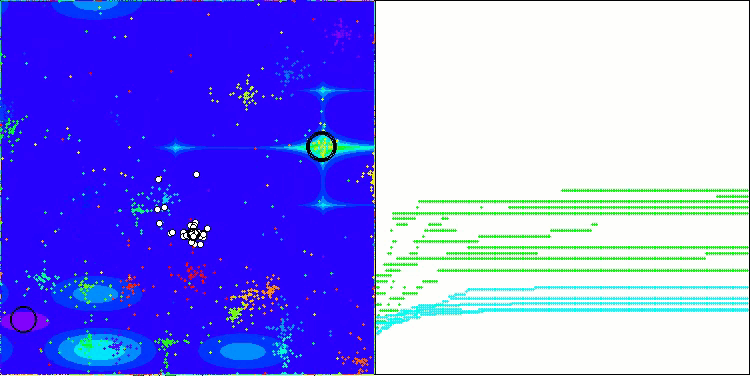
NOA mit der Testfunktion Megacity
Nach den Tests steht der NOA-Algorithmus in einer separaten Zeile (er hat keine Seriennummer), da bei hochdimensionalen Funktionen keine Testergebnisse erzielt wurden. Die nachstehenden Tabellen dienen der vergleichenden Analyse der Ergebnisse mit anderen an der Bewertungstabelle beteiligten Algorithmen.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Code-Sperr-Algorithmus (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | Zeit-Evolutions-Reise-Algorithmus (Joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | BOAm | Billard-Optimierungsalgorithmus M | 0.95757 | 0.82599 | 0.25235 | 2.03590 | 1.00000 | 0.90036 | 0.30502 | 2.20538 | 0.73538 | 0.52523 | 0.09563 | 1.35625 | 5.598 | 62.19 |
| 9 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 10 | ESG | Entwicklung sozialer Gruppen (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 11 | SIA | Simuliertes isotropes Glühen (Joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 12 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 13 | DA | dialektischer Algorithmus | 0.86183 | 0.70033 | 0.33724 | 1.89940 | 0.98163 | 0.72772 | 0.28718 | 1.99653 | 0.70308 | 0.45292 | 0.16367 | 1.31967 | 5.216 | 57.95 |
| 14 | BHAm | Algorithmus für schwarze Löcher M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 15 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 16 | RFO | Optimierung des Royal Flush (joo) | 0.83361 | 0.73742 | 0.34629 | 1.91733 | 0.89424 | 0.73824 | 0.24098 | 1.87346 | 0.63154 | 0.50292 | 0.16421 | 1.29867 | 5.089 | 56.55 |
| 17 | AOSm | Suche nach atomaren Orbitalen M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 18 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 19 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 20 | SRA | Algorithmus für erfolgreiche Gastronomen (joo) | 0.96883 | 0.63455 | 0.29217 | 1.89555 | 0.94637 | 0.55506 | 0.19124 | 1.69267 | 0.74923 | 0.44031 | 0.12526 | 1.31480 | 4.903 | 54.48 |
| 21 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 22 | BIO | Optimierung der Blutvererbung (joo) | 0.81568 | 0.65336 | 0.30877 | 1.77781 | 0.89937 | 0.65319 | 0.21760 | 1.77016 | 0.67846 | 0.47631 | 0.13902 | 1.29378 | 4.842 | 53.80 |
| 23 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 24 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 25 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 26 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 27 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 28 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 29 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 30 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 31 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 32 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 33 | AEO | Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 34 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 35 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 36 | SOA | einfacher Optimierungsalgorithmus | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 37 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 38 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 39 | ADAMm | adaptive Momentabschätzung M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 40 | CGO | Chaos Game Optimization | 0.57256 | 0.37158 | 0.32018 | 1.26432 | 0.61176 | 0.61931 | 0.62161 | 1.85267 | 0.37538 | 0.21923 | 0.19028 | 0.78490 | 3.902 | 43.35 |
| 41 | ATAm | Algorithmus für künstliche Stämme M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 42 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 43 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 44 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 45 | CSA | Kreis-Such-Algorithmus | 0.66560 | 0.45317 | 0.29126 | 1.41003 | 0.68797 | 0.41397 | 0.20525 | 1.30719 | 0.37538 | 0.23631 | 0.10646 | 0.71815 | 3.435 | 38.17 |
| NOA | neuroboids optimierungsalgorithmus (joo) | 0.70135 | 0.40129 | 0.00000 | 1.10264 | 0.62230 | 0.30830 | 0.00000 | 0.93060 | 0.45231 | 0.20892 | 0.00000 | 0.66123 | 2.694 | 29.94 | |
| RW | Random Walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Zusammenfassung
Bei der Entwicklung von NOA habe ich versucht, zwei Welten miteinander zu verbinden: neuronale Netze und Optimierungsalgorithmen. Das Ergebnis war sowohl vorhersehbar als auch unerwartet.
Was mich an diesem Algorithmus begeistert, ist vor allem seine biologische Plausibilität. Wir versuchen oft, komplexe Modelle zu entwerfen, während die Natur seit Millionen von Jahren durch die kollektive Intelligenz einfacher Organismen effiziente Lösungen demonstriert hat. Neuroboids sind ein Versuch, diese natürliche Weisheit in algorithmischer Form zu verkörpern.
Tests mit verschiedenen Funktionen zeigten vielversprechende Ergebnisse. Ein Wirkungsgrad von etwa 45 % ist ein guter Anfang für einen konzeptionell neuen Ansatz. Ich sehe, dass der Algorithmus bei Aufgaben mittlerer Komplexität gut abschneidet. Allerdings gibt es auch erhebliche Einschränkungen. Probleme mit der Skalierbarkeit werden kritisch, wenn das Problem sehr groß ist. Bei 1000 Variablen wird die Rechenlast unpraktisch, da mehrere neuronale Netze trainiert werden müssen, ein Prozess, der selbst ressourcenintensiv ist.
Was mich an NOA besonders reizt, ist die Fähigkeit, Suchstrategien selbst zu erlernen. Im Gegensatz zu herkömmlichen Metaheuristiken mit festen Regeln passen Neuroboids ihr Verhalten durch Lernen an.
Die von mir beobachtete Variabilität der Ergebnisse zwischen den einzelnen Läufen hat zwei Gründe. Zum einen ist es die fehlende Vorhersehbarkeit. Andererseits ist es ein Zeichen für die Vielfalt der Explorationsstrategien, die in komplexen Optimierungslandschaften von Vorteil sein kann.
Ich sehe mehrere Möglichkeiten für die Entwicklung des NOA-Algorithmus:
- Optimierung der Architektur neuronaler Netze zur Verringerung der Rechenlast
- Implementierung von Wissenstransfermechanismen zwischen Neuroboiden
Letztendlich ist NOA nicht nur eine weitere Optimierungsmethode. Dies ist ein Schritt zum Verständnis, wie einfache Systeme komplexes Verhalten erzeugen können. Hier wird die Grenze zwischen maschinellem Lernen und metaheuristischer Optimierung, zwischen individueller und kollektiver Intelligenz erforscht.
Ich glaube, dass dieser Ansatz nicht nur in der Funktionsoptimierung eine Zukunft hat, sondern auch in weiteren Bereichen – von der Modellierung adaptiven Verhaltens bis hin zur Entwicklung grundlegend neuer Architekturen für künstliche Intelligenz. In einer Welt, in der Komplexität immer mehr zur Norm wird, kann die Einfachheit, wenn sie richtig organisiert ist, manchmal unerwartet interessante Lösungen hervorbringen.
Insgesamt sollte der NOA-Algorithmus nicht als vollständige Lösung von Optimierungsproblemen betrachtet werden, sondern vielmehr als grundlegende Plattform und Ausgangspunkt für viele Forschungsbereiche und die Schaffung vielversprechender Lösungen im Bereich der Optimierung im Allgemeinen und des maschinellen Lernens im Besonderen.
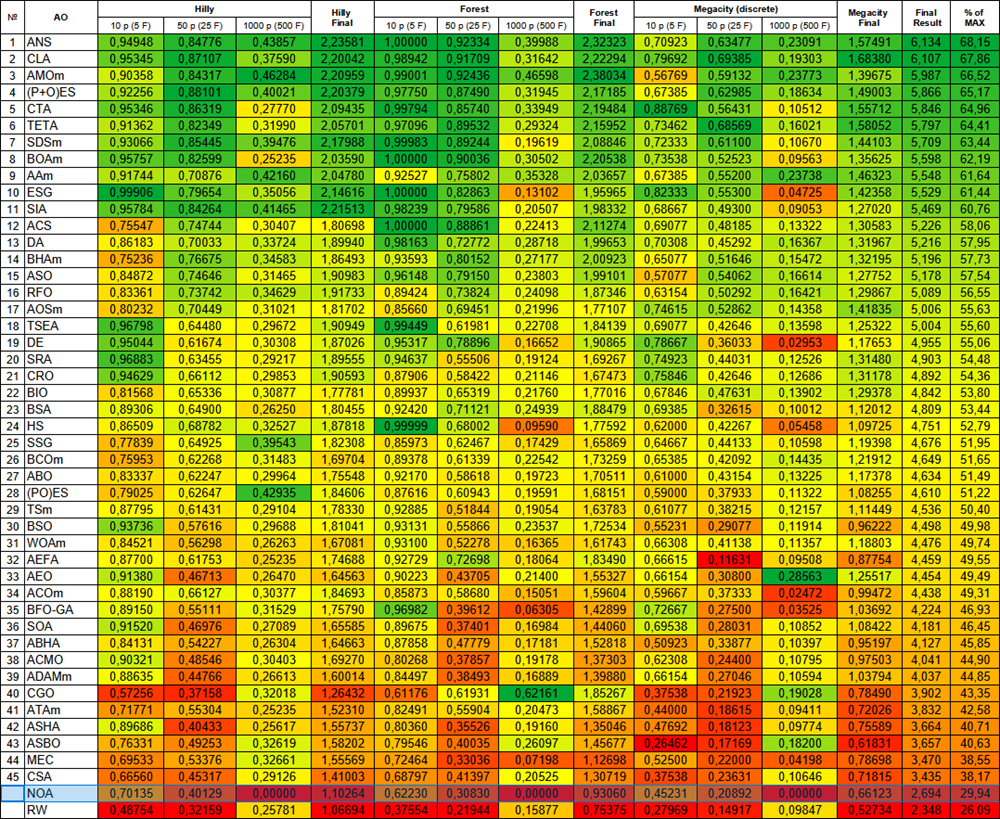
Abbildung 2. Farbabstufung der Algorithmen nach den entsprechenden Tests
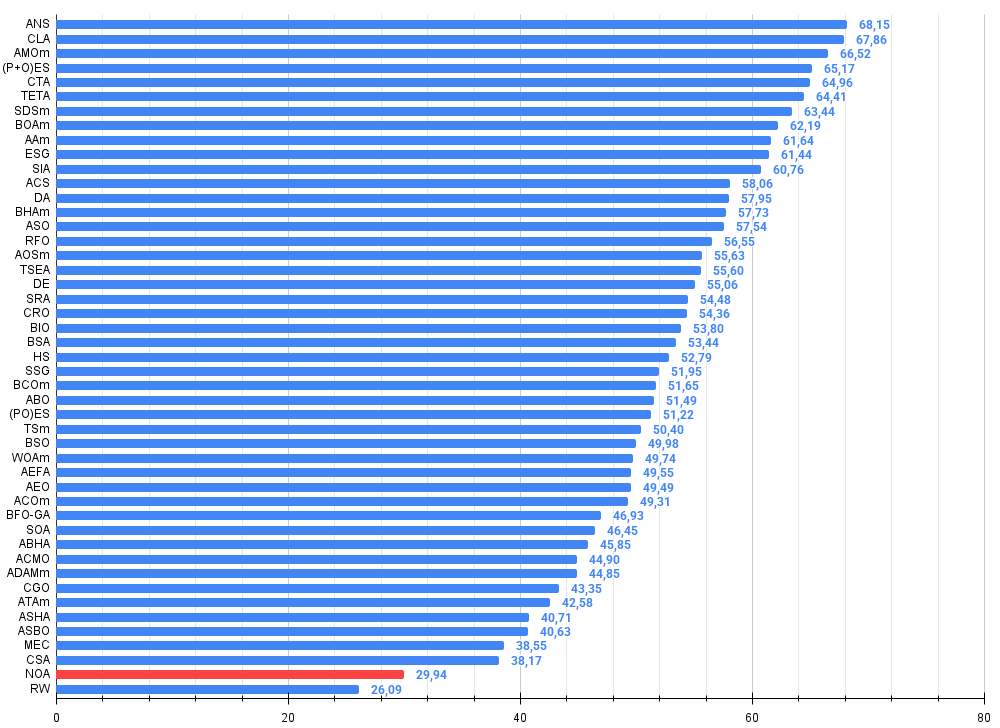
Abbildung 3. Histogramm der Algorithmus-Testergebnisse (Skala von 0 bis 100, je höher, desto besser, wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Bewertungstabelle)
Vor- und Nachteile von NOA:
Vorteile:
- Einfache Umsetzung.
- Interessante Ergebnisse.
Nachteile
- Aufgrund der langen Ausführungszeit wurden keine Ergebnisse für mehrdimensionale Räume erzielt.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Elternklasse der Populationsoptimierung Algorithmen |
| 2 | #C_AO_enum.mqh | Include | Enumeration der Algorithmen zur Populationsoptimierung |
| 3 | MLPa.mqh | Include | Neuronales MLP-Netz mit ADAM |
| 4 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 5 | TestStandFunctions.mqh | Include | Bibliothek mit Funktionen für den Prüfstand |
| 6 | Utilities.mqh | Include | Bibliothek mit Hilfsfunktionen |
| 7 | CalculationTestResults.mqh | Include | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 8 | Testing AOs.mq5 | Skript | Der einheitliche Prüfstand für alle Algorithmen zur Populationsoptimierung |
| 9 | Simple use of population optimization algorithms.mq5 | Skript | Ein einfaches Beispiel für die Verwendung von Algorithmen zur Populationsoptimierung ohne Visualisierung |
| 10 | Test_AO_NOA.mq5 | Skript | NOA-Prüfstand |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16992
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Arbitrage-Handel im Forex: Ein einfacher synthetischer Market-Maker-Bot für den Einstieg
Arbitrage-Handel im Forex: Ein einfacher synthetischer Market-Maker-Bot für den Einstieg
 Vom Neuling zum Experten: Zeitlich gefilterter Handel
Vom Neuling zum Experten: Zeitlich gefilterter Handel
 Einführung in MQL5 (Teil 26): Aufbau eines EAs mit Hilfe von Unterstützungs- und Widerstandszonen
Einführung in MQL5 (Teil 26): Aufbau eines EAs mit Hilfe von Unterstützungs- und Widerstandszonen
 Vom Neuling zum Experten: Prädiktive Preispfade
Vom Neuling zum Experten: Prädiktive Preispfade
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.