Otimização por neuroboides — Neuroboids Optimization Algorithm (NOA)

Conteúdo

1. Introdução
2. Implementação do algoritmo
3. Resultados dos testes

Introdução

Durante o estudo de algoritmos de otimização, sempre me atraiu a ideia de criar soluções simples, porém eficazes. Ao observar como a natureza resolve problemas complexos por meio da interação de organismos simples, desenvolvi um novo algoritmo de otimização, o Neuroboids Optimization Algorithm (NOA).

A base do algoritmo está na ideia de agentes neurais minimalistas, chamados de neuroboides. Cada neuroboide é uma rede neural simples, com duas camadas de neurônios, treinada com o algoritmo Adam. A singularidade dessa abordagem está no fato de que, apesar da extrema simplicidade de cada agente individual, o comportamento coletivo do grupo é capaz de explorar eficientemente o espaço de soluções de tarefas complexas de otimização.

A inspiração para a criação do NOA veio dos processos de auto-organização em sistemas naturais, onde unidades simples, seguindo regras básicas, formam estruturas complexas e adaptativas. Neste artigo, apresento o embasamento teórico do algoritmo, seu modelo matemático e os resultados da pesquisa experimental sobre sua eficácia em funções-padrão de teste de otimização.

Implementação do algoritmo

Imagine que você está caminhando por um jardim após a chuva. Há minhocas por toda parte, criaturas simples com um sistema nervoso primitivo. Elas não pensam como os humanos, mas de algum modo conseguem encontrar caminhos em um solo complexo, evitar perigos, localizar alimento e parceiros. Seu minúsculo cérebro, com apenas alguns milhares de neurônios, é suficiente para que sobrevivam há milhões de anos. Assim nasceu a ideia dos neuroboides.

E se uníssemos a simplicidade de uma minhoca à força da inteligência coletiva? Na natureza, organismos simples alcançam resultados extraordinários quando atuam em conjunto, como as formigas, que constroem colônias complexas; as abelhas, que resolvem problemas de otimização ao coletar néctar; e os bandos de pássaros, que formam estruturas dinâmicas elaboradas sem qualquer controle centralizado.

Meus neuroboides são como essas minhocas que aparecem após a chuva. Cada um possui sua própria pequena rede neural, não uma arquitetura massiva com milhões de parâmetros, mas apenas alguns neurônios nas entradas e saídas. Eles não conhecem todo o espaço de busca; apenas enxergam o ambiente ao seu redor. Quando uma dessas pequenas criaturas encontra uma área fértil do solo, rica em nutrientes, as outras se aproximam gradualmente desse ponto. No entanto, elas não seguem cegamente: cada uma mantém sua individualidade e sua própria estratégia de movimento. Meus neuroboides não precisam conhecer toda a matemática da otimização. Eles aprendem sozinhos, por tentativa e erro. Quando um deles encontra uma boa solução, os demais não apenas copiam suas coordenadas, mas também aprendem a entender por que aquela solução é boa e como chegar até ela pelo seu próprio caminho.

Lembram-se dos pores do sol no mar? O sol se reflete em milhões de brilhos sobre as ondas, e cada um deles é uma pequena história da interação entre a luz e a água. Assim também são os meus neuroboides: cada um reflete uma parte da solução e, juntos, eles compõem o quadro completo. À distância, seu movimento pode parecer caótico. Mas, dentro desse aparente caos nasce a ordem: um sistema auto-organizado de busca por soluções ótimas.

Os neuroboides também não têm um comandante central. Em vez disso, cada um usa sua pequena rede neural para decidir se deve seguir em direção à melhor solução conhecida ou explorar uma nova área, se deve copiar a estratégia bem-sucedida de um vizinho ou arriscar-se a criar a sua própria. 

Num mundo obcecado por complexidade e escala, os neuroboides nos lembram que os maiores sistemas são, muitas vezes, construídos a partir dos elementos mais simples. Assim como grãos de areia formam praias e montanhas, e gotas, oceanos, meus pequenos vermes digitais, cada um com sua diminuta rede neural, unem forças para resolver problemas diante dos quais algoritmos gigantescos e monolíticos fracassam.

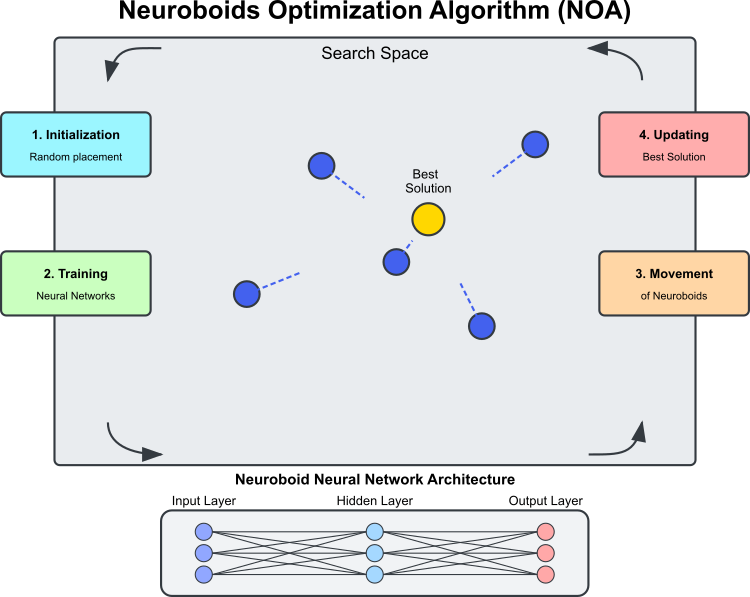
Figura 1. Diagrama do algoritmo NOA

A Figura 1 mostra os principais componentes e o princípio de funcionamento do NOA. O espaço de busca é a região em que os neuroboides (círculos azuis) procuram a solução ótima. Os neuroboides são agentes de otimização e cada um possui sua própria rede neural. A melhor solução é o melhor resultado encontrado até o momento (círculo dourado), em direção ao qual os neuroboides se movem. A arquitetura da rede neural é a seguinte: cada neuroboide usa sua própria rede para determinar a direção de movimento. O processo cíclico do algoritmo consiste nas seguintes etapas: inicialização, com posicionamento aleatório dos neuroboides; treinamento das redes neurais, com aprendizado baseado na melhor solução encontrada; movimento dos neuroboides, controlado pelas redes treinadas; e atualização da melhor solução, caso uma melhor seja encontrada. As linhas tracejadas indicam as direções de movimento dos neuroboides, determinadas pelas saídas de suas redes neurais, voltadas para a melhor solução com um elemento de aleatoriedade.

O termo "neuroboide" une os conceitos de rede neural e de "boid" (uma "ave" artificial em modelos de comportamento coletivo). Cada agente-neuroboide é uma combinação de uma posição no espaço de solução
e de uma rede neural pessoal, que define sua estratégia de movimento.

Ao contrário dos algoritmos metaheurísticos tradicionais (como os algoritmos genéticos ou os métodos de enxame), nos quais o comportamento dos agentes é regido por regras fixas, cada neuroboide no NOA possui sua própria rede neural, que aprende ao longo do processo de otimização. As redes neurais aprendem gradualmente a identificar as direções de busca mais promissoras e o aprendizado ocorre com base na melhor solução encontrada (vetor-alvo). Assim, o algoritmo de otimização incorpora duas estratégias de busca: a primeira é o próprio NOA e a segunda é o ADAM integrado à rede neural. O mecanismo de propagação reversa do erro permite usar o ADAM dentro do contexto do NOA como uma ferramenta independente para ajustar os pesos da rede neural de cada neuroboide. Dessa forma o número total de pesos de todos os neuroboides pode ser muito maior do que a dimensão do problema, e não é necessário otimizar manualmente os pesos das redes neurais de toda a população, pois isso ocorre de maneira natural e automática.

O comportamento dos neuroboides apresenta certas semelhanças com: o aprendizado social na natureza (observação de indivíduos bem-sucedidos), com a neuroplasticidade (capacidade do sistema nervoso de se adaptar a condições em mudança) e com a inteligência coletiva (otimização emergente resultante da interação de muitos agentes simples).

Podem ser destacadas as principais características técnicas do algoritmo NOA:

• propagação para frente e propagação reversa do erro dentro do próprio processo de otimização,
• treinamento distribuído de múltiplas redes neurais, cada uma formando sua própria estratégia,
• ajuste adaptativo do comportamento com base no estado atual da busca,
• uso das funções de ativação das redes neurais para criar uma dinâmica de busca não linear.

Essa combinação torna o NOA uma abordagem híbrida interessante, unindo as paradigmas do aprendizado de máquina e da otimização. Em vez de usar redes neurais para aproximar a função objetivo (como em modelos substitutos), o NOA as utiliza para controlar indiretamente o próprio processo de busca, criando uma espécie de "meta-aprendizado" voltado à resolução de problemas de otimização.

Agora podemos compor o pseudocódigo do algoritmo NOA:

Inicialização:

1. Criar uma população de N redes neurais (neuroboides)
2. Cada rede neural possui uma estrutura cujo número de entradas e saídas é igual à dimensionalidade do problema de otimização
3. Definir os parâmetros:
   • popSize (tamanho da população)
   • actFunc (função de ativação dos neurônios)
   • dispScale (escala de deslocamento)
   • eliteProb (probabilidade de copiar coordenadas da elite)

Algoritmo:

1. Se for a primeira iteração (revision = false):
   • Para cada neuroboide na população:
     • Inicializar aleatoriamente as coordenadas no espaço de busca
     • Converter as coordenadas em valores discretos válidos
   • Definir revision = true e encerrar a iteração atual
2. Para as iterações seguintes:
   • Para a maioria dos neuroboides (todos, exceto os 5 últimos):
     • Para cada coordenada:
       • Com probabilidade eliteProb, substituir o valor da coordenada pelo valor da melhor solução encontrada (cB)
   • Para cada neuroboide na população:
     • Escalonar a melhor solução encontrada (cB) e a posição atual do neuroboide para o intervalo [-1, 1]
     • Executar a propagação para frente pela rede neural do neuroboide atual
     • Calcular o erro entre o valor alvo (cB escalonado) e a saída da rede neural
     • Executar a propagação reversa do erro para treinar a rede neural
     • Atualizar as coordenadas do neuroboide deslocando-as na direção determinada pela saída da rede neural
     • Converter as coordenadas em valores discretos válidos
3. Avaliação e atualização:
   • Para cada neuroboide na população:
     • Calcular o valor da função objetivo para as coordenadas atuais
     • Se o valor for melhor do que o melhor encontrado até o momento (fB):
       • Atualizar o melhor valor encontrado (fB)
       • Salvar as coordenadas atuais como as melhores (cB)

Agora passamos à implementação do código do algoritmo. Definimos a classe "C_AO_NOA", derivada da classe "C_AO". Isso significa que ela herda as propriedades e métodos de "C_AO", além de adicionar seus próprios. Os principais elementos da classe são:

Destrutor C_AO_NOA(): remove os objetos de função de ativação alocados dinamicamente para cada elemento do array "nn", ou seja, a rede neural individual de cada neuroboide. Isso ajuda a evitar vazamentos de memória.

Construtor C_AO_NOA():

• Inicializa os parâmetros do algoritmo de otimização.
• Define valores iniciais para os parâmetros: "popSize" — tamanho da população, "actFunc" — função de ativação dos neurônios, "dispScale" — escala dos deslocamentos e a probabilidade de copiar coordenadas da elite.
• Reserva o array "params" para armazenar os parâmetros.

Método SetParams(): define os parâmetros com base nos valores armazenados no array "params".

Método Init(): é definido para inicializar a classe com os intervalos de valores rangeMinP, rangeMaxP, rangeStepP e o número de épocas "epochsP". 

Moving() e Revision(): esses métodos são responsáveis por mover os indivíduos dentro da população e realizar a avaliação e atualização das soluções.

Array nn: representa o conjunto de instâncias da classe de rede neural correspondente a cada neuroboide.

Métodos privados: ScaleInp() e ScaleOut() — métodos utilizados para escalonar os dados de entrada e de saída, respectivamente.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_NOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_NOA ()
  {
    for (int i = 0; i < ArraySize (nn); i++) if (CheckPointer (nn [i].actFunc)) delete nn [i].actFunc;
  }
  C_AO_NOA ()
  {
    ao_name = "NOA";
    ao_desc = "Neuroboids Optimization Algorithm (joo)";
    ao_link = "https://www.mql5.com/en/articles/16992";

    popSize   = 50;   // population size
    actFunc   = 0;    // neuron activation function
    dispScale = 0.01; // scale of movements
    eliteProb = 0.1;  // probability of copying elite coordinates

    ArrayResize (params, 4);
    params [0].name = "popSize";   params [0].val  = popSize;
    params [1].name = "actFunc";   params [1].val  = actFunc;
    params [2].name = "dispScale"; params [2].val  = dispScale;
    params [3].name = "eliteProb"; params [3].val  = eliteProb;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    actFunc   = (int)params [1].val;
    dispScale = params      [2].val;
    eliteProb = params      [3].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum values
             const double &rangeMaxP  [],  // maximum values
             const double &rangeStepP [],  // step change
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    actFunc;   // neuron activation function
  double dispScale; // scale of movements
  double eliteProb; // probability of copying elite coordinates

  private: //-------------------------------------------------------------------
  C_MLPa nn [];

  void ScaleInp (double &inp [], double &out []);
  void ScaleOut (double &inp [], double &out []);
};
//——————————————————————————————————————————————————————————————————————————————

O método Init é projetado para inicializar uma instância da classe "C_AO_NOA". Ele recebe um conjunto de parâmetros que definem os intervalos de valores e o número de épocas, executando as operações necessárias para configurar o algoritmo.

Assinatura do método: indica o sucesso da inicialização. Parâmetros:

• MinP[] — valores mínimos para os parâmetros.
• MaxP[] — valores máximos para os parâmetros.
• StepP[] — passo de variação dos parâmetros.
• epochsP — número de épocas.

Inicialização padrão: a primeira linha do método chama a função "StandardInit" com os intervalos fornecidos.

Configuração da rede neural:

• É criado o array "nnConf", que contém os tamanhos das camadas de entrada e saída da rede neural.
• Em seguida, é chamada a função "ArrayResize" para ajustar o tamanho do array "nnConf" para 2 (camada de entrada e camada de saída).
• Ambos os elementos do array são inicializados com o valor "coords", que corresponde à dimensionalidade dos dados de entrada.

Declaração do enumerador E_Act: é criado um enumerador que define as diferentes funções de ativação dos neurônios (eActTanh, eActAlgSigm, eActRatSigm, etc.).

Reserva do array de redes neurais: o tamanho do array "nn" (conjunto de redes neurais) é ajustado para "popSize", valor previamente definido no construtor.

Inicialização das redes neurais:

• A variável "cnt" é inicializada com zero e usada para gerar uma semente aleatória (seed) única para a inicialização de cada rede neural, garantindo que os pesos sejam inicializados de forma independente em todas as redes.
• No laço "for", ocorre a inicialização de cada rede neural. O método "nn[i].Init()" é chamado com a configuração "nnConf", a função de ativação "actFunc" e a semente baseada no valor atual de "cnt" combinado com o número de milissegundos decorridos desde o início do sistema.
• O valor de "cnt" é incrementado a cada iteração, assegurando a geração de sementes exclusivas para cada inicialização.

Retorno do resultado: se todas as operações forem concluídas com sucesso, o método retorna "true", indicando que a inicialização foi realizada corretamente.

O método "Init" da classe "C_AO_NOA" é um componente essencial na configuração do algoritmo de otimização, responsável pela correta inicialização das redes neurais e dos parâmetros associados. 

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_NOA::Init (const double &rangeMinP  [], // minimum values
                     const double &rangeMaxP  [], // maximum values
                     const double &rangeStepP [], // step change
                     const int     epochsP = 0)   // number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  int nnConf [];
  ArrayResize (nnConf, 2);
  nnConf [0] = coords;
  nnConf [1] = coords;

  enum E_Act
  {
    eActTanh,      //0
    eActAlgSigm,   //1
    eActRatSigm,   //2

    eActSoftPlus,  //3
    eActBentIdent, //4
    eActSiLU,      //5

    eActACON,      //6
    eActSERF,      //7
    eActSnake      //8
  };

  ArrayResize (nn, popSize);
  int cnt = 0;
  for (int i = 0; i < popSize; i++)
  {
    nn [i].Init (nnConf, actFunc, (int)GetTickCount64 () + cnt);
    cnt++;
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

O método "Moving()" implementa o processo de deslocamento dos indivíduos na população dentro do algoritmo de otimização por neuroboides. Vamos analisá-lo por etapas:

Inicialização dos valores iniciais: se "revision" for igual a "false", o método realiza a primeira inicialização. Para cada elemento da população "popSize" e para cada dimensão "coords", o método define os valores iniciais no array "a[i].c[c]", que representa os agentes de busca:

• u.RNDfromCI() — gera um valor aleatório dentro do intervalo "rangeMin[c]" e "rangeMax[c]".
• u.SeInDiSp() — função que utiliza o passo de variação para ajustar o valor de "a[i].c[c]" dentro do intervalo permitido.
• Após a conclusão da inicialização, a variável "revision" é definida como "true" e o controle retorna do método. 

Atualização das coordenadas: ocorre a atualização das coordenadas dos indivíduos com base na probabilidade de elitismo. Para os primeiros "popSize - 5" elementos da população, é realizada uma verificação aleatória, e, se o número gerado for menor que "eliteProb", as coordenadas "a[i].c[c]" são definidas iguais às coordenadas da elite "cB[c]".

Processamento dos dados da rede neural: são criados arrays para os dados de entrada, saída, valores-alvo e erros, dimensionados de acordo com "coords". Para cada elemento da população:

• ScaleInp() — escala as coordenadas do alvo "cB" e as armazena em "targVal".
• ScaleInp() — escala a coordenada atual da população e a armazena em "inpData".
• nn[i].ForwProp() — executa a propagação para frente na rede neural para obter os dados de saída.
• Calcula-se o erro (diferença entre o valor alvo e o valor obtido) para cada coordenada.
• nn[i].BackProp(err) — realiza a propagação reversa do erro para ajustar os pesos.
• A atualização das coordenadas "a[i].c[c]" é feita considerando a saída da rede neural, o fator de escala e um elemento aleatório da amostragem.
• No final, o valor de "a[i].c[c]" é normalizado pela função "u.SeInDiSp".

Dessa forma, o método "Moving()" é responsável pelo deslocamento dos indivíduos no modelo, inicializando-os no início e atualizando suas posições com base nas saídas das redes neurais e na seleção probabilística. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    // Initialize the initial values of anchors in all parallel universes
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd  = 0.0;
  double val  = 0.0;
  int    pair = 0.0;

  for (int i = 0; i < popSize - 5; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < eliteProb)
      {
        a [i].c [c] = cB [c];
      }
    }
  }

  double inpData []; ArrayResize (inpData, coords);
  double outData []; ArrayResize (outData, coords);
  double targVal []; ArrayResize (targVal, coords);
  double err     []; ArrayResize (err,     coords);

  for (int i = 0; i < popSize; i++)
  {
    ScaleInp (cB,      targVal);
    ScaleInp (a [i].c, inpData);

    nn [i].ForwProp (inpData, outData);

    for (int c = 0; c < coords; c++) err [c] = targVal [c] - outData [c];

    nn [i].BackProp (err);

    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] += outData [c] * (rangeMax [c] - rangeMin [c]) * dispScale * u.RNDprobab ();
      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

A seguir, analisamos o método "Revision", que executa a avaliação e atualização da melhor solução atual dentro da população. Ele compara os valores da função objetivo de cada indivíduo com o valor atualmente considerado o melhor e o atualiza caso encontre um resultado superior. Assim, o método garante a manutenção contínua da melhor solução encontrada durante o processo de otimização. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::Revision ()
{
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "ScaleInp" é responsável por escalonar os dados de entrada do intervalo definido por "rangeMin" e "rangeMax" para o intervalo de -1 a 1. Cada valor "inp[c]" é ajustado utilizando a função "u.Scale", que realiza um escalonamento linear, convertendo o valor para o intervalo de -1 a 1. O método "ScaleInp" prepara os dados para os cálculos subsequentes, garantindo sua normalização dentro da faixa adequada.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::ScaleInp (double &inp [], double &out [])
{
  for (int c = 0; c < coords; c++) out [c] = u.Scale (inp [c], rangeMin [c], rangeMax [c], -1, 1);
}
//——————————————————————————————————————————————————————————————————————————————

De forma análoga ao "ScaleInp", o método "ScaleOut" realiza o escalonamento inverso, convertendo os valores do intervalo de -1 a 1 de volta para o intervalo definido por "rangeMin" e "rangeMax".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::ScaleOut (double &inp [], double &out [])
{
  for (int c = 0; c < coords; c++) out [c] = u.Scale (inp [c], -1, 1, rangeMin [c], rangeMax [c]);
}
//——————————————————————————————————————————————————————————————————————————————

Resultados dos testes

O algoritmo apresentou resultados interessantes em funções com baixa e média dimensionalidade. Quando a dimensionalidade do problema foi aumentada para 1000 variáveis, o tempo de cálculo tornou-se excessivamente longo, razão pela qual esses testes não foram incluídos. O desempenho alcançou aproximadamente 45% (em 6 dos 9 testes) do valor ótimo nas avaliações.

NOA|Neuroboids Optimization Algorithm (joo)|50.0|0.0|0.01|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.7013521128826248
25 Hilly's; Func runs: 10000; result: 0.40128968110640306
=============================
5 Forest's; Func runs: 10000; result: 0.6222984295200933
25 Forest's; Func runs: 10000; result: 0.30830340651626337
=============================
5 Megacity's; Func runs: 10000; result: 0.4523076923076924
25 Megacity's; Func runs: 10000; result: 0.20892307692307693
=============================
All score: 2.69447 (44.91%)

Vale destacar alguns aspectos da visualização do funcionamento do algoritmo NOA. É possível observar que o algoritmo forma estruturas em forma de leque bastante peculiares. Na essência, essas estruturas representam a visualização dos resultados produzidos pelas redes neurais dos neuroboides. 

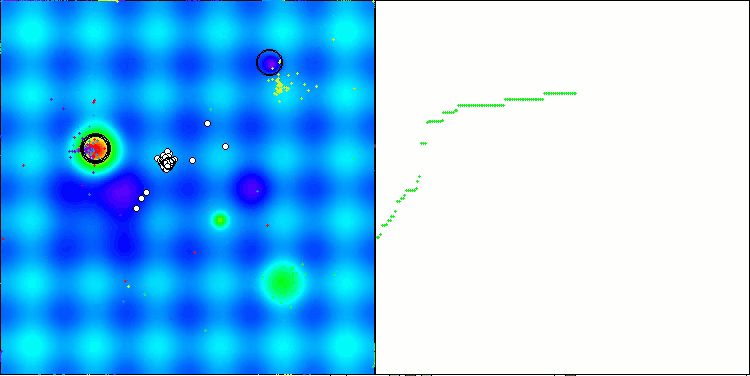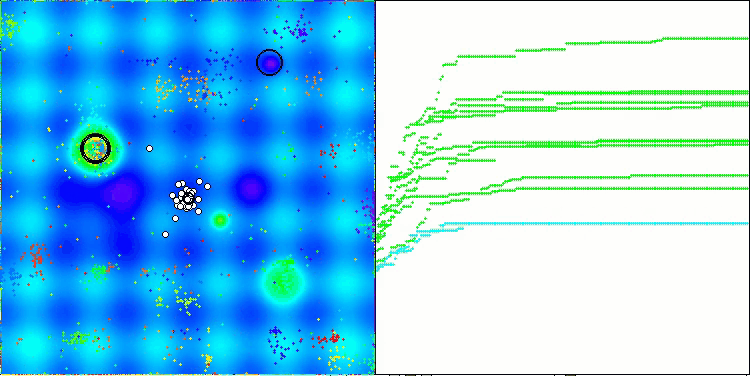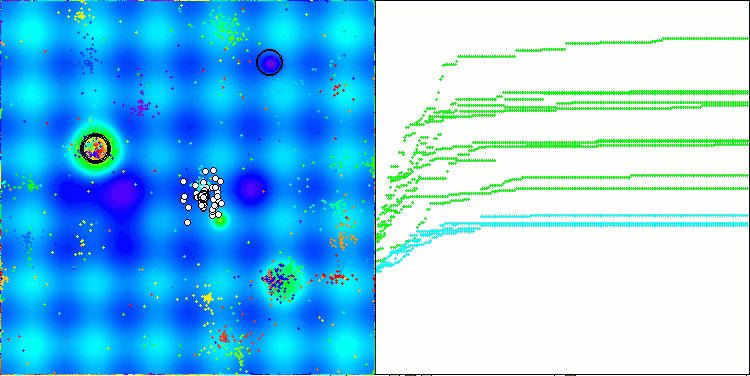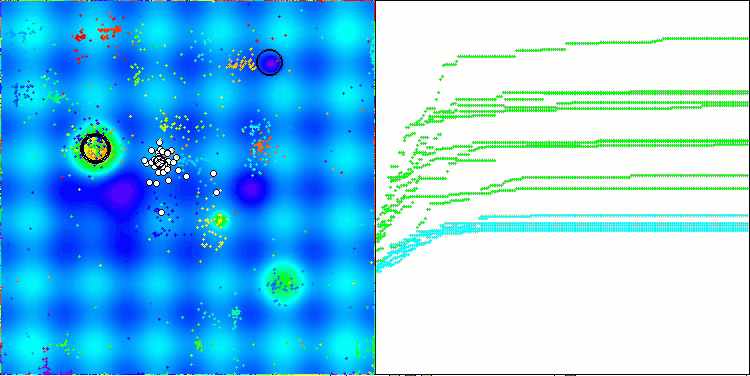
NOA na função de teste Hilly

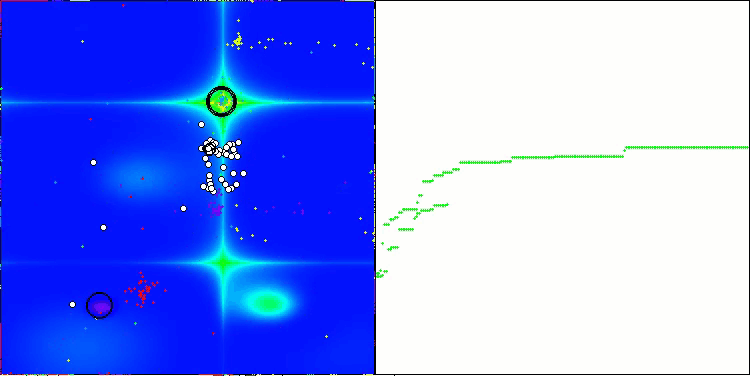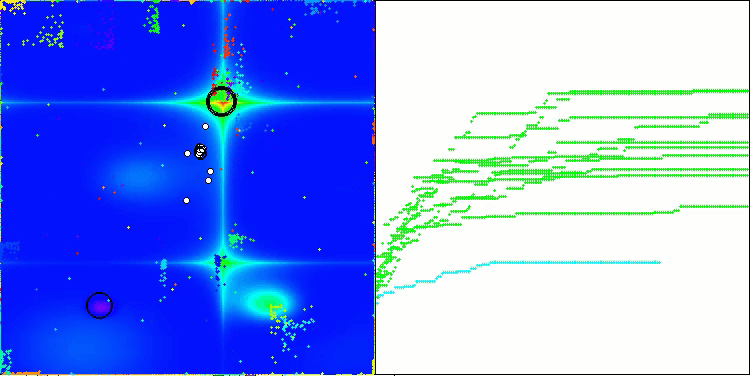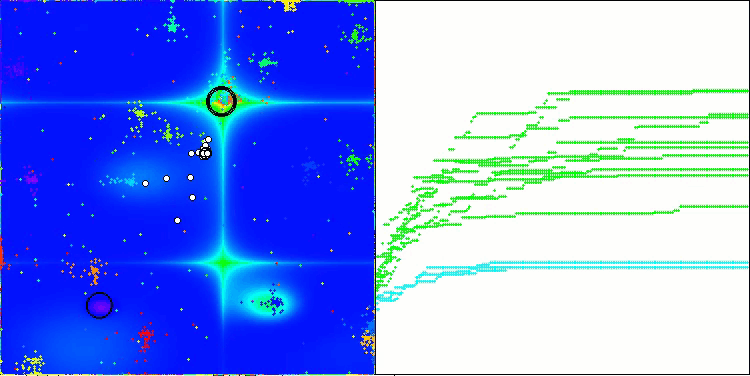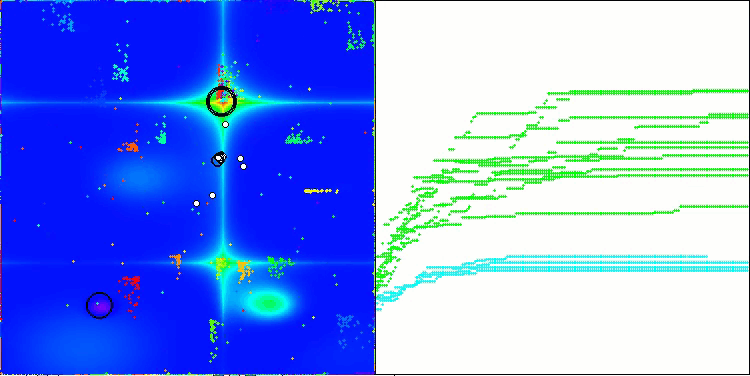
NOA na função de teste Forest

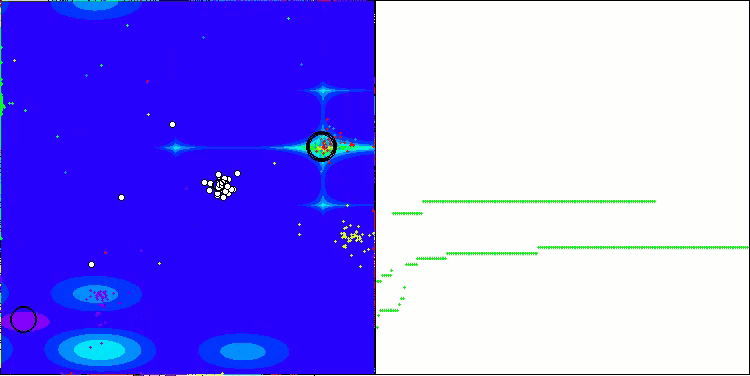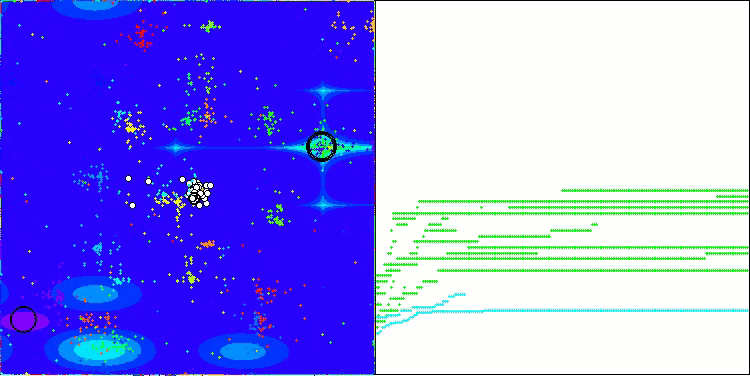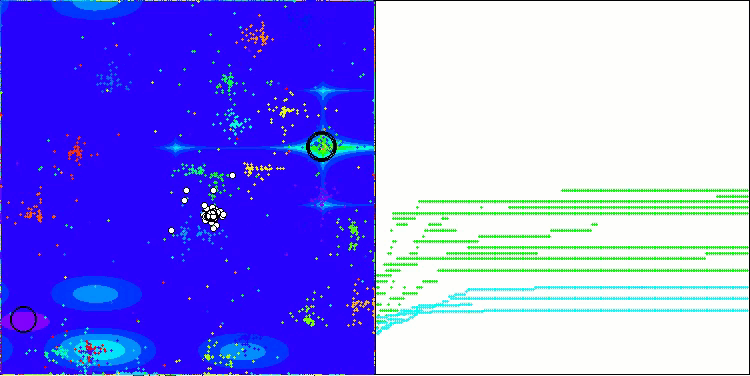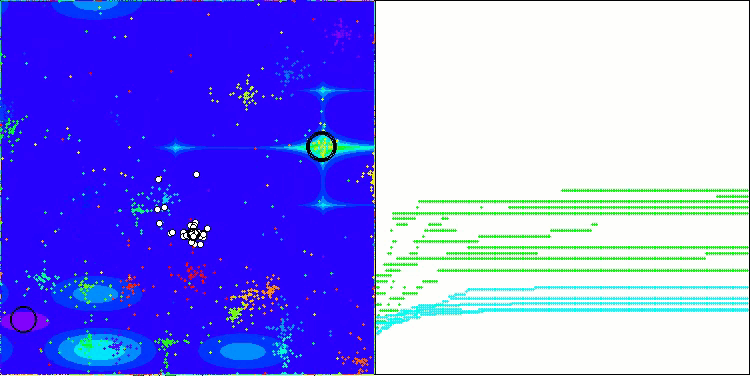
NOA na função de teste Megacity

Após os testes realizados, o algoritmo NOA foi colocado em uma linha separada (sem número de ordem), pois não foram obtidos resultados de testes em funções de alta dimensionalidade. As tabelas apresentadas abaixo servem para a análise comparativa dos resultados com os demais algoritmos participantes da tabela de classificação.

#	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	code lock algorithm (joo)	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	animal migration ptimization M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O) evolution strategies	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	comet tail algorithm (joo)	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	TETA	time evolution travel algorithm (joo)	0.91362	0.82349	0.31990	2.05701	0.97096	0.89532	0.29324	2.15952	0.73462	0.68569	0.16021	1.58052	5.797	64.41
7	SDSm	stochastic diffusion search M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
8	BOAm	billiards optimization algorithm M	0.95757	0.82599	0.25235	2.03590	1.00000	0.90036	0.30502	2.20538	0.73538	0.52523	0.09563	1.35625	5.598	62.19
9	AAm	archery algorithm M	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
10	ESG	evolution of social groups (joo)	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
11	SIA	simulated isotropic annealing (joo)	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
12	ACS	artificial cooperative search	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
13	DA	dialectical algorithm	0.86183	0.70033	0.33724	1.89940	0.98163	0.72772	0.28718	1.99653	0.70308	0.45292	0.16367	1.31967	5.216	57.95
14	BHAm	black hole algorithm M	0.75236	0.76675	0.34583	1.86493	0.93593	0.80152	0.27177	2.00923	0.65077	0.51646	0.15472	1.32195	5.196	57.73
15	ASO	anarchy society optimization	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
16	RFO	royal flush optimization (joo)	0.83361	0.73742	0.34629	1.91733	0.89424	0.73824	0.24098	1.87346	0.63154	0.50292	0.16421	1.29867	5.089	56.55
17	AOSm	atomic orbital search M	0.80232	0.70449	0.31021	1.81702	0.85660	0.69451	0.21996	1.77107	0.74615	0.52862	0.14358	1.41835	5.006	55.63
18	TSEA	turtle shell evolution algorithm (joo)	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
19	DE	differential evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
20	SRA	successful restaurateur algorithm (joo)	0.96883	0.63455	0.29217	1.89555	0.94637	0.55506	0.19124	1.69267	0.74923	0.44031	0.12526	1.31480	4.903	54.48
21	CRO	chemical reaction optimization	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
22	BIO	blood inheritance optimization (joo)	0.81568	0.65336	0.30877	1.77781	0.89937	0.65319	0.21760	1.77016	0.67846	0.47631	0.13902	1.29378	4.842	53.80
23	BSA	bird swarm algorithm	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
24	HS	harmony search	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
25	SSG	saplings sowing and growing	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
26	BCOm	bacterial chemotaxis optimization M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
27	ABO	african buffalo optimization	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
28	(PO)ES	(PO) evolution strategies	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
29	TSm	tabu search M	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
30	BSO	brain storm optimization	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
31	WOAm	wale optimization algorithm M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
32	AEFA	artificial electric field algorithm	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
33	AEO	artificial ecosystem-based optimization algorithm	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
34	ACOm	ant colony optimization M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
35	BFO-GA	bacterial foraging optimization - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
36	SOA	simple optimization algorithm	0.91520	0.46976	0.27089	1.65585	0.89675	0.37401	0.16984	1.44060	0.69538	0.28031	0.10852	1.08422	4.181	46.45
37	ABHA	artificial bee hive algorithm	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
38	ACMO	atmospheric cloud model optimization	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
39	ADAMm	adaptive moment estimation M	0.88635	0.44766	0.26613	1.60014	0.84497	0.38493	0.16889	1.39880	0.66154	0.27046	0.10594	1.03794	4.037	44.85
40	CGO	chaos game optimization	0.57256	0.37158	0.32018	1.26432	0.61176	0.61931	0.62161	1.85267	0.37538	0.21923	0.19028	0.78490	3.902	43.35
41	ATAm	artificial tribe algorithm M	0.71771	0.55304	0.25235	1.52310	0.82491	0.55904	0.20473	1.58867	0.44000	0.18615	0.09411	0.72026	3.832	42.58
42	ASHA	artificial showering algorithm	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
43	ASBO	adaptive social behavior optimization	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
44	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
45	CSA	circle search algorithm	0.66560	0.45317	0.29126	1.41003	0.68797	0.41397	0.20525	1.30719	0.37538	0.23631	0.10646	0.71815	3.435	38.17
	NOA	neuroboids optimization algorithm (joo)	0.70135	0.40129	0.00000	1.10264	0.62230	0.30830	0.00000	0.93060	0.45231	0.20892	0.00000	0.66123	2.694	29.94
	RW	random walk	0.48754	0.32159	0.25781	1.06694	0.37554	0.21944	0.15877	0.75375	0.27969	0.14917	0.09847	0.52734	2.348	26.09

 

Considerações finais

Ao criar o NOA, procurei unir dois mundos: as redes neurais e os algoritmos de otimização. O resultado foi, ao mesmo tempo, previsível e surpreendente.

O que mais me inspira neste algoritmo é sua plausibilidade biológica. Frequentemente tentamos construir modelos complexos, quando a natureza já demonstra há milhões de anos soluções eficientes por meio da inteligência coletiva de organismos simples. Os neuroboides são uma tentativa de traduzir essa sabedoria natural em forma algorítmica.

Os testes realizados em diferentes funções mostraram resultados promissores. Uma eficiência de cerca de 45% é um começo respeitável para uma abordagem conceitualmente nova. Percebo que o algoritmo se sai muito bem em tarefas de complexidade moderada. No entanto, há limitações significativas. Os problemas de escalabilidade se tornam críticos em casos de alta dimensionalidade. Com mil variáveis, a carga computacional se torna impraticável, consequência do treinamento simultâneo de múltiplas redes neurais, um processo naturalmente exigente em termos de recursos.

O que mais me fascina no NOA é sua capacidade de aprender autonomamente estratégias de busca. Diferente das metaheurísticas clássicas, baseadas em regras fixas, os neuroboides ajustam seu comportamento por meio do aprendizado.

A variabilidade dos resultados entre as execuções, que observei durante os testes, tem uma natureza dupla. De um lado, representa uma falta de previsibilidade. De outro, indica diversidade nas estratégias de exploração, o que pode ser uma vantagem em paisagens de otimização complexas.

Vejo alguns caminhos promissores para o desenvolvimento futuro do algoritmo NOA:

1. Otimização da arquitetura das redes neurais para reduzir a carga computacional.
2. Implementação de mecanismos de transferência de conhecimento entre neuroboides.

Em última análise, o NOA não é apenas mais um método de otimização. É um passo em direção à compreensão de como sistemas simples podem gerar comportamentos complexos. É um estudo na fronteira entre aprendizado de máquina e otimização metaheurística, entre o aprendizado individual e a inteligência coletiva.

Acredito que essa abordagem tem potencial não apenas para a otimização de funções, mas também para áreas mais amplas, como o modelamento de comportamentos adaptativos e a busca por novas arquiteturas de inteligência artificial. Num mundo em que a complexidade se torna o padrão, a simplicidade, quando bem estruturada, pode oferecer soluções surpreendentemente eficazes.

De modo geral, o algoritmo NOA deve ser visto não como uma solução final para problemas de otimização, mas como uma plataforma básica e um ponto de partida para diversas linhas de pesquisa e desenvolvimento de soluções promissoras, tanto no campo da otimização quanto no aprendizado de máquina.

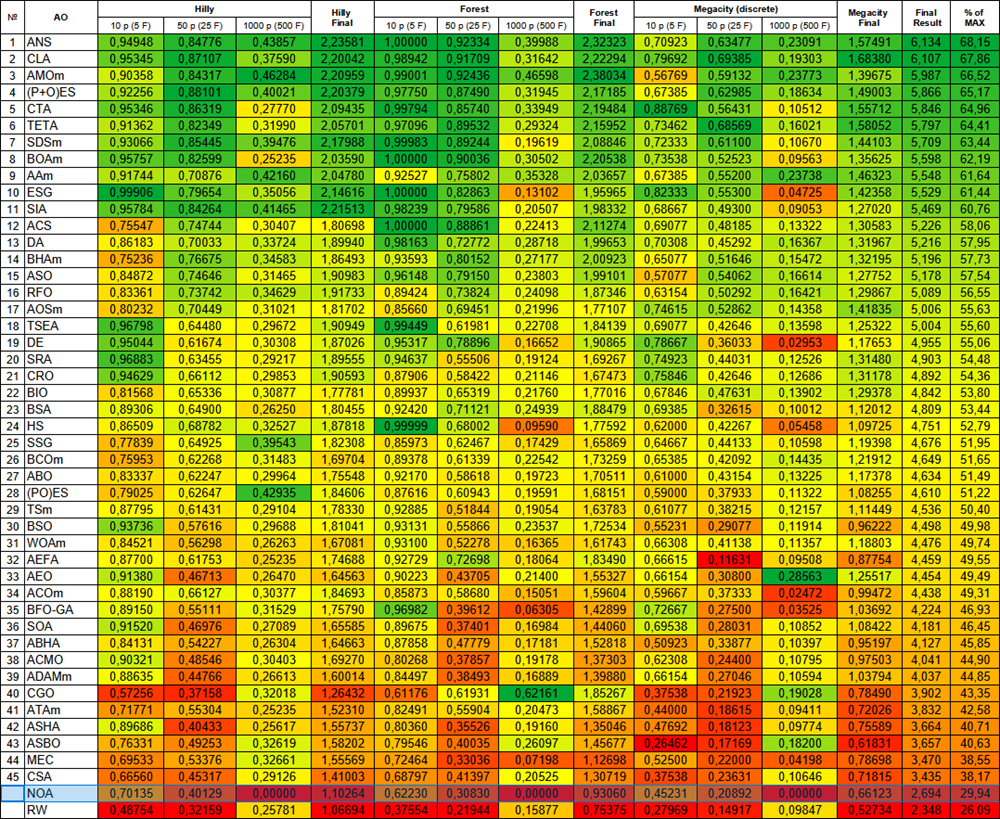
Figura 2. Gradação de cores dos algoritmos nos testes correspondentes

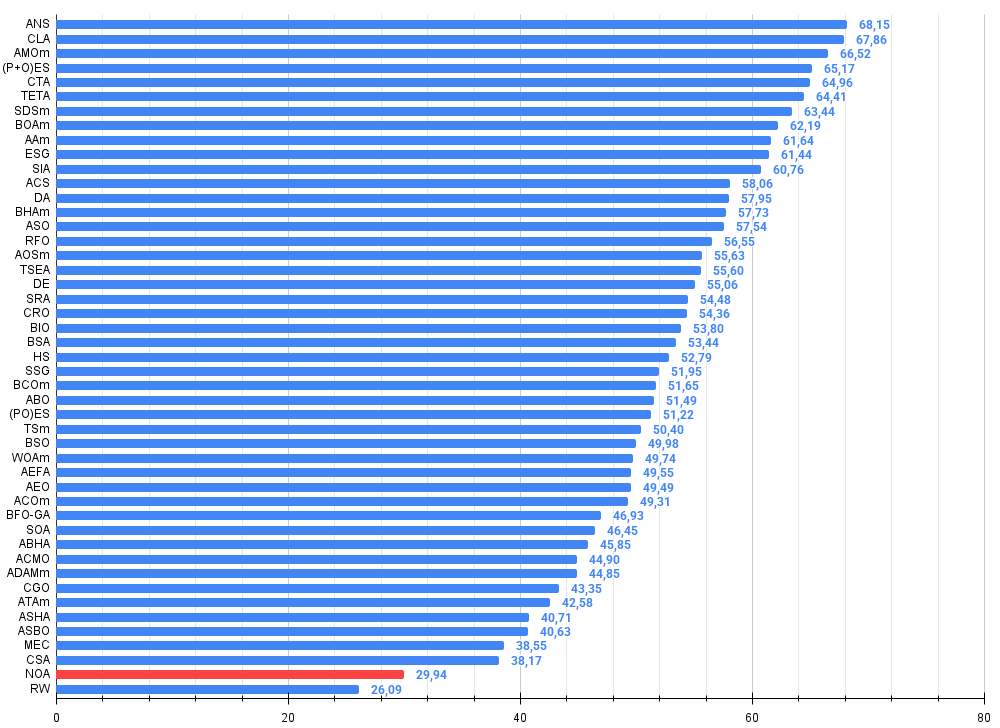
Figura 3. Histograma dos resultados dos testes dos algoritmos (na escala de 0 a 100, quanto maior melhor, onde 100 — o resultado teórico máximo possível, no arquivo o script para cálculo da tabela de classificação)

Vantagens e desvantagens do algoritmo NOA:

Vantagens:

1. Implementação simples.
   
2. Resultados interessantes.

Desvantagens:

1. Devido ao longo tempo de execução, não foram obtidos resultados para espaços de alta dimensionalidade.
   

O artigo inclui um arquivo compactado com as versões atuais dos códigos dos algoritmos. O autor não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, já que muitos deles foram modificados para aprimorar suas capacidades de busca. As conclusões e observações apresentadas baseiam-se nos resultados experimentais obtidos.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	C_AO.mqh	Arquivo incluído	Classe base dos algoritmos populacionais de otimização
2	C_AO_enum.mqh	Arquivo incluído	Enumeração dos algoritmos populacionais de otimização
3	MLPa.mqh	Arquivo incluído	Rede neural MLP com ADAM
4	TestFunctions.mqh	Arquivo incluído	Biblioteca de funções de teste
5	TestStandFunctions.mqh	Arquivo incluído	Biblioteca de funções do ambiente de testes
6	Utilities.mqh	Arquivo incluído	Biblioteca de funções auxiliares
7	CalculationTestResults.mqh	Arquivo incluído	Script para cálculo dos resultados e compilação em tabela comparativa
8	Testing AOs.mq5	Script	Ambiente de testes unificado para todos os algoritmos populacionais de otimização
9	Simple use of population optimization algorithms.mq5	Script	Exemplo simples de uso dos algoritmos populacionais de otimização sem visualização
10	Test_AO_NOA.mq5	Script	Ambiente de testes dedicado ao NOA