Visualizza questo! Libreria grafica di MQL5 simile a 'plot' del linguaggio R
Quando si studia la logica del trading, la rappresentazione visiva sotto forma di grafici è di grande importanza. Alcuni linguaggi di programmazione popolari tra la comunità scientifica (come R e Python) dispongono della speciale funzione "plot" utilizzata per la visualizzazione. Permette di disegnare linee, distribuzioni di punti e istogrammi per visualizzare i modelli.
L'importante vantaggio della funzione 'plot' è che bastano poche righe di codice per tracciare qualsiasi grafico. È sufficiente passare l'array di dati come parametro, specificare il tipo di grafico e il gioco è fatto! La funzione 'plot' esegue tutte le operazioni di routine come il calcolo della scala, la costruzione degli assi, la selezione del colore, ecc.
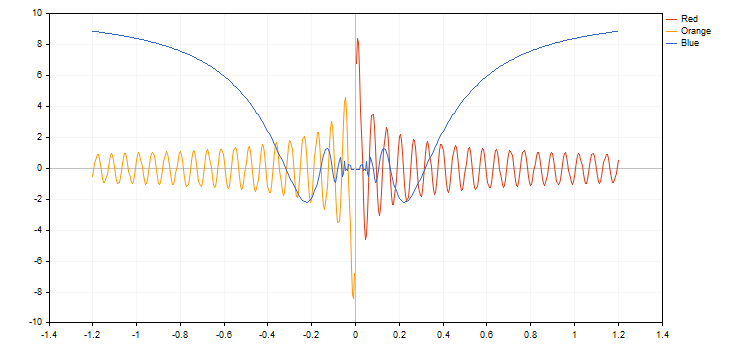
In MQL5, tutte le caratteristiche della funzione sono rappresentate dal metodo della libreria grafica della Standard Library. Di seguito sono riportati il codice di esempio e il risultato della sua esecuzione:
#define RESULT_OR_NAN(x,expression) ((x==0)?(double)"nan":expression)
//--- Funzioni
double BlueFunction(double x) { return(RESULT_OR_NAN(x,10*x*sin(1/x))); }
double RedFunction(double x) { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(x))); }
double OrangeFunction(double x) { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(-x))); }
//+------------------------------------------------------------------+
//| Funzione di avvio del programma Script |
//+------------------------------------------------------------------+
void OnStart()
{
double from=-1.2;
double to=1.2;
double step=0.005;
CGraphic graphic;
graphic.Create(0,"G",0,30,30,780,380);
//--- colori
CColorGenerator generator;
uint blue= generator.Next();
uint red = generator.Next();
uint orange = generator.Next();
//--- traccia tutte le curve
graphic.CurveAdd(RedFunction,from,to,step,red,CURVE_LINES,"Red");
graphic.CurveAdd(OrangeFunction,from,to,step,orange,CURVE_LINES,"Orange");
graphic.CurveAdd(BlueFunction,from,to,step,blue,CURVE_LINES,"Blue");
graphic.CurvePlotAll();
graphic.Update();
}
La classe base CCanvas e il suo sviluppo
La libreria standard contiene la classe di base CCanvas, progettata per tracciare in modo rapido e comodo le immagini direttamente sui grafici dei prezzi. La classe si basa sulla creazione di una risorsa grafica e sul tracciamento di semplici primitivi (punti, linee rette e polilinee, cerchi, triangoli e poligoni) sull’area di lavoro. La classe implementa le funzioni per il riempimento delle forme e la visualizzazione del testo utilizzando il carattere, il colore e la dimensione necessari.
Inizialmente, CCanvas conteneva solo due modalità di visualizzazione delle primitive grafiche — con antialiasing (AA) e senza antialiasing. Poi sono state aggiunte le nuove funzioni per il tracciamento delle primitive basate sull’algoritmo di Wu:
- LineWu — linea retta
- PolylineWu — polilinea
- PolygonWu — poligono
- TriangleWu — triangolo
- CircleWu — cerchio
- EllipseWu — ellisse
L'algoritmo di Wu combina l'eliminazione dell'aliasing di alta qualità con una velocità di funzionamento vicina a quella dell' algoritmo di Bresenham senza anti-aliasing. Inoltre, differisce visivamente dall'algoritmo di anti-aliasing standard (AA) implementato in CCanvas. Di seguito è riportato un esempio del tracciamento di una circonferenza utilizzando tre diverse funzioni:
CCanvas canvas;
//+------------------------------------------------------------------+
//| Funzione di avvio del programma Script |
//+------------------------------------------------------------------+
void OnStart()
{
int Width=800;
int Height=600;
//--- creazione area di lavoro
if(!canvas.CreateBitmapLabel(0,0,"CirclesCanvas",30,30,Width,Height))
{
Print("Errore nella creazione del canvas: ",GetLastError());
}
//--- Disegnare
canvas.Erase(clrWhite);
canvas.Circle(70,70,25,clrBlack);
canvas.CircleAA(120,70,25,clrBlack);
canvas.CircleWu(170,70,25,clrBlack);
//---
canvas.Update();
}
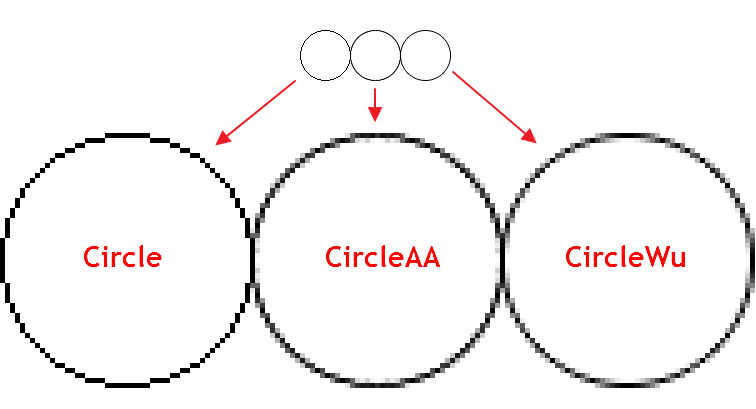
Come si può notare, CircleAA() con l'algoritmo di smoothing standard traccia una linea più spessa rispetto alla funzione CircleWu() secondo l'algoritmo di Wu. Grazie allo spessore ridotto e al miglior calcolo delle tonalità di transizione, CircleWu appare più ordinato e naturale.
Ci sono anche altri miglioramenti nella classe CCanvas:
- Aggiunta la nuova primitiva ellisse con due opzioni di anti-aliasing — EllipseAA() e EllipseWu()
- Aggiunto il sovraccarico della funzione dell’area di riempimento con il nuovo parametro responsabile della "sensibilità di riempimento" (il parametro threshould).
L'algoritmo per lavorare con la libreria
1. Dopo aver collegato la libreria, dobbiamo creare l'oggetto della classe CGraphic. Le curve da disegnare verranno aggiunte ad esso.
Successivamente, occorre richiamare il metodo Create() per l'oggetto creato. Il metodo contiene i parametri principali del grafico:
- ID del grafico
- Nome dell’oggetto
- Indice della finestra
- Punto di ancoraggio del grafico
- Larghezza e altezza del grafico
Il metodo applica i parametri definiti per creare un oggetto grafico e una risorsa grafica da utilizzare per tracciare un grafico.
CGraphic graphic;
//--- creazione area di lavoro
graphic.Create(0,"Graphic",0,30,30,830,430);
Come risultato, abbiamo un’area già pronta.
2. Ora, riempiamo il nostro oggetto con le curve. L'aggiunta viene eseguita con il metodo CurveAdd() che consente di tracciare le curve in quattro modi diversi:
- Basato sull'array monodimensionale di tipo double. In questo caso, i valori dell’array vengono visualizzati sull'asse Y, mentre gli indici dell’array fungono da coordinate X.
- Basato su due array di tipo double x[] e y[].
- Basato sull’array CPoint2D.
- Basato sul puntatore CurveFunction() e tre valori per costruire gli argomenti della funzione: initial, final e increment per argomento.
Il metodo CurveAdd() restituisce il puntatore alla classe CCurve, consentendo un accesso rapido alla curva appena creata e la possibilità di modificarne le proprietà.
double y[]={-5,4,-10,23,17,18,-9,13,17,4};
CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);3. Tutte le curve aggiunte possono poi essere visualizzate sul grafico. Questo può essere fatto in tre modi.
- Utilizzando il metodo CurvePlotAll() che disegna automaticamente tutte le curve aggiunte al grafico. graphic.CurvePlotAll();
- Utilizzando il metodo CurvePlot() che disegna una curva in base all'indice specificato. graphic.CurvePlot(0);
- Utilizzando il metodo Redraw() e impostando la proprietà Visible della curva su 'true'. curve.Visible(true);
graphic.Redraw();
4. Per tracciare un grafico sul grafico, richiamare il metodo Update(). Di conseguenza, si ottiene l'intero codice dello script per tracciare un semplice grafico:
//+------------------------------------------------------------------+
//| Funzione di avvio del programma Script |
//+------------------------------------------------------------------+
void OnStart()
{
CGraphic graphic;
graphic.Create(0,"Graphic",0,30,30,780,380);
double x[]={-10,-4,-1,2,3,4,5,6,7,8};
double y[]={-5,4,-10,23,17,18,-9,13,17,4};
CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
graphic.CurvePlotAll();
graphic.Update();
}
Di seguito è riportato il grafico risultante:
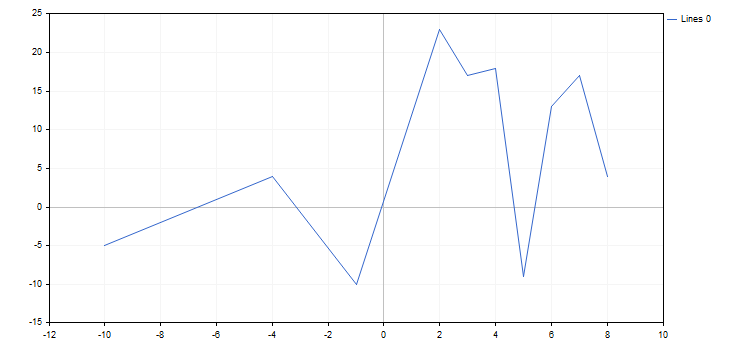
Le proprietà del grafico e di qualsiasi sua funzione possono essere modificate in qualsiasi momento. Ad esempio, è possibile aggiungere etichette agli assi del grafico, modificare il nome della curva e attivare la modalità di approssimazione spline:
//+------------------------------------------------------------------+
//| Funzione di avvio del programma Script |
//+------------------------------------------------------------------+
void OnStart()
{
CGraphic graphic;
graphic.Create(0,"Graphic",0,30,30,780,380);
double x[]={-10,-4,-1,2,3,4,5,6,7,8};
double y[]={-5,4,-10,23,17,18,-9,13,17,4};
CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
curve.Name("Example");
curve.LinesIsSmooth(true);
graphic.XAxis().Name("X - axis");
graphic.XAxis().NameSize(12);
graphic.YAxis().Name("Y - axis");
graphic.YAxis().NameSize(12);
graphic.YAxis().ValuesWidth(15);
graphic.CurvePlotAll();
graphic.Update();
DebugBreak();
}
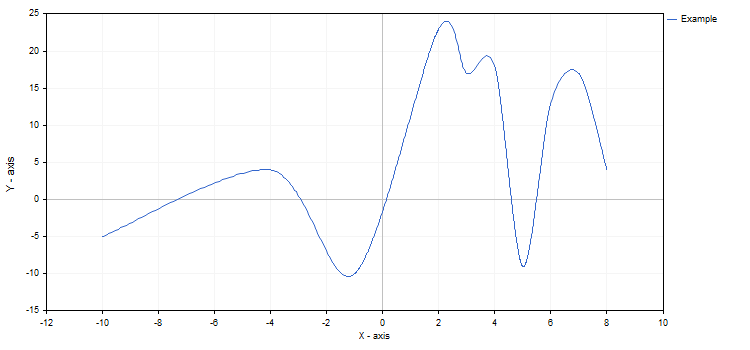
Se le modifiche fossero state impostate dopo aver chiamato CurvePlotAll, avremmo dovuto chiamare anche il metodo Redraw per vederle.
Come molte librerie moderne, Graphics contiene vari algoritmi già pronti che semplificano notevolmente il tracciamento dei grafici:
- La libreria è in grado di generare automaticamente colori contrastanti delle curve se non sono specificati esplicitamente.
- Gli assi del grafico sono dotati di una modalità di scalatura parametrica automatica che può essere disabilitata se necessario.
- I nomi delle curve vengono generati automaticamente in base al loro tipo e all'ordine di aggiunta.
- L'area di lavoro del grafico viene allineata automaticamente e vengono impostati gli assi reali.
- È possibile smussare le curve quando si utilizzano le linee.
La libreria Graphics dispone anche di alcuni metodi aggiuntivi per aggiungere nuovi elementi al grafico:
- TextAdd() — aggiunge un testo in una posizione arbitraria del grafico. Le coordinate devono essere impostate in scala reale. Utilizzare il metodo FontSet per configurare con precisione il testo visualizzato.
- LineAdd() — aggiunge una linea in una posizione arbitraria del grafico. Le coordinate devono essere impostate in scala reale.
- MarksToAxisAdd() - aggiunge nuove etichette alle coordinate di un asse specificato.
I dati sull'aggiunta degli elementi non vengono memorizzati da nessuna parte. Dopo aver tracciato una nuova curva sul grafico o averne ridisegnata una precedente, scompaiono.
Tipi di grafico
La libreria Graphics supporta i tipi di base di tracciatura delle curve. Tutti sono specificati nell'enumerazione ENUM_CURVE_TYPE:
- CURVE_POINTS — disegna una curva puntiforme
- CURVE_LINES — disegna una linea curva
- CURVE_POINTS_AND_LINES — disegna curve di punti e di linee
- CURVE_STEPS — disegna una curva a gradini
- CURVE_HISTOGRAM — disegna una curva dell'istogramma
- CURVE_NONE — non disegna una curva
Ciascuna di queste modalità ha le proprie proprietà che influenzano la visualizzazione di una curva sul grafico. Il puntatore a una curva CCurve consente di modificare rapidamente queste proprietà. Pertanto, si raccomanda di ricordare tutti i puntatori restituiti dal metodo CurveAdd. Il nome di una proprietà inizia sempre con la modalità di disegno della curva in cui viene utilizzata.
Vediamo nel dettaglio le proprietà di ciascun tipo.
1. CURVE_POINTS è la modalità più semplice e veloce. Ogni coordinata della curva viene visualizzata come un punto con le proprietà specificate:
- PointsSize - dimensione del punto
- PointsFill - flag che indica se il riempimento è presente
- PointsColor - colore di riempimento
- PointsType - tipo di punti
In questo caso, il colore della curva stessa definisce il colore dei bordi dei punti.
curve.PointsSize(20);
curve.PointsFill(true);
curve.PointsColor(ColorToARGB(clrRed,255));
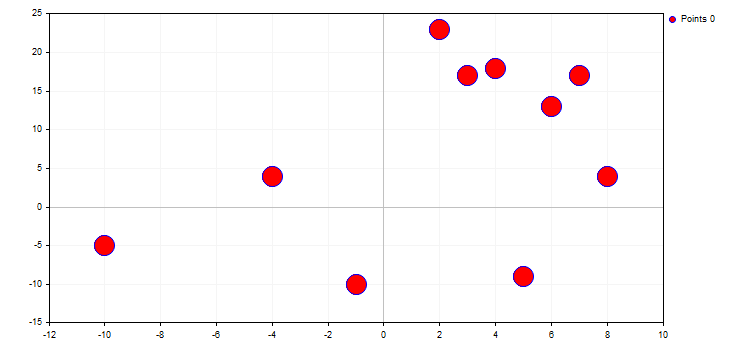
Il tipo di punti definisce una determinata forma geometrica dall'enumerazione ENUM_POINT_TYPE. Questa forma deve essere utilizzata per visualizzare tutti i punti della curva. In totale, ENUM_POINT_TYPE comprende dieci forme geometriche principali:
- POINT_CIRCLE - cerchio (usato per impostazione predefinita)
- POINT_SQUARE — quadrato
- POINT_DIAMOND — rombo
- PUNTO_TRIANGOLO — triangolo
- POINT_TRIANGLE_DOWN — triangolo invertito
- PUNTO_X_CROSS — croce
- POINT_PLUS — più
- POINT_STAR — stella
- POINT_HORIZONTAL_DASH — linea orizzontale
- POINT_VERTICAL_DASH — linea verticale
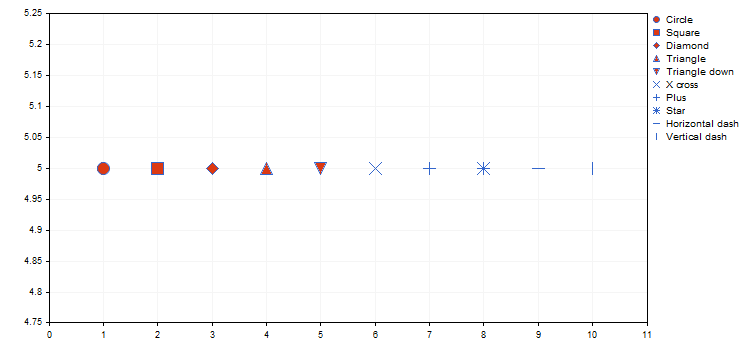
Sotto è riportato un esempio di rappresentazione visiva di diversi tipi di iride (vedi l'articolo “Utilizzo di feature map auto-organizzanti (mappe Kohonen) in MetaTrader 5) dallo script IrisSample.mq5allegato.
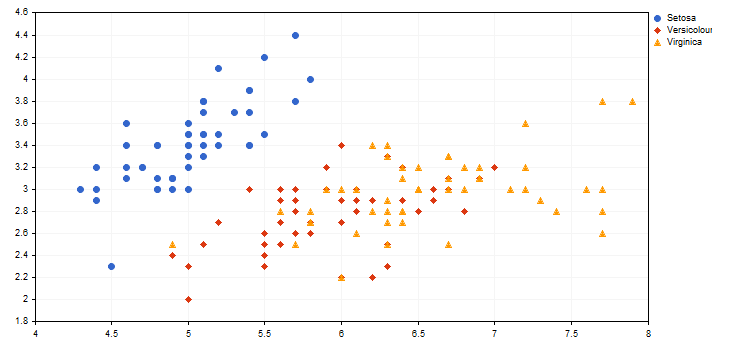
2. La modalità di visualizzazione CURVE_LINES è la modalità principale per la visualizzazione delle curve, in cui ogni coppia di punti è collegata da una o più (in caso di smussamento) linee rette. Le proprietà della modalità sono le seguenti:
- LinesStyle — stile di linea dall'enumerazione ENUM_LINE_STYLE
- LineeSmooth — flag che indica se deve essere eseguito la smussatura
- LineeSmoothTension — grado di smussatura
- LinesSmoothStep — lunghezza delle linee di approssimazione durante la smussatura
Graphics presenta l'algoritmo parametrico standard di smussatura delle curve. Si compone di due parti.
- Per ogni coppia di punti vengono definiti due punti di riferimento sulla base delle loro derivate
- Una Curva di Bèzier con un passo di approssimazione specificato viene tracciata sulla base di questi quattro punti
Il parametro LinesSmoothTension assume i valori (0,0; 1,0). Se LinesSmoothTension è impostato su 0,0, non viene eseguito alcuna smussatura. Aumentando questo parametro, si ottiene una curva sempre più smussata.
curve.LinesStyle(STYLE_DOT);
curve.LinesSmooth(true);
curve.LinesSmoothTension(0.8);
curve.LinesSmoothStep(0.2);
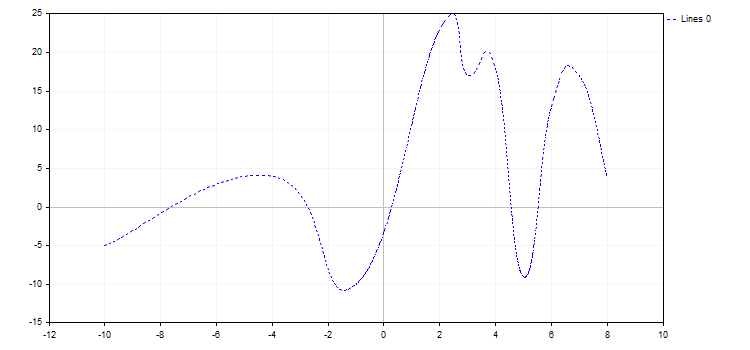
3. CURVE_POINTS_AND_LINES combina le due precedenti modalità di visualizzazione e le loro proprietà.
4. Nella modalità CURVE_STEPS, ogni coppia di punti è collegata da due linee come passo. La modalità ha due proprietà:
- LinesStyle — questa proprietà è presa da CURVE_POINTS e definisce lo stile della linea.
- StepsDimension — dimensione del passo: 0 — x (una linea orizzontale seguita da una verticale) o 1 — y (una linea verticale seguita da una orizzontale).
curve.LinesStyle(STYLE_DASH);
curve.StepsDimension(1);

5. La modalità CURVA_ISTOGRAMMA disegna un istogramma a barre standard. La modalità prevede un'unica proprietà:
- HistogramWidth — larghezza della barra
Se il valore è troppo grande, le barre possono sovrapporsi e le barre con un valore Y maggiore "assorbono" le barre adiacenti con valori più piccoli.
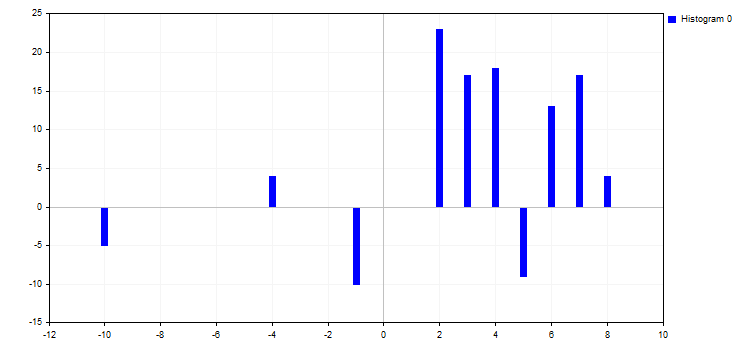
6. La modalità CURVE_NONE disabilita la rappresentazione grafica delle curve, indipendentemente dalla loro visibilità.
Quando si esegue il ridimensionamento automatico, tutte le curve aggiunte al grafico hanno determinati valori. Pertanto, anche se la curva non è tracciata o è impostata sulla modalità CURVE_NONE, i suoi valori vengono comunque presi in considerazione.
Grafici con le funzioni: generazione rapida in poche righe
Un altro vantaggio della libreria è quello di lavorare con i puntatori alle funzioni CurveFunction. In MQL5, i puntatori alle funzioni accettano solo funzioni globali o statiche, mentre la sintassi della funzione dovrebbe corrispondere completamente a quella del puntatore. Nel nostro caso, CurveFunction è configurato per le funzioni che ricevono un parametro di tipo double che riceve anche double.
Per costruire una curva mediante un puntatore a una funzione, è necessario impostare con precisione i valori iniziali (da) e finali (a) dell'argomento, nonché il suo incremento (passo). Minore è il valore di incremento, più punti funzione abbiamo per costruirlo. Per creare una serie di dati, utilizzare CurveAdd() , mentre per tracciare una funzione, applicare CurvePlot() oppure CurvePlotAll().
Ad esempio, creiamo una funzione parabolica e disegniamola in vari incrementi:
//+------------------------------------------------------------------+
//| Parabola |
//+------------------------------------------------------------------+
double Parabola(double x) { return MathPow(x,2); }
//+------------------------------------------------------------------+
//| Funzione di avvio del programma Script |
//+------------------------------------------------------------------+
void OnStart()
{
double from1=-5;
double to1=0;
double step1=1;
double from2=0;
double to2=5;
double step2=0.2;
CurveFunction function = Parabola;
CGRAPHIC graph;
graph.Create(0,"Graph",0,30,30,780,380);
graph.CurveAdd(function,from1,to1,step1,CURVE_LINES);
graph.CurveAdd(function,from2,to2,step2,CURVE_LINES);
graph.CurvePlotAll();
graph.Update();
}
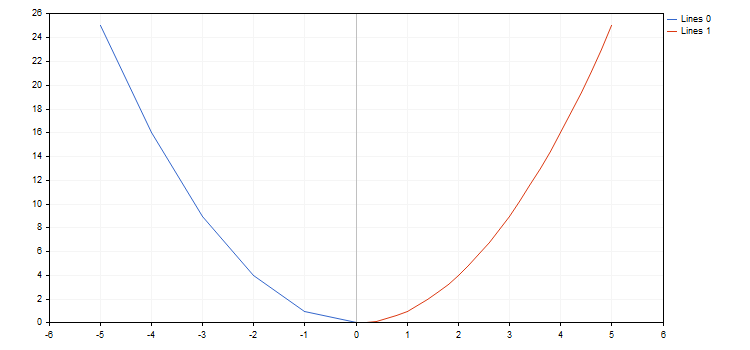
La libreria funziona con funzioni che presentano punti di interruzione (una delle coordinate ha il valore più o meno infinito o è non numerica). L'incremento per funzione deve essere preso in considerazione, poiché a volte si può semplicemente perdere un punto di interruzione. In questo caso, un grafico non soddisfa le aspettative. Ad esempio, disegniamo due funzioni iperboliche all'interno del segmento [-5,0; 5,0] con la prima funzione che ha un passo di 0,7 e la seconda di 0,1. Il risultato viene visualizzato di seguito:
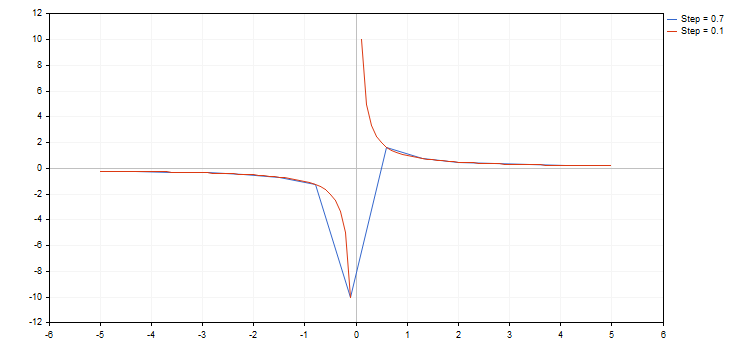
Come si può vedere nell'immagine qui sopra, abbiamo semplicemente perso il punto di rottura quando abbiamo utilizzato un passo di 0,7. Di conseguenza, la curva risultante non ha quasi nulla a che vedere con la funzione iperbolica reale.
Durante l'utilizzo delle funzioni potrebbe verificarsi un errore di divisione per zero. Ci sono due modi per gestire questo problema:
- disabilitare il controllo della divisione per zero in metaeditor.ini
[Experts]
FpNoZeroCheckOnDivision=1 - o analizzare un'equazione utilizzata in una funzione e restituire un valore valido per questi casi. Un esempio di questa gestione tramite macro si trova nei file 3Functions.mq5 e bat.mq5 allegati.
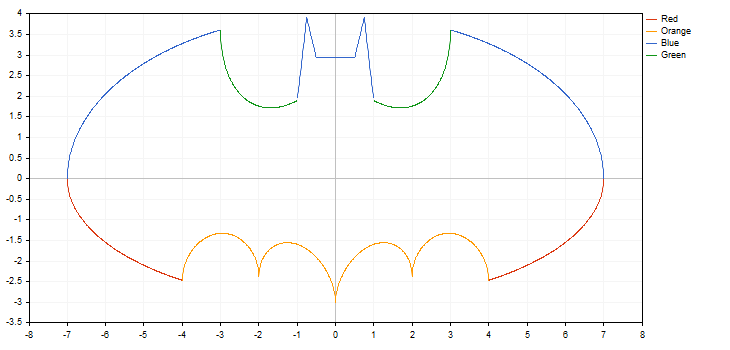
Funzioni di tracciamento rapido
La libreria Graphics include anche una serie di funzioni globali GraphPlot() che eseguono tutte le fasi di tracciamento del grafico in base ai dati disponibili e restituiscono come risultato il nome di un oggetto sul grafico. Queste funzioni sono simili a 'plot' dei linguaggi R o Phyton e consentono di visualizzare istantaneamente i dati disponibili in differenti formati.
La funzione GraphPlot ha 10 diversi sovraccarichi che consentono di tracciare un numero svariato di curve su un singolo grafico e di impostarle in modi diversi. Tutto quello che hai bisogno di fare è formare i dati per tracciare una curva utilizzando uno dei metodi disponibili. Ad esempio, il codice sorgente per il tracciamento rapido degli array x[] e y[] si presenta come segue:
{
double x[]={-10,-4,-1,2,3,4,5,6,7,8};
double y[]={-5,4,-10,23,17,18,-9,13,17,4};
GraphPlot(x,y);
}
Sembra simile su R:
> y<-c(-5,4,-10,23,17,18,-9,13,17,4)
> plot(x,y)
Risultati del confronto tra i grafici delle tre principali modalità di visualizzazione costruiti con la funzione GraphPlot di MQL5 e con la funzione plot di R:
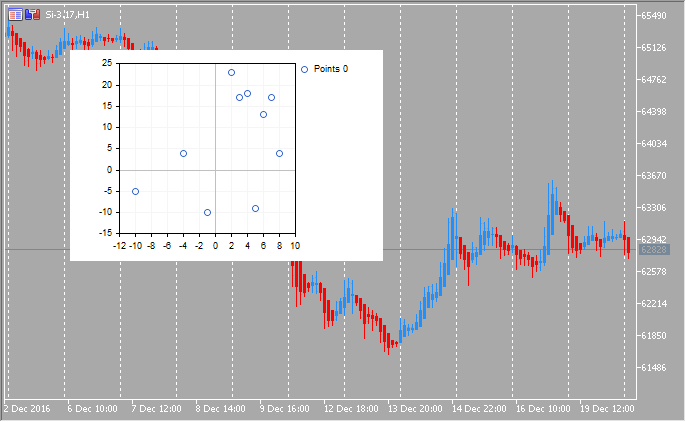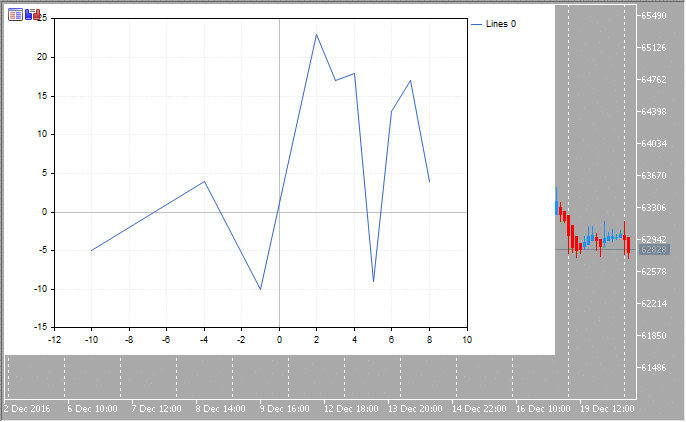
1. Curve puntiformi
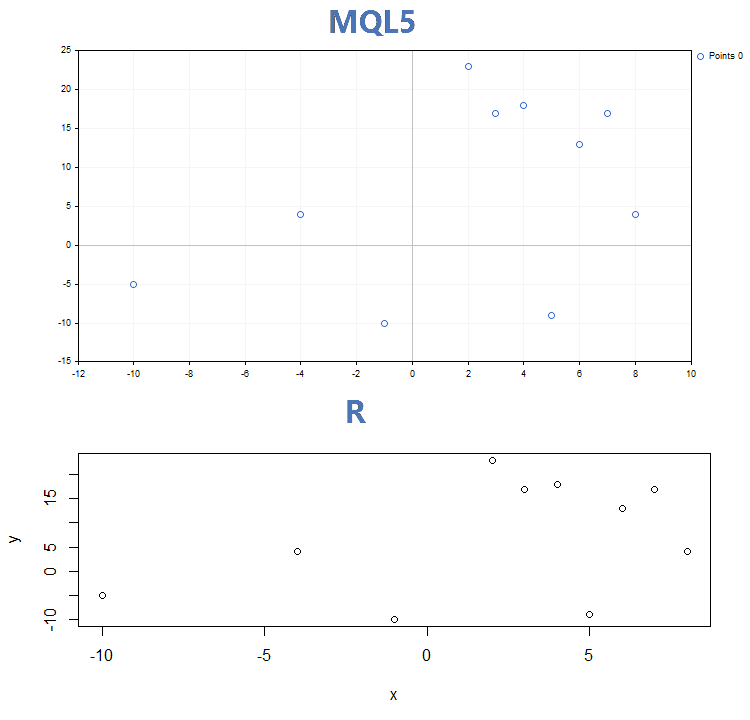
2. Linee
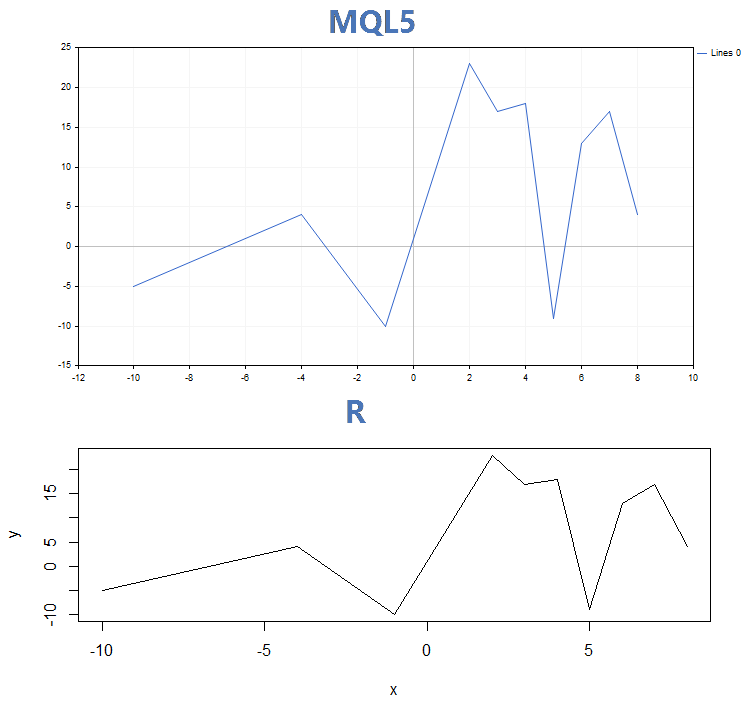
3. Istogramma
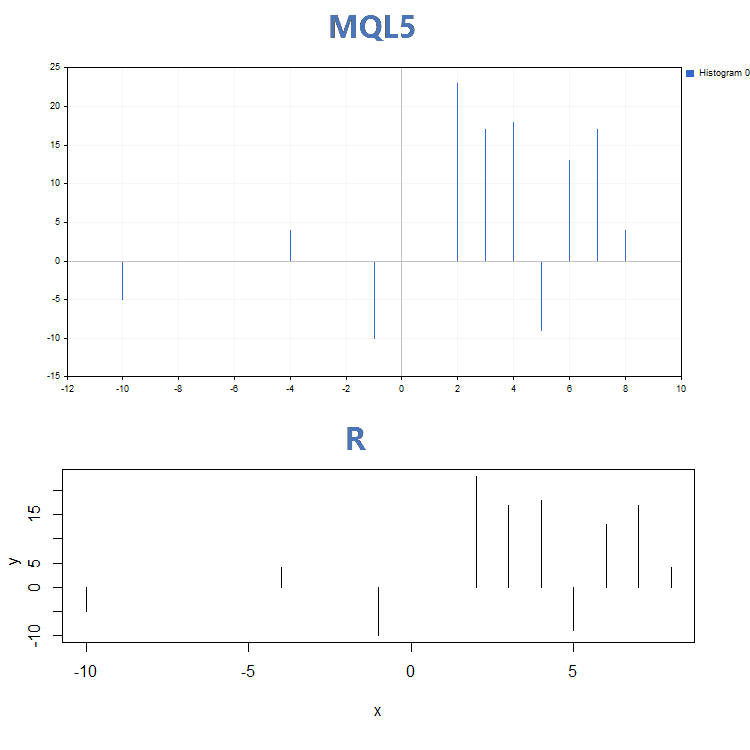
Oltre a differenze visive piuttosto significative delle funzioni GraphPlot() e plot(), esse applicano parametri di input diversi. Mentre la funzione plot() consente di impostare parametri specifici della curva (ad esempio, 'lwd' che modifica la larghezza delle linee), la funzione GraphPlot() include solo i parametri chiave necessari per la costruzione dei dati.
Diamo loro un nome:
- I dati della curva in uno dei quattro formati descritti sopra.
- Tipo di tracciato (l'impostazione predefinita è CURVE_POINTS).
- Nome dell'oggetto (l'impostazione predefinita è NULL).
Ogni grafico creato con la libreria Graphics consiste in un oggetto grafico e in una risorsa grafica ad esso assegnata. Il nome della risorsa grafica viene formato in base al nome dell'oggetto, aggiungendo semplicemente "::" prima di esso. Ad esempio, se il nome dell'oggetto è "SomeGraphic", il nome della sua risorsa grafica è "::SomeGraphic".
La funzione GraphPlot() ha un punto di ancoraggio fisso su un grafico x=65 e y=45. La larghezza e l'altezza del grafico sono calcolate in base alle dimensioni del grafico: la larghezza comprende il 60% del grafico, mentre l'altezza è pari al 65% dell'altezza del grafico. Pertanto, se le dimensioni attuali del grafico sono inferiori a 65-45, la funzione GraphPlot() non è in grado di funzionare correttamente.
Se si applica il nome di un oggetto già creato durante la creazione di un grafico, la libreria Graphics tenta di visualizzare il grafico su quell'oggetto dopo aver controllato il suo tipo di risorsa. Se il tipo di risorsa è OBJ_BITMAP_LABEL, il tracciamento viene eseguito sulla stessa coppia oggetto-risorsa.
Se il nome di un oggetto viene passato esplicitamente alla funzione GraphPlot(), si cerca di trovare quell'oggetto e di visualizzare il grafico su di esso. Se l'oggetto non viene trovato, viene creata automaticamente una nuova coppia oggetto-risorsa in base al nome specificato. Quando si utilizza la funzione GraphPlot() senza un nome di oggetto esplicitamente specificato, viene utilizzato il nome standard "Graphic".
In questo caso, è possibile specificare un punto di ancoraggio del grafico e le sue dimensioni. A tale scopo, creare una coppia oggetto-risorsa con i parametri necessari e passare il nome dell'oggetto creato alla funzione GraphPlot(). Creando una coppia con il nome dell'oggetto Graphic, ridefiniamo e fissiamo l’area di lavoro standard per la funzione GraphPlot, eliminando la necessità di passare il nome dell'oggetto a ogni chiamata.
Ad esempio, prendiamo i dati dell'esempio precedente e impostiamo una nuova dimensione del grafico pari a 750х350. Inoltre, spostiamo il punto di ancoraggio nell'angolo superiore sinistro:
{
//--- crea oggetto su grafico e risorsa dinamica
string name="Graphic";
long x=0;
long y=0;
int width=750;
int height=350;
int data[];
ArrayResize(data,width*height);
ZeroMemory(data);
ObjectCreate(0,name,OBJ_BITMAP_LABEL,0,0,0);
ResourceCreate(":"+name,data,width,height,0,0,0,COLOR_FORMAT_XRGB_NOALPHA);
ObjectSetInteger(0,name,OBJPROP_XDISTANCE,x);
ObjectSetInteger(0,name,OBJPROP_YDISTANCE,y);
ObjectSetString(0,name,OBJPROP_BMPFILE,"::"+name);
//--- crea l'array x e y
double arr_x[]={-10,-4,-1,2,3,4,5,6,7,8};
double arr_y[]={-5,4,-10,23,17,18,-9,13,17,4};
//--- traccia gli array x e y
GraphPlot(arr_x,arr_y,CURVE_LINES);
}
Grafici scientifici di esempio
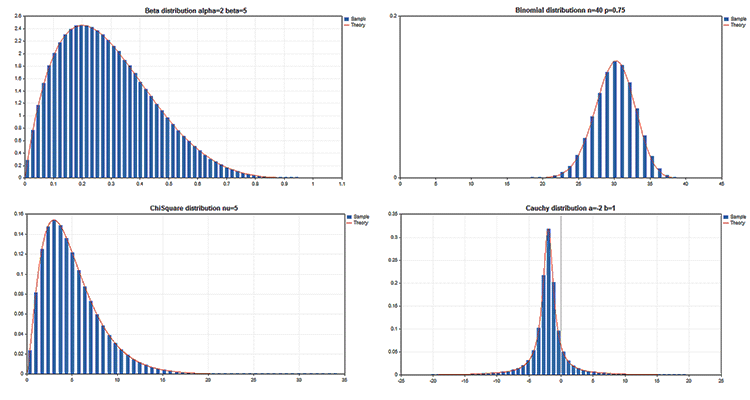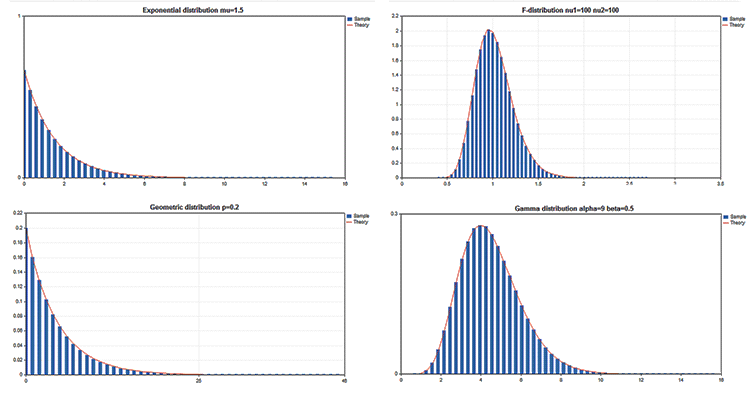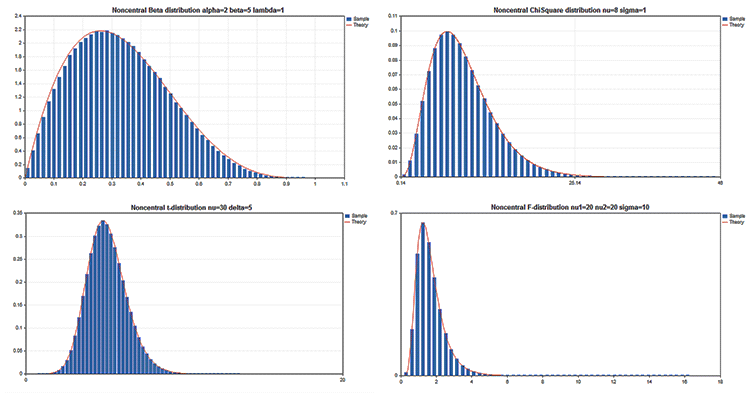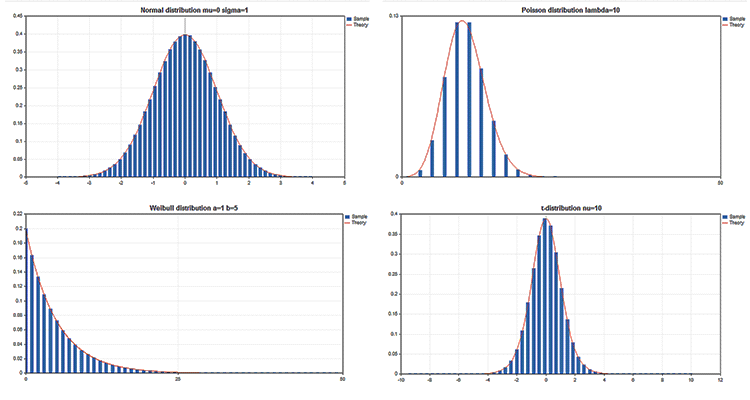
La Libreria standard comprende la sezione Statistica, dotata di funzioni per lavorare con le distribuzioni statistiche multiple della teoria della probabilità. Ogni distribuzione è accompagnata da un grafico di esempio e da un codice per recuperarla. In questo caso, visualizziamo semplicemente questi grafici in un'unica GIF. I codici sorgente degli esempi sono allegati al file MQL5.zip. Scompattarli in MQL5\Scripts.
Tutti questi esempi hanno un grafico dei prezzi disabilitato dalla proprietà CHART_SHOW:
ChartSetInteger(0,CHART_SHOW,false);
Questo ci permette di trasformare la finestra del grafico in un'unica grande area di lavoro e di disegnare oggetti di qualsiasi complessità applicando le risorse grafiche.
Vantaggi principali della libreria grafica
Il linguaggio MQL5 consente agli sviluppatori non solo di creare robot di trading e indicatori tecnici, ma anche di eseguire complessi calcoli matematici utilizzando le librerie ALGLIB, Fuzzy e Statistics. I dati ottenuti possono essere facilmente visualizzati grazie alla libreria grafica fornita. La maggior parte delle operazioni sono automatizzate e la biblioteca offre ampie funzionalità:
- 5 tipi di visualizzazione del grafico
- 10 tipi di indicatori grafici
- ridimensionamento automatico dei grafici per gli assi X e Y
- selezione automatica del colore anche se un grafico presenta diversi costrutti
- smussatura delle linee utilizzando l'anti-aliasing standard o il più avanzato algoritmo di Bresenham
- possibilità di impostare parametri di approssimazione della spline per la visualizzazione delle linee
- capacità di tracciare un grafico utilizzando una singola riga di codice basata sugli array x[] e y[]
- capacità di tracciare grafici utilizzando puntatori a funzioni
La libreria grafica semplifica il tracciamento di grafici scientifici e porta lo sviluppo di applicazioni di trading a un nuovo livello. La piattaforma MetaTrader 5 consente di eseguire calcoli matematici di qualsiasi complessità e di visualizzare i risultati direttamente nella finestra del terminale in modo professionale.
Prova i codici allegati. Non avete più bisogno di pacchetti di terze parti!
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/2866
Avvertimento: Tutti i diritti su questi materiali sono riservati a MetaQuotes Ltd. La copia o la ristampa di questi materiali in tutto o in parte sono proibite.
 SQLite: Gestione nativa dei database SQL in MQL5
SQLite: Gestione nativa dei database SQL in MQL5
 Sviluppare un Expert Advisor per il trading da zero (Parte 10): Accesso agli indicatori personalizzati
Sviluppare un Expert Advisor per il trading da zero (Parte 10): Accesso agli indicatori personalizzati
 Sviluppare un Expert Advisor per il trading da zero (Parte 9): Un salto concettuale (II)
Sviluppare un Expert Advisor per il trading da zero (Parte 9): Un salto concettuale (II)
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso
Abbiamo bisogno di una nuova classe con meno funzioni di CCanvas. È meglio rendere questa classe il più simile possibile a JS canvas, che non ha molte funzioni in sostanza, per facilitare l'apprendimento e l'adozione, dato che l'intera informatica si sta spostando verso il web.
ma questo è l'ideale.
Probabilmente potrei scrivere qualcosa di simile da solo, ma ci vorrebbe almeno mezzo anno a tempo pieno
anche se personalmente non mi piace tutto ciò che c'è in JS Canvas, ma per la standardizzazione sarebbe giusto implementare qualcosa di simile con piccole modifiche per fare a meno del parsing delle stringhe.
Ma per il lavoro normale abbiamo bisogno di rifare il modello di eventi di MT5, perché è semplicemente orribile.
È chiaro che tutto è "sotto i ferri", ma la domanda era comunque un po' diversa. Cosa è auspicabile cambiare/raffinare nella classe esistente...
È chiaro che tutto è "sotto i ferri", ma la domanda era comunque un po' diversa. Cosa è auspicabile cambiare/migliorare nella classe esistente...
metodi lisci per dar loro vita. Ora penso che ci siano anche funzioni in CCanvas che non sono documentate.
metodi di smussamento per dar loro vita. Ora sembra che in CCanvas ci siano persino funzioni non documentate.
Davvero? Non ci ho fatto caso... Dovrò dare un'occhiata al mio tempo libero....
Ho bisogno dei grafici del tipo "cassetti con i baffi", è prevista la loro aggiunta?
Manca anche la possibilità di usare le sottofinestre/basi, cioè quando si vogliono usare due scale diverse.
Salve.
La classe CGraphic ha metodi incorporati per disegnare mappe di calore?