
Usar Mapas Auto-organizáveis (mapas de Kohonen) no MetaTrader 5
Introdução
Um mapa auto-organizável (SOM) é um tipo de rede neural artificial que é treinada a partir da utilização de aprendizagem não supervisionada para produzir uma representação discretizada do espaço de entrada das amostras de treinamento, denominado mapa.
Esses mapas são úteis para a classificação e visualização de panoramas de baixa dimensão de dados de alta dimensão, semelhante ao escalonamento multidimensional. O modelo foi primeiramente descrito como uma rede neural artificial pelo professor finlandês Teuvo Kohonen e às vezes é chamado de mapa de Kohonen.
Há muitos algoritmos disponíveis. Seguiremos o código apresentado em http://www.ai-junkie.com. Para visualizar os dados no terminal do cliente MetaTrader, usaremos o cIntBMP - uma biblioteca para a criação de imagens em BMP. Neste artigo, serão apresentadas diversas aplicações simples dos mapas de Kohonen.
1. Mapas auto-organizáveis
Os mapas auto-organizáveis foram primeiramente descritos por Teuvo Kohonen em 1982. Ao contrário de muitas redes neurais, não há necessidade de correspondência exata (um a um) entre a entrada e os dados alvo de saída. Esta rede neural é treinada através da utilização de aprendizagem não supervisionada.
O SOM poderá ser descrito formalmente como um mapeamento harmonioso, não linear, ordenado, de dados de entrada de alta dimensão em elementos de um array regular, de baixa dimensão. Em seu formato básico, ele produz um gráfico de similaridade dos dados de entrada.
O SOM converte a relação estatística não linear entre dados de alta dimensão em uma relação geométrica simples de seus pontos de imagem em uma rede bidimensional regular de nodos. Os mapas SOM podem ser usados para a classificação e visualização de dados de alta dimensão.
1.1. Arquitetura da rede
O mapa de Kohonen simples em forma de rede de 16 nodos (4x4, cada um deles está conectado a um vetor de entrada tridimensional) é apresentado na Figura 1.
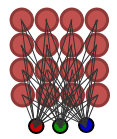
Figura 1. Mapa de Kohonen simples (16 nodos)
Cada nodo tem coordenadas (x,y) em retículo e vetor de pesos com componentes, definidos com base no vetor de entrada.
1.2. Algoritmo de aprendizagem
Ao contrário de muitos outros tipos de redes neurais, o SOM não precisa que uma saída alvo seja especificada. Em vez disso, quando os pesos do nodo correspondem ao vetor de entrada, aquela área do retículo é seletivamente otimizada para se parecer mais com os dados da classe a que pertence o vetor de entrada.
A partir de uma distribuição inicial de pesos aleatórios após muitas iterações, o SOM finalmente organiza-se em um mapa de zonas estáveis. Cada zona é efetivamente um classificador de características, então você pode pensar na saída gráfica como um tipo de mapa de características do espaço de entrada.
O treinamento ocorre em vários passos e ao longo de muitas iterações.
- Os pesos de cada nodo são inicializados com valores aleatórios.
- Um vetor é selecionado aleatoriamente a partir do conjunto de dados de treinamento.
- Cada nodo é examinado para calcular qual deles apresenta os pesos mais semelhantes ao vetor de entrada. O nodo vencedor é conhecido como Unidade de Melhor Ajuste (Best Matching Unit - BMU).
- O raio da vizinhança da BMU é calculado. Inicialmente, este valor é estabelecido como o raio do retículo, mas é diminuído a cada etapa de tempo.
- Para quaisquer nodos encontrados dentro do raio da BMU, os pesos do nodo são ajustados para torná-los mais semelhantes ao vetor de entrada. Quanto mais perto um nodo estiver da BMU, mais os seus pesos serão alertados.
- Repita o passo 2 para N iterações.
Os detalhes podem ser encontrados em http://www.ai-junkie.com.
2. Estudos de caso
2.1. Exemplo 1. "Olá Mundo!" em SOM
O exemplo clássico de mapa de Kohonen é um problema de agrupamento de cores.
Imagine que nós tenhamos um conjunto de 8 cores. Cada uma delas está representada como um vetor tridimensional no modelo de cores RGB.
-
 Vermelho: (255,0,0);
Vermelho: (255,0,0);  Verde: (0.128,0);
Verde: (0.128,0); Azul: (0,0,255);
Azul: (0,0,255); Verde escuro: (0.100,0);
Verde escuro: (0.100,0); Azul escuro: (0,0,139);
Azul escuro: (0,0,139); Amarelo: (255.255,0);
Amarelo: (255.255,0); Laranja: (255.165,0);
Laranja: (255.165,0); Roxo: (128,0,128).
Roxo: (128,0,128).
Ao trabalhar com mapas de Kohonen em linguagem MQL5, nós seguiremos o paradigma de orientação a objetos.
Precisamos de duas classes: Classe CSOMNode para um nodo da rede regular e CSOM, que é uma classe de rede neural.
//+------------------------------------------------------------------+ //| CSOMNode class | //+------------------------------------------------------------------+ class CSOMNode { protected: int m_x1; int m_y1; int m_x2; int m_y2; double m_x; double m_y; double m_weights[]; public: //--- class constructor CSOMNode(); //--- class destructor ~CSOMNode(); //--- node initialization void InitNode(int x1,int y1,int x2,int y2); //--- return coordinates of the node's center double X() const { return(m_x);} double Y() const { return(m_y);} //--- returns the node coordinates void GetCoordinates(int &x1,int &y1,int &x2,int &y2); //--- returns the value of weight_index component of weight's vector double GetWeight(int weight_index); //--- returns the squared distance between the node weights and specified vector double CalculateDistance(double &vector[]); //--- adjust weights of the node void AdjustWeights(double &vector[],double learning_rate,double influence); };
A implementação de métodos de classe pode ser encontrada em som_ex1.mq5. O código possui vários comentários. Nós iremos focar na ideia.
A descrição da classe CSOM tem o seguinte aspecto:
//+------------------------------------------------------------------+ //| CSOM class | //+------------------------------------------------------------------+ class CSOM { protected: //--- class for using of bmp images cIntBMP m_bmp; //--- grid mode int m_gridmode; //--- bmp image size int m_xsize; int m_ysize; //--- number of nodes int m_xcells; int m_ycells; //--- array with nodes CSOMNode m_som_nodes[]; //--- total items in training set int m_total_training_sets; //--- training set array double m_training_sets_array[]; protected: //--- radius of the neighbourhood (used for training) double m_map_radius; //--- time constant (used for training) double m_time_constant; //--- initial learning rate (used for training) double m_initial_learning_rate; //--- iterations (used for training) int m_iterations; public: //--- class constructor CSOM(); //--- class destructor ~CSOM(); //--- net initialization void InitParameters(int iterations,int xcells,int ycells,int bmpwidth,int bmpheight); //--- finds the best matching node, closest to the specified vector int BestMatchingNode(double &vector[]); //--- train method void Train(); //--- render method void Render(); //--- shows the bmp image on the chart void ShowBMP(bool back); //--- adds a vector to training set void AddVectorToTrainingSet(double &vector[]); //--- shows the pattern title void ShowPattern(double c1,double c2,double c3,string name); //--- adds a pattern to training set void AddTrainPattern(double c1,double c2,double c3); //--- returns the RGB components of the color void ColToRGB(int col,int &r,int &g,int &b); //--- returns the color by RGB components int RGB256(int r,int g,int b) const {return(r+256*g+65536*b); } //--- deletes image from the chart void NetDeinit(); };
O uso da classe CSOM é simples:
CSOM KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ void OnInit() { MathSrand(200); //--- initialize net, 10000 iterations will be used for training //--- the net contains 15x20 nodes, bmp image size 400x400 KohonenMap.InitParameters(10000,15,20,400,400); //-- add RGB-components of each color from training set KohonenMap.AddTrainPattern(255, 0, 0); // Red KohonenMap.AddTrainPattern( 0,128, 0); // Green KohonenMap.AddTrainPattern( 0, 0,255); // Blue KohonenMap.AddTrainPattern( 0,100, 0); // Dark green KohonenMap.AddTrainPattern( 0, 0,139); // Dark blue KohonenMap.AddTrainPattern(255,255, 0); // Yellow KohonenMap.AddTrainPattern(255,165, 0); // Orange KohonenMap.AddTrainPattern(128, 0,128); // Purple //--- train net KohonenMap.Train(); //--- render map to bmp KohonenMap.Render(); //--- show patterns and titles for each color KohonenMap.ShowPattern(255, 0, 0,"Red"); KohonenMap.ShowPattern( 0,128, 0,"Green"); KohonenMap.ShowPattern( 0, 0,255,"Blue"); KohonenMap.ShowPattern( 0,100, 0,"Dark green"); KohonenMap.ShowPattern( 0, 0,139,"Dark blue"); KohonenMap.ShowPattern(255,255, 0,"Yellow"); KohonenMap.ShowPattern(255,165, 0,"Orange"); KohonenMap.ShowPattern(128, 0,128,"Purple"); //--- show bmp image on the chart KohonenMap.ShowBMP(false); //--- }
O resultado é apresentado na Figura 2.
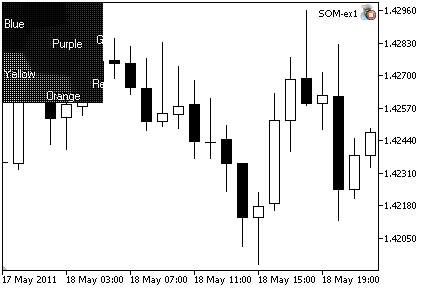
Figura 2. A saída do Expert Advisor SOM_ex1.mq5
A dinâmica de aprendizagem do mapa de Kohonen é apresentada na Figura 3 (veja os passos abaixo da imagem):
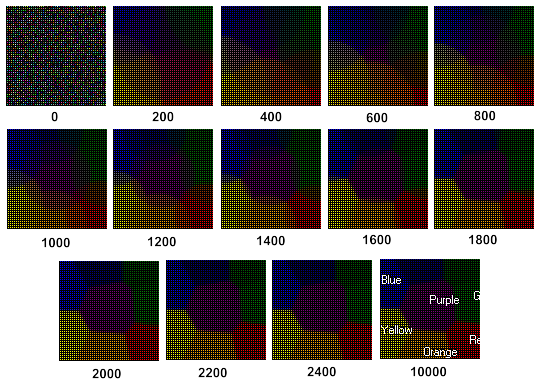
Figura 3. Dinâmica de aprendizagem do mapa de Kohonen
É possível perceber na Figura 3 que o mapa de Kohonen Map é formado após 2400 etapas.
Se criarmos um retículo de 300 nodos e especificarmos o tamanho da imagem em 400x400:
//--- lattice of 15x20 nodes, image size 400x400 KohonenMap.InitParameters(10000,15,20,400,400);
Iremos obter a imagem apresentada na Figura 4:
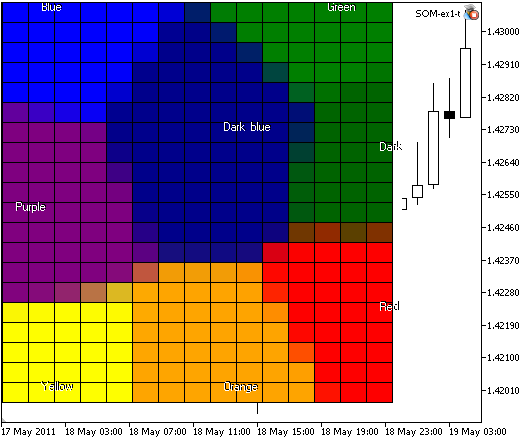
Figura 4. Mapa de Kohonen com 300 nodos, tamanho da imagem 400x400
Se você ler o livro Visual Explorations in Finance: with Self-Organizing Maps, escrito por Guido Dboeck e Teuvo Kohonen, você lembrará que os nodos do retículo também podem ser representados como células hexagonais. Ao modificar o código do Expert Advisor, nós podemos implementar outra visualização.
O resultado do SOM-ex1-hex.mq5 é apresentado na Figura 5:
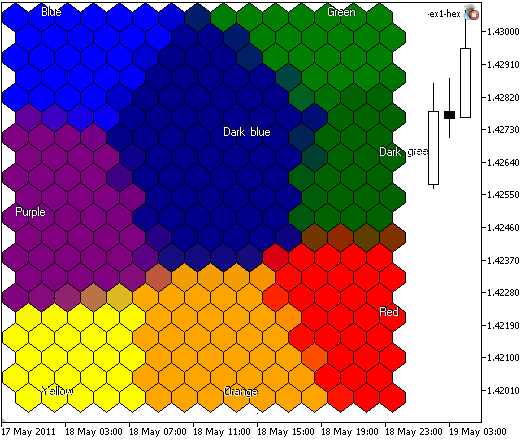
Figura 5. Mapa de Kohonen com 300 nodos, tamanho da imagem 400x400, nodos representados como células hexagonais
Nesta versão, podemos definir a exibição de bordas de célula utilizando os parâmetros de entrada:
// input parameter, used to show hexagonal cells input bool HexagonalCell=true; // input parameter, used to show borders input bool ShowBorders=true;
Em alguns casos, não é preciso exibir as bordas das células. Se você especificar ShowBorders=false, você obterá a seguinte imagem (veja a Figura 6):
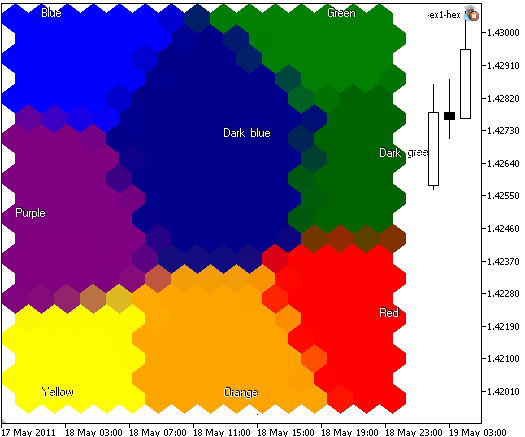
Figura 6. Mapa de Kohonen com 300 nodos, imagem 400x400, nodos organizados em células hexagonais, bordas desabilitadas
No primeiro exemplo, usamos 8 cores no conjunto de treinamento com os componentes de cores especificados. é possível aumentar o conjunto de treinamento e simplificar a especificação de componentes de cor ao adicionar dois métodos à classe CSOM.
Observe que, neste caso, os mapas de Kohonen são simples porque há apenas poucas cores, separadas no espaço de cores. Como resultado, obtivemos os agrupamentos localizados.
O problema surge quando consideramos mais cores com componentes mais próximos.
2.2. Exemplo 2. Utilizar Cores hexadecimais como amostras de treinamento
Em linguagem MQL5, as Cores hexadecimais são constantes predefinidas.
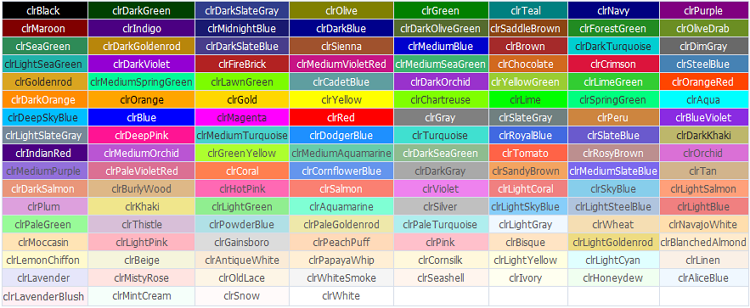
Figura 7. Cores hexadecimais
E se aplicarmos o algoritmo de Kohonen a um conjunto de vetores que tenham componentes similares?
Podemos criar uma classe CSOMWeb derivada da classe CSOM:
//+------------------------------------------------------------------+ //| CSOMWeb class | //+------------------------------------------------------------------+ class CSOMWeb : public CSOM { public: //--- adds a color to training set (used for colors, instead of AddTrainPattern) void AddTrainColor(int col); //--- method of showing of title of the pattern (used for colors, instead of ShowPattern) void ShowColor(int col,string name); };
Como você pode ver, para simplificar o trabalho com as cores, adicionamos dois novos métodos. Agora não é preciso especificar explicitamente os componentes de cores.
A implementação dos métodos de classe tem o seguinte aspecto:
//+------------------------------------------------------------------+ //| Adds a color to training set | //| (used for colors, instead of AddTrainPattern) | //+------------------------------------------------------------------+ void CSOMWeb::AddTrainColor(int col) { double vector[]; ArrayResize(vector,3); int r=0; int g=0; int b=0; ColToRGB(col,r,g,b); vector[0]=r; vector[1]=g; vector[2]=b; AddVectorToTrainingSet(vector); ArrayResize(vector,0); } //+------------------------------------------------------------------+ //| Method of showing of title of the pattern | //| (used for colors, instead of ShowPattern) | //+------------------------------------------------------------------+ void CSOMWeb::ShowColor(int col,string name) { int r=0; int g=0; int b=0; ColToRGB(col,r,g,b); ShowPattern(r,g,b,name); }
Todas as cores hexadecimais podem ser combinadas no array web_colors[]:
//--- web colors array color web_colors[132]= { clrBlack, clrDarkGreen, clrDarkSlateGray, clrOlive, clrGreen, clrTeal, clrNavy, clrPurple, clrMaroon, clrIndigo, clrMidnightBlue, clrDarkBlue, clrDarkOliveGreen, clrSaddleBrown, clrForestGreen, clrOliveDrab, clrSeaGreen, clrDarkGoldenrod, clrDarkSlateBlue, clrSienna, clrMediumBlue, clrBrown, clrDarkTurquoise, clrDimGray, clrLightSeaGreen, clrDarkViolet, clrFireBrick, clrMediumVioletRed, clrMediumSeaGreen, clrChocolate, clrCrimson, clrSteelBlue, clrGoldenrod, clrMediumSpringGreen, clrLawnGreen, clrCadetBlue, clrDarkOrchid, clrYellowGreen, clrLimeGreen, clrOrangeRed, clrDarkOrange, clrOrange, clrGold, clrYellow, clrChartreuse, clrLime, clrSpringGreen, clrAqua, clrDeepSkyBlue, clrBlue, clrMagenta, clrRed, clrGray, clrSlateGray, clrPeru, clrBlueViolet, clrLightSlateGray, clrDeepPink, clrMediumTurquoise, clrDodgerBlue, clrTurquoise, clrRoyalBlue, clrSlateBlue, clrDarkKhaki, clrIndianRed, clrMediumOrchid, clrGreenYellow, clrMediumAquamarine, clrDarkSeaGreen, clrTomato, clrRosyBrown, clrOrchid, clrMediumPurple, clrPaleVioletRed, clrCoral, clrCornflowerBlue, clrDarkGray, clrSandyBrown, clrMediumSlateBlue, clrTan, clrDarkSalmon, clrBurlyWood, clrHotPink, clrSalmon, clrViolet, clrLightCoral, clrSkyBlue, clrLightSalmon, clrPlum, clrKhaki, clrLightGreen, clrAquamarine, clrSilver, clrLightSkyBlue, clrLightSteelBlue, clrLightBlue, clrPaleGreen, clrThistle, clrPowderBlue, clrPaleGoldenrod, clrPaleTurquoise, clrLightGray, clrWheat, clrNavajoWhite, clrMoccasin, clrLightPink, clrGainsboro, clrPeachPuff, clrPink, clrBisque, clrLightGoldenrod, clrBlanchedAlmond, clrLemonChiffon, clrBeige, clrAntiqueWhite, clrPapayaWhip, clrCornsilk, clrLightYellow, clrLightCyan, clrLinen, clrLavender, clrMistyRose, clrOldLace, clrWhiteSmoke, clrSeashell, clrIvory, clrHoneydew, clrAliceBlue, clrLavenderBlush, clrMintCream, clrSnow, clrWhite };
A função OnInit() tem formato simples:
CSOMWeb KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ void OnInit() { MathSrand(200); int total_web_colors=ArraySize(web_colors); //--- initialize net, 10000 iterations will be used for training //--- the net contains 15x20 nodes, bmp image size 400x400 KohonenMap.InitParameters(10000,50,50,500,500); //-- add all web colors to training set for(int i=0; i<total_web_colors; i++) { KohonenMap.AddTrainColor(web_colors[i]); } //--- train net KohonenMap.Train(); //--- render map to bmp KohonenMap.Render(); //--- show patterns and titles for each color for(int i=0; i<total_web_colors; i++) { KohonenMap.ShowColor(web_colors[i],ColorToString(web_colors[i],true)); } //--- show bmp image on the chart KohonenMap.ShowBMP(false); }
Se lançarmos o som-ex2-hex.mq5, obteremos a imagem apresentada na Figura 8.
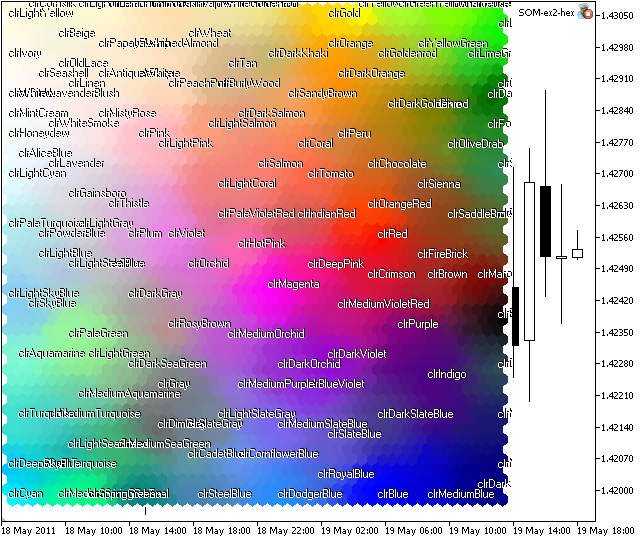
Figura 8. Mapa de Kohonen para cores hexadecimais
Como você pode ver, há alguns agrupamentos, mas algumas cores (como xxxBlue) estão localizadas em regiões diferentes.
A razão para isto é a estrutura do grupo de treinamento. Há muitos vetores com componentes próximos.
2.3. Exemplo 3. Agrupamento de produtos
A seguir, consideraremos um exemplo simples que tentará agrupar vinte e cinco alimentos em regiões de semelhança com base em três parâmetros, que são proteína, carboidrato e gordura.
| Alimento | Proteína | Carboidrato | Gordura | |
|---|---|---|---|---|
| 1 | Maçãs | 0,4 | 11,8 | 0,1 |
| 2 | Abacate | 1,9 | 1,9 | 19,5 |
| 3 | Bananas | 1,2 | 23,2 | 0,3 |
| 4 | Carne bovina | 20,9 | 0 | 7,9 |
| 5 | Big Mac | 13 | 19 | 11 |
| 6 | Castanhas-do-pará | 15,5 | 2,9 | 68,3 |
| 7 | Pão | 10,5 | 37 | 3,2 |
| 8 | Manteiga | 1 | 0 | 81 |
| 9 | Queijo | 25 | 0,1 | 34,4 |
| 10 | Cheesecake | 6,4 | 28,2 | 22,7 |
| 11 | Biscoitos | 5,7 | 58,7 | 29,3 |
| 12 | Cereal de milho | 7 | 84 | 0,9 |
| 13 | Ovos | 12,5 | 0 | 10,8 |
| 14 | Frango frito | 17 | 7 | 20 |
| 15 | Batatas fritas | 3 | 36 | 13 |
| 16 | Chocolate quente | 3,8 | 19,4 | 10,2 |
| 17 | Pepperoni | 20,9 | 5,1 | 38,3 |
| 18 | Pizza | 12,5 | 30 | 11 |
| 19 | Torta de carne suína | 10,1 | 27,3 | 24,2 |
| 20 | Batatas | 1,7 | 16,1 | 0,3 |
| 21 | Arroz | 6,9 | 74 | 2,8 |
| 22 | Frango assado | 26,1 | 0,3 | 5,8 |
| 23 | Açúcar | 0 | 95,1 | 0 |
| 24 | Filé de atum | 25,6 | 0 | 0,5 |
| 25 | Água | 0 | 0 | 0 |
Tabela 1. Proteína, carboidrato e gordura de 25 alimentos.
Este problema é interessante porque os vetores de entrada possuem diferentes valores e cada componente tem a sua própria variação de valores. é importante para a visualização, porque usaremos o modelo de cores RGB com componentes que variam de 0 a 255.
Felizmente, neste caso os vetores de entrada também são tridimensionais e nós podemos utilizar o modelo de cores RGB para a visualização do mapa de Kohonen.
//+------------------------------------------------------------------+ //| CSOMFood class | //+------------------------------------------------------------------+ class CSOMFood : public CSOM { protected: double m_max_values[]; double m_min_values[]; public: void Train(); void Render(); void ShowPattern(double c1,double c2,double c3,string name); };
Como você pode ver, nós adicionamos arrays m_max_values[] e m_min_values[] para armazenamento de valores máximos e mínimos do conjunto de treinamento. O "escalonamento" é necessário para visualização no modelo de cores RGB, então nós sobrecarregamos os métodos Train(), Render() e ShowPattern().
A busca pelos valores máximos e mínimos é implementada no método Train().
//--- find minimal and maximal values of the training set ArrayResize(m_max_values,3); ArrayResize(m_min_values,3); for(int j=0; j<3; j++) { double maxv=m_training_sets_array[3+j]; double minv=m_training_sets_array[3+j]; for(int i=1; i<m_total_training_sets; i++) { double v=m_training_sets_array[3*i+j]; if(v>maxv) {maxv=v;} if(v<minv) {minv=v;} } m_max_values[j]=maxv; m_min_values[j]=minv; Print(j,"m_min_value=",m_min_values[j],"m_max_value=",m_max_values[j]); }
Para exibir os componentes no modelo de cores RGB, nós precisamos modificar o método Render():
// int r = int(m_som_nodes[ind].GetWeight(0)); // int g = int(m_som_nodes[ind].GetWeight(1)); // int b = int(m_som_nodes[ind].GetWeight(2)); int r=int ((255*(m_som_nodes[ind].GetWeight(0)-m_min_values[0])/(m_max_values[0]-m_min_values[0]))); int g=int ((255*(m_som_nodes[ind].GetWeight(1)-m_min_values[1])/(m_max_values[1]-m_min_values[1]))); int b=int ((255*(m_som_nodes[ind].GetWeight(2)-m_min_values[2])/(m_max_values[2]-m_min_values[2])));
O resultado do som_ex3.mq5 é apresentado na Figura 9.
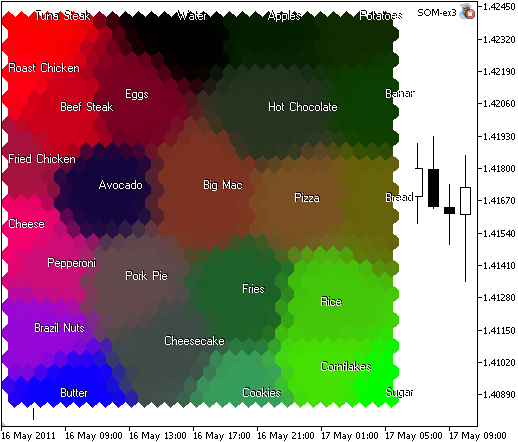
Figura 9. Mapa de alimentos agrupados em regiões de semelhança, com base em proteína, carboidrato e gordura
Análise de componentes é possível ver no mapa que açúcar, arroz e cereal de milho estão organizados com a cor verde devido ao Carboidrato (2º componente). A manteiga está na zona verde e contém muita gordura (3º componente). Carne bovina, frango assado e filé de atum contêm muita proteína (1º componente, vermelho).
Você pode aumentar o conjunto de treinamento adicionando novos alimentos das Tabelas de composição de alimentos (tabela alternativa).
Como você pode perceber, o problema é resolvido para direções R, G, B "puras". E os outros alimentos com diversos componentes iguais (ou quase iguais)? A seguir, iremos apresentar os Planos de componentes. Isso é muito útil, especialmente nos casos em que os vetores de entrada possuem dimensão maior que 3.
2.4. Exemplo 4. Caso tetradimensional. Conjunto de dados da íris de Fisher CMYK
Para vetores tridimensionais, não há problemas com a visualização. Os resultados são claros devido ao modelo de cores RGB, usado para visualizar componentes de cor.
Ao trabalhar com dados de alta dimensão, precisamos encontrar uma forma de visualizá-los. A solução simples é marcar um mapa de gradiente (preto/branco, por exemplo), com cores proporcionais ao comprimento do vetor. A outra maneira é utilizar outros espaços de cores. Neste exemplo, utilizaremos o modelo de cores CMYK para o conjunto de dados da íris de Fisher. Posteriormente, apresentaremos uma solução melhor.
O conjunto de dados íris ou conjunto de dados da íris de Fisher é um conjunto de dados multivariados apresentados por Ronald Fisher (1936) como um exemplo de análise discriminante. O conjunto de dados consiste em 50 amostras de cada uma das três espécies de flores íris (Iris setosa, Iris virginica e Iris versicolor).
Quatro características foram medidas em cada amostra: o comprimento e a largura da sépala e da pétala, em centímetros.

Figura 10. íris
Cada amostra possui 4 características:
- Comprimento da sépala;
- Largura da sépala;
- Comprimento da pétala;
- Largura da pétala.
O conjunto de dados íris pode ser encontrado em SOM_ex4.mq5.
Neste exemplo, utilizaremos o espaço de cores CMYK intermediário para a marcação. Ou seja, consideraremos os pesos do nodo como vetores no espaço CMYK. Para visualizar os resultados, a conversão CMYK->RGB é utilizada. Um novo método int CSOM::CMYK2Col(uchar c,uchar m,uchar y,uchar k) é adicionado à classe CSOM. Ele foi usado no método CSOM::Render(). Ademais, temos que modificar as classes para que elas suportem vetores tetradimensionais.
O resultado é apresentado na Figura 11.
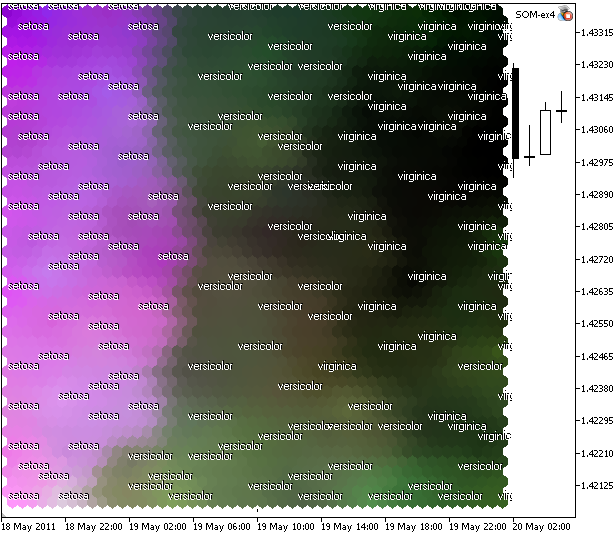
Figura 11. Mapa de Kohonen para conjunto de dados íris, organizados no modelo de cores CMYK
O que é possível perceber? Não obtivemos o agrupamento completo (devido às características do problema), mas é possível perceber a separação linear da iris setosa.
O motivo dessa separação linear da setosa é um grande componente "Magenta" (2º) no espaço CMYK.
2.6. Análise de plano de componente
é possível perceber que há um problema com a visualização de dados nos exemplos anteriores (alimentos e agrupamentos de dados íris).
Por exemplo, no problema dos alimentos, analisamos o mapa de Kohonen utilizando as informações em determinadas cores (vermelha, verde, azul). Além dos agrupamentos básicos, havia alguns alimentos com diversos componentes. Ademais, a análise se tornou difícil quando os componentes eram quase iguais.
Os planos de componentes oferecem a possibilidade de visualizar a intensidade relativa de cada um dos alimentos.
Precisamos adicionar as instâncias (m_bmp[] array) da classe CIntBMP à classe CSOM e modificar os métodos de renderização correspondentes. Além disso, precisamos de um mapa de gradiente par visualizar a intensidade de cada componente (os valores menores são exibidos na cor azul e os maiores, na cor vermelha).
![]()
Figura 12. Paleta de gradientes
Nós adicionamos o array Palette[768] e os métodos GetPalColor() e Blend(). O desenho de um nodo é posicionado no método RenderCell().
Conjunto de dados íris
Os resultados do som-ex4-cpr.mq5 são apresentados na Figura 13.
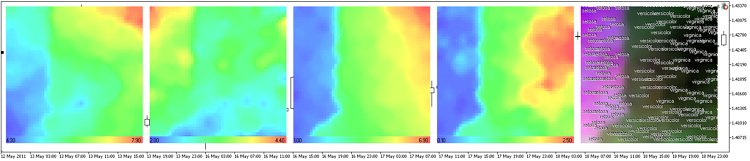
Figura 13. Representação de planos de componentes do conjunto de dados íris
Neste caso, usamos a rede com 30x30 nodos e tamanho de imagem 300x300.
Os planos de componentes desempenham um papel importante na detecção de correlações: ao comparar estes planos, mesmo as variáveis parcialmente correlacionadas podem ser detectadas por inspeção visual. Isto se torna mais fácil se os planos de componentes forem reorganizados para que os que forem correlacionados fiquem próximos uns dos outros. Desta forma, é fácil selecionar combinações de componentes interessantes para melhor investigação.
Vamos observar os planos de componentes (Figura 14).
Os valores máximos e mínimos de componentes são exibidos na tabela de gradientes.
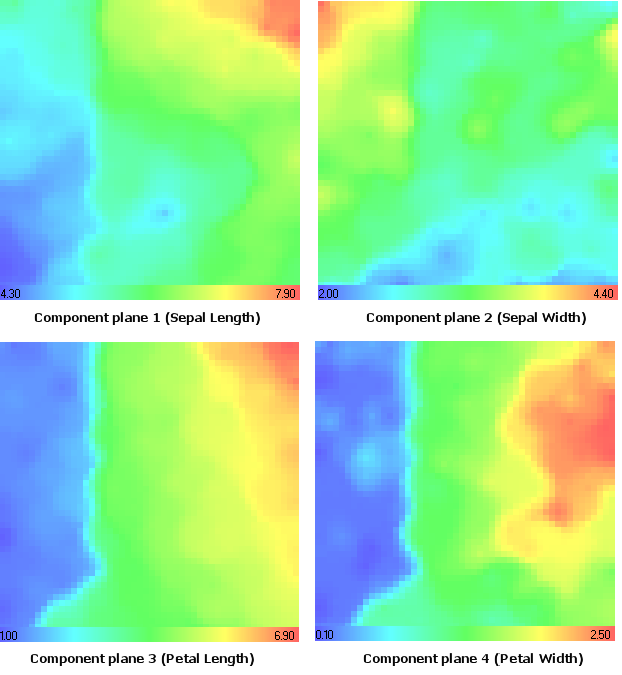
Figura 14. Conjunto de dados íris. Planos de componentes
Todos esses planos de componentes, representados no modelo de cores CMYK, são exibidos na Figura 15.

Figura 15. Conjunto de dados íris. Mapa de Kohonen em modelo de cores CMYK
Vamos recordar a espécie íris setosa. Utilizando a análise de planos de componentes (Figura 14), é possível perceber que ela possui valores mínimos no 1º (comprimento de sépala), 3º (comprimento de pétala) e 4º (largura de pétala) plano de componentes.
é notável que ela possua valores máximos no 2º plano de componentes (largura da sépala) - o mesmo resultado que obtivemos no modelo de cores CMYK (componente magenta, Figura 15).
Agrupamento de alimentos
Agora vamos considerar o problema do agrupamento de alimentos utilizando a análise de plano de componente (som-ex3-cpr.mq5).
O resultado é apresentado na Figura 16 (30x30 nodos, tamanho da imagem 300x300, células hexagonais sem bordas).
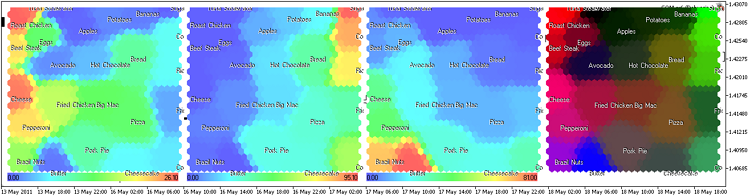
Figura 16. Mapa de Kohonen para alimentos, representação de plano de componente
Adicionamos a opção de exibição de títulos no método ShowPattern() da classe CSOM (input parameter ShowTitles=true).
Os planos de componentes (proteína, carboidrato, gordura) têm o seguinte aspecto:
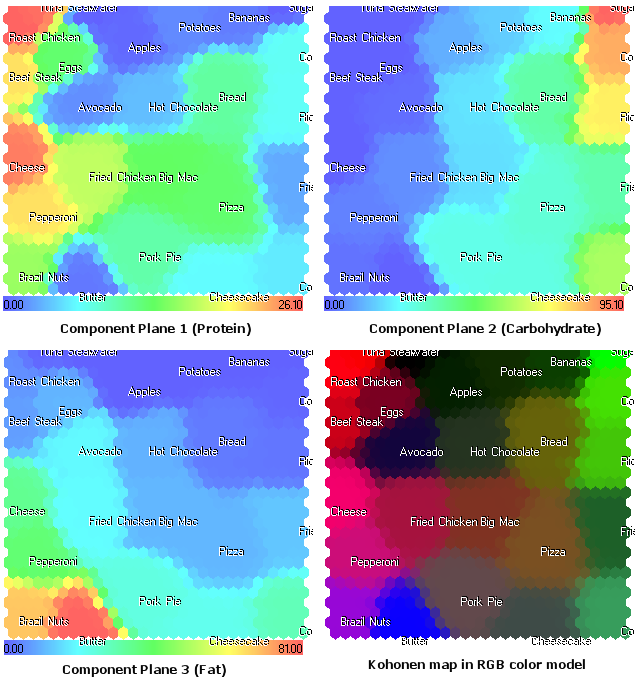
Figura 17. Mapa de Kohonen para alimentos. Planos de componentes e modelo de cores RGB
A representação de planos de componentes, apresentada na Figura 17, cria uma nova perspectiva sobre a estrutura dos componentes de alimentos. Ademais, fornece informações adicionais que não podem ser visualizadas no modelo de cores RGB, apresentado na Figura 9.
Por exemplo, agora é possível visualizar o queijo no 1º plano de componente (proteína). No modelo de cores RGB, ele foi exibido perto da cor magenta, devido à gordura (2º componente).
2.5. Implementação dos planos de componentes para o caso de dimensão arbitrária
Os exemplos que analisamos possuem algumas características específicas: a dimensão era fixa e o algoritmo de visualização era diferente para cada representação diferente (modelos de cores RGB e CMYK).
Agora podemos generalizar o algoritmo para dimensões arbitrárias, mas, neste caso, iremos visualizar somente os planos de componentes. O programa deve ser capaz de carregar os dados arbitrários a partir do arquivo CSV.
Por exemplo, o arquivo food.csv tem o seguinte aspecto:
Protein;Carbohydrate;Fat;Title 0.4;11.8;0.1;Apples 1.9;1.9;19.5;Avocado 1.2;23.2;0.3;Bananas 20.9;0.0;7.9;Beef Steak 13.0;19.0;11.0;Big Mac 15.5;2.9;68.3;Brazil Nuts 10.5;37.0;3.2;Bread 1.0;0.0;81.0;Butter 25.0;0.1;34.4;Cheese 6.4;28.2;22.7;Cheesecake 5.7;58.7;29.3;Cookies 7.0;84.0;0.9;Cornflakes 12.5;0.0;10.8;Eggs 17.0;7.0;20.0;Fried Chicken 3.0;36.0;13.0;Fries 3.8;19.4;10.2;Hot Chocolate 20.9;5.1;38.3;Pepperoni 12.5;30.0;11.0;Pizza 10.1;27.3;24.2;Pork Pie 1.7;16.1;0.3;Potatoes 6.9;74.0;2.8;Rice 26.1;0.3;5.8;Roast Chicken 0.0;95.1;0.0;Sugar 25.6;0.0;0.5;Tuna Steak 0.0;0.0;0.0;Water
A primeira linha do arquivo contém os nomes (títulos) do vetor de dados de entrada. Os títulos são necessários para diferenciar os planos de componentes. Colocaremos os nomes deles no painel de gradientes.
O nome do padrão está localizado na última coluna. Neste caso, é o nome do alimento.
O código do SOM.mq5 (função OnInit) é simplificado:
CSOM KohonenMap; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { MathSrand(200); //--- load patterns from file if(!KohonenMap.LoadTrainDataFromFile(DataFileName)) { Print("Error in loading data for training."); return(1); } //--- train net KohonenMap.Train(); //--- render map KohonenMap.Render(); //--- show patterns from training set KohonenMap.ShowTrainPatterns(); //--- show bmp on the chart KohonenMap.ShowBMP(false); return(0); }
O nome do arquivo com padrões de treinamento é especificado no parâmetro de entrada DataFileName, que em nosso caso é "food.csv".
O resultado é apresentado na Figura 18.

Figura 18. Mapa de Kohonen para alimentos em gradiente preto/branco.
Também adicionamos o parâmetro de entrada ColorScheme para a seleção do esquema de gradiente.
Atualmente, há 4 esquemas de cores disponíveis (ColorScheme=0,1,2,4=preto-branco, azul escuro-azul-verde-amarelo-vermelho, vermelho-preto-verde, vermelho-branco-verde).

Você pode adicionar o seu próprio esquema facilmente adicionando o gradiente ao método CSOM::InitParameters().
O esquema de cores pode ser selecionado a partir dos parâmetros de entrada do Expert Advisor:
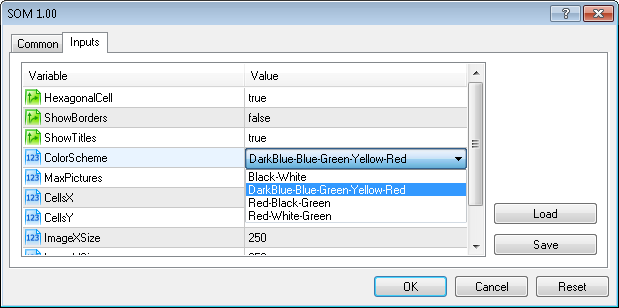
De maneira similar, podemos preparar o conjunto de dados íris (iris-fisher.csv):
Sepal length;Sepal width;Petal length;Petal width;Title 5.1;3.5;1.4;0.2;setosa 4.9;3.0;1.4;0.2;setosa 4.7;3.2;1.3;0.2;setosa 4.6;3.1;1.5;0.2;setosa 5.0;3.6;1.4;0.2;setosa 5.4;3.9;1.7;0.4;setosa 4.6;3.4;1.4;0.3;setosa 5.0;3.4;1.5;0.2;setosa 4.4;2.9;1.4;0.2;setosa 4.9;3.1;1.5;0.1;setosa 5.4;3.7;1.5;0.2;setosa 4.8;3.4;1.6;0.2;setosa 4.8;3.0;1.4;0.1;setosa 4.3;3.0;1.1;0.1;setosa 5.8;4.0;1.2;0.2;setosa 5.7;4.4;1.5;0.4;setosa 5.4;3.9;1.3;0.4;setosa 5.1;3.5;1.4;0.3;setosa 5.7;3.8;1.7;0.3;setosa 5.1;3.8;1.5;0.3;setosa 5.4;3.4;1.7;0.2;setosa 5.1;3.7;1.5;0.4;setosa 4.6;3.6;1.0;0.2;setosa 5.1;3.3;1.7;0.5;setosa 4.8;3.4;1.9;0.2;setosa 5.0;3.0;1.6;0.2;setosa 5.0;3.4;1.6;0.4;setosa 5.2;3.5;1.5;0.2;setosa 5.2;3.4;1.4;0.2;setosa 4.7;3.2;1.6;0.2;setosa 4.8;3.1;1.6;0.2;setosa 5.4;3.4;1.5;0.4;setosa 5.2;4.1;1.5;0.1;setosa 5.5;4.2;1.4;0.2;setosa 4.9;3.1;1.5;0.2;setosa 5.0;3.2;1.2;0.2;setosa 5.5;3.5;1.3;0.2;setosa 4.9;3.6;1.4;0.1;setosa 4.4;3.0;1.3;0.2;setosa 5.1;3.4;1.5;0.2;setosa 5.0;3.5;1.3;0.3;setosa 4.5;2.3;1.3;0.3;setosa 4.4;3.2;1.3;0.2;setosa 5.0;3.5;1.6;0.6;setosa 5.1;3.8;1.9;0.4;setosa 4.8;3.0;1.4;0.3;setosa 5.1;3.8;1.6;0.2;setosa 4.6;3.2;1.4;0.2;setosa 5.3;3.7;1.5;0.2;setosa 5.0;3.3;1.4;0.2;setosa 7.0;3.2;4.7;1.4;versicolor 6.4;3.2;4.5;1.5;versicolor 6.9;3.1;4.9;1.5;versicolor 5.5;2.3;4.0;1.3;versicolor 6.5;2.8;4.6;1.5;versicolor 5.7;2.8;4.5;1.3;versicolor 6.3;3.3;4.7;1.6;versicolor 4.9;2.4;3.3;1.0;versicolor 6.6;2.9;4.6;1.3;versicolor 5.2;2.7;3.9;1.4;versicolor 5.0;2.0;3.5;1.0;versicolor 5.9;3.0;4.2;1.5;versicolor 6.0;2.2;4.0;1.0;versicolor 6.1;2.9;4.7;1.4;versicolor 5.6;2.9;3.6;1.3;versicolor 6.7;3.1;4.4;1.4;versicolor 5.6;3.0;4.5;1.5;versicolor 5.8;2.7;4.1;1.0;versicolor 6.2;2.2;4.5;1.5;versicolor 5.6;2.5;3.9;1.1;versicolor 5.9;3.2;4.8;1.8;versicolor 6.1;2.8;4.0;1.3;versicolor 6.3;2.5;4.9;1.5;versicolor 6.1;2.8;4.7;1.2;versicolor 6.4;2.9;4.3;1.3;versicolor 6.6;3.0;4.4;1.4;versicolor 6.8;2.8;4.8;1.4;versicolor 6.7;3.0;5.0;1.7;versicolor 6.0;2.9;4.5;1.5;versicolor 5.7;2.6;3.5;1.0;versicolor 5.5;2.4;3.8;1.1;versicolor 5.5;2.4;3.7;1.0;versicolor 5.8;2.7;3.9;1.2;versicolor 6.0;2.7;5.1;1.6;versicolor 5.4;3.0;4.5;1.5;versicolor 6.0;3.4;4.5;1.6;versicolor 6.7;3.1;4.7;1.5;versicolor 6.3;2.3;4.4;1.3;versicolor 5.6;3.0;4.1;1.3;versicolor 5.5;2.5;4.0;1.3;versicolor 5.5;2.6;4.4;1.2;versicolor 6.1;3.0;4.6;1.4;versicolor 5.8;2.6;4.0;1.2;versicolor 5.0;2.3;3.3;1.0;versicolor 5.6;2.7;4.2;1.3;versicolor 5.7;3.0;4.2;1.2;versicolor 5.7;2.9;4.2;1.3;versicolor 6.2;2.9;4.3;1.3;versicolor 5.1;2.5;3.0;1.1;versicolor 5.7;2.8;4.1;1.3;versicolor 6.3;3.3;6.0;2.5;virginica 5.8;2.7;5.1;1.9;virginica 7.1;3.0;5.9;2.1;virginica 6.3;2.9;5.6;1.8;virginica 6.5;3.0;5.8;2.2;virginica 7.6;3.0;6.6;2.1;virginica 4.9;2.5;4.5;1.7;virginica 7.3;2.9;6.3;1.8;virginica 6.7;2.5;5.8;1.8;virginica 7.2;3.6;6.1;2.5;virginica 6.5;3.2;5.1;2.0;virginica 6.4;2.7;5.3;1.9;virginica 6.8;3.0;5.5;2.1;virginica 5.7;2.5;5.0;2.0;virginica 5.8;2.8;5.1;2.4;virginica 6.4;3.2;5.3;2.3;virginica 6.5;3.0;5.5;1.8;virginica 7.7;3.8;6.7;2.2;virginica 7.7;2.6;6.9;2.3;virginica 6.0;2.2;5.0;1.5;virginica 6.9;3.2;5.7;2.3;virginica 5.6;2.8;4.9;2.0;virginica 7.7;2.8;6.7;2.0;virginica 6.3;2.7;4.9;1.8;virginica 6.7;3.3;5.7;2.1;virginica 7.2;3.2;6.0;1.8;virginica 6.2;2.8;4.8;1.8;virginica 6.1;3.0;4.9;1.8;virginica 6.4;2.8;5.6;2.1;virginica 7.2;3.0;5.8;1.6;virginica 7.4;2.8;6.1;1.9;virginica 7.9;3.8;6.4;2.0;virginica 6.4;2.8;5.6;2.2;virginica 6.3;2.8;5.1;1.5;virginica 6.1;2.6;5.6;1.4;virginica 7.7;3.0;6.1;2.3;virginica 6.3;3.4;5.6;2.4;virginica 6.4;3.1;5.5;1.8;virginica 6.0;3.0;4.8;1.8;virginica 6.9;3.1;5.4;2.1;virginica 6.7;3.1;5.6;2.4;virginica 6.9;3.1;5.1;2.3;virginica 5.8;2.7;5.1;1.9;virginica 6.8;3.2;5.9;2.3;virginica 6.7;3.3;5.7;2.5;virginica 6.7;3.0;5.2;2.3;virginica 6.3;2.5;5.0;1.9;virginica 6.5;3.0;5.2;2.0;virginica 6.2;3.4;5.4;2.3;virginica 5.9;3.0;5.1;1.8;virginica
O resultado é apresentado na Figura 19.

Figura 19. Conjunto de dados íris. Planos de componentes em esquema de cores vermelho-preto-verde (ColorScheme=2, iris-fisher.csv)
Agora temos uma ferramenta para os aplicativos reais.
2.6. Exemplo 5. Mapas de calor de mercado
Mapas auto-organizáveis podem ser usados em mapas de movimento de mercado. ás vezes é necessário ter um panorama global do mercado e o mapa de calor de mercado é uma ferramenta muito útil. As ações são agrupadas de acordo com setores econômicos.
A cor atual da ação depende de sua taxa atual de crescimento (em %):

Figura 20. Mapa de calor de mercado para ações do S&P 500
O mapa de calor semanal das ações do S&P (http://finviz.com) é apresentado na Figura 20. A cor depende da taxa de crescimento (em %):
![]()
O tamanho do retângulo de ações depende da capitalização de mercado. A mesma análise pode ser feita no terminal do cliente MetaTrader5 com o uso de mapas de Kohonen.
A ideia é utilizar as taxas de crescimento (em %) para diversos períodos de tempo. Nós temos a ferramenta para trabalhar com os mapas de Kohonen, então apenas precisaremos do script que armazena os dados em arquivo .csv.
Os dados de preços CFD das ações norte-americanas (#AA, #AIG, #AXP, #BA, #BAC, #C, #CAT, #CVX, #DD, #DIS, #EK, #GE, #HD, #HON, #HPQ, #IBM, #INTC, #IP, #JNJ, #JPM, #KFT, #KO, #MCD, #MMM, #MO, #MRK, #MSFT, #PFE, #PG, #T, #TRV, #UTX, #VZ, #WMT и #XOM) podem ser encontrados no servidor Demo da MetaQuotes.
O script que prepara o arquivo dj.csv é muito simples:
//+------------------------------------------------------------------+ //| DJ.mq5 | //| Copyright 2011, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" string s_cfd[35]= { "#AA","#AIG","#AXP","#BA","#BAC","#C","#CAT","#CVX","#DD","#DIS","#EK","#GE", "#HD","#HON","#HPQ","#IBM","#INTC","#IP","#JNJ","#JPM","#KFT","#KO","#MCD","#MMM", "#MO","#MRK","#MSFT","#PFE","#PG","#T","#TRV","#UTX","#VZ","#WMT","#XOM" }; //+------------------------------------------------------------------+ //| Returns price change in percents | //+------------------------------------------------------------------+ double PercentChange(double Open,double Close) { return(100.0*(Close-Open)/Close); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { ResetLastError(); int filehandle=FileOpen("dj.csv",FILE_WRITE|FILE_ANSI); if(filehandle==INVALID_HANDLE) { Alert("Error opening file"); return; } //--- MqlRates MyRates[]; ArraySetAsSeries(MyRates,true); string t="M30;M60;M90;M120;M150;M180;M210;M240;Title"; FileWrite(filehandle,t); Print(t); int total_symbols=ArraySize(s_cfd); for(int i=0; i<total_symbols; i++) { string cursymbol=s_cfd[i]; int copied1=CopyRates(cursymbol,PERIOD_M30,0,8,MyRates); if(copied1>0) { string s=""; s=s+DoubleToString(PercentChange(MyRates[1].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[2].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[3].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[4].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[5].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[6].open,MyRates[0].close),3)+";"; s=s+DoubleToString(PercentChange(MyRates[7].open,MyRates[0].close),3)+";"; s=s+cursymbol; Print(s); FileWrite(filehandle,s); } else { Print("Error in request of historical data on symbol ",cursymbol); return; } } Alert("OK"); FileClose(filehandle); } //+------------------------------------------------------------------+
Os dados históricos devem ser baixados. Você pode fazer isso automaticamente utilizando o script DownloadHistory.
Como resultado do script dj.mq5, iremos obter o arquivo dj.csv com os seguintes dados:
M30;M60;M90;M120;M150;M180;M210;M240;Title 0.063;-0.564;-0.188;0.376;0.251;0.313;0.627;0.439;#AA -0.033;0.033;0.067;-0.033;0.067;-0.133;0.266;0.533;#AIG -0.176;0.039;0.039;0.274;0.196;0.215;0.430;0.646;#AXP -0.052;-0.328;-0.118;0.315;0.223;0.367;0.288;0.328;#BA -0.263;-0.351;-0.263;0.000;-0.088;0.088;0.000;-0.088;#BAC -0.224;-0.274;-0.374;-0.100;-0.274;-0.224;-0.324;-0.598;#C -0.069;-0.550;-0.079;0.766;0.727;0.638;0.736;0.589;#CAT -0.049;-0.168;0.099;0.247;0.187;0.049;0.355;0.266;#CVX 0.019;-0.058;0.058;0.446;0.174;0.349;0.136;-0.329;#DD -0.073;-0.219;-0.146;0.267;0.170;0.292;0.170;0.267;#DIS -1.099;-1.923;-1.099;0.275;0.275;0.275;-0.549;-1.374;#EK -0.052;-0.310;-0.103;0.362;0.258;0.362;0.465;0.258;#GE -0.081;-0.244;-0.326;-0.136;0.081;0.326;0.489;0.489;#HD -0.137;-0.427;-0.171;0.427;0.445;0.342;0.325;0.359;#HON -0.335;-0.363;-0.112;0.112;0.168;0.307;0.475;0.251;#HPQ 0.030;-0.095;0.065;0.190;0.071;0.214;0.279;0.327;#IBM 0.000;-0.131;-0.044;-0.088;-0.044;0.000;0.000;0.044;#INTC -0.100;-0.200;-0.166;0.100;-0.067;0.033;-0.532;-0.798;#IP -0.076;0.076;0.259;0.473;0.427;0.336;0.336;-0.076;#JNJ -0.376;-0.353;-0.494;-0.259;-0.423;-0.329;-0.259;-0.541;#JPM -0.057;-0.086;-0.029;0.086;0.114;0.057;0.257;-0.114;#KFT 0.059;-0.030;0.119;0.282;0.119;0.193;0.208;-0.119;#KO -0.109;-0.182;0.206;0.352;0.279;0.473;0.521;0.194;#MCD -0.043;-0.195;-0.151;0.216;0.270;0.227;0.411;0.206;#MMM -0.036;-0.072;0.072;0.144;-0.072;-0.108;0.108;0.072;#MO 0.081;-0.081;0.027;0.081;-0.054;0.027;-0.027;-0.108;#MRK 0.083;0.083;0.041;0.331;0.083;0.248;0.166;0.041;#MSFT 0.049;0.000;0.243;0.680;0.194;0.243;0.340;0.097;#PFE -0.045;0.060;0.104;0.015;-0.179;-0.149;-0.224;-0.224;#PG 0.097;-0.032;0.000;0.129;0.129;0.064;0.097;0.064;#T -0.277;-0.440;-0.326;-0.358;-0.537;-0.619;-0.570;-0.733;#TRV -0.081;-0.209;0.035;0.325;0.198;0.093;0.128;-0.035;#UTX 0.054;0.000;0.054;0.190;0.136;0.326;0.380;0.353;#VZ -0.091;-0.091;-0.036;0.036;-0.072;0.000;0.145;-0.127;#WMT -0.062;-0.211;0.087;0.198;0.186;0.050;0.347;0.508;#XOM
Após lançar o som.mq5(ColorScheme=3, CellsX=30,CellsY=30, ImageXSize=200, ImageXSize=200, DataFileName="dj.csv"), iremos obter 8 imagens. Cada uma delas corresponde aos intervalos de tempo de 30, 60, 90, 120, 150, 180, 210 e 240 minutos.
Os mapas de Kohonen dos dados de taxa de crescimento de mercado (ações norte-americanas) das últimas 4 horas da sessão de negociações de 23 de maio de 2011 são apresentados na Figura 21.
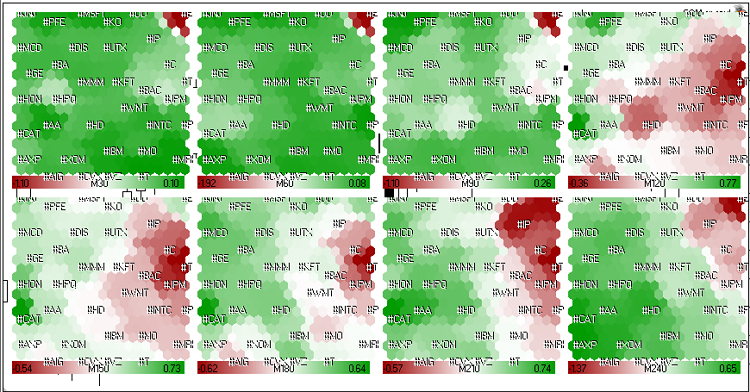
Figura 21. Mapas de Kohonen das ações norte-americanas (últimas 4 horas da sessão de negociações de 23 de maio de 2011).
É possível perceber, através da Figura 21, que a dinâmica de #C (Citigroup Inc.), #T (AT&T Inc.), #JPM (JPMorgan Chase & Co) e #BAC (Bank of America) é similar. Eles foram agrupados em um conjunto vermelho de longo prazo.
Durante a última hora e meia (M30, M60, M90) a dinâmica tornou-se verde, mas em geral (M240), as ações estavam na zona vermelha.
Com o uso dos mapas de Kohonen, é possível visualizar a dinâmica relativa das ações, encontrar líderes e perdedores e o ambiente deles. Os elementos com dados similares formam agrupamentos.
Como é possível ver na Figura 21a, o preço das ações da Citigroup Inc. foi líder em queda. Em geral, todas as ações das instituições financeiras estavam na zona vermelha.
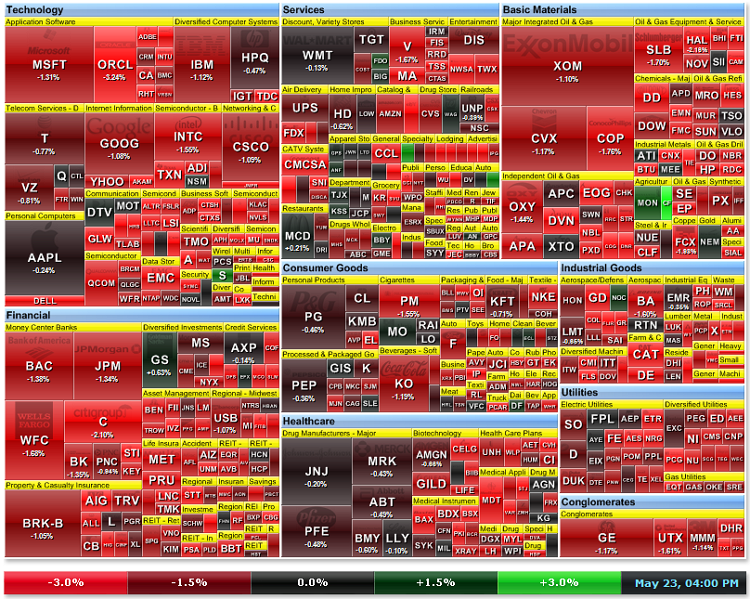
Figura 21a. Mapa de calor de mercado de 23 de maio de 2011 (fonte: http://finviz.com)
De maneira similar, podemos calcular os mapas de Kohonen do mercado FOREX (Figura 22):
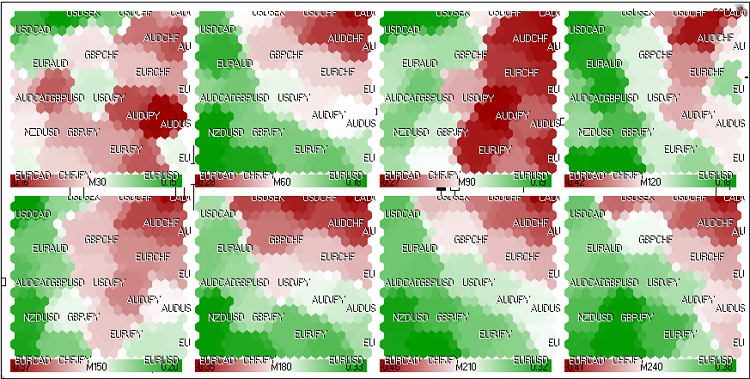
Figura 22. Mapa de Kohonen do mercado FOREX (24 de maio de 2011, sessão europeia)
Foram utilizados os seguintes pares: EURUSD, GBPUSD, USDCHF, USDJPY, USDCAD, AUDUSD, NZDUSD, USDSEK, AUDNZD, AUDCAD, AUDCHF, AUDJPY, CHFJPY, EURGBP, EURAUD, EURCHF, EURJPY, EURNZD, EURCAD, GBPCHF, GBPJPY, CADCHF.
As taxas de crescimento são exportadas para fx.csv com a utilização do script fx.mq5.
M30;M60;M90;M120;M150;M180;M210;M240;Title 0.058;-0.145;0.045;-0.113;-0.038;-0.063;0.180;0.067;EURUSD 0.046;-0.100;0.078;0.094;0.167;0.048;0.123;0.160;GBPUSD -0.048;0.109;-0.142;-0.097;-0.219;-0.143;-0.277;-0.236;USDCHF 0.042;0.097;0.043;-0.024;-0.009;-0.067;0.024;0.103;USDJPY -0.045;0.162;0.155;0.239;0.217;0.246;0.157;0.227;USDCAD 0.095;-0.126;-0.018;-0.141;-0.113;-0.062;0.081;-0.005;AUDUSD 0.131;-0.028;0.167;0.096;-0.013;0.147;0.314;0.279;NZDUSD -0.047;0.189;-0.016;0.107;0.084;0.076;-0.213;-0.133;USDSEK -0.034;-0.067;-0.188;-0.227;-0.102;-0.225;-0.234;-0.291;AUDNZD 0.046;0.039;0.117;0.102;0.097;0.170;0.234;0.216;AUDCAD 0.057;-0.016;-0.158;-0.226;-0.328;-0.215;-0.180;-0.237;AUDCHF 0.134;-0.020;0.024;-0.139;-0.124;-0.127;0.107;0.098;AUDJPY 0.083;-0.009;0.184;0.084;0.208;0.082;0.311;0.340;CHFJPY 0.025;-0.036;-0.030;-0.200;-0.185;-0.072;0.058;-0.096;EURGBP -0.036;-0.028;0.061;0.010;0.074;-0.006;0.088;0.070;EURAUD 0.008;-0.049;-0.098;-0.219;-0.259;-0.217;-0.094;-0.169;EURCHF 0.096;-0.043;0.085;-0.124;-0.049;-0.128;0.206;0.157;EURJPY -0.073;-0.086;-0.119;-0.211;-0.016;-0.213;-0.128;-0.213;EURNZD 0.002;0.009;0.181;0.119;0.182;0.171;0.327;0.284;EURCAD -0.008;0.004;-0.077;-0.015;-0.054;-0.127;-0.164;-0.080;GBPCHF 0.079;-0.005;0.115;0.079;0.148;-0.008;0.144;0.253;GBPJPY 0.013;-0.060;-0.294;-0.335;-0.432;-0.376;-0.356;-0.465;CADCHF
Além dos preços, você pode utilizar os valores dos indicadores em diferentes períodos de tempo.
2.6. Exemplo 6. Análise dos resultados da otimização
O Provador de Estratégia do terminal do cliente MetaTrader 5 oferece uma oportunidade para explorar a estrutura do espaço de parâmetro e encontrar o melhor conjunto de parâmetros de estratégia. Você também pode exportar os resultados da otimização utilizando a opção "Exportar para XML (MS Office Excel)" do menu de contexto da aba "Resultados de Otimização".
As Estatísticas do Provador também estão incluídas nos resultados da otimização (41 colunas):
- Resultado.
- Lucro.
- Lucro bruto.
- Perda bruta.
- Retirada.
- Lucro esperado.
- Fator de lucro.
- Fator de recuperação.
- índice de Sharpe.
- Nível de margem.
- Personalizado.
- Balanço mínimo.
- Balanço DD máximo.
- Balanço DD máximo (%).
- Balanço DD relativo.
- Balanço DD relativo (%).
- Participação mínima.
- Participação DD máxima.
- Participação DD máxima (%).
- Participação DD relativa.
- Participação DD relativa (%).
- Negociações.
- Acordos.
- Negociações curtas.
- Lucro de negociações curtas.
- Negociações longas.
- Lucro de negociações longas.
- Lucro de negociações.
- Perda de negociações.
- Máx. de lucro de negociação.
- Máx. de perda de negociação.
- Máx. de ganhos consecutivos.
- Máx. de ganhos consecutivos ($).
- Máx. de lucro consecutivo.
- Total de lucros consecutivos máx.
- Máx. de perdas consecutivas.
- Máx. de perdas consecutivas ($).
- Máx. de perda consecutiva.
- Total de perdas consecutivas máx.
- Média de ganhos consecutivos.
- Média de perdas consecutivas.
O uso das estatísticas do provador permite ajudar a análise do espaço de parâmetros. é notável que muitos parâmetros das estatísticas são intimamente relacionados e dependem dos resultados do desempenho de negociação.
Por exemplo, os melhores resultados de negociação têm os maiores valores de parâmetros de lucro, fator de lucro, fator de recuperação e índice de Sharpe. Este fato permite utilizá-los na análise dos resultados.
Resultados da otimização do Expert Advisor MovingAverage.mq5
Neste capítulo, iremos fazer considerações acerca da análise dos resultados da otimização do Expert Advisor MovingAverage.mq5, incluso no pacote padrão do terminal do cliente MetaTrader 5. Este Expert Advisor é baseado em preços cruzados e indicador de média móvel. Ele possui dois parâmetros de entrada: MovingPeriod e MovingShift. Ou seja, como resultado, nós teremos o arquivo XML com 43 colunas.
Não iremos considerar o espaço de parâmetros de 43 dimensões. Os mais interessantes são:
- Lucro.
- Fator de lucro.
- Fator de recuperação.
- índice de Sharpe.
- Negociações.
- Lucro das negociações (%).
- Período móvel (MovingPeriod).
- Alteração móvel (MovingShift).
Perceba que adicionamos o parâmetro Lucro das negociações (%) (ele está ausente nos resultados). Isso significa que o percentual de acordos lucrativos é calculado como resultado da divisão dos Lucros das negociações (28) por Negociações (22), multiplicados por 100.
Vamos preparar o arquivo optim.csv com 9 colunas para 400 grupos de parâmetros de entrada do provador de estratégia do MetaTrader 5.
Profit;Profit Factor;Recovery Factor;Sharpe Ratio;Trades;ProfitTrades(%);MovingPeriod;MovingShift;Title -372.3;0.83;-0.51;-0.05;71;28.16901408;43;6;43 -345.79;0.84;-0.37;-0.05;66;27.27272727;50;6;50 ...
Note que nós usamos o valor do período móvel como título de coluna. Ele será usado para "marcar" os padrões nos mapas de Kohonen.
No provador de estratégia, nós otimizamos os valores do MovingPeriod e MovingShift com os seguintes parâmetros:
- Símbolo - EURUSD.
- Período - H1.
- Modo de geração de tick - "OHLC de 1 minuto".
- Intervalo de teste - 2011.01.01-2011.05.24.
- Otimização - Rápida (algoritmo genético).
- Otimização - Máx. balanço.
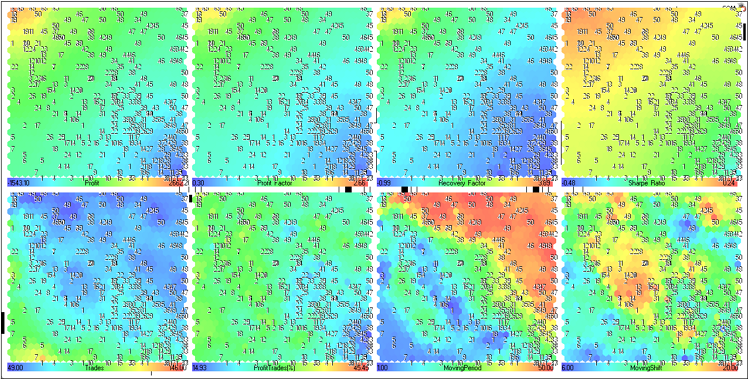
Figura 23. Mapa de Kohonen para os resultados da otimização do EA MovingAverage (representação de planos de componentes)
Vamos considerar os planos de componentes da linha superior (Lucro, Fator de lucro, Fator de recuperação e índice de Sharpe).
Eles foram combinados na Figura 24.
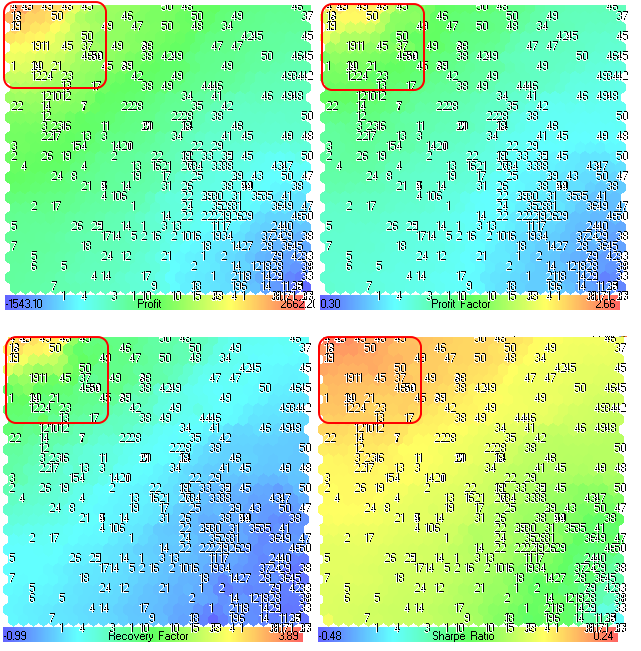
Figura 24. Planos de componentes para os parâmetros Lucro, Fator de lucro, Fator de recuperação e índice de Sharpe
Primeiramente, precisávamos encontrar as regiões com os melhores resultados de otimização.
é possível observar na Figura 24 que as regiões com valores máximos estão localizadas no canto superior esquerdo. Os números correspondem ao período de média do indicador Média Móvel (parâmetro MovingPeriod, utilizado como título). A localização dos números é a mesma para todos os planos de componentes. Cada plano de componentes tem a sua própria variação de valores. Os valores estão inscritos no painel de gradientes.
Os melhores resultados de otimização têm os maiores valores de Lucro, Fator de Lucro, Fator de Recuperação e índice de Sharpe, então temos as informações sobre as regiões no mapa (delineadas na Figura 24).
Os planos de componentes para Negociações, Lucro das negociações (%), MovingPeriod e MovingShift são apresentados na Figura 25.
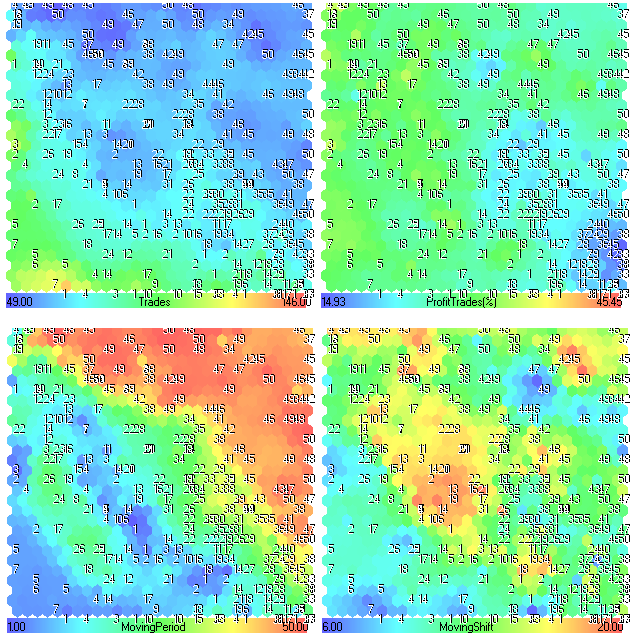
Figura 25. Planos de componentes para os parâmetros Negociações, Lucro das negociações (%), MovingPeriod e MovingShift
Análise de plano de componente
À primeira vista, não há qualquer informação interessante. Os 4 primeiros planos de componentes (Lucro, Fator de Lucro, Fator de recuperação e índice de Sharpe) parecem similares, porque eles dependem diretamente do desempenho do sistema de negociação.
É possível observar na Figura 24 que a região superior esquerda é muito interessante (por exemplo, os melhores resultados podem ser obtidos se nós estabelecermos o MovingPeriod de 45 a 50.
O Expert Advisor foi testado em período de uma hora em EURUSD, com estratégia baseada em tendência. Podemos considerar esses valores como uma memória de "tendência de mercado". Se for verdadeira, a memória de tendência de mercado para a primeira metade de 2011 é igual a 2 dias.
Vamos observar outros planos de componentes.
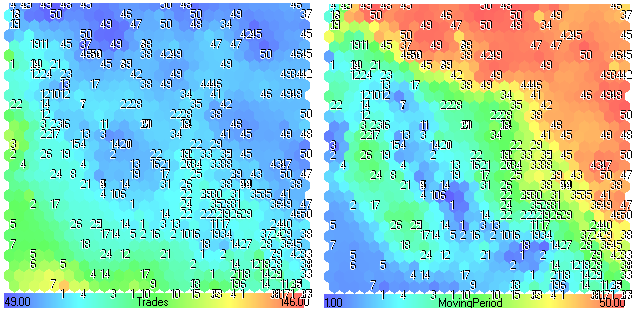
Figura 26. Planos de componentes Negociações-MovingPeriod
Ao observar a Figura 26, podemos ver que os menores valores de MovingPeriod (regiões azuis) levam a maiores valores de Negociações (regiões amarelas-vermelhas). Se o período de média móvel é baixo, há muitos crossovers (negociações).
Também podemos observar isto no plano de componentes de Negociações (regiões verdes com números inferiores a 20).
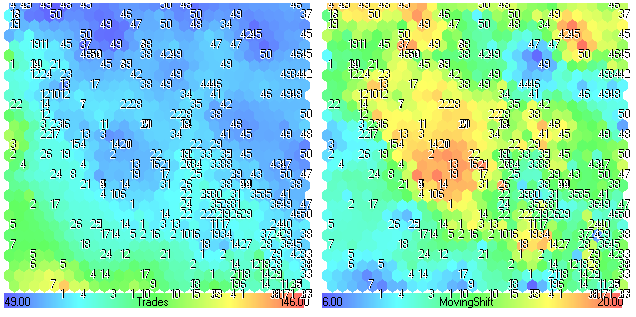
Figura 27. Planos de componentes Negociações-MovingShift
O número de negociações diminui (regiões azuis) com o aumento de MovingShift (regiões amarelas-vermelhas). Comparando os planos de componentes para MovingShift e a Figura 24, é possível perceber que o parâmetro MovingShift não é muito importante para o desempenho desta estratégia de negociação.
O percentual de negociações lucrativas, Lucro das negociações (%), não depende diretamente do MovingPeriod ou do MovingShift - é uma característica integral do sistema de negociação. Em outras palavras, a análise da sua correlação com os parâmetros de entrada não tem significado.
Estratégias de negociação mais complexas podem ser analisadas de maneira semelhante. Você precisa encontrar o(s) parâmetro(s) mais importante(s) do seu sistema de negociação e usá-lo(s) como título.
Conclusão
A principal vantagem dos mapas auto-organizáveis é a possibilidade de produzir uma representação bidimensional discretizada de dados de alta dimensão. Os dados com características similares formam agrupamentos que simplificam a análise de correlação.
Os detalhes e outros aplicativos podem ser encontrados no excelente livro Visual Explorations in Finance: with Self-Organizing Maps, de Guido Deboeck e Teuvo Kohonen.
Apêndice
Após a publicação, Alex Sergeev propôs uma versão melhorada de classes (SOM_Alex-Sergeev_en.zip).
Lista de alterações:
1. A exibição de imagens foi alterada: cIntBMP::Show(int aX, int aY, string aBMPFileName, string aObjectName, bool aFromImages=true).
2. Adição do recurso abrir arquivo com imagens:
#import "shell32.dll" int ShellExecuteW(int hwnd, string oper, string prog, string param, string dir, int show); #import input bool OpenAfterAnaliz=true; // open folder with maps after finish
Alterações na classe CSOM:
- Adição do método CSOM::HideChart - ocultar gráfico.
- Adição dos membros de classe m_chart, m_wnd, m_x0, m_y0 - (gráfico, janela e coordenadas para exibir imagens).
+ prefixo m_sID - nomes de objeto adicionado. O prefixo usa o nome do arquivo. De forma padrão, utiliza-se o prefixo "SOM". - Todos os mapas são salvos no arquivo com o nome m_sID.
- Os arquivos bmp são nomeados pelo nome de coluna dos padrões.
- O método CSOM::ShowBMP foi alterado (mapas armazenados em \Files em vez de \Images - é muito mais rápido).
- O CSOM::NetDeinit foi alterado por CSOM::HideBMP.
- O método CSOM::ReadCSVData foi modificado. A primeira coluna contém títulos.
- Uma bandeira foi adicionada para mostrar mapas intermediários em CSOM::Train(bool bShowProgress).
- A exibição de mapas intermediários em CSOM::Train é feita a cada 2 segundos (em vez de iteração). O progresso é exibido no gráfico através da utilização do Comentário.
- Os nomes de algumas variáveis foram otimizados. Os métodos de classe foram ordenados por categoria.
O desenho de bmp é um processo muito lento. Se você não precisa realmente dele, não o desenhe todas as vezes.
Os exemplos de imagens de SOM com otimização de resultados estão inclusos no arquivo.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/283
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
 Criar critérios personalizados de otimização de Expert Advisors
Criar critérios personalizados de otimização de Expert Advisors
 Estimativas estatísticas
Estimativas estatísticas
 Teoria dos indicadores adaptativosavançados e sua implementação em MQL5
Teoria dos indicadores adaptativosavançados e sua implementação em MQL5
 Pagamentos e métodos de pagamento
Pagamentos e métodos de pagamento
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
eles não sabem como fazer isso, há treinamento para implantar vetores de pesos NS em conjuntos de treinamento - o resultado é agrupar os dados, mas a resposta da própria rede está ausente em outros dados - ou melhor, estará, mas produzirá valores aleatórios.
sobre a raiz... o nome não é rede Kohonen, mas Self Organising Maps (SOM).
UPD: Não vejo sentido em continuar a discussão, pois pela segunda vez a discussão é reduzida ao que está escrito na Wiki e, agora, ao que foi escrito por alguém "Citando S. Osovsky". Concordo em permanecer no cativeiro de meu raciocínio, que não é apoiado pela frase "SOM Kohonen" pode prever, e o inverso - eles não podem
Sempre se vê o que se quer ver.
Isso é exatamente o que você confirmou com a postagem acima - não tenho vontade de discutir a tradução correta de "Kohonen's self-organising maps" - se havia algum espaço nessa tradução:
Eu sempre olho para a raiz, sabia que ninguém a chamaria de rede neural se os mapas de Kohonen não pudessem prever.
Assim como não há absolutamente nenhum interesse em discutir "citações de S. Osovsky", como mostra a prática - reimpressões de trabalhos de recursos ingleses prevalecem no runet, não tenho certeza de que Osovsky escreveu seu próprio trabalho, e discuto com os membros do fórum, não com o escritor?
No link, mostrei minhas pesquisas sobre esse tópico na runet, no site autorizado, na minha opinião, BaseGroup Labs, também não há confirmação.....
.... ok, terminei - não quero me repetir, apenas preveja )))).
lista de alterações anexa:
1. pequena alteração na função cIntBMP::Show(int aX, int aY, string aBMPFileName, string aObjectName, bool aFromImages=true)
2. adicionada ao script principal
Alterações na classe CSOM
1. Adicionada a função CSOM::HideChart - ela escurece o gráfico, a grade, etc. sob a cor de fundo
2. Adicionados os parâmetros m_chart, m_wnd, m_x0, m_y0 - indicando em qual gráfico e em qual janela exibir os mapas.
+ prefixo dos nomes de objetos m_sID. O prefixo é automaticamente adotado pelo nome do arquivo, caso contrário, é atribuído a "SOM"
3. Os mapas são gravados na pasta chamada m_sID
4. Os nomes dos arquivos bmp são dados pelo nome da coluna do padrão de treinamento.
4. Função CSOM::ShowBMP alterada - os mapas não são copiados para a pasta Images, mas permanecem em Files (caso contrário, isso consumiria muito tempo)
5. Em vez da função CSOM::NetDeinit , agora existe a função CSOM::HideBMP
7. A função CSOM::ReadCSVData foi reconfigurada para ler o arquivo de modo que a primeira coluna seja a coluna de nomes
6. Adicionado sinalizador à função CSOM::Train para mostrar mapas intermediários CSOM::Train( bool bShowProgress)
8. Na função CSOM::Train, os dados intermediários são exibidos a cada 2 segundos em vez de iterações,
e também a notificação de progresso é movida do registro para o comentário
9. Alguns nomes de variáveis foram encurtados e as funções foram categorizadas.
A renderização de Bmp torna o processo muito mais lento. Portanto, é melhor não usá-la desnecessariamente.
Os mapas de Kohonen são adequados para classificar grandes quantidades de dados diferentes. Por exemplo, 100 animais diferentes. Nesse caso, você terá que classificar por um parâmetro - cor da pelagem. A matemática dessa abordagem não permite reunir diferentes parâmetros.
Essa abordagem é a mais estúpida possível para decisões em Forex. Imagine que a classificação por um parâmetro seja reduzida a uma decisão de "comprar" ou "não comprar". Então, você pode criar dois nós no mapa de Kohonen e isso será muito engraçado. É claro que há mastodontes que criarão 10 mil nós e olharão para esse mapa com desejo, dizendo: ah, como ele é lindamente colorido.
Aqui está um exemplo com o período e o deslocamento de um Expert Advisor MT5 padrão - um mapa (rede?) de Kohonen separado para o período de suavização e outro separado para o deslocamento. Você se senta e pensa no que fazer com isso.
Um perseptron multicamadas é uma caixa preta, para a qual, se tudo for feito corretamente, você precisará inserir parâmetros diferentes e, na saída, poderá obter uma resposta inequívoca - mais do que o limite (resposta "sim") ou menos do que o limite (resposta "não"). Isso é mais adequado para mim.
Depois de ler vários livros sobre o tópico de aprendizado de máquina, percebi uma ideia que sempre se repete: não existe um modelo único para criar uma rede neural. Cada tarefa exige um estudo extremamente individual dos dados, a preparação dos dados, a descoberta da estrutura da rede e o ajuste dessa rede. Em outras palavras, há opções que não são adequadas para o Forex e para tomar uma decisão de "comprar" ou "não comprar". Acredito que os mapas de Kohonen não são adequados para isso.
Embora nós, pessoas talentosas, muitas vezes estejamos errados, pois os erros são a principal força do talento.
Embora nós, pessoas talentosas, cometamos erros com frequência, os erros são a principal força do talento.
Quase vomitei
Os mapas de Kohonen são adequados para classificar um grande número de dados diferentes. Por exemplo, 100 animais diferentes. Nesse caso, você terá que classificar por um parâmetro - cor da pelagem. A matemática dessa abordagem não permite reunir diferentes parâmetros.
Essa abordagem é a mais estúpida possível para decisões em Forex. Imagine que a classificação por um parâmetro seja reduzida a uma decisão de "comprar" ou "não comprar". Então, você pode criar dois nós no mapa de Kohonen e isso será muito engraçado. É claro que há mastodontes que criarão 10 mil nós e olharão para esse mapa com desejo, dizendo: ah, como ele é lindamente colorido.
Aqui está um exemplo com o período e o deslocamento de um Expert Advisor MT5 padrão - um mapa (rede?) de Kohonen separado para o período de suavização e outro separado para o deslocamento. Você se senta e pensa no que fazer com isso.
Acho que os mapas de Kohonen não são adequados para isso.
Você simplesmente não entende.
Um mapa não precisa necessariamente responder à pergunta "para onde".
Ele pode destacar padrões semelhantes no histórico, de modo que você não precise ficar procurando-os manualmente por meio ano.
Quando um macaco recebe uma ferramenta, há uma chance de que ele comece a martelar pregos com uma régua.