Visualisez le ! Bibliothèque graphique MQL5 similaire à 'plot' du langage R

Lors de l'étude de la logique de trading, la représentation visuelle sous forme de graphiques est d’une grande importance. Un certain nombre de langages de programmation populaires dans la communauté scientifique (tels que R et Python) contiennent une fonction spéciale "plot" utilisée pour la visualisation. Elle permet de dessiner des lignes, des distributions de points et des histogrammes pour visualiser les modèles.

Le principal avantage de la fonction "plot" est que vous n'avez besoin que de quelques lignes de code pour tracer n'importe quel graphique. Il suffit de passer le tableau de données en paramètre et de spécifier le type de graphique, c'est tout ! La fonction "plot" effectue toutes les opérations : calcul d'une échelle, construction d'axes, sélection d'une couleur, etc.

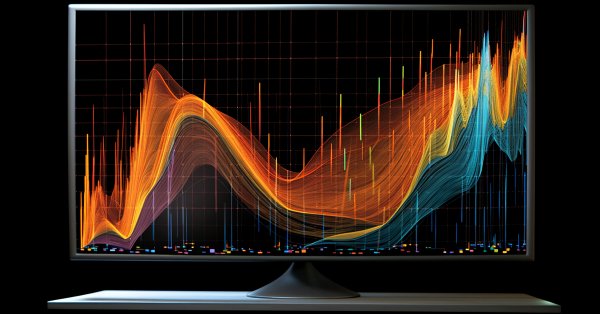
En MQL5, toutes les caractéristiques de la fonction sont représentées par la méthode de la bibliothèque graphique de la Bibliothèque Standard. L'exemple de code et le résultat de son exécution sont ci-dessous :

#include <Graphics\Graphic.mqh>
#define RESULT_OR_NAN(x, expression) ((x==0) ? (double)"nan" : expression)
//--- Fonctions
double BlueFunction(double x) { return(RESULT_OR_NAN(x, 10*x*sin(1/x))) ; }
double RedFunction(double x) { return(RESULT_OR_NAN(x, sin(100*x)/sqrt(x))) ; }
double OrangeFunction(double x) { return(RESULT_OR_NAN(x, sin(100*x)/sqrt(-x))); }
//+------------------------------------------------------------------+
//| Fonction de démarrage du programme de script                     |
//+------------------------------------------------------------------+
void OnStart()
  {
   double from=-1.2;
   double to=1.2;
   double step=0.005;
   CGraphic graphic;
   graphic.Create(0, "G", 0, 30, 30, 780, 380);
//--- couleurs
   CColorGenerator generator;
   uint blue= generator.Next();
   uint red = generator.Next();
   uint orange=generator.Next();
//--- trace toutes les courbes
   graphic.CurveAdd(RedFunction, from, to, step, red, CURVE_LINES, "Red");
   graphic.CurveAdd(OrangeFunction, from, to, step, orange, CURVE_LINES, "Orange");
   graphic.CurveAdd(BlueFunction, from, to, step, blue, CURVE_LINES, "Blue");
   graphic.CurvePlotAll();
   graphic.Update();
  }

La classe de base CCanvas et son développement

La bibliothèque standard contient la classe de base CCanvas, conçue pour le traçage rapide et facile d'images directement sur les graphiques des prix. La classe est basée sur la création d'une ressource graphique et sur le dessin de primitives simples (points, lignes droites et polylignes, cercles, triangles et polygones) sur le canevas. Cette classe implémente les fonctions permettant de remplir les formes et d'afficher le texte en utilisant la police, la couleur et la taille nécessaires.

Au départ, CCanvas ne contenait que deux modes d'affichage des primitives graphiques : avec anti-crénelage, ou anti-aliasing, (AA) et sans. Les nouvelles fonctions ont ensuite été ajoutées pour le traçage des primitives sur la base de l'algorithme de Wu :

• LineWu — ligne droite
• PolylineWu — polyligne
  
• PolygonWu — polygone
  
• TriangleWu — triangle
  
• CircleWu — cercle
• EllipseWu — ellipse

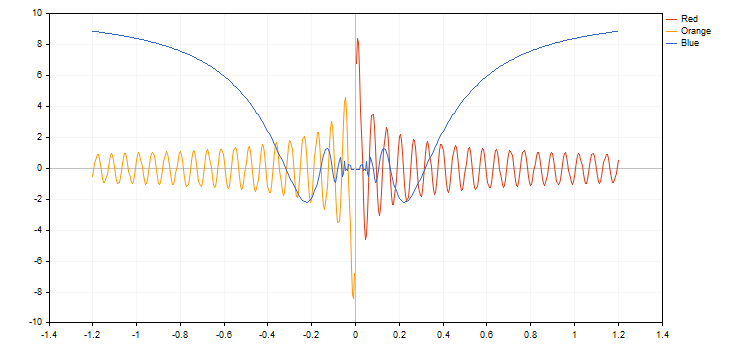
L'algorithme de Wu combine une élimination de haute qualité du crénelage avec une vitesse d'exécution proche de celle de l'algorithme de Bresenham sans anti-crénelage. Il diffère également visuellement de l'algorithme d'anti-crénelage standard (AA) implémenté dans CCanvas. Vous trouverez ci-dessous un exemple de tracé d'un cercle à l'aide des trois fonctions différentes :

#include<Canvas\Canvas.mqh>
CCanvas canvas;
//+------------------------------------------------------------------+
//| Fonction de démarrage du programme de script                     |
//+------------------------------------------------------------------+
void OnStart()
  {
   int Width=800;
   int Height=600;
//--- création du canevas
   if (!canvas.CreateBitmapLabel(0, 0, "CirclesCanvas", 30, 30, Width, Height))
     {
      Print("Erreur lors de la création du canevas : ", GetLastError());
     }
//--- dessin
   canvas.Erase(clrWhite);
   canvas.Circle(70, 70, 25, clrBlack);
   canvas.CircleAA(120, 70, 25, clrBlack);
   canvas.CircleWu(170, 70, 25, clrBlack);
//---
   canvas.Update();  
  }

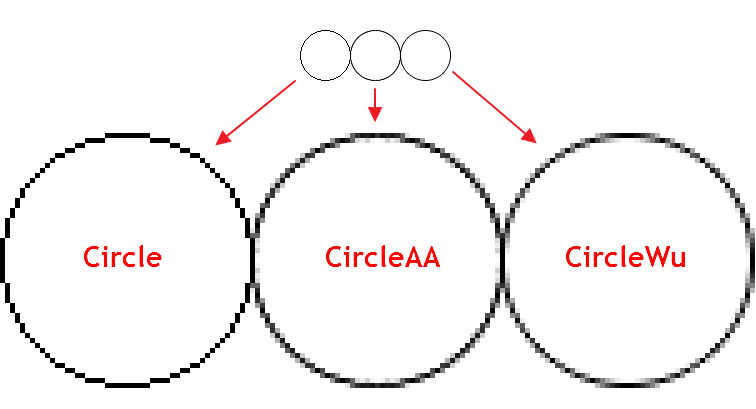
Comme nous pouvons le voir, CircleAA(), avec l'algorithme de lissage standard, dessine une ligne plus épaisse que la fonction CircleWu() selon l'algorithme de Wu. Grâce à sa plus faible épaisseur et à un meilleur calcul des teintes de transition, CircleWu a un aspect plus soigné et plus naturel.

D'autres améliorations ont également été apportées à la classe CCanvas :

1. Ajout de la nouvelle primitive ellipse avec deux options d'anticrénelage : EllipseAA() et EllipseWu()
   
2. Ajout de la surcharge de la fonction de remplissage d’une aire avec le nouveau paramètre de la "sensibilité de remplissage" (le seuil).

Utilisation de la bibliothèque

1. Après avoir connecté la bibliothèque, nous devons créer un objet de classe CGraphic. Nous y ajouterons les courbes à dessiner.

Nous devons ensuite appeler la méthode Create() pour créer l'objet. La méthode contient les paramètres principaux du graphique :

1. Identifiant du graphique
2. Nom de l'objet
3. Index de la fenêtre
   
4. Point d'ancrage du graphique
5. Largeur et hauteur du graphique

La méthode applique les paramètres donnés pour créer un objet graphique et une ressource graphique à utiliser lors du tracé d'un graphique.

   //--- objet pour la création ultérieure des graphiques
   CGraphic graphic;
   //--- création du canevas
   graphic.Create(0, "Graphic", 0, 30, 30, 830, 430);

Suite à ces lignes, nous disposons d'un canevas prêt à l'emploi.

2. Maintenant, nous allons pouvoir remplir notre objet avec des courbes. L'ajout est effectué grâce à la méthode CurveAdd() qui permet de tracer des courbes de quatre manières différentes :

1. A partir d’un tableau unidimensionnel de type double. Dans ce cas, les valeurs du tableau sont affichées sur l'axe Y, et les indices du tableau servent de coordonnées X.
2. A partir de 2 tableaux de type double x[] et y[].
3. A partir d’un tableau de CPoint2D.
4. A partir d’un pointeur CurveFunction() et de 3 valeurs pour construire les arguments de la fonction : initial, final et le pas.

La méthode CurveAdd() renvoie une pointeur vers un objet de type CCurve, qui permet un accès rapide à la courbe nouvellement créée et la possibilité de modifier ses propriétés.

   double x[]={-10, -4, -1, 2, 3, 4, 5, 6, 7, 8};

   double y[]={-5, 4, -10, 23, 17, 18, -9, 13, 17, 4};

   CCurve *curve=graphic.CurveAdd(x, y, CURVE_LINES);

3. Toutes les courbes ajoutées peuvent maintenant être affichées sur le graphique. Cela peut se faire de 3 manières :

1. Avec la méthode CurvePlotAll() qui dessine automatiquement toutes les courbes ajoutées au graphique.
   graphic.CurvePlotAll();
2. Avec la méthode CurvePlot() qui dessine la courbe correspondant à l’index spécifié.
   graphic.CurvePlot(0);
3. Avec la méthode Redraw() et en donnant la valeur "true" à la propriété Visible de la courbe.
   curve.Visible(true);
   graphic.Redraw();

4. Afin de tracer un élément graphique sur le graphique, appelez la méthode Update(). Nous obtenons du coup le code complet du script pour tracer un graphique simple :

#include <Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| Fonction de démarrage du programme de script                     |
//+------------------------------------------------------------------+
void OnStart()
  {
   CGraphic graphic;
   graphic.Create(0, "Graphic", 0, 30, 30, 780, 380);
   double x[]={-10, -4, -1, 2, 3, 4, 5, 6, 7, 8};
   double y[]={-5, 4, -10, 23, 17, 18, -9, 13, 17, 4};
   CCurve *curve=graphic.CurveAdd(x, y, CURVE_LINES);
   graphic.CurvePlotAll();
   graphic.Update();
  }

Voici le graphique résultat :

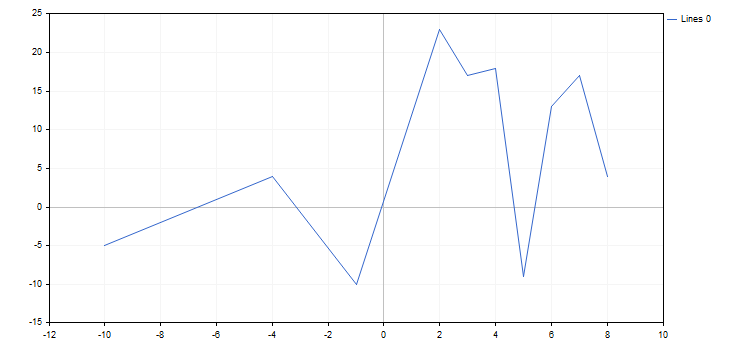
Les propriétés du graphique et de n'importe laquelle de ses fonctions peuvent être modifiées à tout moment. Nous pouvons par exemple ajouter des étiquettes aux axes du graphique, changer le nom de la courbe et activer le mode d'approximation spline :

#include <Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| Fonction de démarrage du programme de script                     |
//+------------------------------------------------------------------+
void OnStart()
  {
   CGraphic graphic;
   graphic.Create(0, "Graphic", 0, 30, 30, 780, 380);
   double x[]={-10, -4, -1, 2, 3, 4, 5, 6, 7, 8};
   double y[]={-5, 4, -10, 23, 17, 18, -9, 13, 17, 4};
   CCurve *curve=graphic.CurveAdd(x, y, CURVE_LINES);
   curve.Name("Example");                
   curve.LinesIsSmooth(true);           
   graphic.XAxis().Name("X - axis");      
   graphic.XAxis().NameSize(12);          
   graphic.YAxis().Name("Y - axis");      
   graphic.YAxis().NameSize(12);
   graphic.YAxis().ValuesWidth(15);
   graphic.CurvePlotAll();
   graphic.Update();
   DebugBreak();
  }

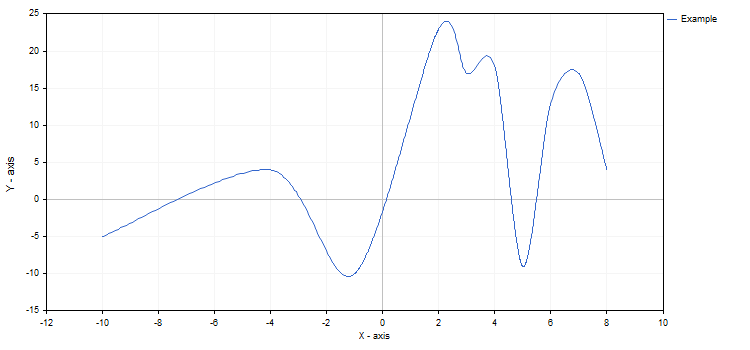
Si les changements avaient été faits après l'appel de CurvePlotAll, nous aurions dû ensuite appeler la méthode Redraw pour les voir.

Comme de nombreuses bibliothèques modernes, Graphics contient divers algorithmes prêts à être utilisés simplifiant considérablement le tracé des graphiques :

1. La bibliothèque est capable de générer automatiquement des couleurs contrastées pour les courbes si elles ne sont pas explicitement spécifiées.
2. Les axes du graphique disposent du mode de mise à l'échelle automatique, qui peut être désactivé si nécessaire.
3. Les noms des courbes sont générés automatiquement en fonction de leur type et de leur ordre d'ajout.
4. La zone de travail du graphique est automatiquement tracée et les axes sont automatiquement définis.
5. Il est possible de lisser les courbes lorsque vous utilisez des lignes.

La bibliothèque Graphics dispose également de méthodes supplémentaires pour ajouter de nouveaux éléments au graphique :

1. TextAdd() - ajoute un texte sur le graphique, à une position arbitraire. Les coordonnées doivent être définies sur l'échelle réelle. Vous devez utiliser la méthode FontSet pour configurer précisément le texte affiché.
   
2. LineAdd() - ajoute une ligne sur le graphique, à une position arbitraire. Les coordonnées doivent être définies sur l'échelle réelle.
3. MarksToAxisAdd() - ajoute de nouvelles étiquettes sur l’axe de coordonnées spécifié.

Les données relatives à l'ajout des éléments ne sont pas stockées. Elles disparaissent après avoir tracé une nouvelle courbe sur le graphique ou redessiné une courbe précédente.

Types de graphiques

La bibliothèque Graphics prend en charge les types de base de dessin des courbes. Ils sont tous spécifiés dans l'énumération ENUM_CURVE_TYPE :

1. CURVE_POINTS - dessine une courbe de points
2. CURVE_LINES - dessine une ligne courbe
3. CURVE_POINTS_AND_LINES - dessine à la fois des courbes de points et les lignes courbes
4. CURVE_STEPS - dessine une courbe par paliers (en escalier)
   
5. CURVE_HISTOGRAM - dessine un histogramme
6. CURVE_NONE - ne dessine rien
   

Chacun de ces modes a ses propres propriétés qui affectent chacune l'affichage d'une courbe sur le graphique. Le pointeur CCurve sur une courbe permet de modifier ses propriétés rapidement. Il est donc recommandé de conserver tous les pointeurs renvoyés par la méthode CurveAdd. Le nom d'une propriété commence toujours par le mode de dessin de la courbe dans lequel elle est utilisée.

Examinons maintenant plus en détail les propriétés de chacun de ces types.

1. CURVE_POINTS est le mode le plus rapide et le plus simple. Chaque coordonnée de la courbe est affichée comme un point ayant des propriétés spécifiques :

• PointsSize - taille du point
• PointsFill - marqueur indiquant si la zone est remplie.
  
• PointsColor - couleur de remplissage
  
• PointsType - type de points
  

La couleur de la courbe elle-même définit la couleur des bords des points.

   CCurve *curve = graphic.CurveAdd(x, y, ColorToARGB(clrBlue, 255), CURVE_POINTS);
   curve.PointsSize(20);
   curve.PointsFill(true);
   curve.PointsColor(ColorToARGB(clrRed, 255));

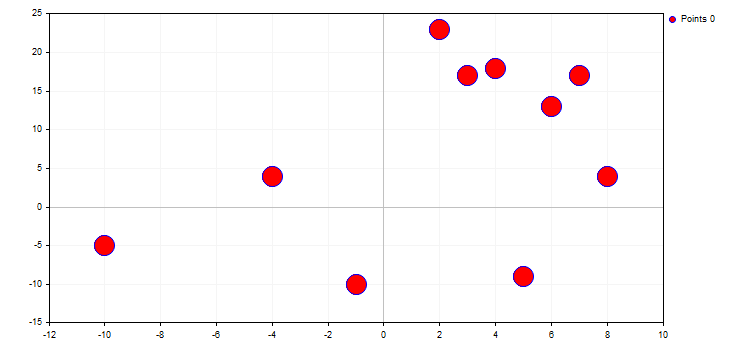
Le type de point définit une certaine forme géométrique de l'énumération ENUM_POINT_TYPE. Cette forme est utilisée pour afficher tous les points de la courbe. Au total, ENUM_POINT_TYPE comprend 10 formes géométriques principales :

1. POINT_CIRCLE - cercle (par défaut)
   
2. POINT_SQUARE - carré
   
3. POINT_DIAMOND - diamant
   
4. POINT_TRIANGLE - triangle
   
5. POINT_TRIANGLE_DOWN - triangle inversé
   
6. POINT_X_CROSS - croix
   
7. POINT_PLUS - plus
   
8. POINT_STAR - étoile
   
9. POINT_HORIZONTAL_DASH - ligne horizontale
   
10. POINT_VERTICAL_DASH - ligne verticale
    

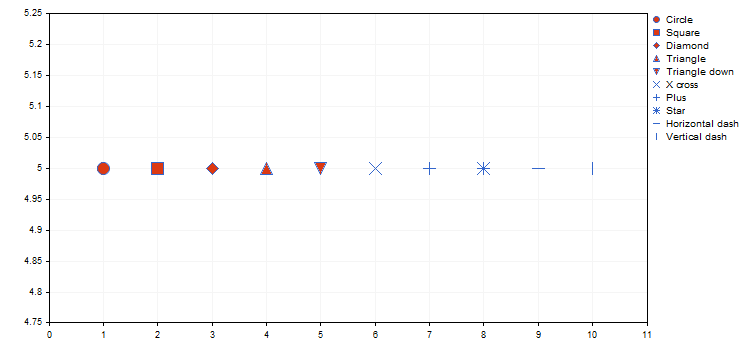
Vous trouverez ci-dessous un exemple de représentation visuelle de différents types d'iris (voir l'article "Utiliser des cartes topologiques auto-adaptatives (Cartes de Kohonen) in MetaTrader 5") à partir du script IrisSample.mq5ci-joint.

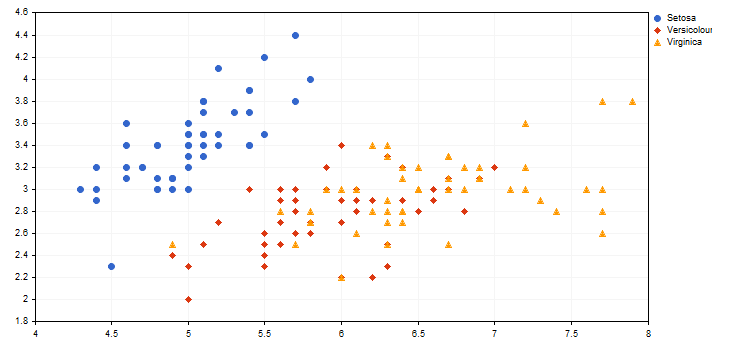
2. Le mode d'affichage CURVE_LINES est le mode principal de visualisation des courbes, dans lequel chaque paire de points est reliée par une ou plusieurs (en cas de lissage) lignes droites. Les propriétés de ce mode sont les suivantes :

• LinesStyle - style de ligne, de l'énumération ENUM_LINE_STYLE
• LinesSmooth - marqueur indiquant si le lissage doit être effectué
  
• LinesSmoothTension - degré de lissage
  
• LinesSmoothStep - longueur des lignes d’approximation lors du lissage
  

Les graphiques utilisent l'algorithme standard de lissage paramétrique des courbes. Il est constitué de 2 lignes :

1. Deux points de référence sont définis pour chaque paire de points sur la base de leurs dérivées
2. Une courbe de Bezier avec un pas d'approximation spécifié est tracée sur la base de ces 4 points

Le paramètre LinesSmoothTension prend les valeurs (0.0 ; 1.0). Si LinesSmoothTension est défini sur 0.0, aucun lissage n'est effectué. En augmentant ce paramètre, on obtient une courbe de plus en plus lissée.

   CCurve *curve = graphic.CurveAdd(x, y, ColorToARGB(clrBlue, 255), CURVE_LINES);
   curve.LinesStyle(STYLE_DOT);
   curve.LinesSmooth(true);
   curve.LinesSmoothTension(0.8);
   curve.LinesSmoothStep(0.2);

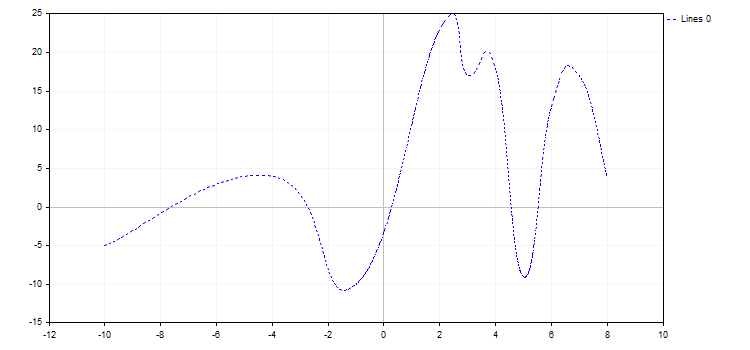
3. CURVE_POINTS_AND_LINES combine les deux modes d'affichage précédents ainsi que leurs propriétés respectives.

4. Dans le mode CURVE_STEPS, chaque paire de points est reliée par deux lignes. Ce mode a 2 propriétés :

• LinesStyle - provient de CURVE_POINTS et définit le style de la ligne.
• StepsDimension - dimension des pas : 0 - x (une ligne horizontale suivie d'une ligne verticale) ou 1 - y (une ligne verticale suivie d'une ligne horizontale).
  

   CCurve *curve=graphic.CurveAdd(x, y, ColorToARGB(clrBlue, 255), CURVE_STEPS);
   curve.LinesStyle(STYLE_DASH);
   curve.StepsDimension(1);

5. Le mode CURVE_HISTOGRAM dessine un histogramme à barres. Ce mode ne présente qu’une seule propriété :

• HistogramWidth - largeur de la barre

Si la valeur est trop grande, les barres peuvent se chevaucher, et les barres ayant une valeur Y supérieure "absorbent" les barres adjacentes ayant des valeurs plus petites.

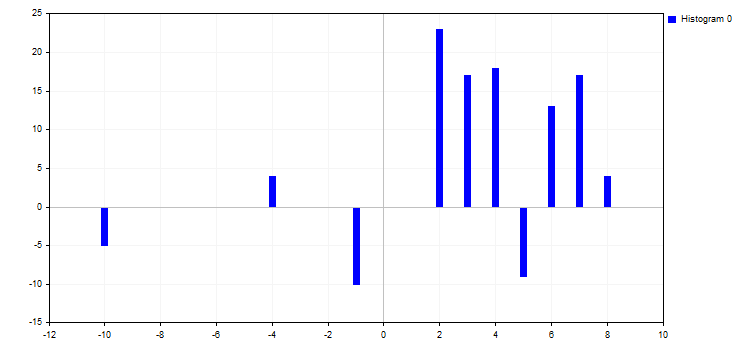
6. Le mode CURVE_NONE désactive la représentation graphique de toutes les courbes, quelle que soit leurs visibilités.

Lors de la mise à l'échelle automatique, toutes les courbes ajoutées au graphique ont certaines valeurs par défaut. Par conséquent, même si la courbe n'est pas tracée ou si elle est réglée sur le mode CURVE_NONE, ses valeurs sont toujours prises en compte.

Graphiques sur les fonctions - génération rapide en quelques lignes

Un autre avantage de la bibliothèque est de travailler avec des pointeurs de fonction CurveFunction. En MQL5, les pointeurs de fonctions n'acceptent que les fonctions globales ou statiques. La syntaxe de la fonction doit correspondre entièrement à celle du pointeur. Dans notre cas, CurveFunction est configuré pour que les fonctions prenant un paramètre de type double reçoivent également le double.

Pour construire une courbe à l'aide d'un pointeur vers une fonction, nous devons aussi définir avec précision les valeurs initiale (début) et finale (fin) de l'argument, ainsi que son incrément (pas). Plus la valeur de l'incrément est faible, plus on dispose de points de fonction pour le construire. Pour créer une série de données, utilisez CurveAdd(). Pour tracer une fonction, appelez CurvePlot() ou CurvePlotAll().

Créons par exemple une fonction parabolique et dessinons-la en plusieurs incréments :

#include <Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| Parabole                                                         |
//+------------------------------------------------------------------+
double Parabola(double x) { return MathPow(x, 2) ; }
//+------------------------------------------------------------------+
//| Fonction de démarrage du programme de script                     |
//+------------------------------------------------------------------+
void OnStart()
  {
   double from1 = -5;
   double to1 = 0;
   double step1 = 1;
  
   double from2 = 0;
   double to2 = 5;
   double step2 = 0.2;
  
   CurveFunction function = Parabola;
  
   CGraphic graph;
   graph.Create(0, "Graph", 0, 30, 30, 780, 380);
   graph.CurveAdd(function, from1, to1, step1, CURVE_LINES);
   graph.CurveAdd(function, from2, to2, step2, CURVE_LINES);
   graph.CurvePlotAll();
   graph.Update();
  }

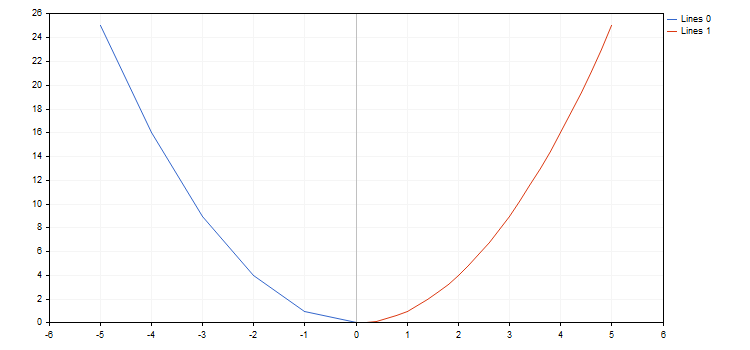
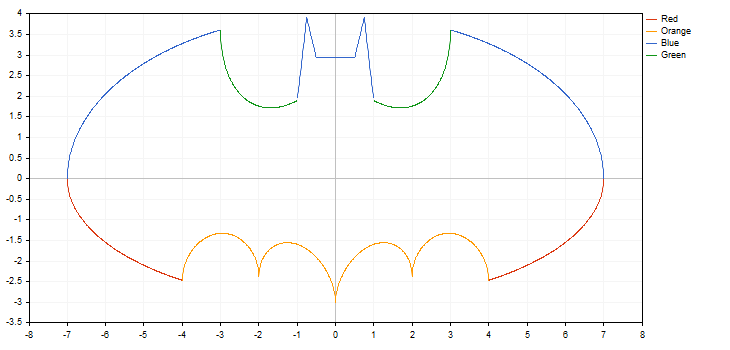
La bibliothèque fonctionne avec des fonctions ayant des points d'arrêt (l'une des coordonnées a la valeur +/- l'infini ou est non-numérique). L'incrémentation par fonction doit être envisagée, car parfois, nous pouvons simplement manquer un point de rupture (break point). Dans ce cas, le graphique ne répond pas aux attentes. Par exemple, dessinons deux fonctions hyperboliques dans le segment [-5,0 ; 5,0], la première ayant un pas de 0,7 et la seconde un pas de 0,1. Voici le résultat :

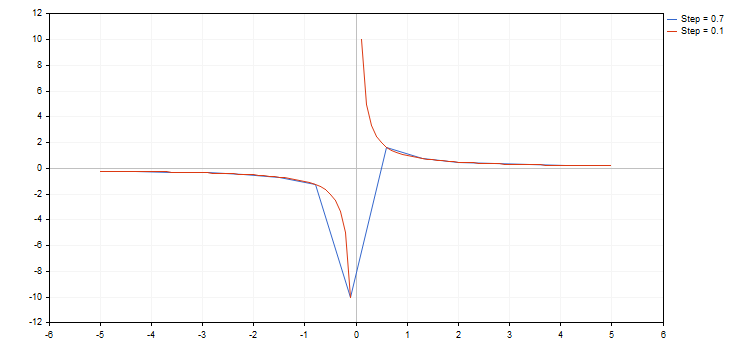
Comme nous pouvons le voir dans l'image ci-dessus, nous avons manqué le point de rupture en utilisant un pas de 0,7. Par conséquent, la courbe résultante est différente de la fonction hyperbolique réelle.

Une erreur de division par zéro peut aussi se produire lors de l'utilisation de ces fonctions. Il existe deux façons de traiter ce point :

• désactiver la vérification de la division par zéro dans le fichier metaeditor.ini
  
  [Experts]
  FpNoZeroCheckOnDivision = 1
• ou analyser une équation utilisée dans une fonction et renvoyer une valeur valide dans ce cas. Vous trouverez un exemple de cette manipulation à l'aide d'une macro dans les fichiers 3Functions.mq5 et bat.mq5 joints.

  
  
  
  

  
  

Fonctions de traçage rapide

La bibliothèque Graphics comprend également un certain nombre de fonctions globales GraphPlot() qui effectuent toutes les étapes de traçage de la géométrie en fonction des données disponibles et renvoient en résultat un nom d'objet sur le graphique. Ces fonctions sont similaires aux fonctions "plot" des langages R ou Python et vous permettent de visualiser instantanément les données disponibles dans différents formats.

Il existe 10 surcharges différentes de la fonction GraphPlot permettant de tracer un nombre différent de courbes sur un seul graphique et de les définir de différentes manières. Tout ce que vous avez à faire est de former les données pour tracer une courbe en utilisant l'une des méthodes disponibles. Le code source pour un tracé rapide des tableaux x[] et y[] par exemple se présente comme suit :

void OnStart()
  {
   double x[]={-10, -4, -1, 2, 3, 4, 5, 6, 7, 8};
   double y[]={-5, 4, -10, 23, 17, 18, -9, 13, 17, 4};
   GraphPlot(x, y);
  }

C'est similaire avec le langage R :

> x<-c(-10, -4, -1, 2, 3, 4, 5, 6, 7, 8)
> y<-c(-5, 4, -10, 23, 17, 18, -9, 13, 17, 4)
> plot(x, y)

Résultats de la comparaison des graphiques avec les 3 principaux modes d'affichage construits par la fonction GraphPlot el MQL5 et la fonction plot sur R :

1. Courbes de points

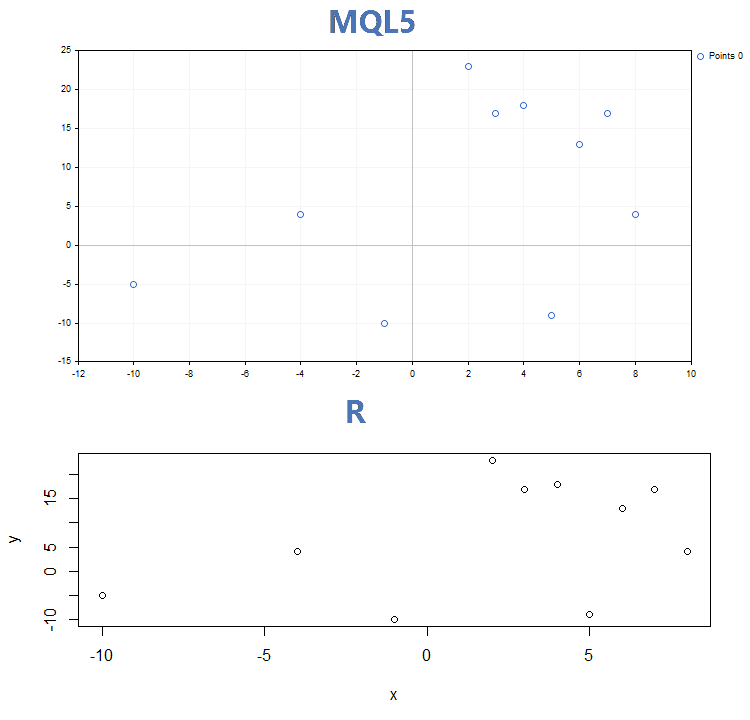
2. Lignes

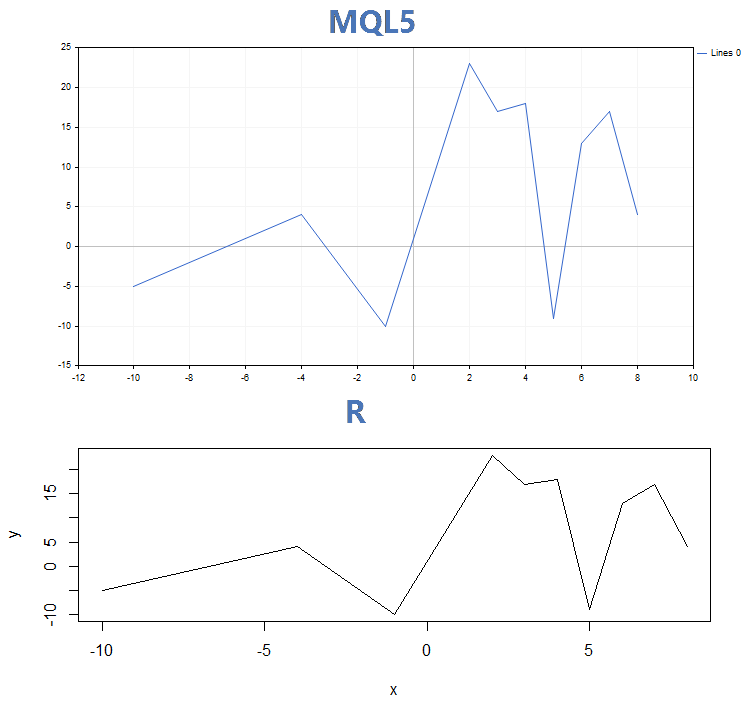
3. Histogramme

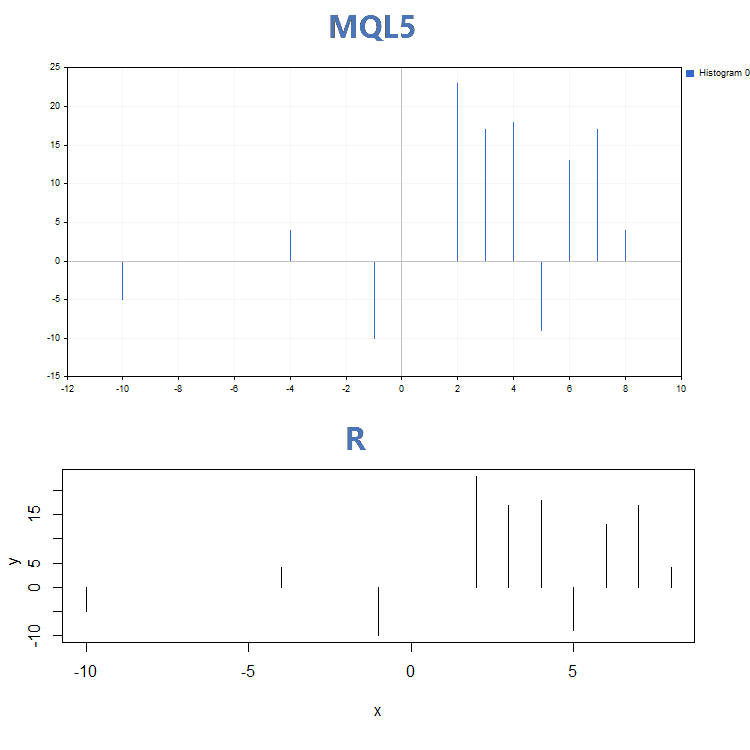
En plus des différences visuelles assez importantes du fonctionnement des fonctions GraphPlot() et plot(), elles appliquent des paramètres d'entrée différents. Alors que la fonction plot() permet de définir des paramètres de courbe spécifiques (par exemple 'lwd' qui modifie la largeur des lignes), la fonction GraphPlot() ne comprend que les paramètres clés nécessaires à la construction des données.

Ces paramètres sont les suivants :

1. Les données des courbes dans l'un des 4 formats décrits ci-dessus
   
2. Le type de tracé (par défaut, CURVE_POINTS)
   
3. Le nom de l'objet (par défaut, NULL)

Chaque graphique créé à l'aide de la bibliothèque Graphics se compose d'un objet graphique et d'une ressource graphique qui lui est directement attribuée. Le nom de la ressource graphique est formé à partir du nom de l'objet simplement préfixé de "::". Par exemple, si le nom de l'objet est "SomeGraphic", le nom de sa ressource graphique sera "::SomeGraphic".

La fonction GraphPlot() a un point d'ancrage fixe sur un graphique : x=65 et y=45. La largeur et la hauteur de l’élément graphique sont calculées en fonction de la taille du graphique : la largeur correspond à 60 % de celle du graphique, et la hauteur correspond à 65 % de la hauteur du graphique. Donc, si les dimensions actuelles du graphique sont inférieures à 65 sur 45, la fonction GraphPlot() ne peut pas fonctionner correctement.

Si vous appliquez le nom d'un objet déjà créé lors de la création d'un graphique, la bibliothèque Graphics tente d'afficher le graphique sur cet objet après avoir vérifié son type de ressource. Si la ressource est de type OBJ_BITMAP_LABEL, le traçage est effectué sur la même paire objet-ressource.

Si un nom d'objet est explicitement passé à la fonction GraphPlot(), une tentative est faite pour trouver cet objet et afficher l’élément graphique dessus. Si l'objet n'est pas trouvé, une nouvelle paire objet-ressource est automatiquement créée à partir du nom spécifié. Lors de l'utilisation de la fonction GraphPlot() sans nom d'objet spécifié, le nom standard "Graphic" est utilisé. 

Dans ce cas, vous pouvez spécifier un point d'ancrage du graphique ainsi que sa taille. Pour cela, créez une paire objet-ressource avec les paramètres nécessaires et passez le nom de l'objet créé à la fonction GraphPlot(). En créant une paire avec le nom de l'objet graphique, nous redéfinissons et fixons le canevas standard de la fonction GraphPlot en éliminant la nécessité de passer le nom de l'objet à chaque appel.

Prenons par exemple les données de l'exemple ci-dessus et définissons une nouvelle taille de graphique de 750х350. Déplaçons aussi le point d'ancrage dans le coin supérieur gauche :

void OnStart()
  {
//--- crée un objet sur le graphique et la ressource dynamique
   string name = "Graphic";
   long x = 0;
   long y = 0;
   int width = 750;
   int height = 350;
   int data[];
   ArrayResize(data, width*height);
   ZeroMemory(data);
   ObjectCreate(0, name, OBJ_BITMAP_LABEL, 0, 0, 0);
   ResourceCreate("::"+name, data, width, height, 0, 0, 0, COLOR_FORMAT_XRGB_NOALPHA);
   ObjectSetInteger(0, name, OBJPROP_XDISTANCE, x);
   ObjectSetInteger(0, name, OBJPROP_YDISTANCE, y);
   ObjectSetString(0, name,OBJPROP_BMPFILE, "::"+name);
//--- crée les tableaux x et y
   double arr_x[] = {-10, -4, -1, 2, 3, 4, 5, 6, 7, 8};
   double arr_y[] = {-5, 4, -10, 23, 17, 18, -9, 13, 17, 4};
//--- tracé des tableaux x et y
   GraphPlot(arr_x, arr_y, CURVE_LINES);
  }

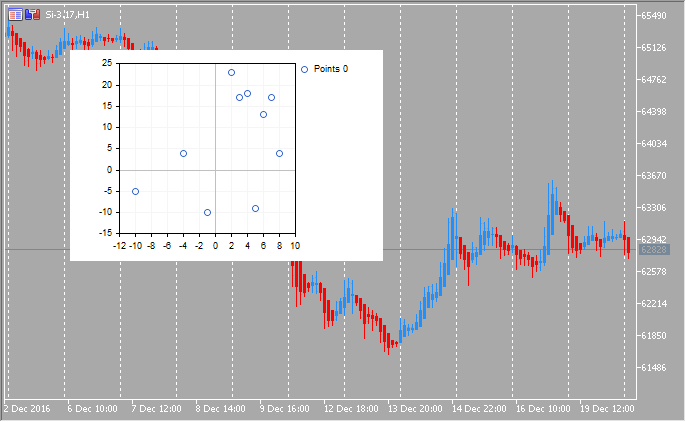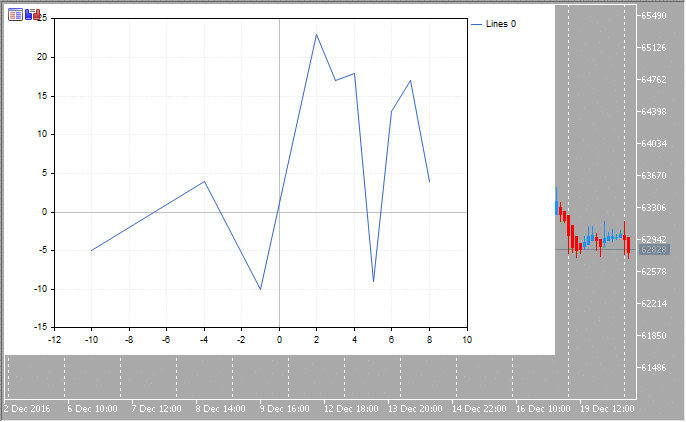
Exemples de graphiques scientifiques

La Bibliothèque Standard comporte la section Statistiques, qui propose des fonctions permettant de travailler avec de multiples distributions statistiques issues de la théorie des probabilités. Chaque distribution est accompagnée d'un exemple de graphique et du code correspondant. Nous affichons ici simplement ces graphiques dans un seul GIF. Le code source des exemples est joints dans le fichier MQL5.zip. Décompressez-le dans MQL5\Scripts.

Dans tous ces exemples, le graphique des prix est désactivé via la propriété CHART_SHOW :

//--- désactive le graphique des prix
   ChartSetInteger(0, CHART_SHOW, false);

Cela nous permet de transformer une fenêtre de graphique en un seul grand canevas et de dessiner des objets de n'importe quelle complexité en appliquant les ressources graphiques.

Lisez l'article "Un exemple de développement d'une stratégie de spread pour les futures du Moscow Exchange" qui montre l'application de la bibliothèque Graphics pour afficher l'échantillon d'entraînement et les résultats de la régression linéaire obtenus avec la bibliothèque Alglib.

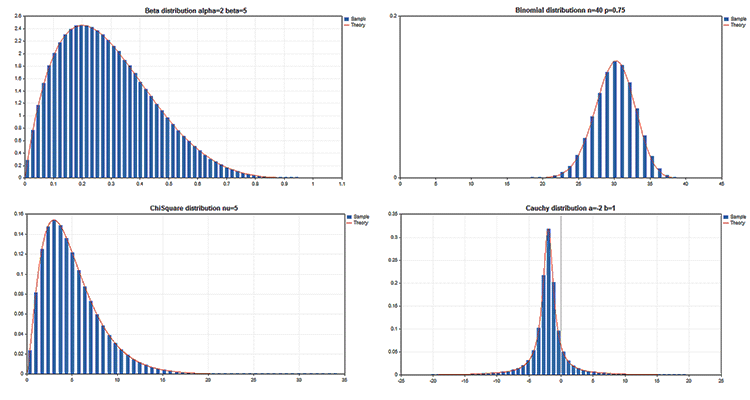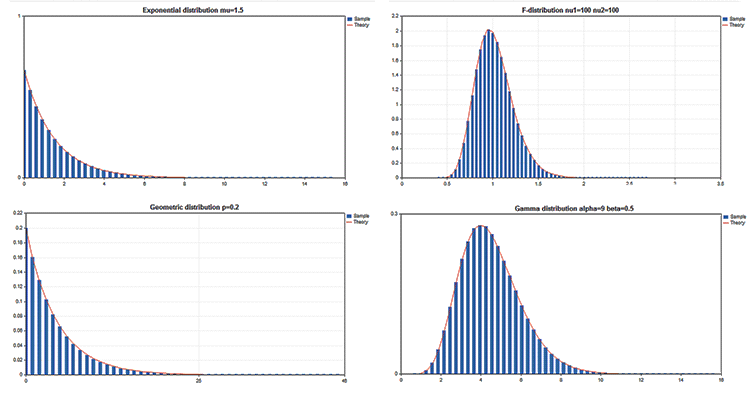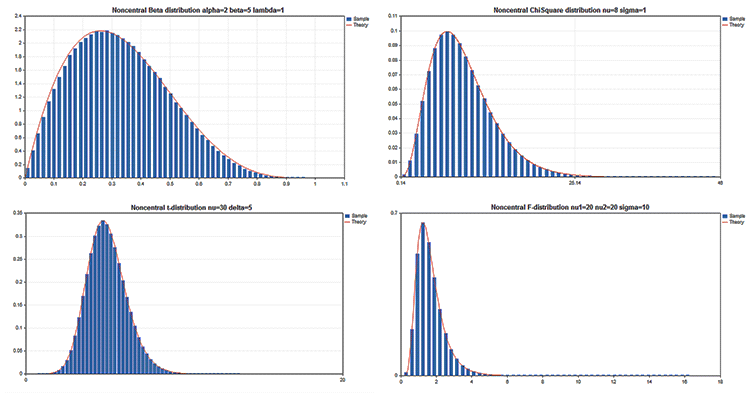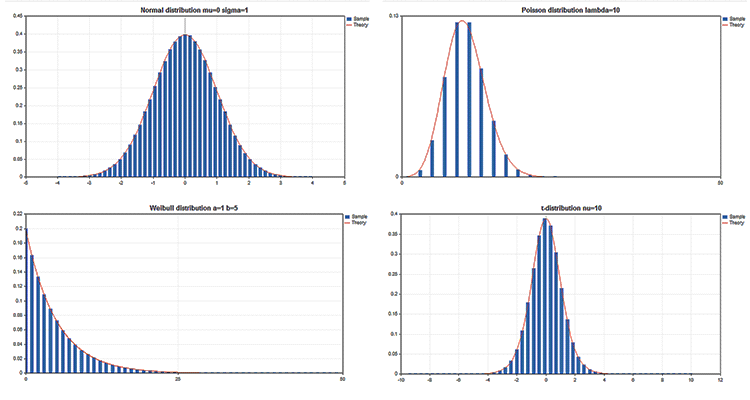
Principaux avantages de la bibliothèque Graphics

Le langage MQL5 permet aux développeurs de créer non seulement des robots de trading et des indicateurs techniques, mais aussi d'effectuer des calculs mathématiques complexes à l'aide des bibliothèques ALGLIB, Fuzzy et Statistics. Les données obtenues sont ensuite facilement visualisées avec la bibliothèque Graphics fournie. La plupart des opérations sont automatisées, et la bibliothèque offre des fonctionnalités étendues :

• 5 types d'affichage de graphiques
• 10 types de marqueurs graphiques
  
• mise à l'échelle automatique des graphiques sur les axes X et Y
• sélection automatique de la couleur, même si un graphique comporte plusieurs constructions
  
• lissage des lignes à l'aide de l'anti-crénelage standard ou de l’algorithme de Bresenham plus avancé
• possibilité de définir les paramètres d'approximation des courbes
  
• capacité de tracer un graphique en utilisant en une ligne de code basée sur les tableaux x[] et y[]
• capacité à tracer des graphiques en utilisant des pointeurs de fonctions
  

La bibliothèque Graphics simplifie le tracé des graphiques scientifiques et permet le développement des applications de trading à un niveau supérieur. La plateforme MetaTrader 5 vous permet d'effectuer des calculs mathématiques de différentes complexités et d'afficher les résultats directement dans la fenêtre du terminal de manière professionnelle.

Vous devez essayez le code des exemples joints. Vous n'avez plus besoin d’outils supplémentaires !