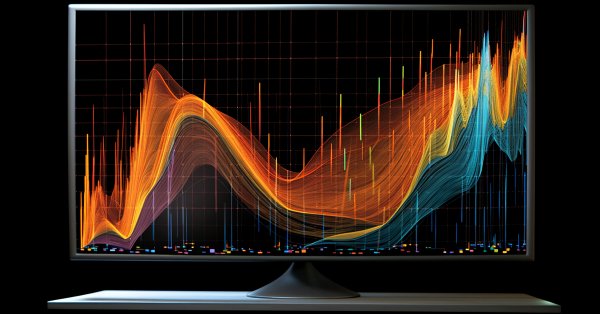
可視化の可能性 Rのプロットに似たMQL5のグラフィックス ライブラリ

トレードロジックを勉強する際、チャートの視覚的な表現は非常に重要です。科学分野で人気のある数々のプログラミング言語 (R や Python など) は可視化のための関数”プロット”があります。これらは視覚化するために、線、点の分布、ヒストグラムなどを描くことができます。

Plot 関数の重要な利点は、任意のチャートをプロットするためにわずかなコードしか必要としないことです。単純にパラメーターとしてデータ配列を使い、グラフタイプを指定するだけで利用できます。プロット関数はスケール、軸、色などの一般的なものを実行することが可能です。

MQL5では、すべての関数は、標準のライブラリからグラフィック ライブラリのメソッドによって表されます。サンプル コードとその結果は以下のとおりです。

#include<Graphics\Graphic.mqh>
#define RESULT_OR_NAN(x,expression) ((x==0)?(double)"nan":expression)
//---関数
double BlueFunction(double x)   { return(RESULT_OR_NAN(x,10*x*sin(1/x)));      }
double RedFunction(double x)    { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(x))); }
double OrangeFunction(double x) { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(-x)));}
//+------------------------------------------------------------------+
//プログラム開始関数をスクリプト |
//+------------------------------------------------------------------+
void OnStart()
  {
   double from=-1.2;
   double to=1.2;
   double step=0.005;
   CGraphic graphic;
   graphic.Create(0,"G",0,30,30,780,380);
//---色
   CColorGenerator generator;
   uint blue= generator.Next();
   uint red = generator.Next();
   uint orange=generator.Next();
//---すべての曲線のプロット
   graphic.CurveAdd(RedFunction,from,to,step,red,CURVE_LINES,"Red");
   graphic.CurveAdd(OrangeFunction,from,to,step,orange,CURVE_LINES,"Orange");
   graphic.CurveAdd(BlueFunction,from,to,step,blue,CURVE_LINES,"Blue");
   graphic.CurvePlotAll();
   graphic.Update();
  }

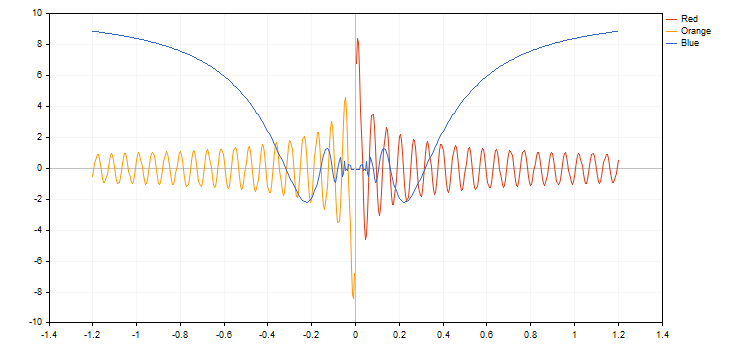
CCanvas 基本クラスとその開発

標準ライブラリには、基本クラスの価格のチャート上で、迅速かつ便利なCCanvasがあります。このクラスは、グラフィカルリソースを作成して、キャンバス上のプリミティブ (ドット、ストレート ライン、ポリライン、円、３角形、多角形) に基づいています。このクラスは、図形の塗りつぶしと必要なフォント、色およびサイズの関数を実装しています。

当初は、CCanvas には、グラフィカルなプリミティブ—アンチエイリアシング (AA)とを表示するだけの 2 つのモードしかありませんでした。その後、Wuのアルゴリズムに基づくプリミティブのプロットに追加されました。

• LineWu -直線
• PolylineWu -ポリライン
  
• PolygonWu — ポリゴン
  
• TriangleWu -３角形
  
• CircleWu -円
• EllipseWu -楕円

Wuのアルゴリズムは、アンチ エイリアスなしで、高品質かつ高速なブレゼンハムのアルゴリズムを組み合わせています。また、視覚的に標準アンチ エイリアスのアルゴリズム (AA) CCanvas の実装とは異なります。以下3つの異なる関数を使用した円のプロットの例です。

#include<Canvas\Canvas.mqh>
CCanvas canvas;
//+------------------------------------------------------------------+
//プログラム開始関数をスクリプト |
//+------------------------------------------------------------------+
void OnStart()
  {
   int      Width=800;
   int      Height=600;
//---キャンバスを作成する
   if(!canvas.CreateBitmapLabel(0,0,"CirclesCanvas",30,30,Width,Height))
     {
      Print("Error creating canvas: ",GetLastError());
     }
//---描画
   canvas.Erase(clrWhite);
   canvas.Circle(70,70,25,clrBlack);
   canvas.CircleAA(120,70,25,clrBlack);
   canvas.CircleWu(170,70,25,clrBlack);
//---
   canvas.Update();  
  }

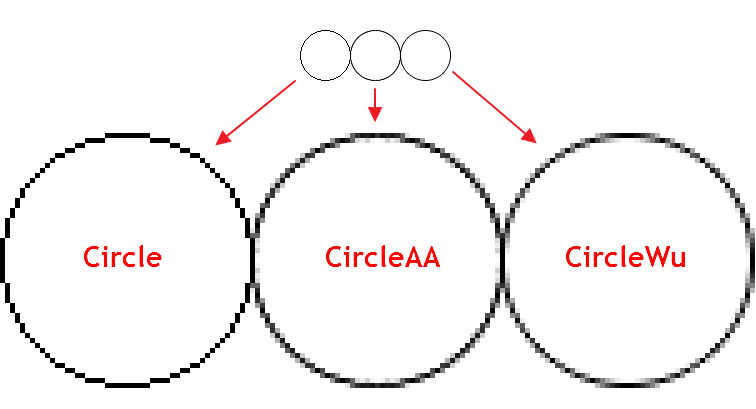
ご覧の通り、標準平滑化アルゴリズムのCircleAA()は、WuのアルゴリズムのCircleWu()に比べて太い線を描画します。その厚さと過渡的な色合いのため CircleWuより自然に見えます。

CCanvas クラスには他の改善もあります。

1. 2 つのアンチ エイリアス オプションと新しい楕円プリミティブを追加- （EllipseAA()とEllipseWu() ）
   
2. 新しいパラメータ充填領域関数のオーバー ロードを追加 (閾値パラメータ)。

ライブラリの操作のアルゴリズム

1. ライブラリに接続した後 CGraphic クラスのオブジェクトを作成する必要があります。描画する曲線が追加されます。

次に、作成されたオブジェクトの Create() メソッドを呼び出す必要があります。このメソッドには、メインのチャートのパラメータがあります。

1. チャート ID
2. オブジェクト名
3. ウィンドウ インデックス
   
4. アンカー ポイント
5. チャートの幅と高さ

このメソッドは、チャートをPrintするときに使用するグラフィカル リソースを作成する定義済みのパラメータを適用します。

   //---チャートを作成するためのオブジェクト
   CGraphic graphic;
   //---キャンバスを作成する
   graphic.Create(0,"Graphic",0,30,30,830,430);

結果として、 既製のキャンバスがあります。

2。曲線オブジェクトを塗りつぶしましょう。4 つのメソッドで曲線をプロットすることができるCurveAdd()メソッドを使用されます。

1. Double 型の 1 次元配列に基づいています。この場合、配列のインデックスとして X 座標を提供しながら、配列からの値は Y 軸に表示されます。
2. 2つの x[] と y[] のダブル型配列に基づいています。
3. CPoint2D 配列に基づいています。
4. CurveFunction() ポインターと関数の引数を構築するための 3 つの値に基づきます。

CurveAdd() メソッドは、新しく作成した曲線とそのプロパティを変更する関数に高速アクセスを提供するCCurveクラスへのポインターを返します。

   double x[]={-10,-4,-1,2,3,4,5,6,7,8};

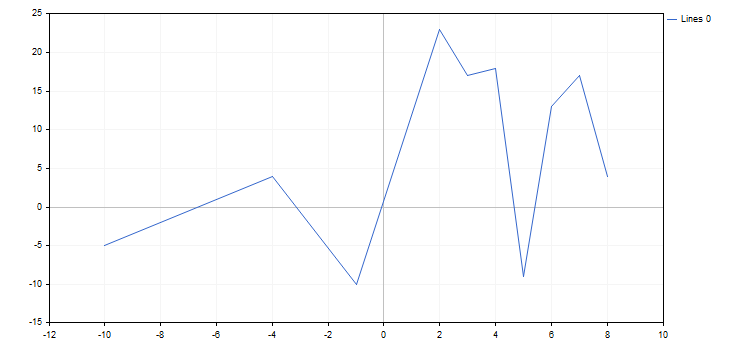
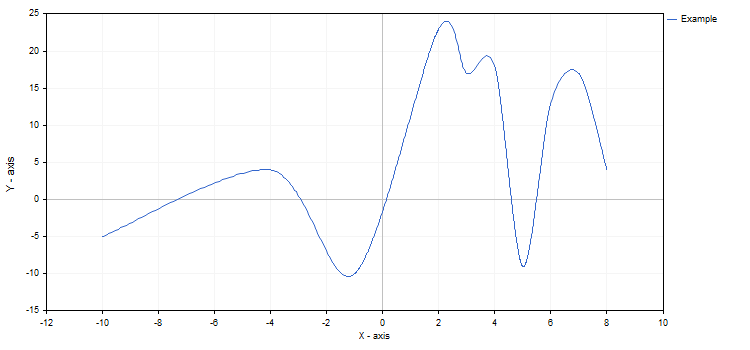
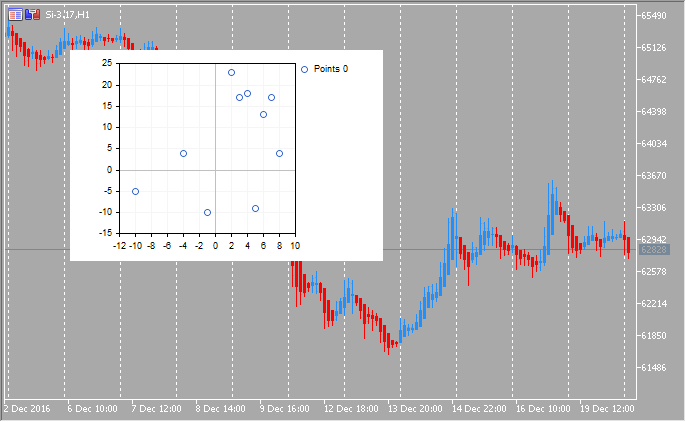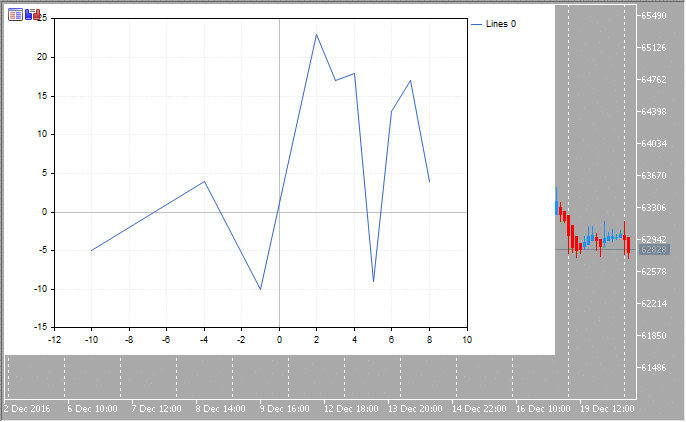
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};

   CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);

3. 追加の曲線をいずれかのチャートに表示することができます。3つのメソッドで行うことができます。

1. 自動的にすべての曲線を描画するCurvePlotAll()メソッドを使用します。
   graphic.CurvePlotAll();
2. CurvePlot()メソッドを使用して指定されたインデックスを使用して曲線を描画します。
   graphic.CurvePlot(0);
3. Redraw() メソッドを使用して、曲線の Visible プロパティを 'true' に設定。
   curve.Visible(true);
   graphic.Redraw();

4. チャートをプロットするためにUpdate()メソッドを呼び出します。その結果、チャートを作成するためのスクリプトの全体のコードを取得します。

#include<Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//プログラム開始関数をスクリプト |
//+------------------------------------------------------------------+
void OnStart()
  {
   CGraphic graphic;
   graphic.Create(0,"Graphic",0,30,30,780,380);
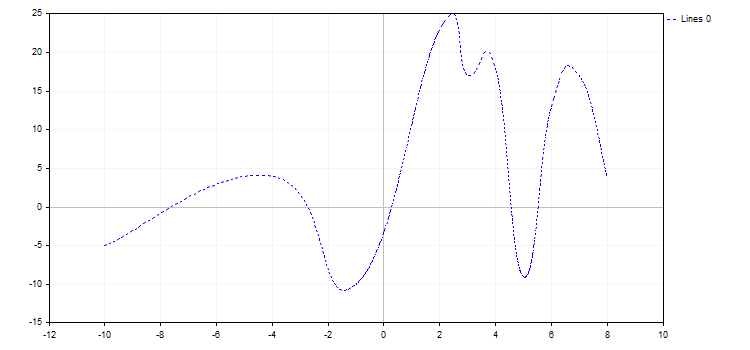
   double x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};
   CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
   graphic.CurvePlotAll();
   graphic.Update();
  }

結果のチャートを次に示します。

チャートとその関数のいずれかのプロパティは、任意の時点で変更できます。たとえば、ラベル曲線の名前の変更や、スプライン近似のモードを有効にできます。

#include<Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//プログラム開始関数をスクリプト |
//+------------------------------------------------------------------+
void OnStart()
  {
   CGraphic graphic;
   graphic.Create(0,"Graphic",0,30,30,780,380);
   double x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};
   CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
   curve.Name("Example");                
   curve.LinesIsSmooth(true);            
   graphic.XAxis().Name("X - axis");      
   graphic.XAxis().NameSize(12);          
   graphic.YAxis().Name("Y - axis");      
   graphic.YAxis().NameSize(12);
   graphic.YAxis().ValuesWidth(15);
   graphic.CurvePlotAll();
   graphic.Update();
   DebugBreak();
  }

CurvePlotAll を呼び出した後、変更された場合、さらにを表示する再描画メソッドを呼び出します。

多くの現代のライブラリのグラフィックスには、プロット図をかなり簡素化するさまざまな既製のアルゴリズムがあります。

1. そのライブラリは、明示的に指定されていない場合、曲線の対照的な色を生成するすることが可能です。
2. パラメトリックにスケーリングモードに応じて無効にすることができます。
3. 曲線の名前は、その型およびオーダーに応じて自動的に生成されます。
4. チャートのタスク領域で自動的に、実際の軸が設定されます。
5. 線を使用するときに曲線を滑らかにすることも可能です。

グラフィックスライブラリは、チャートに新しい要素を追加する追加メソッドもあります。

1. TextAdd() -チャート上の任意のポジションにテキストを追加します。座標は、リアル スケールで設定する必要があります。表示されるテキストの正確な構成は、フォントセットのメソッドを使用します。
   
2. LineAdd() -チャート上の任意のポジションにラインを追加します。座標は、リアル スケールで設定する必要があります。
3. MarksToAxisAdd() — 指定した座標軸に新しいラベルを追加します。

要素を追加する上でのデータはどこにも格納されません。チャートに新しい曲線をプロットまたは再描画後、消えます。

チャートの種類

グラフィックス ライブラリは、カーブの種類をプロットの基本的な種類をサポートします。ENUM_CURVE_TYPE 列挙体で指定されます。

1. CURVE_POINTS -ポイント曲線を描画します。
2. CURVE_LINES -ラインの曲線を描画します。
3. CURVE_POINTS_AND_LINES -点と線の両方の曲線を描く
4. CURVE_STEPS -段付き曲線を描画します。
   
5. CURVE_HISTOGRAM -ヒストグラム曲線を描画します。
6. CURVE_NONE -曲線を描画しません。
   

各モードは、チャートの曲線の表示に影響を与える独自のプロパティがあります。CCurve ポインターは、プロパティを変更できます。したがって、CurveAdd メソッドによって返されるすべてのポインターを覚えておくことをお勧めします。プロパティ名は、図面モードで使用される曲線で始まります。

種類ごとのプロパティをより詳細に見てみましょう。

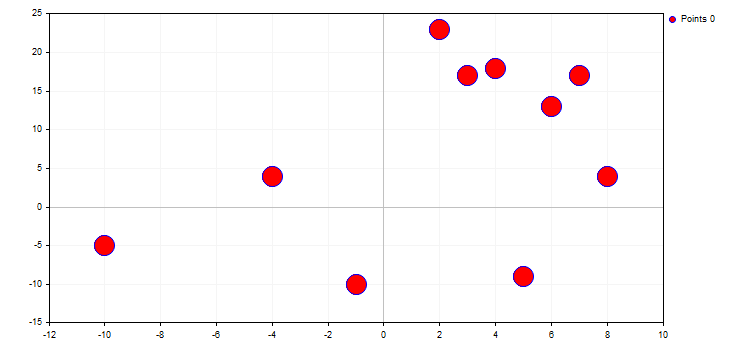
1. CURVE_POINTS最速かつ最も簡単なモードです。各曲線の座標が指定されたプロパティを持つポイントとして表示されます。

• PointsSize-ポイント サイズ
• PointsFill　－　充填されているかどうかを示す
  
• PointsColor-塗りつぶし色
  
• PointsType-ポイントの種類
  

この場合、曲線自体の色はポイントの枠線の色を定義します。

   CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_POINTS);
   curve.PointsSize(20);
   curve.PointsFill(true);
   curve.PointsColor(ColorToARGB(clrRed,255));

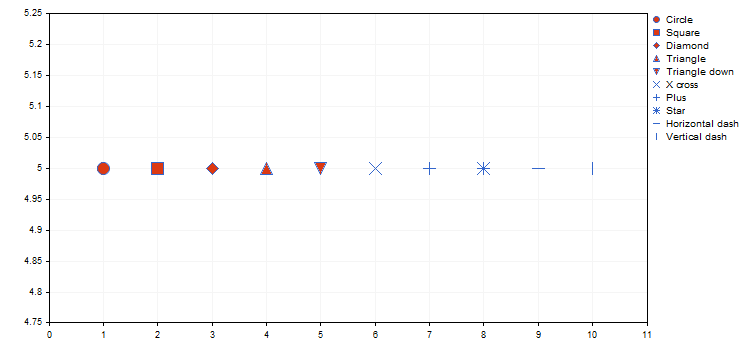
ポイントの種類は、ENUM_POINT_TYPE 列挙から特定の幾何学的な形を定義します。この図形はすべてのカーブ ポイントを表示するために使用されます。合計で、ENUM_POINT_TYPE には 10の幾何学的図形があります。

1. POINT_CIRCLE　-　円（デフォルト）
   
2. POINT_SQUARE-四角
   
3. POINT_DIAMOND-ダイヤモンド
   
4. POINT_TRIANGLE-トライアングル
   
5. POINT_TRIANGLE_DOWN-逆３角形
   
6. POINT_X_CROSS-クロス
   
7. POINT_PLUS- プラス
   
8. POINT_STAR-スター
   
9. POINT_HORIZONTAL_DASH-水平線
   
10. POINT_VERTICAL_DASH-垂直線
    

さまざまな種類のビジュアル表現の例を次に添付します。(参照記事特徴マップ (Kohonen) MT５による自己組織化" IrisSample.mq)

2. CURVE_LINES表示モードは、接続されている曲線を可視化するメインモードです。モードのプロパティは次のとおりです。

• LinesStyle-ENUM_LINE_STYLE列挙体の線のスタイル
• LinesSmooth-スムージングを示すフラグ
  
• LinesSmoothTension-平滑度
  
• LinesSmoothStep-スムージングするときの近似線の長さ
  

グラフィックは、標準的なパラメトリック曲線のスムージング アルゴリズムを備えています。2つの段階で構成されます。

1. 2つの参照点は、その誘導体に基づいてポイントの各ペアに対して定義されています。
2. 指定したベジエ曲線は、 4 つのポイントに基づいてプロットされます。

LinesSmoothTension パラメータは、値 (0.0; 1.0]。LinesSmoothTension は、0.0 に設定されている場合、平滑化されません。このパラメータを増加させることにより、カーブがスムーズになります。

   CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_LINES);
   curve.LinesStyle(STYLE_DOT);
   curve.LinesSmooth(true);
   curve.LinesSmoothTension(0.8);
   curve.LinesSmoothStep(0.2);

3. CURVE_POINTS_AND_LINESは、前の 2 つの表示モードとその特性を兼ね備えています。

4. CURVE_STEPSモードでは、ポイントの各ペアが2 本線で接続されています。このモードには、次の 2 つのプロパティがあります。

• LinesStyle-このプロパティは CURVE_POINTS から取得され、線のスタイルを定義します
• StepsDimension-ステップ ディメンション: 0-(水平線垂直） x または 1-y (垂直線を水平)。
  

   CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_STEPS);
   curve.LinesStyle(STYLE_DASH);
   curve.StepsDimension(1);

5. CURVE_HISTOGRAMモードを描画する標準ヒストグラム バー。このモードは、1 つのプロパティです。

• HistogramWidth-バーの幅

値が大きすぎる場合、バーが重なる可能性があります。

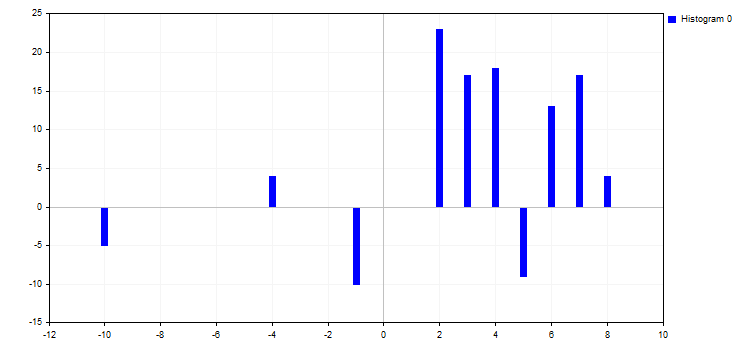
6. CURVE_NONEモードでは、可視性に関係なく曲線のグラフィカルな表示を無効にします。

自動スケーリングの際、すべてのチャートは特定の値を持ちます。したがって、CURVE_NONE モードに設定されていない場合でも、その値も考慮に取られます。

関数のチャート-ラインの高速生成

ライブラリの別の利点として、CurveFunction 関数へのポインターがあります。MQL5では、グローバルまたはスタティック関数の構文は、1 つポインターと完全に一致する必要があります。ここで、CurveFunction はdouble 型パラメータを受け取る関数に対して設定されます。

この関数へのポインターによって曲線を構築するために、そのインクリメント (ステップ) と同様、 最初と最後に引数の値を正確に設定する必要があります。増分値が少なければ少ないほど、関数のポインタを構築します。データ系列を作成するため、CurveAdd()関数を使います。 CurvePlot()または CurvePlotAll() を適用します。

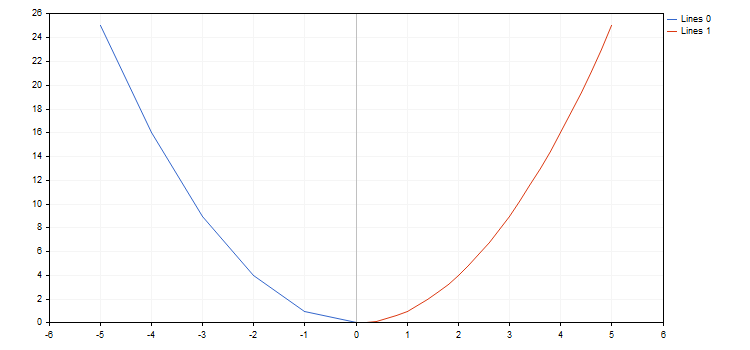
たとえば、放物線関数を作成し、描画してみましょう。

#include<Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| Parabola                                                         |
//+------------------------------------------------------------------+
double Parabola(double x) { return MathPow(x,2); }
//+------------------------------------------------------------------+
//プログラム開始関数をスクリプト |
//+------------------------------------------------------------------+
void OnStart()
  {
   double from1=-5;
   double to1=0;
   double step1=1;
  
   double from2=0;
   double to2=5;
   double step2=0.2;
  
   CurveFunction function = Parabola;

   CGraphic graph;
   graph.Create(0,"Graph",0,30,30,780,380);
   graph.CurveAdd(function,from1,to1,step1,CURVE_LINES);
   graph.CurveAdd(function,from2,to2,step2,CURVE_LINES);
   graph.CurvePlotAll();
   graph.Update();
  }

このライブラリは、ブレーク ・ ポイントを持つ関数で動作します。 (座標の1つがプラスまたはマイナス無限大の値を持つ。または数値ではない) インクリメント関数によって検討されるべきことに、 ブレイクポイントを見逃すことがあります。この場合、チャートでは条件を満たしていません。たとえば、2つの双曲線関数を描いてみましょう。[-5.0; 5.0]結果は下のようになります。

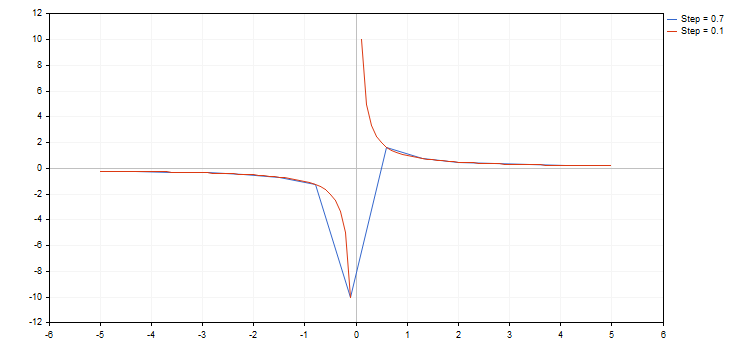
画像から分かるように、 0.7 のステップを使用したブレイクポイントです。その結果、結果のカーブは実際の双曲線関数とはほとんど何も関係ありません。

ゼロの除算エラーが発生する可能性があります。この問題に対処する 2 つの方法があります。

• metaeditor.ini でゼロ除算のチェックを無効にします。
  
  [Experts]
  FpNoZeroCheckOnDivision=1
• または、関数で使用される式を分析し、このような場合に有効な値を返します。3Functions.mq5とbat.mq5の添付ファイルからマクロを使用して、このような処理の例を見つけることができます。

  
  
  
  

  
  

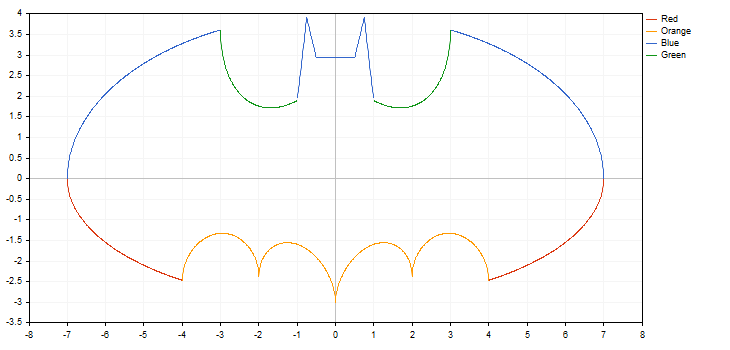
簡単なプロット関数

グラフィック ライブラリには、利用可能なデータに基づいています。その結果、チャートのオブジェクト名を返すGraphPlot()グローバル関数があります。この関数は、さまざまな形式で利用可能なデータを即座に視覚化でき、RまたはPhytonの「plot」に似ています。

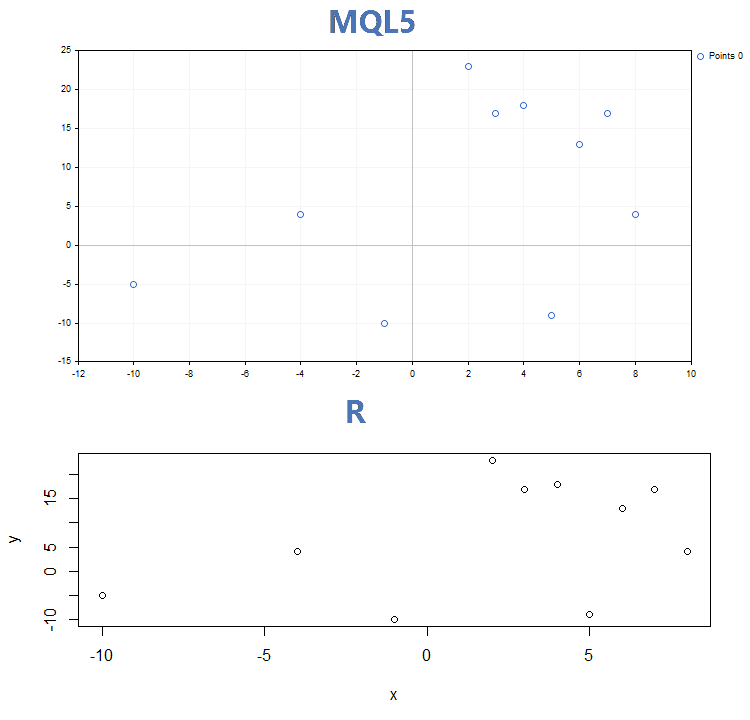
GraphPlot 関数は、1 つのチャート上の曲線をプロットし、さまざまなメソッドでを設定することができます。やるべきことは、利用可能なメソッドを利用して曲線を描くことです。たとえば、x[] と y[]配列 は次のようになります。

void OnStart()
  {
   double x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};
   GraphPlot(x,y);
  }

これはRに似ています。

> x<-c(-10,-4,-1,2,3,4,5,6,7,8)
> y<-c(-5,4,-10,23,17,18,-9,13,17,4)
> plot(x,y)

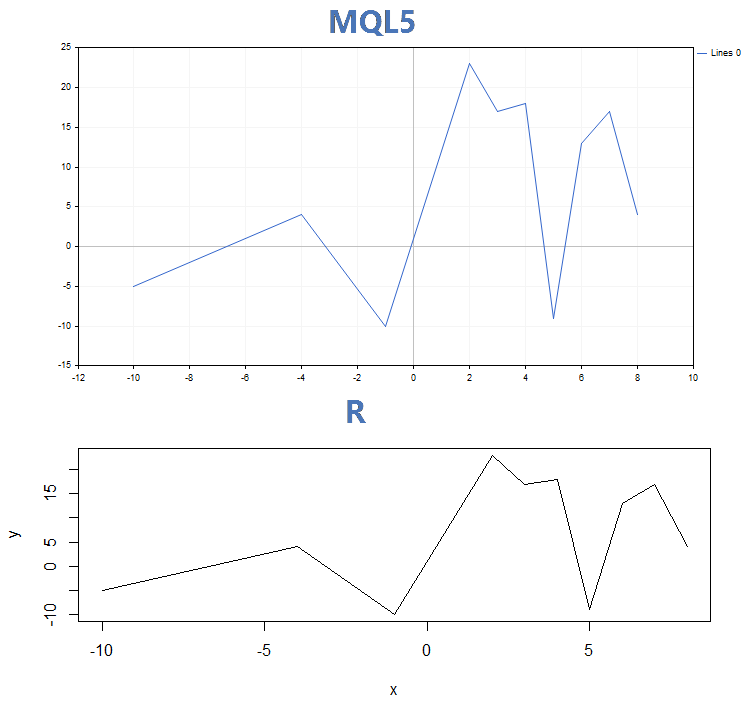
この結果は、MQL5 と R上のプロット関数 GraphPlot 関数によって建てられました。

1. ポイント カーブ

2. Lines

3. Histogram

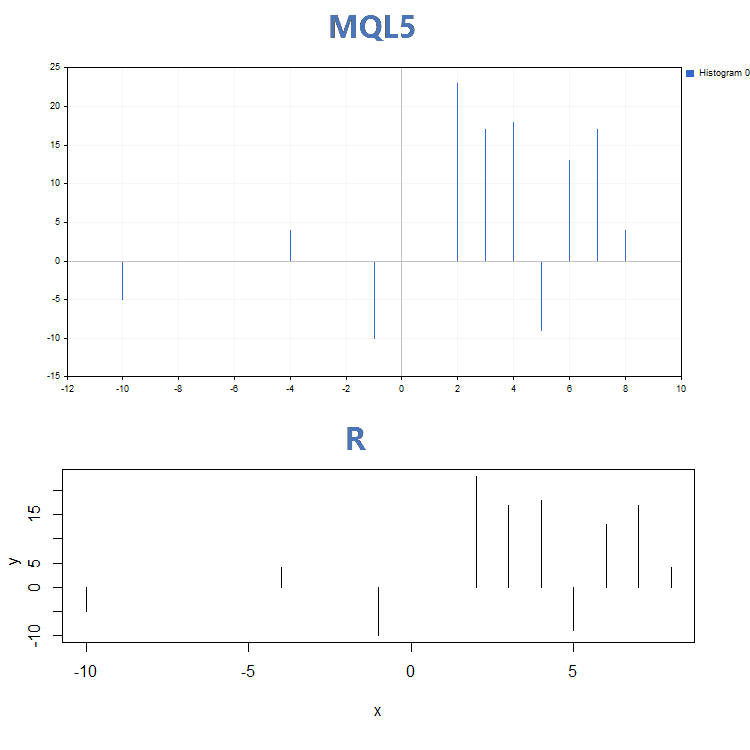
GraphPlot()、plot() 関数の操作の視覚的な差から離れて、別のエントリーパラメータを適用します。Plot() 関数は、特定のカーブ パラメータ (たとえば、' lwd' 線の幅を変更する) を設定することができます。GraphPlot() 関数にはデータを構築するために必要な唯一の重要パラメータが含まれます。

名前を付けてみましょう。

1. 上記の4 つの形式のいずれかでデータを記述します。
   
2. プロット タイプ(デフォルトは CURVE_POINTS) 。
   
3. オブジェクト名 (デフォルトは NULL)。

グラフィックライブラリを使用して作成された各チャートは、チャート オブジェクトと割り当てられたグラフィカル リソースで構成されます。グラフィカルリソース名に基づいて形成されるオブジェクト名に「::」を追加するだけです。たとえば、オブジェクトの名前が"SomeGraphic"の場合、そのグラフィカル リソースの名前は":: SomeGraphic"です。

GraphPlot() 関数は固定アンカー x = 65, y = 45です。幅とチャートの高さは、チャートのサイズに基づいて計算されます。幅は65%、高さは60% で構成されています。したがって、現在のチャートの次元が65から45未満である場合は、GraphPlot() 関数は正常に動作できません。

作成済みのオブジェクトの名前を適用すると、グラフィックス ライブラリは、そのリソースの種類を確認した後そのオブジェクトのチャートを表示します。リソースの種類がOBJ_BITMAP_LABELの場合、同じオブジェクト リソースのペアで実行されます。

オブジェクト名がGraphPlot() 関数に渡される場合、そのオブジェクトを検索し、チャート表示されます。オブジェクトが見つからない場合、新しいオブジェクト リソースのペアが自動的に指定した名前に基づいて作成します。明示的に指定されたオブジェクト名がないGraphPlot() 関数を使用して、「グラフィック」の標準的な名前が使用されます。 

この場合、チャートのアンカー ポイントとそのサイズを指定することができます。これを行うには、必要なパラメータとオブジェクト リソース ペアを作成し、作成したオブジェクトの名前を GraphPlot() 関数に渡します。グラフィック オブジェクトの名前のペアの作成では、各呼び出しでオブジェクトの名前を渡す必要性を除去し、 GraphPlot 関数の標準的なキャンバスを修正します。

例として、上記の例からデータを取得し、750х350 の新しいグラフ サイズを設定しましょう。また、アンカー ポイントを左上に移しましょう。

void OnStart()
  {
//---チャートと動的リソース オブジェクトを作成
   string name="Graphic";
   long x=0;
   long y=0;
   int width=750;
   int height=350;
   int data[];
   ArrayResize(data,width*height);
   ZeroMemory(data);
   ObjectCreate(0,name,OBJ_BITMAP_LABEL,0,0,0);
   ResourceCreate("::"+name,data,width,height,0,0,0,COLOR_FORMAT_XRGB_NOALPHA);
   ObjectSetInteger(0,name,OBJPROP_XDISTANCE,x);
   ObjectSetInteger(0,name,OBJPROP_YDISTANCE,y);
   ObjectSetString(0,name,OBJPROP_BMPFILE,"::"+name);
//--- x および y 配列
   double arr_x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double arr_y[]={-5,4,-10,23,17,18,-9,13,17,4};
//---x および y 配列をプロット
   GraphPlot(arr_x,arr_y,CURVE_LINES);
  }

サンプル チャート

標準ライブラリには、複数の統計分布を操作するための関数を搭載した統計情報セクションがあります。各ディストリビューションは、サンプル チャートを取得するコードに伴われます。ここでは、 シンプルに 1 つの GIF にチャートを表示します。例のソース コードは、MQL5.zip ファイルにアタッチされます。MQL5\Scripts に解凍します。

すべての例で価格チャート CHART_SHOWプロパティが無効になっています:

//---価格チャートを無効にする
   ChartSetInteger(0,CHART_SHOW,false);

1つの大きなキャンバスにチャート ウィンドウを切り替え、グラフィカル リソースを適用する複雑なオブジェクトを描画することができます。

モスクワ為替先物のスプレッド戦略の例を参照してください。ここにはグラフィックス ライブラリの適用例などが示されています。

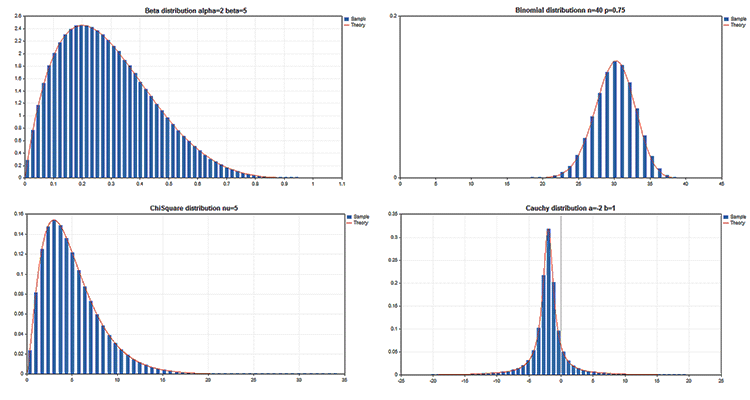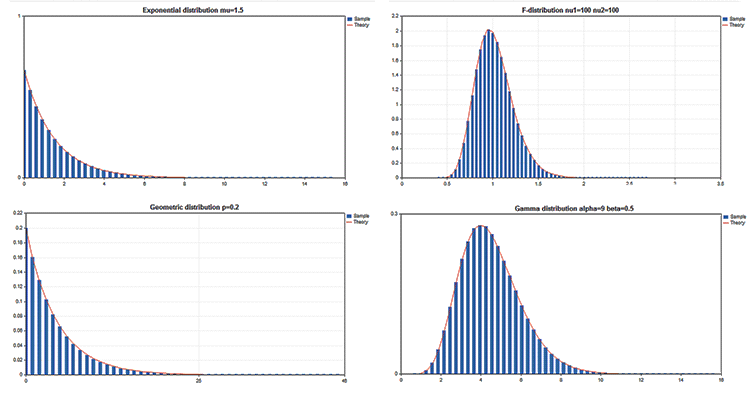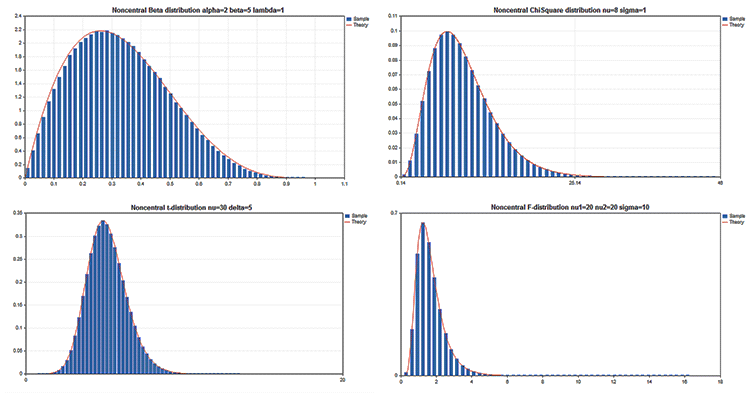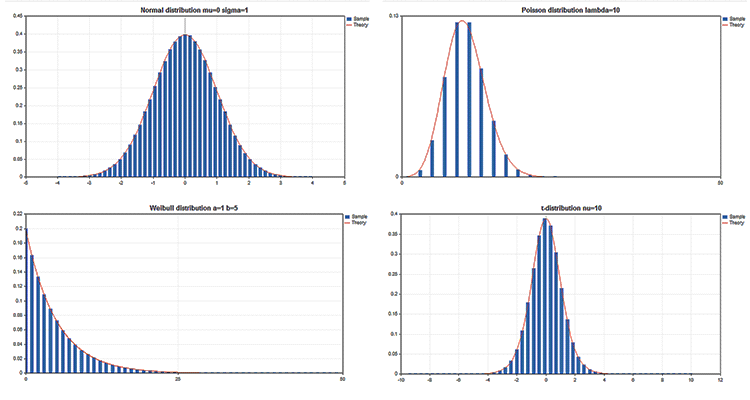
グラフィックス ライブラリの重要な利点

MQL5により、開発者はトレードロボットとテクニカルインジケーターを作成することができます。　また、 ALGLIBやファジィを用いた複雑な数学的計算を実行するだけでなく、統計ライブラリを使って得られたデータをグラフィック ライブラリでシンプルに可視化することができます。ライブラリが提供する広範な関数で、ほとんどの操作が自動化されています。

• 5 チャートの種類を表示
• 10 のチャートのマーカーの種類
  
• X軸とY軸の自動スケーリング
• 色の自動選択
  
• 標準のアンチエイリアシングやより高度なブレゼンハムのアルゴリズムを使用した平滑化
• ラインを表示するためのスプライン近似パラメータを設定する関数
  
• 配列 x[] と y[] に基づいて、ラインのコードを使用したチャートをプロットする関数
• 関数へのポインターを使用してチャートをプロットする関数
  

グラフィックス ライブラリはプロット チャートを簡素化し、トレードに新たなレベルのアプリケーションを発生させます。MT５プラットフォームでは、複雑な数学的計算を実行し、ターミナル ウィンドウで直接結果を表示することができます。

添付のコードを是非みてください。サードパーティ製のパッケージはもう必要ありません!