EA baseado em um aproximador universal MLP

Conteúdo

1. Introdução
2. Imersão no problema do aprendizado
   
3. Aproximador universal
4. Implementação do MLP dentro de um EA

Introdução

Quando se fala em redes neurais, muitos imaginam algoritmos complexos e detalhes técnicos complicados. Na essência, uma rede neural é uma composição de funções, em que cada camada combina uma transformação linear com uma função de ativação não linear. Se representarmos isso com uma fórmula, podemos escrever da seguinte forma:

F(x) = f2(f1(x))

onde f1 é a função da primeira camada, e f2 é a função da segunda camada.

Muita gente acredita que redes neurais são algo extremamente difícil de entender, mas quero explicar isso de forma simples, para que todos possam enxergar por outro ângulo. Existem muitas arquiteturas de redes neurais, cada uma voltada para uma tarefa específica. Neste artigo, vamos focar no MLP (Perceptron Multicamadas) mais simples, que transforma informações de entrada por meio de funções não lineares. Conhecendo a arquitetura da rede, conseguimos expressá-la de forma analítica, onde cada função de ativação nos neurônios atua como um transformador não linear.

Cada camada da rede tem um grupo de neurônios que processa informações ao passar por várias transformações não lineares. Um MLP é capaz de executar tarefas como aproximação, classificação e extrapolação. A fórmula geral que descreve o funcionamento do perceptron é ajustada com pesos, permitindo que ele se adapte a diferentes tarefas.

É interessante notar que podemos integrar esse aproximador em qualquer sistema de trading. Se considerarmos a rede neural sem mencionar otimizadores como SGD ou ADAM, o MLP pode ser usado como um transformador de informação. Por exemplo, ele pode analisar o estado do mercado — seja lateralização, tendência ou transição — e, com base nisso, aplicar diferentes estratégias de trading. Também podemos usar a rede neural para transformar dados de indicadores em sinais de negociação.

Neste artigo, buscamos desfazer o mito sobre a complexidade de aplicar redes neurais e mostrar como, deixando de lado os detalhes complicados do ajuste de pesos e da otimização, é possível criar um EA baseado em rede neural sem precisar de conhecimento aprofundado em aprendizado de máquina. Vamos explorar passo a passo o processo de criação do EA, desde a coleta e preparação dos dados até o treinamento do modelo e sua integração na estratégia de trading.

Imersão no problema do aprendizado

Existem três tipos principais de aprendizado. O nosso foco está nos detalhes desses tipos quando aplicados à análise de dados de mercado. A abordagem apresentada neste artigo visa considerar as limitações desses tipos de aprendizado.

Aprendizado supervisionado. O modelo é treinado com dados rotulados, gerando previsões com base em exemplos. A função objetivo: minimizar o erro entre a previsão e o valor-alvo (por exemplo, erro MSE). No entanto, essa abordagem possui várias limitações. Ela exige um grande volume de dados rotulados com qualidade, o que representa um dos principais desafios no contexto de séries temporais. Se tivermos exemplos claros e confiáveis para treinar, como ocorre em tarefas de reconhecimento de texto manuscrito ou conteúdo de imagens, o processo de treinamento transcorre sem problemas. A rede neural aprende exatamente aquilo para o qual foi treinada.

No caso de séries temporais, a situação é diferente: é extremamente difícil rotular os dados de forma a garantir que sejam confiáveis e relevantes. Na prática, a rede acaba aprendendo aquilo que nós presumimos, e não necessariamente o que realmente está ligado ao processo que estamos investigando. Muitos autores destacam que, para um aprendizado supervisionado bem-sucedido, é preciso usar rótulos “bons”, porém, a qualidade desses rótulos no contexto de séries temporais é algo difícil de definir antecipadamente.

Como resultado, surgem avaliações subjetivas da qualidade do aprendizado, como o “overfitting”. Também surge o conceito artificial de “ruído”, sugerindo que uma rede “muito sobreajustada” pode ter memorizado dados ruidosos em vez de padrões fundamentais. Você não encontrará definições claras ou medidas quantitativas de “ruído” e “overfitting”, justamente porque são conceitos subjetivos quando se trata da análise de séries temporais. Por isso, é necessário reconhecer que o uso de aprendizado supervisionado em séries temporais exige considerar muitos fatores de difícil formalização, que impactam diretamente na robustez do modelo com novos dados.

Aprendizado não supervisionado. O modelo busca identificar estruturas ocultas nos dados sem rótulos. A função objetivo: varia conforme o método usado. É difícil avaliar a qualidade dos resultados obtidos, pois não há rótulos definidos para validação. O modelo pode não encontrar padrões úteis se os dados não tiverem uma estrutura clara, e nem mesmo é possível afirmar com certeza se as estruturas detectadas têm relação direta com o “processo portador”.

Os métodos tradicionalmente atribuídos ao aprendizado não supervisionado incluem: K-means, Mapas Auto-organizáveis (SOM) e outros. Todos esses métodos são treinados com base em funções objetivo específicas para cada um.

Vamos a alguns exemplos correspondentes:

• K-médias (K-means). Minimização da dispersão intracluster, definida como a soma dos quadrados das distâncias entre cada ponto e o centro do seu cluster.
• Análise de Componentes Principais (PCA). Maximização da variância das projeções dos dados sobre novos eixos (componentes principais).
• Árvores de Decisão (DT). Minimização da entropia, índice de Gini, variância e outros.
  

Aprendizado por reforço. Função objetivo: recompensa acumulada. É um método de aprendizado de máquina no qual o agente (por exemplo, um programa ou robô) aprende a tomar decisões ao interagir com o ambiente. O agente recebe uma recompensa ou punição dependendo das ações que realiza. O objetivo do agente é maximizar a recompensa total, aprendendo com base na experiência.

Os resultados podem ser instáveis por causa da natureza aleatória do aprendizado, dificultando a previsão do comportamento do modelo e nem sempre sendo adequado para tarefas onde não há um sistema claro de recompensas e penalizações, o que pode tornar o aprendizado menos eficiente. O aprendizado por reforço geralmente vem acompanhado de diversos problemas práticos: dificuldade em representar a função objetivo de reforço ao utilizar algoritmos de aprendizado de redes neurais como o ADAM e similares, já que é necessário normalizar os valores da função objetivo para a faixa próxima de [-1;1]. Isso está ligado ao cálculo das derivadas das funções de ativação nos neurônios e à propagação reversa do erro pela rede para ajustar os pesos, evitando assim a “explosão de pesos” e outros efeitos que levam à paralisação da rede neural.

Acima analisamos a classificação clássica dos tipos de aprendizado. Como se pode notar, todos eles se baseiam na minimização ou maximização de alguma função objetivo. Torna-se evidente então que a principal diferença entre eles está apenas em um ponto — a presença ou ausência de um “professor”, e, quando não há um, a distinção entre os tipos de aprendizado se resume à natureza específica da função objetivo que se busca otimizar.

Assim, na minha visão, a classificação dos tipos de aprendizado pode ser representada como aprendizado supervisionado, quando existem valores-alvo (minimização do erro da previsão em relação ao alvo), e aprendizado não supervisionado, quando não há valores-alvo. Os subtipos de aprendizado não supervisionado se diferenciam pelo tipo de função objetivo com base nas propriedades dos dados (distâncias, densidade etc.), nos resultados do sistema (métricas integrais como lucro, desempenho etc.), nas distribuições (no caso de modelos generativos) e em outros critérios de avaliação.

Aproximador universal

A abordagem que proponho pertence ao segundo tipo, isto é, ao aprendizado não supervisionado. Nesse método, não tentamos “ensinar” a rede neural a operar corretamente nem indicamos onde abrir ou fechar posições, porque nós mesmos não sabemos as respostas para essas perguntas. Em vez disso, permitimos que a rede tome as decisões de trading por conta própria, e nossa tarefa é avaliar seus resultados acumulados de negociação.

Não há necessidade de normalizar a função de avaliação nem de se preocupar com problemas como “explosão de pesos” e “paralisação da rede”, pois esses problemas não ocorrem nesse tipo de abordagem. Separamos logicamente a rede neural do algoritmo de otimização e atribuímos a ela apenas a função de transformar os dados de entrada em uma nova forma de informação que represente as habilidades de um trader. Por essência, estamos apenas convertendo um tipo de informação em outro, sem precisar entender os padrões da série temporal nem como negociar para obter lucro.

Para essa função, um tipo de rede neural ideal é o MLP (perceptron multicamadas), conforme afirma o teorema da aproximação universal. Esse teorema garante que redes neurais podem aproximar qualquer função contínua. No nosso caso, “função contínua” se refere ao processo observado na série temporal em análise. Com essa abordagem, não é necessário recorrer a conceitos artificiais e subjetivos, como “ruído” e “overfitting”, que não têm medidas quantitativas.

Para entender como isso funciona, basta observar a figura 1. Alimentamos o MLP com informações relacionadas ao mercado no momento atual (como preços OHLC das barras, valores de indicadores etc.), e recebemos na saída sinais de trading prontos para uso. Após rodar a rede com o histórico de um ativo, podemos calcular a função objetivo, que representa uma avaliação integral (ou um conjunto de avaliações) dos resultados da negociação, e ajustar os pesos da rede com um algoritmo de otimização externo, maximizando a função objetivo que descreve a qualidade dos resultados de trading da rede neural.

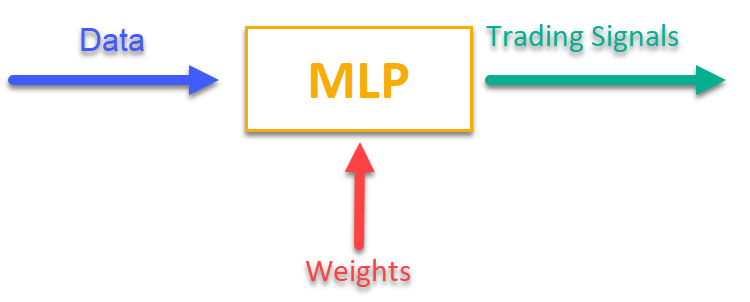
Figura 1. Transformação de um tipo de informação em outro

Implementação do MLP dentro de um EA

Primeiro escreveremos a classe MLP e depois integraremos essa classe ao EA. Há muitas implementações diferentes de redes com várias arquiteturas descritas em artigos, mas aqui vou apresentar minha própria versão de um MLP, que é uma rede neural propriamente dita, sem otimizador.

Declaramos a classe "C_MLP", que implementa um perceptron multicamadas (MLP). As funções principais:

1. Init() — inicialização, configura a rede de acordo com o número necessário de camadas e a quantidade de neurônios em cada camada e retorna o número total de pesos.

2. ANN() — propagação para frente, do primeiro layer de entrada até o último layer de saída; o método recebe os dados de entrada e os pesos, calcula os valores de saída da rede (ver figura 1).

3. GetWcount() — método que retorna a quantidade total de pesos da rede.

4. LayerCalc() — realiza o cálculo de uma camada da rede.

Elementos internos:

• layers — armazena os valores dos neurônios
• weightsCNT — número total de pesos
• layersCNT — número total de camadas

A classe permite criar uma rede neural MLP com qualquer número de camadas ocultas e qualquer quantidade de neurônios nelas.

//+----------------------------------------------------------------------------+
//| Multilayer Perceptron (MLP) class                                          |
//| Implement a forward pass through a fully connected neural network          |
//| Architecture: Lin -> L1 -> L2 -> ... Ln -> Lout                            |
//+----------------------------------------------------------------------------+
class C_MLP
{
  public: //--------------------------------------------------------------------

  // Initialize the network with the given configuration
  // Return the total number of weights in the network, or 0 in case of an error
  int Init (int &layerConfig []);

  // Calculate the values of all layers sequentially from input to output
  void ANN (double &inLayer  [],  // input values
            double &weights  [],  // network weights (including biases)
            double &outLayer []); // output layer values

  // Get the total number of weights in the network
  int GetWcount () { return weightsCNT; }

  int layerConf []; // Network configuration - number of neurons in each layer

  private: //-------------------------------------------------------------------
  // Structure for storing the neural network layer
  struct S_Layer
  {
      double l [];     // Neuron values
  };

  S_Layer layers [];    // Array of all network layers
  int     weightsCNT;   // Total number of weights in the network (including biases)
  int     layersCNT;    // Total number of layers (including input and output ones)
  int     cnt_W;        // Current index in the weights array when traversing the network
  double  temp;         // Temporary variable to store the sum of the weighted inputs

  // Calculate values of one layer of the network
  void LayerCalc (double   &inLayer  [], // values of neurons of the previous layer
                  double   &weights  [], // array of weights and biases of the entire network
                  double   &outLayer [], // array for writing values of the current layer
                  const int inSize,      // number of neurons in the input layer
                  const int outSize);    // outSize  - number of neurons in the output layer
};

O MLP é inicializado com a configuração especificada das camadas. Etapas principais:

1. Verificação da configuração:

• Confere se a rede tem pelo menos 2 camadas (entrada e saída).
• Verifica se cada camada contém pelo menos 1 neurônio. Caso essas condições não sejam cumpridas, exibe uma mensagem de erro e a função retorna 0.

2. Armazena a configuração de cada camada para acesso rápido no array "layerConf".

3. Criação dos arrays de camadas: aloca memória para armazenar os neurônios em cada camada.

4. Cálculo dos pesos: calcula o número total de pesos da rede, incluindo os bias para cada neurônio.

A função retorna o total de pesos ou 0 em caso de erro.

//+----------------------------------------------------------------------------+
//| Initialize the network                                                     |
//| layerConfig - array with the number of neurons in each layer               |
//| Returns the total number of weights needed, or 0 in case of an error       |
//+----------------------------------------------------------------------------+
int C_MLP::Init (int &layerConfig [])
{
  // Check that the network has at least 2 layers (input and output)
  layersCNT = ArraySize (layerConfig);
  if (layersCNT < 2)
  {
    Print ("Error Net config! Layers less than 2!");
    return 0;
  }

  // Check that each layer has at least 1 neuron
  for (int i = 0; i < layersCNT; i++)
  {
    if (layerConfig [i] <= 0)
    {
      Print ("Error Net config! Layer No." + string (i + 1) + " contains 0 neurons!");
      return 0;
    }
  }

  // Save network configuration
  ArrayCopy (layerConf, layerConfig, 0, 0, WHOLE_ARRAY);

  // Create an array of layers
  ArrayResize (layers, layersCNT);

  // Allocate memory for neurons of each layer
  for (int i = 0; i < layersCNT; i++)
  {
    ArrayResize (layers [i].l, layerConfig [i]);
  }

  // Calculate the total number of weights in the network
  weightsCNT = 0;
  for (int i = 0; i < layersCNT - 1; i++)
  {
    // For each neuron of the next layer we need:
    // - one bias value
    // - weights for connections with all neurons of the current layer
    weightsCNT += layerConf [i] * layerConf [i + 1] + layerConf [i + 1];
  }

  return weightsCNT;
}

O método "LayerCalc" executa os cálculos para uma camada da rede neural, usando a tangente hiperbólica como função de ativação. Etapas principais:

1. Parâmetros de entrada e saída:

• inLayer[] — array com os valores de entrada vindos da camada anterior
• weights[] — array de pesos que contém os bias e os pesos das conexões
• outLayer[] — array que armazenará os valores de saída da camada atual
• inSize — número de neurônios na camada de entrada
• outSize — número de neurônios na camada de saída

2. Laço sobre os neurônios da camada de saída. Para cada neurônio:

• começa com o valor do bias
• soma os valores de entrada ponderados (cada valor de entrada é multiplicado pelo peso correspondente)
• calcula o valor da função de ativação do neurônio

3. Aplicação da função de ativação:

• utiliza a tangente hiperbólica para fazer a transformação não linear, levando o valor para a faixa entre -1 e 1
• o resultado é armazenado no array de saída "outLayer[]"

//+----------------------------------------------------------------------------+
//| Calculate values of one layer of the network                               |
//| Implement the equation: y = tanh(bias + w1*x1 + w2*x2 + ... + wn*xn)       |
//+----------------------------------------------------------------------------+
void C_MLP::LayerCalc (double    &inLayer  [],
                       double    &weights  [],
                       double    &outLayer [],
                       const int  inSize,
                       const int  outSize)
{
  // Calculate the value for each neuron in the output layer
  for (int i = 0; i < outSize; i++)
  {
    // Start with the bias value for the current neuron
    temp = weights [cnt_W];
    cnt_W++;

    // Add weighted inputs from each neuron in the previous layer
    for (int u = 0; u < inSize; u++)
    {
      temp += inLayer [u] * weights [cnt_W];
      cnt_W++;
    }

    // Apply the "hyperbolic tangent" activation function
    // f(x) = 2/(1 + e^(-x)) - 1
    // Range of values f(x): [-1, 1]
    outLayer [i] = 2.0 / (1.0 + exp (-temp)) - 1.0;
  }
}

A rede neural artificial é executada calculando sequencialmente os valores de todas as camadas, isto é, da camada de entrada até a camada de saída. 

1. Parâmetros de entrada e saída:

• inLayer[] — array com os valores de entrada que são fornecidos à rede neural
• weights[] — array de pesos, que inclui tanto os pesos das conexões entre neurônios quanto os bias
• outLayer[] — array onde serão armazenados os valores de saída da última camada da rede neural

2. Reinicialização do contador de pesos: a variável "cnt_W", que rastreia a posição atual no array de pesos, é zerada antes do início dos cálculos.

3. Cópia dos dados de entrada: os dados de entrada de "inLayer" são copiados para a primeira camada da rede usando a função "ArrayCopy".

4. Laço pelas camadas:

• o laço percorre todas as camadas da rede neural
• para cada camada é chamada a função "LayerCalc", que calcula os valores da camada atual com base nos valores de saída da camada anterior, nos pesos e nos tamanhos das camadas

5. Após finalizar os cálculos de todas as camadas, os valores de saída da última camada são copiados para o array "outLayer" utilizando a função "ArrayCopy".

//+----------------------------------------------------------------------------+
//| Calculate the values of all layers sequentially from input to output       |
//+----------------------------------------------------------------------------+
void C_MLP::ANN (double &inLayer  [],  // input values
                 double &weights  [],  // network weights (including biases)
                 double &outLayer [])  // output layer values
{
  // Reset the weight counter before starting the pass
  cnt_W = 0;

  // Copy the input data to the first layer of the network
  ArrayCopy (layers [0].l, inLayer, 0, 0, WHOLE_ARRAY);

  // Calculate the values of each layer sequentially
  for (int i = 0; i < layersCNT - 1; i++)
  {
    LayerCalc (layers    [i].l,     // output of the previous layer
               weights,             // network weights (including bias)
               layers    [i + 1].l, // next layer
               layerConf [i],       // size of current layer
               layerConf [i + 1]);  // size of the next layer
  }

  // Copy the values of the last layer to the output array
  ArrayCopy (outLayer, layers [layersCNT - 1].l, 0, 0, WHOLE_ARRAY);
}

Agora é a vez de escrever o EA para a estratégia de trading automatizada com aprendizado de máquina baseado na rede neural MLP.

1. Incluímos as bibliotecas para operações de trading, manipulação de informações do símbolo, funções matemáticas, perceptron multicamadas (MLP) e algoritmos de otimização.

2. Parâmetros de negociação — volume da posição, horário de início e fim do trading. Parâmetros de aprendizado — escolha do otimizador, estrutura da rede neural, número de barras para análise, profundidade do histórico para treinamento, período de validade do modelo e limiar do sinal.

3. Declaração de classes e variáveis — objetos de classes utilitárias, da rede neural, e variáveis para armazenar os dados de entrada, pesos e o momento do último treinamento.

#include "#Symbol.mqh"
#include <Math\AOs\Utilities.mqh>
#include <Math\AOs\NeuroNets\MLP.mqh>
#include <Math\AOs\PopulationAO\#C_AO_enum.mqh>

//------------------------------------------------------------------------------
input group    "---Trade parameters-------------------";
input double   Lot_P              = 0.01;   // Position volume
input int      StartTradeH_P      = 3;      // Trading start time
input int      EndTradeH_P        = 12;     // Trading end time

input group    "---Training parameters----------------";
input E_AO     OptimizerSelect_P  = AO_CLA; // Select optimizer
input int      NumbTestFuncRuns_P = 5000;   // Total number of function runs
input string   MLPstructure_P     = "1|1";  // Hidden layers, <4|6|2> - three hidden layers
input int      BarsAnalysis_P     = 3;      // Number of bars to analyze
input int      DepthHistoryBars_P = 10000;  // History depth for training in bars 
input int      RetrainingPeriod_P = 12;     // Duration in hours of the model's relevance
input double   SigThr_P           = 0.5;    // Signal threshold

//------------------------------------------------------------------------------
C_AO_Utilities U;
C_MLP          NN;
int            InpSigNumber;
int            WeightsNumber;
double         Inputs  [];
double         Weights [];
double         Outs    [1];
datetime       LastTrainingTime = 0;

C_Symbol       S;
C_NewBar       B;
int            HandleS;
int            HandleR;

Como dados para serem processados pela rede neural, escolhi a primeira ideia que veio à mente: OHLC — preços das barras (por padrão, definidos como os 3 últimos candles antes do atual) e os valores dos indicadores RSI e Stochastic dessas mesmas barras. A função "OnInit()" inicializa a estratégia de trading usando a rede neural. 

1. Inicialização dos indicadores — são criados os objetos para RSI e Stochastic.

2. Cálculo da quantidade de sinais de entrada para a rede com base no parâmetro "BarsAnalysis_P".

3. Configuração da estrutura da rede neural — a string de configuração da rede informada pelo usuário é dividida e verificada quanto à validade do número de camadas e de neurônios. O parâmetro de entrada em formato string define a quantidade de camadas ocultas e de neurônios nelas. Por padrão, esse parâmetro é "1|1", o que significa 2 camadas ocultas com 1 neurônio em cada.

4. Inicialização da rede neural — é chamado o método de inicialização da rede, são criados os arrays para os pesos e os dados de entrada.

5. Exibição de informações — são impressos os dados sobre o número de camadas e os parâmetros da rede.

6. Retorna o status de inicialização bem-sucedida.

A função garante a preparação de todos os componentes necessários para a operação da estratégia de trading.

//——————————————————————————————————————————————————————————————————————————————
int OnInit ()
{
  //----------------------------------------------------------------------------
  // Initializing indicators: Stochastic and RSI
  HandleS = iStochastic (_Symbol, PERIOD_CURRENT, 5, 3, 3, MODE_EMA, STO_LOWHIGH);
  HandleR = iRSI        (_Symbol, PERIOD_CURRENT, 14, PRICE_TYPICAL);

  // Calculate the number of inputs to the neural network based on the number of bars to analyze
  InpSigNumber = BarsAnalysis_P * 2 + BarsAnalysis_P * 4;

  // Display information about the number of inputs
  Print ("Number of network logins  : ", InpSigNumber);

  //----------------------------------------------------------------------------
  // Initialize the structure of the multilayer MLP
  string sepResult [];
  int layersNumb = StringSplit (MLPstructure_P, StringGetCharacter ("|", 0), sepResult);

  // Check if the number of hidden layers is greater than 0
  if (layersNumb < 1)
  {
    Print ("Network configuration error, hidden layers < 1...");
    return INIT_FAILED; // Return initialization error
  }

  // Increase the number of layers by 2 (input and output)
  layersNumb += 2;

  // Initialize array for neural network configuration
  int nnConf [];
  ArrayResize (nnConf, layersNumb);

  // Set the number of inputs and outputs in the network configuration
  nnConf [0] = InpSigNumber;   // Input layer
  nnConf [layersNumb - 1] = 1; // Output layer

  // Filling the hidden layers configuration
  for (int i = 1; i < layersNumb - 1; i++)
  {
    nnConf [i] = (int)StringToInteger (sepResult [i - 1]); // Convert a string value to an integer

    // Check that the number of neurons in a layer is greater than 0
    if (nnConf [i] < 1)
    {
      Print ("Network configuration error, in layer ", i, " <= 0 neurons...");
      return INIT_FAILED; // Return initialization error
    }
  }

  // Initialize the neural network and get the number of weights
  WeightsNumber = NN.Init (nnConf);
  if (WeightsNumber <= 0)
  {
    Print ("Error initializing MLP network...");
    return INIT_FAILED; // Return initialization error
  }

  // Resize the input array and weights
  ArrayResize (Inputs,  InpSigNumber);
  ArrayResize (Weights, WeightsNumber);

  // Initialize weights with random values in the range [-1, 1] (for debugging)
  for (int i = 0; i < WeightsNumber; i++)
      Weights [i] = 2 * (rand () / 32767.0) - 1;

  // Output network configuration information
  Print ("Number of all layers     : ", layersNumb);
  Print ("Number of network parameters: ", WeightsNumber);

  //----------------------------------------------------------------------------
  // Initialize the trade and bar classes
  S.Init (_Symbol);
  B.Init (_Symbol, PERIOD_CURRENT);

  return (INIT_SUCCEEDED); // Return successful initialization result
}
//——————————————————————————————————————————————————————————————————————————————

A lógica principal da estratégia está implementada na função "OnTick()". A estratégia é simples: se o sinal do neurônio da camada de saída ultrapassar o limiar definido nos parâmetros, o sinal é interpretado como uma indicação para compra ou venda. Se não houver posições abertas e o horário atual estiver dentro do período permitido para negociações, abre-se uma posição. A posição é fechada caso a rede gere um sinal contrário ou de forma forçada, caso o tempo permitido para operar tenha se encerrado. Vamos aos passos principais da estratégia:

1. Verificação da necessidade de novo treinamento. Se passou tempo suficiente desde o último treinamento, inicia-se o processo de treinamento da rede neural. Em caso de erro, uma mensagem é exibida.

2. Verificação de novo candle. Se o tick atual não marca o início de uma nova barra, a execução da função é interrompida.

3. Coleta de dados. O código solicita os dados de preços (abertura, fechamento, máxima e mínima) e os valores dos indicadores (RSI e Stochastic).

4. Normalização dos dados. São identificados os valores máximos e mínimos entre os dados de preços coletados, e então todos os dados são normalizados no intervalo de -1 a 1.

5. Previsão. Os dados normalizados são passados à rede neural para gerar os sinais de saída.

6. Geração do sinal de trading. Com base nos dados de saída, é gerado um sinal de compra (1) ou venda (-1).

7. Gerenciamento de posições. Se a posição atual estiver em desacordo com o sinal, ela é encerrada. Se houver um sinal de abertura e o horário for permitido, uma nova posição é aberta. Caso contrário, se já houver uma posição aberta, ela é encerrada.

Dessa forma, a lógica em OnTick() implementa o ciclo completo de uma operação automatizada: aprendizado, coleta de dados, normalização, previsão e gestão de posições.

//——————————————————————————————————————————————————————————————————————————————
void OnTick ()
{
  // Check if the neural network needs to be retrained
  if (TimeCurrent () - LastTrainingTime >= RetrainingPeriod_P * 3600)
  {
    // Start the neural network training
    if (Training ()) LastTrainingTime = TimeCurrent (); // Update last training time
    else             Print ("Training error...");      // Display an error message

    return; // Complete function execution
  }

  //----------------------------------------------------------------------------
  // Check if the current tick is the start of a new bar
  if (!B.IsNewBar ()) return;

  //----------------------------------------------------------------------------
  // Declare arrays to store price and indicator data
  MqlRates rates [];
  double   rsi   [];
  double   sto   [];

  // Get price data
  if (CopyRates (_Symbol, PERIOD_CURRENT, 1, BarsAnalysis_P, rates) != BarsAnalysis_P) return;

  // Get Stochastic values
  if (CopyBuffer (HandleS, 0, 1, BarsAnalysis_P, sto) != BarsAnalysis_P) return;
  // Get RSI values
  if (CopyBuffer (HandleR, 0, 1, BarsAnalysis_P, rsi) != BarsAnalysis_P) return;

  // Initialize variables to normalize data
  int wCNT   = 0;
  double max = -DBL_MAX; // Initial value for maximum
  double min =  DBL_MAX; // Initial value for minimum

  // Find the maximum and minimum among high and low
  for (int b = 0; b < BarsAnalysis_P; b++)
  {
    if (rates [b].high > max) max = rates [b].high; // Update the maximum
    if (rates [b].low  < min) min = rates [b].low;  // Update the minimum
  }

  // Normalization of input data for neural network
  for (int b = 0; b < BarsAnalysis_P; b++)
  {
    Inputs [wCNT] = U.Scale (rates [b].high,  min, max, -1, 1); wCNT++; // Normalizing high
    Inputs [wCNT] = U.Scale (rates [b].low,   min, max, -1, 1); wCNT++; // Normalizing low
    Inputs [wCNT] = U.Scale (rates [b].open,  min, max, -1, 1); wCNT++; // Normalizing open
    Inputs [wCNT] = U.Scale (rates [b].close, min, max, -1, 1); wCNT++; // Normalizing close

    Inputs [wCNT] = U.Scale (sto   [b],       0,   100, -1, 1); wCNT++; // Normalizing Stochastic
    Inputs [wCNT] = U.Scale (rsi   [b],       0,   100, -1, 1); wCNT++; // Normalizing RSI
  }

  // Convert data from Inputs to Outs
  NN.ANN (Inputs, Weights, Outs);

  //----------------------------------------------------------------------------
  // Generate a trading signal based on the output of a neural network
  int signal = 0;
  if (Outs [0] >  SigThr_P) signal =  1; // Buy signal
  if (Outs [0] < -SigThr_P) signal = -1; // Sell signal

  // Get the type of open position
  int posType = S.GetPosType ();
  S.GetTick ();

  if ((posType == 1 && signal == -1) || (posType == -1 && signal == 1))
  {
    if (!S.PosClose ("", ORDER_FILLING_FOK) != 0) posType = 0;
    else return;
  }

  MqlDateTime time;
  TimeToStruct (TimeCurrent (), time);

  // Check the allowed time for trading
  if (time.hour >= StartTradeH_P && time.hour < EndTradeH_P)
  {
    // Open a new position depending on the signal
    if (posType == 0 && signal != 0) S.PosOpen (signal, Lot_P, "", ORDER_FILLING_FOK, 0, 0.0, 0.0, 1);
  }
  else
  {
    if (posType != 0) S.PosClose ("", ORDER_FILLING_FOK);
  }
}
//——————————————————————————————————————————————————————————————————————————————

A seguir, abordamos o treinamento da rede neural com dados históricos:

1. Coleta de dados. São carregados os dados históricos de preços, além dos valores dos indicadores RSI e Stochastic.

2. Definição do horário de negociação. É criado um array que marca quais barras estão dentro do horário permitido para operações.

3. Configuração dos parâmetros de otimização. São inicializados os limites e os passos dos parâmetros para a otimização.

4. Escolha do algoritmo de otimização. É definido o algoritmo de otimização a ser usado e o tamanho da população.

5. Laço principal de otimização dos pesos da rede neural: 

• para cada solução na população, é calculado o valor da função objetivo que avalia sua qualidade
• a população de soluções é atualizada com base nos resultados

6. Exibição dos resultados. É impresso o nome do algoritmo, o melhor resultado e os melhores parâmetros são copiados para o array de pesos.

7. A memória usada pelo objeto do algoritmo de otimização é liberada.

A função realiza o processo de treinamento da rede neural para encontrar os melhores parâmetros com base em dados históricos.

//——————————————————————————————————————————————————————————————————————————————
bool Training ()
{
  MqlRates rates [];
  double   rsi   [];
  double   sto   [];

  int bars = CopyRates (_Symbol, PERIOD_CURRENT, 1, DepthHistoryBars_P, rates);
  Print ("Training on history of ", bars, " bars");
  if (CopyBuffer (HandleS, 0, 1, DepthHistoryBars_P, sto) != bars) return false;
  if (CopyBuffer (HandleR, 0, 1, DepthHistoryBars_P, rsi) != bars) return false;

  MqlDateTime time;
  bool truTradeTime []; ArrayResize (truTradeTime, bars); ArrayInitialize (truTradeTime, false);
  for (int i = 0; i < bars; i++)
  {
    TimeToStruct (rates [i].time, time);
    if (time.hour >= StartTradeH_P && time.hour < EndTradeH_P) truTradeTime [i] = true;
  }

  //----------------------------------------------------------------------------
  int popSize          = 50;                           // Population size for optimization algorithm
  int epochCount       = NumbTestFuncRuns_P / popSize; // Total number of epochs (iterations) for optimization

  double rangeMin [], rangeMax [], rangeStep [];       // Arrays for storing the parameters' boundaries and steps

  ArrayResize (rangeMin,  WeightsNumber);              // Resize 'min' borders array
  ArrayResize (rangeMax,  WeightsNumber);              // Resize 'max' borders array
  ArrayResize (rangeStep, WeightsNumber);              // Resize the steps array

  for (int i = 0; i < WeightsNumber; i++)
  {
    rangeMax  [i] =  5.0;
    rangeMin  [i] = -5.0;
    rangeStep [i] = 0.01;
  }

  //----------------------------------------------------------------------------
  C_AO *ao = SelectAO (OptimizerSelect_P);             // Select an optimization algorithm

  ao.params [0].val = popSize;                         // Assigning population size....
  ao.SetParams ();                                     //... (optional, then default population size will be used)

  ao.Init (rangeMin, rangeMax, rangeStep, epochCount); // Initialize the algorithm with given boundaries and number of epochs

  // Main loop by number of epochs
  for (int epochCNT = 1; epochCNT <= epochCount; epochCNT++)
  {
    ao.Moving ();                                      // Execute one epoch of the optimization algorithm

    // Calculate the value of the objective function for each solution in the population
    for (int set = 0; set < ArraySize (ao.a); set++)
    {
      ao.a [set].f = TargetFunction (ao.a [set].c, rates, rsi, sto, truTradeTime); //FF.CalcFunc (ao.a [set].c); //ObjectiveFunction (ao.a [set].c); // Apply the objective function to each solution
    }

    ao.Revision ();                                    // Update the population based on the results of the objective function
  }

  //----------------------------------------------------------------------------
  // Output the algorithm name, best result and number of function runs
  Print (ao.GetName (), ", best result: ", ao.fB);
  ArrayCopy (Weights, ao.cB);
  delete ao;                                           // Release the memory occupied by the algorithm object

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Implementamos a função objetivo para avaliar a eficácia da estratégia de trading que utiliza a rede neural.

1. Inicialização das variáveis. São definidas variáveis para acompanhar lucro, prejuízo, número de operações e outros parâmetros.

2. Processamento dos dados históricos. Um laço percorre os dados históricos e verifica se está permitido abrir posições no candle atual.

3. Normalização dos dados. Para cada candle, os valores dos preços (high, low, open, close) e dos indicadores (RSI e Stochastic) são normalizados para posterior envio à rede neural.

4. Previsão dos sinais. Os dados normalizados são alimentados na rede neural, que gera os sinais de trading (compra ou venda).

5. O gerenciamento das posições virtuais é feito de acordo com a lógica da estratégia definida em OnTick().

6. Cálculo do resultado. Ao final da função, calcula-se a razão entre lucro e prejuízo, multiplicada pelo número de operações, considerando um fator de penalização para o desequilíbrio entre operações de compra e venda.

A função avalia a eficácia da estratégia analisando os lucros e perdas com base nos sinais gerados pela rede neural e retorna um valor numérico que representa sua qualidade (na prática, essa função executa um ciclo de backtest a partir da posição atual no tempo do EA).

//——————————————————————————————————————————————————————————————————————————————
double TargetFunction (double &weights [], MqlRates &rates [], double &rsi [], double &sto [], bool &truTradeTime [])
{
  int bars = ArraySize (rates);

  // Initialize variables to normalize data
  int    wCNT       = 0;
  double max        = 0.0;
  double min        = 0.0;
  int    signal     = 0;
  double profit     = 0.0;
  double allProfit  = 0.0;
  double allLoss    = 0.0;
  int    dealsNumb  = 0;
  int    sells      = 0;
  int    buys       = 0;
  int    posType    = 0;
  double posOpPrice = 0.0;
  double posClPrice = 0.0;

  // Run through history
  for (int h = BarsAnalysis_P; h < bars - 1; h++)
  {
    if (!truTradeTime [h])
    {
      if (posType != 0)
      {
        posClPrice = rates [h].open;
        profit = (posClPrice - posOpPrice) * signal - 0.00003;

        if (profit > 0.0) allProfit += profit;
        else              allLoss   += -profit;

        if (posType == 1) buys++;
        else              sells++;

        allProfit += profit;
        posType = 0;
      }

      continue;
    }

    max  = -DBL_MAX; // Initial value for maximum
    min  =  DBL_MAX; // Initial value for minimum

    // Find the maximum and minimum among high and low
    for (int b = 1; b <= BarsAnalysis_P; b++)
    {
      if (rates [h - b].high > max) max = rates [h - b].high; // Update maximum
      if (rates [h - b].low  < min) min = rates [h - b].low;  // Update minimum
    }

    // Normalization of input data for neural network
    wCNT = 0;
    for (int b = BarsAnalysis_P; b >= 1; b--)
    {
      Inputs [wCNT] = U.Scale (rates [h - b].high,  min, max, -1, 1); wCNT++; // Normalizing high
      Inputs [wCNT] = U.Scale (rates [h - b].low,   min, max, -1, 1); wCNT++; // Normalizing low
      Inputs [wCNT] = U.Scale (rates [h - b].open,  min, max, -1, 1); wCNT++; // Normalizing open
      Inputs [wCNT] = U.Scale (rates [h - b].close, min, max, -1, 1); wCNT++; // Normalizing close

      Inputs [wCNT] = U.Scale (sto   [h - b],       0,   100, -1, 1); wCNT++; // Normalizing Stochastic
      Inputs [wCNT] = U.Scale (rsi   [h - b],       0,   100, -1, 1); wCNT++; // Normalizing RSI
    }

    // Convert data from Inputs to Outs
    NN.ANN (Inputs, weights, Outs);

    //----------------------------------------------------------------------------
    // Generate a trading signal based on the output of a neural network
    signal = 0;
    if (Outs [0] >  SigThr_P) signal =  1; // Buy signal
    if (Outs [0] < -SigThr_P) signal = -1; // Sell signal

    if ((posType == 1 && signal == -1) || (posType == -1 && signal == 1))
    {
      posClPrice = rates [h].open;
      profit = (posClPrice - posOpPrice) * signal - 0.00003;

      if (profit > 0.0) allProfit += profit;
      else              allLoss   += -profit;

      if (posType == 1) buys++;
      else              sells++;

      allProfit += profit;
      posType = 0;
    }

    if (posType == 0 && signal != 0)
    {
      posType = signal;
      posOpPrice = rates [h].open;
    }
  }

  dealsNumb = buys + sells;

  double ko = 1.0;
  if (sells == 0 || buys == 0) return -DBL_MAX;
  if (sells / buys > 1.5 || buys / sells > 1.5) ko = 0.001;

  return (allProfit / (allLoss + DBL_EPSILON)) * dealsNumb;
}
//——————————————————————————————————————————————————————————————————————————————

A figura 2 mostra o gráfico de saldo dos resultados de trading obtidos com o uso do EA baseado em MLP sobre dados novos, ainda desconhecidos pela rede neural. Os valores de entrada são os preços normalizados OHLC, além dos indicadores RSI e Stochastic, calculados com base no número de candles especificado. O EA realiza operações enquanto a rede neural se mantém válida; caso contrário, realiza o treinamento da rede e continua operando. Assim, os resultados mostrados na figura 2 representam a eficácia do desempenho em OOS (out of sample).

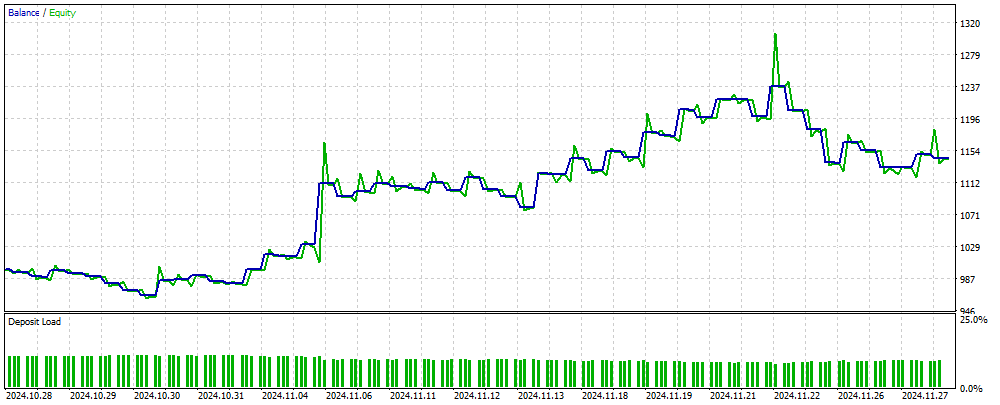
Figura 2. Resultado do desempenho do EA em dados desconhecidos para o MLP

Considerações finais

O artigo apresentou uma forma simples e acessível de usar uma rede neural em um EA, adequada a um público amplo de traders e que não exige conhecimentos profundos em aprendizado de máquina. Este método elimina a necessidade de normalizar os valores da função objetivo antes de enviá-los à rede neural como erro, além de dispensar o uso de técnicas para evitar a “explosão de pesos”. Também resolve o problema de “paralisação da rede” e propõe um aprendizado intuitivo com controle visual dos resultados.

É importante observar que o EA apresentado não contém verificações necessárias para a execução segura de operações de trading, sendo voltado exclusivamente para fins demonstrativos.

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	C_AO.mqh	Arquivo incluído	Classe base para algoritmos populacionais de otimização
2	C_AO_enum.mqh	Arquivo incluído	Enumeração de algoritmos populacionais de otimização
3	Utilities.mqh	Arquivo incluído	Biblioteca de funções auxiliares
4	Symbol.mqh	Arquivo incluído	Biblioteca de funções de trading e utilitários
5	ANN EA.mq5	Expert Advisor	EA baseado em rede neural MLP