
Алгоритм атомарного орбитального поиска — Atomic Orbital Search (AOS): Модификация
Содержание
Введение
В первой части статьи мы подробно рассмотрели алгоритм AOS (Atomic Orbital Search), его основы, вдохновленные атомной орбитальной моделью, и механизмы, лежащие в его основе. Мы обсудили, как алгоритм использует вероятностные распределения и динамику взаимодействий для поиска оптимальных решений в сложных задачах оптимизации.
Во второй части статьи мы сосредоточимся на модификации алгоритма AOS, поскольку не можем пройти мимо такой выдающейся идеи, не стремясь её улучшить. Мы проанализируем концепцию улучшения алгоритма, уделяя особое внимание специфическим операторам, которые присущи этому методу и могут повысить его эффективность и адаптивность.
Работа над алгоритмом AOS открыла передо мной множество интересных аспектов, связанных с его методами поиска в пространстве решений. В процессе исследования я также пришел к ряду идей о том, как можно улучшить этот интересный алгоритм. В частности, я сосредоточился на переработке имеющихся методов, которые могут повысить производительность работы алгоритма, улучшая его способность к исследованию сложных пространств решений. Мы рассмотрим, как эти улучшения могут быть интегрированы в существующую структуру алгоритма AOS, чтобы сделать его еще более мощным инструментом для решения задач оптимизации. Таким образом, наша цель — не только проанализировать существующие механизмы, но и предложить иные подходы, которые могут значительно расширить возможности алгоритма AOS.
Реализация алгоритма
В предыдущей статье мы подробно рассмотрели ключевые компоненты алгоритма AOS. Напомним, что в этом алгоритме популяция рассматривается как молекула, а допустимая область координат, в которой осуществляется поиск оптимальных решений, представлена в виде атома. Каждый атом состоит из различных слоев, которые помогают организовать и направлять поиск.
Конкретные значения по координате, которые мы получаем в процессе оптимизации, можно интерпретировать как электроны. Эти электроны, находясь в пределах атома, представляют собой возможные решения одного из параметров задачи, которую мы оптимизируем. Таким образом, каждая молекула (популяция) стремится к нахождению оптимальных значений (электронов) в пределах заданной области (атома).
В оригинальной версии алгоритма AOS энергия слоя BEk определяется как среднее арифметическое энергии электронов в слое, а связь BSk — как среднее арифметическое их координат. Энергия BEk используется для сравнения с энергией электронов с целью определения способа их последующего перемещения. Связь BSk служит для вычисления приращения к положению электронов, как разницы между наилучшим положением электронов LEk в слое и связью BSk по следующей формуле: Xki[t+1] = Xkit + αi × (βi × LEk − γi × BSk).
Предлагаю отказаться от усредненного положения электронов BSk в пользу персонального лучшего положения электрона. Таким образом, электрон будет двигаться в сторону наилучшего решения в своем слое, основываясь на индивидуальном достижении, а не на усредненном решении по слою. Кроме того, два случайных компонента βi и γi представляются излишними, поскольку уже имеется внешний случайный компонент αi. Это позволит сократить время на генерацию случайных чисел в данной формуле в три раза, не теряя при этом физического смысла.
Теперь давайте рассмотрим структуру, описывающую слой в атоме. Красным цветом выделены элементы, которые будут удалены из кода://—————————————————————————————————————————————————————————————————————————————— struct S_Layer { int pc; // счетчик частиц double BSk; // состояние связи double BEk; // энергия связи double LEk; // минимальная энергия void Init () { pc = 0; BSk = 0.0; BEk = 0.0; LEk = 0.0; } }; //——————————————————————————————————————————————————————————————————————————————
Рассмотрим код метода "CalcLayerParams", который выполняет расчет характеристик слоев, таких как энергия и связь. Строки, выделенные красным, будут удалены, так как они больше не понадобятся. Напомним, что этот метод играет ключевую роль в стратегии поиска AOS, направленной на предотвращение застревания алгоритма в локальных ловушках. Поскольку уровень энергии в слоях не зависит от их расположения (энергия уменьшается от центра к внешним слоям атома), а определяется наличием значимых локальных экстремумов (внешний слой может иметь энергию, превышающую внутренние), слои служат для корректировки движения электронов в пространстве поиска.
Случайное количество слоев на каждой эпохе помогает бороться с застреванием алгоритма в локальных ловушках, не позволяя электронам застаиваться только в одном из слоев. В модифицированной версии также отпадает необходимость в расчете средней энергии по всему атому, поэтому мы удалим соответствующие строки.

Рисунок 1. Разница направления и размера смещения электрона e в зависимости от количества слоев в атоме
Рисунок 1 иллюстрирует различия в поведении электронов в атомах с разным количеством слоев в алгоритме AOS. Верхняя часть показывает атом с тремя слоями, где электрон находится в слое L1 со значением целевой функции B1 и движется в сторону локального лучшего значения LEk1. Нижняя часть рисунка иллюстрирует атом с двумя слоями, где электрон находится так же в слое L1 и движется в сторону локального лучшего значения LEk1 со значением целевой функции B1 (в случае с тремя слоями это была бы точка LEk2).
Ключевые элементы на рисунке:
- B0, B1, B2 — обозначения локальных значений целевой функции для соответствующих слоев,
- LEk0, LEk1, LEk2 — лучшие решения в соответствующих слоях,
- L0, L1, L2 — слои в атоме,
- e — электрон,
- MIN, MAX — границы внешних слоев атомов (граничные условия по оптимизируемым параметрам задачи).
//—————————————————————————————————————————————————————————————————————————————— // Расчет параметров для каждого слоя void C_AO_AOS::CalcLayerParams () { double energy; // Обработка каждой координаты (атома) for (int c = 0; c < coords; c++) { atoms [c].Init (maxLayers); // Обработка каждого слоя for (int L = 0; L < currentLayers [c]; L++) { energy = -DBL_MAX; // Обработка каждого электрона for (int e = 0; e < popSize; e++) { if (electrons [e].layerID [c] == L) { atoms [c].layers [L].pc++; atoms [c].layers [L].BEk += a [e].f; atoms [c].layers [L].BSk += a [e].c [c]; if (a [e].f > energy) { energy = a [e].f; atoms [c].layers [L].LEk = a [e].c [c]; } } } // Расчет средних значений для слоя if (atoms [c].layers [L].pc != 0) { atoms [c].layers [L].BEk /= atoms [c].layers [L].pc; atoms [c].layers [L].BSk /= atoms [c].layers [L].pc; } } } // Расчет общего состояния связей ArrayInitialize (BS, 0); for (int c = 0; c < coords; c++) { for (int e = 0; e < popSize; e++) { BS [c] += a [e].c [c]; } BS [c] /= popSize; } } //——————————————————————————————————————————————————————————————————————————————
Для обновления наилучших индивидуальных решений добавим код в метод "Revision" в класс модифицированной версии "C_AO_AOSm".
//—————————————————————————————————————————————————————————————————————————————— // Метод пересмотра лучших решений void C_AO_AOSm::Revision () { int bestIndex = -1; // Поиск лучшего решения в текущей итерации for (int i = 0; i < popSize; i++) { // Обновление глобального лучшего решения if (a [i].f > fB) { fB = a [i].f; bestIndex = i; } // Обновление персонального лучшего решения if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } // Обновление лучших координат если найдено лучшее решение if (bestIndex != -1) ArrayCopy (cB, a [bestIndex].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
В методе "UpdateElectrons" удалим переменные "β" и "γ", так как они не нужны для генерации соответствующих случайных чисел. Кроме того, исключим деление приращения электрона на количество слоев в случае перемещения в сторону глобального решения. Честно говоря, решение авторов выглядит спорным, и физический смысл этого подхода не совсем ясен. Возможно, авторы стремились сделать степень перемещения электронов в направлении глобального решения вариативной, изменяя её в зависимости от количества слоев: чем меньше слоев, тем интенсивнее должно быть перемещение (хотя мои эксперименты показали, что это ничего не дает).
//—————————————————————————————————————————————————————————————————————————————— // Обновление положения электронов void C_AO_AOS::UpdateElectrons () { double α; // коэффициент скорости double β; // коэффициент веса лучшего решения double γ; // коэффициент веса среднего состояния double φ; // вероятность перехода double newPos; // новая позиция double LE; // лучшая энергия double BSk; // состояние связи int lID; // идентификатор слоя // Обработка каждой частицы for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Случайное рассеивание newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); β = u.RNDprobab (); γ = u.RNDprobab (); // Если текущая энергия частицы меньше средней энергии слоя if (a [p].f < atoms [c].layers [lID].BEk) { // Движение в сторону глобального оптимума---------------------------- LE = cB [c]; newPos = a [p].c [c]+ α * (β * LE - γ * BS [c]) / currentLayers [c]; } else { // Движение в сторону локального оптимума слоя------------------------ LE = atoms [c].layers [lID].LEk; BSk = atoms [c].layers [lID].BSk; newPos = a [p].c [c] + α * (β * LE - γ * BSk); } } // Ограничение новой позиции в пределах диапазона поиска с учетом шага a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Дополнительно в методе "UpdateElectrons" в классе "C_AO_AOSm" вместо случайного рассеивания электрона по пространству поиска реализуем перемещение электрона в центр ядра с некоторой вероятностью. По сути, это означает замену значения по какой-то координате на значение глобального решения, что должно повысить комбинаторные свойства алгоритма. А случайное рассеивание было призвано обеспечивать разнообразие в популяции решений, но это свойство обеспечивало распространение электронов по логнормальному распределению, где была ненулевая вероятность попадания электрона в любую точку пространства при перемещении.
Зеленым показаны изменения в формулах перемещения электронов, теперь приращение считается как разница между локальным лучшим решением слоя и индивидуальным лучшим решением электрона.
//—————————————————————————————————————————————————————————————————————————————— // Обновление положения электронов void C_AO_AOSm::UpdateElectrons () { double α; // коэффициент скорости double φ; // вероятность перехода double newPos; // новая позиция double LE; // лучшая энергия double BSk; // состояние связи int lID; // идентификатор слоя // Обработка каждой частицы for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Случайный переход к центру newPos = cB [c]; } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); // Если текущая энергия частицы меньше средней энергии слоя if (a [p].f < atoms [c].layers [lID].BEk) { // Движение в сторону глобального оптимума---------------------------- LE = cB [c]; newPos = a [p].cB [c]+ α * (LE - a [p].cB [c]); } else { // Движение в сторону локального оптимума слоя------------------------ LE = atoms [c].layers [lID].LEk; newPos = a [p].cB [c]+ α * (LE - a [p].cB [c]); } } // Ограничение новой позиции в пределах диапазона поиска с учетом шага a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Метод "DistributeParticles" распределяет электроны в пространстве поиска, используя логнормальное распределение для каждой координаты. Для каждой частицы и каждой координаты вызывается функция, которая генерирует позицию с учетом заданных параметров (среднее, минимальное и максимальное значения, пик), а затем применяется дополнительная функция для корректировки позиции в заданном диапазоне.
//—————————————————————————————————————————————————————————————————————————————— // Распределение частиц в пространстве поиска void C_AO_AOS::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Используем логнормальное распределение для позиционирования частиц a [i].c [c] = u.LognormalDistribution (cB [c], rangeMin [c], rangeMax [c], peakPosition); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Мы изменим распределение электронов на нормальное. В этом распределении используется среднеквадратичное отклонение, равное 8. Хотя этот параметр можно было бы сделать внешним для алгоритма, я решил не делать этого. Меньшие значения способствуют более широкому исследованию пространства поиска, тогда как более высокие значения повышают точность сходимости при уточнении глобального решения.
//—————————————————————————————————————————————————————————————————————————————— // Распределение частиц в пространстве поиска void C_AO_AOSm::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Используем гауссово распределение для позиционирования частиц a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Были проанализированы все изменения, внесенные в оригинальную версию алгоритма AOS, с целью повышения его эффективности. Поскольку в логику поисковой стратегии были внесены значительные изменения, модифицированную версию алгоритма можно обозначить буквой "m". В дальнейшем в рейтинговой таблице будет представлена только одна модифицированная версия — AOSm.
Пример использования алгоритмов класса C_AO
Поскольку все популяционные алгоритмы оптимизации, рассмотренные ранее, унаследованы от общего класса C_AO, это позволяет использовать их единообразно и с минимальными усилиями для решения различных задач, требующих подбора оптимальных параметров. В приведенном ниже примере представлен скрипт, в котором осуществляется оптимизация целевой функции:
1. В начале скрипта вы можете выбрать, какой алгоритм оптимизации использовать. Если ничего не выбрано, скрипт сообщит об ошибке и остановится.
2. Настройка параметров. Скрипт определяет, сколько раз будет запускаться функция, сколько параметров нужно оптимизировать, размер группы решений и сколько итераций будет выполнено.
3. Границы значений. Для каждого параметра устанавливаются минимальные и максимальные значения (в данном примере от -10 до 10).
4. Скрипт начинает процесс оптимизации:
- Он генерирует решения (наборы параметров) и проверяет, насколько они хороши, используя специальную функцию (целевую функцию).
- На каждой итерации алгоритм обновляет свои решения, основываясь на том, какие из них показали лучшие результаты.
5. Результаты. После завершения оптимизации, скрипт выводит информацию о том, какой алгоритм использовался, какое лучшее значение было найдено, и сколько раз функция была запущена.
6. Целевая функция — это абстрактная задача оптимизации (в данном примере используется решение задачи поиска глобального максимума перевернутой параболы), которая принимает параметры и возвращает оценку их качества.
#property script_show_inputs // Указывает, что скрипт будет показывать входные параметры в окне свойств #include <Math\AOs\PopulationAO\#C_AO_enum.mqh> // Подключение библиотеки для работы с алгоритмами оптимизации input E_AO AOexactly = NONE_AO; // Параметр для выбора алгоритма оптимизации, по умолчанию - NONE_AO //—————————————————————————————————————————————————————————————————————————————— void OnStart() { //---------------------------------------------------------------------------- int numbTestFuncRuns = 10000; // Общее количество запусков тестовой функции int params = 1000; // Количество параметров для оптимизации int popSize = 50; // Размер популяции для алгоритма оптимизации int epochCount = numbTestFuncRuns / popSize; // Общее количество эпох (итераций) для оптимизации double rangeMin [], rangeMax [], rangeStep []; // Массивы для хранения границ и шагов параметров ArrayResize (rangeMin, params); // Изменение размера массива min границ ArrayResize (rangeMax, params); // Изменение размера массива max границ ArrayResize (rangeStep, params); // Изменение размера массива шагов // Инициализация границ и шагов для каждого параметра for (int i = 0; i < params; i++) { rangeMin [i] = -10; // Минимальное значение параметра rangeMax [i] = 10; // Максимальное значение параметра rangeStep [i] = DBL_EPSILON; // Шаг для параметра } //---------------------------------------------------------------------------- C_AO *ao = SelectAO (AOexactly); // Выбор алгоритма оптимизации if (ao == NULL) // Проверка, был ли выбран алгоритм { Print ("AO не выбран..."); // Сообщение об ошибке, если алгоритм не выбран return; } ao.params [0].val = popSize; // Назначение размера популяции.... ao.SetParams (); //... (необязательно, тогда будет использован размер популяции по умолчанию) ao.Init (rangeMin, rangeMax, rangeStep, epochCount); // Инициализация алгоритма с заданными границами и количеством эпох // Основной цикл по количеству эпох for (int epochCNT = 1; epochCNT <= epochCount; epochCNT++) { ao.Moving (); // Выполнение одной эпохи алгоритма оптимизации // Вычисление значения целевой функции для каждого решения в популяции for (int set = 0; set < ArraySize (ao.a); set++) { ao.a [set].f = ObjectiveFunction (ao.a [set].c); // Применение целевой функции к каждому решению } ao.Revision (); // Обновление популяции на основе результатов целевой функции } //---------------------------------------------------------------------------- // Вывод имени алгоритма, лучшего результата и количества запусков функции Print (ao.GetName (), ", best result: ", ao.fB, ", number of function launches: ", numbTestFuncRuns); delete ao; // Освобождение памяти, занятой объектом алгоритма } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Определение целевой функции пользователя, в данном случае как пример - параболоид, F(Xn) ∈ [0.0; 1.0], X ∈ [-10.0; 10.0], максимизация double ObjectiveFunction (double &x []) { double sum = 0.0; // Переменная для накопления результата // Цикл по всем параметрам for (int i = 0; i < ArraySize (x); i++) { // Проверка, находится ли параметр в допустимом диапазоне if (x [i] < -10.0 || x [i] > 10.0) return 0.0; // Если параметр вне диапазона, возвращаем 0 sum += (-x [i] * x [i] + 100.0) * 0.01; // Вычисление значения целевой функции } return sum /= ArraySize (x); } //——————————————————————————————————————————————————————————————————————————————
Результаты тестов
Перейдем к тестированию модифицированной версии алгоритма.
AOS|Atomic Orbital Search|50.0|10.0|20.0|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.8023218355650774
25 Hilly's; Func runs: 10000; result: 0.7044908398821188
500 Hilly's; Func runs: 10000; result: 0.3102116882841442
=============================
5 Forest's; Func runs: 10000; result: 0.8565993699987462
25 Forest's; Func runs: 10000; result: 0.6945107796904211
500 Forest's; Func runs: 10000; result: 0.21996085558228406
=============================
5 Megacity's; Func runs: 10000; result: 0.7461538461538461
25 Megacity's; Func runs: 10000; result: 0.5286153846153846
500 Megacity's; Func runs: 10000; result: 0.1435846153846167
=============================
All score: 5.00645 (55.63%)
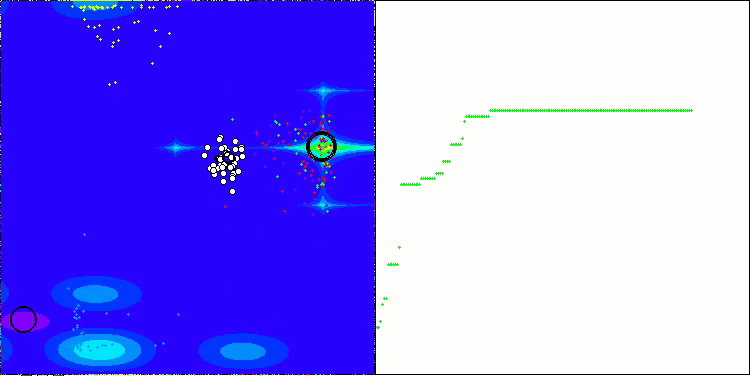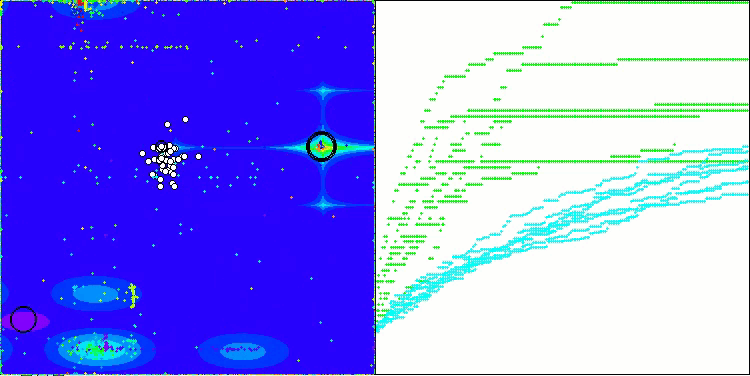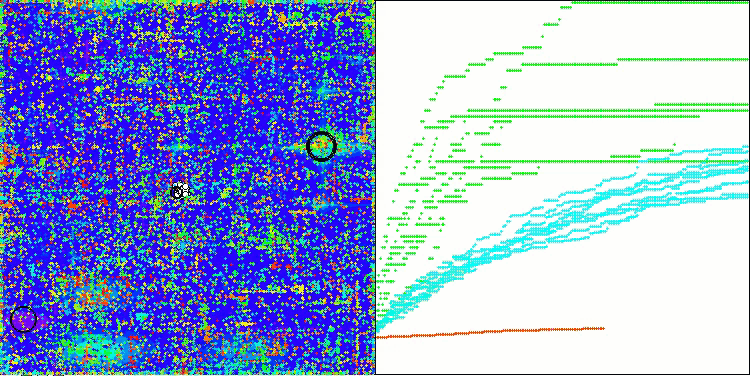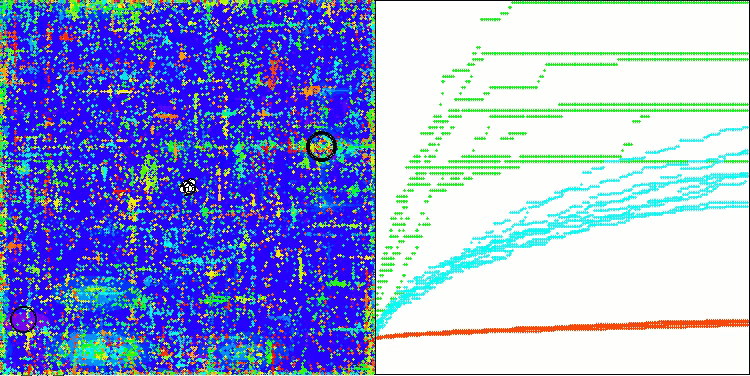
Как можно заметить, результаты модифицированной версии значительно улучшились по сравнению с предыдущими показателями оригинальной версии, где общий балл составил 3.00488 (33.39%). Это улучшение становится очевидным при анализе визуализации, которая демонстрирует не только улучшение сходимости, но и более детальную проработку значимых экстремумов.
Одним из ключевых аспектов, который стоит отметить, является эффект "кучкования" решений по отдельным координатам. Этот феномен наблюдается как в оригинальной версии, так и в модифицированной, что подчеркивает характерную особенность алгоритмов AOS. "Кучкование" решений может свидетельствовать о том, что алгоритм эффективно находит области, где расположены потенциальные оптимальные решения.
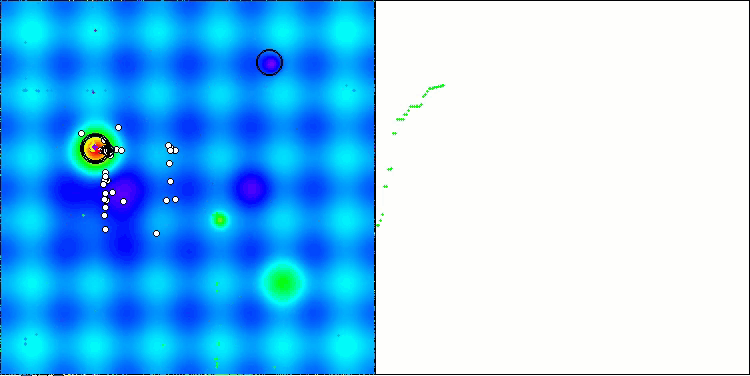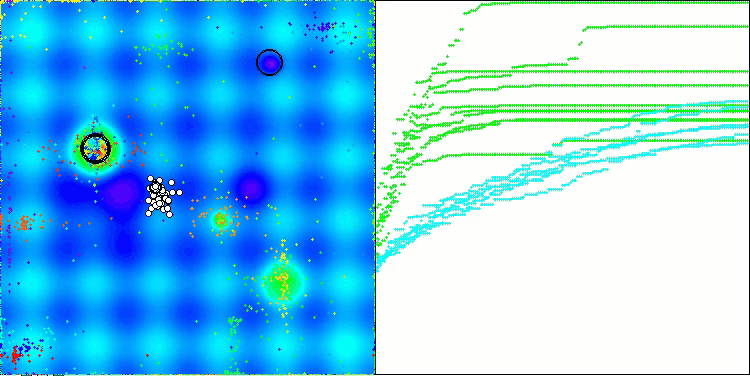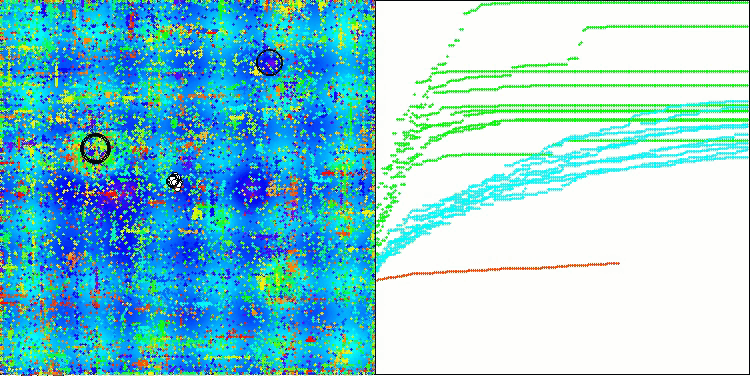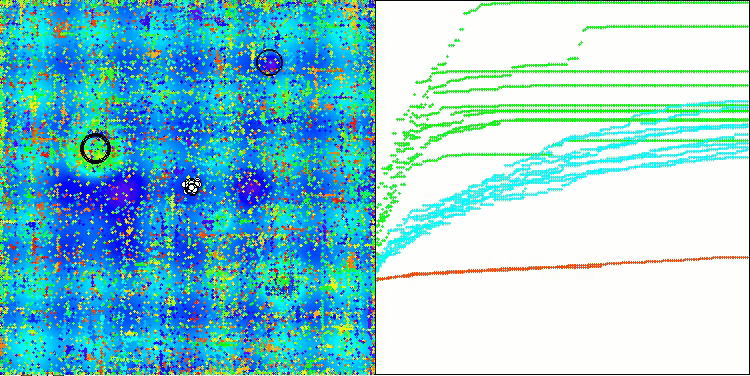
AOSm на тестовой функции Hilly
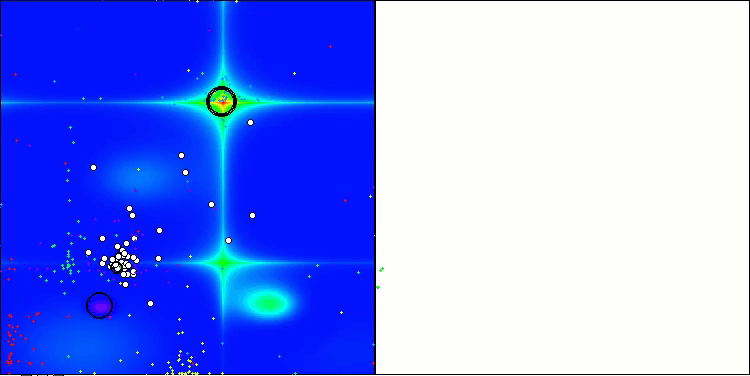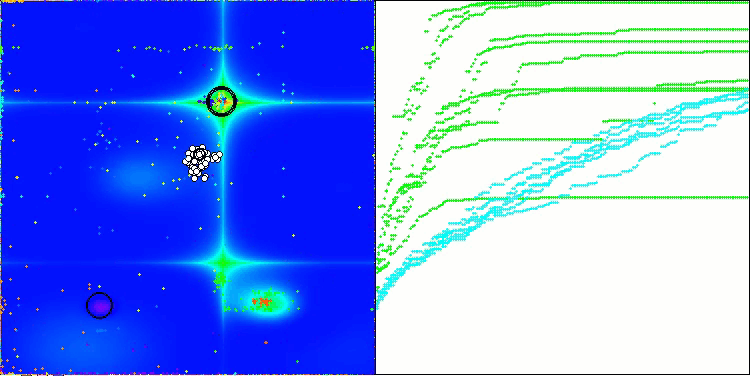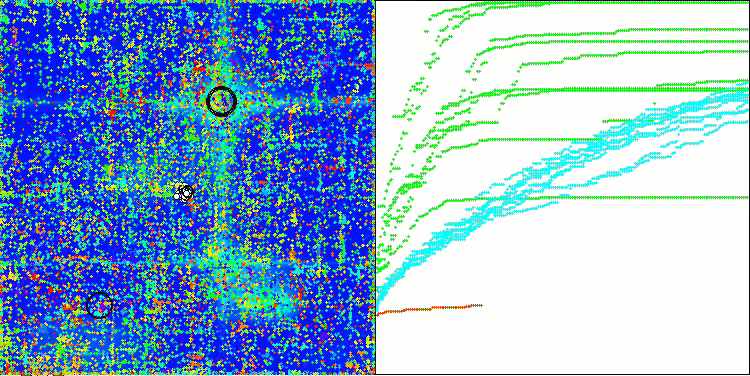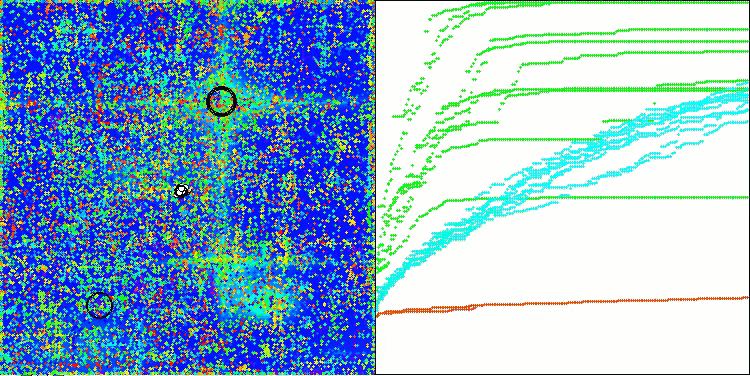
AOSm на тестовой функции Forest
AOSm на тестовой функции Megacity
Модифицированная версия алгоритма Atomic Orbital Search (AOS) значительно улучшила свои показатели по сравнению с оригинальной версией и теперь достигает более 55% от максимально возможного. Это действительно впечатляющий результат! В рейтинговой таблице алгоритм занимает 12-е место, в ее верхней части, что говорит о весьма достойных результатах.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 12 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 13 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 14 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 15 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 16 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 17 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 18 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 19 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 20 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 21 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 22 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 23 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 24 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 25 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 26 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 27 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 28 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 29 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 30 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 31 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 32 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 33 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 34 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 35 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 36 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 37 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 38 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 39 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 40 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 41 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 42 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 43 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 44 | AAA | algae adaptive algorithm | 0,50007 | 0,32040 | 0,25525 | 1,07572 | 0,37021 | 0,22284 | 0,16785 | 0,76089 | 0,27846 | 0,14800 | 0,09755 | 0,52402 | 2,361 | 26,23 |
| 45 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
Выводы
В данной статье была представлена модифицированная версия алгоритма атомарного орбитального поиска (AOSm), в которой я отказался от усредненного положения электронов BSk в слоях атома в пользу индивидуального лучшего положения каждого электрона. Это позволило электронам более эффективно двигаться в сторону наилучшего решения в своем слое, основываясь на личном достижении, а не на усредненном значении. Кроме того, были исключены два случайных компонента βi и γi, что сократило время на генерацию случайных чисел в три раза, не теряя при этом физического смысла алгоритма.
В методе "UpdateElectrons" были удалены теперь ненужные переменные и исключены деления приращения электрона на количество слоев при перемещении к глобальному решению. Хотя авторы оригинальной версии, возможно, стремились сделать степень перемещения вариативной, мои эксперименты показали, что это не приносит значительных преимуществ.
Также были внедрены изменения в метод "UpdateElectrons" в классе "C_AO_AOSm", заменив случайное рассеивание электрона на перемещение к центру ядра с определенной вероятностью. Это повысило комбинаторные свойства алгоритма, позволяя электронам более точно нацеливаться на глобальное решение. Было также заменено логнормальное распределение на нормальное, что увеличило точность сходимости при уточнении глобального решения.
Результаты модифицированной версии AOSm показали значительное улучшение, с общим баллом, превышающим 55% от максимально возможного, что подтверждает высокую эффективность и конкурентоспособность алгоритма. В рейтинговой таблице AOSm занимает 12-е место, что свидетельствует о его значительных достижениях среди других методов оптимизации.
Одним из наиболее заметных аспектов AOSm является улучшение сходимости, которое стало очевидным при визуализации результатов. Алгоритм более детально прорабатывает значимые экстремумы и демонстрирует способность к эффективному поиску оптимальных решений в сложных многомерных пространствах. Эффект "кучкования" решений, наблюдаемый как в оригинальной, так и в модифицированной версиях, подчеркивает способность алгоритма находить и сосредотачиваться на областях с потенциальными оптимумами, что особенно полезно в задачах с высокой размерностью и сложной структурой.
Дополнительный плюс к достоинствам модифицированной версии придает снижение количества внешних параметров, что упрощает его использование и настройку. Впрочем, для всех алгоритмов, представленных ранее в статьях, мной подобраны оптимальные внешние параметры для достижения максимальной результативности в комплексном тестировании на различных типах тестовых задач, поэтому все алгоритмы готовы к использованию и не требуют какой-либо настройки. В данной статье продемонстрировано, что иногда самые незначительные изменения в алгоритмах оптимизации могут кардинально изменить их поисковые свойства, в то время как значительные изменения в логике поисковой стратегии могут не принести заметных изменений в результатах. И конечно же, я делюсь в статьях приемами, которые действительно улучшают результативность оптимизации.
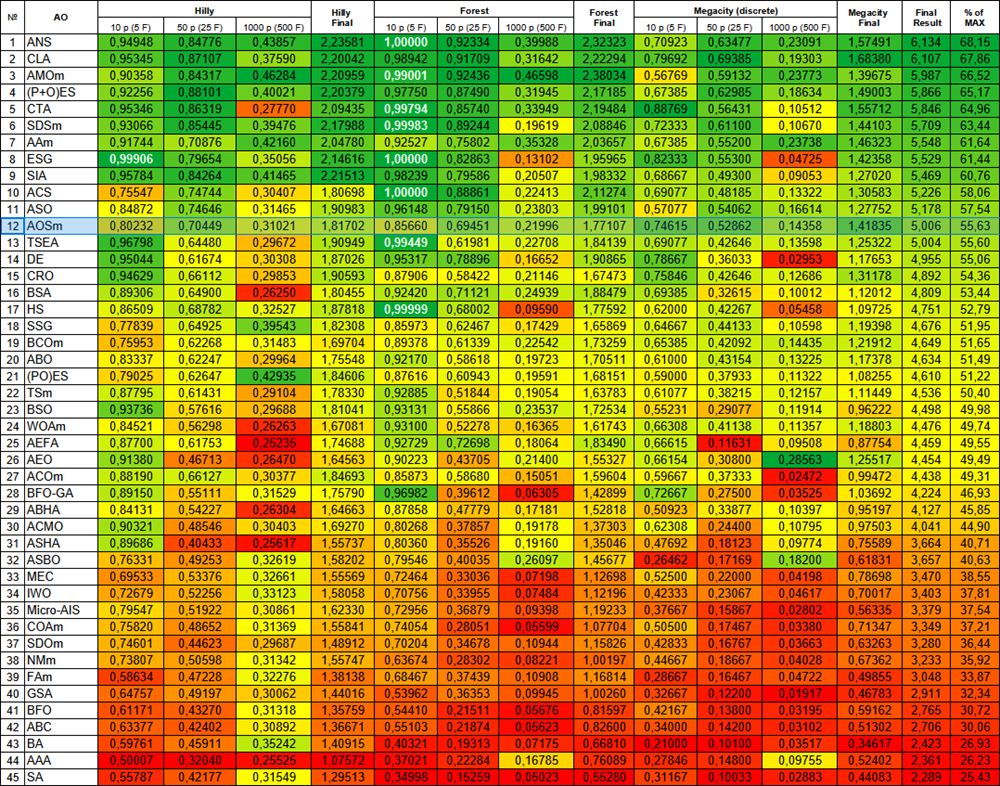
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам. Белым цветом подсвечены результаты больше или равные 0.99
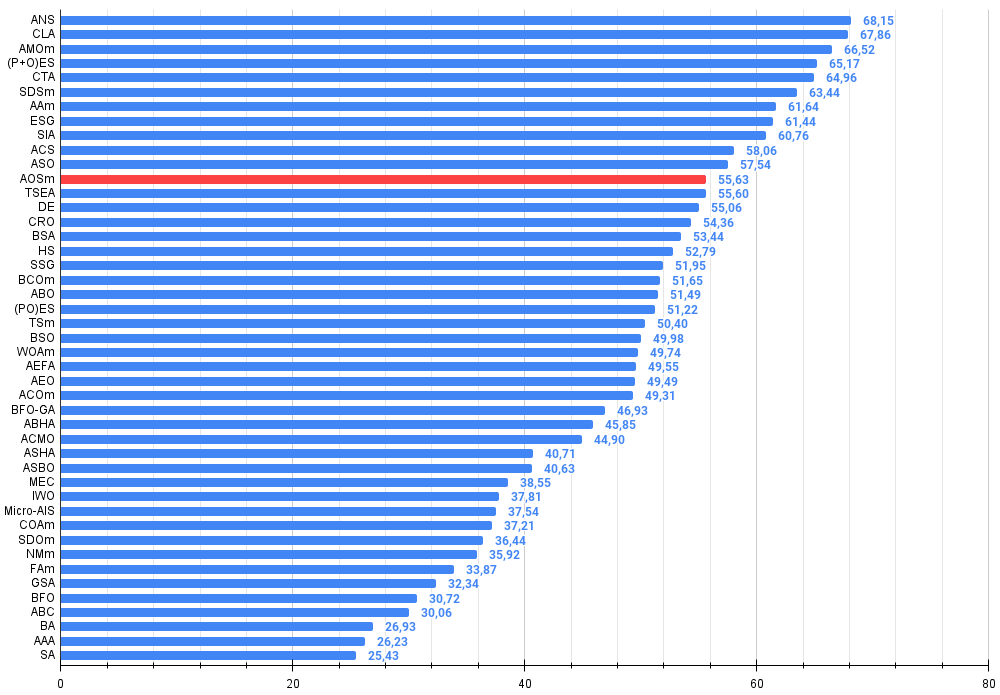
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,
где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма AOSm:
Плюсы:
- Хорошая результативность на различных задачах.
- Малое количество внешних параметров.
- Хорошая масштабируемость.
- Сбалансированный поиск и по локальным экстремумам и глобального.
Минусы:
- Достаточно сложная реализация.
- Средняя по отношению к другим алгоритмам точность сходимости на гладких функциях.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | AO_AOSm_AtomicOrbitalSearch.mqh | Включаемый файл | Класс алгоритма AOSm |
| 10 | Test_AO_AOSm.mq5 | Скрипт | Испытательный стенд для AOSm |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Нейросети в трейдинге: Повышение эффективности Transformer путем снижения резкости (SAMformer)
Нейросети в трейдинге: Повышение эффективности Transformer путем снижения резкости (SAMformer)
 Объемный нейросетевой анализ как ключ к будущим трендам
Объемный нейросетевой анализ как ключ к будущим трендам
 Изучение MQL5 — от новичка до профи (Часть VI): Основы написания советников
Изучение MQL5 — от новичка до профи (Часть VI): Основы написания советников
 Нейросети в трейдинге: Оптимизация Transformer для прогнозирования временных рядов (LSEAttention)
Нейросети в трейдинге: Оптимизация Transformer для прогнозирования временных рядов (LSEAttention)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Благодарю за статью!
Посидел я немного вчера и сегодня над функцией Hilly и алглибовскими методами. И вот какие мысли.
Для того что бы найти максимум данной функции, особенно когда количество параметров от 10 и больше бессмысленно применять градиентные методы, это задача комбинаторных методов оптимизации. Градиентные просто мгновенно застревают в локальном экстремуме. И не имеет значение сколько раз делать рестарт из новой точки пространства параметров, шанс попасть в нужную область пространства из которой градиентный метод мгновенно находит решение стремится к нулю с ростом количества параметров.
Например, точка пространства из которой lbfgs или CG за 2(две) итерации находят максимум для любого количества параметров следующая {x = -1,2 , y = 0.5}
Но шанс попасть в эту область как я уже сказал просто нулевой. Это нужно наверно лет сто случайные числа генерировать.
Поэтому нужно каким-то образом скомбинировать генетические алгоритмы представленные в статье (что бы они провели разведку, сократили пространство поиска) с градиентными методами, которые бы уже далее быстро находили экстремум из более выгодной точки.
Благодарю за статью!
Спасибо за отзыв.
Для того что бы найти максимум данной функции, особенно когда количество параметров от 10 и больше бессмысленно применять градиентные методы
Да, верно.
это задача комбинаторных методов оптимизации.
Комбинаторные, такие как классический "муравьиный", предназначены для проблем типа "задачи коммивояжера" и "задачи о рюкзаке", т.е, предназначены для дискретных задач с фиксированным шагом (ребро графа). Для многомерных "непрерывных" задач эти алгоритмы не предназначены совсем, например, для таких задач, как обучение нейронных сетей. Да, комбинаторные свойства очень полезны для стохастических эвристических методов, но не являются единственным и достаточным свойством для успешного решения подобных, приближенных к реальным, тестовым задачам. Важны ещё и сами поисковые стратегии в алго.
Градиентные просто мгновенно застревают в локальном экстремуме. И не имеет значение сколько раз делать рестарт из новой точки пространства параметров, шанс попасть в нужную область пространства из которой градиентный метод мгновенно находит решение стремится к нулю с ростом количества параметров.
Да, так.
Но шанс попасть в эту область как я уже сказал просто нулевой. Это нужно наверно лет сто случайные числа генерировать.
Да, так. В маломерных пространствах (1-2) попасть в окрестности глобала очень просто, для этого даже могут сгодится простые рандомные генераторы. Но всё совершенно меняется, когда размерность задачи растет, здесь начинают играть важную роль именно поисковые свойства алгоритмов, а не Госпожа Удача.
Поэтому нужно каким-то образом скомбинировать генетические алгоритмы представленные в статье (что бы они провели разведку, сократили пространство поиска) с градиентными методами, которые бы уже далее быстро находили экстремум из более выгодной точки.
"генетические" - наверное имеете ввиду "эвристические". А зачем "рыбке зонтик" и "а зачем нам кузнец? кузнец нам не нужен".))) Есть эффективные способы решения сложных многомерных в непрерывном пространстве задач, которые описаны в статьях о популяционных методах. А для классических градиентных есть свои задачи - одномерные аналитически определимые задачи (в этом им равных нет, там будет быстрая и точная сходимость).
И, вопрос, какие у Вас впечатления от скорости работы эвристики?
ЗЫ:
О сколько нам открытий чудных
Готовят просвещенья дух
И опыт, сын ошибок трудных,
И гений, парадоксов друг,
И случай, бог изобретатель.
ЗЗЫ. Один момент. В неизвестном пространстве поиска никогда невозможно знать в любой момент времени или шаге итерации, что это на самом деле действительно перспективное направление в сторону глобала. Поэтому невозможно сначала разведать, а потом уточнять. Могут работать только цельные стратегии поиска, они либо работают хорошо, либо плохо. Степень "хорошести" и "пригодности для задачи" каждый выбирает сам, для этого ведется рейтинговая таблица, чтобы выбирать алгоритм по специфике задачи.
Да, так. В маломерных пространствах (1-2) попасть в окрестности глобала очень просто, для этого даже могут сгодится простые рандомные генераторы. Но всё совершенно меняется, когда размерность задачи растет, здесь начинают играть важную роль именно поисковые свойства алгоритмов, а не Госпожа Удача.
Так они же не справляются
И, вопрос, какие у Вас впечатления от скорости работы эвристики?
несмотря на то что работают быстро. Результат для 1000 параметров что-то около 0,4.
Вот поэтому я чисто интуитивно подумал, что есть смысл комбинировать ГА и градиентные методы, что бы добраться до максимума. Иначе по отдельности они вашу функцию не разгадают. На практике не проверял.
P.S. Все-таки считаю что данная функция слишком сгущает краски, в реальных задача(обучение нейросетей например) таких проблем нет, хотя там тоже поверхность ошибок вся в локальных минимумах.
1. Так они же не справляются
2. несмотря на то что работают быстро. Результат для 1000 параметров что-то около 0,4.
3. Вот поэтому я чисто интуитивно подумал, что есть смысл комбинировать ГА и градиентные методы, что бы добраться до максимума. Иначе по отдельности они вашу функцию не разгадают. На практике не проверял.
4. P.S. Все-таки считаю что данная функция слишком сгущает краски, в реальных задача(обучение нейросетей например) таких проблем нет, хотя там тоже поверхность ошибок вся в локальных минимумах.
1. Что значит "не справляются"? Есть ограничение на число обращений к целевой функции, кто показал лучше результат - того и тапки.)) Увеличивать количество разрешенных обращений? Ну тогда все равно придут к финишу более проворные и приспособленные к сложным функциям. Попробуйте увеличивать обращения, картина не изменится.
2. Да. А у кого-то 0.3, а у других 0.2, а у третьих 0.001. Лучше те, кто показал 0.4.
3. Не поможет, интуитивно было пробовано и перепробовано сотни комбинаций и вариаций. Лучше тот, кто показывает лучше результат за заданное количество эпох (итераций). Увеличивайте количество обращений к целевой, увидите кто из них достигнет финиша первым.
4. Если на сложных задачах есть лидеры, то считаете, что на легких задачах лидеры покажут результаты хуже чем аутсайдеры? Это не так, мягко говоря. Работаю над более "простой" но реалистичной задачей по обучению сеток. Результатами буду делится, как всегда. Будет интересно.
Просто экспериментируйте, пробуйте разные алгоритмы, разные задачи, не зацикливайтесь на чем-то одном. Весь инструментарий я постарался предоставить для этого.
1. Что значит "не справляются"? Есть ограничение на число обращений к целевой функции, кто показал лучше результат - того и тапки.)) Увеличивать количество разрешенных обращений? Ну тогда все равно придут к финишу более проворные и приспособленные к сложным функциям. Попробуйте увеличивать обращения, картина не изменится.
2. Да. А у кого-то 0.3, а у других 0.2, а у третьих 0.001. Лучше те, кто показал 0.4.
3. Не поможет, интуитивно было пробовано и перепробовано сотни комбинаций и вариаций. Лучше тот, кто показывает лучше результат за заданное количество эпох (итераций). Увеличивайте количество обращений к целевой, увидите кто из них достигнет финиша первым.
4. Если на сложных задачах есть лидеры, то считаете, что на легких задачах лидеры покажут результаты хуже чем аутсайдеры? Это не так, мягко говоря. Работаю над более "простой" но реалистичной задачей по обучению сеток. Результатами буду делится, как всегда. Будет интересно.
Просто экспериментируйте, пробуйте разные алгоритмы, разные задачи, не зацикливайтесь на чем-то одном. Весь инструментарий я постарался предоставить для этого.
да вот экспериментирую,
Про реалистичную задачу это правильно, проверить алгоритмы на задачах приближенных к боевым.
Вдвойне интересно посмотреть как сети на генетике будут обучаться.