初級から中級まで：再帰

はじめに

ここに掲載されている資料は、教育目的のみのものです。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを利用することは避けてください。

前回の「初級から中級まで：共用体(II)」では、多くの人が純粋で単純なMQL5では解決できないと主張する問題を、どのように共用体(union)を用いて解決できるかを探りました。

このような課題は、経験豊富なプログラマーでなければ達成できないと思われがちです。しかし私の視点と理解からすれば、前回取り上げた内容はあくまで基礎的なものであり、初学者レベルのプログラミング学習者でも十分に実装可能です。

ここからは、応用や探求の幅が一気に広がる段階に入ります。見た目には大胆または高度に思えるプログラミングに挑戦することをためらう方も多いですが、これまでの内容からも分かる通り、イベント処理に踏み込まない限り（正しい扱い方や実装方法はまだ学んでいないため）、幅広い解決策を実現することは十分可能です。

改めて強調しておきたいのは、MetaTrader 5はイベント駆動型のプラットフォームであり、その上で動作するアプリケーションもイベントベースで設計されているという点です。ただし例外的に、通常はイベントに依存しない2種類のアプリケーションがあります。それが、今回添付したスクリプトと「サービス」です。サービスについては、MetaTrader 5の動作原理をより深く理解する必要があるため、適切なタイミングで取り上げます。私の考えでは、サービスはMetaTrader 5用アプリケーションの中で最も高度な種類です。

この2種類に加えて、インジケーターとエキスパートアドバイザー(EA)があります。どちらもイベント駆動型プログラミングを前提として設計されていますが、この時点で詳しく解説する段階にはありません。それでもなお、金融市場向けプログラミングを志す方が確かな基礎を築くために欠かせない重要なテーマは、まだ多く残されています。

こうした話をするのは、自分はこの分野に進む準備ができていると信じながらも、いざ実践に臨むと惨敗し、その原因を世界の不公平さに求めてしまう人が少なくないからです。実際には、優れたプログラマーなら容易かつ迅速、効率的に対応できる課題に立ち向かうための十分な準備が整っていなかっただけなのです。

特別な種類のループ

これまでのいくつかの記事で、ループに関連するコマンドについて説明してきました。MQL5では、他の多くの言語と同様に、一般的に3種類のループがあります。まず最初に、そして私の考えでは最も単純なのは、whileとdo...whileです。これに加えて、forループもあります。しかし実際には、ほぼすべてのプログラミング言語で利用できる「第4のループ作成方法」も存在します。私の記憶では、この方法をサポートしていない唯一の言語はBASICです。BASICは関数や手続きに基づいて動作する構造化言語ではないためです。しかし、ここではMQL5を扱っているため、この点は関係ありません。MQL5は関数や手続きを完全にサポートする構造化言語です。ここで、その第4のループ形式について説明します。

通常、ループは大きく分けて2つの方法で作られます。1つは専用のループ制御構造を使う方法、もう1つは関数や手続きを使う方法です。そう、読者の皆さん、関数や手続きを使ってループを作るというのは少し奇妙に聞こえるかもしれません。しかし実際には、皆さんが思うよりもずっと一般的な方法なのです。

ループ構文を使って繰り返し処理をおこなう場合、これを「反復プログラミング」と呼びます。一方、関数や手続きを使って同じことをおこなう場合は「再帰プログラミング」と呼びます。再帰の作り方と適用方法を理解することは、初心者が必ず学んでおくべきことです。再帰ループは、多くの場合、理解しやすいのです。

では、なぜ今になってこの話を持ち出すのでしょうか。それは、コードで再帰を効果的に使うためには、いくつかの重要な概念をしっかり理解しておく必要があるからです。具体的には、if文の使い方、変数と定数の適切な利用、寿命と値の受け渡しの理解、そして何よりもデータ型とその制限の深い理解です。やっていることによっては、最も適切な型を選択することが重要になります。これにより、再帰処理の妨げとなるあいまいさを回避できます。

考えてみてください。反復ループは通常、現在作業しているコードの近くにありますが、再帰ループの重要な部分は、今読んでいる箇所からずっと離れた関数や手続きの中に存在することがあります。そしてエラーや失敗が発生した場合、その原因を突き止めるために、コード全体を追跡して起点を探さなければならないこともよくあります。これこそが再帰の特性であり、初心者にとって難しい理由です。見た目にはループには見えませんが、実際にはループなのです。ただし、特別な種類のループです。

これをよりよく理解するために、実際の例を見ていく必要があります。ただその前に最後に1つだけ注意点を述べておきます。反復ループはすべて再帰として書き直すことができ、再帰ループもすべて反復として書き直すことができます。ただし、変換の難易度はループの性質によって異なります。一般的に、反復ループの方が実行時のパフォーマンスは高くなります。一方で、再帰ループの方がコードを書くのは容易な場合が多いです。つまり、お互いに長所と短所があるのです。再帰を反復に変換するのにかかる時間が、性能向上に見合わない場合もあります。したがって、基本的な指針としては、できるだけシンプルでコストの低い方法を選ぶことです。それでは、始めましょう。

まずは、とても単純な例から始めて、実際にどのように動作するのかを理解しやすくしていきます。以下にその例を示します。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Recursive(5);
07. }
08. //+------------------------------------------------------------------+
09. void Recursive(uchar arg)
10. {
11.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
12.     arg--;
13.     if (arg > 0)
14.         Recursive(arg);
15.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
16. }
17. //+------------------------------------------------------------------+

コード01

コード01を実行すると、下の画像のような結果が表示されます。

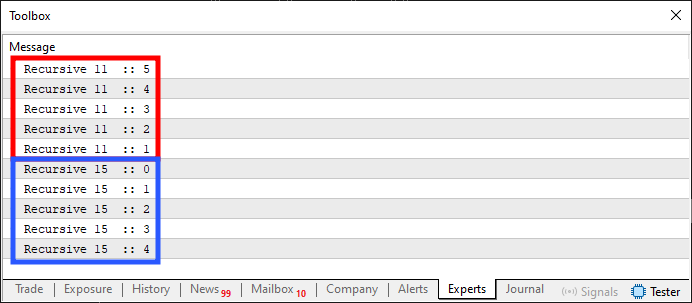
図01

これは一体何の狂気でしょうか。そう、これこそが再帰ルーチンの正体です。最初は少しおかしなことに思えるかもしれませんが、多くの場合、まさにこれこそが私たちが求めているものなのです。図01に示したのと同じ出力は、従来のループ構文を使っても生成できます。しかし、この場合は「再帰」と呼ばれる概念を使って生成しています。つまり、関数や手続きが自分自身、または別の関数や手続きを呼び出し、その間でループを形成するのです。多くの人は再帰というと、1つの関数や手続きが自分自身を呼び出すものだと考えがちです。しかし必ずしもそうではありません。唯一の条件は、標準的なループ命令を使わずにループを形成することです。以下に、再帰のもう1つ興味深い例を示します。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Print("Result: ", Fibonacci(7));
07. }
08. //+------------------------------------------------------------------+
09. uint Fibonacci(uint arg)
10. {
11.     if (arg <= 1)
12.         return arg;
13. 
14.     Print(__FUNCTION__, " ", __LINE__, "  :: ", arg);
15. 
16.     return Fibonacci(arg - 1) + Fibonacci(arg - 2);
17. }
18. //+------------------------------------------------------------------+

コード02

これは、おそらく再帰を学ぶ際に最もよく使われる古典的な例でしょう。なぜなら、コード02は再帰の仕組みを非常にわかりやすく示しているからです。実行すると、そのすぐ下に示すような結果が得られます。

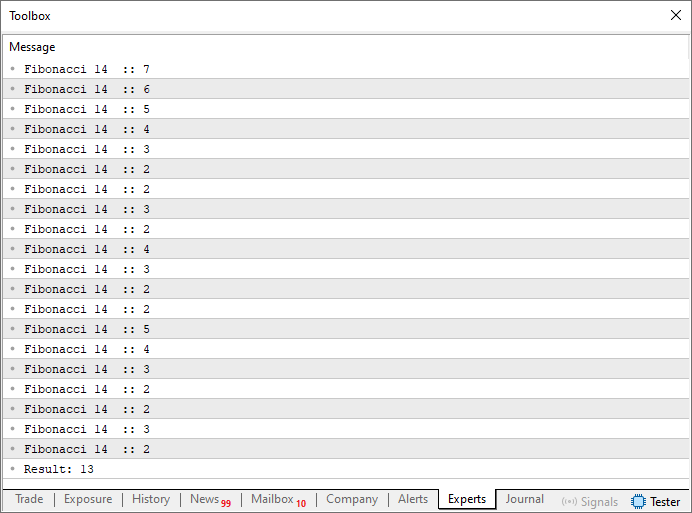
図02

つまり、フィボナッチ数列の7番目の値は13ということです。そして、もし数列に詳しければ、それが正しいことがわかるでしょう。では、このコードがどうやって7番目の値を計算したのか、正確にはどうなっているのでしょうか。正直なところ、すぐに理解できるものではありません。ですが、読者の皆さん、その鍵は16行目にあります。そこにはフィボナッチ数を計算するために必要な最小限の因数分解が含まれているのです。フィボナッチの値を計算するための数学的な式を調べると、以下に示すようなものが見つかるでしょう。

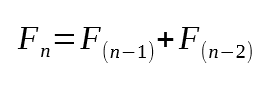
図03

では、改めて16行目を見てみてください。画像03の数学的表現と16行目の記述の類似点が見つかりますか。これこそが再帰ルーチンの基本です。つまり、問題をどんどん分解していき、最終的に答えが既知の最小値に収束するまで続けるのです。では、その最小値とは何でしょうか。フィボナッチ数列の場合、それは0か1です。これは11行目で確認しています。

ここで気づくべきことがあります。コード01と同様に、まずカウントダウン（降順の数列）があり、その後にカウントアップ（昇順の数列）が続くように見えました。同じパターンがコード02にも現れていますが、2つの明確な段階に分かれています。第一段階では、「arg - 1」の値を計算します。関数呼び出しが連鎖的におこなわれ、最終的に12行目に到達します。呼び出すたびに14行目が実行され、現在のargの値が出力されます。そのため、最初は1ステップずつ減少する降順の数列が観察されます。そして、これらの呼び出しがすべて戻り始めると、関数は再び自分自身を呼び出し始めますが、今度は2つ減らした値で呼び出されます。これはまだかなり複雑に思えるかもしれません。そこで、コード02がどのように結果を計算しているのかを視覚的に理解しやすくするために、いくつかの部分を修正してみましょう。更新版を以下に示します。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     Print("Result: ", Fibonacci(5, 0, 0));
07. }
08. //+------------------------------------------------------------------+
09. uint Fibonacci(uint arg, uint call, int who)
10. {
11.     uint value = 0;
12. 
13.     Print(__FUNCTION__, " ", __LINE__, " Entry point [ ", call," ]  ARG: ", arg, " WHO: ", who);
14. 
15.     if (arg <= 1)
16.     {
17.         Print(__FUNCTION__, " ", __LINE__, " Number Callback [ ", call," ]  ARG: ", arg, " WHO: ", who);
18. 
19.         return arg;
20.     }
21. 
22.     value += Fibonacci(arg - 1, call + 1, 1);
23. 
24.     Print(__FUNCTION__, " ", __LINE__, " Value = ", value, "  >> New call with arg: ", arg);
25. 
26.     value += Fibonacci(arg - 2, call + 1, 2);
27. 
28.     Print(__FUNCTION__, " ", __LINE__, " General Return = ", value);
29. 
30.     return value;
31. }
32. //+------------------------------------------------------------------+

コード03

ここで、皆さまにお詫びします。申し訳ないのですが、ここで起きていることを説明する、より簡単な方法は残念ながらありません。コード03を実行した場合の出力は次のとおりです。

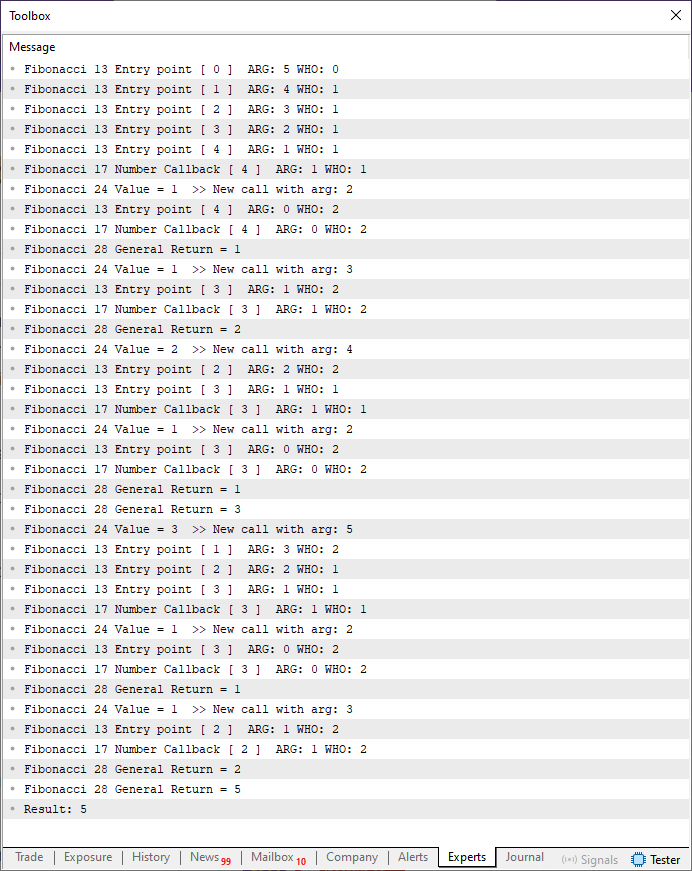
図04

図04はかなり長いですが、ご注意ください。関数呼び出しは7番目の要素を計算するのではなく、5番目の要素に変更しています。この差は大きく見えないかもしれませんが、解析すべき情報量を大幅に減らしています。ただし、非常に重要なことがあります。13行目が実行されるたびに関数に入っていきます。その直後にすぐ戻ることもあれば、さらに再帰呼び出しがおこなわれることもあります。最初は少し混乱するかもしれませんが、11行目の条件が最終結果に影響すると思う方も多いでしょう。しかしそれをそう考えるなら、再帰が関数や手続きに対して実際に何をしているのか、まだ完全に理解していないことになります。

だからこそ、私は図04をできるだけ詳細に示しています。コード02がどのようにして正しい結果を計算しているのか、皆さんにしっかり理解してほしいからです。

これからの説明は集中して読んでほしいので、読者の皆さん、続ける前に周囲の邪魔を排除してください。再帰関数や手続きは、特に初めて触れる際は混乱しやすいものです。

では図04をもとに、本当に何が起きているのか理解していきましょう。まず6行目が実行されると、フィボナッチ関数がループのように呼び出されます。反復的なループではなく、再帰的なループです。これが理解すべき最初のポイントです。

次に、制限条件が必要であることを認識しましょう。コード01でも見たように、再帰を用いるループには必ず終了条件が必要です。今回のコードでは15行目にその条件があります。前述したように、再帰は単純な式に還元されるべきですが、再帰を制限する役割はその式とは異なる概念です。この違いを理解することが重要なポイントです。簡単に言えばこうなります。 

再帰を生み出すのは最小限の数学的表現の実装で、再帰を制限するのは無限ループ化を防ぐ条件です。

したがって、コード04では制限条件が15行目にあり、再帰のメカニズムは22行目と26行目にあります。コード02では制限条件が11行目、再帰呼び出しは16行目でおこなわれています。

ここから処理の流れを追っていきましょう。最初の引数は5です。13行目が呼び出され、続いて22行目に進みます。この行で関数が再度呼び出され、9行目に戻ることでループが形成されます。ただし注意してください。22行目で呼び出す際、引数は1ずつ減少しています。そのため、呼び出しが積み重なっていき、15行目の条件が真になるまで続きます。

その時点で興味深い現象が起きます。4回目の呼び出しで引数の値がどんどん減少しています。15行目が真になると、17行目が実行され、現在の引数の値と関数の呼び出し回数が表示されます。引数が1になったため、その値を呼び出し元に返します。ただし呼び出し元は6行目ではなく22行目です。呼び出しは積み重なっているため、ここからスタックを戻し始めます。最初に返される値は1で、これは変数Valueに加算されます。この変数は呼び出し間で値を失わず、戻るたびに新しい値を蓄積します。これを理解するにはコールスタックの仕組みを知る必要がありますが、今は詳しい説明は割愛します。再帰の本質は把握できますのでご安心ください。ただし、気を付けてください。

こうして最初の戻り値が計算されました。しかし、図03の式からわかるように、もう一度再帰呼び出しをおこなう必要があります。だから26行目で新たな呼び出しをおこなうのです。ここからが複雑なところです。

22行目の呼び出しでは引数を1ずつ減らしていましたが、argが1になって関数が戻ると、前の呼び出し（22行目の呼び出し）の引数はまだ2です。つまり24行目に来たとき、最新の呼び出しではargは1でしたが、現在はarg=2の状態です。

これは最初は混乱しやすいところです。だからこそ、最も単純な再帰例であるフィボナッチ数列を使っています。そして、コード01で見たように、最初にカウントダウンがあり、その後にカウントアップが見えました。このカウントアップは値が積み重なっていたために起こった現象であり、直接実装したものではありません。この挙動は再帰呼び出しの積み重ねと戻りの仕組みが生み出す副産物です。

では慎重に進みましょう。26行目時点でargは2です。ここで2を引くと0になります。15行目の条件が真になり、関数は0を返します。28行目は返された値1を出力します。これは数列の最初のフィボナッチ数です。

なお、5回の呼び出しが積み重なっていて、まだ1回しか戻っていません。次に22行目に戻るとValueは1になります。しかし前回の呼び出し時は1でしたか。いいえ、読者の皆さん。あれは前の呼び出しでの値です。今戻った22行目のValueは0から1に変わります。次に24行目を実行し、1つ戻るとargは2になります。ここが24行目のポイントです。処理の流れをよく追ってください。26行目で2を引き、関数は0で呼び出されます。そしてWHOは2のままです。これは26行目から呼び出されているためです。

argは0なので15行目が真となり、19行目で0が返されます。26行目でその結果(0)を先のValue(1)に加算し、Valueは1になります。これが2番目のフィボナッチ数です。

次に22行目に戻ります。5回の呼び出しのうち、2回だけ戻りました。Valueは1、argは3です。ここが興味深いところで、arg=3です。26行目で2を引くと1となり、関数はarg=1で呼び出されます。15行目が真となり1を返し、Valueは2になります。

これが3番目のフィボナッチ数です。さらに1段戻ると、22行目でValueは2、argは4です。26行目が実行されるとどうなるでしょうか。予想できましたか。関数はarg=2で呼び出されます。26行目で2を引いてから呼び出していることを忘れないでください。

このときargは2なので、15行目の条件は偽となり22行目が再度実行されます。ただし今回はValueが0で、前回の2とは異なります。この値はスタック上に保存されているためです。argが2であり、呼び出す前に1を引く必要があるため15行目ではargは1となり、1が返されます。22行目でValueは1となり26行目が実行されます。ここで2を引くと関数が呼び出され、0を返します。30行目でValueは1となり、どこに返るでしょうか。それは26行目です。この呼び出しは26行目からおこなわれているのを覚えておいてください。Valueは現在2です。戻りが1回あったためValueは3になります。これで数列の4番目の要素が計算できました。残るは1つです（笑）。

ここまで来ると、頭が混乱しているかもしれません。呼び出しと戻りが複雑に絡み合っています。しかし最後の要素は繰り返しを省きます。必要な仕組みはすでに理解できたと思うからです。さて26行目でargは5、Valueは3です。argを半分ずつ減らしながら呼び出しが続きます。ここまで説明した内容で十分だと思います。

重要なのは、この記事冒頭で述べたように「再帰は書くのは簡単だが、実行は遅い」ということです。だからフィボナッチ数を計算するのに、同等の反復的な実装も可能です。こちらは性能が向上しますが、コードはやや複雑になります。

それを証明するために、今度は再帰ではなく反復で同じ計算を行う例を見てみましょう。方法はいくつかありますが、以下はその一例です。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     const uchar who = 6;
07. 
08.     Print("Result: ", Fibonacci_Recursive(who));
09.     Print("Result: ", Fibonacci_Interactive(who));
10. }
11. //+------------------------------------------------------------------+
12. uint Fibonacci_Recursive(uint arg)
13. {
14.     if (arg <= 1)
15.         return arg;
16. 
17.     return Fibonacci_Recursive(arg - 1) +  Fibonacci_Recursive(arg - 2);
18. }
19. //+------------------------------------------------------------------+
20. uint Fibonacci_Interactive(uint arg)
21. {
22.     uint v, i, c;
23. 
24.     for (c = 0, i = 0, v = 1; c < arg; i += v, c += 2)
25.         v += i;
26. 
27.     return (c == arg ? i : v);
28. }
29. //+------------------------------------------------------------------+

コード04

ここではループの2つのアプローチを扱っています。1つ目が再帰、2つ目が反復です。ここでお尋ねしますが、どちらのほうが理解しやすいと感じますか。また、その回答を踏まえて、どちらが実行速度が速いと思いますか。同じ計算をおこなう2つの方法について、既にご存知のことを考慮してください。

20行目から実装されている反復関数は、読者の中には少し変わっていると感じる方もいるかもしれません。そこで、その動作について簡単に説明します。

22行目では必要な変数を宣言しています。続く24行目で計算のメインループに入ります。ここからが面白いところです。計算を始める前に値を初期化していることに注目してください。ここで重要なポイントですが、求めたい要素が奇数番目（1番目、3番目、5番目、7番目…）の場合は、変数vに正しい結果が入っています。しかし、求めたい要素が偶数番目の場合は、正しい値が変数iに入っています。なぜでしょうか。

これはカウンタ変数cがループごとに2ずつ増加し、正しい結果を飛び越えないようにしているからです。さらに、各反復で前の値を新しい値に加算し、iとvの値を入れ替えていないため、このわずかな違いが反復関数に現れています。この問題を避ける実装方法もありますが、私はそれを不要だと考えています。ループの仕組み自体が現在の値と次の値の両方を把握させてくれるためです。したがって、必要なのは三項演算子を使って正しい結果を返すことだけです。この小さな調整がないと、入力（または求める要素）が奇数か偶数か、そしてiかvのどちらの値を返すかによって、次の要素や前の要素を指してしまうことがあります。

このコード04が正しく動作していることを示すため、実行結果をすぐ下に示しています。フィボナッチ数列の他の値を試したり、2つの計算方法を比較したりしたい場合は、6行目の定数を変更してください。ただし、フィボナッチ数列は非常に急速に大きくなることを忘れないでください。コード内で使われているデータ型の制限もありますので、数列のあまり先の値を要求すると、予期せぬ結果やエラーが起こる可能性があることに注意してください。

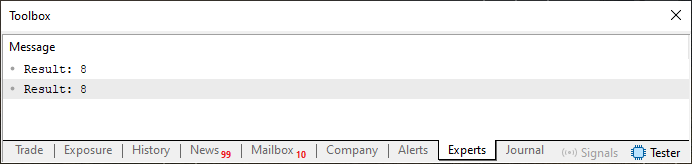
図05

これらの制限を克服する方法も存在し、コンピュータのメモリ容量の範囲内であればどんな数字でも計算可能です。しかしこれはより高度なトピックであり、私の意見ではもっと適切な時期に学ぶのが望ましいでしょう。ただし、興味を引くために少しだけ触れておきます。プログラマーはどうやってπやその他の無理数定数を何千桁もの小数点以下の精度で計算できると思いますか。ほとんどのプログラミング言語で使われている標準のデータ型では、このレベルの精度を達成することは到底不可能だからです。

前述の通り、このテーマはより高度な理解が必要です。これまでに学んだ知識では到底無理、というわけではありません。実際のところ、ここで扱った再帰などの概念を用いてこうした計算を実現することは可能です。しかし、その実装には多くの労力が必要であり、各種の構成要素を直感的ではない形式に適応させる必要があります。

最後に

この記事の目的は、強力で本当に面白いプログラミングの概念を紹介することでした。しかし、この概念は注意と敬意をもって扱うべきものです。再帰を正しく理解せずに使うと、比較的シンプルなプログラムが不必要に複雑になってしまいます。しかし、正しく適切な場面で使用すれば、再帰は非常に強力な味方となり、そうでなければはるかに難しく、時間のかかる問題を解決する助けとなります。

一般的なルールとしては、可能な限り再帰を使うべきです。特に、数学的な表現で反復的な解法が難しい場合はなおさらです。ただし、多くの再帰呼び出しがプログラムのパフォーマンスを著しく低下させることもあります。パフォーマンスが問題になる場合は、再帰のロジックを反復ループに書き換えることを検討してください。設計は最初は複雑かもしれませんが、特に大量のデータや変換が必要なシーケンスでは、反復解法のほうが実行速度が速い傾向にあります。