MetaTrader 5 / 测试者
English Русский Español Deutsch 日本語 Português
preview
原子轨道搜索（AOS）算法：改进与拓展

原子轨道搜索（AOS）算法：改进与拓展

MetaTrader 5 — 测试者 |
266 5
Andrey Dik
Andrey Dik

内容

  1. 概述
  2. 算法实现
  3. C_AO类的使用示例
  4. 测试结果


概述

在本文的第一部分，我们研究了受原子轨道模型启发的 AOS（原子轨道搜索）算法及其基本原理和运行机制。我们探讨了该算法如何利用概率分布和相互作用动态来寻找复杂优化问题的最优解。

在本文的第二部分，我们将专注于改进AOS算法，因为面对这样一个先进的理念，我们不得不尝试对其进行改进。我们将分析改进该算法的概念，特别关注该方法所特有的特定算子，这些算子可以提高其效率和适应性。

对AOS算法的研究让我对其搜索解空间的方法产生了许多有趣的思考。在研究过程中，我也想出了许多关于如何改进这个有趣算法的理念。特别是，我专注于改进现有的方法，这些方法可以通过提高其探索复杂解空间的能力来提升算法的性能。我们将探讨如何将这些改进整合到AOS算法的现有结构中，使其成为解决优化问题的更强大的工具。因此，我们的目标不仅是分析现有机制，还要提出其他能够显著扩展AOS算法能力的方法。


算法实现

在上一篇文章中，我们详细研究了AOS算法的关键组成部分。您可能还记得，在该算法中，种群被视为一个分子，而坐标的有效区域（即搜索最优解的区域）被表示为一个原子。每个原子由不同的层组成，这些层有助于安排和指导搜索。

在优化过程中我们获得的具体坐标值可以被解释为电子。这些电子在原子内，代表了我们正进行优化问题的一个参数的可能解。因此，每个分子（种群）都在努力在给定的区域（原子）内找到最优值（电子）。

在AOS算法的原始版本中，BEk层的能量被定义为该层中电子能量的算术平均值，而BSk键被定义为它们坐标的算术平均值。BEk能量用于与电子的能量进行比较，以确定它们后续运动的模式。BSk键用于计算电子位置的增量，即层中电子的最佳位置LEk与BSk键之间的差值，根据以下公式计算：Xki[t+1] = Xki[t] + αi × (βi × LEk − γi × BSk)。

我建议放弃BSk（电子平均位置），转而使用电子的个体最佳位置。这样一来，电子将根据其个体成就，而不是基于整个层的平均解，向其所在层的最佳解移动。此外，βi和γi这两个随机因子似乎多余，因为已经有一个外部的αi随机因子。这一改进将使该方程中随机数的生成时间缩短至原来的三分之一，同时也不会丧失其物理意义。

现在让我们看看描述原子中一层的结构。代码中删除的元素以红色突出显示：

//——————————————————————————————————————————————————————————————————————————————
struct S_Layer
{
    int    pc;  // particle counter
    double BSk; // connection state
    double BEk; // binding energy
    double LEk; // minimum energy

    void Init ()
    {
      pc  = 0;
      BSk = 0.0;
      BEk = 0.0;
      LEk = 0.0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

让我们看一下CalcLayerParams方法的代码，它计算层的特性，如能量和连通性。以红色突出显示的字符串将被删除，因为它们不再需要。您可能还记得，该方法在AOS搜索策略中起着关键作用，其目标是防止算法陷入局部陷阱。由于层的能量水平并不依赖于它们的位置（能量从原子中心向外层递减），而是由显著的局部极值决定（外层的能量可能超过内层），因此层的作用是纠正电子在搜索空间中的运动。

在每一轮迭代（epoch）中层数随机变化，有助于防止算法陷入局部最优陷阱，避免电子长期停滞在单一层中。此外，改进后的版本无需再计算整个原子的平均能量，因此我们将移除相关的代码行。

AOS层

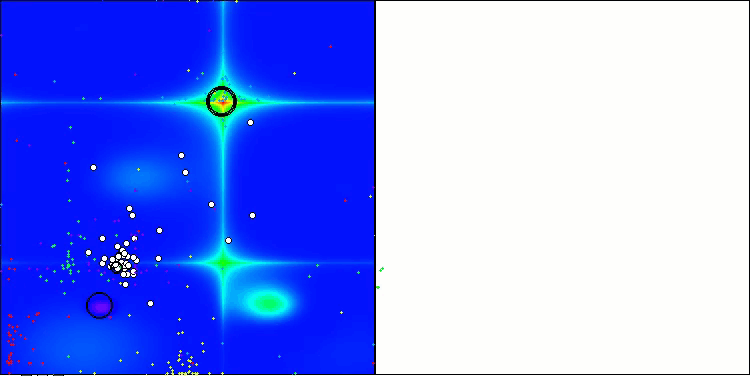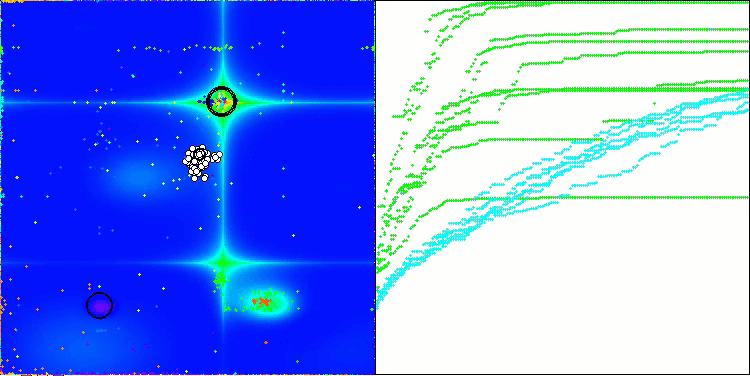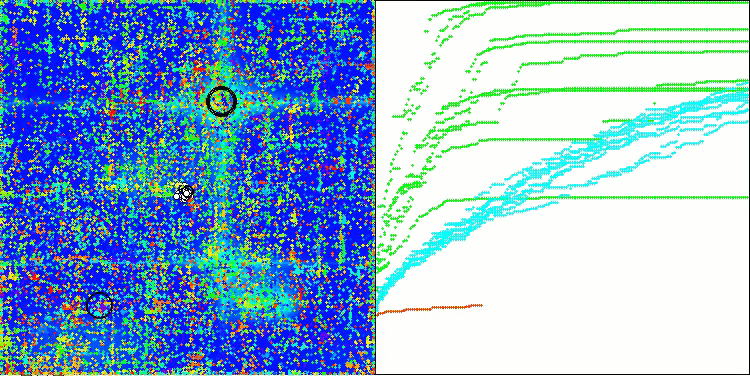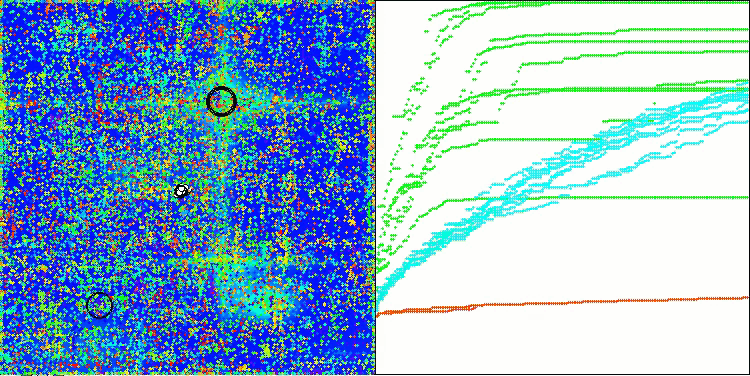
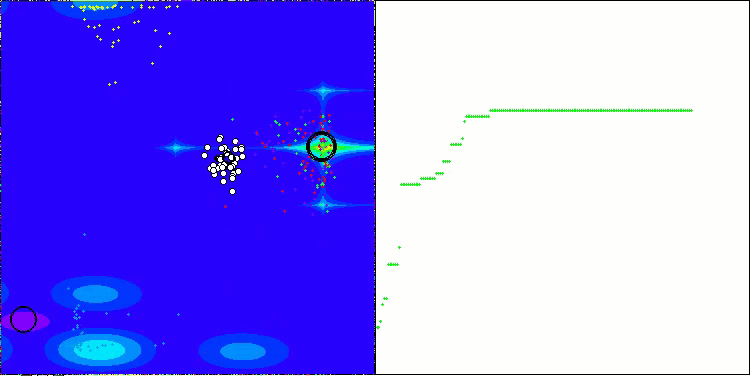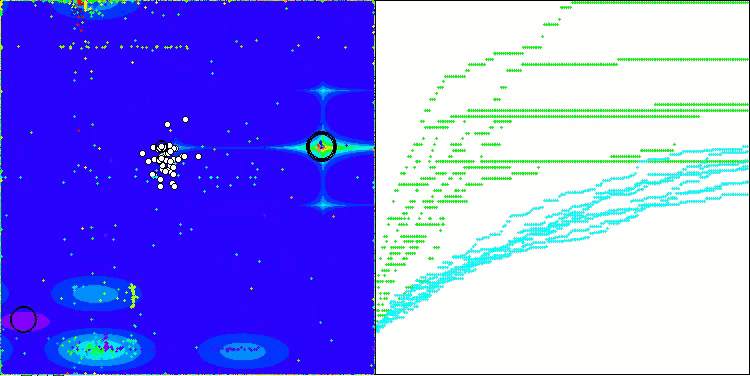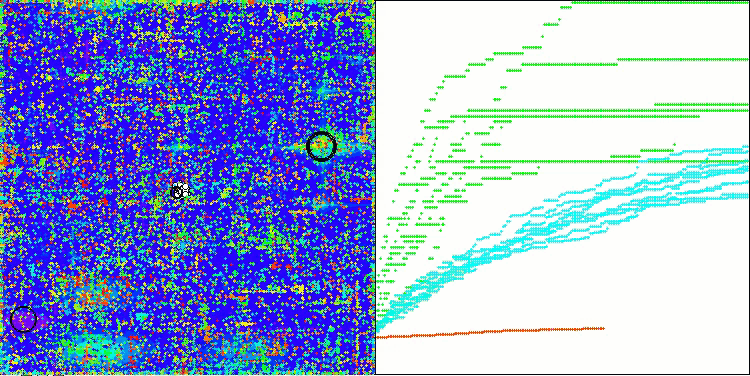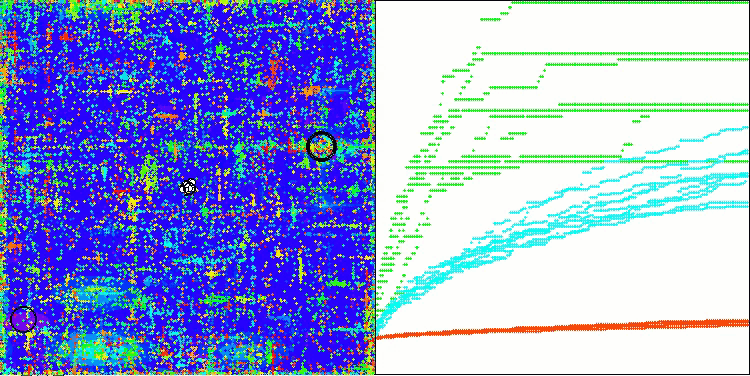
图例1. 原子中层数不同时，e电子的位移方向和大小都会随之变化

图1展示了在AOS算法中，不同层数的原子中电子行为的差异。上图呈现了一个三层原子，其中电子位于L1层，目标函数值为B1，并向局部最优值LEk1移动。下图展示了一个两层原子，其中电子也位于L1层，并向局部最优值LEk1移动，目标函数值为B1（如果是三层原子，这将是点LEk2）。

图中的关键元素：

  • B0, B1, B2 — 相应层目标函数的局部值，
  • LEk0, LEk1, LEk2 — 相应层中的最优解，
  • L0, L1, L2 — 原子层，
  • e — 电子，
  • MIN, MAX — 原子外层的边界（问题优化参数的边界条件）。
//——————————————————————————————————————————————————————————————————————————————
// Calculate parameters for each layer
void C_AO_AOS::CalcLayerParams ()
{
  double energy;

  // Handle each coordinate (atom)
  for (int c = 0; c < coords; c++)
  {
    atoms [c].Init (maxLayers);

    // Handle each layer
    for (int L = 0; L < currentLayers [c]; L++)
    {
      energy = -DBL_MAX;

      // Handle each electron
      for (int e = 0; e < popSize; e++)
      {
        if (electrons [e].layerID [c] == L)
        {
          atoms [c].layers [L].pc++;
          atoms [c].layers [L].BEk += a [e].f;
          atoms [c].layers [L].BSk += a [e].c [c];

          if (a [e].f > energy)
          {
            energy = a [e].f;
            atoms [c].layers [L].LEk = a [e].c [c];
          }
        }
      }

      // Calculate average values for the layer
      if (atoms [c].layers [L].pc != 0)
      {
        atoms [c].layers [L].BEk /= atoms [c].layers [L].pc;
        atoms [c].layers [L].BSk /= atoms [c].layers [L].pc;
      }
    }
  }

  // Calculate the general state of connections
  ArrayInitialize (BS, 0);

  for (int c = 0; c < coords; c++)
  {
    for (int e = 0; e < popSize; e++)
    {
      BS [c] += a [e].c [c];
    }

    BS [c] /= popSize;
  }
}
//——————————————————————————————————————————————————————————————————————————————

若需更新最优个体解，请将相关代码添加至改进版C_AO_AOSm的 Revision 方法中。

//——————————————————————————————————————————————————————————————————————————————
// Method of revising the best solutions
void C_AO_AOSm::Revision ()
{
  int bestIndex = -1;

  // Find the best solution in the current iteration
  for (int i = 0; i < popSize; i++)
  {
    // Update the global best solution
    if (a [i].f > fB)
    {
      fB = a [i].f;
      bestIndex = i;
    }

    // Update the personal best solution
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  // Update the best coordinates if a better solution is found 
  if (bestIndex != -1) ArrayCopy (cB, a [bestIndex].c, 0, 0, WHOLE_ARRAY);
}
//——————————————————————————————————————————————————————————————————————————————

在UpdateElectrons方法中，移除β和γ变量，因为生成对应随机数时无需使用这两个参数。此外，当电子向全局解移动时，取消根据层数对电子增量进行的删除操作。直白地讲，作者提出的解决方案存在争议，且该方法的物理意义尚未完全明确。或许作者希望使电子向全局解移动的幅度可变，并根据层数调整这一幅度：层数越少，移动应越剧烈（尽管我的实验表明实际情况并非如此）。

//——————————————————————————————————————————————————————————————————————————————
// Update electron positions
void C_AO_AOS::UpdateElectrons ()
{
  double α;      // speed coefficient
  double β;      // best solution weight coefficient
  double γ;      // average state weight coefficient
  double φ;      // transition probability
  double newPos; // new position
  double LE;     // best energy
  double BSk;    // connection state
  int    lID;    // layer ID

  // Handle each particle
  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      φ = u.RNDprobab ();

      if (φ < PR)
      {
        // Random scatter
        newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      }
      else
      {
        lID = electrons [p].layerID [c];

        α = u.RNDfromCI (-1.0, 1.0);
        β = u.RNDprobab ();
        γ = u.RNDprobab ();

        // If the current particle energy is less than the average layer energy
        if (a [p].f < atoms [c].layers [lID].BEk)
        {
          // Moving towards the global optimum----------------------------
          LE = cB [c];

          newPos = a [p].c [c]+ α * (β * LE - γ * BS [c]) / currentLayers [c];
        }
        else
        {
          // Movement towards the local optimum of the layer------------------------
          LE  = atoms [c].layers [lID].LEk;
          BSk = atoms [c].layers [lID].BSk;

          newPos = a [p].c [c] + α * (β * LE - γ * BSk);
        }
      }

      // Limiting the new position within the search range taking into account the step
      a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

此外，在C_AO_AOSm类的UpdateElectrons方法中，我们不再让电子在搜索空间中随机分散，而是以一定概率将其移动至核心中心。本质上，这意味着用全局解的值替换部分坐标值，从而提升算法的组合优化性能。随机分散原本旨在保持解群体的多样性，但这一特性导致电子分布服从对数正态分布——即电子在移动过程中，仍有非零概率命中空间中的任意一点。

电子运动方程的改进部分以绿色标出。现在，增量计算方式改为：当前层局部最优解与电子个体最优解的差值。

//——————————————————————————————————————————————————————————————————————————————
// Update electron positions
void C_AO_AOSm::UpdateElectrons ()
{
  double α;      // speed coefficient
  double φ;      // transition probability
  double newPos; // new position
  double LE;     // best energy
  double BSk;    // connection state
  int    lID;    // layer ID

  // Handle each particle
  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      φ = u.RNDprobab ();

      if (φ < PR)
      {
        // Random jump to center
        newPos = cB [c];
      }
      else
      {
        lID = electrons [p].layerID [c];

        α = u.RNDfromCI (-1.0, 1.0);

        // If the current particle energy is less than the average layer energy
        if (a [p].f < atoms [c].layers [lID].BEk)
        {
          // Moving towards the global optimum----------------------------
          LE     = cB [c];

          newPos = a [p].cB [c]+ α * (LE - a [p].cB [c]);
        }
        else
        {
          // Movement towards the local optimum of the layer------------------------
          LE     = atoms [c].layers [lID].LEk;

          newPos = a [p].cB [c]+ α * (LE - a [p].cB [c]);
        }
      }

      // Limiting the new position within the search range taking into account the step
      a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

DistributeParticles方法采用对数正态分布，在搜索空间中为每个坐标分配电子。针对每个粒子及其各坐标，算法首先调用函数根据给定参数（均值、最小/最大值、峰值）生成初始位置，随后通过附加函数将该位置调整至指定范围内。 

//——————————————————————————————————————————————————————————————————————————————
// Distribution of particles in the search space
void C_AO_AOS::DistributeParticles ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Use log-normal distribution to position particles
      a [i].c [c] = u.LognormalDistribution (cB [c], rangeMin [c], rangeMax [c], peakPosition);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

将电子分布改为正态分布。该分布采用标准差为8的参数设置。尽管此参数本可设为算法外部可调项，但我选择保持其内部固定。标准差较小时，算法会加强对搜索空间的广泛探索；标准差较大时，则能在优化全局解时提升收敛精度。

//——————————————————————————————————————————————————————————————————————————————
// Distribution of particles in the search space
void C_AO_AOSm::DistributeParticles ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Use a Gaussian distribution to position particles
      a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

为了提升效率，我们对AOS算法原始版本的所有改进都进行了系统性分析。鉴于搜索策略逻辑已发生重大变更，因此可以用字母“m”来标识算法的改进版本。从现在起，只将改进后的版本展示在排名表中——AOSm。


C_AO类的使用示例

由于前文所探讨的所有群体优化算法均继承自通用C_AO基类，因此可通过统一接口轻松解决各类最优参数选择问题。以下脚本示例展示了如何进行目标函数优化：

1. 在脚本起始处，您可以选择要使用的优化算法。如果没做任何选择，脚本将报告错误并停止运行。
2. 配置参数：脚本定义了函数将运行的次数、需要优化的参数数量、解决方案群体的大小以及将执行的迭代次数。
3. 限制参数值：为每个参数设置最小和最大值（本例中范围为-10至10）。
4. 开始优化脚本：

  • 生成解决方案（参数集合），并使用一个特殊函数（目标函数）评估其质量。
  • 在每次迭代中，算法根据解的表现动态更新最优解。

5. 输出结果：优化完成后，脚本将显示所用算法、找到的最优值及函数的调用次数。
6. 目标函数是一个抽象的优化问题（在本示例中，采用倒置抛物线求解全局最大值问题），该函数接收参数并返回其质量评分。

#property script_show_inputs                           // Specify that the script will show the inputs in the properties window

#include <Math\AOs\PopulationAO\#C_AO_enum.mqh>        // Connect the library for handling optimization algorithms

input E_AO AOexactly = NONE_AO;                        // Parameter for selecting the optimization algorithm, default is NONE_AO

//——————————————————————————————————————————————————————————————————————————————
void OnStart()
{
  //----------------------------------------------------------------------------
  int numbTestFuncRuns = 10000;                        // Total number of function runs
  int params           = 1000;                         // Number of parameters for optimization
  int popSize          = 50;                           // Population size for optimization algorithm
  int epochCount       = numbTestFuncRuns / popSize;   // Total number of epochs (iterations) for optimization
  
  
  double rangeMin [], rangeMax [], rangeStep [];       // Arrays for storing the parameters' boundaries and steps
  
  ArrayResize (rangeMin,  params);                     // Resize 'min' borders array
  ArrayResize (rangeMax,  params);                     // Resize 'max' borders array
  ArrayResize (rangeStep, params);                     // Resize the steps array
  
  // Initialize the borders and steps for each parameter
  for (int i = 0; i < params; i++)
  {
    rangeMin  [i] = -10;                               // Minimum value of the parameter
    rangeMax  [i] =  10;                               // Maximum value of the parameter
    rangeStep [i] =  DBL_EPSILON;                      // Parameter step
  }
  
  //----------------------------------------------------------------------------
  C_AO *ao = SelectAO (AOexactly);                     // Select an optimization algorithm
  if (ao == NULL)                                      // Check if an algorithm has been selected
  {
    Print ("AO not selected...");                         // Error message if no algorithm is selected
    return;
  }
  
  ao.params [0].val = popSize;                         // Assigning population size....
  ao.SetParams ();                                     //... (optional, then default population size will be used)
  
  
  ao.Init (rangeMin, rangeMax, rangeStep, epochCount); // Initialize the algorithm with given boundaries and number of epochs
  
  // Main loop by number of epochs
  for (int epochCNT = 1; epochCNT <= epochCount; epochCNT++)
  {
    ao.Moving ();                                      // Execute one epoch of the optimization algorithm

    // Calculate the value of the objective function for each solution in the population
    for (int set = 0; set < ArraySize (ao.a); set++)
    {
      ao.a [set].f = ObjectiveFunction (ao.a [set].c); // Apply the objective function to each solution
    }

    ao.Revision ();                                    // Update the population based on the results of the objective function
  }
  
  //----------------------------------------------------------------------------
  // Output the algorithm name, best result and number of function runs
  Print (ao.GetName (), ", best result: ", ao.fB, ", number of function launches: ", numbTestFuncRuns);
  
  delete ao;                                           // Release the memory occupied by the algorithm object
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Definition of the user's objective function, in this case as an example - a paraboloid, F(Xn) ∈ [0.0; 1.0], X ∈ [-10.0; 10.0], maximization
double ObjectiveFunction (double &x [])
{
  double sum = 0.0;  // Variable for accumulation of the result

  // Loop through all parameters
  for (int i = 0; i < ArraySize (x); i++)
  {
    // Check if the parameter is in the allowed range
    if (x [i] < -10.0 || x [i] > 10.0) return 0.0;  // If the parameter is out of range, return 0
    sum += (-x [i] * x [i] + 100.0) * 0.01;         // Calculate the value of the objective function
  }
  
  return sum /= ArraySize (x);
}
//——————————————————————————————————————————————————————————————————————————————


测试结果

让我们继续测试算法的改进版本。

AOS|Atomic Orbital Search|50.0|10.0|20.0|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.8023218355650774
25 Hilly's; Func runs: 10000; result: 0.7044908398821188
500 Hilly's; Func runs: 10000; result: 0.3102116882841442
=============================
5 Forest's; Func runs: 10000; result: 0.8565993699987462
25 Forest's; Func runs: 10000; result: 0.6945107796904211
500 Forest's; Func runs: 10000; result: 0.21996085558228406
=============================
5 Megacity's; Func runs: 10000; result: 0.7461538461538461
25 Megacity's; Func runs: 10000; result: 0.5286153846153846
500 Megacity's; Func runs: 10000; result: 0.1435846153846167
=============================
总分: 5.00645 (55.63%)

如您所见，改进版算法的结果较原始版本（整体得分3.00488，对应33.39%）有显著提升。通过可视化分析可以更直观地验证这一改进：不仅收敛速度加快，关键极值区域的探索也更为精细。

值得关注的关键现象之一是解在各个坐标维度上的"聚集效应"。这一特性在原始版与改进版中均有体现，恰恰印证了AOS算法的典型特征。解的聚集性可能表明算法能有效定位潜在最优解所在区域。

Hilly值

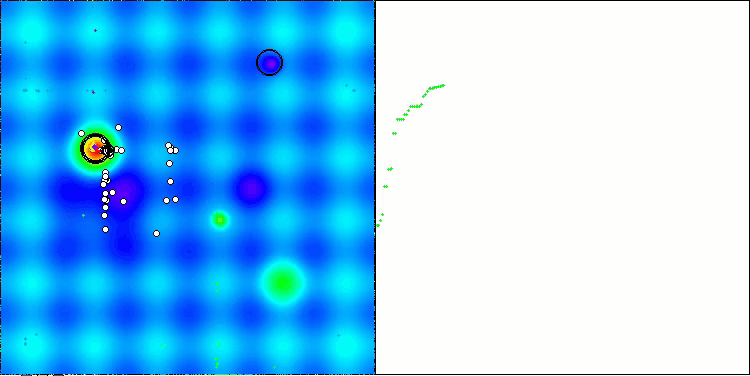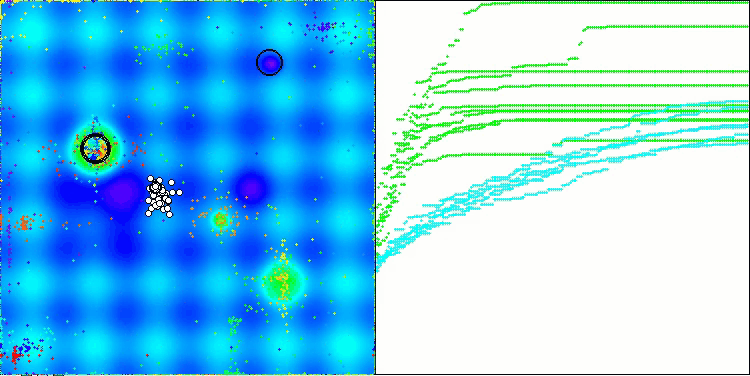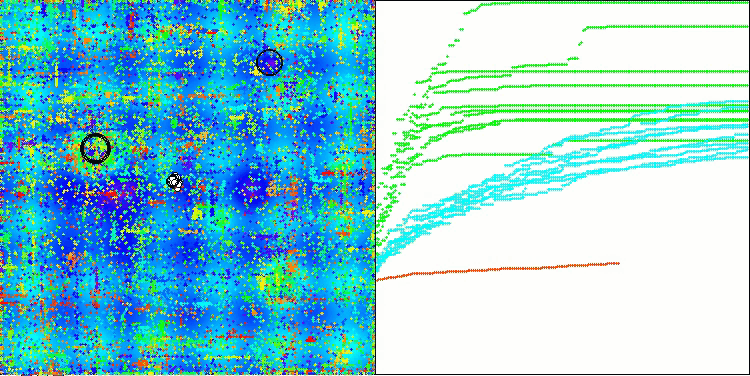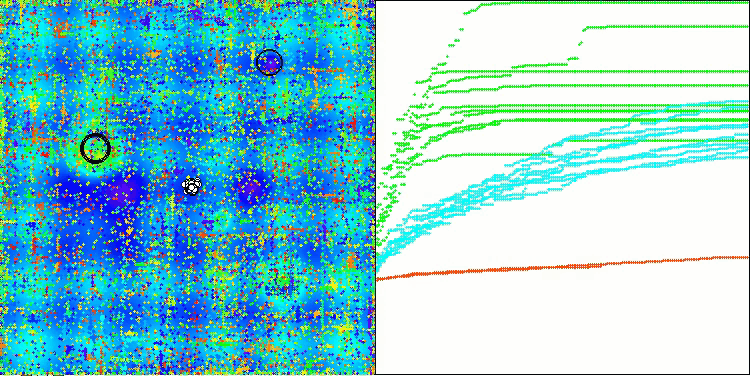
AOSm在Hilly测试函数上

Forest值

AOSm在Forest测试函数上

Megacity

  AOSm在Megacity测试函数上

改进后的原子轨道搜索（AOS）算法性能较原始版本显著提升，现已达到最大可能值的55%以上。这一成果令人惊喜！在评分表中，该算法位列第12名，充分彰显了其优异表现。

# AO 说明 Hilly值 Hilly最终值 Forest值 Forest最终值 Megacity (离散) Megacity最终值 最终结果 最大百分比
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 ANS 跨邻域搜索 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
2 CLA 密码锁算法（joo） 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
3 AMOm 动物迁徙优化M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
4 (P+O)ES (P+O) 进化策略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA 彗星尾算法（joo） 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 AAm 射箭算法M 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
8 ESG 社会群体的进化（joo） 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
9 SIA 模拟各向同性退火（joo） 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
10 ACS 人工协同搜索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
11 ASO 无序社会优化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
12 AOSm 原子轨道搜索M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
13 TSEA 龟壳演化算法（joo） 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
14 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
15 CRO 化学反应优化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
16 BSA 鸟群算法 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
17 HS 和声搜索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
18 SSG 树苗播种和生长 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
19 BCOm 细菌趋化性优化算法M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
20 ABO 非洲水牛优化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
21 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
22 TSm 禁忌搜索M 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
23 BSO 头脑风暴优化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
24 WOAm 鲸鱼优化算法M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
25 AEFA 人工电场算法 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
26 AEO 基于人工生态系统的优化算法 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
27 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
28 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
29 ABHA 人工蜂巢算法 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
30 ACMO 大气云模型优化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
31 ASHA 人工淋浴算法 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
32 ASBO 适应性社会行为优化 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
33 MEC 思维进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
34 IWO 入侵杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
35 Micro-AIS 微型人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
36 COAm 布谷鸟优化算法 M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
37 SDOm 螺旋动力学优化 M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
38 NMm Nelder-Mead方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
39 FAm 萤火虫算法 M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
40 GSA 引力搜索算法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
41 BFO 细菌觅食优化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
42 ABC 人工蜂群 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
43 BA 蝙蝠算法 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
44 AAA 人工藻类算法 0.50007 0.32040 0.25525 1.07572 0.37021 0.22284 0.16785 0.76089 0.27846 0.14800 0.09755 0.52402 2.361 26.23
45 SA 模拟退火 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43


总结

本文提出了改进版原子轨道搜索算法（AOSm），其核心修改在于：摒弃原子层中电子的BSk平均位置，转而采用每个电子的个体最优位置。这一改进使电子能基于个体表现而非平均值，更高效地向本层最优解迁移。此外，移除了βᵢ和γᵢ两个随机分量，在保持算法物理意义的前提下，将随机数生成时间缩短至原来的三分之一。

在UpdateElectrons方法中，我们移除了冗余变量，并取消了电子向全局解迁移时按层数分割增量的操作。尽管原始版本作者可能希望通过可变迁移幅度提升性能，但实验表明此方式收益甚微。

对C_AO_AOSm类中的UpdateElectrons方法还做了另一项关键改进：将电子随机散射替换为以一定概率向核心中心移动。这增强了算法的组合优化能力，使电子能更精准地定位全局最优解。同时，将对数正态分布改为正态分布，显著提升了全局解细化阶段的收敛精度。

改进版AOSm的测试结果表现卓越，整体得分超过最大可能值的55%，充分体现了算法的高效性与竞争力。在排名表中，AOSm位列第12名，彰显了其在众多优化方法中的突出成就。

AOSm最显著的特性之一是收敛性能的提升，这在结果可视化中尤为明显：算法能更细致地探索关键极值区域，展现出在复杂多维空间中高效搜索最优解的能力。原版本与改进版均观察到的解"聚集效应"，印证了算法定位潜在最优区域并聚焦搜索的特性，这对高维复杂问题尤为适用。

改进版的另一优势是减少了外部参数数量，简化了使用与配置流程。不过，对于前文提及的所有算法，我已经预先优化了外部参数配置，以便通过各类复杂的测试任务，确保算法开箱即用，无需额外的配置调整。本文证明：优化算法的微小改动可能彻底改变其搜索特性，而搜索策略的重大逻辑调整未必会带来显著的效果提升。当然，在我的文章中，仅分享经实证能有效提升优化效率的方法。

标签

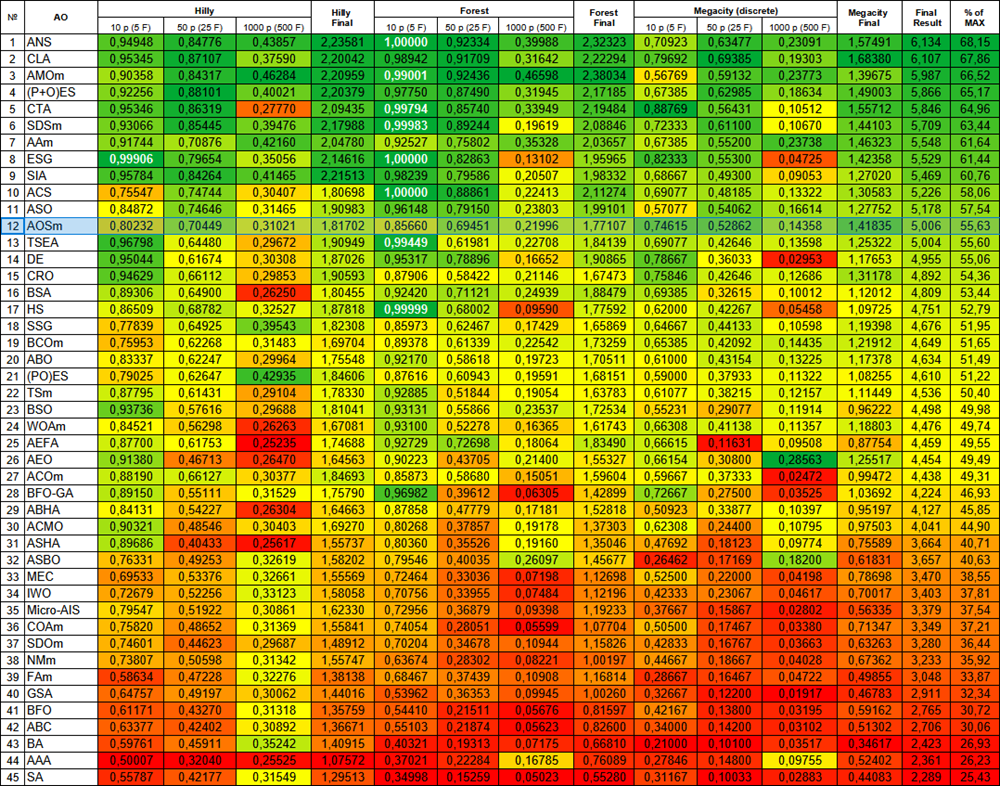
图例2. 根据相关测试，将算法的颜色等级大于或等于0.99的结果以白色突出显示。

图表

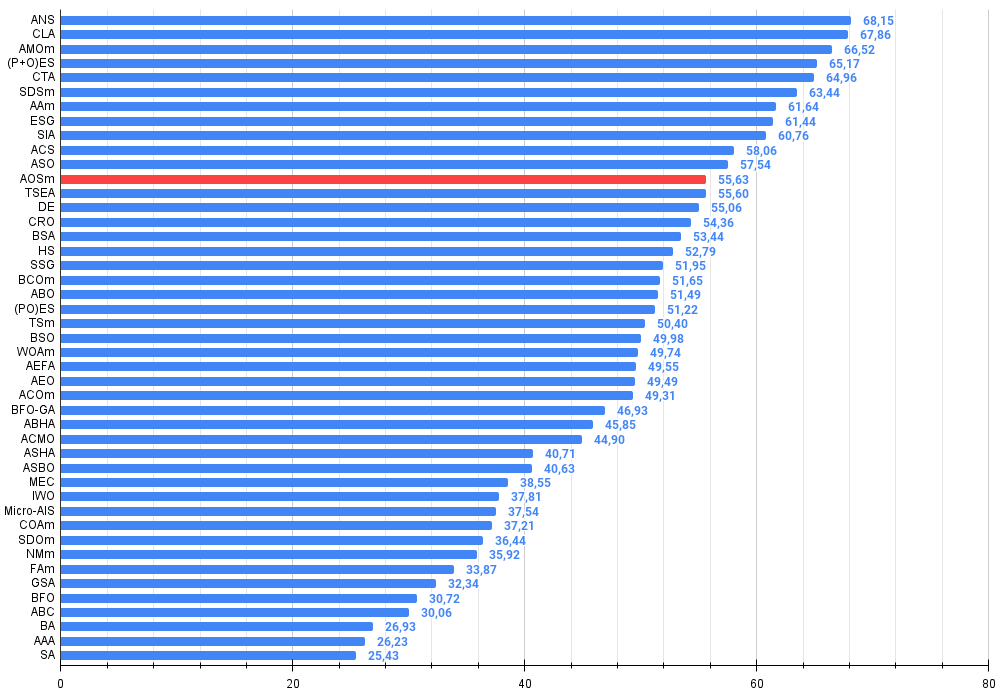
图例 3. 算法测试结果的直方图（标尺从 0 到 100，数字越大结果越好，

其中 100 是理论上的最大可能结果，将计算评级表格的脚本存档）


AOSm优缺点：

优点：

  1. 在各项任务中表现出色。
  2. 少量外部参数。
  3. 良好的扩展性。
  4. 兼顾局部与全局极值的均衡搜索。

缺点：

  1. 实现过程相当复杂。
  2. 相较于其他算法，在平滑函数上只达到平均收敛精度水平。

文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。

文中所用的程序

# 名称 类型 说明
1 #C_AO.mqh
 库
 种群优化算法的基类
2 #C_AO_enum.mqh
 库
 种群优化算法的枚举说明
3 TestFunctions.mqh
 库
 测试函数库
4
 TestStandFunctions.mqh
 库
 测试台函数库
5
 Utilities.mqh
 库
 辅助函数库
6
 CalculationTestResults.mqh
 库
 用于计算比较表结果的脚本
7
 Testing AOs.mq5
 脚本 面向所有种群优化算法的统一测试平台
8
 Simple use of population optimization algorithms.mq5
 脚本
种群优化算法非可视化简易使用案例
9
 AO_AOSm_AtomicOrbitalSearch.mqh
 库 AOSm算法类
10
 Test_AO_AOSm.mq5
 脚本
 AOSm测试脚本

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/16315

附加的文件 |
下载ZIP
AOSm.zip (139.64 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

该作者的其他文章

最近评论 | 前往讨论 (5)
Evgeniy Chernish
Evgeniy Chernish | 15 11月 2024 在 11:51

感谢您的文章！

昨天和今天，我就 Hilly 函数和 alglib 方法坐了一会儿。以下是我的想法。

为了找到这个函数的最大值，尤其是当参数数为 10 或更多时，使用梯度方法是毫无意义的，这是组合优化方法的任务。梯度法会立即陷入局部极值。不管从参数空间的新点重新开始多少次，随着参数数量的增加，梯度法立即找到正确解的空间区域的机会趋于零。

例如，对于任意数量的参数，lbfgs 或 CG 2（2）次迭代找到最大值的空间点是 {x = -1,2 , y = 0.5}。


lbfgs

但正如我所说，进入这一区域的机会为零。随机数的产生需要一百年的时间。

因此，有必要以某种方式将文章中介绍的遗传算法与梯度方法结合起来（这样它们就能进行侦查并缩小搜索空间），以便从一个更有利的点快速找到极值。

Andrey Dik
Andrey Dik | 15 11月 2024 在 16:25
Evgeniy Chernish #:

感谢您的文章！

感谢您的反馈。

为了找到给定函数的最大值，尤其是当参数数为 10 或更多时，使用梯度法是毫无意义的。

是的，没错。

这就是组合优化方法的任务。

组合方法，如经典的 "蚂蚁"，是为 "旅行推销员问题 "和 "knapsack 问题 "等问题而设计的，即它们是为具有固定步长（图边）的离散问题而设计的。而对于多维 "连续 "问题，这些算法根本不是为训练神经网络等任务而设计的。是的，组合特性对随机启发式方法非常有用，但它们并不是成功解决这类近乎真实测试问题的唯一和充分特性。算法中的搜索策略本身也很重要。

基于梯度的搜索策略会立即陷入局部极值。不管从参数空间的一个新点重新开始多少次，随着参数数量的增加，梯度法立即找到正确解的空间区域的机会趋于零。

是的，确实如此。

但正如我已经说过的，到达这个区域的几率根本就是零。生成随机数需要一百年的时间。

是的，没错。在低维空间（1-2）中，进入全局附近是非常容易的，简单的随机发生器甚至可以做到这一点。但是，当问题的维度增加时，一切都会完全改变，此时，算法的搜索特性开始发挥重要作用，而不是 "幸运女神"。

因此，我们需要以某种方式将文章中介绍的遗传算法（它们会进行探索，缩小搜索空间）与梯度法结合起来，这样就能从一个更有利的点快速找到极值。

"遗传"--你可能是指 "启发式"。为什么 "鱼需要一把伞"，"为什么我们需要铁匠？ 我们不需要铁匠。"))))。有一些有效的方法可以解决连续空间中的复杂多维问题，这些方法在有关群体方法的文章中都有描述。而对于经典梯度问题，则有它们自己的任务--一维可分析确定问题（在这一点上，它们不分伯仲，会有快速而精确的收敛）。

还有一个问题，你对启发式方法的速度有何印象？

SZY:

哦，多少奇妙的发现

为启蒙精神做准备

经验，错误之子、

天才，悖论之友、

还有机遇，上帝的发明家。


ZZZY，稍等。在一个未知的探索空间里，我们永远不可能在任何时刻、任何步骤的迭代中，知道它实际上是一个真正有希望通向全球的方向。因此，不可能先侦查后完善。只有整体搜索策略才能发挥作用，它们要么效果好，要么效果差。每个人都会自己选择 "好 "的程度和 "适合任务 "的程度，为此，我们会保留一个评级表，以便根据任务的具体情况选择算法。

Evgeniy Chernish
Evgeniy Chernish | 15 11月 2024 在 16:53
Andrey Dik #:
是的，没错。在低维空间（1-2 维）中，进入全局邻域非常容易，简单的随机发生器甚至可以派上用场。但是，当问题的维度增加时，一切都完全不同了。在这里，算法的搜索特性，而不是幸运女神，开始发挥重要作用。

所以它们失败了

Andrey Dik#:
还有一个问题，你对启发式算法的速度有何印象？

尽管启发式运算速度很快。1000个参数的结果约为0.4。

这就是为什么我凭直觉认为，将遗传算法和梯度法结合起来以达到最大值是有意义的。否则，单独使用这两种方法将无法求解你的函数。我还没有实际测试过。


附注：我仍然认为这个函数太粗了，在实际任务中（比如神经网络的训练）不存在这样的问题，尽管误差面也都是局部最小值。

Andrey Dik
Andrey Dik | 15 11月 2024 在 18:47
Evgeniy Chernish #:

1. 他们做得不好

2. 尽管它们工作得很快。1000 个参数的结果约为 0.4。

3.这就是为什么我凭直觉认为将 GA 和梯度法结合起来求最大值是有意义的。否则，单独使用这两种方法无法求解你的函数。我还没有实际测试过。

4.附注：我仍然认为这个函数太粗了，在实际任务中（比如神经网络训练）不存在这样的问题，尽管在那里误差面也都是局部最小值。

1.你说 "它们应付不了 "是什么意思？对目标函数的访问次数是有限制的，谁的结果更好，谁就是 "应付不了"））。我们应该增加允许的访问次数吗？那么，无论如何，更敏捷、更能适应复杂函数的人都会到达终点。尝试增加引用次数，情况不会改变。

2.是的，有些人是 0.3，有些人是 0.2，有些人是 0.001。

3.这没有用，直观地说，已经有数百种组合和变化被尝试和重新尝试过了。在给定的迭代次数（epochs）下，能显示出更好结果的就是更好的。增加对目标的引用次数，看看哪种方法最先到达终点。

4.如果在困难任务中存在领先者，那么您认为在简单任务中领先者的结果会比局外人差吗？毫不夸张地说，事实并非如此。我正在进行一项更 "简单 "但更现实的网格培训任务。我会一如既往地与大家分享结果。这将会很有趣。


只要做实验，尝试不同的算法、不同的任务，不要拘泥于一件事。我已经尽力提供了这方面的所有工具。

Evgeniy Chernish
Evgeniy Chernish | 15 11月 2024 在 19:18
Andrey Dik #:

1.什么叫 "失败"？对目标函数的访问次数是有限制的，谁的结果最好，谁就是失败者））。我们应该增加允许的访问次数吗？那么，无论如何，更敏捷、更能适应复杂函数的人都会到达终点。试着增加引用次数吧，情况不会改变。

2.是的，有些人是 0.3，有些人是 0.2，有些人是 0.001。

3.这没有用，直观地说，已经有数百种组合和变化被尝试和重新尝试过了。在给定的迭代次数（epochs）下，能显示出更好结果的就是更好的。增加对目标的引用次数，看看哪种方法最先到达终点。

4.如果在困难任务中存在领先者，那么您认为在简单任务中领先者的结果会比局外人差吗？毫不夸张地说，事实并非如此。我正在进行一项更 "简单 "但更现实的网格培训任务。我会一如既往地与大家分享结果。这将会很有趣。


只要做实验，尝试不同的算法、不同的任务，不要专注于一件事。我已尝试提供所有相关工具。

我正在做实验、

ANS

关于现实任务，在接近实战的任务中测试算法是正确的。

看看遗传网络是如何训练的，会让人倍感兴趣。

Connexus观察者模式（第8部分）：添加一个观察者请求 Connexus观察者模式（第8部分）：添加一个观察者请求
在本系列文章的最后一篇中，我们探讨了观察者模式（Observer Pattern） 在Connexus库中的实现，同时对文件路径和方法名进行了必要的重构优化。该系列文章完整地记录了Connexus库的开发过程——这是一个专为简化复杂应用中的HTTP通信而设计的工具库。
Connexus客户端（第七部分）：添加客户端层 Connexus客户端（第七部分）：添加客户端层
在本文中，我们将继续开发connexus库。在本章节中，我们将构建CHttpClient类，该类负责发送请求并接收指令。我们还将介绍模拟对象（mocks）的概念，让该库与WebRequest函数解耦，从而为用户提供更强大的灵活性。
从基础到中级：数组和字符串（二） 从基础到中级：数组和字符串（二）
在本文中，我将展示，尽管我们仍处于编程的一个非常基本的阶段，但我们已经可以实现一些有趣的应用程序。在这种情况下，我们将创建一个相当简单的密码生成器。通过这种方式，我们将能够应用到目前为止已经解释过的一些概念。此外，我们将研究如何为一些具体问题制定解决方案。
开发回放系统（第 67 部分）：完善控制指标 开发回放系统（第 67 部分）：完善控制指标
在本文中，我们将看看通过一点代码改进可以实现什么。这一改进旨在简化我们的代码，更多地使用 MQL5 库调用，最重要的是，使其在我们未来可能开发的其他项目中更加稳定、安全和易于使用。