周期と取引
24
11
はじめに
トレーダーが直面する主な課題は、価格の動きを予測することです。トレーダーは、さまざまなモデルに基づいて予測を立てます。その中で最もシンプルで視覚的に分かりやすいモデルのひとつが、価格の周期モデルです。
あらゆる周期パターンの基本的な考え方は、さまざまな要因が相互に作用して価格の周期を生み出すというものです。これらの周期は、期間や強さがそれぞれ異なる場合があります。もし周期のパラメータが分かれば、取引は非常に簡単になります。周期が最小値に達したときに買いポジションを開き、最大値に達したときに売る、という具合です。
では、このモデルを実際にどのように活用できるか見てみましょう。
単純周期
周期を説明する際、通常は正弦や余弦といった三角関数を用います。しかし、周期は別の方法でも定義できます。https://ja.wikipedia.org/wiki/%E6%9C%89%E9%99%90%E5%B7%AE%E5%88%86title有限差分を使う方法です。
たとえば、2階差分が時系列の値に比例するという方程式を考えてみましょう。
これは調和振動子方程式です。一見すると特別なことはないように見えます。しかし、この方程式には興味深い性質があります。もし比率Rの値が0から4の範囲にある場合、この方程式は正弦波にしかなりえません。この比率はN周期周期に依存します。言い換えれば、方程式が特定の周波数の周期にのみ反応するように、この値を選ぶことができるということです。
では、この方程式を実際にどのように応用できるかを見てみましょう。これを価格データp[]に適用する場合、価格が振動する平均レベルmの値が必要になります。
しかし、この平均レベルを計算する代わりに、ちょっとしたトリックを使います。周期が最大値や最小値に達したときに、数学的には何が起きるかを思い出してみましょう。この瞬間、一次導関数の符号が変わります。
導関数の代わりに、元の方程式の1階差分を使います。これがトレーダーに課せられた厳しい宿命、「差分からさらに差分を求める」ことです。しかし、この方法により計算は大幅に簡単になります。設定すべきは比率Rの値だけです。最終的な方程式の形は次の通りです。
さらに、このような方程式を「取引アルゴリズム方程式」と呼ぶことにします。この方程式に基づいて取引戦略を作ることができます。まず少し補足すると、現在の価格の代わりに任意の移動平均を使用することも可能です。戦略の本質は非常にシンプルです。ポジションのオープンとクローズは、方程式の符号が変わるときにおこないます。
- 負から正に変わるとき：買いをオープン、売りをクローズ
- 正から負に変わるとき：売りをオープン、買いをクローズ
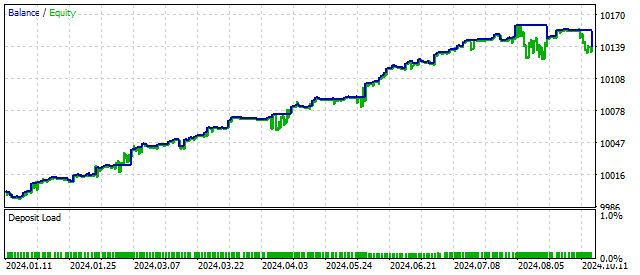
EAの残高推移はこのようになります。
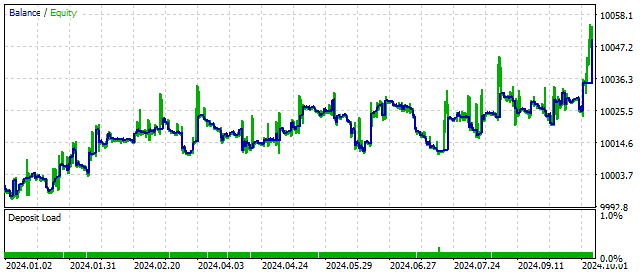
この取引戦略には将来性があります。しかし、いくつかの改善が必要です。
減衰付き周期
先に見た戦略には、ひとつ重大な欠点があります。それは周期がかなり長く続くと仮定している点です。しかし現実では、周期は多くの外的要因に依存しており、始まった直後に崩れることもあります。
この欠点を解消するために、減衰振動を持つ調和振動子モデルを使用できます。このような周期の方程式も有限差分によって設定されます。
パラメータSは、振動がどれくらい速く減衰するかを決定します。その値が大きいほど、減衰は速くなります。このパラメータの臨界値は次の式で求められます。
この値を超えると、振動子の動きは非振動的になります。
こうした方程式に対しても、やることは既にわかっています。1階差分を求め、それを取引シグナルとして利用すればよいのです。
新しいパラメータを追加することで、取引戦略はより柔軟かつ収益性の高いものになります。たとえば、Sの臨界値における残高推移はこのようになります。
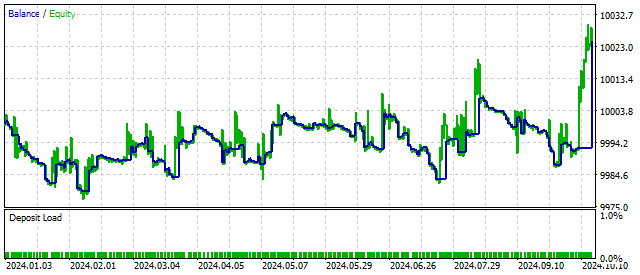
定義上、パラメータSは正の値であるべきです。しかし、この要件は必須ではありません。このパラメータに負の値を設定すると、元の方程式は振幅がどんどん増大する振動を表すことになります。この方法により、EAは周期の始まりに反応し、収益性を高める可能性があります。この場合の取引結果は次のようになります。
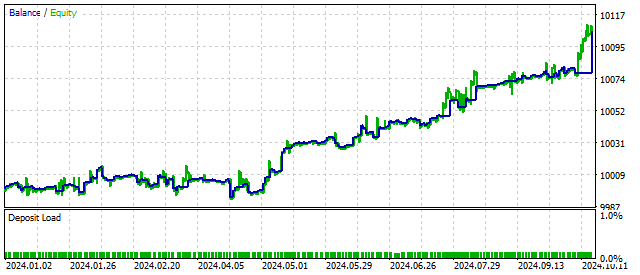
ご覧のとおり、周期モデルを複雑化することで、取引結果を改善できることがわかります。では、さらにモデルを複雑にしてみましょう。
エリオット波動
エリオット波動は長い間知られており、取引でも広く使われています。ここでは、周期モデルをエリオット波動に適用してみましょう。
最初の5つのエリオット波は、異なる振幅と周期を持つ2つの正弦波の和としてシミュレーションできます。
この場合、次の条件を満たす必要があります。
その結果、次のような形を得ることができます。
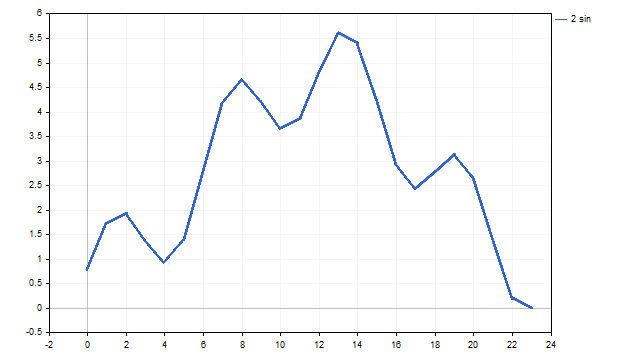
本に載っている形と完全に同じではありませんが、少し角張っている程度で、かなり似ています。
有限差分を用いて、2つの正弦波の和をシミュレーションすることも可能です。
ここで、
は、n次の有限差分の値で、インデックスiの価格データに対するものです。この方程式に対してやることはすでにわかっています。差分の和からさらに差分を求め、取引シグナルを得るのです。
2つの正弦波の和を使うことで、EAをより複雑な市場状況に適応させることができます。この取引アルゴリズムを使用することで、市場へのエントリ回数の増加と、取引の収益性向上の両方が期待できます。
これが、エリオット波動の原理に基づいたEAが示す結果です。
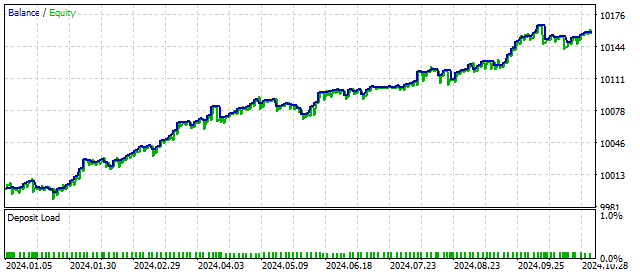
ご覧の通り、周期モデルを少し複雑にするだけでも、ポジティブな結果をもたらすことがわかります。
一般化調和振動子
これまでに、調和振動子に基づく3つのモデルを見てきました。それぞれのモデルは独自の初期仮定に基づいて構築されていました。しかし、最終的にはいずれも有限差分の和として表されました。
ここで、より一般的なモデルを構築することができます。このモデルの本質は非常にシンプルです。まず所定の次数の差分を取り、それを1次の差分まで下位の差分に加えていきます。このとき、低次の各差分にはそれぞれ固有の重み付け比率が与えられます。
たとえば、私は7次の差分を取りました。この場合、取引アルゴリズムの方程式は次のようになります。
このようなモデルは、周期やその挙動のさまざまな組み合わせを含めることができます。先に見たように、モデルを複雑にすることで取引結果が改善されます。この場合、残高推移は次のようになることがあります。
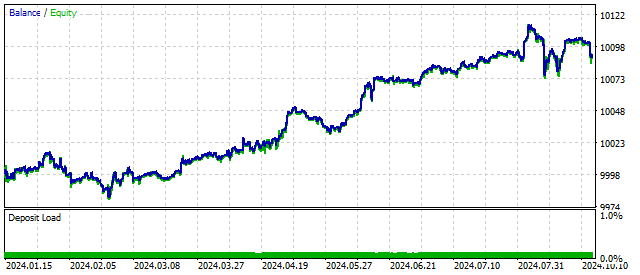
先導差分の次数を上げることで、モデルはより柔軟になります。一般化振動子は特定の価格の組み合わせにのみ反応します。言い換えれば、特定のパターンを探すわけです。同時に、振動子の次数が高くなるほど、そのパターンが現れる頻度は少なくなることを覚えておく必要があります。
このアルゴリズムのもう一つの特徴は、比率が非常に広い範囲で変動可能であることです。この範囲を評価すること自体が難しい場合もあります。一方で、比率の選択により、価格の非周期的パターンにも反応するようにアルゴリズムを設定することができます。
非線形振動子
線形モデルはシンプルで直感的です。しかし、市場の価格挙動は非線形である場合もあります。たとえば、急激な価格変動は非線形モデルを使った方が説明しやすいのです。非線形モデルの最大の利点は、複雑な時系列の挙動をより正確に記述できる点です。カオスやstochasticity（英語）という言葉を耳にしたとき、それはほとんどの場合、非線形モデルと関係しています。
最も単純なモデルのひとつが符号振動子です。その方程式は調和振動子のものにかなり似ています。ここでは非線形関数として符号関数が使われます。取引アルゴリズムの方程式は次のようになります。
ここで、signは符号関数です。
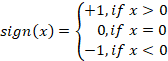
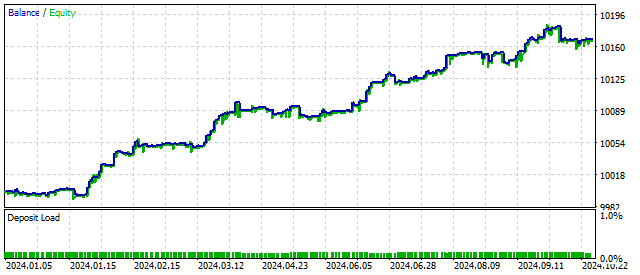
この特徴により、振動子は5つの異なるモードで動作できます。モードの切り替えは価格の動きに依存します。振動子の非線形性は、取引をより柔軟かつ安定的にしてくれる可能性を示しています。このアルゴリズムを使った場合の残高推移は次のようになるでしょう。
次に二次非線形振動子を考えてみます。その方程式は非常にシンプルです。
この方程式を実際に応用するためには、少し修正が必要です。
まず、価格が変動する基準となる平均レベルが必要です。思い出してください。実際の価格の代わりに、平滑化された値(SMA)を使うことができます。この場合、平均レベルは移動平均の平均値となります。
「平均の平均を計算する」と聞くと少し難しそうに思えるかもしれません。しかし1910年、アンドレイ・マルコフは『有限差分の計算』という研究を発表しました。その中で、数多くのSMAの平均を取ることは、全ての時系列データにLWMAを適用することと同じであることを示しました。再び有限差分が計算を簡単にしてくれます。
二次振動子の取引アルゴリズムの方程式は次のようになります。
二次非線形性により、振動子の動作モードをより滑らかに切り替えることができますが、その振幅は大きくなります。これによって取引結果が改善される可能性があります。
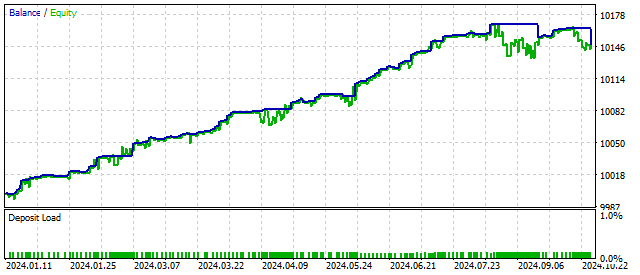
二次非線形性のもうひとつの例がファン・デル・ポール振動子です。これは決定論的カオスをシミュレーションした最初の例のひとつです。その特性から、この方程式は振動理論だけでなく物理学や生物学などの分野にも応用されました。
ファン・デル・ポール振動子は二次非線形振動子の改良版であり、その取引アルゴリズムの方程式は次のようになります。
一見すると、この振動子は不安定に見えるかもしれません。しかし実際には、そのパラメータはかなり広い範囲で変化しても取引結果に大きな影響を与えません。
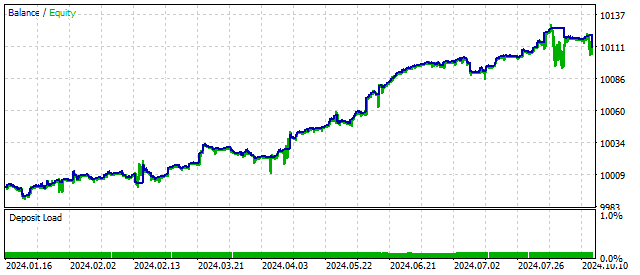
1918年、Georg Duffing（英語）は三次非線形振動子の方程式を研究しました。この振動子もカオス的な価格挙動をシミュレーションできます。しかし、このモデルにはもう一つ特徴があります。それは、外部条件やパラメータに応じて、2つの安定状態を持ちうるという点です。
ダフィング振動子の取引アルゴリズムの方程式は、3次元調和振動子と三次二項展開式の和として表されます。
この振動子の性能は、他の非線形モデルと同等です。
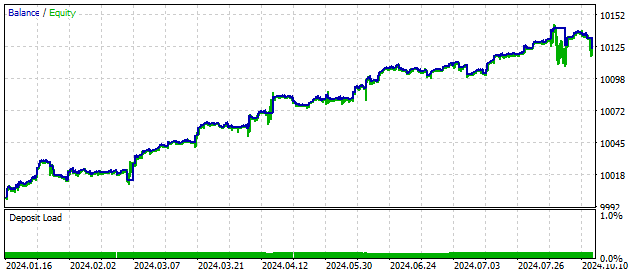
一般的に、多くの非線形モデルを作ることができます。どんな非線形関数でもカオスの生成器になり得ます。これまでに紹介した3つの振動子の非線形性は、いくつかの物理的な原理や考え方に基づいていました。経済物理学は有用な方向性ですが、常にそれに従う必要はまったくありません。
たとえば、私は対数関数に基づいて取引アルゴリズムに非線形性を加えてみます。
これらの対数はどこからきたのか、どんな根拠で加えたのかと聞かれるかもしれません。私の答えはとても単純で、「そうしたかったから」です。
しかし、もし答えを考える時間があるなら、少し違う答えになります。連続する価格の差は何でしょうか。たとえば100ポイント。では、その価格の対数の差はどうでしょうか。ゼロ以外に何か現れるでしょうか。ここでの新しい答えはこうです。左側には通常の振動子があり、右側にはポジションのオープンに影響を与えることができるフィルターがあります。そのフィルターは価格が大きく動いたときにだけ現れます。私たちはその働きを確認します。
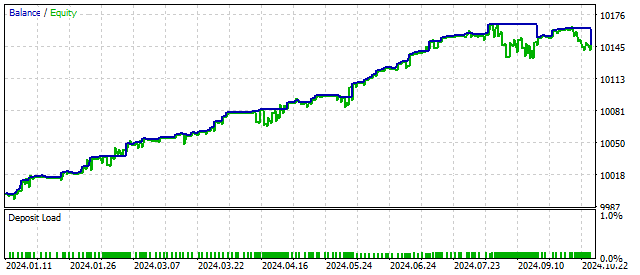
結果は二次非線形振動子の動作に似ています。フィルターは機能しています。しかし重要なのは、すべてのアイデアは実際に適用する前に必ずテスターで検証すべきだということです。
外力
これまで私たちは自律型の振動子を見てきました。振り子を想像してください。それは左右に均等に揺れます。その周期は何度も繰り返されます。なぜこの振り子が揺れるのか、なぜこのように揺れるのかは説明できません。これは自由振動子の一例です。
では、その振り子を押してみましょう。まず一方に、次にもう一方に。すると振り子の周期は変化し、瞬間的な周波数や振幅も変わりました。外力の影響によって、その振り子は自律的ではなくなったのです。
同じアプローチを調和振動子に適用してみましょう。その方程式は次のように変わります。
ここでF[n]は外力です。それがどのような力なのか、どのように作用するのか、どこに向かっているのか、私は何も知りません。ただ、それが存在すると仮定するだけです。ここで、果たしてこのようなモデルの複雑化は正当化されるのかという疑問が生じます。それに答えてみましょう。
私はこの外力が次のように価格値と関連していると仮定することで結果を得ました。
私がこの仮定をした唯一の理由は、記事全体で有限差分について述べていたからです。そしてこの場合も二次差分の比率を用いたのです。もちろん、あなたは自由に独自の仮定を立てることができます。たとえば、外力は終値と始値の差、ティックボリュームなどに関連しているかもしれません。また、非線形要素を加えることもできます。
結局のところ、この未知の力は複数の要素に依存している可能性があります。できる限り要素をまとめてみてください。あなたが立てるどのような仮定も、取引の成果にプラスの影響を与える可能性があります。
結論
ご覧のとおり、取引において周期的パターンを利用することは十分に正当化されます。このようなモデルの主な利点は、長期間にわたって安定した結果をもたらす数百通りのパラメータ組み合わせを持つことです。トレーダーは相関のない数十のオプションを選択する必要があります。
この記事では、最も一般的な振動子のいくつかにしか触れていません。他にも周期モデルを構築するために利用できる解法は数多く存在します。
私は、EUR/USD、上半期、2024年1月1日～2024年10月30日でEAをテストしました。
この記事の執筆には以下のプログラムが使用されました。
| 名前 | 種類 | 詳細 |
|---|---|---|
| Harmonic Oscillator | EA |
|
| Damped Harmonic Oscillator | EA |
|
| scr Elliott wave | スクリプト |
|
| Elliott wave | EA |
|
| Generalized Harmonic Oscillator | EA | 比率の許容値：-1000 ... +1000 |
| Sign Oscillator | EA | |
| Quadratic Oscillator | EA | |
| Van der Pol Oscillator | EA | |
| Duffing Oscillator | EA | |
| Log Oscillator | EA | |
| Non-Autonomous Oscillator | EA |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16494
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
リプレイシステムの開発（第76回）：新しいChart Trade(III)
取引におけるニューラルネットワーク：Segment Attentionを備えたパラメータ効率重視Transformer（最終回）
初級から中級まで：定義(I)
マーケットプロファイルインジケーター
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
これは素晴らしい記事だが、ビスケットジャーでもある。市場の状況を評価し、現在の状況に最適な最適化を選択しようとする適応的なメカニズムを構築することを検討したことがあるか？
適応する一つの方法は、複数のサイクルを一度に評価することだ。しかも、これは案外簡単だ。例えば、このようにできる。最初のサイクル - カウントを連続して取る。2サイクル目 - 価格サンプルを次々に取る。といった具合だ。これらのサイクルを組み合わせることで、現時点での市場の状態を独自の画像で把握することができる。
🚫 レッドフラッグ：
使えないデフォルト・パラメーター：
iPeriod = 870 , R = -940 , S = 450 → 短期取引のための不合理な値
取引がトリガーされない：
EAは新しいバーごとに1回だけ シグナルを評価し、シグナルロジックのしきい値はデフォルトパラメータではほとんどヒットしない。
CalcLWMA()は オリジナルで 静的アキュムレーターを使用して います。
バックテストも コードでの検証もない- そしてインジケータは、リアルタイムの目視検査のために記事で提供されていない。
共有可能な証拠やMQ5 Signalsのリンクなしに、株式成長を誇って いる。
証拠やMQ5シグナルへの参照を提供することなく、株式の成長を自慢して います。
1.値の不合理さについて - あなたはよく知っている。
2.EAは、新しいバーが開かれたときにポジションを開きます。他のロジックが必要な場合は、すべて自分で実装できます。
3. CalcWMAがすべてのSMAの平均を計算するために使用されていることは、記事から明らかでしょう。