Atomic Orbital Search (AOS) algorithm: Modification
1 134
5
Contents
Introduction
In the first part of the article we examined the basics of the AOS (Atomic Orbital Search) algorithm inspired by the atomic orbital model and its underlying mechanisms. We discussed how the algorithm uses probability distributions and interaction dynamics to find optimal solutions to complex optimization problems.
In the second part of the article, we will focus on modifying the AOS algorithm, since we cannot pass by such an outstanding idea without trying to improve it. We will analyze the concept of improving the algorithm, paying special attention to the specific operators that are inherent to this method and can improve its efficiency and adaptability.
Working on the AOS algorithm has opened up many interesting aspects for me regarding its methods of searching the solution space. During the research, I also came up with a number of ideas on how this interesting algorithm could be improved. In particular, I focused on reworking existing methods that can improve the performance of the algorithm by improving its ability to explore complex solution spaces. We will consider how these improvements can be integrated into the existing structure of the AOS algorithm to make it an even more powerful tool for solving optimization problems. Thus, our goal is not only to analyze existing mechanisms, but also to propose other approaches that can significantly expand the capabilities of the AOS algorithm.
Implementation of the algorithm
In the previous article, we took a detailed look at the key components of the AOS algorithm. As you might remember, in this algorithm, the population is considered as a molecule, and the admissible region of coordinates, in which the search for optimal solutions is carried out, is represented as an atom. Each atom is made up of different layers that help arrange and direct the search.
The specific coordinate values that we obtain during the optimization can be interpreted as electrons. These electrons, being within the atom, represent possible solutions to one of the parameters of the problem we are optimizing. Thus, each molecule (population) strives to find optimal values (electrons) within a given region (atom).
In the original version of the AOS algorithm, the BEk layer energy is defined as the arithmetic mean of the energy of electrons in the layer, and the bond BSk is defined as the arithmetic mean of their coordinates. The BEk energy is used to compare with the energy of the electrons to determine the mode of their subsequent movement. The BSk connection is used to calculate the increment to the position of electrons as the difference between the best position of electrons LEk in the layer and the BSk connection according to the following equation: Xki[t+1] = Xkit + αi × (βi × LEk − γi × BSk).
I propose to abandon the BSk average position of electrons in favor of the personal best position of the electron. Thus, the electron will move towards the best solution in its layer based on its individual achievement, not on the average solution across the layer. Moreover, the two βi and γi random components seem redundant since there is already an external αi random component. This will reduce the time for generating random numbers in this equation by three times, without losing physical meaning.
Now let's look at the structure that describes a layer in an atom. Elements removed from the code are highlighted in red://—————————————————————————————————————————————————————————————————————————————— struct S_Layer { int pc; // particle counter double BSk; // connection state double BEk; // binding energy double LEk; // minimum energy void Init () { pc = 0; BSk = 0.0; BEk = 0.0; LEk = 0.0; } }; //——————————————————————————————————————————————————————————————————————————————
Let's consider the CalcLayerParams method code, which calculates layer characteristics such as energy and connectivity. Strings highlighted in red will be removed as they are no longer needed. As you might remember, this method plays a key role in the AOS search strategy, which aims to prevent the algorithm from getting stuck in local traps. Since the energy level in the layers does not depend on their location (the energy decreases from the center to the outer layers of the atom), but is determined by the presence of significant local extremes (the outer layer can have energy exceeding the inner ones), the layers serve to correct the movement of electrons in the search space.
The random number of layers at each epoch helps to combat the algorithm getting stuck in local traps, preventing electrons from stagnating in only one of the layers. The modified version also eliminates the need to calculate the average energy over the entire atom, so we will remove the corresponding lines.
Figure 1. The difference in direction and size of the e electron displacement depending on the number of layers in the atom
Figure 1 illustrates the differences in the behavior of electrons in atoms with different numbers of layers in the AOS algorithm. The top panel shows a three-layer atom where the electron is located in the layer L1 with the B1 objective function value and moves towards the LEk1 local best value. The lower part of the figure illustrates an atom with two layers, where the electron is also in layer L1 and moves towards the local best value LEk1 with the B1 objective function value (in the case of three layers this would be the point LEk2).
Key elements in the figure:
- B0, B1, B2 — designations of local values of the objective function for the corresponding layers,
- LEk0, LEk1, LEk2 — best solutions in the corresponding layers,
- L0, L1, L2 — atom layers,
- e — electron,
- MIN, MAX — boundaries of the outer layers of atoms (boundary conditions for the optimized parameters of the problem).
//—————————————————————————————————————————————————————————————————————————————— // Calculate parameters for each layer void C_AO_AOS::CalcLayerParams () { double energy; // Handle each coordinate (atom) for (int c = 0; c < coords; c++) { atoms [c].Init (maxLayers); // Handle each layer for (int L = 0; L < currentLayers [c]; L++) { energy = -DBL_MAX; // Handle each electron for (int e = 0; e < popSize; e++) { if (electrons [e].layerID [c] == L) { atoms [c].layers [L].pc++; atoms [c].layers [L].BEk += a [e].f; atoms [c].layers [L].BSk += a [e].c [c]; if (a [e].f > energy) { energy = a [e].f; atoms [c].layers [L].LEk = a [e].c [c]; } } } // Calculate average values for the layer if (atoms [c].layers [L].pc != 0) { atoms [c].layers [L].BEk /= atoms [c].layers [L].pc; atoms [c].layers [L].BSk /= atoms [c].layers [L].pc; } } } // Calculate the general state of connections ArrayInitialize (BS, 0); for (int c = 0; c < coords; c++) { for (int e = 0; e < popSize; e++) { BS [c] += a [e].c [c]; } BS [c] /= popSize; } } //——————————————————————————————————————————————————————————————————————————————
To update the best individual solutions, add the code to the Revision method of the modified C_AO_AOSm version.
//—————————————————————————————————————————————————————————————————————————————— // Method of revising the best solutions void C_AO_AOSm::Revision () { int bestIndex = -1; // Find the best solution in the current iteration for (int i = 0; i < popSize; i++) { // Update the global best solution if (a [i].f > fB) { fB = a [i].f; bestIndex = i; } // Update the personal best solution if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } // Update the best coordinates if a better solution is found if (bestIndex != -1) ArrayCopy (cB, a [bestIndex].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
In the UpdateElectrons method, remove the β and γ variables since they are not needed to generate the corresponding random numbers. In addition, exclude deletion of the electron increment by the number of layers in the case of movement towards the global solution. Frankly speaking, the authors' solution seems controversial, and the physical meaning of this approach is not entirely clear. Perhaps the authors wanted to make the degree of electron movement towards the global solution variable, changing it depending on the number of layers: the fewer layers, the more intense the movement should be (although my experiments showed that this is not the case).
//—————————————————————————————————————————————————————————————————————————————— // Update electron positions void C_AO_AOS::UpdateElectrons () { double α; // speed coefficient double β; // best solution weight coefficient double γ; // average state weight coefficient double φ; // transition probability double newPos; // new position double LE; // best energy double BSk; // connection state int lID; // layer ID // Handle each particle for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Random scatter newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); β = u.RNDprobab (); γ = u.RNDprobab (); // If the current particle energy is less than the average layer energy if (a [p].f < atoms [c].layers [lID].BEk) { // Moving towards the global optimum---------------------------- LE = cB [c]; newPos = a [p].c [c]+ α * (β * LE - γ * BS [c]) / currentLayers [c]; } else { // Movement towards the local optimum of the layer------------------------ LE = atoms [c].layers [lID].LEk; BSk = atoms [c].layers [lID].BSk; newPos = a [p].c [c] + α * (β * LE - γ * BSk); } } // Limiting the new position within the search range taking into account the step a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Additionally, in the UpdateElectrons method of the C_AO_AOSm class, instead of randomly scattering the electron across the search space, we implement the movement of the electron to the core center with some probability. In essence, this means replacing the value of some coordinate with the value of the global solution, which should improve the combinatorial properties of the algorithm. Random scattering was intended to provide diversity in the population of solutions, but this property ensured the distribution of electrons according to a lognormal distribution, where there was a non-zero probability of an electron hitting any point in space while moving.
Changes in the electron movement equations are displayed in green. Now the increment is calculated as the difference between the local best solution of the layer and the individual best solution of the electron.
//—————————————————————————————————————————————————————————————————————————————— // Update electron positions void C_AO_AOSm::UpdateElectrons () { double α; // speed coefficient double φ; // transition probability double newPos; // new position double LE; // best energy double BSk; // connection state int lID; // layer ID // Handle each particle for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Random jump to center newPos = cB [c]; } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); // If the current particle energy is less than the average layer energy if (a [p].f < atoms [c].layers [lID].BEk) { // Moving towards the global optimum---------------------------- LE = cB [c]; newPos = a [p].cB [c]+ α * (LE - a [p].cB [c]); } else { // Movement towards the local optimum of the layer------------------------ LE = atoms [c].layers [lID].LEk; newPos = a [p].cB [c]+ α * (LE - a [p].cB [c]); } } // Limiting the new position within the search range taking into account the step a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
The DistributeParticles method distributes electrons in the search space using lognormal distribution for each coordinate. For each particle and each coordinate, a function is called that generates a position given the given parameters (average, minimum and maximum values, peak), and then an additional function is applied to adjust the position within the given range.
//—————————————————————————————————————————————————————————————————————————————— // Distribution of particles in the search space void C_AO_AOS::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Use log-normal distribution to position particles a [i].c [c] = u.LognormalDistribution (cB [c], rangeMin [c], rangeMax [c], peakPosition); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Change the electron distribution to normal. This distribution uses a standard deviation of 8. Although this parameter could have been made external to the algorithm, I chose not to do so. Smaller values encourage a wider exploration of the search space, while higher values improve the accuracy of convergence when refining the global solution.
//—————————————————————————————————————————————————————————————————————————————— // Distribution of particles in the search space void C_AO_AOSm::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Use a Gaussian distribution to position particles a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
All changes made to the original version of the AOS algorithm were analyzed in order to improve its efficiency. Since significant changes were made to the logic of the search strategy, the modified version of the algorithm can be designated by the letter "m". From now on, only the modified version will be presented in the rating table - AOSm.
An example of using the C_AO class
Since all population optimization algorithms discussed earlier are inherited from the general C_AO class, this allows them to be used uniformly and with minimal effort to solve various problems that require the selection of optimal parameters. The example below shows a script that performs optimization of the objective function:
1. At the beginning of the script, you can choose which optimization algorithm to use. If nothing is selected, the script will report an error and stop.
2. Setting up parameters. The script defines how many times the function will be run, how many parameters need to be optimized, the size of the solution group, and how many iterations will be performed.
3. Value limits. Minimum and maximum values are set for each parameter (in this example, from -10 to 10).
4. The script starts optimization:
- It generates solutions (sets of parameters) and checks how good they are using a special function (the objective function).
- At each iteration, the algorithm updates its solutions based on which ones performed best.
5. Results. After the optimization is complete, the script outputs information about which algorithm was used, what the best value was found, and how many times the function was launched.
6. The objective function is an abstract optimization problem (in this example, solving the problem of finding the global maximum of an inverted parabola is used) that takes parameters and returns a score for their quality.
#property script_show_inputs // Specify that the script will show the inputs in the properties window #include <Math\AOs\PopulationAO\#C_AO_enum.mqh> // Connect the library for handling optimization algorithms input E_AO AOexactly = NONE_AO; // Parameter for selecting the optimization algorithm, default is NONE_AO //—————————————————————————————————————————————————————————————————————————————— void OnStart() { //---------------------------------------------------------------------------- int numbTestFuncRuns = 10000; // Total number of function runs int params = 1000; // Number of parameters for optimization int popSize = 50; // Population size for optimization algorithm int epochCount = numbTestFuncRuns / popSize; // Total number of epochs (iterations) for optimization double rangeMin [], rangeMax [], rangeStep []; // Arrays for storing the parameters' boundaries and steps ArrayResize (rangeMin, params); // Resize 'min' borders array ArrayResize (rangeMax, params); // Resize 'max' borders array ArrayResize (rangeStep, params); // Resize the steps array // Initialize the borders and steps for each parameter for (int i = 0; i < params; i++) { rangeMin [i] = -10; // Minimum value of the parameter rangeMax [i] = 10; // Maximum value of the parameter rangeStep [i] = DBL_EPSILON; // Parameter step } //---------------------------------------------------------------------------- C_AO *ao = SelectAO (AOexactly); // Select an optimization algorithm if (ao == NULL) // Check if an algorithm has been selected { Print ("AO not selected..."); // Error message if no algorithm is selected return; } ao.params [0].val = popSize; // Assigning population size.... ao.SetParams (); //... (optional, then default population size will be used) ao.Init (rangeMin, rangeMax, rangeStep, epochCount); // Initialize the algorithm with given boundaries and number of epochs // Main loop by number of epochs for (int epochCNT = 1; epochCNT <= epochCount; epochCNT++) { ao.Moving (); // Execute one epoch of the optimization algorithm // Calculate the value of the objective function for each solution in the population for (int set = 0; set < ArraySize (ao.a); set++) { ao.a [set].f = ObjectiveFunction (ao.a [set].c); // Apply the objective function to each solution } ao.Revision (); // Update the population based on the results of the objective function } //---------------------------------------------------------------------------- // Output the algorithm name, best result and number of function runs Print (ao.GetName (), ", best result: ", ao.fB, ", number of function launches: ", numbTestFuncRuns); delete ao; // Release the memory occupied by the algorithm object } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Definition of the user's objective function, in this case as an example - a paraboloid, F(Xn) ∈ [0.0; 1.0], X ∈ [-10.0; 10.0], maximization double ObjectiveFunction (double &x []) { double sum = 0.0; // Variable for accumulation of the result // Loop through all parameters for (int i = 0; i < ArraySize (x); i++) { // Check if the parameter is in the allowed range if (x [i] < -10.0 || x [i] > 10.0) return 0.0; // If the parameter is out of range, return 0 sum += (-x [i] * x [i] + 100.0) * 0.01; // Calculate the value of the objective function } return sum /= ArraySize (x); } //——————————————————————————————————————————————————————————————————————————————
Test results
Let's move on to testing the modified version of the algorithm.
AOS|Atomic Orbital Search|50.0|10.0|20.0|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.8023218355650774
25 Hilly's; Func runs: 10000; result: 0.7044908398821188
500 Hilly's; Func runs: 10000; result: 0.3102116882841442
=============================
5 Forest's; Func runs: 10000; result: 0.8565993699987462
25 Forest's; Func runs: 10000; result: 0.6945107796904211
500 Forest's; Func runs: 10000; result: 0.21996085558228406
=============================
5 Megacity's; Func runs: 10000; result: 0.7461538461538461
25 Megacity's; Func runs: 10000; result: 0.5286153846153846
500 Megacity's; Func runs: 10000; result: 0.1435846153846167
=============================
All score: 5.00645 (55.63%)
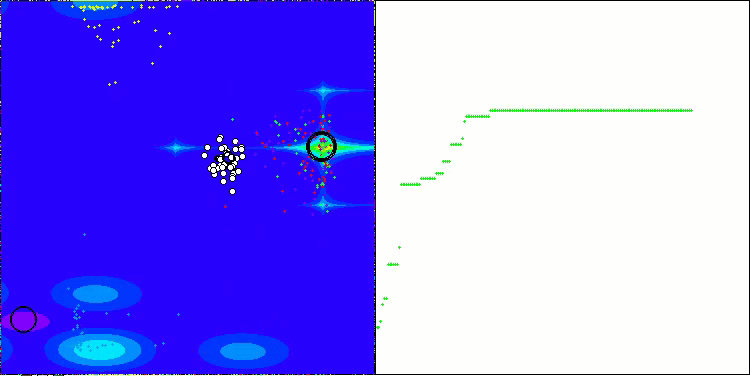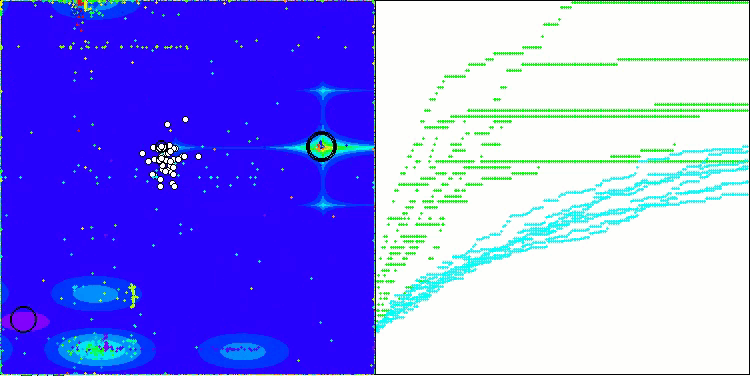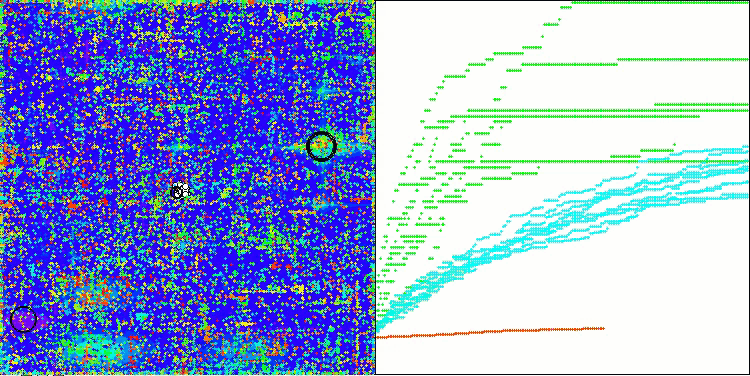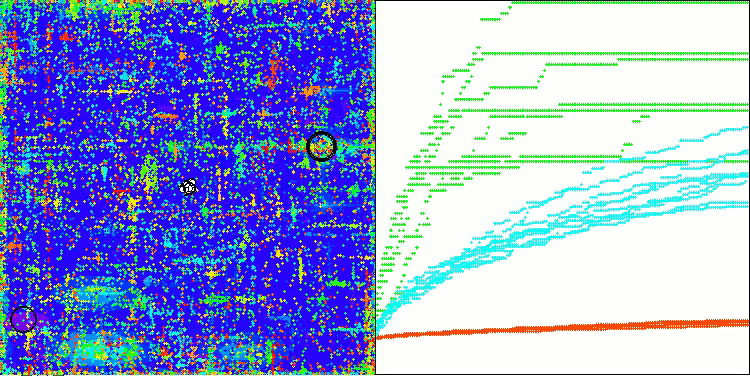
As you can see, the results of the modified version have improved significantly compared to the previous results of the original version, where the overall score was 3.00488 (33.39%). This improvement becomes apparent when analyzing the visualization, which shows not only improved convergence, but also more detailed elaboration of significant extremes.
One of the key aspects worth noting is the effect of "clumping" of solutions on individual coordinates. This phenomenon is observed in both the original and modified versions, which highlights the characteristic feature of AOS algorithms. Clumping of solutions may indicate that the algorithm is effective in finding areas where potential optimal solutions are located.
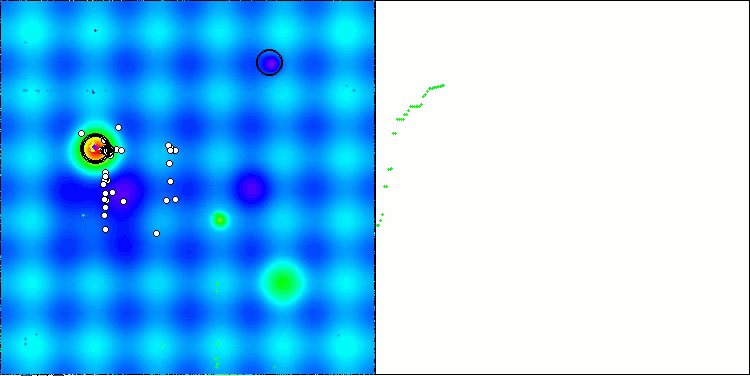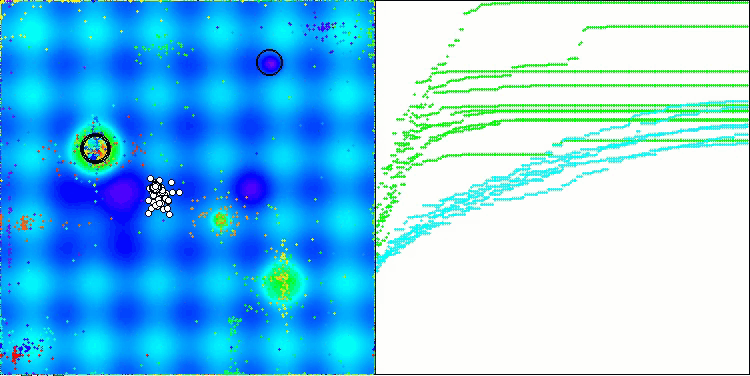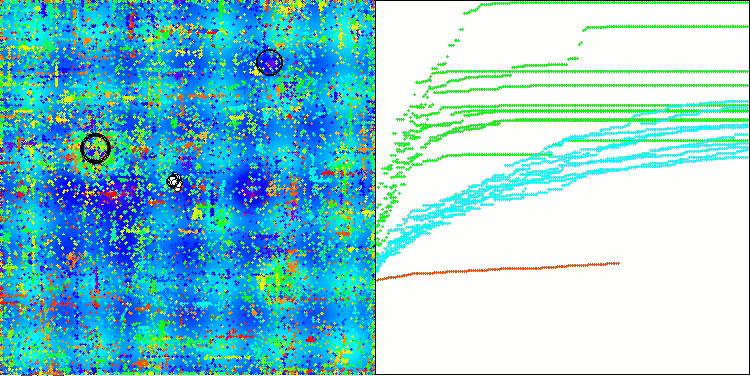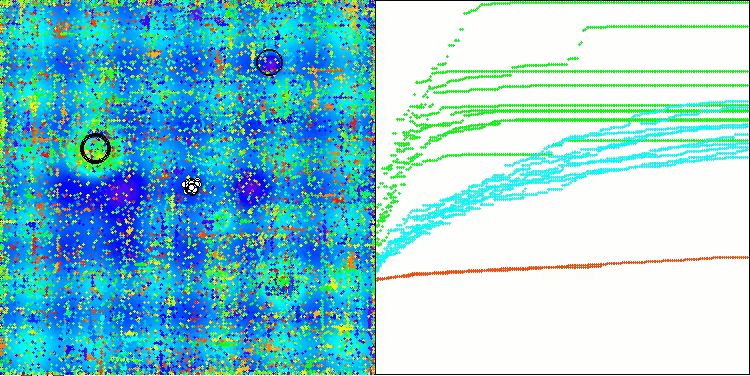
AOSm on the Hilly test function
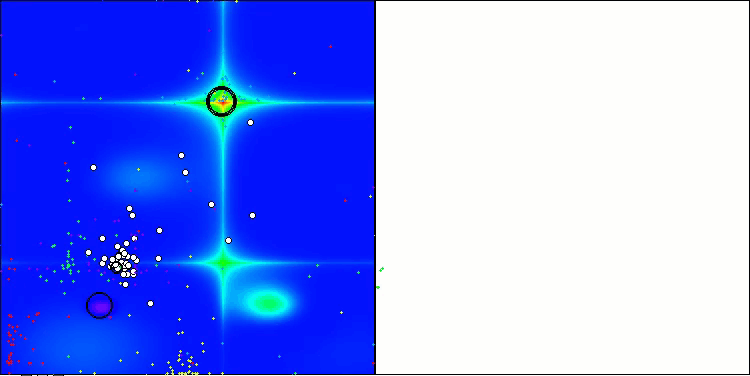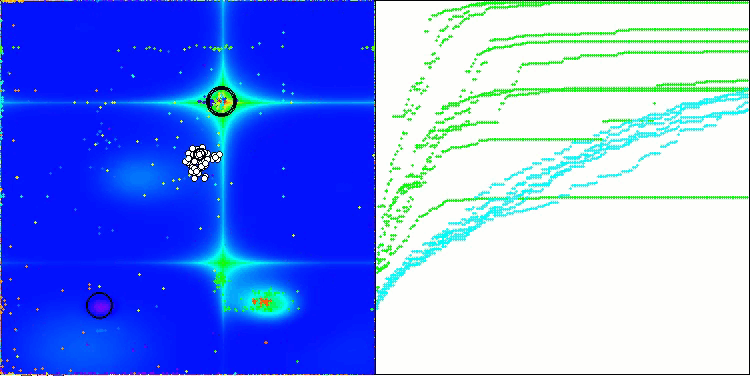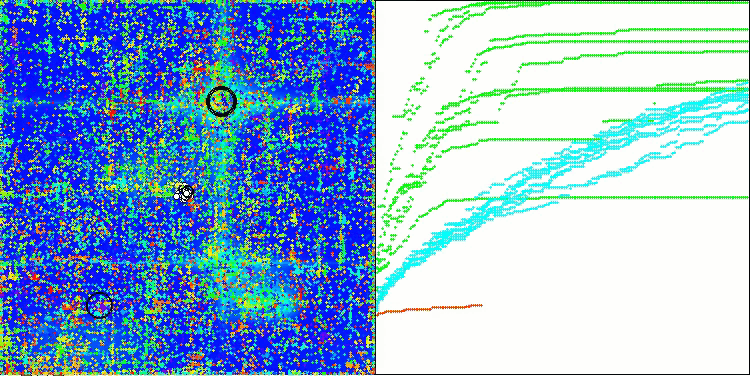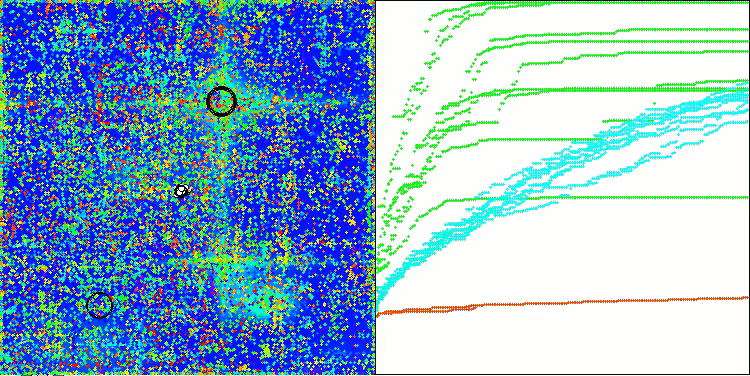
AOSm on the Forest test function
AOSm on the Megacity test function
The modified version of the Atomic Orbital Search (AOS) algorithm has significantly improved its performance compared to the original version and now reaches more than 55% of the maximum possible value. This is a truly impressive result! In the rating table, the algorithm occupies 12 th place, which indicates very decent results.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration ptimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 12 | AOSm | atomic orbital search M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 13 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 14 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 15 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 16 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 17 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 18 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 19 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 20 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 21 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 22 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 23 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 24 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 25 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 26 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 27 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 28 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 29 | ABHA | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 30 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 31 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 32 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 33 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 34 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 35 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 36 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 37 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 38 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 39 | FAm | firefly algorithm M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 40 | GSA | gravitational search algorithm | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 41 | BFO | bacterial foraging optimization | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 42 | ABC | artificial bee colony | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 43 | BA | bat algorithm | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 44 | AAA | algae adaptive algorithm | 0.50007 | 0.32040 | 0.25525 | 1.07572 | 0.37021 | 0.22284 | 0.16785 | 0.76089 | 0.27846 | 0.14800 | 0.09755 | 0.52402 | 2.361 | 26.23 |
| 45 | SA | simulated annealing | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
Summary
In this article, a modified version of the atomic orbital search (AOSm) algorithm was presented, in which I abandoned the BSk average position of electrons in the atom layers in favor of the individual best position of each electron. This allowed electrons to move more efficiently towards the best solution in their layer, based on individual achievement rather than an average value. In addition, two random components βi and γi were excluded, which reduced the time for generating random numbers by three times, without losing the physical meaning of the algorithm.
In the UpdateElectrons method, unnecessary variables have been removed and divisions of the electron increment by the number of layers when moving to the global solution have been eliminated. While the authors of the original versions may have intended for the degree of movement to be variable, my experiments have shown that this does not provide significant benefits.
Changes were also made to the UpdateElectrons method in the C_AO_AOSm class - the random scattering of an electron was replaced with a movement to the center of the core with a certain probability. This increased the combinatorial properties of the algorithm, allowing electrons to more accurately target the global solution. The lognormal distribution was also replaced by a normal one, which increased the accuracy of convergence when refining the global solution.
The results of the modified version of AOSm showed significant improvement, with an overall score exceeding 55% of the maximum possible, which confirms the high efficiency and competitiveness of the algorithm. AOSm ranks 12 th in the ranking table, which shows its significant achievements among other optimization methods.
One of the most noticeable aspects of AOSm is the improvement in convergence, which became evident when visualizing the results. The algorithm works out significant extremes in more detail and demonstrates the ability to effectively search for optimal solutions in complex multidimensional spaces. The "clumping" effect of solutions observed in both the original and modified versions highlights the ability of the algorithm to find and focus on areas with potential optima, which is especially useful in problems with high dimensionality and complex structure.
An additional plus to the advantages of the modified version is the reduction in the number of external parameters, which simplifies its use and configuration. However, for all the algorithms presented earlier in the articles, I have selected the optimal external parameters to achieve maximum efficiency in complex testing on various types of test tasks, so all the algorithms are ready for use and do not require any configuration. The article demonstrates that sometimes the smallest changes in optimization algorithms can dramatically change their search properties, while significant changes in the logic of the search strategy may not bring any noticeable changes in the results. Of course, in my articles, I share the methods that really improve the efficiency of optimization.
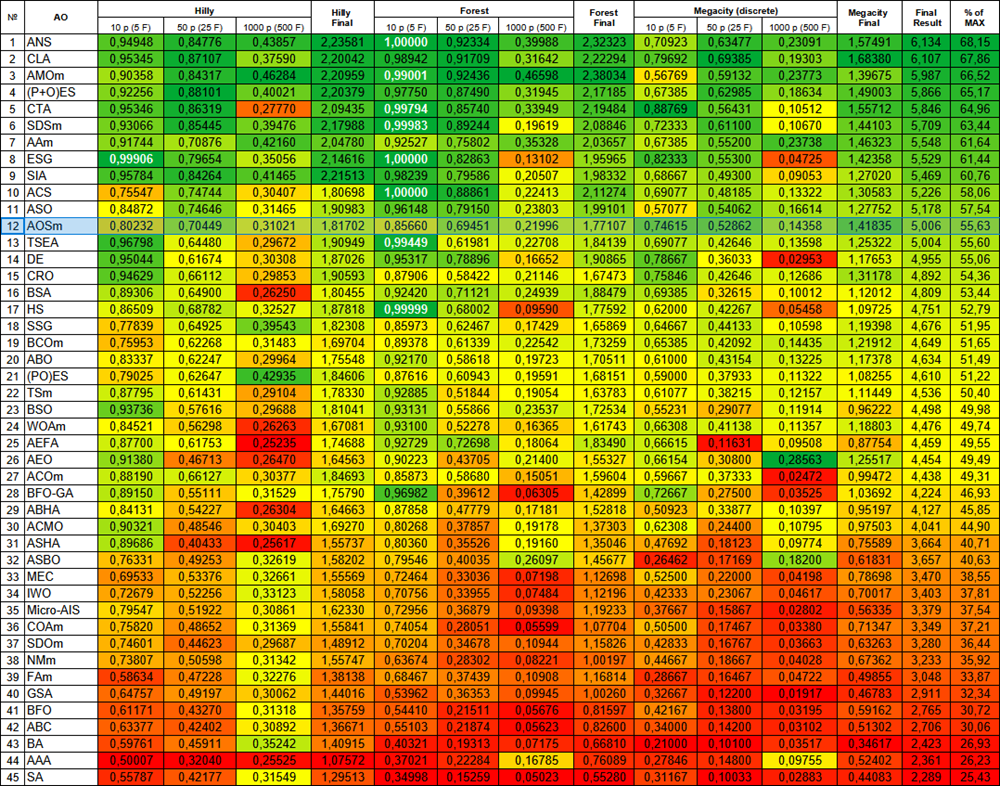
Figure 2. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white
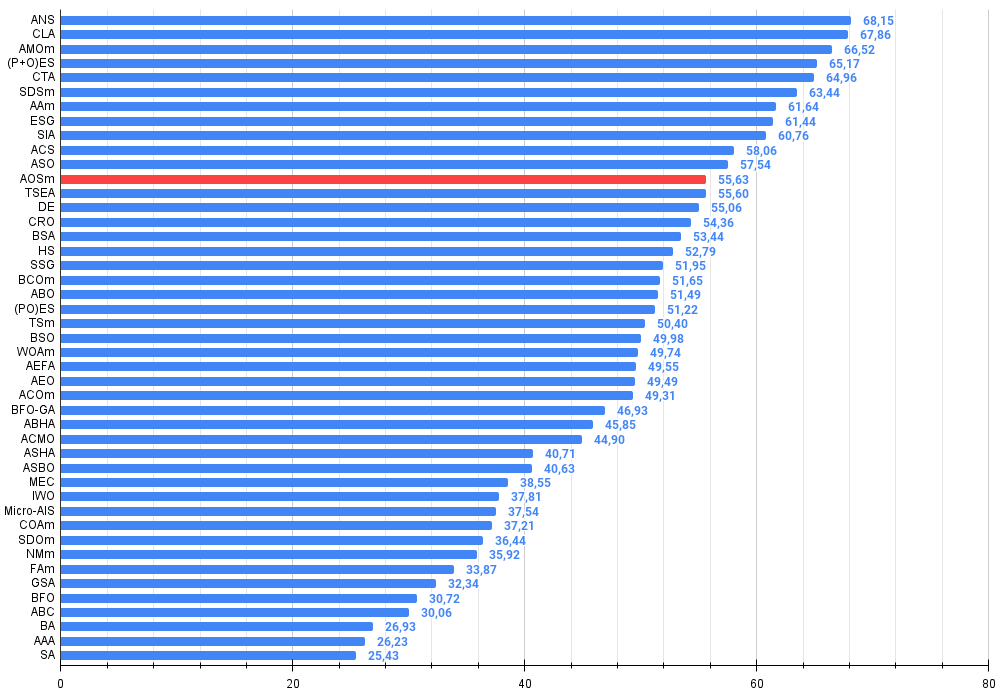
Figure 3. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,
where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)
AOSm pros and cons:
Pros:
- Good performance on various tasks.
- Small number of external parameters.
- Good scalability.
- Balanced search by both local and global extremes.
Cons:
- Quite a complex implementation.
- Average accuracy of convergence on smooth functions compared to other algorithms.
The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.
Programs used in the article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Parent class of population optimization algorithms |
| 2 | #C_AO_enum.mqh | Include | Enumeration of population optimization algorithms |
| 3 | TestFunctions.mqh | Include | Library of test functions |
| 4 | TestStandFunctions.mqh | Include | Test stand function library |
| 5 | Utilities.mqh | Include | Library of auxiliary functions |
| 6 | CalculationTestResults.mqh | Include | Script for calculating results in the comparison table |
| 7 | Testing AOs.mq5 | Script | The unified test stand for all population optimization algorithms |
| 8 | Simple use of population optimization algorithms.mq5 | Script | A simple example of using population optimization algorithms without visualization |
| 9 | AO_AOSm_AtomicOrbitalSearch.mqh | Include | AOSm algorithm class |
| 10 | Test_AO_AOSm.mq5 | Script | AOSm test stand |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/16315
Automating Trading Strategies in MQL5 (Part 21): Enhancing Neural Network Trading with Adaptive Learning Rates
Data Science and ML (Part 45): Forex Time series forecasting using PROPHET by Facebook Model
MQL5 Wizard Techniques you should know (Part 72): Using Patterns of MACD and the OBV with Supervised Learning
From Novice to Expert: Animated News Headline Using MQL5 (III) — Indicator Insights
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Thanks for the article!
I sat for a while yesterday and today on the Hilly function and alglib methods. Here are my thoughts.
In order to find the maximum of this function, especially when the number of parameters is 10 and more, it is pointless to apply gradient methods, this is the task of combinatorial methods of optimisation. Gradient methods just instantly get stuck in the local extremum. And it does not matter how many times to restart from a new point of the parameter space, the chance to get to the right region of space from which the gradient method instantly finds a solution tends to zero as the number of parameters increases.
For example, the point of space from which lbfgs or CG for 2(two) iterations find the maximum for any number of parameters is {x = -1,2 , y = 0.5}.
But the chance to get into this region as I have already said is simply zero. It must be a hundred years to generate random numbers.
Therefore, it is necessary to somehow combine the genetic algorithms presented in the article (so that they could do reconnaissance and reduce the search space) with gradient methods that would quickly find the extremum from a more favourable point.
Thank you for the article!
Thank you for your feedback.
In order to find the maximum of a given function, especially when the number of parameters is 10 or more, it is pointless to use gradient methods.
Yes, that's right.
This is the task of combinatorial methods of optimisation.
Combinatorial methods, such as the classical "ant", are designed for problems like the "travelling salesman problem" and the "knapsack problem", i.e. they are designed for discrete problems with a fixed step (graph edge). For multidimensional "continuous" problems, these algorithms are not designed at all, for example, for tasks such as training neural networks. Yes, combinatorial properties are very useful for stochastic heuristic methods, but they are not the only and sufficient property for successful solution of such near-real test problems. The search strategies themselves in the algo are also important.
Gradient-based ones simply get stuck in a local extremum instantly. And it doesn't matter how many times to restart from a new point of the parameter space, the chance to get to the right region of the space from which the gradient method instantly finds a solution tends to zero as the number of parameters increases.
Yes, it does.
But the chance to get to this region, as I have already said, is simply zero. It would take about a hundred years to generate random numbers.
Yes, that's right. In low-dimensional spaces (1-2) it is very easy to get into the vicinity of the global, simple random generators can even work for this. But everything changes completely when the dimensionality of the problem grows, here search properties of algorithms start to play an important role, not Mistress Luck.
So we need to somehow combine genetic algorithms presented in the article (that they would do exploration, reduce the search space) with gradient methods, which would then quickly find the extremum from a more favourable point.
"genetic" - you probably mean "heuristic". Why "the fish needs an umbrella" and "why do we need a blacksmith? We don't need a blacksmith.")))) There are efficient ways to solve complex multidimensional in continuous space problems, which are described in articles on population methods. And for classical gradient problems there are their own tasks - one-dimensional analytically determinable problems (in this they have no equal, there will be fast and exact convergence).
And, question, what are your impressions of the speed of heuristics?
SZY:
Oh, how many wonderful discoveries
Prepare the spirit of enlightenment
And experience, the son of errors,
And genius, the friend of paradoxes,
And chance, God's inventor.
ZZZY. One moment. In an unknown space of search it is never possible to know at any moment of time or step of iteration that it is actually a really promising direction towards the global. Therefore, it is impossible to scout first and refine later. Only whole search strategies can work, they either work well or poorly. Everyone chooses the degree of "goodness" and "suitability for the task" himself, for this purpose a rating table is kept to choose an algorithm according to the specifics of the task.
Yes, that's right. In low-dimensional spaces (1-2) it is very easy to get into the neighbourhood of a global, simple random generators can even be useful for this. But everything changes completely when the dimensionality of the problem grows, here search properties of algorithms, not Lady Luck, start to play an important role.
So they fail
And, question, what are your impressions of the speed of heuristics?
Despite the fact that they work fast. The result for 1000 parameters something about 0.4.
That's why I intuitively thought that it makes sense to combine GA and gradient methods to get to the maximum. Otherwise, separately they will not solve your function. I haven't tested it in practice.
P.S. I still think that this function is too thick, in real tasks (training of neural networks, for example) there are no such problems, although there too the error surface is all in local minima.
1. They're not doing a good job
2. even though they work fast. The result for 1000 parameters is something around 0.4.
3. That's why I intuitively thought that it makes sense to combine GA and gradient methods to get to the maximum. Otherwise, separately they won't solve your function. I haven't tested it in practice.
4. P.S. I still think that this function is too thick, in real tasks (training of neural networks, for example) there are no such problems, although there too the error surface is all in local minima.
1. What do you mean "they can't cope"? There is a limit on the number of accesses to the target function, the one who showed a better result is the one who can't cope)). Should we increase the number of allowed accesses? Well, then the more agile and adapted to complex functions will come to the finish line anyway. Try to increase the number of references, the picture will not change.
2. Yes. And some have 0.3, and others 0.2, and others 0.001. Better are those who showed 0.4.
3. It won't help, intuitively hundreds of combinations and variations have been tried and re-tried. Better is the one that shows better results for a given number of epochs (iterations). Increase the number of references to the target, see which one reaches the finish line first.
4. If there are leaders on difficult tasks, do you think that on easy tasks leaders will show worse results than outsiders? This is not the case, to put it mildly. I am working on a more "simple" but realistic task of grid training. I will share the results as always. It will be interesting.
Just experiment, try different algorithms, different tasks, don't get stuck on one thing. I have tried to provide all the tools for this.
1. What do you mean "fail"? There is a limit on the number of accesses to the target function, the one who has shown the best result is the one who can't cope)). Should we increase the number of allowed accesses? Well, then the more agile and adapted to complex functions will come to the finish line anyway. Try increasing the number of references, the picture will not change.
2. Yes. And some have 0.3, and others 0.2, and others 0.001. Better are those who showed 0.4.
3. It won't help, intuitively hundreds of combinations and variations have been tried and re-tried. Better is the one that shows better results for a given number of epochs (iterations). Increase the number of references to the target, see which one reaches the finish line first.
4. If there are leaders on difficult tasks, do you think that on easy tasks leaders will show worse results than outsiders? This is not the case, to put it mildly. I am working on a more "simple" but realistic task of grid training. I will share the results as always. It will be interesting.
Just experiment, try different algorithms, different tasks, don't fixate on one thing. I have tried to provide all the tools for this.
I am experimenting,
About the realistic task it is right to test algorithms on tasks close to combat.
It's doubly interesting to see how genetic networks will be trained.