原子軌道探索(AOS)アルゴリズム

MetaTrader 5 — 例 | YYYY年08月DD日, 15:17

Andrey Dik

内容

はじめに

近年では、複雑な最適化問題を解決するための手法として、物理学、特に量子力学の原理から着想を得たアプローチが増えています。この記事では、原子軌道モデルの概念に基づく原子軌道検索(AOS:Atomic Orbital Search)アルゴリズムについて紹介します。このアルゴリズムは、2021年にMahdi Aziziによって提案された新しいメタヒューリスティック手法です。このモデルでは、電子の動きを厳密な軌道としてではなく、原子核の周囲に存在する確率雲として表現します。これは、物理学者エルヴィン・シュレーディンガーによる研究成果に基づいています。

原子軌道とは、量子的な記述によって得られる、電子が存在する確率が最も高い領域のことです。このモデルでは、電子はエネルギー準位を反映する量子数や半径によって定義された仮想的な層内を移動します。量子数nが大きくなるほど、半径が広がりエネルギーも高くなります。電子は、他の粒子との相互作用や光子の影響によって励起され、異なる軌道間を移動する際にエネルギーを吸収したり放出したりします。このような振る舞いにより、電子の動きは非常にダイナミックで変化に富んだものになります。

AOSアルゴリズムは、こうした物理的な原理を活用して、最適化問題の解を探索するプロセスをモデル化しています。確率分布と相互作用のダイナミクスを取り入れることで、解空間を効率よく探索できます。特にこのアルゴリズムでは、候補解（電子）の位置を、それぞれのエネルギーに応じて更新し、その結果としてある層に存在する確率も変わっていきます。これにより、AOSは最適解を見つけるだけでなく、環境の変化にも柔軟に対応することができます。

この記事では、AOSの数学的モデルについて詳しく見ていき、候補解の位置更新のステップや、エネルギーの吸収・放出を制御する仕組みについても説明します。AOSは、単なる最適化手法としてだけでなく、量子の原理を計算問題に応用する新しいアプローチとしても注目されています。

アルゴリズムの実装

AOSアルゴリズムは、原子軌道モデルの原理に基づいています。このモデルでは、原子によるエネルギーの放出や吸収、さらには電子密度の構成が考慮されています。アルゴリズムの初期段階では、複数の候補解がXとして与えられます。これらは、原子核のまわりに存在する電子と見なされます。候補解は電子の雲を構成し、探索空間は同心円状の層に分割された球体として表現されます。候補解の一般的な表記は以下の通りです。

X = [x₁, x₂, ..., xⱼ, ..., xₘ]、ここで、xᵢはi番目の候補解、mは候補解の総数です。

候補解の初期位置はランダムに初期化されます。各電子には目的関数によって決定されるエネルギー準位があり、この関数は最小化されるべきものです。そのため、エネルギーが低い電子は良好な目的関数の値を持つ候補解に対応し、エネルギーが高い電子は悪い値を持つ候補解に対応します。目的関数の値を示すベクトルは以下のように表されます。

E = [E₁, E₂, ..., Eᵢ, ..., Eₘ]、ここで、Eᵢはi番目の候補解のエネルギーです。

原子核のまわりの仮想的な層は、1からL（層数）までの範囲のランダムな整数nを使ってモデル化されます。最も半径が小さい層L₀はコアを表し、他の層Lᵢは電子の存在位置となります（AOSではコア層にも電子が存在することがあります）。候補解の各層への分布は、ある変数が指定された範囲に存在する確率を決定する確率密度関数(PDF)によっておこなわれます。このアルゴリズムでは、電子の波動的挙動をシミュレーションするために対数正規分布を使用しています。候補解はさまざまな層に分布し、各層の候補解を含むベクトルXₖは以下のように表されます。

Xₖ = [Xₖ₁, Xₖ₂, ..., Xₖᵢ, ..., Xₖₚ]、ここで、kは層のインデックス、pはその層内の候補解の数です。

原子軌道モデルに従い、電子は基底状態にあると仮定されます。各層の結合状態BSₖおよび結合エネルギーBEₖは以下のように計算されます。

BSₖ = (1/p) × Σ(Xₖᵢ)

BEₖ = (1/p) × Σ(Eₖᵢ)

原子全体の結合状態と結合エネルギーは次のように定義されます。

BS = (1/m) × Σ(Xᵢ)

BE = (1/m) × Σ(Eᵢ)

電子は、光子や他の粒子との相互作用の影響を受けて位置を変えたり、層を移動したりします。AOSにおける候補解の位置更新は、相互作用確率に基づいておこなわれます。この確率は、[0, 1]の範囲でランダムに生成されるϕという値で表されます。ϕ ≥ PR（光子速度パラメータ）の場合、エネルギーの放出または吸収が発生します。

Eₖᵢ ≥ BEₖの場合（放出）：Xₖᵢ[t+1] = Xₖᵢ[t] + αᵢ × (βᵢ × LE − γᵢ × BS) / k

Eₖᵢ < BEₖの場合（吸収）：Xₖᵢ[t+1] = Xₖᵢ[t] + αᵢ × (βᵢ × LEₖ − γᵢ × BSₖ)

ϕ < PRの場合、磁場の影響や他の粒子との相互作用による位置の変化が考慮されます。Xₖᵢ[t+1] = Xₖᵢ[t] + rᵢ、ここでrᵢは、問題の該当パラメータの最小値から最大値の範囲内でのランダムな増分です。

簡単に言えば、AOSにおいて候補解の集団は分子として比喩的に表現できます。探索空間内の座標が原子に対応し、それぞれの原子内にある電子が具体的な解に相当します。たとえば、候補解が50個ある場合、それぞれの原子には50個の電子が対数正規分布に基づいて層に分布することになります。

アルゴリズムの記述において、著者は原子の最外層の直径をどのように定義するかを明確には示していませんが、原子核が層に対して中心に位置していると仮定しています。つまり、原子とその層は問題空間の指定された範囲内で移動可能です。アルゴリズムの柔軟性を高めるために、原子の外層の直径は、対応する探索空間の座標の[min; max]の範囲に一致するものとします。また、原子核の中心は、その座標における大域最良解の位置に配置されます。視覚的には、AOSの原子モデルは図1のように表現できます。

AOS

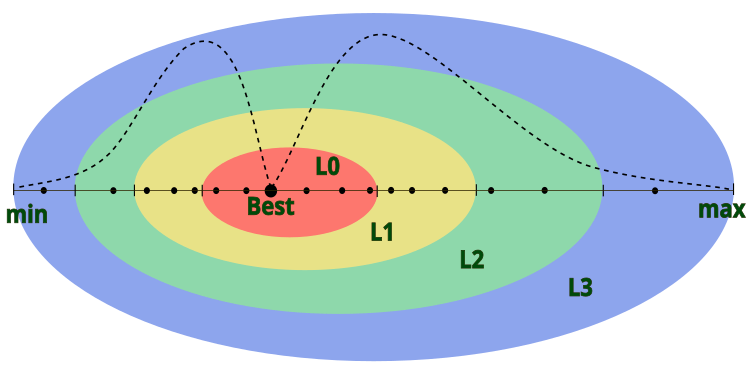
図1：AOSアルゴリズムにおける原子のモデル。点は電子を表し、点線は電子の対数正規分布を表す

以下は、AOSアルゴリズムの疑似コードです。

1. 初期化

1.1 候補解の初期位置(Xi)

候補解（粒子）をm個生成します。
各候補解には、探索空間内のランダムな初期位置が割り当てられます。

1.2 初期適応度(Ei)の計算

各候補解について、目的関数の値を計算します。
この値は粒子のエネルギーを表します。
エネルギーが低いほど、解の質は高くなります。

1.3 原子パラメータの決定

BS（結合状態）：すべての粒子の現在の平均位置
BE（結合エネルギー）：すべての粒子のエネルギーの平均
LE（最低エネルギー）：最もエネルギーが低い粒子（最良解）

2. 層構造の作成

2.1 原子ごとにランダムな層数[1; n]を生成

仮想的な軌道の数をランダムに決定します。
各層は、異なる強度での探索レベルを表します。

2.2 粒子の分布

粒子は確率密度関数(PDF)に基づいて層に分布されます。
内側の層には通常、良好な解が含まれます。
外側の層は探索範囲の拡張に使われます。

2.3 各層kに対する探索処理

3.1 層のパラメータ

BSk：特定の層の結合状態
BEk：その層の結合エネルギー
LEk：その層内で最もエネルギーが低い粒子

3.2 粒子位置の更新

各粒子i（層kに属する）について以下を実行します。

3.3 制御パラメータの生成

φ：移動タイプ
α：スケーリング係数
β：最良解への引力係数
γ：平均状態からの斥力係数
PR：光子移動の確率

3.4 移動タイプの選択

φ ≥ PRの場合
Eki ≥ BEkの場合
// 大域的検索
Xi[t+1] = Xit + αi × (βi × LE - γi × BS) / k
その他の場合
// 局所的検索
Xi[t+1] = Xit + αi × (βi × LEk - γi × BSk)
その他の場合
// ランダムな動き
Xki[t+1] = Xkit + ri

4. 適応度(Ei)の再計算

5. グローバル設定の更新

6. 停止条件を満たすまで1.3から繰り返します

原子核（最良解）のまわりの電子の分布確率を計算するために、さまざまな分布に基づいた乱数生成を使用することができます。著者は対数正規分布を好んでおり、これをコード内で実装する必要があります。生成器のコードを欠きましょう。このアルゴリズムでは、単なる対数正規分布ではなく、中心（コア）に対して非対称にシフトされた分布が必要であり、それが図1に示されています。このため、最適化アルゴリズム用の関数ライブラリに、対数正規分布に従い、与えられた範囲内で偏りを持つ乱数を生成するLognormalDistribution関数を実装します。

この関数は次のパラメータを取ります。

1. center：分布の中心値
2. min_value：生成可能な最小値
3. max_value：生成可能な最大値
4. peakDisplCoeff：分布中心に対するピーク変位の係数（デフォルトは0.2）

関数の説明

1. 境界の確認
min_valueがmax_value以上の場合、関数はmax_valueを返します。
max_valueがmin_value以下の場合、関数はmin_valueを返します。

2. 0から1までの範囲でランダムな数を生成します。

3. 中心値の調整
centerがmin_valueより小さい場合はmin_valueに設定され、randomは1に設定されます。
centerがmax_valueを超える場合はmax_valueに設定され、randomは0に設定されます。

4. 分布ピークの位置を決定するpeak_left値とpeak_right値を計算します。

5. 値の生成
    randomが0.5未満である場合、分布の左側の計算をおこないます。
        mu_leftおよびsigma_leftパラメータを計算します。
        ボックス＝ミュラー法のための乱数u1とu2を生成します。
        ボックス＝ミュラー法を用いて正規分布のz値を得ます。
    左側の分布に基づいた結果を計算します。
    randomが0.5以上である場合、右側について同様の処理をmu_rightおよびsigma_rightパラメータを使用しておこないます。

6. 生成されたresult値がmin_valueとmax_valueの範囲外である場合、RNDfromCI関数が呼び出され、生成された値を許容範囲内に「投げ返す」ことで、乱数の境界への偏りを防ぎます。

//------------------------------------------------------------------------------
//The lognormal distribution of the species:  min|------P---C---P------|max
double C_AO_Utilities :: LognormalDistribution (double center, double min_value, double max_value, double peakDisplCoeff = 0.2)
{
  // Check the right border
  if (min_value >= max_value)
  {
    return max_value;
  }

  // Check the left border
  if (max_value <= min_value)
  {
    return min_value;
  }

  // Generate a random number from 0 to 1
  double random = MathRand () / 32767.0;

  // Correction of the center if it goes beyond the boundaries
  if (center < min_value)
  {
    center = min_value;
    random = 1;
  }

  if (center > max_value)
  {
    center = max_value;
    random = 0;
  }

  // Calculate the position of the peaks
  double peak_left  = center - (center - min_value) * peakDisplCoeff;
  double peak_right = center + (max_value - center) * peakDisplCoeff;

  double result = 0.0;

  if (random < 0.5) // Left side of the distribution
  {
    // Calculate parameters for the left side
    double diff_center_peak = MathMax (center - peak_left, DBL_EPSILON);
    double diff_center_min  = MathMax (center - min_value, DBL_EPSILON);

    double mu_left = MathLog (diff_center_peak);
    double sigma_left = MathSqrt (2.0 * MathLog (MathMax (diff_center_min / diff_center_peak, DBL_EPSILON)) / 9.0);

    // Generate random numbers for the Box-Muller method
    double u1 = MathRand () / 32767.0;
    double u2 = MathRand () / 32767.0;

    // Protection against null values
    u1 = MathMax (u1, DBL_EPSILON);

    // Application of the Box-Muller method
    double z = MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2);

    // Calculate the result for the left side
    result = center - MathExp (mu_left + sigma_left * z);
  }
  else // Right side of the distribution
  {
    // Calculate parameters for the right side
    double diff_peak_center = MathMax (peak_right - center, DBL_EPSILON);
    double diff_max_center  = MathMax (max_value - center,  DBL_EPSILON);

    double mu_right    = MathLog  (diff_peak_center);
    double sigma_right = MathSqrt (2.0 * MathLog (MathMax (diff_max_center / diff_peak_center, DBL_EPSILON)) / 9.0);

    // Generate random numbers for the Box-Muller method
    double u1 = MathRand () / 32767.0;
    double u2 = MathRand () / 32767.0;

    // Protection against null values
    u1 = MathMax (u1, DBL_EPSILON);

    // Application of the Box-Muller method
    double z = MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2);

    // Calculate the result for the right side
    result = center + MathExp (mu_right + sigma_right * z);
  }

  // Check and correct the result if it goes beyond the limits
  if (result < min_value || result > max_value) return RNDfromCI (min_value, max_value);

  return result;
}

分布の生成結果を視覚的に確認するためのスクリプトを作成します。これはテストスクリプトがおこなう内容です（残りのコードは提供しません。テストスタンド用のキャンバス操作クラスについては記事のアーカイブにあります）。

1. グラフィックを描画するためにCanvasオブジェクトを作成します。
2. キャンバスパラメータ（幅：W、高さ：H 、インデント：O）を初期化します。
3. 入力値Inp_Pを基準として、左側と右側の値をカウントするために、CountLおよびCountRの配列を0で初期化して作成します。
4. 指定されたサイズと背景色でグラフィック要素（キャンバス）を作成します。

対数正規分布は、対数が正規分布に従う確率変数を表します。コード内では、この分布を使用して値を生成し、グラフ上に可視化します。

5. forループ内で、U.LognormalDistribution関数を使用してN個の値を生成します。それぞれの値はInp_Pと比較されます。より小さい場合はCountL[i]カウンタが増加され、より大きい場合はCountR[i]カウンタが増加されます。
6. 生成前に、CountLとCountRはゼロで初期化されます。
7. グラフの範囲を決定するために、配列内の最小値と最大値が計算されます。
8. グラフ描画のための座標が計算されます。これにはキャンバスの中心と、左側および右側のステップ幅が含まれます。
9. 範囲内の値の数を表すドットがキャンバス上に描画され、発生頻度に応じた色が使用されます。
10. キャンバスは変更を反映させるために更新されます。

// Function called at startup
void OnStart ()
{
    CCanvas Canvas; // Object for handling graphics (canvas)

    // Canvas parameters
    int W = 750; // Canvas width
    int H = 400; // Canvas height
    int O = 10;  // Margins from canvas borders

    // Arrays for storing count values
    int CountL []; // Count values to the left of the input
    int CountR []; // Count values to the right of the input

    // Initialize arrays
    ArrayResize (CountL, Size_P);  // Resize the CountL array
    ArrayInitialize (CountL, 0);   // Initialize the CountL array with zeros

    ArrayResize (CountR, Size_P);  // Resize the CountR array
    ArrayInitialize (CountR, 0);   // Initialize the CountR array with zeros

    // Create a canvas
    string canvasName = "Test_Probability_Distribution_Canvas"; // Canvas name
    if (!Canvas.CreateBitmapLabel(canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW))
    {
        Print ("Error creating Canvas: ", GetLastError()); // Display an error if creation fails
        return;
    }

    // Set up canvas properties
    ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false);    // Make canvas visible
    ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true); // Make canvas selectable

    // Clear the canvas and draw the border
    Canvas.Erase (COLOR2RGB(clrWhite));                         // Fill with white color
    Canvas.Rectangle (1, 1, W - 1, H - 1, COLOR2RGB(clrBlack)); // Draw a black frame

    int    ind = 0;   // Index for counting
    double X   = 0.0; // Variable for storing values

    // Main loop for generating values
    for (int i = 0; i < CNT_P; i++)
    {
        // Generate log-normal distribution
        X = U.LognormalDistribution (Inp_P, Min_P, Max_P, PeakDisplCoeff_P);

        // Determine which side of the input parameter the value falls on
        if (X < Inp_P)
        {
            // Calculate the index for the left part
            ind = (int) U.Scale(X, Min_P, Inp_P, 0, Size_P, true);
            if (ind >= Size_P) ind = Size_P - 1; // Limit the index
            if (ind < 0) ind = 0;                // Limit the index
            CountL [ind] += 1;                   // Increment the counter for the left side
        }
        else
        {
            // Calculate the index for the right side
            ind = (int) U.Scale (X, Inp_P, Max_P, 0, Size_P, false);
            if (ind >= Size_P) ind = Size_P - 1; // Limit the index
            if (ind < 0) ind = 0;                // Limit the index
            CountR [ind] += 1;                   // Increment the counter for the right side
        }
    }

    // Define minimum and maximum values for the graph
    int minCNT = CNT_P; // Initial value for the minimum counter
    int maxCNT = 0;     // Initial value for the max counter

    // Finding minimum and maximum values in counters
    for (int i = 0; i < Size_P; i++)
    {
        if (CountL [i] > maxCNT) maxCNT = CountL [i]; // Update the max value for the left side
        if (CountR [i] > maxCNT) maxCNT = CountR [i]; // Update the max value for the right side

        if (CountL [i] < minCNT) minCNT = CountL [i]; // Update the min value for the left side
        if (CountR [i] < minCNT) minCNT = CountR [i]; // Update the minimum value for the right side
    }

    // Variables for drawing graphs
    int   x      = 0.0; // X coordinate
    int   y      = 0.0; // Y coordinate
    color clrF;         // Color
    int   centre = 0;   // Canvas center
    int   stepL  = 0;   // Left side step
    int   stH_L  = 0;   // Left side height
    int   stepR  = 0;   // Right side step
    int   stH_R  = 0;   // Right side height

    // Determine the center of the canvas
    centre = (int) U.Scale(Inp_P, Min_P, Max_P, O, W - O - 1, false);

    // Calculate steps and heights for the left side
    stepL = (centre - O) / Size_P;
    stH_L = stepL / 2;
    if (stH_L == 0) stH_L = 1; // Make sure the height is not 0

    // Calculate steps and heights for the right side
    stepR = (W - O - centre) / Size_P;
    stH_R = stepR / 2;
    if (stH_R == 0) stH_R = 1; // Make sure the height is not 0

    // Draw graphs for left and right parts
    for (int i = 0; i < Size_P; i++)
    {
        // Draw for the left side 
        x = (int) U.Scale (i, 0, Size_P - 1, O, centre - stH_L, true); // Calculate the X coordinate
        y = (int) U.Scale (CountL [i], 0, maxCNT, O, H - O - 1, true); // Calculate the Y coordinate

        clrF = DoubleToColor(CountL [i], minCNT, maxCNT, 0, 255); // Define color by value

        // Draw dots for the left side
        Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); // Draw a small circle
        Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); // Draw a larger circle

        // Draw for the right side
        x = (int) U.Scale (i, 0, Size_P - 1, centre + stH_R, W - O - 1, false); // Calculate the X coordinate
        y = (int) U.Scale (CountR[i], 0, maxCNT, O, H - O - 1, true);           // Calculate the Y coordinate

        clrF = DoubleToColor (CountR [i], minCNT, maxCNT, 0, 255); // Define color by value

        // Draw dots for the right side
        Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); // Draw a small circle
        Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); // Draw a larger circle
    }

    Canvas.Update (); // Update the canvas to reflect the changes}

スクリプトを実行して、チャート上に図2のような画像を表示してみましょう。

LogNormDistr

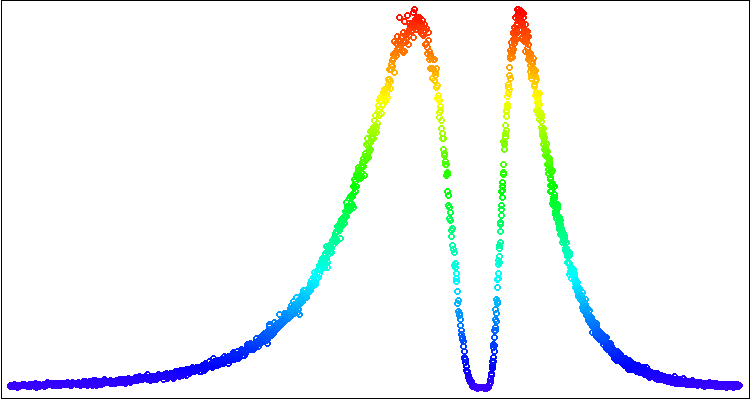
図2：標準Canvasライブラリを使用して非対称対数正規分布プロットを可視化する

アルゴリズムのすべての段階についての理論を詳細に検討したので、いよいよコード実装に直接移りましょう。AOSアルゴリズムは問題の最小化手法ですが、ここでは最大化に対応するようロジックを調整します。S_Layer構造体を実装していきます。これは原子層をシミュレートし、その層に存在する粒子の数などの情報を保持するものです。数値的な特性に加え、初期化用のメソッドも含まれます。以下が構造体フィールドです。

pc：原子のこの層に存在する粒子（電子）のカウンタ。このフィールドによって、特定の層に存在する粒子の数を追跡できます。
BSk：層内の結合状態。この値は、層内の粒子間の相互作用のレベルを表します。
BEk：層内の結合エネルギー。これは、層内の粒子同士がどの程度強く結びついているかを示します。
LEk：層内における最小エネルギー。これは、その層の粒子が達成可能な最低エネルギーレベルを判定するために使用されます。

Initメソッドは、構造体のフィールドをデフォルト値で初期化するためのものであり、必要に応じて層の状態を何度でも簡単にリセットできるようにします。

//——————————————————————————————————————————————————————————————————————————————
struct S_Layer
{
    int    pc;  // particle counter
    double BSk; // connection state
    double BEk; // binding energy
    double LEk; // minimum energy

    void Init ()
    {
      pc  = 0;
      BSk = 0.0;
      BEk = 0.0;
      LEk = 0.0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

次に、S_Atom構造体とそのInitメソッドを見てみましょう。S_Atomは、複数の層から構成される原子を表す構造体です。各層は、先ほど説明したS_Layer構造体のlayers []配列を使ってシミュレートされます。以下が構造体フィールドです。

Init：原子層の配列を初期化するメソッドであり、この配列内の各層を初期化します。
layersNumb：この原子に対して作成される層の数を指定する整数パラメータです。

//——————————————————————————————————————————————————————————————————————————————
struct S_Atom
{
    S_Layer layers [];  // array of atom layers

    void Init (int layersNumb)
    {
      ArrayResize (layers, layersNumb);
      for (int i = 0; i < layersNumb; i++) layers [i].Init ();
    }
};
//——————————————————————————————————————————————————————————————————————————————

次に、S_Electron構造体とそのInitメソッドについて見ていきます。この構造体は電子を表しており、解の個体群の一員です。また、この電子が原子内のどの層に存在するかに関する情報を保持します。フィールドlayerID []は整数の配列であり、この電子が属する層のIDを格納します。各IDは原子内の特定の層に対応しており、電子がどのエネルギーレベルにいるかを追跡することができます。

//——————————————————————————————————————————————————————————————————————————————
struct S_Electron
{
    int layerID [];  // array of layer IDs for the electron

    void Init (int coords)
    {
      ArrayResize (layerID, coords);
    }
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_AOSクラスは、基底クラスであるC_AOから継承されたAOSアルゴリズムのクラスであり、原子軌道に関連する共通の機能を備えていることを意味します。

クラスパラメータ：

popSize：アルゴリズムにおける個体群のサイズ
maxLayers：原子モデルで使用可能な層の最大数。
photonEmissions：最適化プロセスで使用されるフォトン放出の回数
PR：光子遷移係数（状態間の遷移確率）
peakPosition：対数正規分布のピーク位置

クラスのメソッド

1. SetParams：params配列から値を読み取ってアルゴリズムのパラメータを設定します。
2. Init：最小・最大範囲、探索ステップ、エポック数などの探索パラメータを用いてアルゴリズムを初期化します。
3. Moving：検索空間内で粒子を移動させるメソッド
4. Revision：最適化中に見つかった最良解を更新・検討するメソッド

クラスのprivateフィールド

atomStage：原子プロセスの現在の段階
currentLayers []：各原子における現在の層の数。各エポックで、各原子の層数は[1; maxLayers]の範囲でランダムに決まります。
S_Atom atoms []：アルゴリズムで使用される座標数に対応した原子の配列
S_Electron electrons []：個体群サイズに対応する電子の配列
BS []：個体群全体における電子間の結合状態の配列

privateクラスメソッド

1. GetOrbitBandID：層の数や範囲などのパラメータに基づいて軌道帯IDを取得します。
2. DistributeParticles：粒子を探索空間内に分布させます。
3. LayersGenerationInAtoms：原子内の層数を生成します。
4. UpdateElectronsIDs：電子に対応する層IDを更新します。
5. CalcLayerParams：層のパラメータ（エネルギーレベルや結合状態）を計算します。
6. UpdateElectrons：電子の位置を更新します。

//——————————————————————————————————————————————————————————————————————————————
// Class implementing the atomic optimization algorithm (Atomic Orbital Search)
class C_AO_AOS : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AOS () { }
  C_AO_AOS ()
  {
    ao_name = "AOS";
    ao_desc = "Atomic Orbital Search";
    ao_link = "https://www.mql5.com/ja/articles/16276";

    popSize         = 50;      // population size

    maxLayers       = 5;       // maximum number of layers
    photonEmissions = 1;       // number of photon emissions
    PR              = 0.1;     // photon transition coefficient
    peakPosition    = 0.05;    // peak position in the log-normal distribution

    ArrayResize (params, 5);

    params [0].name = "popSize";         params [0].val = popSize;
    params [1].name = "maxLayers";       params [1].val = maxLayers;
    params [2].name = "photonEmissions"; params [2].val = photonEmissions;
    params [3].name = "photonRate";      params [3].val = PR;
    params [4].name = "peakPsition";     params [4].val = peakPosition;
  }

  // Setting algorithm parameters
  void SetParams ()
  {
    popSize         = (int)params [0].val;
    maxLayers       = (int)params [1].val;
    photonEmissions = (int)params [2].val;
    PR              = params      [3].val;
    peakPosition    = params      [4].val;
  }

  // Initialization of the algorithm with the given search parameters
  bool Init (const double &rangeMinP  [], // minimum search range
             const double &rangeMaxP  [], // maximum search range
             const double &rangeStepP [], // search step
             const int     epochsP = 0);  // number of epochs

  void Moving   (); // Method of moving particles
  void Revision (); // Method of revising the best solutions

  //----------------------------------------------------------------------------
  int    maxLayers;       // maximum number of layers
  int    photonEmissions; // number of photon emissions
  double PR;              // photon transition coefficient
  double peakPosition;    // peak position in the log-normal distribution

  private: //-------------------------------------------------------------------
  int        atomStage;        // current stage of the atom
  int        currentLayers []; // current number of layers for the corresponding atom (coordinates)
  S_Atom     atoms         []; // atoms with their size corresponding to the number of coordinates
  S_Electron electrons     []; // electrons corresponding to the population size
  double     BS            []; // connection states

  // Get orbital band for given parameters
  int  GetOrbitBandID          (int layersNumb, double min, double max, double center, double p);

  // Distribution of particles in the search space
  void DistributeParticles     ();

  // Generate layers in atoms
  void LayersGenerationInAtoms ();

  // Update electron IDs
  void UpdateElectronsIDs      ();

  // Calculate layer parameters 
  void CalcLayerParams         ();

  // Update electron positions
  void UpdateElectrons         ();
};
//——————————————————————————————————————————————————————————————————————————————

AOSアルゴリズムクラスのInitメソッドで何が起こるかを見てみましょう。

1. 標準初期化：このメソッドはまずStandardInitを呼び出し、座標範囲の設定など、共通の初期化ステップを実行します。

2. 変数の初期化

atomStage：0に設定され、アルゴリズムが初期段階から開始することを意味します。
ArrayResize (currentLayers, coords)：currentLayers配列のサイズをcoords座標の数に応じて変更します。
ArrayResize (atoms, coords)：atoms配列のサイズを座標数に合わせて変更し、各座標（すなわち各原子）に対応するオブジェクトを作成します。各原子に対して、Init (maxLayers)メソッドが呼び出され、最大層数で初期化されます。
ArrayResize (electrons, popSize)：electrons配列のサイズを個体群サイズ(popSize)に合わせて変更します。各電子に対してlayerID配列が作成され、この配列のサイズは座標数に対応します。
ArrayResize (BS, coords)：結合状態を保持するBS配列のサイズを座標数に合わせて変更します。

4. すべての初期化操作が成功した場合、メソッドはtrueを返します。

//——————————————————————————————————————————————————————————————————————————————
// Initialize the algorithm
bool C_AO_AOS::Init (const double &rangeMinP [],
                     const double &rangeMaxP [],
                     const double &rangeStepP [],
                     const int epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  atomStage = 0;

  ArrayResize (currentLayers, coords);

  ArrayResize (atoms, coords);
  for (int i = 0; i < coords; i++) atoms [i].Init (maxLayers);

  ArrayResize (electrons,   popSize);
  for (int i = 0; i < popSize; i++) ArrayResize (electrons [i].layerID, coords);

  ArrayResize (BS, coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

粒子移動メソッド、Movingメソッドについて説明しましょう。

1. 初期のランダム配置

revision変数がfalseの場合、アルゴリズムはまだ実行を開始していないことを意味します。この場合、粒子（電子）のランダムな初期配置がおこなわれます。
次に、入れ子のforループが全電子（個体群のサイズ）に対して実行され、各座標についてu.RNDfromCIメソッドを用いてランダムな値が生成されます。このメソッドは、rangeMinとrangeMaxで指定された範囲から値を取得します。その後、この値はu.SeInDiSpによって調整され、指定されたstepに従って値が設定されます。

2. 原子の進化段階の実行

revisionがtrueの場合、アルゴリズムはすでに初期化されており、主要なステージの実行が可能な状態です。現在のatomStageの値に応じて、以下のように異なるメソッドが呼び出されます。
atomStageが0の場合、DistributeParticles()が呼び出され、非対称な対数正規分布に基づいて粒子の空間分布がおこなわれます。
それ以外の場合、原子内の層を生成するメソッド、電子IDを更新するメソッド、層パラメータを計算するメソッド、電子の位置を更新するメソッドなどが順次呼び出されます。

3. 必要な操作がすべて完了すると、atomStageが1増加します。atomStageは、photonEmissionsの値を超えた場合には0にリセットされ、アルゴリズムのステージが周期的に繰り返されるようになります。

//——————————————————————————————————————————————————————————————————————————————
// Particle displacement method
void C_AO_AOS::Moving ()
{
  // Initial random positioning
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  // Execute the corresponding stage of the algorithm
  if (atomStage == 0)
  {
    DistributeParticles ();
  }
  else
  {
    LayersGenerationInAtoms ();
    UpdateElectronsIDs      ();
    CalcLayerParams         ();
    UpdateElectrons         ();
  }

  // Proceed to the next stage
  atomStage++;
  if (atomStage > photonEmissions) atomStage = 0;
}
//——————————————————————————————————————————————————————————————————————————————

具体的なメソッドの解析に進みましょう。C_AO_AOSクラスのGetOrbitBandIDメソッドは、粒子の位置が与えられた中心に対してどの軌道帯に属しているかを判定するためのものです。層数、最小値と最大値、粒子pの中心と位置を取得します。

1. 中心から左右に分かれた軌道帯の幅を計算します。
2. 粒子pの位置が中心より小さい場合は、左側のどの軌道帯にあるかを検索します。
3. 粒子pの位置が中心より大きい場合は、右側のどの軌道帯にあるかどうかを検索します。
4. 位置が中心と等しい場合は、0（中心の軌道帯）を返します。

このようにして、関数は与えられた位置に対応する軌道帯のインデックスを返します。

//——————————————————————————————————————————————————————————————————————————————
// Determining the orbital band for a particle
int C_AO_AOS::GetOrbitBandID (int layersNumb, double min, double max, double center, double p)
{
  // Calculate the width of the bands to the left and right of the center
  double leftWidth  = (center - min) / layersNumb;
  double rightWidth = (max - center) / layersNumb;

  // Define the band index
  if (p < center)
  {
    // The object is located to the left of the center
    for (int i = 1; i <= layersNumb; i++)
    {
      if (p >= center - i * leftWidth) return i - 1;
    }
    return layersNumb - 1; // If the object is in the leftmost band
  }
  else
    if (p > center)
    {
      // The object is located to the right of the center
      for (int i = 1; i <= layersNumb; i++)
      {
        if (p <= center + i * rightWidth) return i - 1;
      }
      return layersNumb - 1; // If the object is in the far right band
    }
    else
    {
      // The object is in the center
      return 0;
    }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AOSクラスのDistributeParticlesメソッドは、探索空間における粒子の分布を担当します。このメソッドは、対数正規分布を使用して、粒子を探索空間に分布させます。

各粒子（popSizeによるループ）および各座標（coordsによるループ）に対して、以下をおこないます。

パラメータ（cB、rangeMin、rangeMax、peakPosition）を用いて、対数正規分布に基づいて粒子の位置を生成します。
生成された粒子の位置に対して、SeInDiSp関数を適用し、指定されたステップと範囲に従って値を調整します。

//——————————————————————————————————————————————————————————————————————————————
// Distribution of particles in the search space
void C_AO_AOS::DistributeParticles ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Use log-normal distribution to position particles
      a [i].c [c] = u.LognormalDistribution (cB [c], rangeMin [c], rangeMax [c], peakPosition);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AOSクラスのUpdateElectronsIDsメソッドは、電子の座標と指定されたパラメータに応じて、各電子の層IDを更新します。

//——————————————————————————————————————————————————————————————————————————————
//  Update layer IDs for each electron
void C_AO_AOS::UpdateElectronsIDs ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      electrons [i].layerID [c] = GetOrbitBandID (currentLayers [c], rangeMin [c], rangeMax [c], cB [c], a [i].c [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AOSクラスのCalcLayerParamsメソッドは、システム内の各原子の層に関するパラメータを計算するために設計されたメソッドです。この方法の主な構成要素は次の通りです。

1. 変数の初期化：energyは最大エネルギーを格納するための変数であり、電子を処理する過程で更新されます。

2. システム内のすべての原子（座標）に対してループ処理がおこなわれ、cインデックスが現在の原子を示します。

3. 各原子に対してInitメソッドが呼び出され、maxLayersで指定された最大層数に基づいて各パラメータが初期化されます。

4. 層のループ処理：内部ループでは、現在の原子に関連付けられたすべての層を繰り返し処理します。currentLayers [c]は、原子cに対する層の数を示します。

5. 電子の処理：さらに内側のループでは、すべての電子eに対してループ処理をおこない、その電子が原子cの層Lに属しているかを判定します。

6. 層パラメータの更新：

電子が該当層に属している場合、その層の粒子カウンタ(pc)がインクリメントされます。
層のBEkおよびBSkの値が、電子の性質に基づいて更新されます。
電子エネルギーa[e].fが現在の最大energyを超える場合は、最大energyおよびLEk状態の値も更新されます。

7. 層の平均値の計算：粒子カウンターpcが0でない場合、エネルギーと結合状態の平均値が計算されます。

8. 全体の結合状態の計算：各原子に対するBSは、電子の集団全体にわたって同様の方法で計算されます。

//——————————————————————————————————————————————————————————————————————————————
// Calculate parameters for each layer
void C_AO_AOS::CalcLayerParams ()
{
  double energy;

  // Handle each coordinate (atom)
  for (int c = 0; c < coords; c++)
  {
    atoms [c].Init (maxLayers);

    // Handle each layer
    for (int L = 0; L < currentLayers [c]; L++)
    {
      energy = -DBL_MAX;

      // Handle each electron
      for (int e = 0; e < popSize; e++)
      {
        if (electrons [e].layerID [c] == L)
        {
          atoms [c].layers [L].pc++;
          atoms [c].layers [L].BEk = a [e].f;
          atoms [c].layers [L].BSk = a [e].c [c];

          if (a [e].f > energy)
          {
            energy = a [e].f;
            atoms [c].layers [L].LEk = a [e].c [c];
          }
        }
      }

      // Calculate average values for the layer
      if (atoms [c].layers [L].pc != 0)
      {
        atoms [c].layers [L].BEk /= atoms [c].layers [L].pc;
        atoms [c].layers [L].BSk /= atoms [c].layers [L].pc;
      }
    }
  }

  // Calculate the general state of connections
  ArrayInitialize (BS, 0);

  for (int c = 0; c < coords; c++)
  {
    for (int e = 0; e < popSize; e++)
    {
      BS [c] += a [e].c [c];
    }

    BS [c] /= popSize;
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AOSクラスのUpdateElectronsメソッドは、システム内の電子の位置を更新する役割を担っています。

1. パラメータの初期化：速度係数、最良解の重み、平均状態の重み、遷移確率が設定されます。

2. 各粒子と各座標について

ランダムな確率φが生成されます。
φがPRの閾値を下回る場合は、ランダムな分散が発生し、指定された範囲内で新たな位置がランダムに選ばれます。
それ以外の場合

現在の粒子に対するlID（層ID）が取得されます。

各係数（重み）のためのランダム値が生成されます。

粒子の現在のエネルギーが、その層の平均エネルギーよりも小さい場合、大域最良解に向かって移動がおこなわれます。

そうでない場合は、層内の局所的最良解に向かって移動がおこなわれます。

最後に、ステップ幅を考慮して、新しい位置が指定範囲内に制限されます。

//——————————————————————————————————————————————————————————————————————————————
// Update electron positions
void C_AO_AOS::UpdateElectrons ()
{
  double α;      // speed coefficient
  double β;      // best solution weight coefficient
  double γ;      // average state weight coefficient
  double φ;      // transition probability
  double newPos; // new position
  double LE;     // best energy
  double BSk;    // connection state
  int    lID;    // layer ID

  // Handle each particle
  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      φ = u.RNDprobab ();

      if (φ < PR)
      {
        // Random scatter
        newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      }
      else
      {
        lID = electrons [p].layerID [c];

        α = u.RNDfromCI (-1.0, 1.0);
        β = u.RNDprobab ();
        γ = u.RNDprobab ();

        // If the current particle energy is less than the average layer energy
        if (a [p].f < atoms [c].layers [lID].BEk)
        {
          // Moving towards the global optimum----------------------------
          LE = cB [c];

          newPos = a [p].c [c]+ α * (β * LE - γ * BS [c]) / currentLayers [c];
        }
        else
        {
          // Movement towards the local optimum of the layer
          LE  = atoms [c].layers [lID].LEk;
          BSk = atoms [c].layers [lID].BSk;

          newPos = a [p].c [c] + α * (β * LE - γ * BSk);
        }
      }

      // Limiting the new position within the search range taking into account the step
      a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AOSクラスのRevisionメソッドは、反復処理中に最良解（または最良状態）を見直し、更新するために設計されています。以下がメソッドの処理手順です。

1. 最良解のインデックスを格納するための変数bestIndexが初期化されます。

2. 最適解の探索：現在の解a [i].fの関数値（もしくは評価値）が、大域最良解fBの現在値を上回っているかどうかを判定します。この条件が真であれば、大域最適値は現在の値に更新され、最良解のインデックスがbestIndexに保存されます。

3. 最良解が見つかった場合、その解の座標a[bestIndex].cが、大域最良座標配列cBにコピーされます。

//——————————————————————————————————————————————————————————————————————————————
// Method of revising the best solutions
void C_AO_AOS::Revision ()
{
  int bestIndex = -1;

  // Find the best solution in the current iteration
  for (int i = 0; i < popSize; i++)
  {
    // Update the global best solution
    if (a [i].f > fB)
    {
      fB = a [i].f;
      bestIndex = i;
    }
  }

  // Update the best coordinates if a better solution is found 
  if (bestIndex != -1) ArrayCopy (cB, a [bestIndex].c, 0, 0, WHOLE_ARRAY);
}
//——————————————————————————————————————————————————————————————————————————————

テスト結果

テストスタンドを実行すると、次のAOS操作結果が取得されます。

AOS|Atomic Orbital Search|50.0|5.0|1.0|0.1|0.05|
=============================
5 Hilly's; Func runs:10000; result:0.6521321213930082
25 Hilly's; Func runs:10000; result:0.39883708808831186
500 Hilly's; Func runs:10000; result:0.2602779698842558
=============================
5 Forest's; Func runs:10000; result:0.5165008091396371
25 Forest's; Func runs:10000; result:0.30233740723010416
500 Forest's; Func runs:10000; result:0.1926906342754638
=============================
5 Megacity's; Func runs:10000; result:0.39384615384615385
25 Megacity's; Func runs:10000; result:0.1892307692307692
500 Megacity's; Func runs:10000; result:0.09903076923077013
=============================
All score:3.00488 (33.39%)

AOSアルゴリズムの可視化においては、原子の軌道上に特有の「集中」領域が見られるという興味深い挙動が確認できますが、収束の精度はあまり高くありません。

Hilly

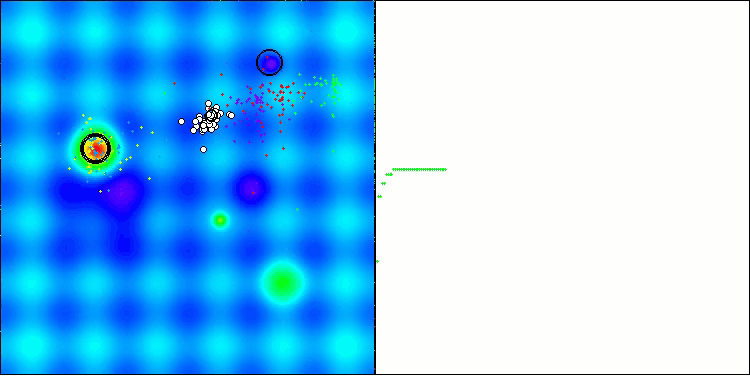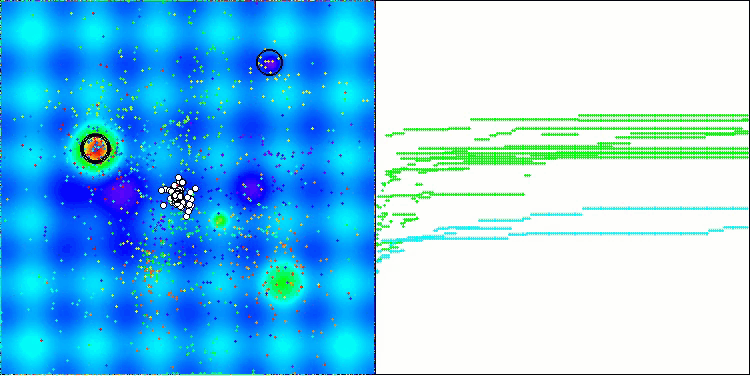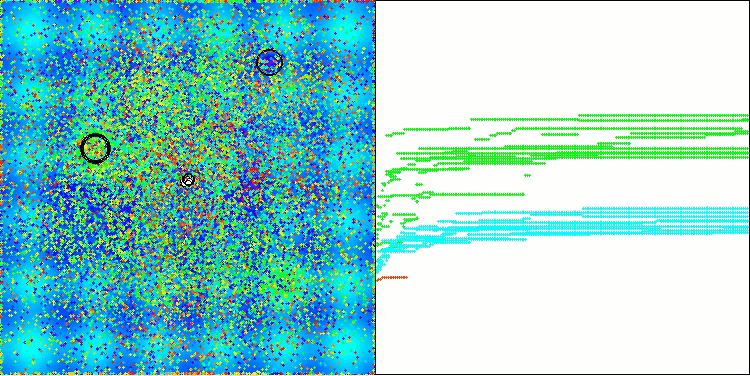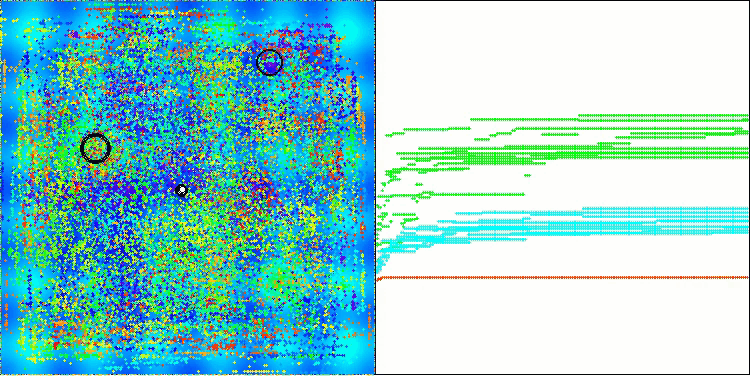
Hillyテスト関数のAOS

Forest

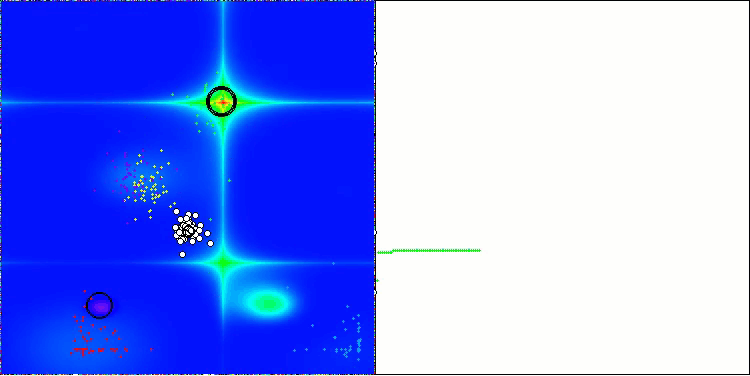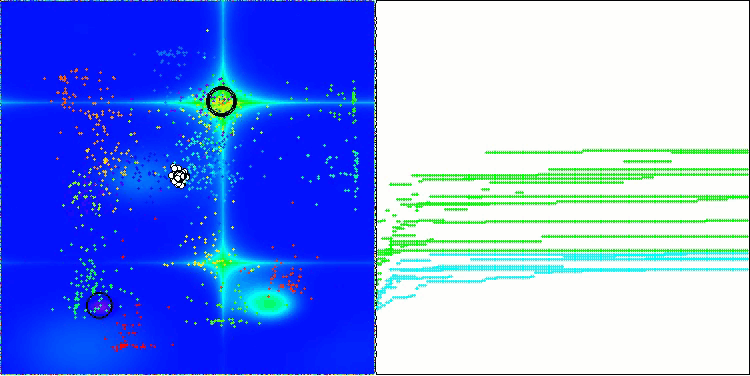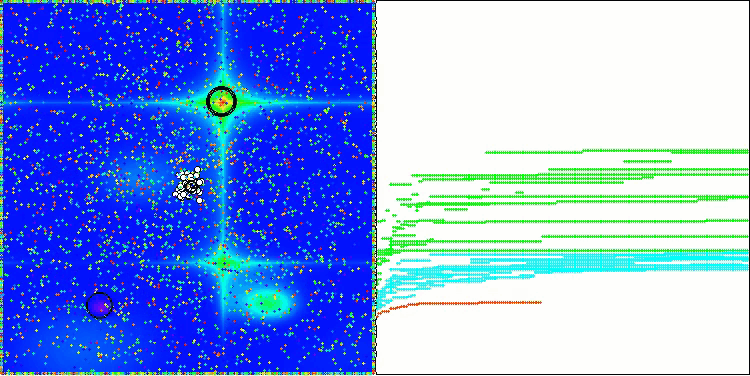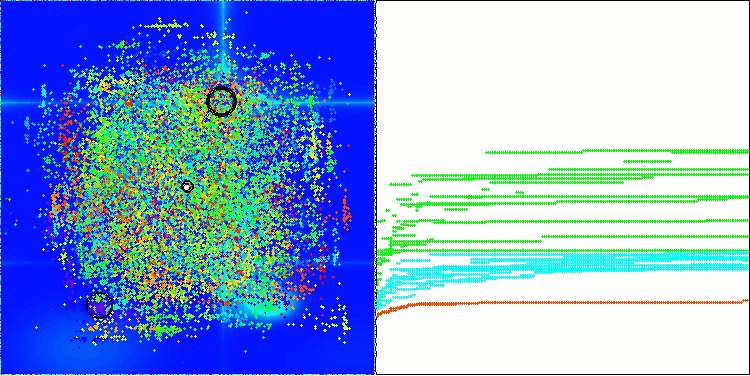
Forestテスト関数のAOS

Megacity

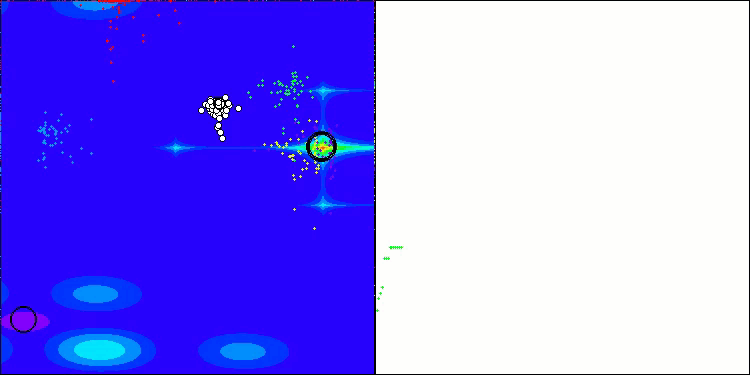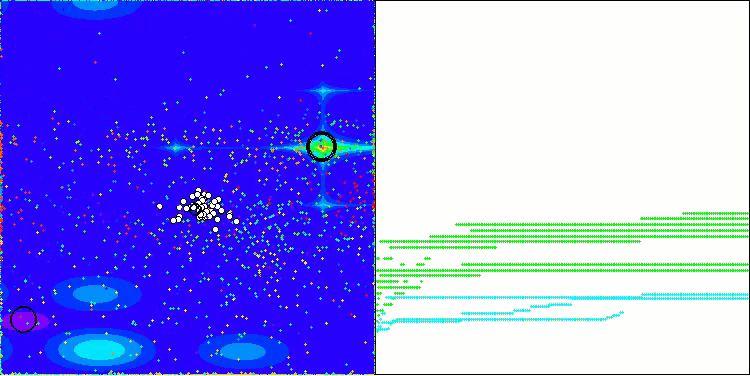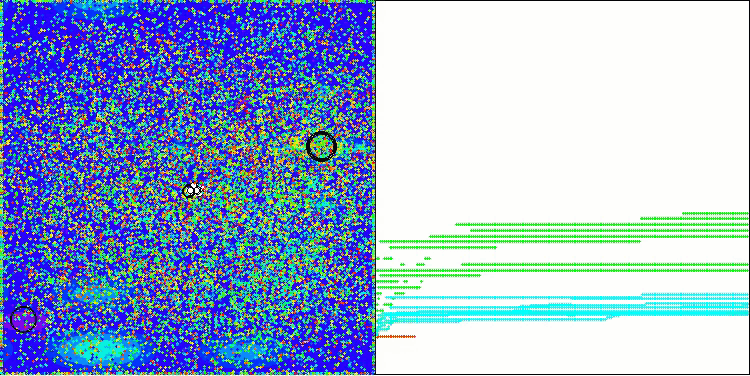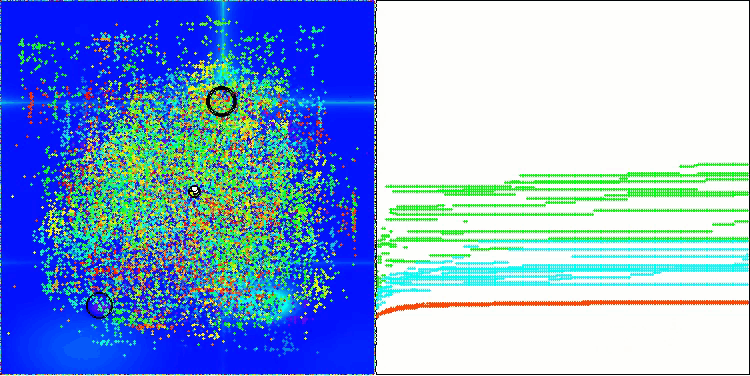
Megacityテスト関数のAOS

テスト結果に基づいて、AOSアルゴリズムは評価表で39位にランクされました。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
#	AO	詳細	10p(5F)	50p(25F)	1000p(500F)	Hilly最終	10p(5F)	50p(25F)	1000p(500F)	Forest最終	10p(5F)	50p(25F)	1000p(500F)	Megacity最終	最終結果	MAXの%
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	コードロックアルゴリズム(joo)	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	動物移動最適化m	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O)進化戦略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	彗星の尾アルゴリズム(joo)	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	AAm	アーチェリーアルゴリズムM	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
8	ESG	社会集団の進化(joo)	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
9	SIA	等方的焼きなまし(joo)	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
10	ACS	人工協調探索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
11	ASO	無政府社会最適化	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
12	TSEA	亀甲進化アルゴリズム(joo)	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
13	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
14	CRO	化学反応の最適化	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
15	BSA	鳥群アルゴリズム	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
16	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
17	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
18	BCOm	細菌走化性最適化M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
19	ABO	アフリカ水牛の最適化	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
20	(PO)ES	(PO)進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
21	TSm	タブーサーチM	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
22	BSO	ブレインストーム最適化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
23	WOAm	鯨最適化アルゴリズムM	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
24	AEFA	人工電界アルゴリズム	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
25	AEO	人工生態系ベースの最適化アルゴリズム	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
26	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
27	BFO-GA	細菌採食の最適化：Ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
28	ABHA	人工蜂の巣アルゴリズム	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
29	ACMO	大気雲モデルの最適化	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
30	ASHA	人工シャワーアルゴリズム	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
31	ASBO	適応型社会行動最適化(ASBO)	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
32	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
33	IWO	侵入雑草最適化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
34	Micro-AIS	微小人工免疫系	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
35	COAm	カッコウ最適化アルゴリズムM	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
36	SDOm	螺旋ダイナミクス最適化M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
37	NMm	ネルダー=ミード法M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
38	FAm	ホタルアルゴリズムM	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
39	AOS	原子軌道探索	0.65213	0.39884	0.26028	1.31125	0.51650	0.30234	0.19269	1.01153	0.39385	0.18923	0.09903	0.68211	3.005	33.39
40	GSA	重力探索法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
41	BFO	細菌採餌最適化	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
42	ABC	人工蜂コロニー	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
43	BA	コウモリアルゴリズム	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
44	AAA	藻類適応アルゴリズム	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23
45	SA	焼きなまし	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43

まとめ

大域的探索と局所的結果の洗練に革新的なアプローチを用いる、興味深い原子軌道探索(AOS: Atomic Orbital Search)アルゴリズムについて考察しました。原子の動的な軌道層のおかげで、電子は安定した原子状態を求めてバランスよく移動します。このアルゴリズムは滑らかな関数に対しては性能が限定的であるものの、問題の次元が増加した場合や、離散的なMegacity関数においては良好な結果を示します。

本アルゴリズムは将来性のあるアイデアの一例ですが、効率性は小さなものの重要ないくつかの要因によって損なわれているのが現状です。次回の記事では、私のAOSの改良版を取り上げ、この優れた軌道探索コンセプトが実際にどこまでの可能性を持っているのかを分析していきます。

Tab

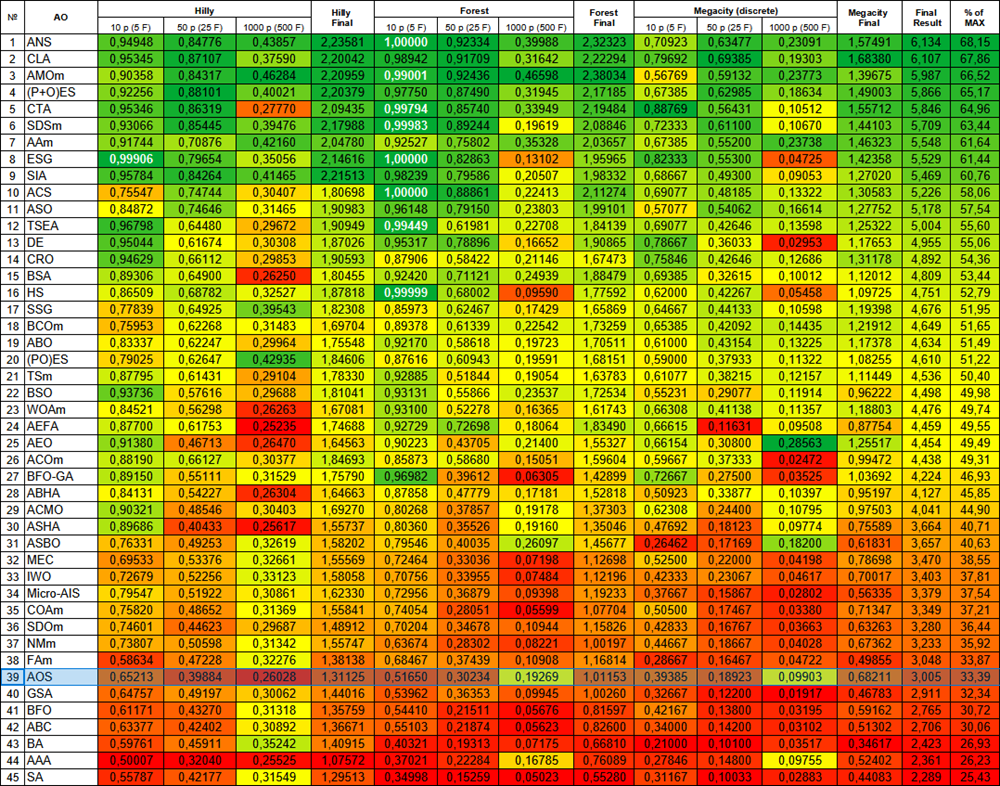
図3：関連するテスト結果に基づくアルゴリズムの色分け。0.99以上の結果は白色で強調表示されている

チャート

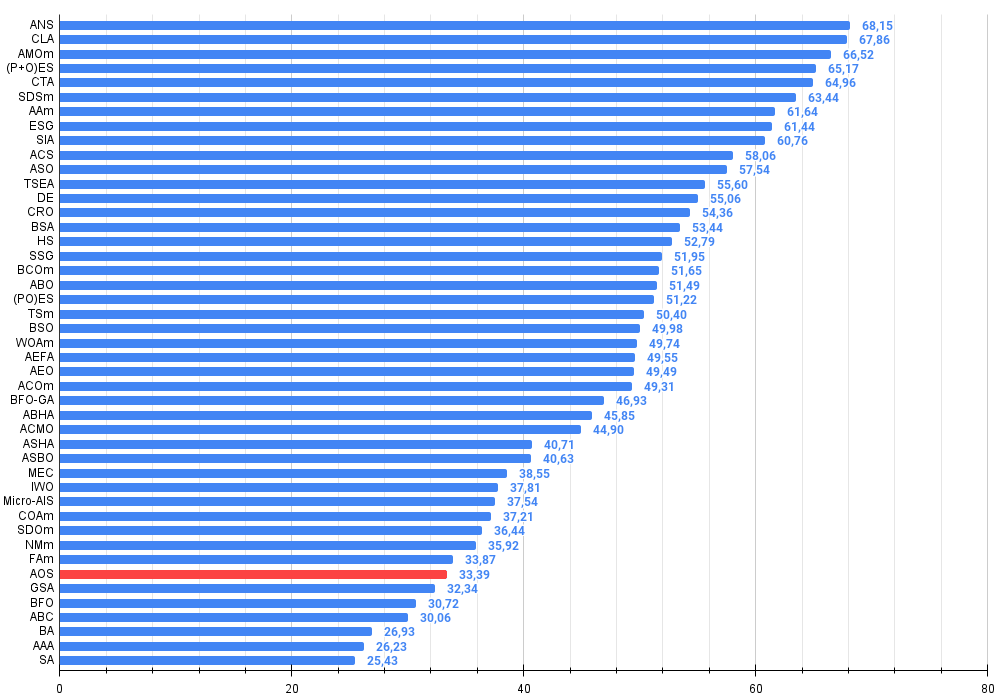
図4：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良い、

ここで、100は理論的に可能な最大の結果であり、アーカイブには評価表を計算するスクリプトが含まれている）

AOSの長所と短所

長所

アルゴリズムの改善のための有望な基盤
外部パラメータが少ない

短所

乱数が頻繁に生成されるため遅くなる
実装がかなり複雑
収束精度が低い

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

記事で使用されているプログラム

#	名前	種類	詳細
1	#C_AO.mqh	インクルード	集団最適化アルゴリズムの親クラス
2	#C_AO_enum.mqh	インクルード	集団最適化アルゴリズムの列挙
3	TestFunctions.mqh	インクルード	テスト関数のライブラリ
4	TestStandFunctions.mqh	インクルード	テストスタンド関数ライブラリ
5	Utilities.mqh	インクルード	補助関数のライブラリ
6	CalculationTestResults.mqh	インクルード	比較表の結果を計算するスクリプト
7	Testing AOs.mq5	スクリプト	すべての集団最適化アルゴリズムの統一テストスタンド
8	AO_AOS_AtomicOrbitalSearch.mqh	インクルード	AOSアルゴリズムクラス
9	Test_AO_AOS.mq5	スクリプト	AOSテストスタンド

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16276

添付されたファイル |

ZIPをダウンロード

AOS.zip (131.48 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

最後のコメント | ディスカッションに移動 (1)

Pavel Ustinov | 24 6月 2025 において 18:42

MetaQuotes:

原子軌道探索アルゴリズム - 原子軌道探索（AOS）が発表されました：

著者：Andrey Dik

これは物理学、数学、チェスなどを含むシステム全体です。

Numbaを使用したPythonの高速取引ストラテジーテスター

この記事では、Numbaを使った機械学習モデルのための高速ストラテジーテスターを実装しています。純粋なPythonのストラテジーテスターと比べて50倍速く動作します。このライブラリを使って特にループを含む数学計算を高速化することを推奨しています

取引におけるニューラルネットワーク：双曲潜在拡散モデル（最終回）

HypDiffフレームワークで提案されているように、双曲潜在空間における初期データのエンコーディングに異方性拡散プロセスを用いることで、現在の市場状況におけるトポロジー的特徴を保持しやすくなり、分析の質を向上させることができます。前回の記事では、提案されたアプローチの実装をMQL5を用いて開始しました。今回はその作業を継続し、論理的な完結に向けて進めていきます。

未来のトレンドを見通す鍵としての取引量ニューラルネットワーク分析

この記事では、テクニカル分析の原理とLSTMニューラルネットワークの構造を統合することで、取引量分析に基づく価格予測の改善可能性を探ります。特に、異常な取引量の検出と解釈、クラスタリングの活用、および機械学習の文脈における取引量に基づく特徴量の作成と定義に注目しています。

取引におけるニューラルネットワーク：双曲潜在拡散モデル(HypDiff)

この記事では、異方性拡散プロセスを用いた双曲潜在空間における初期データのエンコーディング手法について検討します。これにより、現在の市場状況におけるトポロジー的特徴をより正確に保持でき、分析の質が向上します。