
Der Algorithmus Atomic Orbital Search (AOS) Modifizierung
Inhalt
- Einführung
- Implementierung des Algorithmus
- Ein Beispiel für die Verwendung der Klasse C_AO
- Testergebnisse
Einführung
Im ersten Teil des Artikels haben wir die Grundlagen des Algorithmus AOS (Atomic Orbital Search) untersucht, der sich am Atomorbitalmodell und den ihm zugrunde liegenden Mechanismen orientiert. Wir erörterten, wie der Algorithmus Wahrscheinlichkeitsverteilungen und Interaktionsdynamik nutzt, um optimale Lösungen für komplexe Optimierungsprobleme zu finden.
Im zweiten Teil des Artikels werden wir uns auf die Modifizierung des AOS-Algorithmus konzentrieren, da wir an einer so hervorragenden Idee nicht vorbeigehen können, ohne zu versuchen, sie zu verbessern. Wir werden das Konzept zur Verbesserung des Algorithmus analysieren und dabei besonderes Augenmerk auf die spezifischen Operatoren legen, die dieser Methode eigen sind und ihre Effizienz und Anpassungsfähigkeit verbessern können.
Die Arbeit am AOS-Algorithmus hat mir viele interessante Aspekte in Bezug auf seine Methoden zur Suche im Lösungsraum eröffnet. Während der Recherche habe ich auch eine Reihe von Ideen entwickelt, wie dieser interessante Algorithmus verbessert werden könnte. Insbesondere habe ich mich auf die Überarbeitung bestehender Methoden konzentriert, die die Leistung des Algorithmus durch die Verbesserung seiner Fähigkeit, komplexe Lösungsräume zu erkunden, erhöhen können. Wir werden untersuchen, wie diese Verbesserungen in die bestehende Struktur des AOS-Algorithmus integriert werden können, um ihn zu einem noch leistungsfähigeren Werkzeug für die Lösung von Optimierungsproblemen zu machen. Unser Ziel ist es also nicht nur, die bestehenden Mechanismen zu analysieren, sondern auch andere Ansätze vorzuschlagen, die die Möglichkeiten des AOS-Algorithmus erheblich erweitern können.
Implementierung des Algorithmus
Im vorangegangenen Artikel haben wir einen detaillierten Blick auf die wichtigsten Komponenten des AOS-Algorithmus geworfen. Wie Sie sich vielleicht erinnern, wird bei diesem Algorithmus die Population als Molekül betrachtet, und der zulässige Koordinatenbereich, in dem die Suche nach optimalen Lösungen durchgeführt wird, wird als Atom dargestellt. Jedes Atom besteht aus verschiedenen Schichten, die dazu beitragen, die Suche zu ordnen und zu lenken.
Die spezifischen Koordinatenwerte, die wir während der Optimierung erhalten, können als Elektronen interpretiert werden. Diese Elektronen, die sich innerhalb des Atoms befinden, stellen mögliche Lösungen für einen der Parameter des zu optimierenden Problems dar. So strebt jedes Molekül (Population) danach, innerhalb einer bestimmten Region (Atom) optimale Werte (Elektronen) zu finden.
In der ursprünglichen Version des AOS-Algorithmus ist die Schichtenergie BEk als das arithmetische Mittel der Energie der Elektronen in der Schicht und die Bindung BSk als das arithmetische Mittel ihrer Koordinaten definiert. Die BEk-Energie wird mit der Energie der Elektronen verglichen, um die Art ihrer anschließenden Bewegung zu bestimmen. Die BSk-Verbindung wird verwendet, um den Positionszuwachs der Elektronen als Differenz zwischen der besten Position der Elektronen LEk in der Schicht und der BSk-Verbindung gemäß der folgenden Gleichung zu berechnen: Xki[t+1] = Xkit + αi × (βi × LEk − γi × BSk).
Ich schlage vor, die BSk-Durchschnittsposition der Elektronen zugunsten der persönlich besten Position des Elektrons aufzugeben. Das Elektron bewegt sich also auf die beste Lösung in seiner Schicht zu, basierend auf seiner individuellen Leistung, nicht auf der durchschnittlichen Lösung in der gesamten Schicht. Außerdem scheinen die beiden Zufallskomponenten βi und γi überflüssig, da es bereits eine externe Zufallskomponente αi gibt. Dadurch wird die Zeit für die Erzeugung von Zufallszahlen in dieser Gleichung um das Dreifache reduziert, ohne dass die physikalische Bedeutung verloren geht.
Schauen wir uns nun die Struktur an, die eine Schicht in einem Atom beschreibt. Aus dem Code entfernte Elemente sind rot hervorgehoben://—————————————————————————————————————————————————————————————————————————————— struct S_Layer { int pc; // particle counter double BSk; // connection state double BEk; // binding energy double LEk; // minimum energy void Init () { pc = 0; BSk = 0.0; BEk = 0.0; LEk = 0.0; } }; //——————————————————————————————————————————————————————————————————————————————
Betrachten wir den Code der CalcLayerParams-Methode, mit der die Eigenschaften der Schicht wie Energie und Konnektivität berechnet werden. Die rot markierten Zeichenfolgen werden entfernt, da sie nicht mehr benötigt werden. Wie Sie sich vielleicht erinnern, spielt diese Methode eine Schlüsselrolle in der AOS-Suchstrategie, die verhindern soll, dass der Algorithmus in lokalen Fallen stecken bleibt. Da das Energieniveau in den Schichten nicht von ihrer Lage abhängt (die Energie nimmt vom Zentrum zu den äußeren Schichten des Atoms ab), sondern durch das Vorhandensein signifikanter lokaler Extreme bestimmt wird (die äußere Schicht kann eine höhere Energie haben als die innere), dienen die Schichten dazu, die Bewegung der Elektronen im Suchraum zu korrigieren.
Die zufällige Anzahl der Schichten in jeder Epoche trägt dazu bei, dass der Algorithmus nicht in lokalen Fallen stecken bleibt und die Elektronen nicht nur in einer der Schichten stagnieren. Mit der geänderten Version entfällt auch die Notwendigkeit, die durchschnittliche Energie über das gesamte Atom zu berechnen, sodass wir die entsprechenden Zeilen entfernen.

Abbildung 1. Der Unterschied in Richtung und Größe der Elektronenverschiebung e in Abhängigkeit von der Anzahl der Schichten im Atom
Abbildung 1 veranschaulicht die Unterschiede im Verhalten der Elektronen in Atomen mit unterschiedlicher Anzahl von Schichten im AOS-Algorithmus. Das obere Feld zeigt ein Drei-Schichten-Atom, bei dem sich das Elektron in der Schicht L1 mit dem B1-Zielfunktionswert befindet und sich in Richtung des lokal besten Wertes LEk1 bewegt. Der untere Teil der Abbildung zeigt ein Atom mit zwei Schichten, bei dem sich das Elektron ebenfalls in der Schicht L1 befindet und sich auf den lokal besten Wert LEk1 mit dem Zielfunktionswert B1 zubewegt (im Falle von drei Schichten wäre dies der Punkt LEk2).
Schlüsselelemente in der Abbildung:
- B0, B1, B2 - Bezeichnungen der lokalen Werte der Zielfunktion für die entsprechenden Schichten,
- LEk0, LEk1, LEk2 - beste Lösungen in den entsprechenden Schichten,
- L0, L1, L2 - Atomschichten,
- e - Elektron,
- MIN, MAX - Grenzen der äußeren Schichten von Atomen (Randbedingungen für die optimierten Parameter des Problems).
//—————————————————————————————————————————————————————————————————————————————— // Calculate parameters for each layer void C_AO_AOS::CalcLayerParams () { double energy; // Handle each coordinate (atom) for (int c = 0; c < coords; c++) { atoms [c].Init (maxLayers); // Handle each layer for (int L = 0; L < currentLayers [c]; L++) { energy = -DBL_MAX; // Handle each electron for (int e = 0; e < popSize; e++) { if (electrons [e].layerID [c] == L) { atoms [c].layers [L].pc++; atoms [c].layers [L].BEk += a [e].f; atoms [c].layers [L].BSk += a [e].c [c]; if (a [e].f > energy) { energy = a [e].f; atoms [c].layers [L].LEk = a [e].c [c]; } } } // Calculate average values for the layer if (atoms [c].layers [L].pc != 0) { atoms [c].layers [L].BEk /= atoms [c].layers [L].pc; atoms [c].layers [L].BSk /= atoms [c].layers [L].pc; } } } // Calculate the general state of connections ArrayInitialize (BS, 0); for (int c = 0; c < coords; c++) { for (int e = 0; e < popSize; e++) { BS [c] += a [e].c [c]; } BS [c] /= popSize; } } //——————————————————————————————————————————————————————————————————————————————
Um die besten Einzellösungen zu aktualisieren, fügen wir den Code in die Methode Revision der geänderten Version von C_AO_AOSm ein.
//—————————————————————————————————————————————————————————————————————————————— // Method of revising the best solutions void C_AO_AOSm::Revision () { int bestIndex = -1; // Find the best solution in the current iteration for (int i = 0; i < popSize; i++) { // Update the global best solution if (a [i].f > fB) { fB = a [i].f; bestIndex = i; } // Update the personal best solution if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } // Update the best coordinates if a better solution is found if (bestIndex != -1) ArrayCopy (cB, a [bestIndex].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
In der Methode UpdateElectrons entfernen wir die Variablen β und γ, da sie für die Generierung der entsprechenden Zufallszahlen nicht benötigt werden. Darüber hinaus ist die Löschung des Elektroneninkrements um die Anzahl der Schichten bei der Bewegung in Richtung der globalen Lösung auszuschließen. Offen gesagt, scheint die Lösung der Autoren umstritten, und die physikalische Bedeutung dieses Ansatzes ist nicht ganz klar. Vielleicht wollten die Autoren den Grad der Elektronenbewegung in Richtung Globallösung variabel gestalten, indem sie ihn von der Anzahl der Schichten abhängig machten: je weniger Schichten, desto intensiver sollte die Bewegung sein (obwohl meine Experimente gezeigt haben, dass dies nicht der Fall ist).
//—————————————————————————————————————————————————————————————————————————————— // Update electron positions void C_AO_AOS::UpdateElectrons () { double α; // speed coefficient double β; // best solution weight coefficient double γ; // average state weight coefficient double φ; // transition probability double newPos; // new position double LE; // best energy double BSk; // connection state int lID; // layer ID // Handle each particle for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Random scatter newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); β = u.RNDprobab (); γ = u.RNDprobab (); // If the current particle energy is less than the average layer energy if (a [p].f < atoms [c].layers [lID].BEk) { // Moving towards the global optimum---------------------------- LE = cB [c]; newPos = a [p].c [c]+ α * (β * LE - γ * BS [c]) / currentLayers [c]; } else { // Movement towards the local optimum of the layer------------------------ LE = atoms [c].layers [lID].LEk; BSk = atoms [c].layers [lID].BSk; newPos = a [p].c [c] + α * (β * LE - γ * BSk); } } // Limiting the new position within the search range taking into account the step a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Außerdem wird in der Methode UpdateElectrons der Klasse C_AO_AOSm das Elektron nicht zufällig über den Suchraum gestreut, sondern mit einer gewissen Wahrscheinlichkeit zum Kernzentrum bewegt. Im Wesentlichen bedeutet dies, dass der Wert einer bestimmten Koordinate durch den Wert der globalen Lösung ersetzt wird, was die kombinatorischen Eigenschaften des Algorithmus verbessern dürfte. Die zufällige Streuung sollte für Vielfalt in der Lösungspopulation sorgen, aber diese Eigenschaft gewährleistete die Verteilung der Elektronen gemäß einer Log-Normalverteilung, bei der die Wahrscheinlichkeit, dass ein Elektron während seiner Bewegung auf einen beliebigen Punkt im Raum trifft, von Null verschieden ist.
Änderungen in den Gleichungen für die Elektronenbewegung werden in Grün angezeigt. Nun wird der Zuwachs als Differenz zwischen der lokal besten Lösung der Schicht und der individuell besten Lösung des Elektrons berechnet.
//—————————————————————————————————————————————————————————————————————————————— // Update electron positions void C_AO_AOSm::UpdateElectrons () { double α; // speed coefficient double φ; // transition probability double newPos; // new position double LE; // best energy double BSk; // connection state int lID; // layer ID // Handle each particle for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Random jump to center newPos = cB [c]; } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); // If the current particle energy is less than the average layer energy if (a [p].f < atoms [c].layers [lID].BEk) { // Moving towards the global optimum---------------------------- LE = cB [c]; newPos = a [p].cB [c]+ α * (LE - a [p].cB [c]); } else { // Movement towards the local optimum of the layer------------------------ LE = atoms [c].layers [lID].LEk; newPos = a [p].cB [c]+ α * (LE - a [p].cB [c]); } } // Limiting the new position within the search range taking into account the step a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode DistributeParticles verteilt die Elektronen im Suchraum unter Verwendung einer Log-Normalverteilung für jede Koordinate. Für jedes Partikel und jede Koordinate wird eine Funktion aufgerufen, die eine Position mit den gegebenen Parametern (Mittelwert, Minimal- und Maximalwert, Spitzenwert) generiert, und dann wird eine weitere Funktion angewendet, um die Position innerhalb des gegebenen Bereichs anzupassen.
//—————————————————————————————————————————————————————————————————————————————— // Distribution of particles in the search space void C_AO_AOS::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Use log-normal distribution to position particles a [i].c [c] = u.LognormalDistribution (cB [c], rangeMin [c], rangeMax [c], peakPosition); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Ändern Sie die Elektronenverteilung auf normal. Diese Verteilung hat eine Standardabweichung von 8. Obwohl dieser Parameter auch extern in den Algorithmus hätte aufgenommen werden können, habe ich darauf verzichtet. Kleinere Werte fördern eine breitere Erkundung des Suchraums, während höhere Werte die Genauigkeit der Konvergenz bei der Verfeinerung der globalen Lösung verbessern.
//—————————————————————————————————————————————————————————————————————————————— // Distribution of particles in the search space void C_AO_AOSm::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Use a Gaussian distribution to position particles a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Alle Änderungen, die an der ursprünglichen Version des AOS-Algorithmus vorgenommen wurden, wurden analysiert, um seine Effizienz zu verbessern. Da wesentliche Änderungen an der Logik der Suchstrategie vorgenommen wurden, kann die modifizierte Version des Algorithmus mit dem Buchstaben „m“ bezeichnet werden. Von nun an wird nur noch die geänderte Version in der Bewertungstabelle - AOSm - aufgeführt.
Ein Beispiel für die Verwendung der Klasse C_AO
Da alle zuvor besprochenen Algorithmen der Populationsoptimierungen von der allgemeinen Klasse C_AO abgeleitet werden, können sie einheitlich und mit minimalem Aufwand zur Lösung verschiedener Probleme verwendet werden, die die Auswahl optimaler Parameter erfordern. Das folgende Beispiel zeigt ein Skript, das eine Optimierung der Zielfunktion durchführt:
1. Zu Beginn des Skripts können Sie wählen, welchen Optimierungsalgorithmus Sie verwenden möchten. Wenn nichts ausgewählt wird, meldet das Skript einen Fehler und hält an.
2. Einstellung der Parameter. Das Skript legt fest, wie oft die Funktion ausgeführt werden soll, wie viele Parameter optimiert werden müssen, wie groß die Lösungsgruppe ist und wie viele Iterationen durchgeführt werden sollen.
3. Wertgrenzen. Für jeden Parameter werden Mindest- und Höchstwerte festgelegt (in diesem Beispiel von -10 bis 10).
4. Das Skript beginnt mit der Optimierung:
- Es erzeugt Lösungen (Parametersätze) und prüft deren Güte anhand einer speziellen Funktion (der Zielfunktion).
- Bei jeder Iteration aktualisiert der Algorithmus seine Lösungen auf der Grundlage derjenigen, die am besten abgeschnitten haben.
5. Ergebnisse. Nach Abschluss der Optimierung gibt das Skript Informationen darüber aus, welcher Algorithmus verwendet wurde, welcher beste Wert gefunden wurde und wie oft die Funktion aufgerufen wurde.
6. Die Zielfunktion ist ein abstraktes Optimierungsproblem (in diesem Beispiel wird das Problem der Suche nach dem globalen Maximum einer umgekehrten Parabel verwendet), das Parameter annimmt und eine Bewertung für deren Qualität liefert.
#property script_show_inputs // Specify that the script will show the inputs in the properties window #include <Math\AOs\PopulationAO\#C_AO_enum.mqh> // Connect the library for handling optimization algorithms input E_AO AOexactly = NONE_AO; // Parameter for selecting the optimization algorithm, default is NONE_AO //—————————————————————————————————————————————————————————————————————————————— void OnStart() { //---------------------------------------------------------------------------- int numbTestFuncRuns = 10000; // Total number of function runs int params = 1000; // Number of parameters for optimization int popSize = 50; // Population size for optimization algorithm int epochCount = numbTestFuncRuns / popSize; // Total number of epochs (iterations) for optimization double rangeMin [], rangeMax [], rangeStep []; // Arrays for storing the parameters' boundaries and steps ArrayResize (rangeMin, params); // Resize 'min' borders array ArrayResize (rangeMax, params); // Resize 'max' borders array ArrayResize (rangeStep, params); // Resize the steps array // Initialize the borders and steps for each parameter for (int i = 0; i < params; i++) { rangeMin [i] = -10; // Minimum value of the parameter rangeMax [i] = 10; // Maximum value of the parameter rangeStep [i] = DBL_EPSILON; // Parameter step } //---------------------------------------------------------------------------- C_AO *ao = SelectAO (AOexactly); // Select an optimization algorithm if (ao == NULL) // Check if an algorithm has been selected { Print ("AO not selected..."); // Error message if no algorithm is selected return; } ao.params [0].val = popSize; // Assigning population size.... ao.SetParams (); //... (optional, then default population size will be used) ao.Init (rangeMin, rangeMax, rangeStep, epochCount); // Initialize the algorithm with given boundaries and number of epochs // Main loop by number of epochs for (int epochCNT = 1; epochCNT <= epochCount; epochCNT++) { ao.Moving (); // Execute one epoch of the optimization algorithm // Calculate the value of the objective function for each solution in the population for (int set = 0; set < ArraySize (ao.a); set++) { ao.a [set].f = ObjectiveFunction (ao.a [set].c); // Apply the objective function to each solution } ao.Revision (); // Update the population based on the results of the objective function } //---------------------------------------------------------------------------- // Output the algorithm name, best result and number of function runs Print (ao.GetName (), ", best result: ", ao.fB, ", number of function launches: ", numbTestFuncRuns); delete ao; // Release the memory occupied by the algorithm object } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Definition of the user's objective function, in this case as an example - a paraboloid, F(Xn) ∈ [0.0; 1.0], X ∈ [-10.0; 10.0], maximization double ObjectiveFunction (double &x []) { double sum = 0.0; // Variable for accumulation of the result // Loop through all parameters for (int i = 0; i < ArraySize (x); i++) { // Check if the parameter is in the allowed range if (x [i] < -10.0 || x [i] > 10.0) return 0.0; // If the parameter is out of range, return 0 sum += (-x [i] * x [i] + 100.0) * 0.01; // Calculate the value of the objective function } return sum /= ArraySize (x); } //——————————————————————————————————————————————————————————————————————————————
Testergebnisse
Testen wir nun die geänderte Version des Algorithmus.
AOS|Atomic Orbital Search|50.0|10.0|20.0|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.8023218355650774
25 Hilly's; Func runs: 10000; result: 0.7044908398821188
500 Hilly's; Func runs: 10000; result: 0.3102116882841442
=============================
5 Forest's; Func runs: 10000; result: 0.8565993699987462
25 Forest's; Func runs: 10000; result: 0.6945107796904211
500 Forest's; Func runs: 10000; result: 0.21996085558228406
=============================
5 Megacity's; Func runs: 10000; result: 0.7461538461538461
25 Megacity's; Func runs: 10000; result: 0.5286153846153846
500 Megacity's; Func runs: 10000; result: 0.1435846153846167
=============================
All score: 5.00645 (55.63%)
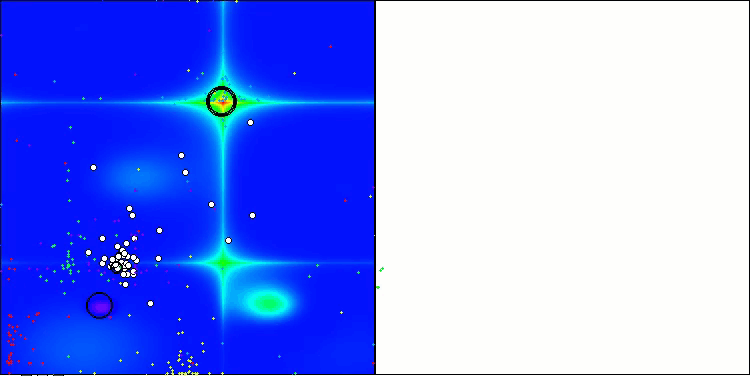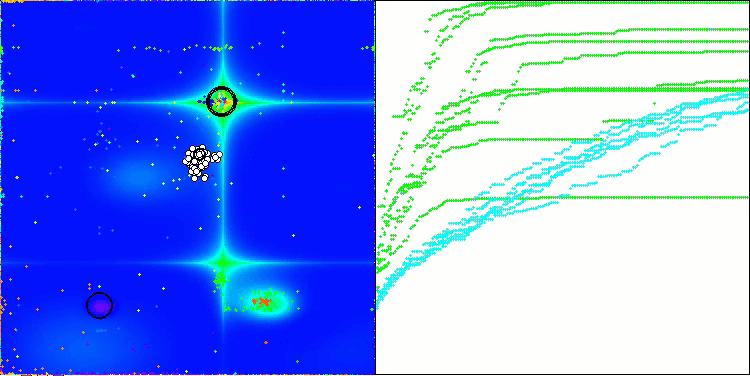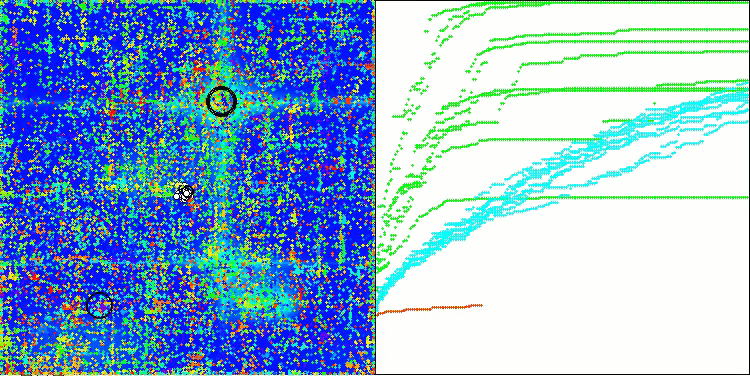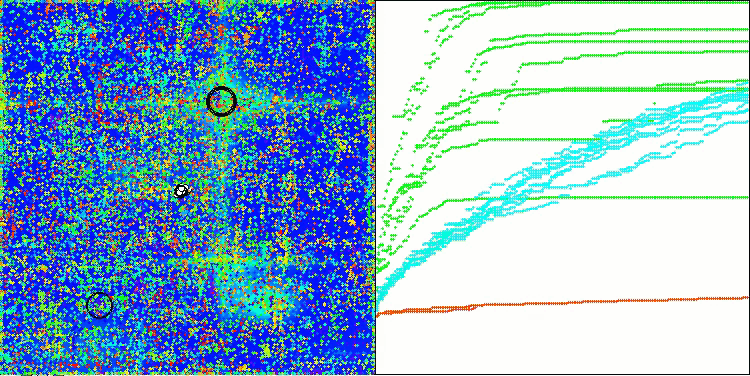
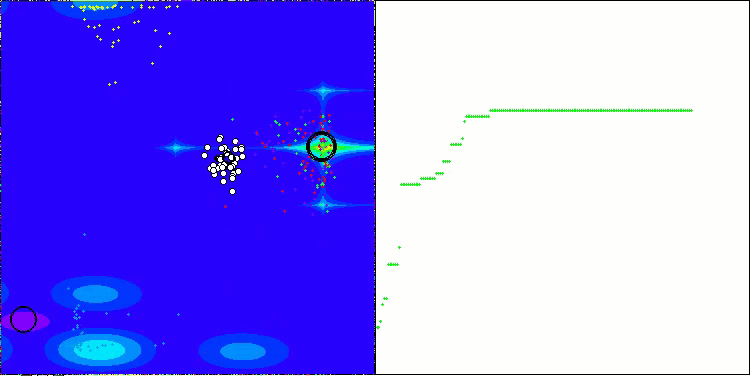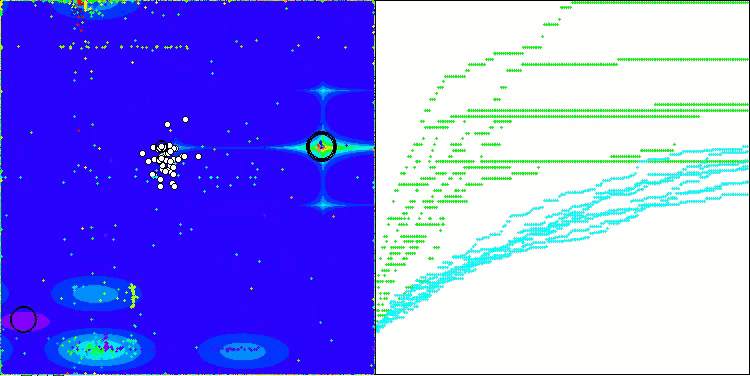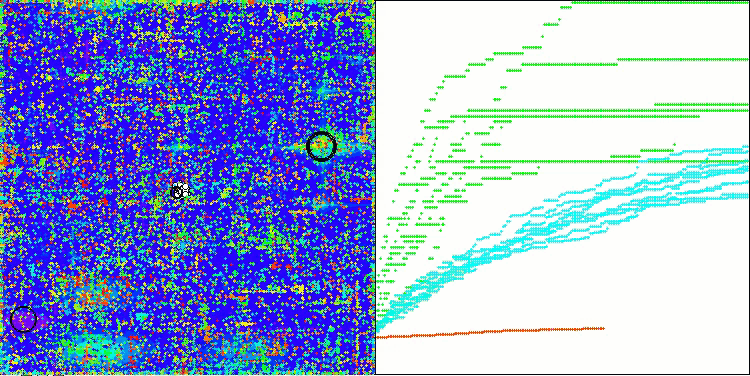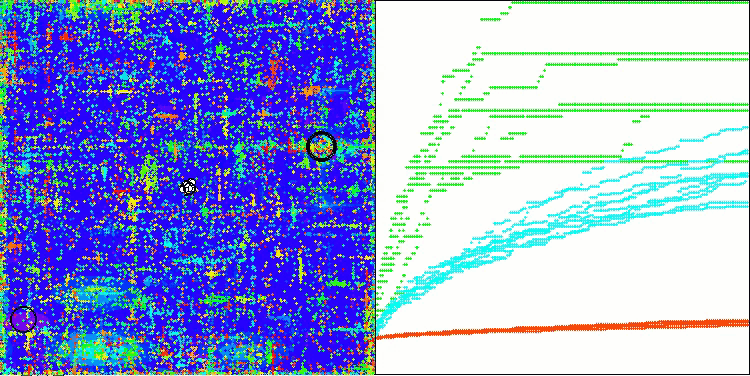
Wie man sehen kann, haben sich die Ergebnisse der geänderten Version im Vergleich zu den früheren Ergebnissen der ursprünglichen Version, bei der die Gesamtpunktzahl 3,00488 (33,39 %) betrug, erheblich verbessert. Diese Verbesserung wird bei der Analyse der Visualisierung deutlich, die nicht nur eine verbesserte Konvergenz, sondern auch eine detailliertere Ausarbeitung signifikanter Extremwerte zeigt.
Einer der wichtigsten Aspekte ist die Auswirkung der „Verklumpung“ von Lösungen auf einzelne Koordinaten. Dieses Phänomen ist sowohl in der ursprünglichen als auch in der modifizierten Version zu beobachten, was die charakteristische Eigenschaft der AOS-Algorithmen unterstreicht. Die Verklumpung von Lösungen kann darauf hindeuten, dass der Algorithmus effektiv Bereiche findet, in denen sich potenziell optimale Lösungen befinden.
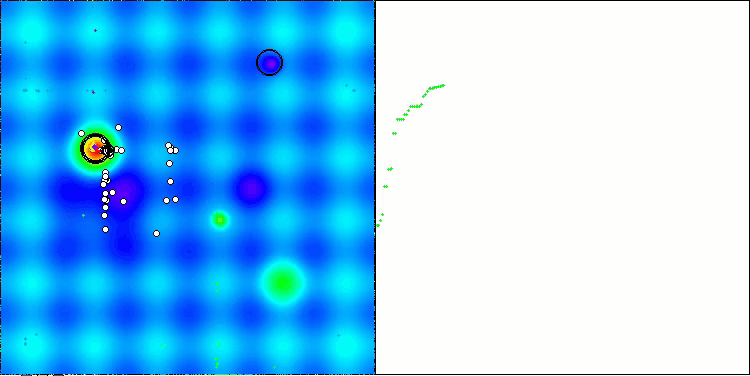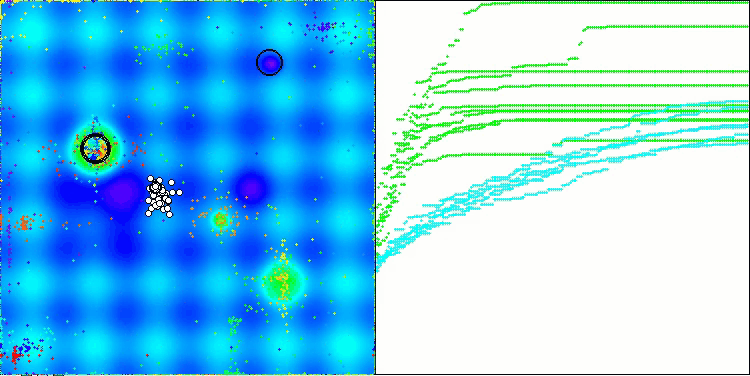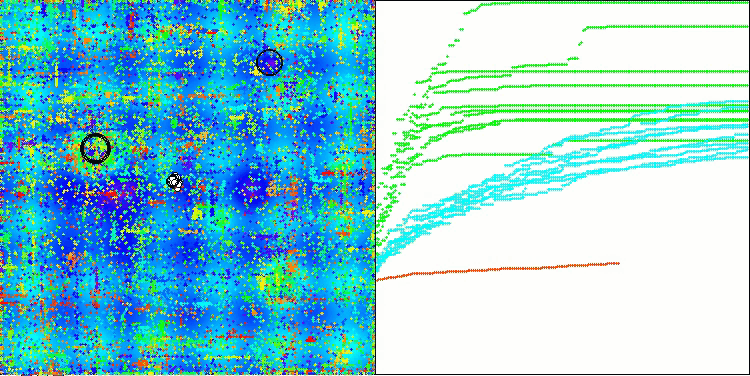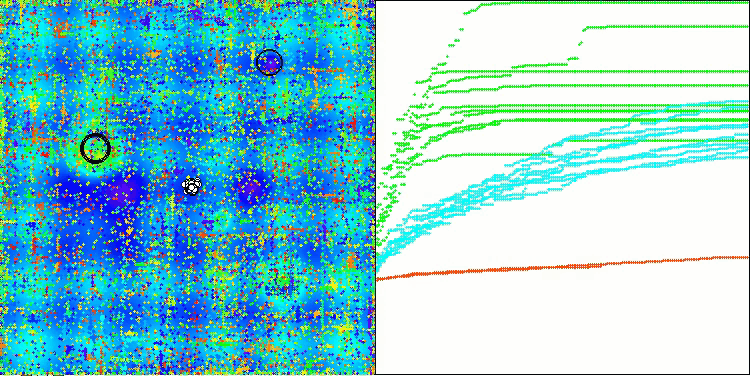
AOSm mit der Testfunktion Hilly
AOSm mit der Testfunktion Forest
AOSm mit der Testfunktion Megacity
Die modifizierte Version des Atomic Orbital Search (AOS)-Algorithmus hat seine Leistung im Vergleich zur ursprünglichen Version erheblich verbessert und erreicht nun mehr als 55 % des maximal möglichen Wertes. Das ist ein wirklich beeindruckendes Ergebnis! In der Bewertungstabelle nimmt der Algorithmus den 12. Platz ein, was auf sehr gute Ergebnisse schließen lässt.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Code-Sperr-Algorithmus (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | Entwicklung sozialer Gruppen (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | Simuliertes isotropes Glühen (Joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 12 | AOSm | Suche nach atomaren Orbitalen M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 13 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 14 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 15 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 16 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 17 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 18 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 19 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 20 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 21 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 22 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 23 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 24 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 25 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 26 | AEO | Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 27 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 28 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 29 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 30 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 31 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 32 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 33 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 34 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 35 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 36 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 37 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 38 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 39 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 40 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 41 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 42 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 43 | BA | Fledermaus-Algorithmus | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 44 | AAA | Künstlicher Algenalgorithmus (AAA) | 0.50007 | 0.32040 | 0.25525 | 1.07572 | 0.37021 | 0.22284 | 0.16785 | 0.76089 | 0.27846 | 0.14800 | 0.09755 | 0.52402 | 2.361 | 26.23 |
| 45 | SA | Simuliertes Abkühlen | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
Zusammenfassung
In diesem Artikel wurde eine modifizierte Version des Algorithmus zur Suche von Atomorbitalen (AOSm) vorgestellt, in der ich die BSk-Durchschnittsposition der Elektronen in den Atomschichten zugunsten der individuell besten Position jedes Elektrons aufgegeben habe. Dadurch konnten sich die Elektronen effizienter zur besten Lösung in ihrer Schicht bewegen, basierend auf der individuellen Leistung und nicht auf einem Durchschnittswert. Außerdem wurden zwei Zufallskomponenten βi und γi ausgeschlossen, was die Zeit für die Erzeugung von Zufallszahlen um das Dreifache reduzierte, ohne dass die physikalische Bedeutung des Algorithmus verloren ging.
In der Methode UpdateElectrons wurden unnötige Variablen entfernt und die Unterteilung des Elektroneninkrements durch die Anzahl der Schichten beim Übergang zur globalen Lösung eliminiert. Auch wenn die Autoren der Originalversionen beabsichtigt haben mögen, dass der Grad der Bewegung variabel ist, haben meine Experimente gezeigt, dass dies keine signifikanten Vorteile bringt.
Änderungen wurden auch an der UpdateElectrons-Methode in der Klasse C_AO_AOSm vorgenommen - die zufällige Streuung eines Elektrons wurde durch eine Bewegung zum Zentrum des Kerns mit einer bestimmten Wahrscheinlichkeit ersetzt. Dadurch wurden die kombinatorischen Eigenschaften des Algorithmus verbessert, sodass die Elektronen die globale Lösung genauer anpeilen können. Außerdem wurde die Log-Normalverteilung durch eine Normalverteilung ersetzt, was die Genauigkeit der Konvergenz bei der Verfeinerung der globalen Lösung erhöhte.
Die Ergebnisse der modifizierten Version von AOSm zeigten eine signifikante Verbesserung, mit einer Gesamtpunktzahl von mehr als 55 % der maximal möglichen Punktzahl, was die hohe Effizienz und Wettbewerbsfähigkeit des Algorithmus bestätigt. AOSm belegt den 12. Platz in der Rangliste, was zeigt, dass es im Vergleich zu anderen Optimierungsmethoden sehr erfolgreich ist.
Einer der auffälligsten Aspekte von AOSm ist die Verbesserung der Konvergenz, die bei der Visualisierung der Ergebnisse deutlich wurde. Der Algorithmus arbeitet signifikante Extreme detaillierter aus und demonstriert die Fähigkeit, in komplexen mehrdimensionalen Räumen effektiv nach optimalen Lösungen zu suchen. Der „Klumpen“-Effekt der Lösungen, der sowohl in der ursprünglichen als auch in der modifizierten Version zu beobachten ist, unterstreicht die Fähigkeit des Algorithmus, Bereiche mit potenziellen Optima zu finden und sich darauf zu konzentrieren, was besonders bei Problemen mit hoher Dimensionalität und komplexer Struktur nützlich ist.
Ein zusätzliches Plus zu den Vorteilen der modifizierten Version ist die Verringerung der Anzahl der externen Parameter, was die Nutzung und Konfiguration vereinfacht. Für alle in den Artikeln vorgestellten Algorithmen habe ich jedoch die optimalen externen Parameter ausgewählt, um eine maximale Effizienz bei komplexen Tests für verschiedene Arten von Testaufgaben zu erreichen. Alle Algorithmen sind also sofort einsatzbereit und müssen nicht konfiguriert werden. Der Artikel zeigt, dass manchmal kleinste Änderungen an Optimierungsalgorithmen deren Sucheigenschaften dramatisch verändern können, während bedeutende Änderungen in der Logik der Suchstrategie möglicherweise keine spürbaren Veränderungen in den Ergebnissen bewirken. In meinen Artikeln teile ich natürlich die Methoden, die die Effizienz der Optimierung wirklich verbessern.
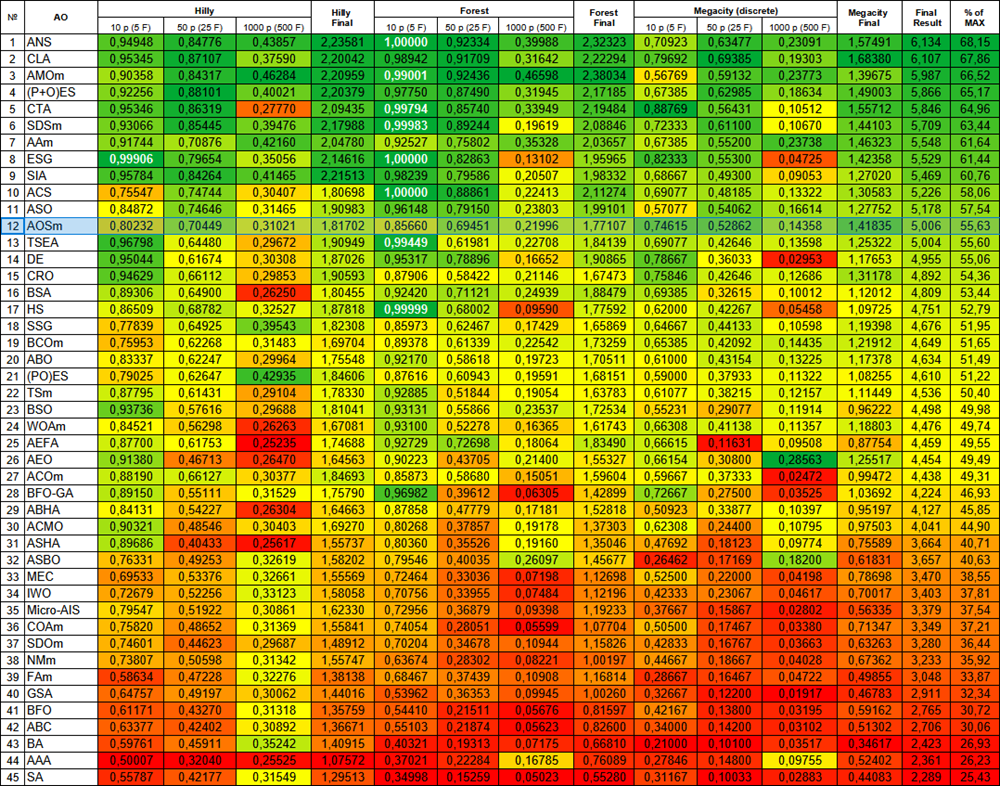
Abbildung 2. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben
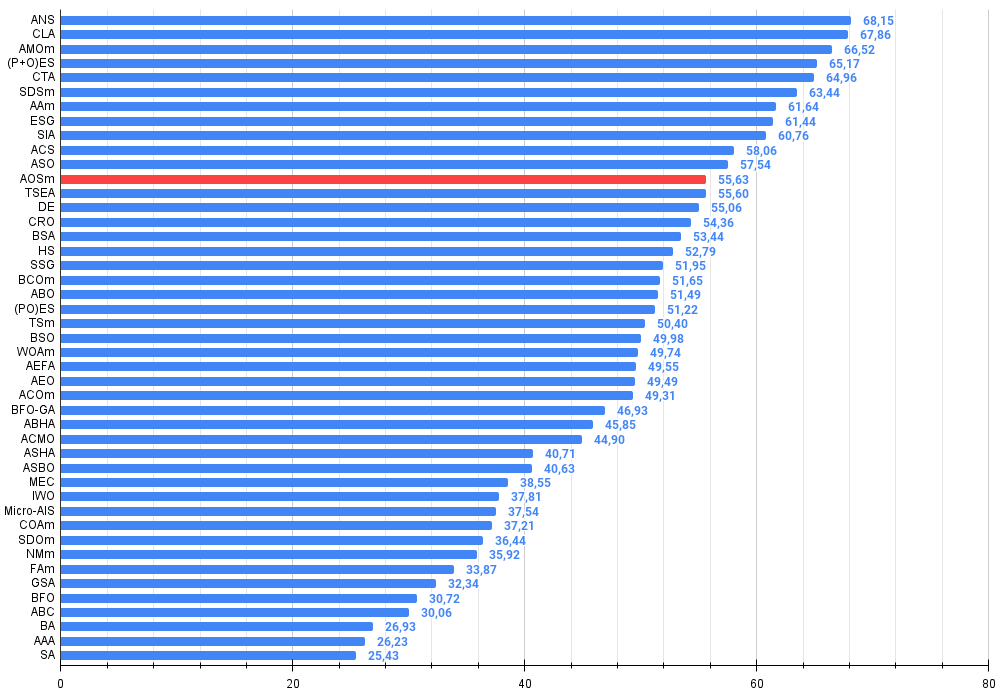
Abbildung 3. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Wertungstabelle)
Vor- und Nachteile von AOSm:
Vorteile:
- Gute Leistung bei verschiedenen Aufgaben.
- Geringe Anzahl von externen Parametern.
- Gute Skalierbarkeit.
- Ausgewogene Suche sowohl nach lokalen als auch nach globalen Extremen.
Nachteile
- Eine recht komplexe Umsetzung.
- Durchschnittliche Genauigkeit der Konvergenz bei glatten Funktionen im Vergleich zu anderen Algorithmen.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Übergeordnete Klasse von Populationsoptimierungsalgorithmen |
| 2 | #C_AO_enum.mqh | Include | Enumeration von Algorithmen zur Bevölkerungsoptimierung |
| 3 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 4 | TestStandFunctions.mqh | Include | Bibliothek der Testfunktionen |
| 5 | Utilities.mqh | Include | Bibliothek der Hilfsfunktionen |
| 6 | CalculationTestResults.mqh | Include | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 7 | Testing AOs.mq5 | Skript | Der einheitliche Test für alle Algorithmen zur Populationsoptimierung |
| 8 | Simple use of population optimization algorithms.mq5 | Skript | Ein einfaches Beispiel für die Verwendung von Algorithmen zur Bevölkerungsoptimierung ohne Visualisierung |
| 9 | AO_AOSm_AtomicOrbitalSearch.mqh | Include | AOSm-Algorithmus-Klasse |
| 10 | Test_AO_AOSm.mq5 | Skript | AOSm-Test |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16315
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Schneller Handelsstrategie-Tester in Python mit Numba
Schneller Handelsstrategie-Tester in Python mit Numba
 Die Verwendung von Assoziationsregeln in der Forex-Datenanalyse
Die Verwendung von Assoziationsregeln in der Forex-Datenanalyse
 Volumetrische neuronale Netzwerkanalyse als Schlüssel zu zukünftigen Trends
Volumetrische neuronale Netzwerkanalyse als Schlüssel zu zukünftigen Trends
 Entwicklung eines Replay-Systems (Teil 75): Neuer Chart-Handel (II)
Entwicklung eines Replay-Systems (Teil 75): Neuer Chart-Handel (II)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Vielen Dank für den Artikel!
Ich habe mich gestern und heute eine Weile mit der Hilly-Funktion und den Alglib-Methoden beschäftigt. Hier sind meine Gedanken.
Um das Maximum dieser Funktion zu finden, insbesondere wenn die Anzahl der Parameter 10 und mehr beträgt, ist es sinnlos, Gradientenmethoden anzuwenden, das ist die Aufgabe der kombinatorischen Optimierungsmethoden. Gradientenmethoden bleiben einfach sofort im lokalen Extremum stecken. Und es spielt keine Rolle, wie oft man von einem neuen Punkt des Parameterraums neu startet, die Chance, in den richtigen Bereich des Raums zu gelangen, von dem aus die Gradientenmethode sofort eine Lösung findet, tendiert gegen Null, wenn die Anzahl der Parameter steigt.
Der Punkt des Raums, von dem aus lbfgs oder CG für 2(zwei) Iterationen das Maximum für eine beliebige Anzahl von Parametern findet, ist beispielsweise {x = -1,2 , y = 0.5}.
Aber die Chance, in diesen Bereich zu gelangen, ist wie gesagt einfach Null. Es muss hundert Jahre dauern, um Zufallszahlen zu erzeugen.
Daher ist es notwendig, die im Artikel vorgestellten genetischen Algorithmen irgendwie mit Gradientenmethoden zu kombinieren (so dass sie eine Erkundung durchführen und den Suchraum reduzieren können), um das Extremum schnell von einem günstigeren Punkt aus zu finden.
Vielen Dank für diesen Artikel!
Vielen Dank für Ihr Feedback.
Um das Maximum einer gegebenen Funktion zu finden, insbesondere wenn die Anzahl der Parameter 10 oder mehr beträgt, ist es sinnlos, Gradientenmethoden zu verwenden.
Ja, das ist richtig.
Dies ist die Aufgabe der kombinatorischen Optimierungsverfahren.
Kombinatorische Methoden, wie die klassische "Ameise", sind für Probleme wie das "Travelling Salesman Problem" und das "Knapsack-Problem" konzipiert, d.h. sie sind für diskrete Probleme mit einem festen Schritt (Graphenrand) konzipiert. Für mehrdimensionale "kontinuierliche" Probleme sind diese Algorithmen überhaupt nicht geeignet, zum Beispiel für Aufgaben wie das Training neuronaler Netze. Ja, kombinatorische Eigenschaften sind sehr nützlich für stochastische heuristische Methoden, aber sie sind nicht die einzige und ausreichende Eigenschaft für die erfolgreiche Lösung solcher realitätsnahen Testprobleme. Die Suchstrategien im Algo selbst sind ebenfalls wichtig.
Gradientenbasierte Verfahren bleiben einfach sofort in einem lokalen Extremum stecken. Und es spielt keine Rolle, wie oft man von einem neuen Punkt des Parameterraums neu startet, die Chance, in die richtige Region des Raums zu gelangen, von der aus die Gradientenmethode sofort eine Lösung findet, tendiert gegen Null, wenn die Anzahl der Parameter steigt.
Ja, das stimmt.
Aber die Chance, in diesen Bereich zu gelangen, ist, wie ich bereits sagte, einfach Null. Es würde etwa hundert Jahre dauern, um Zufallszahlen zu erzeugen.
Ja, das ist richtig. In niedrigdimensionalen Räumen (1-2) ist es sehr einfach, in die Nähe des Globalen zu kommen, einfache Zufallsgeneratoren können sogar dafür arbeiten. Aber alles ändert sich völlig, wenn die Dimensionalität des Problems zunimmt, hier beginnen die Sucheigenschaften von Algorithmen eine wichtige Rolle zu spielen, nicht das Glück von Mistress Luck.
Daher müssen wir die in dem Artikel vorgestellten genetischen Algorithmen (die die Erkundung übernehmen und den Suchraum verkleinern) irgendwie mit Gradientenmethoden kombinieren, die dann das Extremum schnell von einem günstigeren Punkt aus finden würden.
"Genetisch" - Sie meinen wahrscheinlich "heuristisch". Warum "der Fisch braucht einen Regenschirm" und "warum brauchen wir einen Schmied? Wir brauchen keinen Schmied.")))) Es gibt effiziente Methoden zur Lösung komplexer mehrdimensionaler Probleme im kontinuierlichen Raum, die in Artikeln über Populationsmethoden beschrieben werden. Und für klassische Gradientenprobleme gibt es eigene Aufgaben - eindimensionale analytisch bestimmbare Probleme (hier gibt es nichts Vergleichbares, es gibt eine schnelle und exakte Konvergenz).
Und, Frage, was sind Ihre Eindrücke von der Geschwindigkeit der Heuristiken?
SZY:
Oh, wie viele wundersame Entdeckungen
Bereiten den Geist der Erleuchtung vor
Und die Erfahrung, den Sohn der Irrtümer,
Und das Genie, den Freund der Paradoxien,
Und den Zufall, den Erfinder Gottes.
ZZZY: Einen Moment. In einem unbekannten Raum der Suche ist es nie möglich, zu irgendeinem Zeitpunkt oder Schritt der Iteration zu wissen, dass es sich tatsächlich um eine vielversprechende Richtung zum Globalen handelt. Daher ist es unmöglich, erst zu suchen und dann zu verfeinern. Nur ganze Suchstrategien können funktionieren, sie funktionieren entweder gut oder schlecht. Jeder wählt den Grad der "Güte" und "Eignung für die Aufgabe" selbst aus, zu diesem Zweck wird eine Bewertungstabelle geführt, um einen Algorithmus entsprechend den Besonderheiten der Aufgabe auszuwählen.
Ja, das ist richtig. In niedrigdimensionalen Räumen (1-2) ist es sehr einfach, in die Nähe eines Globals zu gelangen, einfache Zufallsgeneratoren können dafür sogar nützlich sein. Aber alles ändert sich völlig, wenn die Dimensionalität des Problems zunimmt, hier beginnen die Sucheigenschaften der Algorithmen, nicht die Glücksfee, eine wichtige Rolle zu spielen.
Sie versagen also
Und, Frage, was halten Sie von der Geschwindigkeit der Heuristiken?
Trotz der Tatsache, dass sie schnell arbeiten. Das Ergebnis für 1000 Parameter etwas über 0,4.
Deshalb habe ich intuitiv gedacht, dass es sinnvoll ist, GA und Gradientenmethoden zu kombinieren, um das Maximum zu erreichen. Andernfalls werden sie einzeln Ihre Funktion nicht lösen. Ich habe es nicht in der Praxis getestet.
P.S. Ich denke immer noch, dass diese Funktion zu dick ist, bei realen Aufgaben (z.B. Training von neuronalen Netzen) gibt es solche Probleme nicht, obwohl auch dort die Fehleroberfläche in lokalen Minima liegt.
1. sie machen ihre Arbeit nicht gut
2. auch wenn sie schnell arbeiten. Das Ergebnis für 1000 Parameter liegt bei etwa 0,4.
3. Deshalb dachte ich intuitiv, dass es sinnvoll ist, GA- und Gradientenmethoden zu kombinieren, um das Maximum zu erreichen. Andernfalls werden sie einzeln die Funktion nicht lösen. Ich habe es nicht in der Praxis getestet.
4. P.S. Ich denke immer noch, dass diese Funktion zu dick ist, bei realen Aufgaben (z.B. Training von neuronalen Netzen) gibt es keine solchen Probleme, obwohl auch dort die Fehleroberfläche in lokalen Minima liegt.
1. Was meinen Sie mit "sie können es nicht bewältigen"? Es gibt eine Begrenzung der Anzahl der Zugriffe auf die Zielfunktion, und derjenige, der ein besseres Ergebnis erzielt hat, ist derjenige, der es nicht schafft)). Sollten wir die Anzahl der erlaubten Zugriffe erhöhen? Nun, dann werden die agileren und besser an komplexe Funktionen angepassten ohnehin die Ziellinie erreichen. Versuchen Sie, die Anzahl der Verweise zu erhöhen, das Bild wird sich nicht ändern.
2. Ja. Und manche haben 0,3, andere 0,2, wieder andere 0,001. Besser sind die, die 0,4 angegeben haben.
3. es hilft nichts, intuitiv wurden hunderte von Kombinationen und Variationen ausprobiert und wieder ausprobiert. Besser ist diejenige, die für eine bestimmte Anzahl von Epochen (Iterationen) bessere Ergebnisse zeigt. Erhöhen Sie die Anzahl der Verweise auf das Ziel, und sehen Sie, wer zuerst die Ziellinie erreicht.
4. Wenn es bei schwierigen Aufgaben Spitzenreiter gibt, glauben Sie dann, dass bei leichten Aufgaben die Spitzenreiter schlechtere Ergebnisse erzielen als die Außenseiter? Das ist nicht der Fall, um es milde auszudrücken. Ich arbeite an einer "einfacheren", aber realistischen Aufgabe zum Gittertraining. Ich werde die Ergebnisse wie immer mitteilen. Es wird interessant sein.
Experimentieren Sie einfach, probieren Sie verschiedene Algorithmen und Aufgaben aus, bleiben Sie nicht an einer Sache hängen. Ich habe versucht, alle Werkzeuge dafür bereitzustellen.
1. Was meinen Sie mit "scheitern"? Es gibt eine Begrenzung der Anzahl der Zugriffe auf die Zielfunktion, derjenige, der das beste Ergebnis erzielt hat, ist derjenige, der es nicht schafft)). Sollten wir die Anzahl der erlaubten Zugriffe erhöhen? Nun, dann werden die agileren und besser an komplexe Funktionen angepassten ohnehin die Ziellinie erreichen. Versuchen Sie, die Anzahl der Verweise zu erhöhen, das Bild wird sich nicht ändern.
2. Ja. Und einige haben 0,3, und andere 0,2, und andere 0,001. Besser sind diejenigen, die 0,4 zeigten.
3. es hilft nichts, intuitiv wurden hunderte von Kombinationen und Variationen ausprobiert und wieder ausprobiert. Besser ist diejenige, die für eine bestimmte Anzahl von Epochen (Iterationen) bessere Ergebnisse zeigt. Erhöhen Sie die Anzahl der Verweise auf das Ziel, und sehen Sie, wer zuerst die Ziellinie erreicht.
4. Wenn es bei schwierigen Aufgaben Spitzenreiter gibt, glauben Sie dann, dass bei leichten Aufgaben die Spitzenreiter schlechtere Ergebnisse erzielen als die Außenseiter? Das ist nicht der Fall, um es milde auszudrücken. Ich arbeite an einer "einfacheren", aber realistischen Aufgabe zum Gittertraining. Ich werde die Ergebnisse wie immer mitteilen. Es wird interessant werden.
Experimentieren Sie einfach, probieren Sie verschiedene Algorithmen und Aufgaben aus, fixieren Sie sich nicht auf eine Sache. Ich habe versucht, alle Werkzeuge dafür bereitzustellen.
Ich experimentiere,
Was die realistische Aufgabe angeht, so ist es richtig, Algorithmen an kampfnahen Aufgaben zu testen.
Es ist doppelt interessant zu sehen, wie genetische Netzwerke trainiert werden.