ALGLIBライブラリの最適化手法（第2回）：

MetaTrader 5 — テスター | YYYY年08月DD日, 08:40

Andrey Dik

内容

はじめに
ALGLIBライブラリの最適化方法

ALGLIB手法で使用される関数の表
テスト方法

はじめに

本研究の第1回では、MetaTrader 5に標準搭載されているALGLIBライブラリの最適化アルゴリズムについて検討し、アルゴリズムBLEIC (Boundary, Linear Equality-Inequality Constraints)、L-BFGS (Limited-memory Broyden–Fletcher–Goldfarb–Shanno)、NS（箱制約・線形制約・非線形制約付き非滑らか非凸最適化）を詳しく取り上げました。これらのアルゴリズムの理論的基礎を確認しただけでなく、最適化問題への適用方法についても簡単に解説しました。

この記事では、ALGLIBが提供する残りの手法を引き続き探究していきます。特に、複雑な多次元関数に対するテストに重点を置くことで、各手法の効率性を包括的に把握することを目指します。最後に、得られた結果に基づいて総合的な分析を行い、特定のタスクに対して最適なアルゴリズムを選ぶための実践的な推奨事項を提示します。

BC (Box Constrained Optimization)

ボックス制約付き最適化では、サブルーチンがF(x)関数（N個の引数を持つ）を、ボックス制約のもとで最小化します（一部のボックス制約は実際には等式制約となります）。この最適化手法は、BLEIC（線形制約付き最適化）アルゴリズムに似た手法を使用していますが、ボックス制約のみが存在するため、より高速な制約活性化戦略を取ることが可能です。特に、解に多数の制約がアクティブとなる大規模問題においては、この最適化手法はBLEICよりも高速に動作する可能性があります。

ボックス制約付き最適化について、簡単に説明します。それは、最良の解を探す最適化アルゴリズムであり、ボックス制約（各変数がある一定の範囲内に収まる必要がある）を扱います。つまり、すべての変数が指定された範囲内にあるという条件のもとで、関数の最小値を探します。このアルゴリズムの主な特徴は、BLEICに似ているものの、より高速で、範囲制約への対応に特化して最適化されている点です。

要件：開始点は実行可能であるか、または実行可能領域に近い必要があります。また、関数は実行可能領域全体で定義されていなければなりません。

BCをはじめとするALGLIBライブラリの最適化手法を使用するには、ライブラリのファイルをプロジェクトに含める必要があります。このライブラリはMetaTrader 5に標準搭載されているため、ユーザーが追加でインストールする必要はありません。

#include <Math\Alglib\alglib.mqh>

ALGLIB手法を効果的に活用するためのスクリプト（例）を作成していきましょう。ここでは、ALGLIB手法を使用する際に典型的な主なステップを示します。同一のコードブロックも適切な色で強調されています。

1. 問題の境界条件を定義します。たとえば、適応度関数（目的関数）の呼び出し回数、最適化するパラメータの範囲とそのステップです。ALGLIB手法では、最適化されるパラメータ「x」の開始値を割り当てる必要があります（メソッドは決定論的であり、結果は完全に初期値に依存するため、問題のパラメータ範囲内で乱数生成を適用します）。また、「s」スケールも設定します（メソッドはパラメータ同士のスケールに敏感であるため、この場合スケールは1に設定します）。

2. アルゴリズムの動作に必要なオブジェクトを宣言します。

3. アルゴリズムの外部パラメータ（設定）を指定します。

4. 最適化を初期化します。これには、最適化するパラメータの範囲とステップ、およびアルゴリズムの外部パラメータをメソッドに渡すことが含まれます。

5. 最適化を実行します。

6. 最適化結果を取得し、今後の使用のために保存します。

注意しておくべき点として、ユーザーは最適化プロセスに影響を与えたり、途中で停止したりすることはできません。メソッドはすべての操作を自動的に実行し、プロセス内で適応度関数を呼び出します。アルゴリズムは、任意の回数だけ適応度関数を呼び出す可能性があります（ただし、ユーザーが指定したパラメータを参考にしています）。ユーザーは、メソッドに停止コマンドを渡すことで、呼び出し回数の上限を制御することができます。

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  // Initialization of optimization parameters---------------------------------------
  int numbTestFuncRuns = 10000;
  int params           = 1000;

  // Create and initialize arrays for range bounds---------------------
  CRowDouble rangeMin, rangeMax;
  rangeMin.Resize (params);
  rangeMax.Resize (params);
  double rangeStep;

  for (int i = 0; i < params; i++)
  {
    rangeMin.Set (i, -10);
    rangeMax.Set (i,  10);
  }
  rangeStep =  DBL_EPSILON;

  CRowDouble x; x.Resize (params);
  CRowDouble s; s.Resize (params);
  s.Fill (1);

  // Generate random initial parameter values in given ranges----
  for (int i = 0; i < params; i++)
  {
    x.Set (i, rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0));
  }

  // Create objects for optimization------------------------------------------
  C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns);
  CObject             obj;
  CNDimensional_Rep   frep;
  CMinBCReport        rep;

  // Set the parameters of the BC optimization algorithm------------------------------
  double diffStep = 0.00001;
  double epsg     = 1e-16;
  double epsf     = 1e-16;

  CAlglib::MinBCCreateF  (x, diffStep, fFunc.state);
  CAlglib::MinBCSetBC    (fFunc.state, rangeMin, rangeMax);
  CAlglib::MinBCSetScale (fFunc.state, s);
  CAlglib::MinBCSetCond  (fFunc.state, epsg, epsf, rangeStep, numbTestFuncRuns);
  CAlglib::MinBCOptimize (fFunc.state, fFunc, frep, obj);
  CAlglib::MinBCResults  (fFunc.state, x, rep);

  // Output of optimization results-----------------------------------------------
  Print ("BC, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches);
}
//——————————————————————————————————————————————————————————————————————————————

メソッドが適応度関数を自ら呼び出す仕様であるため（ユーザープログラム側から呼び出されるわけではない）、適応度関数の呼び出しをALGLIBの親クラスを継承したクラスでラップする必要があります（なお、親クラスは使用するメソッドごとに異なります）。このラッパークラスをC_OptimizedFunctionとして宣言し、以下のメソッドをクラス内に設定します。

1. Func：派生クラスでオーバーライドされる仮想メソッドです。
2. Init ()：クラスのパラメータを初期化します。メソッド内では次の処理をおこないます。

関数の呼び出し回数や、これまでに見つかった最良の値に関連する変数の初期化
c配列とcB配列を初期化し、座標値を格納できるように準備する

変数

state：BCメソッド専用の型であるCMinBCState型オブジェクト。アルゴリズムの静的メソッド呼び出しや、stopメソッドの使用時に必要です。
numberLaunches：現在の呼び出し回数（適応度関数の暴走や過剰な実行を防ぐために使用）
maxNumbLaunchesAllowed：許容される最大の呼び出し回数
fB：適応度関数で見つかった最良の値
c []：現在の座標値を格納する配列
cB []：最良探索座標を保存するための配列

//——————————————————————————————————————————————————————————————————————————————
// Class for function optimization, inherits from CNDimensional_Func
class C_OptimizedFunction : public CNDimensional_Func
{
  public: //--------------------------------------------------------------------
  C_OptimizedFunction (void) { }
  ~C_OptimizedFunction (void) { }

  // A virtual function to contain the function being optimized--------
  virtual void Func (CRowDouble &x, double &func, CObject &obj);

  // Initialization of optimization parameters---------------------------------------
  void Init (int coords,
             int maxNumberLaunchesAllowed)
  {
    numberLaunches         = 0;
    maxNumbLaunchesAllowed = maxNumberLaunchesAllowed;
    fB = -DBL_MAX;

    ArrayResize (c,  coords);
    ArrayResize (cB, coords);
  }

  //----------------------------------------------------------------------------
  CMinBCState state;             // State 
  int         numberLaunches;    // Launch counter 

  double fB;                     // Best found value of the objective function (maximum)
  double cB [];                  // Coordinates of the point with the best function value

  private: //-------------------------------------------------------------------
  double c  [];                  // Array for storing current coordinates
  int    maxNumbLaunchesAllowed; // Maximum number of function calls allowed
};
//——————————————————————————————————————————————————————————————————————————————

C_OptimizedFunctionクラスのFuncメソッドは、ユーザーが定義した適応度関数へアクセスするために使用されます。このメソッドは次の引数を取ります。xベクトル：最適化メソッドが提案する、問題のパラメータの一つの候補解、func：計算された目的関数の値を返すための変数、obj：本メソッドの目的においては明確な用途は不明ですが、おそらく追加情報の受け渡しを可能にするために予約されていると考えられます。メソッドの主な処理手順は以下の通りです。

numberLaunchesカウンタがインクリメントされます。このカウンタはFuncメソッドの呼び出し回数を記録するために使用されます。
実行回数がmaxNumbLaunchesAllowedを超えた場合、funcにDBL_MAXを設定します。ALGLIBのメソッドは関数の最小化を目的としているため、この値は最悪の解を意味します。次に、MinBCRequestTermination関数を呼び出して、BCメソッドに最適化の終了を指示します。
次にループ処理で、xベクトルの値をc配列にコピーします。これは、ユーザー定義の適応度関数にこれらの値を渡して使用するために必要です。
ObjectiveFunction関数が呼び出され、現在のc配列の値に対する目的関数の値を計算します。結果はffValに保存され、funcにはffVal（負の値）が設定されます。これは、最適化対象が最大化すべき反転した放物面であり、BCメソッドは最小化をおこなうため、値を反転する必要があるためです。
ffValの現在の値が、これまでに記録された最良値fBを上回る場合、fBを更新し、cB配列に現在のcの状態をコピーします。これにより、目的関数の最良値とそれに対応するパラメータを記録・参照できるようになります。

Func関数は、カスタム目的関数の呼び出しを実装し、呼び出し回数の管理や最良結果の更新、設定された制限回数を超えた場合の停止処理を実行するものです。

//——————————————————————————————————————————————————————————————————————————————
// Implementation of the function to be optimized
void C_OptimizedFunction::Func (CRowDouble &x, double &func, CObject &obj)
{
  // Increase the function launch counter and limitation control----------------
  numberLaunches++;
  if (numberLaunches >= maxNumbLaunchesAllowed)
  {
    func = DBL_MAX;
    CAlglib::MinBCRequestTermination (state);
    return;
  }

  // Copy input coordinates to internal array-------------------------
  for (int i = 0; i < x.Size (); i++) c [i] = x [i];

  // Calculate objective function value----------------------------------------
  double ffVal = ObjectiveFunction (c);
  func = -ffVal;

  // Update the best solution found--------------------------------------
  if (ffVal > fB)
  {
    fB = ffVal;
    ArrayCopy (cB, c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

BCアルゴリズムを用いて放物面関数の最適化をおこなうテストスクリプトを実行したところ、次の結果が出力されました。

BC, best result:0.6755436156375465, number of function launches:84022

残念ながら、MinBCRequestTerminationメソッドを使って最適化の停止を要求したにもかかわらず、アルゴリズムは処理を継続し、許容回数である10,000回を大きく超えました。

ここで、BCを制限せず、制限を設けずに最適化させてみましょう。結果は以下のとおりです。

BC, best result:1.0, number of function launches:56015

ご覧のとおり、BCは放物面関数に対して完全に収束することができますが、この場合、目的関数の呼び出し回数を事前に見積もることはできません。

アルゴリズムにおいては、微分ステップが重要です。たとえば、0.00001の代わりに非常に小さいステップ（例：1e-16）を使用した場合、アルゴリズムは途中で早期停止し、事実上スタックしてしまいます。その際の出力結果は次のとおりです：

BC, best result:0.6625662039929793, number of function launches:4002

NLC（前処理付き拡張ラグランジュアルゴリズムによる非線形制約最適化）

この制約付き非線形最適化アルゴリズムは、変数がN個ある複雑な目的関数F(x)を、変数の境界制約(min <= x <= max)、線形の不等式・等式制約、非線形等式制約 G(x) = 0、および非線形不等式制約 H(x) <= 0のようなさまざまな制約を考慮しながら最小化することを可能にします。

たとえば、達成したい難しい目標があると想像してください。ただし、それには絶対に破ってはならない制限があるとします。たとえば、売上利益を最大化したいけれど、一定の経費を超えてはいけないというようなケースです。ALGLIBのアルゴリズムは、このような制約付き最適化問題を解決するのに役立ちます。仕組みは以下のようになります。

1. まず、アルゴリズムにスタート地点（初期推定値）を与えます。これは、目標をどう達成するかに関する仮の案であり、すべての制約を満たしている必要があります。

2. 次に、アルゴリズムはその初期点からゆっくりと動き出し、一歩一歩最適解へと近づいていきます。各ステップでは、次にどちらの方向へ進むべきかを判断するための補助的な問題を解いています。

3. このプロセスを加速するために、アルゴリズムは「前処理(preconditioning)」と呼ばれる特殊な手法を使います。これは問題の構造に合わせて「歩幅」を調整するようなもので、より速く収束するように工夫されています。

4. 最終的に、数回の繰り返しの後、すべての制約を満たしながら目的関数（たとえば経費）を最小化する解を見つけ出します。

ユーザーは、ALGLIBに実装されている中から問題の規模や複雑さに応じて適切な3つのソルバーを選択することができます。

SQPSQP（逐次二次計画法）：中規模で目的関数が複雑な問題に推奨されます。
AUL（前処理付き拡張ラグランジュ法）：大規模問題や、目的関数の評価が軽量（高速）な場合に適しています。
SLP（逐次線形計画法）：処理速度は遅いものの、複雑なケースでもより堅牢です。

テスト関数を使った実験では、AULソルバーの効率性が示されており、他のソルバーはコード内でコメントアウトされています。

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  // Initialization of optimization parameters---------------------------------------
  int numbTestFuncRuns = 10000;
  int params           = 1000;

  // Create and initialize arrays for range bounds---------------------
  CRowDouble rangeMin, rangeMax;
  rangeMin.Resize (params);
  rangeMax.Resize (params);
  double rangeStep;

  for (int i = 0; i < params; i++)
  {
    rangeMin.Set (i, -10);
    rangeMax.Set (i,  10);
  }
  rangeStep = DBL_EPSILON;

  CRowDouble x; x.Resize (params);
  CRowDouble s; s.Resize (params);
  s.Fill (1);

  // Generate random initial parameter values in given ranges----
  for (int i = 0; i < params; i++)
  {
    x.Set (i, rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0));
  }

  // Create objects for optimization------------------------------------------
  C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns);
  CObject             obj;
  CNDimensional_Rep   frep;
  CMinNLCReport       rep;

  // Setting parameters of the NLC optimization algorithm-----------------------------
  double diffStep = 0.00001;
  double rho      = 1000.0;
  int    outerits = 5;

  CAlglib::MinNLCCreateF    (x, diffStep, fFunc.state);
  CAlglib::MinNLCSetBC      (fFunc.state, rangeMin, rangeMax);
  CAlglib::MinNLCSetScale   (fFunc.state, s);
  CAlglib::MinNLCSetCond    (fFunc.state, rangeStep, numbTestFuncRuns);

  //CAlglib::MinNLCSetAlgoSQP (fFunc.state);
  CAlglib::MinNLCSetAlgoAUL (fFunc.state, rho, outerits);
  //CAlglib::MinNLCSetAlgoSLP (fFunc.state);

  CAlglib::MinNLCOptimize   (fFunc.state, fFunc, frep, obj);
  CAlglib::MinNLCResults    (fFunc.state, x, rep);

  // Output of optimization results-----------------------------------------------
  Print ("NLC, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches);
}
//——————————————————————————————————————————————————————————————————————————————

NLCでは、state変数はCMinNLCState型です。

//——————————————————————————————————————————————————————————————————————————————
// Class for function optimization, inherits from CNDimensional_FVec
class C_OptimizedFunction : public CNDimensional_FVec
{
  public: //--------------------------------------------------------------------
  C_OptimizedFunction (void) { }
  ~C_OptimizedFunction (void) { }

  // A virtual function to contain the function being optimized--------
  virtual void FVec (CRowDouble &x, CRowDouble &fi, CObject &obj);

  // Initialization of optimization parameters---------------------------------------
  void Init (int coords,
             int maxNumberLaunchesAllowed)
  {
    numberLaunches         = 0;
    maxNumbLaunchesAllowed = maxNumberLaunchesAllowed;
    fB = -DBL_MAX;

    ArrayResize (c,  coords);
    ArrayResize (cB, coords);
  }

  //----------------------------------------------------------------------------
  CMinNLCState state;            // State 
  int          numberLaunches;   // Launch counter 

  double fB;                     // Best found value of the objective function (maximum)
  double cB [];                  // Coordinates of the point with the best function value

  private: //-------------------------------------------------------------------
  double c  [];                  // Array for storing current coordinates
  int    maxNumbLaunchesAllowed; // Maximum number of function calls allowed
};
//——————————————————————————————————————————————————————————————————————————————

MinNLCRequestTermination関数を使用して最適化プロセスの停止を要求します。

//——————————————————————————————————————————————————————————————————————————————
// Implementation of the function to be optimized
void C_OptimizedFunction::FVec (CRowDouble &x, CRowDouble &fi, CObject &obj)
{
  // Increase the function launch counter and limitation control----------------
  numberLaunches++;
  if (numberLaunches >= maxNumbLaunchesAllowed)
  {
    fi.Set (0, DBL_MAX);
    CAlglib::MinNLCRequestTermination (state);
    return;
  }

  // Copy input coordinates to internal array-------------------------
  for (int i = 0; i < x.Size (); i++) c [i] = x [i];

  // Calculate objective function value----------------------------------------
  double ffVal = ObjectiveFunction (c);
  fi.Set (0, -ffVal);

  // Update the best solution found--------------------------------------
  if (ffVal > fB)
  {
    fB = ffVal;
    ArrayCopy (cB, c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

NLCアルゴリズムを用いて放物面関数の最適化をおこなうテストスクリプトを実行したところ、次の結果が出力されました。

NLC, best result:0.8858935739350294, number of function launches:28007

目的関数の起動回数に制限がないため、NLCは完全に収束しますが、その過程で100万回を超える反復処理を実行します。

NLC, best result:1.0, number of function launches:1092273

1e-16という非常に小さなステップを使用すると、アルゴリズムは、たとえばBCメソッドのように途中で停止することはありませんが、0.00001のステップの場合よりもわずかに悪い結果を示します。

NLC, best result:0.8543715192632731, number of function launches:20005

LM（レーベンバーグ・マルカート法）

レベンバーグ・マーカート法(LM)は、非線形最小二乗問題を解くために広く使われている最適化アルゴリズムです。この手法は、曲線あてはめや曲面あてはめの問題に対して非常に効果的です。

LMの基本的な考え方は、2つの最適化技術、すなわち勾配降下法とガウス・ニュートン法を組み合わせることにあります。これにより、目的関数の形状に応じて柔軟に適応できるアルゴリズムとなっています。動作の仕組みは以下の通りです。

各反復ステップで、アルゴリズムは勾配降下法と二次近似（ガウス・ニュートン法）を組み合わせてステップ方向を計算します。
減衰係数(λ)は自動的に調整され、ステップサイズや両手法のバランスを制御します。

たとえるなら、地図の輪郭がぼやけた山岳地帯で一番低い地点を探すようなものです。レベンバーグ・マーカート法は、以下の2つの探索方法を組み合わせた賢いナビゲーターのようなものです。

1. 最初の方法（ガウス・ニュートン法）は高速ですが、リスクが高いです。これは、斜面を一気に駆け下りるようなものです。目標に近い時は非常に効率的ですが、地形が難しいと転倒してしまう可能性があります。

2. 2番目の方法（勾配降下法）は遅いですが、信頼性があります。これは、小さなステップで慎重に降りていくようなものです。時間はかかりますが、安全で、複雑な地形でも対応できます。

このアルゴリズムは、状況に応じて両者を賢く切り替えます。道が明確なときは高速な方法を選び、困難な状況では慎重モードに切り替え、ステップサイズを自動的に調整します。

ただし、局所最小値に陥る可能性もあるため、良好な初期推定（どこを探せばよいか大まかにわかっている状態）が必要です。また、パラメータの数が100を超えるような大規模問題にはあまり効果的ではありません。

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  // Initialization of optimization parameters---------------------------------------
  int numbTestFuncRuns = 10000;
  int params           = 1000;

  double rangeMin [], rangeMax [], rangeStep;
  ArrayResize (rangeMin,  params);
  ArrayResize (rangeMax,  params);

  for (int i = 0; i < params; i++)
  {
    rangeMin  [i] = -10;
    rangeMax  [i] =  10;
  }
  rangeStep = DBL_EPSILON;

  double x [];
  double s [];
  ArrayResize (x, params);
  ArrayResize (s, params);
  ArrayInitialize (s, 1);

  // Generate random initial parameter values in given ranges----
  for (int i = 0; i < params; i++)
  {
    x [i] = rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0);
  }

  // Create objects for optimization------------------------------------------
  C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns);
  CObject             obj;
  CNDimensional_Rep   frep;
  CMinLMReportShell   rep;

  // Set the parameters of the LM optimization algorithm------------------------------
  double diffStep = 1e-16;//0.00001;

  CAlglib::MinLMCreateV  (1, x, diffStep, fFunc.state);
  CAlglib::MinLMSetBC    (fFunc.state, rangeMin, rangeMax);
  CAlglib::MinLMSetScale (fFunc.state, s);
  CAlglib::MinLMSetCond  (fFunc.state, rangeStep, numbTestFuncRuns);
  CAlglib::MinLMOptimize (fFunc.state, fFunc, frep, 0, obj);
  CAlglib::MinLMResults  (fFunc.state, x, rep);

  // Output of optimization results-----------------------------------------------
  Print ("LM, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches);
}
//——————————————————————————————————————————————————————————————————————————————

LMでは、state変数はCMinLMStateShell型です。

//——————————————————————————————————————————————————————————————————————————————
// Class for function optimization, inherits from CNDimensional_FVec
class C_OptimizedFunction : public CNDimensional_FVec
{
  public: //--------------------------------------------------------------------
  C_OptimizedFunction (void) { }
  ~C_OptimizedFunction (void) { }

  // A virtual function to contain the function being optimized--------
  virtual void FVec (CRowDouble &x, CRowDouble &fi, CObject &obj);

  // Initialization of optimization parameters---------------------------------------
  void Init (int coords,
             int maxNumberLaunchesAllowed)
  {
    numberLaunches         = 0;
    maxNumbLaunchesAllowed = maxNumberLaunchesAllowed;
    fB = -DBL_MAX;

    ArrayResize (c,  coords);
    ArrayResize (cB, coords);
  }

  //----------------------------------------------------------------------------
  CMinLMStateShell state;          // State 
  int              numberLaunches; // Launch counter 

  double fB;                       // Best found value of the objective function (maximum)
  double cB [];                    // Coordinates of the point with the best function value

  private: //-------------------------------------------------------------------
  double c  [];                    // Array for storing current coordinates
  int    maxNumbLaunchesAllowed;   // Maximum number of function calls allowed
};
//——————————————————————————————————————————————————————————————————————————————

前の最適化手法と同様に、LM法でも目的関数の呼び出し回数を制限しますが、LM法は唯一、停止コマンドが用意されていない手法です。そのため、MinLMRequestTerminationのような関数が存在することを期待するのは理にかなっています。

//——————————————————————————————————————————————————————————————————————————————
// Implementation of the function to be optimized
void C_OptimizedFunction::FVec (CRowDouble &x, CRowDouble &fi, CObject &obj)
{
  // Increase the function launch counter and limitation control----------------
  numberLaunches++;
  if (numberLaunches >= maxNumbLaunchesAllowed)
  {
    fi.Set (0, DBL_MAX);
    //CAlglib::MinLMRequestTermination (state); // such method does not exist
    return;
  }

  // Copy input coordinates to internal array-------------------------
  for (int i = 0; i < x.Size (); i++) c [i] = x [i];

  // Calculate objective function value----------------------------------------
  double ffVal = ObjectiveFunction (c);
  fi.Set (0, -ffVal);

  // Update the best solution found--------------------------------------
  if (ffVal > fB)
  {
    fB = ffVal;
    ArrayCopy (cB, c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

LMアルゴリズムを用いて放物面関数の最適化をおこなうテストスクリプトを実行したところ、次の結果が出力されました。

LM, best result:0.6776047308612422, number of function launches:4003

LM法は、目的関数の4003回目の呼び出しで停止しました。つまり、最大呼び出し数（たとえば10,000回）という上限を設定していても、実際にはその「天井」に達する前にアルゴリズムが停止したということです。

LM, best result:0.6776047308612422, number of function launches:4003

1e-16という非常に小さなステップサイズを使用すると、アルゴリズムは目的関数の2001回目の実行でさらに早く停止します。

LM, best result:0.6670839162547625, number of function launches:2001

ALGLIB手法で使用される関数の一覧表

ALGLIBの最適化手法では、初期値やボックス制約に使われる変数の型、目的関数の親クラスの種類、最適化に必要なオブジェクト群、呼び出す関数のセットがそれぞれ異なります。そのため、これらのメソッドを使って直感的にプログラムを書くのは簡単ではありません。

この違いを整理して、ALGLIBの最適化手法についての理解を深め、正確に使い分けられるようにするために、以下のような要約表を用意しました。これにより、プログラマが自分の目的に合った最適化アルゴリズムをすぐに選び、正しく実装を開始できるようになります。

最適化アルゴリズム	目的関数	変数の種類	オブジェクト	呼び出すメソッド
BLEIC	Func	double	1) Cobject 2) CNDimensional_Rep 3) CMinBLEICReportShell 4) CminBLEICStateShell	1) Calglib::MinBLEICCreateF 2) Calglib::MinBLEICSetBC 3) Calglib::MinBLEICSetInnerCond 4) Calglib::MinBLEICSetOuterCond 5) Calglib::MinBLEICOptimize 6) Calglib::MinBLEICResults 7) Calglib::MinBLEICRequestTermination
LBFGS	Func	double	1) Cobject 2) CNDimensional_Rep 3) CminLBFGSReportShell 4) CminLBFGSStateShell	1) Calglib::MinLBFGSCreateF 2) Calglib::MinLBFGSSetCond 3) Calglib::MinLBFGSSetScale 4) Calglib::MinLBFGSOptimize 5) Calglib::MinLBFGSResults 6) Calglib::MinLBFGSRequestTermination
NS	FVec	CRowDouble	1) CObject 2) CNDimensional_Rep 3) CminNSReport 4) CminNSState	1) Calglib::MinNSCreateF 2) CAlglib::MinNSSetBC 3) CAlglib::MinNSSetScale 4) CAlglib::MinNSSetCond 5) CAlglib::MinNSSetAlgoAGS 6) CAlglib::MinNSOptimize 7) Calglib::MinNSResults 8) Calglib::MinNSRequestTermination
BC	Func	CRowDouble	1) CObject 2) CNDimensional_Rep 3) CminBCReport 4) CminBCState	1) CAlglib::MinBCCreateF 2) CAlglib::MinBCSetBC 3) CAlglib::MinBCSetScale 4) CAlglib::MinBCSetCond 5) CAlglib::MinBCOptimize 6) Calglib::MinBCResults 7) Calglib::MinBCRequestTermination
NLC	Fvec	CRowDouble	1) Cobject 2) CNDimensional_Rep 3) CminNLCReport 4) CminNLCState	1) CAlglib::MinNLCCreateF 2) CAlglib::MinNLCSetBC 3) CAlglib::MinNLCSetScale 4) CAlglib::MinNLCSetCond 5) Calglib::MinNLCSetAlgoAUL 6) Calglib::MinNLCOptimize 7) Calglib::MinNLCResults 8) Calglib::MinNLCRequestTermination
LM	FVec	double	1) Cobject 2) CNDimensional_Rep 3) CminLMReportShell 4) CminLMStateShell	1) Calglib::MinLMCreateV 2) Calglib::MinLMSetBC 3) Calglib::MinLMSetScale 4) Calglib::MinLMSetCond 5) Calglib::MinLMOptimize 6) Calglib::MinLMResults 7) Calglib::MinLMRequestTermination (does not exist)

テスト方法

ALGLIBライブラリの最適化手法を学んだ後、どの手法を特定のタスクに選ぶべきかという疑問が自然に生じます。最適化問題の種類によって、選択する手法によって解決効率は異なります。この重要な疑問に答えるために、現実の問題に最も近いとされる複雑なテスト関数を用います。これらの関数は典型的なケースを表しており、滑らかな関数はHillyテスト関数、滑らかだが鋭い頂点を持つ関数（定義域全体で微分可能ではないもの）はForest、純粋に離散的な関数はMegacityで表されます。

テストは各関数につき50回再実行をおこない、目的関数の呼び出し回数は最大10,000回に制限します。BC法を例にベンチマーク用のスクリプトを準備します。この方法により、より正確で代表的な結果を得て、それぞれの特定タスクに最適な最適化手法を選択する助けとします。

対応するALGLIB手法を用いて最適化のテスト実行をおこなうFuncTests関数を実装しましょう。この関数は、各手法の性能データを収集し、動作を可視化し、収束グラフを作成することを可能にします。

FuncTests関数がおこなう処理を簡単に列挙します。

テスト対象の目的関数、テスト回数、可視化用の色、全体結果用の変数を受け取る。
グラフ描画が有効な場合、関数をプロットする。
テストの境界を設定し、結果用の変数を初期化する。
ランダムな入力データを生成し、CAlglibライブラリを使って最適化を実行する。
目的関数の呼び出し回数と最良結果を追跡する。
平均結果を計算して表示する。
現在のテスト結果に基づき全体のスコアを更新する。

//——————————————————————————————————————————————————————————————————————————————
void FuncTests (C_Function    &f,                  // Reference to the target function object
                const  int     funcCount,          // Number of functions to test
                const  color   clrConv,            // Visualization color
                double        &allScore,           // Total score of all tests
                double        &allTests)           // Total number of tests
{
  if (funcCount <= 0) return;                      // If the number of functions = 0, exit the function

  allTests++;                                      // Increase the total number of tests

  if (Video_P)                                     // If visualization is enabled
  {
    ST.DrawFunctionGraph (f);                      // Draw the function graph
    ST.SendGraphToCanvas ();                       // Send the graph to the canvas
    ST.MaxMinDr          (f);                      // Determine the maximum and minimum of the function
    ST.Update            ();                       // Update the visualization
  }

  //----------------------------------------------------------------------------
  C_AO_Utilities Ut;                               // Utilities for handling numbers
  int    xConv      = 0.0;                         // Variable for converting along the X axis
  int    yConv      = 0.0;                         // Variable for converting along the Y axis
  double aveResult  = 0.0;                         // Average test result
  int    aveRunsFF  = 0;                           // Average number of function runs
  int    params     = funcCount * 2;               // Number of parameters (2 for each function)
  int    epochCount = NumbTestFuncRuns_P / PopSize_P; // Number of epochs

  //----------------------------------------------------------------------------
  CRowDouble bndl; bndl.Resize (params);          // Array for lower bounds
  CRowDouble bndu; bndu.Resize (params);          // Array for upper bounds

  for (int i = 0; i < funcCount; i++)             // Fill the boundaries for each function
  {
    bndu.Set (i * 2, f.GetMaxRangeX ());          // Set the upper boundary by X
    bndl.Set (i * 2, f.GetMinRangeX ());          // Set the lower boundary by X

    bndu.Set (i * 2 + 1, f.GetMaxRangeY ());      // Set the upper bound by Y
    bndl.Set (i * 2 + 1, f.GetMinRangeY ());      // Set the lower boundary by Y
  }

  CRowDouble x; x.Resize (params);                // Array for parameter values
  CRowDouble s; s.Resize (params);                // Array for scaling
  s.Fill (1);                                     // Fill the array with ones

  for (int test = 0; test < NumberRepetTest_P; test++) // Run the tests
  {
    for (int i = 0; i < funcCount; i++)          // For each function
    {
      x.Set (i * 2,     Ut.RNDfromCI (bndl [i * 2],     bndu [i * 2]));     // Generate random values by X
      x.Set (i * 2 + 1, Ut.RNDfromCI (bndl [i * 2 + 1], bndu [i * 2 + 1])); // Generate random values by Y
    }

    //--------------------------------------------------------------------------
    CObject             obj;                                                                // Object for storing results
    C_OptimizedFunction fFunc; fFunc.Init (params, NumbTestFuncRuns_P, PopSize_P, clrConv); // Initialize the optimization function
    CNDimensional_Rep   frep;                                                               // Representation of multidimensional space
    CMinBCState         state;                                                              // State of the minimization method
    CMinBCReport        rep;                                                                // Minimization report

    double epsg = 1e-16;                                                                    // Parameter for gradient stop condition
    double epsf = 1e-16;                                                                    // Parameter for the stop condition by function value

    CAlglib::MinBCCreateF  (x, DiffStep_P, state);                                          // Create minimization state
    CAlglib::MinBCSetBC    (state, bndl, bndu);                                             // Set the boundaries
    CAlglib::MinBCSetScale (state, s);                                                      // Set scaling 
    CAlglib::MinBCSetCond  (state, epsg, epsf, ArgumentStep_P, NumbTestFuncRuns_P);         // Set conditions
    CAlglib::MinBCOptimize (state, fFunc, frep, obj);                                       // Optimization
    CAlglib::MinBCResults  (state, x, rep);                                                 // Get results
    //--------------------------------------------------------------------------

    aveRunsFF += fFunc.numberLaunches;  // Sum up the number of function runs
    aveResult += -fFunc.bestMIN;        // Sum up the best minimum found
  }

  aveRunsFF /= NumberRepetTest_P;       // Calculate the average number of runs
  aveResult /= NumberRepetTest_P;       // Calculate the average result

  double score = aveResult;             // Estimate based on average result

  Print (funcCount, " ", f.GetFuncName (), "'s; Func runs: ", aveRunsFF, "(", NumbTestFuncRuns_P, "); result: ", aveResult); // Output test results
  allScore += score;                    // Update the overall score
}
//——————————————————————————————————————————————————————————————————————————————

ALGLIBライブラリで検討したすべての最適化手法について、テストベンチを順次実行していきましょう。以下に各手法のテスト結果の出力例を示します。これらの結果は、以下のように読み取ってください。

BLEIC|bound-constrained limited-memory optimizer with equality and inequality constraints|0.8|：メソッドの略語、完全な名前、微分化ステップ（オプションで、追加のメソッドパラメータ）

5 Hilly：多変量問題における対応するテスト目的関数の数

Func runs:2178(10000)：目的関数の実行回数 - 目的関数へのメソッドの呼び出し試行回数と、実行回数の指定された希望「上限」

result:0.38483704535107116：50回のテスト実行の平均結果。

テスト目的関数に対するBLEIC法のパフォーマンス出力結果：

BLEIC|bound-constrained limited-memory optimizer with equality and inequality constraints|0.8|
=============================
5 Hilly's; Func runs:2178(10000); result:0.38483704535107116
25 Hilly's; Func runs:10130(10000); result:0.3572376879336238
500 Hilly's; Func runs:11989(10000); result:0.2676346390264618
=============================
5 Forest's; Func runs:1757(10000); result:0.28835869530001046
25 Forest's; Func runs:9383(10000); result:0.22629722977214342
500 Forest's; Func runs:14978(10000); result:0.16606494305819486
=============================
5 Megacity's; Func runs:1211(10000); result:0.13815384615384615
25 Megacity's; Func runs:9363(10000); result:0.12640000000000004
500 Megacity's; Func runs:15147(10000); result:0.09791692307692391
=============================
All score:2.05290 (22.81%)

テスト目的関数に対するL-BFGS法のパフォーマンス出力結果：

L-BFGS|limited memory BFGS method for large scale optimization|0.9|
=============================
5 Hilly's; Func runs:5625(10000); result:0.38480050402327626
25 Hilly's; Func runs:10391(10000); result:0.2944296786579764
500 Hilly's; Func runs:41530(10000); result:0.25091140645623417
=============================
5 Forest's; Func runs:3514(10000); result:0.2508946897150378
25 Forest's; Func runs:9105(10000); result:0.19753907736098766
500 Forest's; Func runs:40010(10000); result:0.1483916309143011
=============================
5 Megacity's; Func runs:916(10000); result:0.12430769230769222
25 Megacity's; Func runs:4639(10000); result:0.10633846153846153
500 Megacity's; Func runs:39369(10000); result:0.09022461538461606
=============================
All score:1.84784 (20.53%)

テスト目的関数に対するNS法のパフォーマンス出力結果：

NS|nonsmooth nonconvex optimization|0.5|0.8|50.0|
=============================
5 Hilly's; Func runs:10171(10000); result:0.3716823351189392
25 Hilly's; Func runs:11152(10000); result:0.30271115043870767
500 Hilly's; Func runs:1006503(10000); result:0.2481831526729561
=============================
5 Forest's; Func runs:10167(10000); result:0.4432983184931045
25 Forest's; Func runs:11221(10000); result:0.20891527876847327
500 Forest's; Func runs:1006503(10000); result:0.15071828612481414
=============================
5 Megacity's; Func runs:7530(10000); result:0.15076923076923068
25 Megacity's; Func runs:11069(10000); result:0.12480000000000002
500 Megacity's; Func runs:1006503(10000); result:0.09143076923076995
=============================
All score:2.09251 (23.25%)

テスト目的関数に対するBC法のパフォーマンス出力結果：

BC|box constrained optimization with fast activation of multiple box constraints|0.9|
=============================
5 Hilly's; Func runs:1732(10000); result:0.37512809463286956
25 Hilly's; Func runs:9763(10000); result:0.3542591015005374
500 Hilly's; Func runs:22312(10000); result:0.26434986025328294
=============================
5 Forest's; Func runs:1564(10000); result:0.28431712294752914
25 Forest's; Func runs:8844(10000); result:0.23891148588644037
500 Forest's; Func runs:15202(10000); result:0.16925473100070892
=============================
5 Megacity's; Func runs:1052(10000); result:0.12307692307692313
25 Megacity's; Func runs:9095(10000); result:0.12787692307692308
500 Megacity's; Func runs:20002(10000); result:0.09740000000000082
=============================
All score:2.03457 (22.61%)

テスト目的関数に対するNLC法のパフォーマンス出力結果：

NLC|nonlinearly constrained optimization with preconditioned augmented lagrangian algorithm|0.8|1000.0|5|
=============================
5 Hilly's; Func runs:8956(10000); result:0.4270442612182801
25 Hilly's; Func runs:10628(10000); result:0.3222093696838907
500 Hilly's; Func runs:48172(10000); result:0.24687323917487405
=============================
5 Forest's; Func runs:8357(10000); result:0.3230697968403923
25 Forest's; Func runs:10584(10000); result:0.2340843463074393
500 Forest's; Func runs:48572(10000); result:0.14792910131023018
=============================
5 Megacity's; Func runs:5673(10000); result:0.13599999999999995
25 Megacity's; Func runs:10560(10000); result:0.1168615384615385
500 Megacity's; Func runs:47611(10000); result:0.09196923076923148
=============================
All score:2.04604 (22.73%)

テスト目的関数に対するLM法のパフォーマンス出力結果：

LM|improved levenberg-marquardt algorithm|0.0001|
=============================
5 Hilly's; Func runs:496(10000); result:0.2779179366819541
25 Hilly's; Func runs:4383(10000); result:0.26680986645907423
500 Hilly's; Func runs:10045(10000); result:0.27253276065962373
=============================
5 Forest's; Func runs:516(10000); result:0.1549127879839302
25 Forest's; Func runs:3727(10000); result:0.14964009375922901
500 Forest's; Func runs:10051(10000); result:0.1481206726095718
=============================
5 Megacity's; Func runs:21(10000); result:0.0926153846153846
25 Megacity's; Func runs:101(10000); result:0.09040000000000001
500 Megacity's; Func runs:2081(10000); result:0.08909230769230835
=============================
All score:1.54204 (17.13%)

これでテスト関数上でのアルゴリズムの挙動を明確に分析できます。ほとんどの手法は、目的関数の呼び出し回数の上限（今回設定した10,000回）に達する前に早期に処理を終了する傾向があります。たとえば、離散的なMegacity問題（パラメータ数1,000）の場合、レベンバーグ・マーカート法(LM)は平均で2,081回のイテレーションで停止し、パラメータ数10の場合はわずか21回で終了しました。一方、滑らかなHilly関数に対しては、この方法はより多くの反復で最小値を探そうとしました。対照的に、他の手法は目的関数の呼び出し回数が100万回を超えることもありました。

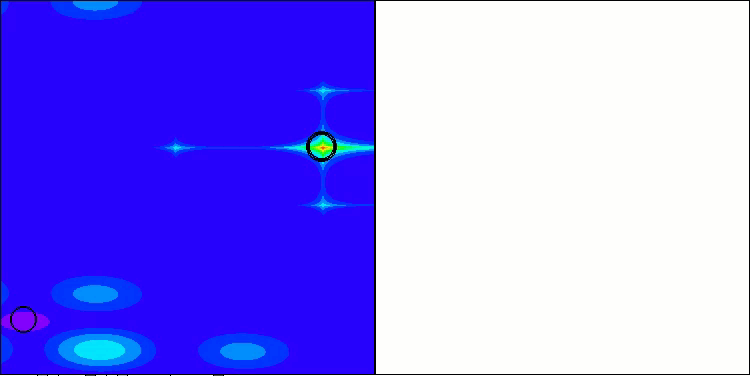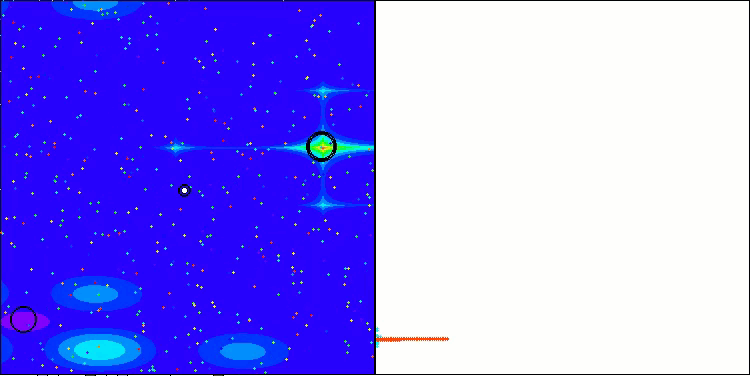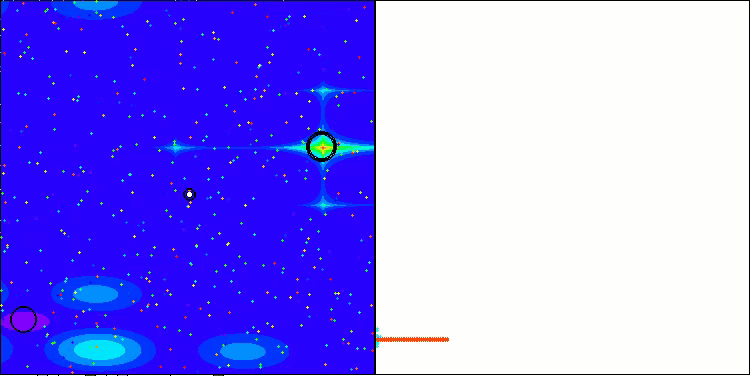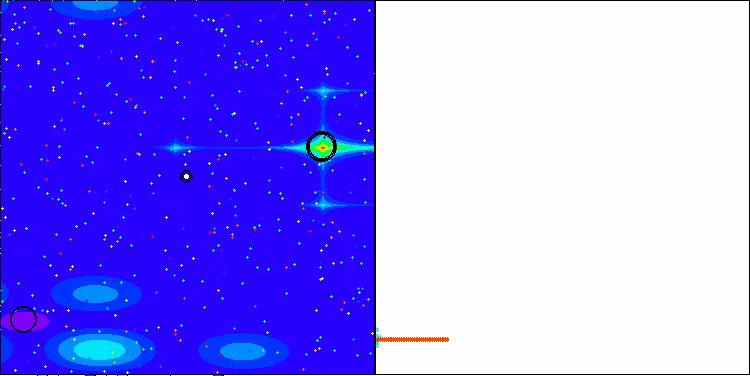
以下に、最も高いスコアを獲得したNS法と、最も低かったLM法のパフォーマンス可視化を示します。

NS Hilly

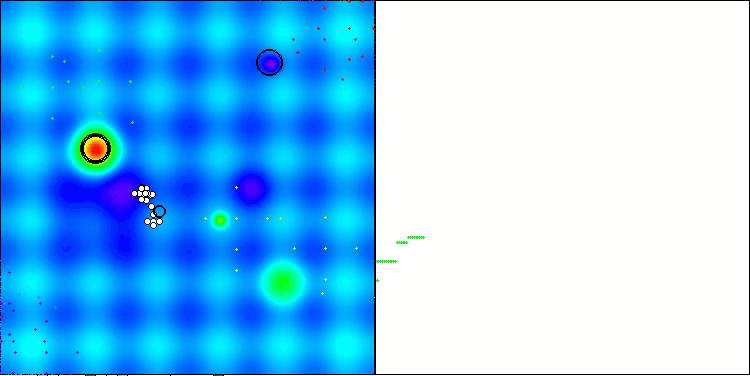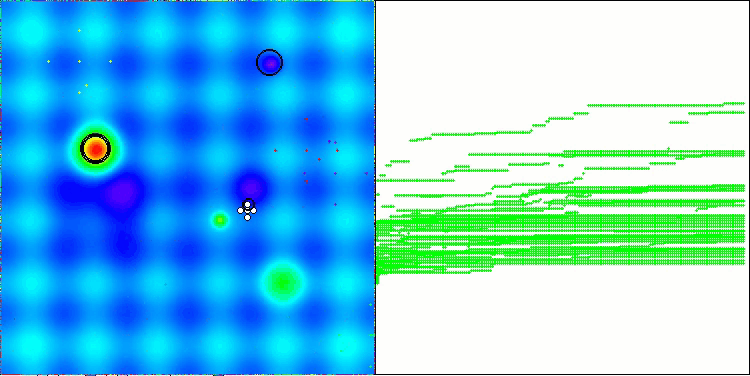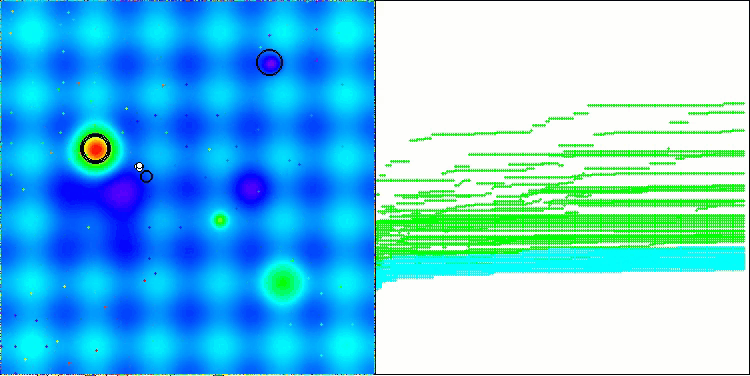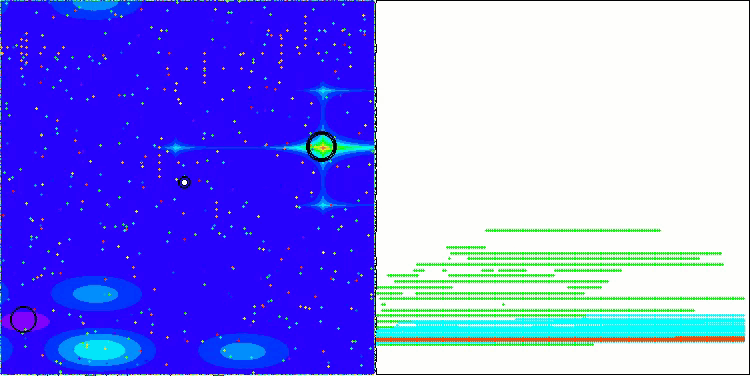
Hillyテスト関数のNS

NS Forest

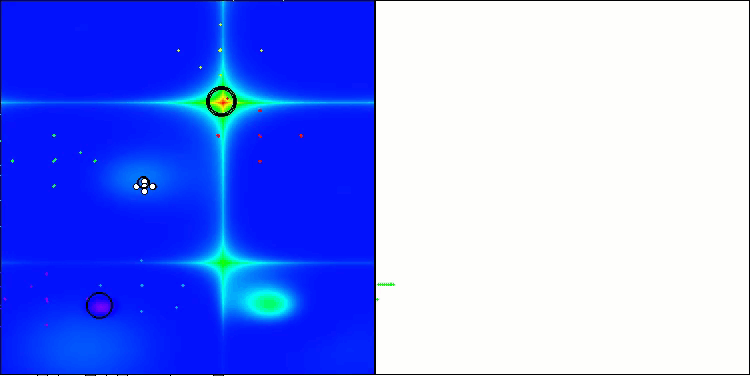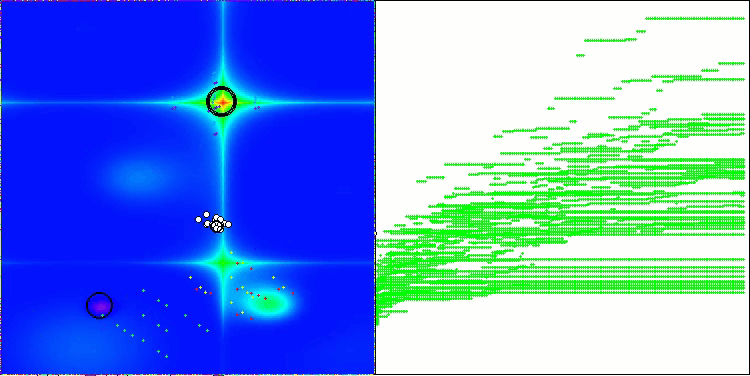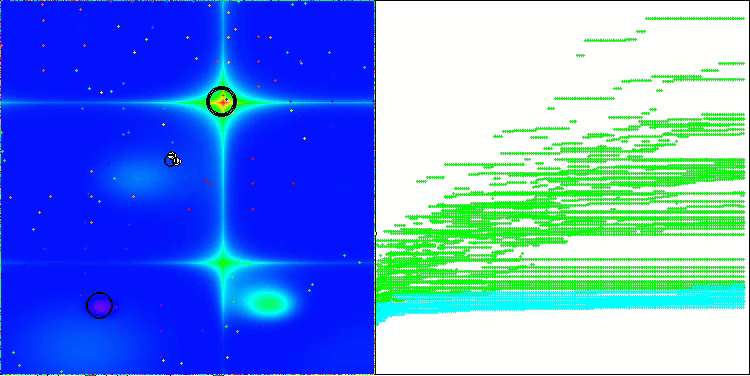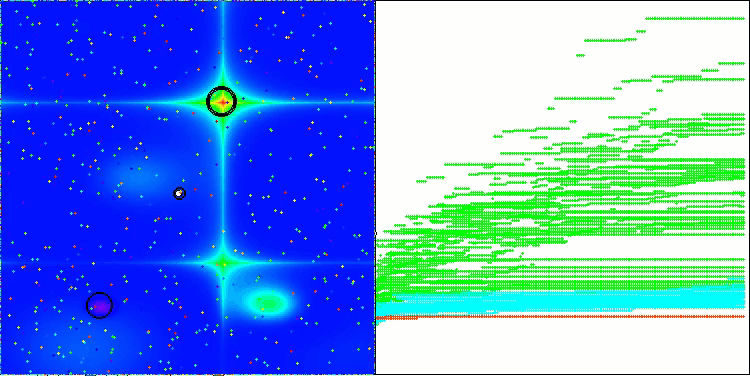
Forestテスト関数のNS

NS Megacity

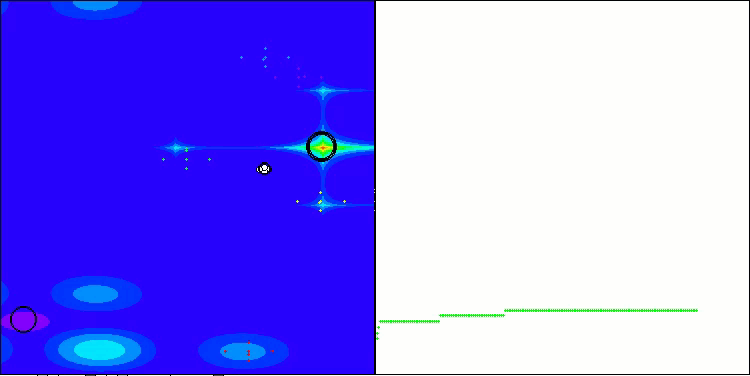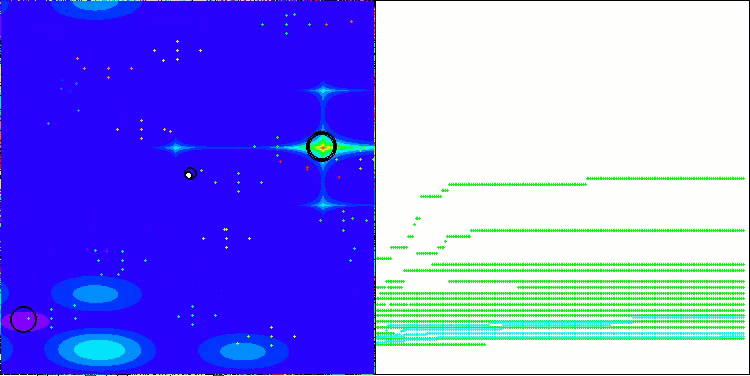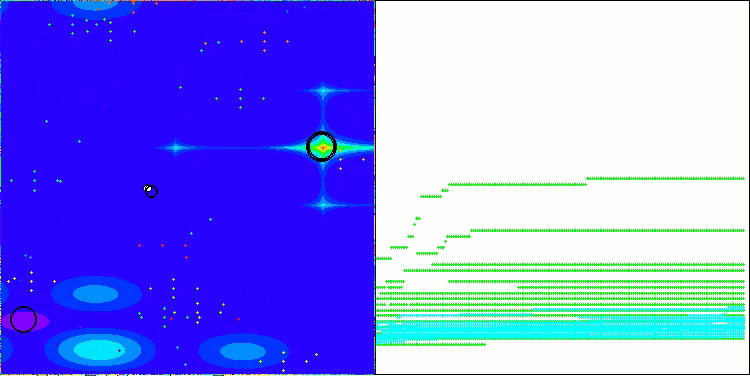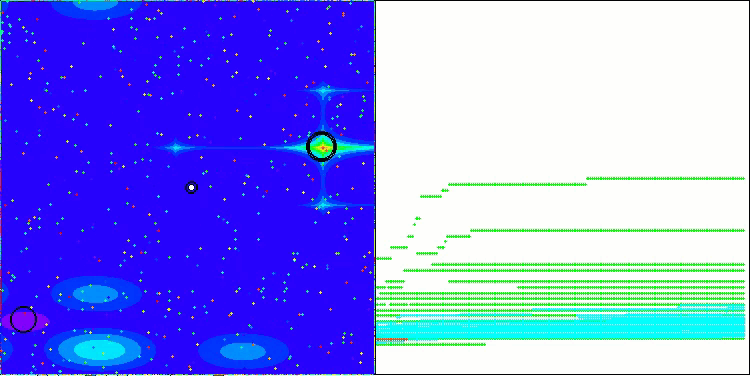
Megacityテスト関数のNS

LM Hilly

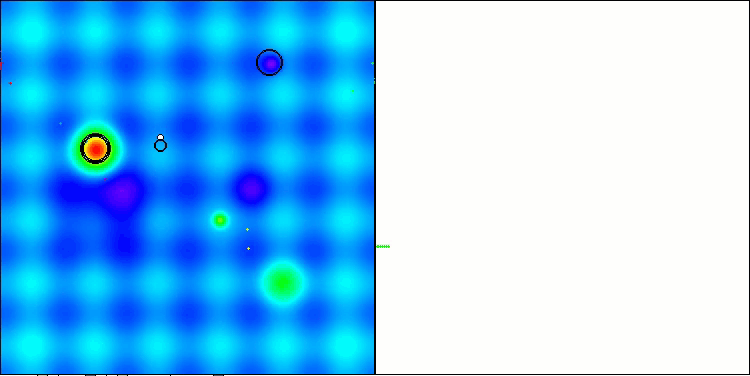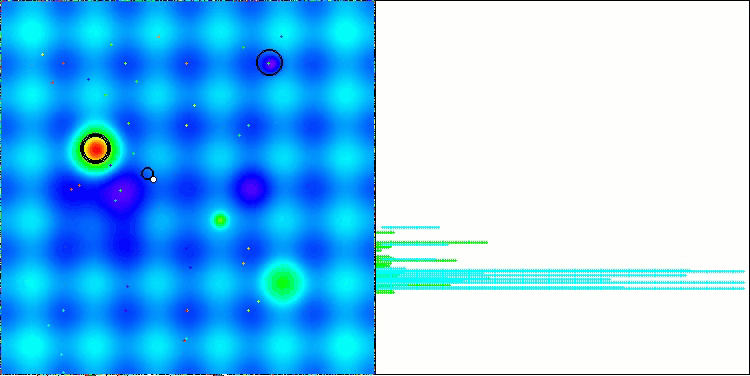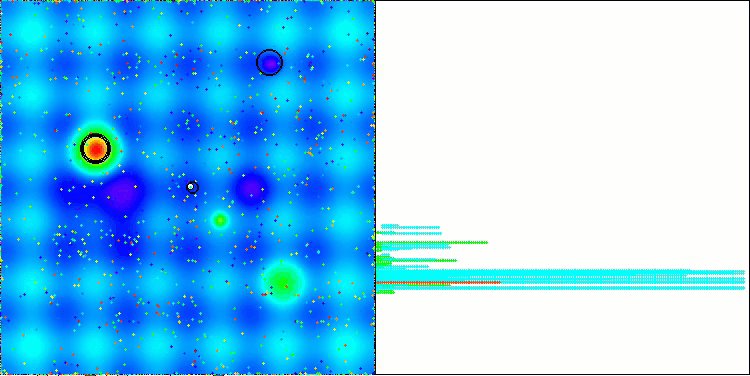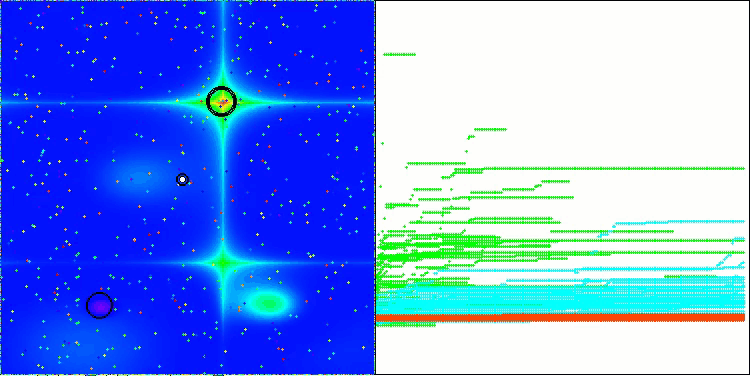
Hillyテスト関数のLM

LM Forest

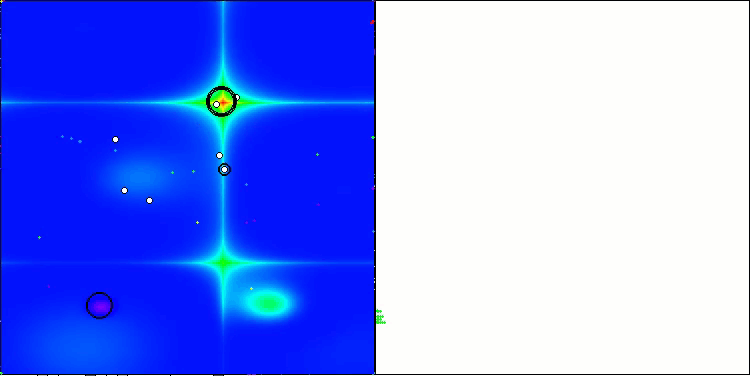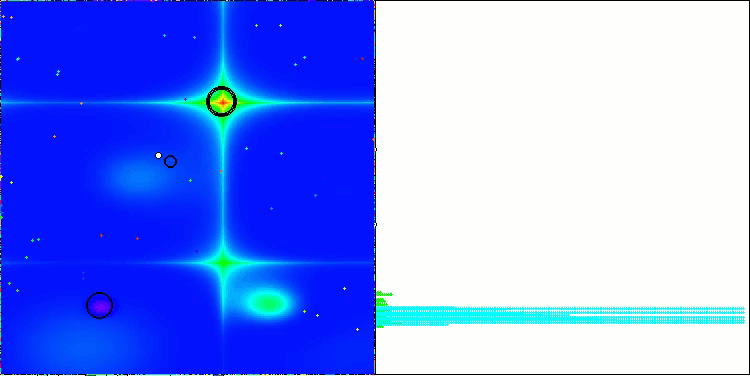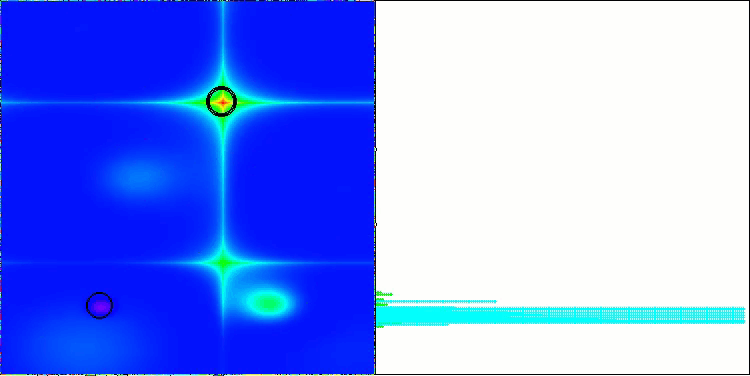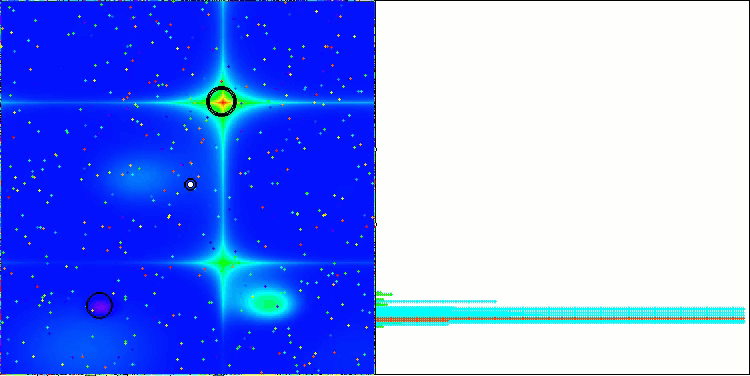
Forestテスト関数のLM

LM Megacity

Megacityテスト関数のLM

得られた結果を表にまとめてみましょう。

Tab

対応するテストに応じたアルゴリズムのカラーグラデーション

まとめ

2つの記事を通して、ALGLIBライブラリの最適化手法を学び、それらをユーザープログラムに統合する方法や、メソッド関数とのやり取りの特徴についても解説しました。さらに、アルゴリズムの強みと弱みを明らかにするためのテストも実施しました。ここで簡単にまとめます。

低次元の滑らかな関数(Hilly)では、NLC法が最良の結果を示しましたが、高次元ではLM法がリードしました。
鋭い極値を持つ滑らかな関数(Forest)では、低次元でNS法が最も良い結果を出し、高次元ではBC法が最優秀でした。
離散的なMegacity問題では、小規模次元でNS法がトップに立ち、大規模次元ではBLEIC法が首位となりました。

手法間の結果の差は大きくなく、各手法の結果範囲内に収まっていますが、NS法はより汎用性が高いと言えます。ただし、強制停止ができない点は留意が必要です。

記事に添付されたコードには、最適化手法をプロジェクトにすぐに導入できる内容がすべて含まれており、それらの能力を視覚的に確認し評価することも可能です。

記事で使用されているプログラム

#	名前	種類	詳細
1	Simple test ALGLIB BLEIC.mq5	スクリプト	BLEIC動作テスト用スクリプト
2	Simple test ALGLIB LBFGS.mq5	スクリプト	L-BFGS動作テスト用スクリプト
3	Simple test ALGLIB NS.mq5	スクリプト	NS動作テスト用スクリプト
4	Simple test ALGLIB BC.mq5	スクリプト	BC動作テスト用スクリプト
5	Simple test ALGLIB NLC.mq5	スクリプト	NLC動作テスト用スクリプト
6	Simple test ALGLIB LM.mq5	スクリプト	LM動作テスト用スクリプト
7	Test_minBLEIC.mq5	スクリプト	BLEIC用テストベンチ
8	Test_minLBFGS.mq5	スクリプト	L-BFGS用テストベンチ
9	Test_minNS.mq5	スクリプト	NS用テストベンチ
10	Test_minBC.mq5	スクリプト	BC用テストベンチ
11	Test_minNLC.mq5	スクリプト	NLC用テストベンチ
12	Test_minLM.mq5	スクリプト	LM用テストベンチ
13	CalculationTestResults.mq5	スクリプト	比較表の結果を計算するスクリプト
14	TestFunctions.mqh	インクルード	テスト関数のライブラリ
15	TestStandFunctions.mqh	インクルード	テストスタンド関数ライブラリ
16	Utilities.mqh	インクルード	補助関数のライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16164

添付されたファイル |

ZIPをダウンロード

Test_ALGLIB_optimization_methods.zip (59.15 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

最後のコメント | ディスカッションに移動 (49)

Andrey Dik | 3 11月 2024 において 13:06

Maxim Dmitrievsky #:
1. 。

2.何かを最適化するタスクがあり、それを最適化し、正常な結果を得た。関数は複雑なので、普通に最適化される。

1.1.質問するのは自由だが、完全なソースコードと正しい再現性のあるテストの立場から話す方が、常に建設的である。

2.90億人に、関数の表面は隠されている白紙にランダムに指を突っ込んでもらえば、2次元のメガシティで最適な結果を得ることができる（そのうちの1人は必ずグローバルに非常に近くなり、問題をうまく解いたのは自分だと言うだろう）。しかし、私たちは90億回の試行で最適解を見つけるのではなく、戦略を用いて1万回で最適解を見つける必要がある。

一連の独立したテスト（結果の安定性、再現性）の平均結果が高ければ高いほど、テストされた方法は特定のタイプの問題に対してランダムポークと比較して高い（ある問題に対してはランダムポークと大差ない方法もあれば、非常に効果的な方法もある）。

これは、異なるアルゴリズムをテストし比較するポイントであり、1つのテスト関数だけでなく、異なる特性を持つ3つの異なる関数をベンチマークとすることで、異なるタスクに対する異なるアルゴリズムの適用可能性、異なるタスクでの限界と能力を明確に見ることができる。これにより、最適化問題の解決に有意義な方法でアプローチすることができます。

今後は、記事の内容やコードに関する具体的な質問にお答えしたいと思います。

Maxim Dmitrievsky | 3 11月 2024 において 13:44

局所最適化の手法をグローバルな問題に適用し、グローバル最適化の手法と比較する。それが私の言っていることだ。

これらの方法をグローバル最適化に適応させる方法について話しているのです。最も単純な方法は、初期化の回数を増やすことです。

Rorschach | 3 11月 2024 において 14:30

私の理解が正しければ、アダムなどは品質ではなくスピードのために磨かれる。

反復回数ではなく時間で制限した場合の評価を見るのは興味深い。

Andrey Dik | 3 11月 2024 において 17:30

Rorschach #:

私の理解が正しければ、アダムなどはクオリティではなくスピードに磨きをかけている。

反復回数ではなく時間で制限した場合の評価を見るのは興味深い。

ADAMアルゴリズムファミリー（AdamW、RAdam、AdaBeliefなど）やSGD、SGRADなど（たくさんあります）は、古典的な勾配法に代わる現代的なアルゴリズムとして開発され、解析式の知識がなくても大きな次元の問題を解くことができるように設計されています。また、グーグル（2023年）の興味深いライオン法や、ごく最近のものもある。このトピックは、特にニューラルネットワークのトレーニングの文脈では、研究するのに非常に興味深く、いくつかの簡単な例（あるいは複雑な例）でターゲットサーフェスを構築し、実験（その内部を解析し、メソッドの特性を深く研究し、その能力を慎重に評価する - すべてが私たちの好きなように）を行うことが有用で有益であろう。

時間の制約があれば、何も縛られることはない。あるユーザーは1分間にターゲットに100万回アクセスするだろうし、別のユーザーは10億回アクセスするだろう。このような状況でどうやってアルゴを比較できるだろうか？そのため、ヒット数に制限を設け、その制限内で効率を比較するのだ。

Rorschach | 3 11月 2024 において 18:32

Andrey Dik #:

時間的な制約があれば、縛るものは何もない。あるユーザーは1分間にターゲットに100万回アクセスするが、別のユーザーは10億回アクセスする。このような状況で、どうやって両者のアルゴを比較できるだろうか？そのため、ヒット数に制限を設け、その制限内で効率を比較するのだ。

筆者のPCにバインド。ANSの10000反復の時間を基準とする。

fxsaberのコードでの結果：

	pso	*72秒*	40.8 KB、	BestResult = -14.0：	TPdist = 0.41、	SLdist = 0.68
	ブガ	22秒	38.5 KB	BestResult = -14.0：	TPdist = 0.32、	SLdist = 1.04
4	pOeS	23秒	19.9 KB	BestResult = -14.0：	TPdist = 0.54、	SLdist = 1.12
6	sdsm	23秒	21.1 KB	BestResult = -14.0：	TPdist = 0.42、	SLdist = 1.28
	SDS	22秒	14.5 KB	BestResult = -14.0：	TPdist = 0.89、	SLdist = 1.34
8	ESG	22秒	23.3 KB	BestResult = -14.0：	TPdist = 0.82、	SLdist = 0.36
9	アジア	23秒	19.2 KB	BestResult = -14.0：	TPdist = 0.82、	SLdist = 1.02
13	デ	22秒	13.3 KB、	BestResult = -14.0：	TPdist = 0.6 、	SLdist = 0.74
16	hs		16.5 KB
17	ssg	22秒	22.7 KB	BestResult = -14.0：	TPdist = 0.57、	SLdist = 0.4
20	ポーズ	23秒	18.8 KB	BestResult = -14.0：	TPdist = 0.42、	SLdist = 2.0
26	アコム	22秒	21.3 KB	BestResult = -14.0：	TPdist = 0.46、	SLdist = 0.98
27	bfoga	*30秒*	22.9 KB	BestResult = -14.0：	TPdist = 0.1 、	SLdist = 0.2
32	メック	22秒	23.7 KB	BestResult = -14.0：	TPdist = 0.91、	SLdist = 0.58
33	iwo	23秒	25.4 KB	BestResult = -14.0：	???
34	メス	23秒	21.0 KB、	BestResult = -14.0：	TPdist = 0.54、	SLdist = 1.44
35	コーム	22秒	16.9 KB	BestResult = -14.0：	TPdist = 0.32、	SLdist = 1.96
36	sdom	22秒	13.9 KB	BestResult = -14.0：	TPdist = 0.72、	SLdist = 2.0
37	nmm	22秒	32.9 KB	BestResult = -14.0：	TPdist = 1.0 、	SLdist = 1.58
38	ファム	22秒	17.3 KB	BestResult = -14.0：	TPdist = 0.83、	SLdist = 0.48
39	gsa	22秒	23.1 KB	BestResult = -14.0：	TPdist = 0.83、	SLdist = 1.44
40	ボフォ	22秒	19.5 KB	BestResult = -14.0：	TPdist = 0.62、	SLdist = 1.6
41	abc	(err)	32.0 KB
42	バ	23秒	20.0 KB	BestResult = -14.0：	TPdist = 0.49、	SLdist = 1.18
44	サ	23秒	12.5 KB	BestResult = -14.0：	TPdist = 0.8 、	SLdist = 1.6
45	iwdm	23秒	27.3 KB	BestResult = -14.0：	TPdist = 0.32、	SLdist = 0.72
	pso	23秒	12.8 KB	BestResult = -14.0：	TPdist = 0.74、	SLdist = 1.42
	マ	22秒	18.0 KB	BestResult = -14.0：	TPdist = 0.88、	SLdist = 0.62
	sfl		29.8 KB
	fss	22秒	24.5 KB	BestResult = -14.0：	TPdist = 0.78、	SLdist = 1.96
	rnd		16.6 KB
	グー	22秒	17.0 KB	BestResult = -14.0：	TPdist = 0.72、	SLdist = 1.56
	css	22秒	17.2 KB	BestResult = -14.0：	TPdist = 0.74、	SLdist = 1.3
	em		17.7 KB
	sc	23秒	18.8 KB	BestResult = -14.0：	TPdist = 0.51、	SLdist = 1.3

追加指標としてのPSコードサイズ（アルゴリズムの実装がどれだけ複雑か）

取引におけるニューラルネットワーク：対照パターンTransformer（最終回）

本連載の前回の記事では、Atom-Motif Contrastive Transformer (AMCT)フレームワークについて取り上げました。これは、対照学習を用いて、基本要素から複雑な構造に至るまでのあらゆるレベルで重要なパターンを発見することを目的とした手法です。この記事では、MQL5を用いたAMCTアプローチの実装を引き続き解説していきます。

ALGLIBライブラリの最適化手法（第1回）：

この記事では、MQL5におけるALGLIBライブラリの最適化手法について紹介します。記事には、最適化問題を解決するためにALGLIBを使用するシンプルで分かりやすい例が含まれており、これらの手法をできるだけ身近に感じられるように構成されています。BLEIC、L-BFGS、NSといったアルゴリズムのつながりを詳しく見ていき、それらを使って簡単なテスト問題を解いてみます。

エラー 146 (「トレードコンテキストビジー」) と、その対処方法

この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。

多通貨エキスパートアドバイザーの開発（第19回）：Pythonで実装されたステージの作成

これまでは、標準のストラテジーテスター内で最適化タスクを順に自動実行することだけを考えてきました。しかし、もしそれらの実行の合間に、別の手段で得られたデータを処理したいとしたらどうなるでしょうか。ここでは、Pythonで記述されたプログラムによって新たな最適化ステージを作成する機能の追加を試みます。