
Algoritmo de busca orbital atômica — Atomic Orbital Search (AOS): Modificação
Conteúdo
- Introdução
- Implementação do algoritmo
- Exemplo de uso dos algoritmos da classe C_AO
- Resultados dos testes
Introdução
Na primeira parte do artigo, examinamos em detalhes o algoritmo AOS (Atomic Orbital Search), seus fundamentos inspirados no modelo orbital atômico e os mecanismos que sustentam seu funcionamento. Discutimos como o algoritmo utiliza distribuições probabilísticas e a dinâmica das interações para buscar soluções ótimas em problemas de otimização complexos.
Na segunda parte do artigo, focaremos na modificação do algoritmo AOS, pois não podemos ignorar uma ideia tão notável sem buscar aprimorá-la. Analisaremos o conceito de melhoria do algoritmo, com especial atenção para os operadores específicos que pertencem a este método e que podem aumentar sua eficiência e adaptabilidade.
Trabalhar no algoritmo AOS abriu para mim muitos aspectos interessantes relacionados aos seus métodos de busca no espaço de soluções. Durante a pesquisa, também cheguei a várias ideias sobre como melhorar esse algoritmo interessante. Em particular, concentrei-me na reformulação dos métodos existentes que podem melhorar o desempenho do algoritmo, aprimorando sua capacidade de explorar espaços de soluções complexos. Veremos como essas melhorias podem ser integradas à estrutura existente do algoritmo AOS, tornando-o uma ferramenta ainda mais poderosa para resolver problemas de otimização. Assim, nosso objetivo é não apenas analisar os mecanismos existentes, mas também propor novas abordagens que podem ampliar significativamente as capacidades do algoritmo AOS.
Implementação do algoritmo
No artigo anterior, examinamos em detalhes os componentes-chave do algoritmo AOS. Lembramos que neste algoritmo a população é considerada como uma molécula, e a área admissível de coordenadas, onde ocorre a busca por soluções ótimas, é representada como um átomo. Cada átomo é composto por diferentes camadas, que ajudam a organizar e direcionar a busca.
Os valores específicos obtidos em cada coordenada no processo de otimização podem ser interpretados como elétrons. Esses elétrons, localizados dentro do átomo, representam possíveis soluções para um dos parâmetros do problema em questão. Assim, cada molécula (população) busca encontrar os valores ótimos (elétrons) dentro da área definida (átomo).
Na versão original do algoritmo AOS, a energia da camada BEk é definida como a média aritmética da energia dos elétrons na camada, e a ligação BSk é definida como a média aritmética de suas coordenadas. A energia BEk é usada para comparar com a energia dos elétrons, a fim de determinar a maneira de seu deslocamento subsequente. A ligação BSk serve para calcular o incremento na posição dos elétrons, ou seja, a diferença entre a melhor posição dos elétrons, LEk, na camada, e a ligação BSk, pela seguinte fórmula: Xki[t+1] = Xkit + αi × (βi × LEk − γi × BSk).
Proponho abandonar a posição média dos elétrons BSk em favor da melhor posição individual de cada um. Dessa forma, o elétron se moverá em direção à melhor solução em sua camada, com base em seu próprio desempenho, e não em uma solução média da camada. Além disso, os dois componentes aleatórios βi e γi parecem ser redundantes, já que já existe um componente aleatório externo αi. Isso permitirá reduzir o tempo de geração de números aleatórios nesta fórmula em três vezes, sem que o sentido físico seja perdido.
Agora vamos analisar a estrutura que descreve a camada no átomo. Vermelho são destacados os elementos que serão removidos do código://—————————————————————————————————————————————————————————————————————————————— struct S_Layer { int pc; // particle counter double BSk; // connection state double BEk; // binding energy double LEk; // minimum energy void Init () { pc = 0; BSk = 0.0; BEk = 0.0; LEk = 0.0; } }; //——————————————————————————————————————————————————————————————————————————————
Vamos analisar o código do método "CalcLayerParams", responsável pelo cálculo das características das camadas, como energia e ligação. As linhas destacadas em vermelho serão removidas, pois não serão mais necessárias. Lembramos que este método desempenha um papel fundamental na estratégia de busca do AOS, voltada para evitar que o algoritmo fique preso em armadilhas locais. Como o nível de energia nas camadas não depende de sua localização (a energia diminui do centro para as camadas externas do átomo), mas é determinado pela presença de extremos locais significativos (a camada externa pode ter energia superior às internas), as camadas servem para ajustar o movimento dos elétrons no espaço de busca.
A quantidade aleatória de camadas a cada época ajuda a combater o aprisionamento do algoritmo em armadilhas locais, impedindo que os elétrons fiquem presos apenas em uma camada. Na versão modificada, também não será mais necessário calcular a energia média de todo o átomo, portanto removeremos as linhas correspondentes.

Figura 1. Diferenças na direção e no tamanho do deslocamento do elétron e em função da quantidade de camadas no átomo
A Figura 1 ilustra as diferenças no comportamento dos elétrons em átomos com diferentes quantidades de camadas no algoritmo AOS. A parte superior mostra um átomo com três camadas, no qual o elétron está na camada L1 com o valor da função objetivo B1 e se move em direção ao melhor valor local LEk1. A parte inferior da figura ilustra um átomo com duas camadas, onde o elétron também está na camada L1 e se move em direção ao melhor valor local LEk1, com o valor da função objetivo B1 (no caso de três camadas, esse seria o ponto LEk2).
Elementos-chave na figura:
- B0, B1, B2 — designações dos valores locais da função objetivo para as respectivas camadas,
- LEk0, LEk1, LEk2 — melhores soluções nas respectivas camadas,
- L0, L1, L2 — camadas no átomo,
- e — elétron,
- MIN, MAX — limites das camadas externas dos átomos (condições de fronteira para os parâmetros do problema de otimização).
//—————————————————————————————————————————————————————————————————————————————— // Calculate parameters for each layer void C_AO_AOS::CalcLayerParams () { double energy; // Handle each coordinate (atom) for (int c = 0; c < coords; c++) { atoms [c].Init (maxLayers); // Handle each layer for (int L = 0; L < currentLayers [c]; L++) { energy = -DBL_MAX; // Handle each electron for (int e = 0; e < popSize; e++) { if (electrons [e].layerID [c] == L) { atoms [c].layers [L].pc++; atoms [c].layers [L].BEk += a [e].f; atoms [c].layers [L].BSk += a [e].c [c]; if (a [e].f > energy) { energy = a [e].f; atoms [c].layers [L].LEk = a [e].c [c]; } } } // Calculate average values for the layer if (atoms [c].layers [L].pc != 0) { atoms [c].layers [L].BEk /= atoms [c].layers [L].pc; atoms [c].layers [L].BSk /= atoms [c].layers [L].pc; } } } // Calculate the general state of connections ArrayInitialize (BS, 0); for (int c = 0; c < coords; c++) { for (int e = 0; e < popSize; e++) { BS [c] += a [e].c [c]; } BS [c] /= popSize; } } //——————————————————————————————————————————————————————————————————————————————
Para atualizar as melhores soluções individuais, adicionaremos código ao método "Revision" na classe da versão modificada "C_AO_AOSm".
//—————————————————————————————————————————————————————————————————————————————— // Method of revising the best solutions void C_AO_AOSm::Revision () { int bestIndex = -1; // Find the best solution in the current iteration for (int i = 0; i < popSize; i++) { // Update the global best solution if (a [i].f > fB) { fB = a [i].f; bestIndex = i; } // Update the personal best solution if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } // Update the best coordinates if a better solution is found if (bestIndex != -1) ArrayCopy (cB, a [bestIndex].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
No método "UpdateElectrons", removeremos as variáveis "β" e "γ", pois elas não serão mais necessárias para gerar os números aleatórios correspondentes. Além disso, eliminaremos a divisão do incremento do elétron pelo número de camadas no caso de movimento em direção à solução global. Para ser sincero, a decisão dos autores parece discutível, e o sentido físico dessa abordagem não é totalmente claro. Talvez os autores quisessem tornar a intensidade do movimento dos elétrons em direção à solução global variável, mudando-a de acordo com o número de camadas: quanto menos camadas, mais intenso deveria ser o movimento (embora meus experimentos tenham mostrado que isso não traz benefício algum).
//—————————————————————————————————————————————————————————————————————————————— // Update electron positions void C_AO_AOS::UpdateElectrons () { double α; // speed coefficient double β; // best solution weight coefficient double γ; // average state weight coefficient double φ; // transition probability double newPos; // new position double LE; // best energy double BSk; // connection state int lID; // layer ID // Handle each particle for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Random scatter newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); β = u.RNDprobab (); γ = u.RNDprobab (); // If the current particle energy is less than the average layer energy if (a [p].f < atoms [c].layers [lID].BEk) { // Moving towards the global optimum---------------------------- LE = cB [c]; newPos = a [p].c [c]+ α * (β * LE - γ * BS [c]) / currentLayers [c]; } else { // Movement towards the local optimum of the layer------------------------ LE = atoms [c].layers [lID].LEk; BSk = atoms [c].layers [lID].BSk; newPos = a [p].c [c] + α * (β * LE - γ * BSk); } } // Limiting the new position within the search range taking into account the step a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Adicionalmente, no método "UpdateElectrons" da classe "C_AO_AOSm", em vez de espalhar aleatoriamente o elétron pelo espaço de busca, implementaremos o movimento do elétron para o centro do núcleo com certa probabilidade. Na prática, isso significa substituir o valor de alguma coordenada pelo valor da solução global, o que deve melhorar as propriedades combinatórias do algoritmo. Já a dispersão aleatória era destinada a proporcionar diversidade na população de soluções, mas essa propriedade acabava promovendo a propagação dos elétrons conforme uma distribuição lognormal, onde havia uma probabilidade diferente de zero de o elétron atingir qualquer ponto do espaço durante o movimento.
Verde são indicadas as mudanças nas fórmulas de movimentação dos elétrons, agora o incremento é calculado como a diferença entre a melhor solução local da camada e a melhor solução individual do elétron.
//—————————————————————————————————————————————————————————————————————————————— // Update electron positions void C_AO_AOSm::UpdateElectrons () { double α; // speed coefficient double φ; // transition probability double newPos; // new position double LE; // best energy double BSk; // connection state int lID; // layer ID // Handle each particle for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Random jump to center newPos = cB [c]; } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); // If the current particle energy is less than the average layer energy if (a [p].f < atoms [c].layers [lID].BEk) { // Moving towards the global optimum---------------------------- LE = cB [c]; newPos = a [p].cB [c]+ α * (LE - a [p].cB [c]); } else { // Movement towards the local optimum of the layer------------------------ LE = atoms [c].layers [lID].LEk; newPos = a [p].cB [c]+ α * (LE - a [p].cB [c]); } } // Limiting the new position within the search range taking into account the step a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
O método "DistributeParticles" distribui os elétrons no espaço de busca, utilizando uma distribuição lognormal para cada coordenada. Para cada partícula e cada coordenada, é chamada uma função que gera a posição considerando os parâmetros definidos (valor médio, mínimo e máximo, pico), e depois é aplicada uma função adicional para ajustar a posição dentro do intervalo especificado.
//—————————————————————————————————————————————————————————————————————————————— // Distribution of particles in the search space void C_AO_AOS::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Use log-normal distribution to position particles a [i].c [c] = u.LognormalDistribution (cB [c], rangeMin [c], rangeMax [c], peakPosition); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Vamos alterar a distribuição dos elétrons para uma distribuição normal. Nesta distribuição é utilizado o desvio padrão igual a 8. Embora esse parâmetro pudesse ser exposto externamente ao algoritmo, decidi não fazer isso. Valores menores favorecem uma exploração mais ampla do espaço de busca, enquanto valores mais altos aumentam a precisão da convergência ao refinar a solução global.
//—————————————————————————————————————————————————————————————————————————————— // Distribution of particles in the search space void C_AO_AOSm::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Use a Gaussian distribution to position particles a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Todas as mudanças feitas na versão original do algoritmo AOS foram analisadas com o objetivo de aumentar sua eficiência. Como alterações significativas foram feitas na lógica da estratégia de busca, a versão modificada do algoritmo pode ser indicada pela letra "m". A partir de agora, apenas uma versão modificada será apresentada na tabela de classificação — AOSm.
Exemplo de uso dos algoritmos da classe C_AO
Como todos os algoritmos populacionais de otimização discutidos anteriormente foram herdados da classe comum C_AO, isso permite usá-los de maneira uniforme e com mínimo esforço para resolver diferentes problemas que exigem a busca de parâmetros ótimos. No exemplo abaixo é apresentado um script no qual é realizada a otimização de uma função objetivo:
1. No início do script você pode escolher qual algoritmo de otimização utilizar. Se nada for selecionado, o script informará o erro e será interrompido.
2. Configuração de parâmetros. O script define quantas vezes a função será chamada, quantos parâmetros precisam ser otimizados, o tamanho do grupo de soluções e quantas iterações serão executadas.
3. Limites de valores. Para cada parâmetro são definidos valores mínimos e máximos (neste exemplo de -10 a 10).
4. O script inicia o processo de otimização:
- Ele gera soluções (conjuntos de parâmetros) e verifica o quão boas elas são, utilizando uma função especial (função objetivo).
- A cada iteração, o algoritmo atualiza suas soluções com base naquelas que apresentaram melhores resultados.
5. Resultados. Após a conclusão da otimização, o script exibe informações sobre qual algoritmo foi utilizado, qual o melhor valor encontrado e quantas vezes a função foi executada.
6. A função objetivo — é uma tarefa abstrata de otimização (neste exemplo, a solução de encontrar o máximo global de uma parábola invertida), que recebe os parâmetros e retorna uma avaliação da sua qualidade.
#property script_show_inputs // Specify that the script will show the inputs in the properties window #include <Math\AOs\PopulationAO\#C_AO_enum.mqh> // Connect the library for handling optimization algorithms input E_AO AOexactly = NONE_AO; // Parameter for selecting the optimization algorithm, default is NONE_AO //—————————————————————————————————————————————————————————————————————————————— void OnStart() { //---------------------------------------------------------------------------- int numbTestFuncRuns = 10000; // Total number of function runs int params = 1000; // Number of parameters for optimization int popSize = 50; // Population size for optimization algorithm int epochCount = numbTestFuncRuns / popSize; // Total number of epochs (iterations) for optimization double rangeMin [], rangeMax [], rangeStep []; // Arrays for storing the parameters' boundaries and steps ArrayResize (rangeMin, params); // Resize 'min' borders array ArrayResize (rangeMax, params); // Resize 'max' borders array ArrayResize (rangeStep, params); // Resize the steps array // Initialize the borders and steps for each parameter for (int i = 0; i < params; i++) { rangeMin [i] = -10; // Minimum value of the parameter rangeMax [i] = 10; // Maximum value of the parameter rangeStep [i] = DBL_EPSILON; // Parameter step } //---------------------------------------------------------------------------- C_AO *ao = SelectAO (AOexactly); // Select an optimization algorithm if (ao == NULL) // Check if an algorithm has been selected { Print ("AO not selected..."); // Error message if no algorithm is selected return; } ao.params [0].val = popSize; // Assigning population size.... ao.SetParams (); //... (optional, then default population size will be used) ao.Init (rangeMin, rangeMax, rangeStep, epochCount); // Initialize the algorithm with given boundaries and number of epochs // Main loop by number of epochs for (int epochCNT = 1; epochCNT <= epochCount; epochCNT++) { ao.Moving (); // Execute one epoch of the optimization algorithm // Calculate the value of the objective function for each solution in the population for (int set = 0; set < ArraySize (ao.a); set++) { ao.a [set].f = ObjectiveFunction (ao.a [set].c); // Apply the objective function to each solution } ao.Revision (); // Update the population based on the results of the objective function } //---------------------------------------------------------------------------- // Output the algorithm name, best result and number of function runs Print (ao.GetName (), ", best result: ", ao.fB, ", number of function launches: ", numbTestFuncRuns); delete ao; // Release the memory occupied by the algorithm object } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Definition of the user's objective function, in this case as an example - a paraboloid, F(Xn) ∈ [0.0; 1.0], X ∈ [-10.0; 10.0], maximization double ObjectiveFunction (double &x []) { double sum = 0.0; // Variable for accumulation of the result // Loop through all parameters for (int i = 0; i < ArraySize (x); i++) { // Check if the parameter is in the allowed range if (x [i] < -10.0 || x [i] > 10.0) return 0.0; // If the parameter is out of range, return 0 sum += (-x [i] * x [i] + 100.0) * 0.01; // Calculate the value of the objective function } return sum /= ArraySize (x); } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Vamos passar para o teste da versão modificada do algoritmo.
AOS|Atomic Orbital Search|50.0|10.0|20.0|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.8023218355650774
25 Hilly's; Func runs: 10000; result: 0.7044908398821188
500 Hilly's; Func runs: 10000; result: 0.3102116882841442
=============================
5 Forest's; Func runs: 10000; result: 0.8565993699987462
25 Forest's; Func runs: 10000; result: 0.6945107796904211
500 Forest's; Func runs: 10000; result: 0.21996085558228406
=============================
5 Megacity's; Func runs: 10000; result: 0.7461538461538461
25 Megacity's; Func runs: 10000; result: 0.5286153846153846
500 Megacity's; Func runs: 10000; result: 0.1435846153846167
=============================
All score: 5.00645 (55.63%)
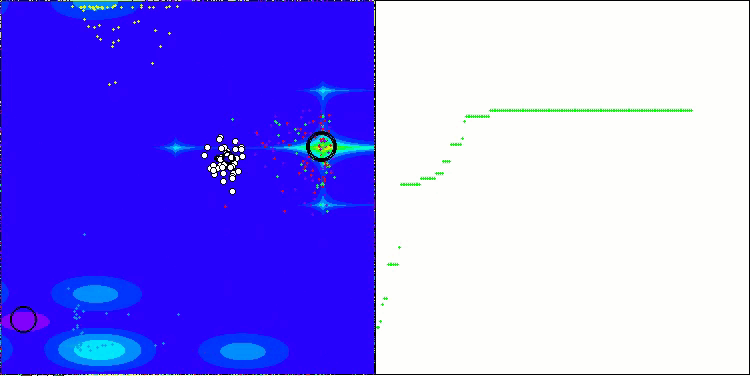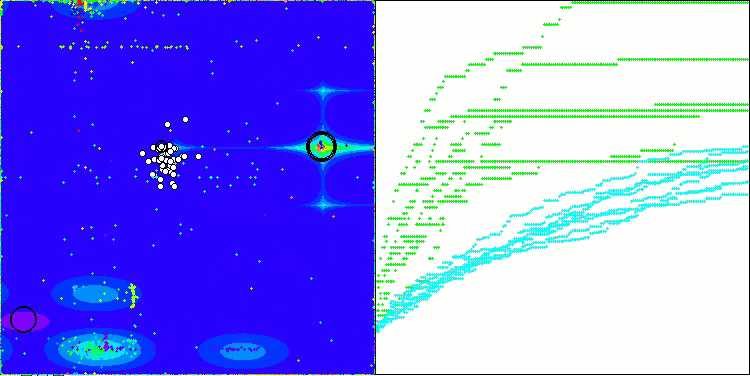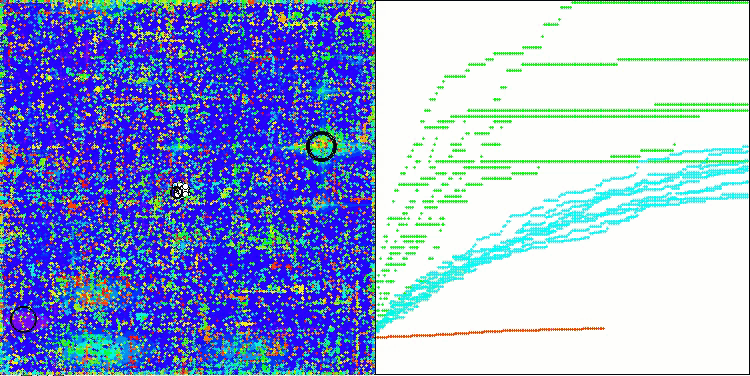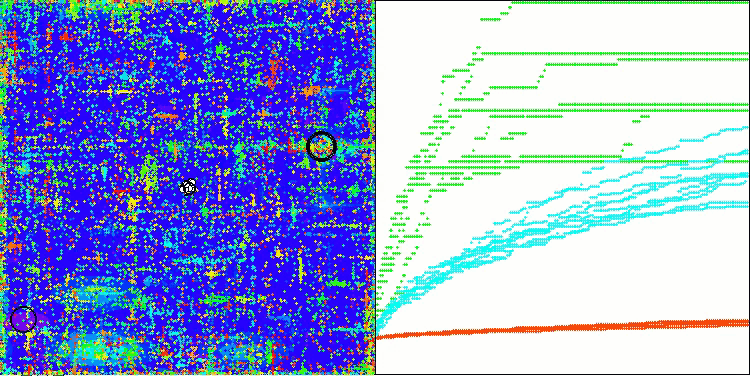
Como pode ser observado, os resultados da versão modificada melhoraram significativamente em comparação com os indicadores anteriores da versão original, onde a pontuação geral foi de 3.00488 (33.39%). Essa melhoria torna-se evidente na análise da visualização, que demonstra não apenas uma melhor convergência, mas também uma exploração mais detalhada dos extremos significativos.
Um dos principais aspectos que merece destaque é o efeito de "agrupamento" das soluções em coordenadas específicas. Esse fenômeno é observado tanto na versão original quanto na modificada, o que ressalta uma característica típica dos algoritmos AOS. O "agrupamento" de soluções pode indicar que o algoritmo está encontrando de forma eficiente as regiões onde se localizam possíveis soluções ótimas.
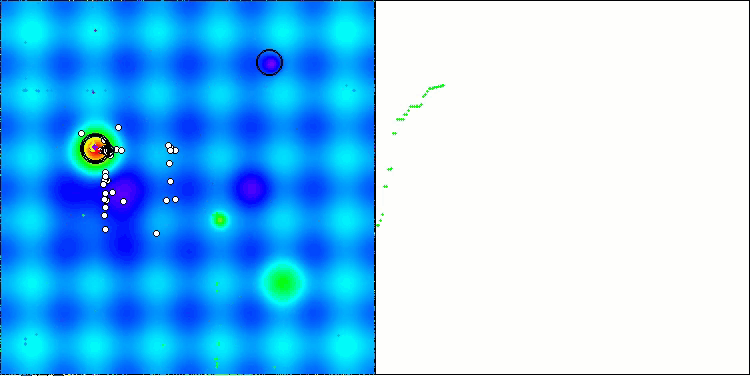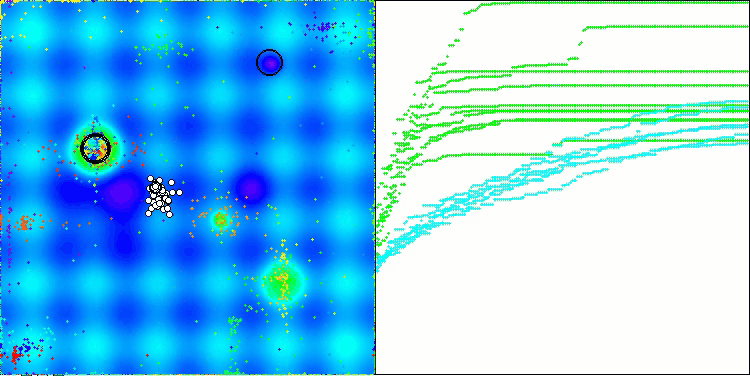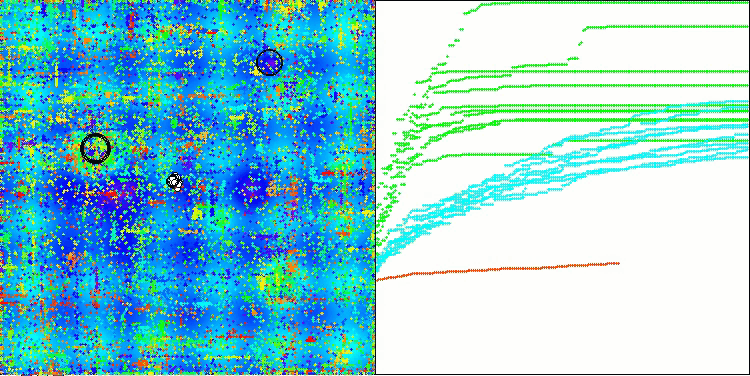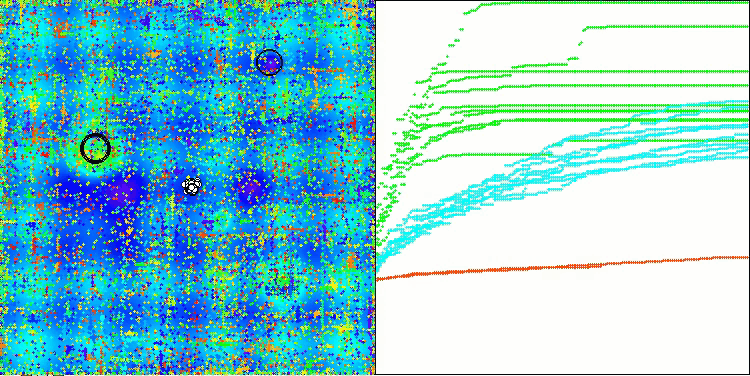
AOSm na função de teste Hilly
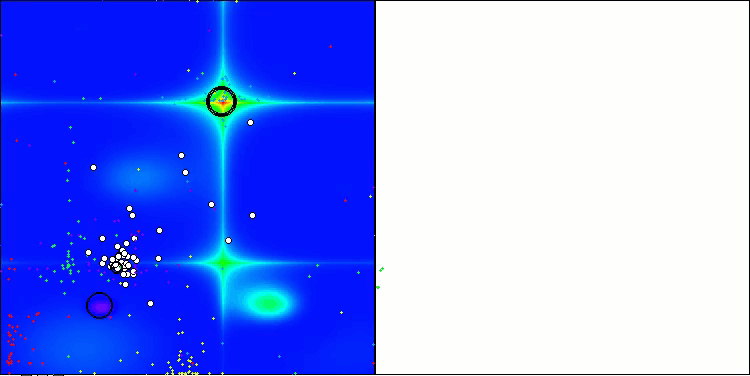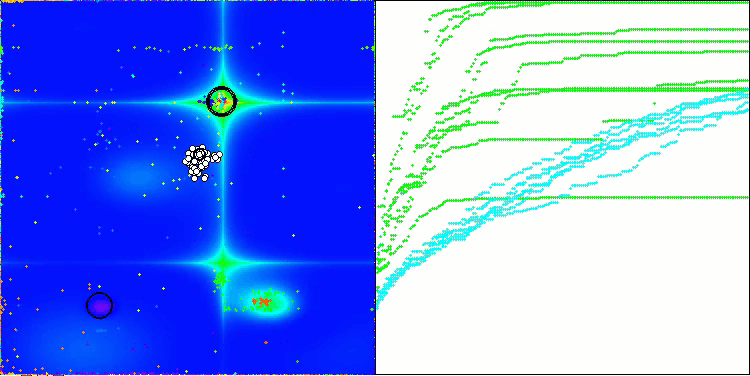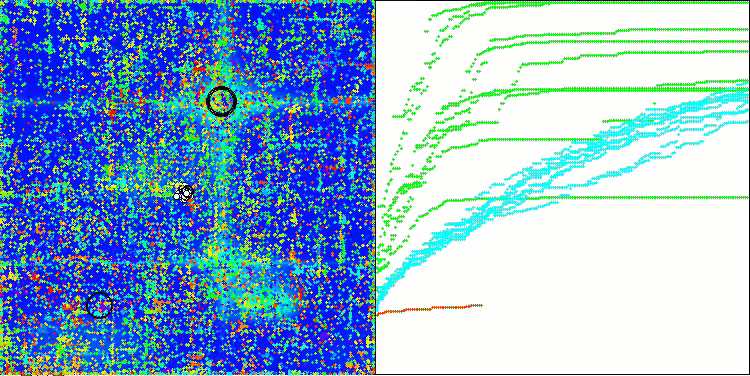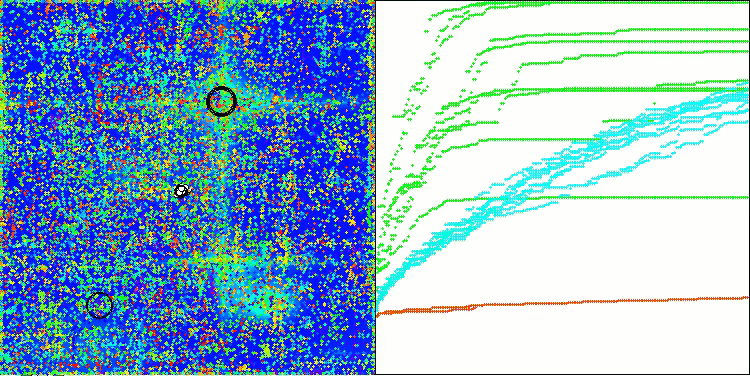
AOSm na função de teste Forest
AOSm na função de teste Megacity
A versão modificada do algoritmo Atomic Orbital Search (AOS) melhorou significativamente seus indicadores em relação à versão original e agora atinge mais de 55% do máximo possível. Este é realmente um resultado impressionante! Na tabela de classificação, o algoritmo ocupa o 12º lugar, na parte superior, o que indica resultados bastante respeitáveis.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration ptimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 12 | AOSm | atomic orbital search M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 13 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 14 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 15 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 16 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 17 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 18 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 19 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 20 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 21 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 22 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 23 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 24 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 25 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 26 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 27 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 28 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 29 | ABHA | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 30 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 31 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 32 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 33 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 34 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 35 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 36 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 37 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 38 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 39 | FAm | firefly algorithm M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 40 | GSA | gravitational search algorithm | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 41 | BFO | bacterial foraging optimization | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 42 | ABC | artificial bee colony | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 43 | BA | bat algorithm | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 44 | AAA | algae adaptive algorithm | 0.50007 | 0.32040 | 0.25525 | 1.07572 | 0.37021 | 0.22284 | 0.16785 | 0.76089 | 0.27846 | 0.14800 | 0.09755 | 0.52402 | 2.361 | 26.23 |
| 45 | SA | simulated annealing | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
Considerações finais
Neste artigo foi apresentada a versão modificada do algoritmo de busca orbital atômica (AOSm), na qual abandonei a posição média dos elétrons BSk nas camadas do átomo em favor da melhor posição individual de cada elétron. Isso permitiu que os elétrons se movessem de forma mais eficiente em direção à melhor solução em sua camada, baseando-se em suas próprias conquistas e não em uma média geral. Além disso, foram eliminados dois componentes aleatórios βi e γi, o que reduziu em três vezes o tempo de geração de números aleatórios, sem perder o sentido físico do algoritmo.
No método "UpdateElectrons", foram removidas as variáveis que se tornaram desnecessárias e foi eliminada a divisão do incremento do elétron pelo número de camadas durante o movimento em direção à solução global. Embora os autores da versão original possivelmente tenham buscado tornar a intensidade de movimento variável, meus experimentos mostraram que isso não trouxe benefícios significativos.
Também foram implementadas mudanças no método "UpdateElectrons" da classe "C_AO_AOSm", substituindo a dispersão aleatória do elétron pelo movimento em direção ao centro do núcleo com uma determinada probabilidade. Isso melhorou as propriedades combinatórias do algoritmo, permitindo que os elétrons focassem com mais precisão no objetivo global. Além disso, a distribuição lognormal foi substituída pela distribuição normal, o que aumentou a precisão da convergência na busca pelo refinamento da solução global.
Os resultados da versão modificada AOSm mostraram uma melhoria significativa, com uma pontuação geral superior a 55% do máximo possível, o que confirma a alta eficiência e competitividade do algoritmo. Na tabela de classificação, o AOSm ocupa a 12ª posição, o que evidencia suas conquistas significativas entre outros métodos de otimização.
Um dos aspectos mais notáveis do AOSm é a melhoria na convergência, que se tornou evidente na visualização dos resultados. O algoritmo trabalha de forma mais detalhada os extremos significativos e demonstra capacidade de busca eficiente por soluções ótimas em espaços complexos e multidimensionais. O efeito de "agrupamento" de soluções, observado tanto na versão original quanto na modificada, destaca a habilidade do algoritmo em encontrar e se concentrar em regiões com potenciais ótimos, o que é especialmente útil em problemas de alta dimensionalidade e estrutura complexa.
Um benefício adicional da versão modificada é a redução do número de parâmetros externos, o que simplifica seu uso e configuração. Contudo, para todos os algoritmos apresentados anteriormente nos artigos, selecionei parâmetros externos otimizados para alcançar o máximo desempenho em testes complexos com diferentes tipos de problemas, portanto, todos os algoritmos estão prontos para uso e não requerem ajustes. Nesta série de artigos ficou demonstrado que, às vezes, pequenas alterações nos algoritmos de otimização podem mudar radicalmente suas propriedades de busca, enquanto grandes mudanças na lógica da estratégia de busca podem não resultar em melhorias perceptíveis. E, claro, compartilho nos artigos técnicas que realmente aumentam a eficiência da otimização.
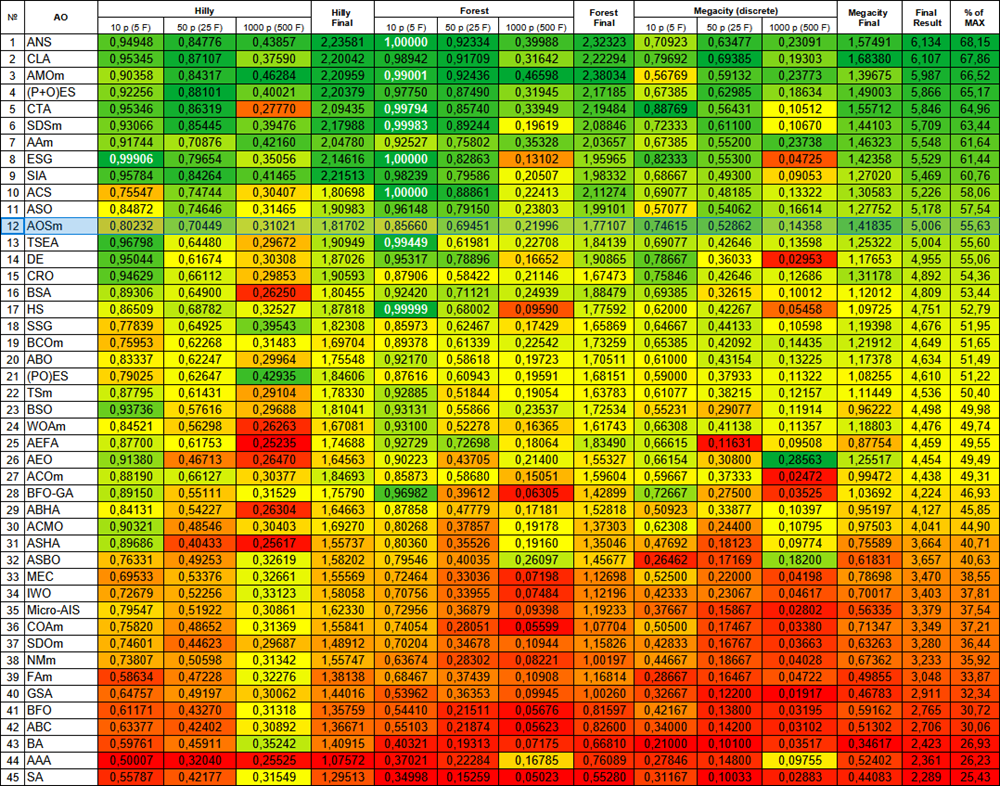
Figura 2. Graduação de cores dos algoritmos conforme os respectivos testes. Os resultados maiores ou iguais a 0.99 são destacados em branco
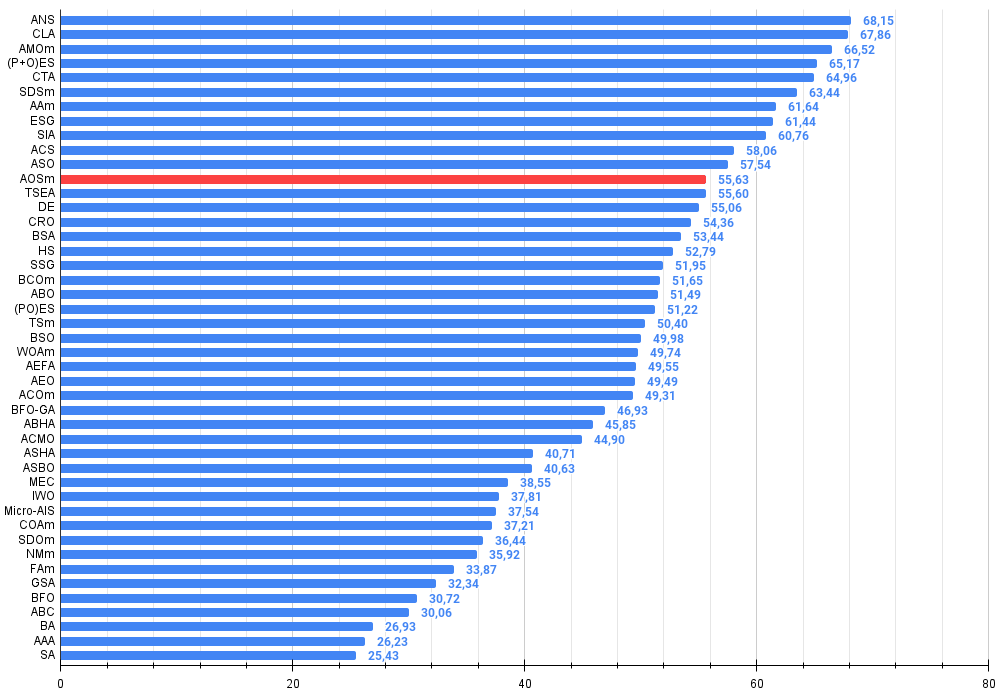
Figura 3. Histograma dos resultados dos testes dos algoritmos (na escala de 0 a 100, quanto maior, melhor,
onde 100 é o resultado teórico máximo possível, no arquivo compactado há o script para o cálculo da tabela de classificação)
Prós e contras do algoritmo AOSm:
Prós:
- Boa performance em diferentes tipos de problemas.
- Pequeno número de parâmetros externos.
- Boa escalabilidade.
- Busca equilibrada tanto em extremos locais quanto globais.
Contras:
- Implementação relativamente complexa.
- Precisão de convergência média em comparação com outros algoritmos em funções suaves.
Está anexado ao artigo um arquivo compactado com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitas alterações foram feitas para melhorar suas capacidades de busca. As conclusões e julgamentos apresentados nos artigos baseiam-se nos resultados dos experimentos realizados.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | #C_AO.mqh | Arquivo incluído | Classe pai dos algoritmos populacionais de otimização |
| 2 | #C_AO_enum.mqh | Arquivo incluído | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluído | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluído | Biblioteca de funções da bancada de testes |
| 5 | Utilities.mqh | Arquivo incluído | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluído | Script para cálculo dos resultados na tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Bancada de testes unificada para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso dos algoritmos populacionais de otimização sem visualização |
| 9 | AO_AOSm_AtomicOrbitalSearch.mqh | Arquivo incluído | Classe do algoritmo AOSm |
| 10 | Test_AO_AOSm.mq5 | Script | Bancada de testes para o AOSm |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16315
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Aprendendo MQL5 do iniciante ao profissional (Parte VI): Fundamentos da criação de EAs
Aprendendo MQL5 do iniciante ao profissional (Parte VI): Fundamentos da criação de EAs
 Exemplo de Análise de Rede de Causalidade (CNA) e Modelo de Autorregressão Vetorial para Predição de Eventos de Mercado
Exemplo de Análise de Rede de Causalidade (CNA) e Modelo de Autorregressão Vetorial para Predição de Eventos de Mercado
 Construindo um Modelo de Restrição de Tendência de Candlestick (Parte 8): Desenvolvimento do Expert Advisor (II)
Construindo um Modelo de Restrição de Tendência de Candlestick (Parte 8): Desenvolvimento do Expert Advisor (II)
 Criando um Expert Advisor Integrado MQL5-Telegram (Parte 4): Modularizando Funções de Código para Maior Reutilização
Criando um Expert Advisor Integrado MQL5-Telegram (Parte 4): Modularizando Funções de Código para Maior Reutilização
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Obrigado pelo artigo!
Fiquei sentado por um tempo ontem e hoje na função Hilly e nos métodos alglib. Aqui estão meus pensamentos.
Para encontrar o máximo dessa função, especialmente quando o número de parâmetros é 10 ou mais, não faz sentido aplicar métodos de gradiente, pois essa é a tarefa dos métodos combinatórios de otimização. Os métodos de gradiente ficam instantaneamente presos no extremo local. E não importa quantas vezes se reinicie a partir de um novo ponto no espaço de parâmetros, a chance de chegar à região correta do espaço a partir da qual o método gradiente encontra instantaneamente uma solução tende a zero à medida que o número de parâmetros aumenta.
Por exemplo, o ponto do espaço a partir do qual o lbfgs ou o CG para 2(duas) iterações encontram o máximo para qualquer número de parâmetros é {x = -1,2 , y = 0,5}.
Mas a chance de chegar a essa região, como eu disse, é simplesmente zero. Deve levar cem anos para gerar números aleatórios.
Portanto, é necessário combinar, de alguma forma, os algoritmos genéticos apresentados no artigo (para que eles possam fazer o reconhecimento e reduzir o espaço de pesquisa) com métodos de gradiente que encontrariam rapidamente o extremo a partir de um ponto mais favorável.
Obrigado pelo artigo!
Obrigado por seus comentários.
Para encontrar o máximo de uma determinada função, especialmente quando o número de parâmetros é 10 ou mais, não faz sentido usar métodos de gradiente.
Sim, é isso mesmo.
Essa é a tarefa dos métodos combinatórios de otimização.
Os métodos combinatórios, como o clássico "ant", são projetados para problemas como o "problema do caixeiro viajante" e o "problema da mochila", ou seja, são projetados para problemas discretos com uma etapa fixa (borda do gráfico). Para problemas multidimensionais "contínuos", esses algoritmos não foram projetados de forma alguma, por exemplo, para tarefas como o treinamento de redes neurais. Sim, as propriedades combinatórias são muito úteis para os métodos heurísticos estocásticos, mas não são a única e suficiente propriedade para a solução bem-sucedida desses problemas de teste quase reais. As próprias estratégias de pesquisa no algoritmo também são importantes.
As baseadas em gradiente simplesmente ficam presas em um extremo local instantaneamente. E não importa quantas vezes se reinicie a partir de um novo ponto do espaço de parâmetros, a chance de chegar à região correta do espaço a partir da qual o método de gradiente encontra instantaneamente uma solução tende a zero à medida que o número de parâmetros aumenta.
Sim, isso acontece.
Mas a chance de chegar a essa região, como eu já disse, é simplesmente zero. Levaria cerca de cem anos para gerar números aleatórios.
Sim, é isso mesmo. Em espaços de baixa dimensão (1-2), é muito fácil chegar à vizinhança do global, e geradores aleatórios simples podem até funcionar para isso. Mas tudo muda completamente quando a dimensionalidade do problema aumenta, e aqui as propriedades de pesquisa dos algoritmos começam a desempenhar um papel importante, e não a Senhora Sorte.
Portanto, precisamos combinar de alguma forma os algoritmos genéticos apresentados no artigo (que fariam a exploração, reduziriam o espaço de pesquisa) com os métodos de gradiente, que encontrariam rapidamente o extremo a partir de um ponto mais favorável.
"genético" - você provavelmente quer dizer "heurístico". Por que "o peixe precisa de um guarda-chuva" e "por que precisamos de um ferreiro? Não precisamos de um ferreiro.")))) Existem maneiras eficientes de resolver problemas complexos multidimensionais em um espaço contínuo, que são descritos em artigos sobre métodos populacionais. E, para os problemas clássicos de gradiente, há suas próprias tarefas - problemas unidimensionais analiticamente determináveis (nesse caso, eles não têm igual, haverá convergência rápida e exata).
E, pergunta, quais são suas impressões sobre a velocidade da heurística?
SZY:
Oh, quantas descobertas maravilhosas
Preparam o espírito do esclarecimento
E a experiência, o filho dos erros,
E o gênio, o amigo dos paradoxos,
E o acaso, o inventor de Deus.
ZZZY. Um momento. Em um espaço de busca desconhecido, nunca é possível saber, em qualquer momento ou etapa da iteração, se essa é realmente uma direção promissora para o global. Portanto, é impossível explorar primeiro e refinar depois. Somente estratégias de pesquisa completas podem funcionar, e elas funcionam bem ou mal. Cada um escolhe o grau de "bondade" e "adequação à tarefa" por conta própria. Para isso, é mantida uma tabela de classificação para escolher um algoritmo de acordo com as especificidades da tarefa.
Sim, é isso mesmo. Em espaços de baixa dimensão (1-2), é muito fácil chegar à vizinhança de um global, e geradores aleatórios simples podem até ser úteis para isso. Mas tudo muda completamente quando a dimensionalidade do problema aumenta, e aí as propriedades de pesquisa dos algoritmos, e não a sorte, começam a desempenhar um papel importante.
Portanto, eles falham
E, pergunta, quais são suas impressões sobre a velocidade da heurística?
Apesar do fato de que elas funcionam rapidamente. O resultado para 1000 parâmetros é algo em torno de 0,4.
É por isso que intuitivamente pensei que faz sentido combinar os métodos GA e gradiente para chegar ao máximo. Caso contrário, separadamente, eles não resolverão sua função. Não testei isso na prática.
P.S. Ainda acho que essa função é muito grossa, pois em tarefas reais (treinamento de redes neurais, por exemplo) não há problemas desse tipo, embora a superfície de erro também esteja toda em mínimos locais.
1. eles não estão fazendo um bom trabalho
2. apesar de trabalharem rapidamente. O resultado para 1000 parâmetros é algo em torno de 0,4.
3. É por isso que intuitivamente pensei que faz sentido combinar os métodos GA e gradiente para chegar ao máximo. Caso contrário, separadamente, eles não resolverão sua função. Não testei isso na prática.
4. P.S. Ainda acho que essa função é muito grossa, em tarefas reais (treinamento de redes neurais, por exemplo) não há problemas desse tipo, embora a superfície de erro também esteja toda em mínimos locais.
1. O que você quer dizer com "eles não conseguem lidar com isso"? Há um limite para o número de acessos à função de destino, aquele que apresentou um resultado melhor é aquele que não consegue lidar com isso)). Devemos aumentar o número de acessos permitidos? Bem, então os mais ágeis e adaptados a funções complexas chegarão à linha de chegada de qualquer maneira. Se tentarmos aumentar o número de referências, o quadro não mudará.
2. Sim, e alguns têm 0,3, outros têm 0,2 e outros têm 0,001. Melhor ainda são aqueles que mostraram 0,4.
3. não vai adiantar, intuitivamente centenas de combinações e variações foram tentadas e re-tentadas. Melhor é aquela que mostra melhores resultados para um determinado número de épocas (iterações). Aumente o número de referências ao alvo e veja qual delas chega primeiro à linha de chegada.
4. Se houver líderes em tarefas difíceis, você acha que, em tarefas fáceis, os líderes apresentarão resultados piores do que os não líderes? Esse não é o caso, para dizer o mínimo. Estou trabalhando em uma tarefa mais "simples", mas realista, de treinamento de grade. Como sempre, compartilharei os resultados. Será interessante.
Faça experimentos, tente algoritmos diferentes, tarefas diferentes, não fique preso a uma única coisa. Tentei fornecer todas as ferramentas para isso.
1. O que você quer dizer com "falhar"? Há um limite no número de acessos à função de destino, aquele que mostrou o melhor resultado é aquele que não consegue lidar com isso)). Devemos aumentar o número de acessos permitidos? Bem, então os mais ágeis e adaptados a funções complexas chegarão à linha de chegada de qualquer maneira. Tente aumentar o número de referências, mas o quadro não mudará.
2. Sim. E alguns têm 0,3, outros 0,2 e outros 0,001. Melhor ainda são aqueles que apresentaram 0,4.
3. não vai adiantar, intuitivamente centenas de combinações e variações foram tentadas e re-tentadas. Melhor é aquela que mostra melhores resultados para um determinado número de épocas (iterações). Aumente o número de referências ao alvo e veja qual delas chega primeiro à linha de chegada.
4. Se houver líderes em tarefas difíceis, você acha que, em tarefas fáceis, os líderes apresentarão resultados piores do que os não líderes? Esse não é o caso, para dizer o mínimo. Estou trabalhando em uma tarefa mais "simples", mas realista, de treinamento de grade. Como sempre, compartilharei os resultados. Será interessante.
Faça experimentos, tente algoritmos diferentes, tarefas diferentes, não se fixe em uma coisa só. Tentei fornecer todas as ferramentas para isso.
Estou experimentando,
Sobre a tarefa realista, é correto testar algoritmos em tarefas próximas ao combate.
É duplamente interessante ver como as redes genéticas serão treinadas.