
取引におけるニューラルネットワーク:時系列予測のためのTransformerの最適化(LSEAttention)
はじめに
多変量時系列予測は、金融や医療など幅広い分野で重要な役割を果たしており、過去のデータに基づいて将来の値を予測することが目的です。このタスクは、長期予測において特に難しく、多変量時系列データの特徴量間の相関や長期依存関係を効果的に捉えられるモデルが求められます。近年の研究では、複雑な時間的相互作用のモデリングに優れたSelf-Attention機構を備えたTransformerアーキテクチャを、時系列予測に活用する動きが高まっています。しかし、その潜在能力にもかかわらず、多くの最新手法は依然として線形モデルに大きく依存しており、Transformerの真の効果に疑問が呈されています。
Transformerアーキテクチャの中核をなすSelf-Attention機構は次のように定義されます。
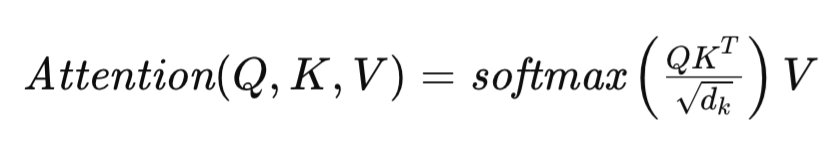
ここでQ、K、VはそれぞれQuery、Key、Valueの行列を表し、dkは各シーケンス要素を記述するベクトルの次元を示します。この定式化により、Transformerは入力シーケンスの異なる要素の関連性を動的に評価できるようになり、データ内の複雑な依存関係のモデリングを可能にします。
長期の時系列予測タスクにおける性能向上のために、Transformerアーキテクチャの様々な適応手法が提案されています。たとえば、FEDformerは、高度なフーリエモジュールを組み込み、時間および空間の両面で線形の計算量を実現し、長い入力シーケンスに対してスケーラビリティと効率性を大幅に向上させています。
一方、PatchTSTは点ごとのAttentionを廃止し、パッチレベルの表現に注目します。これは個々のタイムステップではなく連続するセグメントに焦点を当てるもので、多変量時系列におけるより広範な意味情報の捉え方を可能にし、効果的な長期予測に重要な役割を果たします。
コンピュータビジョンや自然言語処理の分野においては、Attention行列がエントロピー崩壊やランク崩壊を起こすことがあります。この問題は時系列予測において、時間に基づくデータの頻繁な変動によりさらに悪化し、モデル性能の大幅な劣化を招くことが多いです。エントロピー崩壊の根本的な原因は未だ十分に理解されておらず、そのメカニズムやモデルの一般化能力への影響についてのさらなる調査が求められています。これらの課題を中心に扱った論文が「LSEAttention is All You Need for Time Series Forecasting」です。
1. LSEAttentionアルゴリズム
多変量時系列予測の目的は、Cチャネルそれぞれの最もあり得る未来の値Pを推定することであり、これはテンソルY ∈ RC×Pとして表されます。この予測は、長さLかつCチャネルの履歴時系列データを含む入力行列X ∈ RC×Lに基づいておこなわれます。課題は、パラメータωを持つ予測モデルfωRC×L →RC×Pを学習し、予測値と実測値の間の平均二乗誤差(MSE)を最小化することです。
Transformerは時系列の関連性を捉えるために、点ごとのSelf-Attention機構に大きく依存しています。しかし、この依存は「Attention崩壊」と呼ばれる現象を引き起こすことがあり、これは異なる入力シーケンスに対してAttention行列がほぼ同一の値に収束してしまう問題です。この現象はモデルのデータ一般化能力の低下をもたらします。
LSEAttentionの著者らは、Softmax関数を用いて計算される依存係数とLog-Sum-Exp (LSE)演算との類似性に着目しました。彼らは、この定式化における数値的な不安定性がAttention崩壊の根本原因であると仮説を立てています。
関数の条件数は、入力のわずかな変動に対する出力の感度を表します。条件数が高い場合、入力のわずかな摂動でも出力が大きく変化することを意味します。
Attention機構の文脈では、この不安定性は過剰Attentionやエントロピー崩壊として現れ、Attention行列の対角成分が非常に高い値(オーバーフローを示す)を持ち、非対角成分が極端に低い値(アンダーフローを示す)になるのが特徴です。
これらの問題に対処するため、著者らはLog-Sum-Exp (LSE)トリックとGELU (Gaussian Error Linear Unit)活性化関数を統合したLSEAttentionモジュールを提案しました。LSEトリックは正規化を通じてオーバーフローやアンダーフローによる数値的不安定性を軽減します。Softmax関数はLSEを用いて以下のように再定式化可能です。
![]()
ここでLSE(x)の指数部はlog-sum-exp関数の指数値を示しており、これにより数値的安定性が向上します。
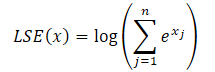
指数関数の性質を利用すると、任意の指数関数の項は、2つの指数関数の積として表現できます。
![]()
ここで、aは正規化に用いられる定数で、実際には通常最大値が定数として使われます。指数関数の積をLSEの式に代入し、全体の値を総和記号の外に出すと、次のようになります。
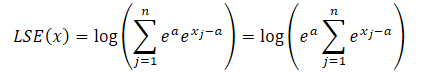
積の対数は対数の和に変換され、指数関数の自然対数は指数そのものに等しくなります。これにより、提示された式を簡略化することが可能になります。
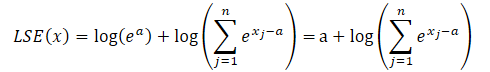
得られた式をSoftmax関数に代入し、指数関数の性質を利用します。
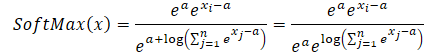
ご覧のように、分子と分母に共通する定数の指数値は打ち消し合います。自然対数の指数は対数の式に等しいため、数値的に安定したSoftmaxの表現が得られます。
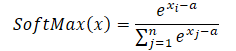
定数として最大値a = max(x)を使用すると、常にx-a≤0となります。この場合、x-aの指数関数の値は0を含まない範囲で0から1の間にあります。したがって、関数の分母は(1, n]の範囲内にあります。
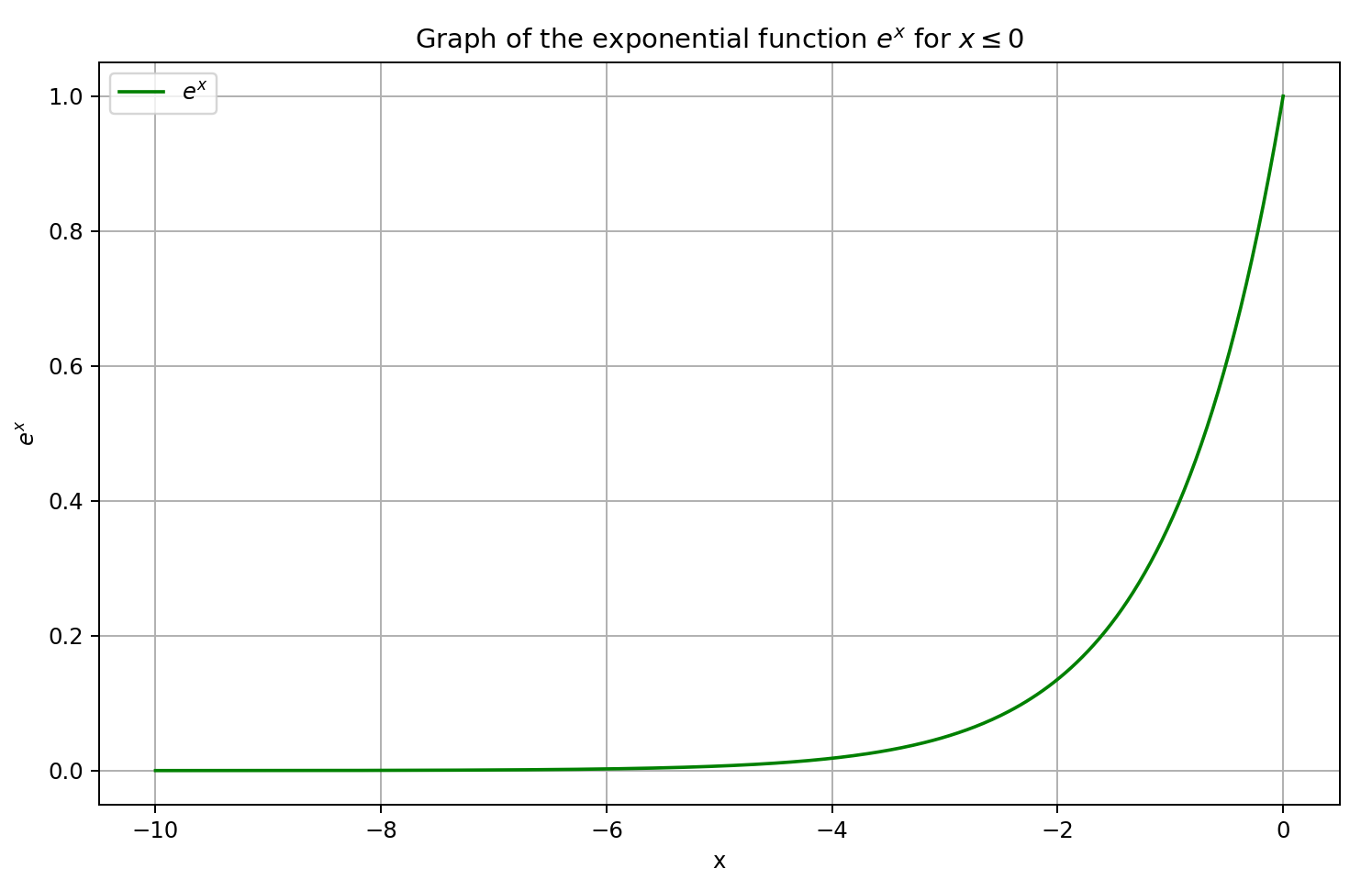
さらに、LSEAttentionフレームワークの著者らは、より滑らかな確率的活性化を提供するGELU活性化関数の使用を提案しています。これは、指数関数を適用する前の対数確率の極端な値を安定化させるのに役立ち、Attentionスコアの急激な変化を和らげます。GELUは標準正規分布の累積分布関数(CDF)を用いた滑らかな曲線によってReLU関数を近似するため、従来のReLUで見られる活性化の急激な変化を減少させます。この特性は、急激な活性化のスパイクが数値的な不安定性や勾配爆発を引き起こしやすいTransformerベースのAttention機構の安定化に特に有効です。
GELU関数は以下のように定義されます。
![]()
ここでΦ(x)は標準正規分布のCDFを表します。この定式化により、GELUは入力値の大きさに応じて異なるスケーリングを適用し、極端な値の増幅を抑制します。GELUの滑らかで確率的な特性は、入力活性化の徐々の遷移を可能にし、その結果、学習時の大きな勾配変動を軽減します。
この特性は、Softmax関数を数値的に安定化させるLog-Sum-Exp (LSE)トリックと組み合わせることで特に効果的になります。LSEとGELUは、Softmaxの指数計算におけるオーバーフローやアンダーフローを効果的に防ぎ、安定した範囲のAttention重みを実現します。この相乗効果により、Transformerモデルのロバスト性が向上し、トークン間でAttention係数が均等に割り当てられるようになります。結果として、より安定した勾配と学習時の収束改善がもたらされます。
従来のTransformerアーキテクチャでは、Feed-Forward Network (FFN)ブロックで使用されるReLU (Rectified Linear Unit)活性化関数が「dying ReLU」問題を起こしやすく、負の入力に対して常にゼロを出力するニューロンが不活性化します。これにより該当ニューロンの勾配がゼロとなり、学習が停止し、訓練の不安定化に繋がります。
この問題に対処するために、パラメトリックReLU(PReLU)関数が代替として用いられます。PReLUは負の入力に対しても学習可能な傾きを導入し、非ゼロの出力を可能にします。この適応により、dying ReLU問題が緩和されるだけでなく、負の活性化と正の活性化の間で滑らかな遷移が実現し、モデルの学習能力が入力空間全体にわたって向上します。負の値に対しても非ゼロの勾配が存在することで、深いネットワークの訓練に不可欠な勾配伝播が促進されます。その結果、PReLUの使用は全体的な学習の安定化に寄与し、活性表現の維持に役立ち、最終的にモデル性能の向上へと繋がります。
LSEAttentionベースの時系列Transformer (LATST)アーキテクチャでは、訓練データとテストデータ間の分布差を効果的に解消するために、可逆的なデータ正規化も組み込まれています。
このアーキテクチャは、従来の時系列Self-Attention機構を保持しつつ、LSEAttentionモジュール内に組み込んでいます。
全体として、LATSTアーキテクチャは置換モジュールを組み合わせた単層のTransformer構造で構成されており、適応的な学習を可能にしながらAttention機構の信頼性を維持しています。この設計により、時系列の依存関係を効率的にモデル化し、時系列予測タスクの性能を向上させています。以下にフレームワークの元のビジュアルが示されています。
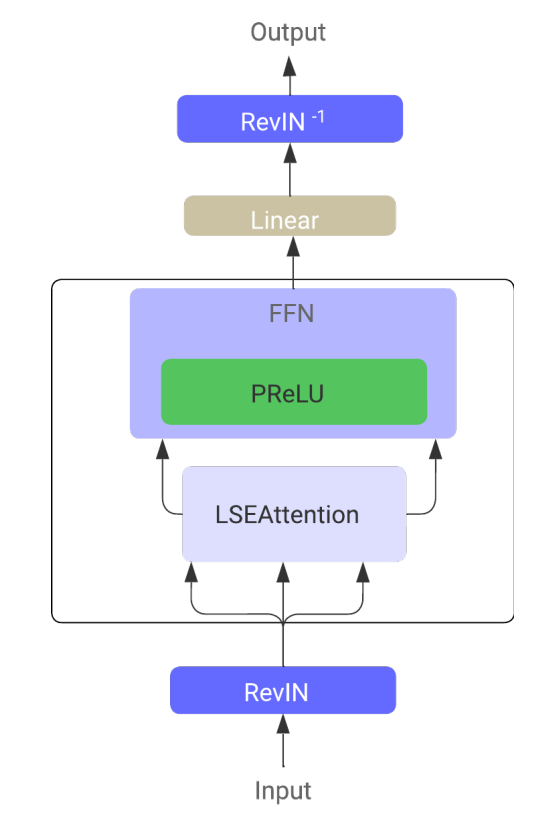
2.MQL5での実装
LSEAttentionフレームワークの理論的側面を確認したので、ここからは提案手法をMQL5を用いて実装する一例について説明します。重要な点として、この実装は従来のものとは大きく異なります。具体的には、新しいオブジェクトを作成して提案手法を実装するのではなく、既存のクラスに統合します。
2.1 Softmax層の調整
ここでは、Softmax関数層を処理するCNeuronSoftMaxOCLクラスを考えます。このクラスは、モデルの単独コンポーネントとしても、さまざまなフレームワークの一部としても広く利用されています。たとえば、依存パターンに基づくプーリングモジュール(CNeuronMHAttentionPooling)を構築する際にもCNeuronSoftMaxOCLオブジェクトを使用しており、このモジュールは最近のいくつかの研究でも適用しています。したがって、このクラスのアルゴリズムに数値的に安定したSoftmax計算を組み込むのは論理的な流れです。
これを実現するために、SoftMax_FeedForwardカーネルの動作を変更します。このカーネルは、入力値用と出力結果用の2つのデータバッファへのポインタをパラメータとして受け取ります。
__kernel void SoftMax_FeedForward(__global float *inputs, __global float *outputs) { const uint total = (uint)get_local_size(0); const uint l = (uint)get_local_id(0); const uint h = (uint)get_global_id(1);
カーネルの実行を2次元のタスク空間で計画します。第1の次元は、1つの単位シーケンス内で正規化される値の数に対応します。第2の次元は、そのような単位シーケンス(または正規化ヘッド)の数を表します。各単位シーケンス内でスレッドをワークグループにまとめます。
カーネル本体内では、まず全次元におけるタスク空間内の現在のスレッドを特定します。
次に、ワークグループ内でのデータ交換を容易にするためのローカルメモリ配列を宣言します。
__local float temp[LOCAL_ARRAY_SIZE];
次に、グローバルデータバッファ内の関連要素を指す定数オフセットを定義します。
const uint ls = min(total, (uint)LOCAL_ARRAY_SIZE); uint shift_head = h * total;
グローバルメモリへのアクセスを最小限に抑えるため、入力値をローカル変数にコピーし、結果の値を検証します。
float inp = inputs[shift_head + l]; if(isnan(inp) || isinf(inp) || inp<-120.0f) inp = -120.0f;
ここで、入力値を下限「-120」に制限している点は注目に値します。これはfloat形式で表現可能な最小の指数値を近似しており、アンダーフローを防ぐための追加対策です。上限は設定していませんが、オーバーフローの可能性は最大値を引く処理で対処します。
次に、現在の単位シーケンス内の最大値を求めます。これは、ワークグループ内の各サブグループの最大値を収集し、それらをローカルメモリ配列の要素に格納するループで実行されます。
for(int i = 0; i < total; i += ls) { if(l >= i && l < (i + ls)) temp[l] = (i > 0 ? fmax(inp, temp[l]) : inp); barrier(CLK_LOCAL_MEM_FENCE); }
次にローカル配列を反復して、現在のワークグループのグローバル最大値を特定します。
uint count = min(ls, (uint)total); do { count = (count + 1) / 2; if(l < ls) temp[l] = (l < count && (l + count) < total ? fmax(temp[l + count],temp[l]) : temp[l]); barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); float max_value = temp[0]; barrier(CLK_LOCAL_MEM_FENCE);
得られた最大値はローカル変数に保存し、この段階でスレッド同期を確保します。ローカルメモリ配列の要素が変更される前に、すべてのスレッドが正しい最大値を保持することが重要です。
次に、各元の入力値から最大値を引きます。再び下限チェックをおこないます。正の最大値を引くことで結果が有効範囲を下回る可能性があるためです。その後、調整後の値の指数を計算します。
inp = fmax(inp - max_value, -120); float inp_exp = exp(inp); if(isinf(inp_exp) || isnan(inp_exp)) inp_exp = 0;
2つのループを使って、ワークグループ全体で指数の合計を求めます。このループ構造は最大値計算時と似ていますが、ループ内の演算内容を加算に置き換えています。
for(int i = 0; i < total; i += ls) { if(l >= i && l < (i + ls)) temp[l] = (i > 0 ? temp[l] : 0) + inp_exp; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)total); do { count = (count + 1) / 2; if(l < ls) temp[l] += (l < count && (l + count) < total ? temp[l + count] : 0); if(l + count < ls) temp[l + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
必要な値がすべて揃ったので、各指数値をワークグループ内の指数合計で割ることで最終的なSoftmax値を計算できます。
//--- float sum = temp[0]; outputs[shift_head+l] = inp_exp / (sum + 1.2e-7f); }
この演算の結果は、グローバル結果バッファの適切な要素に書き込まれます。
重要なのは、順伝播時のSoftmax計算に加えた変更は、逆伝播アルゴリズムの修正を必要としないという点です。この記事の前半で示した数式によれば、LSEトリックの使用はSoftmax関数の最終出力を変えるものではありません。そのため、入力データが最終結果に与える影響は変わらず、既存の勾配誤差分配アルゴリズムをそのまま利用できます。
2.2 相対Attentionモジュールの修正
Softmaxアルゴリズムは、必ずしも単独層として使用されるわけではありません。異なるSelf-Attentionブロック設計を含むほぼすべての実装バージョンでは、そのロジックが統合Attentionカーネル内に直接組み込まれています。ここではCNeuronRelativeSelfAttentionモジュールを見てみます。このモジュールでは、修正版Self-Attention機構のアルゴリズム全体がMHRelativeAttentionOutカーネル内に実装されています。そしてもちろん、すべてのモデルアーキテクチャで安定した学習プロセスを確保することを目指します。そのため、このようなすべてのカーネルに数値的に安定したSoftmaxを実装する必要があります。可能な限り、既存のカーネルパラメータやタスク空間構成は維持します。MHRelativeAttentionOutカーネルのアップグレードでも同じアプローチが用いられました。
ただし、カーネルパラメータやタスク空間レイアウトに変更を加える場合は、このカーネルを実行キューに入れるメインプログラム内のすべてのラッパーメソッドにも反映させなければなりません。これを怠ると、カーネルディスパッチ時に重大なランタイムエラーが発生する可能性があります。これは、グローバルタスク空間の変更だけでなく、ワークグループサイズの変更にも当てはまります。
__kernel void MHRelativeAttentionOut(__global const float *q, ///<[in] Matrix of Querys __global const float *k, ///<[in] Matrix of Keys __global const float *v, ///<[in] Matrix of Values __global const float *bk, ///<[in] Matrix of Positional Bias Keys __global const float *bv, ///<[in] Matrix of Positional Bias Values __global const float *gc, ///<[in] Global content bias vector __global const float *gp, ///<[in] Global positional bias vector __global float *score, ///<[out] Matrix of Scores __global float *out, ///<[out] Matrix of attention const int dimension ///< Dimension of Key ) { //--- init const int q_id = get_global_id(0); const int k_id = get_local_id(1); const int h = get_global_id(2); const int qunits = get_global_size(0); const int kunits = get_local_size(1); const int heads = get_global_size(2);
カーネル本体内では、前と同様に、タスク空間内の現在のスレッドを特定し、必要なすべての次元を定義します。
次に、グローバルデータバッファへのオフセットや補助的な値を含む、一連の必要な定数を宣言します。
const int shift_q = dimension * (q_id * heads + h); const int shift_kv = dimension * (heads * k_id + h); const int shift_gc = dimension * h; const int shift_s = kunits * (q_id * heads + h) + k_id; const int shift_pb = q_id * kunits + k_id; const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE); float koef = sqrt((float)dimension);
また、各ワークグループ内でのスレッド間データ交換のために、ローカルメモリ配列を定義します。
__local float temp[LOCAL_ARRAY_SIZE];
従来のSelf-Attentionアルゴリズムに従ってAttentionスコアを計算するために、まずQueryテンソルとKeyテンソルの対応するベクトル間でドット積をおこないます。しかし、R-MATフレームワークの著者らは、文脈依存のバイアス項とグローバルバイアス項を追加しています。すべてのベクトルは同じ長さであるため、これらの処理はベクトルサイズと同じ回数の反復を持つ単一のループで実行できます。ループ本体内では、要素ごとの乗算をおこない、その後に総和を計算します。
//--- score float sc = 0; for(int d = 0; d < dimension; d++) { float val_q = q[shift_q + d]; float val_k = k[shift_kv + d]; float val_bk = bk[shift_kv + d]; sc += val_q * val_k + val_q * val_bk + val_k * val_bk + gc[shift_q + d] * val_k + gp[shift_q + d] * val_bk; } sc = sc / koef;
得られたスコアは、ベクトルの次元数の平方根でスケーリングされます。従来のTransformerの著者によれば、この操作はモデルの安定性を向上させるとされており、私たちもこの手法に従います。
その後、得られた値をSoftmax関数を用いて確率に変換します。ここで、数値的安定性を確保するための処理を挿入します。まず、各ワークグループ内のAttentionスコアの中で最大値を求めます。これをおこなうために、スレッドをサブグループに分け、それぞれのグループが自分のローカル最大値をローカルメモリ配列の要素に書き込みます。
//--- max value for(int cur_k = 0; cur_k < kunits; cur_k += ls) { if(k_id >= cur_k && k_id < (cur_k + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_k == 0 ? sc : fmax(temp[shift_local], sc)); } barrier(CLK_LOCAL_MEM_FENCE); }
次に、その配列をループ処理して、グローバルな最大値を求めます。
uint count = min(ls, (uint)kunits); //--- do { count = (count + 1) / 2; if(k_id < ls) temp[k_id] = (k_id < count && (k_id + count) < kunits ? fmax(temp[k_id + count], temp[k_id]) : temp[k_id]); barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
現在のAttentionスコアは、この最大値を減算してから指数関数を適用することで調整されます。ここではスレッドの同期も必要です。なぜなら次のステップでローカル配列の要素を変更する際、ワークグループ内のすべてのスレッドが最大値を使用し終える前に、その値が上書きされてしまう危険があるためです。
sc = exp(fmax(sc - temp[0], -120)); if(isnan(sc) || isinf(sc)) sc = 0; barrier(CLK_LOCAL_MEM_FENCE);
次に、ワークグループ内のすべての指数値の合計を計算します。これまでと同様に、連続するループからなる二段階のリダクションアルゴリズムを使用します。
//--- sum of exp for(int cur_k = 0; cur_k < kunits; cur_k += ls) { if(k_id >= cur_k && k_id < (cur_k + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_k == 0 ? 0 : temp[shift_local]) + sc; } barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k_id < ls) temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0); if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
これで、各Attentionスコアを合計値で割ることで確率に変換できます。
//--- score float sum = temp[0]; if(isnan(sum) || isinf(sum) || sum <= 1.2e-7f) sum = 1; sc /= sum; score[shift_s] = sc; barrier(CLK_LOCAL_MEM_FENCE);
得られた確率は、対応するグローバル出力バッファの要素に書き込まれ、ワークグループ内でスレッドの同期をおこないます。
最後に、入力シーケンスの各要素に対して、Valueテンソルの要素の重み付き和を計算します。これは、上で計算したAttention係数を基にValueを重み付けする操作です。シーケンスの1要素内では、Attention係数のベクトルとValueテンソルを乗算し、さらにR-MATフレームワークの著者が追加したグローバルバイアステンソルを加える形で表現されます。
この処理はループ構造で実装されており、外側のループはValueテンソルの最終次元を反復します。
//--- out for(int d = 0; d < dimension; d++) { float val_v = v[shift_kv + d]; float val_bv = bv[shift_kv + d]; float val = sc * (val_v + val_bv); if(isnan(val) || isinf(val)) val = 0;
ループ内では、各スレッドが対応する要素への寄与を計算し、それらの寄与はワークグループ内の入れ子になった連続的なリダクションループを使って集約されます。
//--- sum of value for(int cur_v = 0; cur_v < kunits; cur_v += ls) { if(k_id >= cur_v && k_id < (cur_v + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_v == 0 ? 0 : temp[shift_local]) + val; } barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k_id < count && (k_id + count) < kunits) temp[k_id] += temp[k_id + count]; if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
合計値は、そのうちの一つのスレッドによってグローバル結果バッファの該当要素に書き込まれます。
//--- if(k_id == 0) out[shift_q + d] = (isnan(temp[0]) || isinf(temp[0]) ? 0 : temp[0]); barrier(CLK_LOCAL_MEM_FENCE); } }
その後、次のループ反復に進む前に再度スレッドの同期をおこないます。
先に述べたように、Softmax関数に加えた変更は、結果が入力データに依存する度合いには影響を与えません。したがって、既存の逆伝播アルゴリズムをそのまま変更なしで再利用できます。
2.3 GELU活性化関数
Softmax関数の数値安定化に加えて、LSEAttentionフレームワークの著者らはGELU活性化関数の使用も推奨しています。著者らはこの関数の2つのバージョンを提案しています。そのうちの1つを以下に示します。
![]()
この活性化関数の実装は非常に簡単です。既存の活性化関数ハンドラに新しいバリアントを追加するだけです。
float Activation(const float value, const int function) { if(isnan(value) || isinf(value)) return 0; //--- float result = value; switch(function) { case 0: result = tanh(clamp(value, -20.0f, 20.0f)); break; case 1: //Sigmoid result = 1 / (1 + exp(clamp(-value, -20.0f, 20.0f))); break; case 2: //LReLU if(value < 0) result *= 0.01f; break; case 3: //SoftPlus result = (value >= 20.0f ? 1.0f : (value <= -20.0f ? 0.0f : log(1 + exp(value)))); break; case 4: //GELU result = value / (1 + exp(clamp(-1.702f * value, -20.0f, 20.0f))); break; default: break; } //--- return result; }
しかし、順伝播の見かけ上の単純さの裏には、逆伝播(バックプロパゲーション)の実装というより複雑な課題があります。これは、GELUの導関数が元の入力値とシグモイド関数に依存しているためです。そして、この両方が私たちの標準実装には含まれていません。
![]()
さらに、GELU関数の導関数を順伝播の結果だけで正確に表現することはできません。そのため、いくつかのヒューリスティックや近似手法に頼らざるを得ませんでした。
まずは、シグモイド関数の形状を確認しましょう。
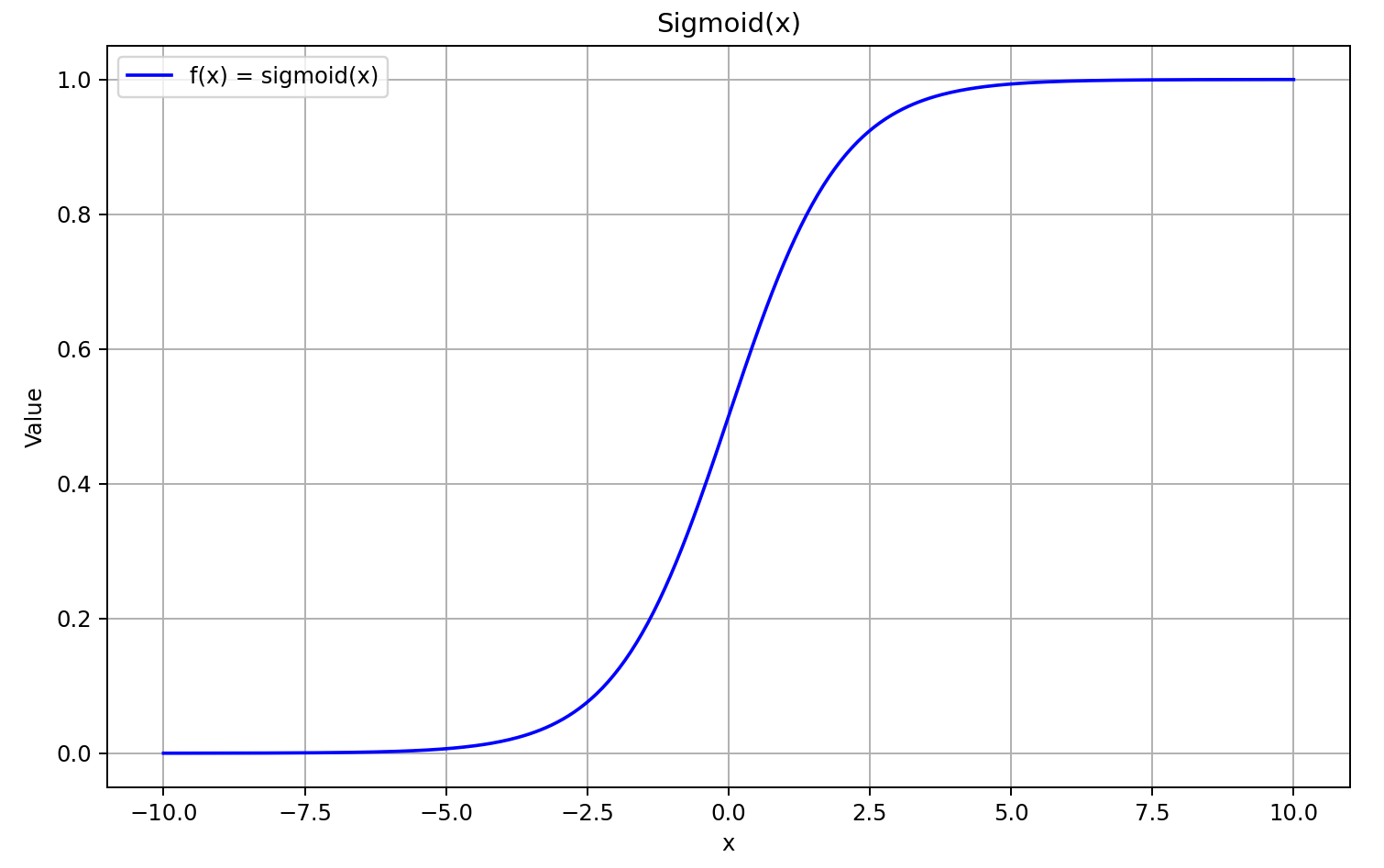
入力値が5より大きい場合、シグモイド関数は1に近づき、-5より小さい場合は0に近づきます。したがって、Xの値が十分に負のとき、微分式の左側の因子が0に近づくため、GELUの導関数は0に収束します。一方、Xの値が大きく正のときは、両方の乗算因子が1に収束するため、導関数は1に近づきます。これらの挙動は、以下のグラフによって確認できます。
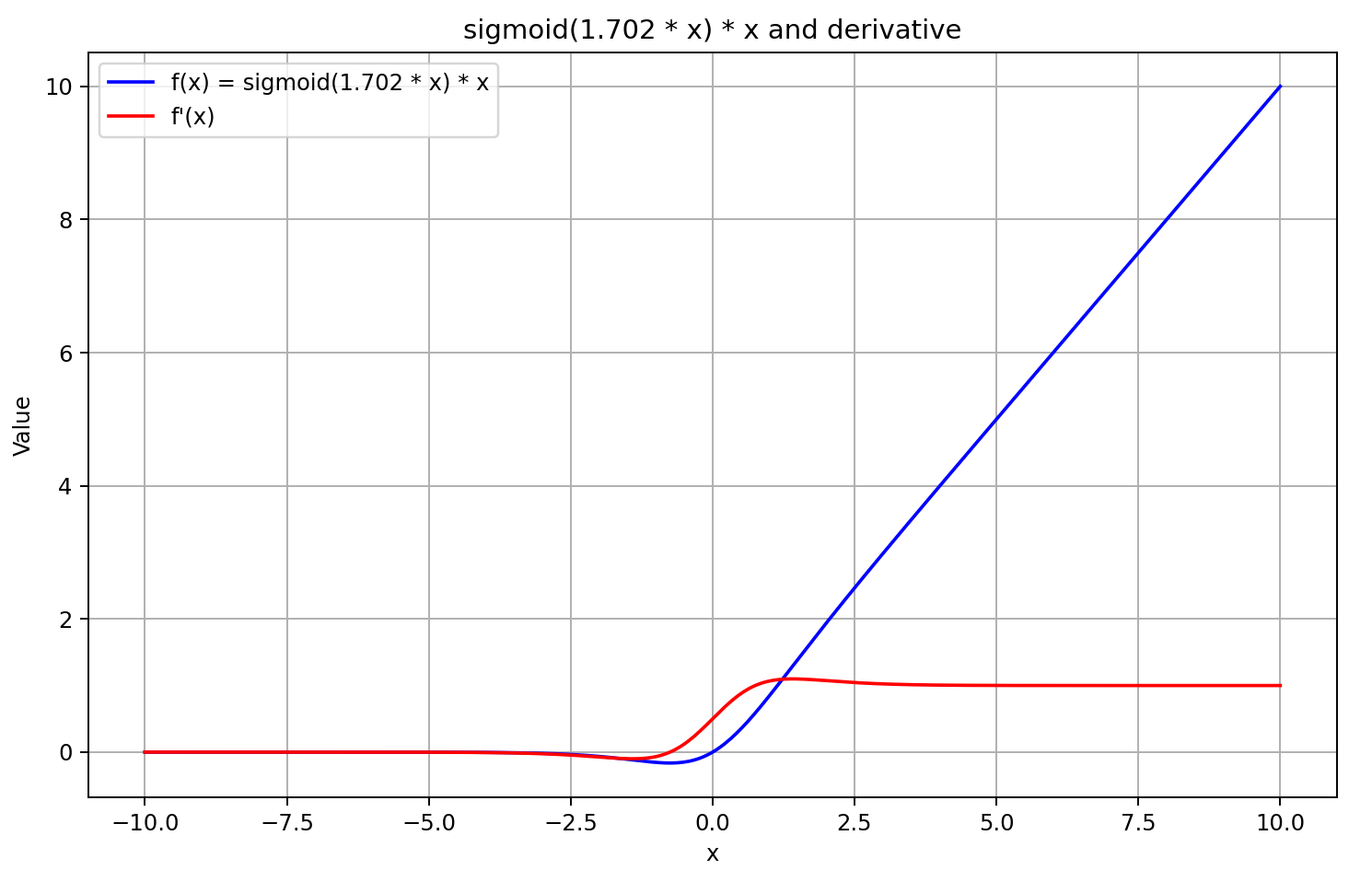
この理解に基づき、導関数の値を順伝播の結果に5を掛けたシグモイド関数として近似します。この方法は計算が高速で、GELUの出力が0以上の場合に良い近似をもたらします。しかし、負の出力値に対しては導関数を0.5に固定しているため、モデルのさらなる学習が困難になります。実際には、導関数は0に近づくべきであり、これにより誤差勾配の伝播が実質的に遮断されます。
![]()
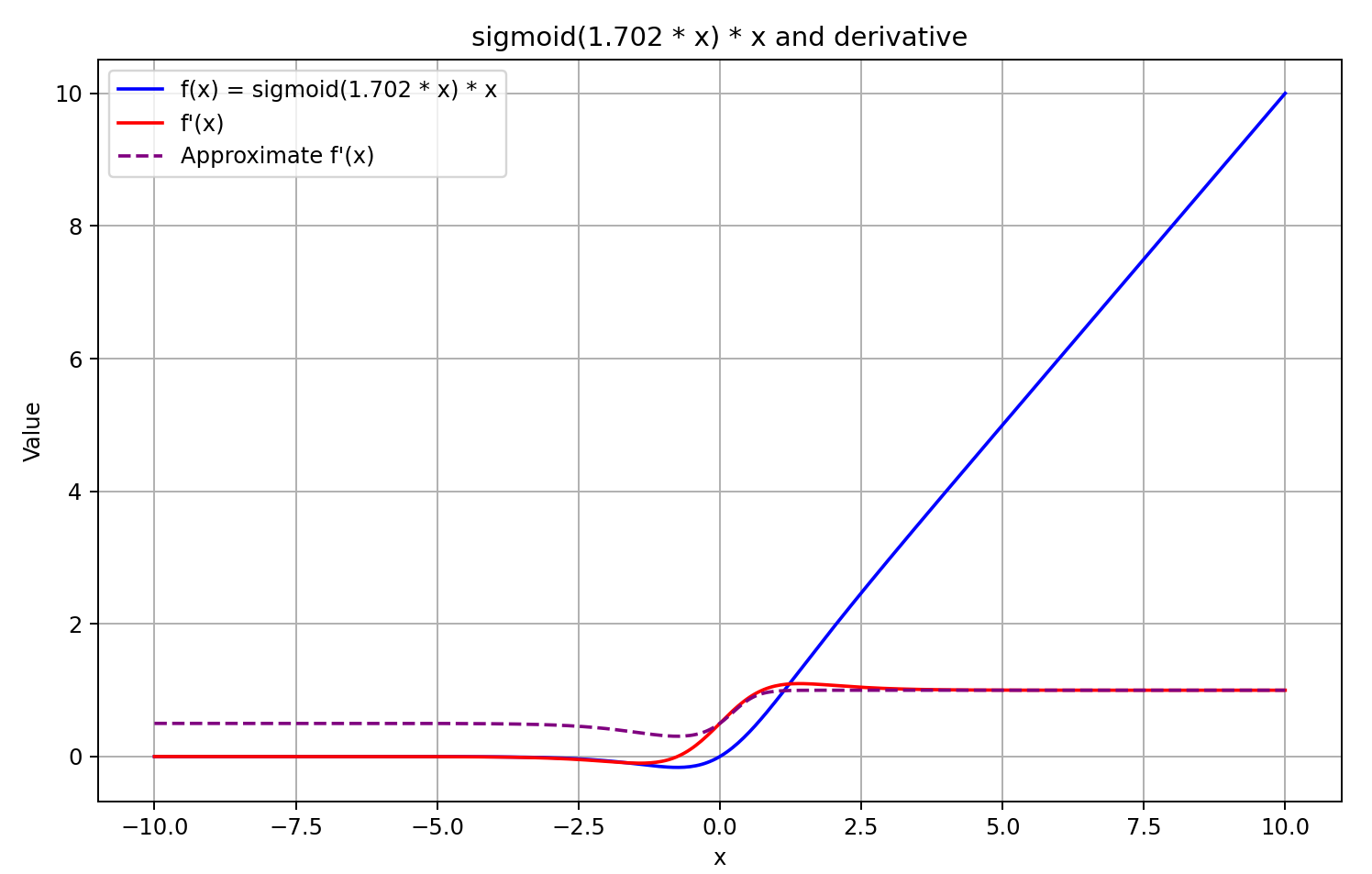
方針は決定しました。実装を始めましょう。これを実現するために、微分計算関数に別のケースを追加しました。
float Deactivation(const float grad, const float inp_value, const int function) { float result = grad; //--- if(isnan(inp_value) || isinf(inp_value) || isnan(grad) || isinf(grad)) result = 0; else switch(function) { case 0: //TANH result = clamp(grad + inp_value, -1.0f, 1.0f) - inp_value; result *= 1.0f - pow(inp_value, 2.0f); break; case 1: //Sigmoid result = clamp(grad + inp_value, 0.0f, 1.0f) - inp_value; result *= inp_value * (1.0f - inp_value); break; case 2: //LReLU if(inp_value < 0) result *= 0.01f; break; case 3: //SoftPlus result *= Activation(inp_value, 1); break; case 4: //GELU if(inp_value < 0.9f) result *= Activation(5 * inp_value, 1); break; default: break; } //--- return clamp(result, -MAX_GRAD, MAX_GRAD); }
順伝播の結果が0.9未満の場合にのみ活性化関数の導関数の値を計算することに注意してください。それ以外の場合は導関数の値を1とみなしますが、これは正確な近似です。これにより、勾配伝播時の演算回数を削減できます。
フレームワークの著者らは、FeedForwardブロック内の層間の非線形性としてGELU関数の使用を推奨しています。私たちのCNeuronRMATクラスでは、このブロックをフィードバック畳み込みモジュールCResidualConvを使って実装しています。このモジュール内で層間に使われる活性化関数を修正します。この操作はクラスの初期化メソッド内でおこなわれます。具体的な更新箇所はコード中で下線が引かれています。
bool CResidualConv::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * count, optimization_type, batch)) return false; //--- if(!cConvs[0].Init(0, 0, OpenCL, window, window, window_out, count, optimization, iBatch)) return false; if(!cNorm[0].Init(0, 1, OpenCL, window_out * count, iBatch, optimization)) return false; cNorm[0].SetActivationFunction(GELU); if(!cConvs[1].Init(0, 2, OpenCL, window_out, window_out, window_out, count, optimization, iBatch)) return false; if(!cNorm[1].Init(0, 3, OpenCL, window_out * count, iBatch, optimization)) return false; cNorm[1].SetActivationFunction(None); //--- ........ ........ ........ //--- return true; }
これでLSEAttentionフレームワークの著者らが提案した技術の実装が完了しました。すべての変更内容を含む完全なコードは添付ファイルにあり、本記事の準備に使用した全プログラムのコードも含まれています。
なお、環境とのやり取りやモデルの学習プログラムは前回の記事から完全に再利用しており、モデルアーキテクチャも変更していません。そのため、今回導入した最適化の影響を評価する上で非常に興味深いものとなっています。なぜなら、唯一の違いはアルゴリズム面での改良だけだからです。
3.テスト
本記事では、LSEAttentionフレームワークの著者らが提案した最適化手法を、時系列予測における従来のTransformerアルゴリズムに対して実装しました。前述の通り、本研究はこれまでの研究とは異なり、新たなニューラル層を作成するのではなく、既存のコンポーネントに提案された改良を統合しています。本質的には、前回の記事で実装したHypDiffフレームワークに対して、モデルアーキテクチャを変更せずにアルゴリズムの最適化を加え、FeedForwardFブロック内の活性化関数も変更しました。これらの調整は主に数値安定性の向上によって内部計算機構に影響を与えています。当然ながら、これらの変更がモデルの学習結果にどのような影響をもたらすかに関心があります。
公平な比較をおこなうために、HypDiffモデルの学習アルゴリズムを完全に再現し、同じ訓練データセットを使用しました。ただし、今回は訓練セットに対する反復的な更新はおこないませんでした。これにより学習性能が若干低下する可能性はありますが、アルゴリズム最適化前後のモデルを正確に比較することが可能となります。
モデルは2024年第1四半期の実データを用いて評価されました。以下にテスト結果を示します。
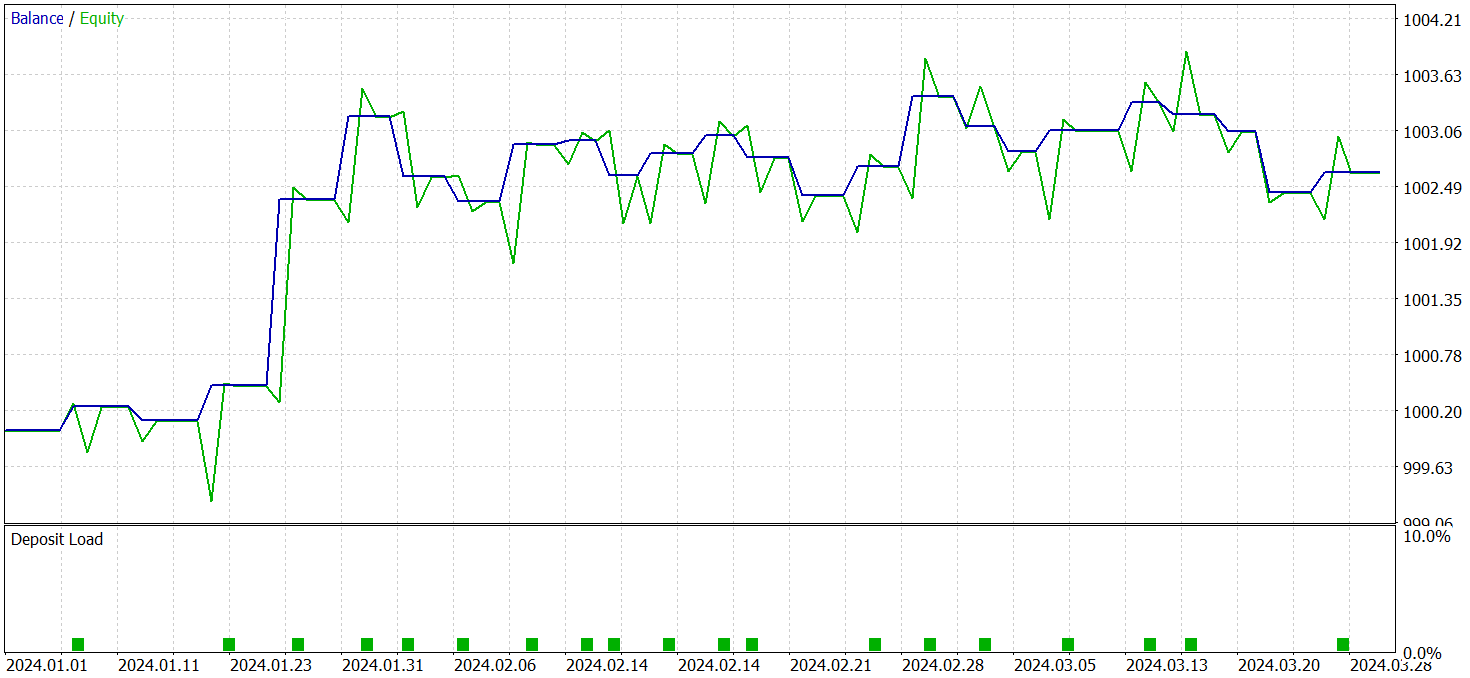
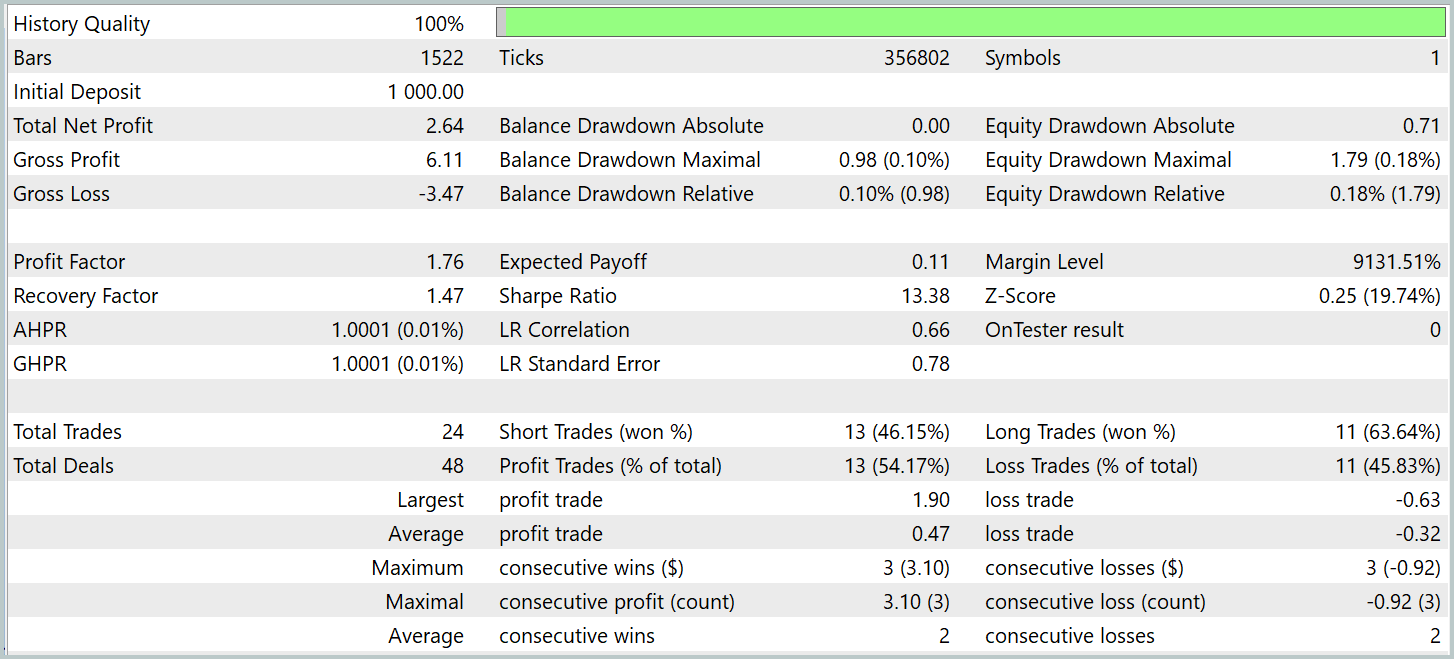
モデルの改良前後での性能はかなり近いものであったことに注意してください。テスト期間中、更新後のモデルは24回の取引を実行しました。これはベースラインモデルとの差がわずか1回の取引に過ぎず、誤差の範囲内と言えます。両モデルともに13回の利益を出した取引がありました。唯一目に見える改善点は、2月にドローダウンがなかったことです。
結論
LSEAttentionは、特にノイズやデータの変動に強い耐性を求められるタスクに効果的な、Attention機構の進化形を示しています。LSEAttentionの主な利点は、Log-Sum-Exp関数を用いた対数的平滑化の活用にあり、これにより深層ニューラルネットワークで問題となる数値のオーバーフローや勾配消失を回避できます。
実践部分では、提案された手法をMQL5で実装し、既存のモジュールに統合しました。実際の過去データを用いてモデルを学習および評価しました。テスト結果から、これらの手法がモデル学習の安定性を向上させることが確認できました。
参照文献
記事で使用されているプログラム
| # | 名前 | 種類 | 詳細 |
|---|---|---|---|
| 1 | Research.mq5 | EA | 事例収集用EA |
| 2 | ResearchRealORL.mq5 | EA | Real-ORL法を用いた例収集用EA |
| 3 | Study.mq5 | EA | モデル学習用EA |
| 4 | Test.mq5 | EA | モデルテスト用EA |
| 5 | Trajectory.mqh | クラスライブラリ | システム状態記述の構造体 |
| 6 | NeuroNet.mqh | クラスライブラリ | ニューラルネットワークを作成するためのクラスのライブラリ |
| 7 | NeuroNet.cl | ライブラリ | OpenCLプログラムコードライブラリ |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16360
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 初心者からプロまでMQL5をマスターする(第6回):エキスパートアドバイザー開発の基礎
初心者からプロまでMQL5をマスターする(第6回):エキスパートアドバイザー開発の基礎
 初級から中級まで:共用体(II)
初級から中級まで:共用体(II)
 原子軌道探索(AOS)アルゴリズム:改良版
原子軌道探索(AOS)アルゴリズム:改良版
 リプレイシステムの開発(第74回):新しいChart Trade(I)
リプレイシステムの開発(第74回):新しいChart Trade(I)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索