初心者からエキスパートへ：自動幾何解析システム

内容

1. はじめに
2. 背景
3. 概要
4. 実装
5. 結果とテスト
6. 結論

はじめに

本日の議論は、幾何学的手法を用いたローソク足パターンの分析という課題に取り組むことを目的としています。前回の「初心者からエキスパートへ：ローソク足プログラミング」では、通常は数本のローソク足で構成される単純なパターンの識別に焦点を当てました。しかし、より長く連続したローソク足を扱う場合、パターン認識はより複雑になり、長期的には一貫性が低下する傾向があります。

それでも、明確な洞察として、データ内の主要な高値と安値を特定することは可能です。これらのポイントを結ぶことで、トレンドをより効果的に把握できます。

私たちが初めて外国為替取引を学び始めたとき、多くの教育リソースは三角形の形成やその他の市場プライスアクションにおける幾何学的パターンの概念を紹介していました。実際、市場には幾何学的な要素が存在し、市場の動きを簡略化して視覚的にまとめることが可能です。

ほとんどのトレーダーは、チャート上にトレンドラインを描いたり幾何学的オブジェクトを配置することで、これらの形状を手動で識別することに慣れています。本記事では、このプロセスを一歩進め、MQL5を活用して自動化し、手動介入を不要にし、より迅速かつ一貫した分析を可能にすることを目指します。

背景

オブジェクト指向プログラミング(OOP)の利点は、現実世界の計算問題を効率的にモデル化し、解決する強力な能力にあります。MQL5はC++を基にした言語であり、この強みを受け継ぎ、取引アルゴリズムの開発に特化した貴重な資産です。本記事で扱う問題を考慮すると、OOPが提供する構造的かつモジュール化された利点により、すでに大きなアドバンテージを持っています。

本セクションでは、まず対象に関連する主要な用語を簡単に定義し、その後、取引における幾何学的形状の識別に用いられる従来の手法を紹介します。テクニカル分析には多くの形状が存在しますが、ここでは一般的な例として長方形と三角形に焦点を当てます。

幾何学とは何か

幾何学は、空間の性質や関係を扱う数学の分野です。距離、形状、大きさ、角度、図形の相対位置などを研究します。幾何学は、空間的関係をモデル化・分析することで、現実世界を解釈するためのしっかりとした枠組みを提供します。

取引において幾何学が重要な理由

幾何学は、市場行動を理解・解釈するための視覚的かつ構造的なフレームワークを提供します。トレーダーは価格変動から現れるパターンや形状に依存することが多く、これらのパターンは本質的に幾何学的です。幾何学はパターン認識を助け、以下のような一般的なパターンがあります。

• 三角形（上昇、下降、対称）
• 長方形（保ち合い相場）
• チャネル（平行トレンドライン）
• 三尊、ダブルトップ/ボトムはすべて幾何学的対称性に依存

これらのパターンを用いることで、トレーダーは以下をおこなうことができます。

• ブレイクアウトや反転の可能性を特定する
• トレンドの強さを測定する
• エントリー/エグジットポイントを設定する

下表に、市場価格データに幾何学的分析を適用する際の主要な考慮点をまとめました。

側面	幾何学の役割
視覚的な明瞭さ	複雑な市場データを認識可能な形に簡略化
意思決定支援	形状がエントリー、エグジット、取引セットアップをガイド
客観性	正確な空間的論理を用いることで推測を減少
自動化	パターンや重要水準のアルゴリズム検出を可能に
市場心理	形状は集団的なトレーダー行動を反映（例：三角形は圧縮を示す）

次に、三角形と長方形の幾何学が従来、取引でどのように応用されているかを見ていきます。ここでは各三角形パターンが価格動向について示唆する一般的な意味を概説しますが、特定の取引戦略には踏み込みません。これは、一般的に受け入れられているルールの多くが、実際の市場条件では無効になることがあるためです。これらのパターンはある程度機能しますが、幾何学的構造が形成される前の価格の動きに十分注意を払うことが賢明です。

たとえば、上昇三角形は一般的に強気のブレイクアウトを示唆しますが、逆に動くケースも多数あります。これらの形状は市場の判断点を示すものであり、保証ではありません。したがって、パターンが示す方向性に従う場合でも、形成前の実際の価格コンテキストと照らし合わせることが重要です。教科書的な期待だけに依存すると誤解を招く可能性があります。

三角形

三角形は三辺と三つの頂点で定義される基本的な幾何学形状です。外国為替取引において、三角形パターンはトレンドの継続または反転の可能性を示します。主要な三角形パターンの種類は次の通りです。

1. 対称三角形:

ボラティリティが低下する期間のレンジ形成を示し、通常はいずれの方向へのブレイクアウトの前兆となります。

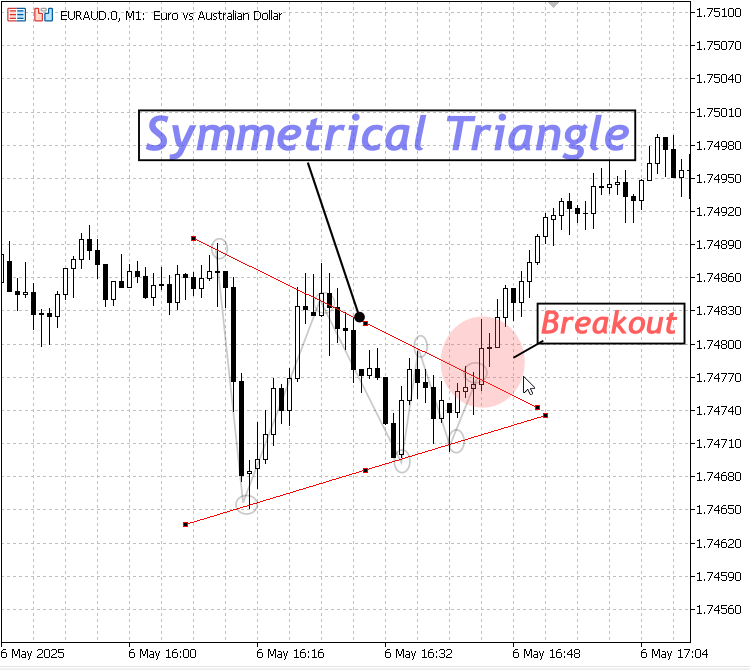
対称三角形

2. 上昇三角形

水平またはわずかに傾いたレジスタンスラインと上昇するサポートラインを特徴とします。典型的には強気のパターンで、上方向へのブレイクアウトの可能性を示唆します。

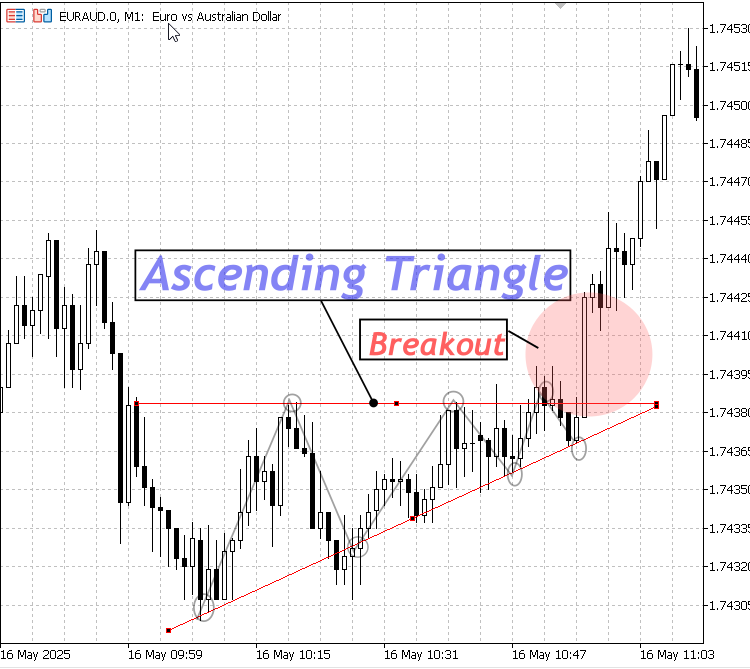
上昇三角形

3. 下降三角形

水平またはわずかに傾いたサポートラインと下降するレジスタンスラインを特徴とします。通常は弱気のパターンで、下方向へのブレイクアウトの可能性を示唆します。

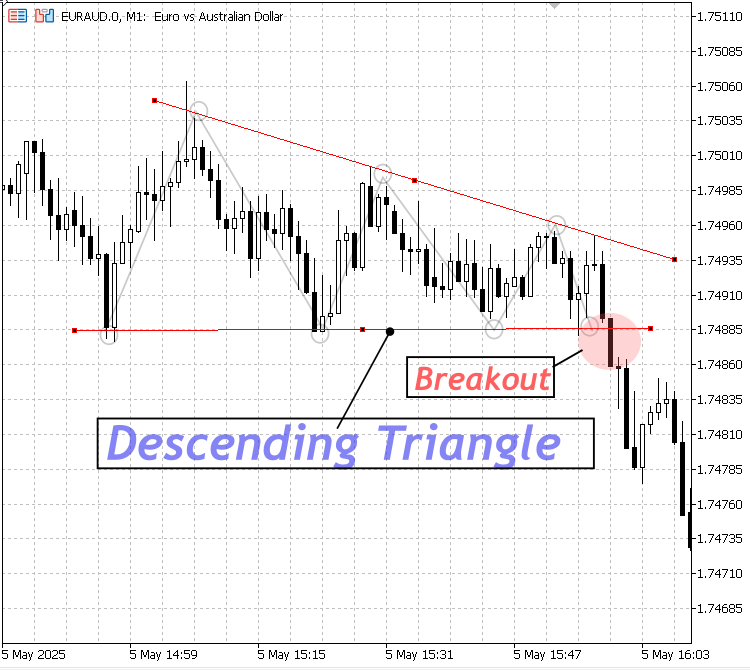
下降三角形

長方形

長方形は、対辺が等しく平行な四辺形の幾何学形状です。各頂点には直角（90度）が存在します。 外国為替やテクニカル分析において、長方形（トレーディングレンジや保ち合い相場とも呼ばれる）は、価格が水平のサポートラインとレジスタンスラインの間で横ばいに動くチャートパターンを指します。このパターンは、市場が以前のトレンドを継続するか反転するかの判断を迷っている期間を示します。Meta Trader 5ターミナル上の市場分析ツールでも利用可能です。

主な特徴は次のとおりです。

• 価格は明確な上方のレジスタンスラインと下方のサポートラインの間で振動する
• パターンはチャート上で長方形またはボックスの形状に見える
• レジスタンスの上方ブレイクアウトやサポートの下方ブレイクアウトは、新しいトレンドの開始を示すことが多い

この概念は、内蔵の平行線ツールを用いても示すことができ、サポートおよびレジスタンスラインを水平に配置することで表現できます。平行線で構成されるため、保ち合い中の価格レンジを効果的に強調できます。しかし、特定期間の価格横ばいを視覚的に「ボックス化」できるため、保ち合い相場を示すには長方形が依然として好まれる方法です。重要なのは、保ち合い相場は一時的な段階であり、最終的には市場はそのレンジを突破し、トレンドを継続するか方向を反転させるという点です。

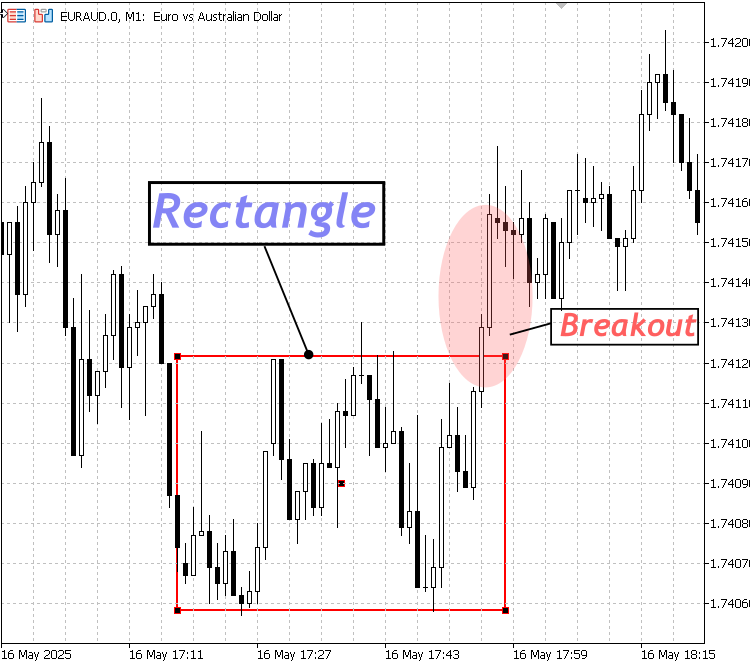
長方形構造

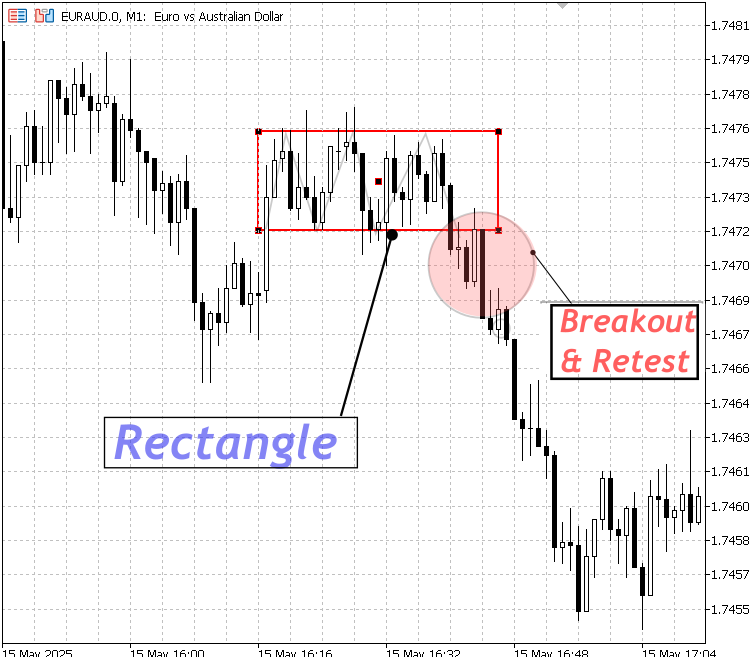
長方形パターンの下方ブレイク

概要

理論的な基盤を整えたところで、ここからは実践的な実装の概要を示します。モジュール化プログラミングの手法を用いて、幾何学構造検出システムのコンポーネントを構築します。具体的には、市場構造における三角形および長方形の形成を検出するためのクラスを個別に開発します。これらはあくまで初期例であり、必要に応じて他の形状への対応も拡張可能です。これは、MQL5のオブジェクト指向およびモジュール化プログラミングの特徴を活かすことで、複雑な現実世界の問題にもクリーンで保守性の高いコードで取り組めるという大きな利点の一つです。

本セクションで作成するヘッダファイルは、メインのエキスパートアドバイザー(EA)やインジケーターに容易に統合可能です。さらに、複数のプロジェクトで再利用できるため、一貫性のある開発と効率的な作業が可能になります。

私のアプローチでは、各幾何学形状には価格データ内の一連の参照点が必要です。通常は、高値のポイント2つと安値のポイント2つを用います。これらのポイントを線で結ぶことで形状を形成します。たとえば、2つのポイントで線を作り、将来的に交わる2本の線で三角形が形成されます。長方形は、レジスタンスラインとサポートラインの双方で2回タッチした場合に検出できます。これらの条件が満たされると、適切な参照点を結ぶことで幾何学形状を描画できます。

以下に、コンピュータロジックを用いてチャート上にこれらの形状を構築する方法を示す図を掲載します。各形状を描くには、通常少なくとも4つの重要なポイントが必要です。図では、最初にポイントa、b、c、dを特定します。これらは形状構造の基礎となるアンカーです。これらのポイントから、形状を予め投影することが可能です。赤の点線は理論上の予想を示しており、価格が形状の境界にどう反応するかを示唆します。この線との価格の関わり方により、将来の価格動向（ブレイクアウトや反発の可能性）に関する重要な手掛かりを得ることができます。

三角形の理論的検出

上図の三角形では、スイングポイントa〜dが参照点として特定され、三角形が構築されます。交わる線は点Xで収束します。ポイントeとfは理論上の将来タッチを表し、必ずしも実際に発生するわけではありません。これらはパターンを概念化し、コードにするための補助です。長方形の図でも、同様のロジックを用いて構造を検出します。ただし、三角形との最大の違いは、長方形の辺が平行である点です。

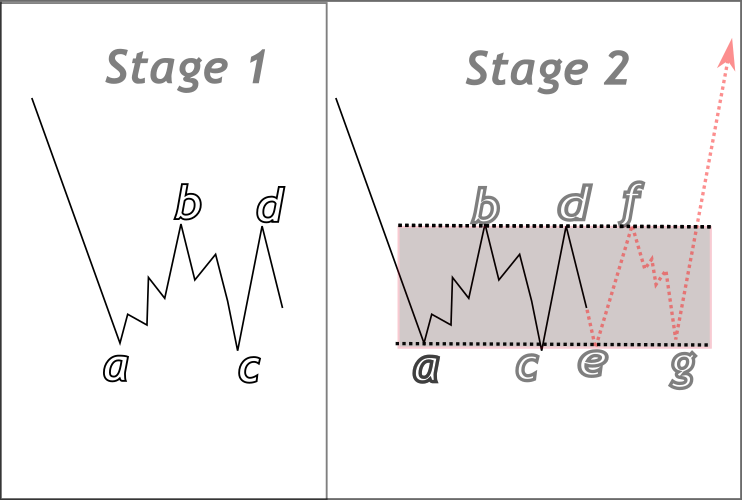
長方形構造の検出

実装

この段階で、実際の開発が始まります。まず、GeometricPatternDetector.mqhという名前のヘッダファイルを作成します。このファイルには、幾何学パターンを検出するために必要なすべてのクラスを含めます。ヘッダファイルの準備が整ったら、これらのクラスを効果的に活用する方法を示すEAの開発に進みます。ここで、すべての要素がどのように組み合わさるかを理解するために、以下のステップを確認します。

必要なヘッダをインクルードする

GeometricPatternDetector.mqhの最上部では、検出器に必要なツールをすべて提供するため、3つの重要なMQL5ライブラリをインクルードします。まず、arrays\ArrayObj.mqhをインクルードすることで、CArrayObjという動的かつオブジェクト指向の配列クラスを利用できるようになります。これにより、スイングのピボットやパターン結果を、ポインタ操作や手動メモリ管理に悩まされることなく格納できます。

次に、Indicators\Indicators.mqhを取り込むことで、MetaTraderに組み込まれたiATR、CopyHigh、CopyLow、CopyTimeなどのインジケーター関数を使用可能になり、過去の価格データの取得やAverage True Range (ATR)の計算をスムーズにおこなえます。最後に、Math\Stat\Math.mqhをインクルードすると、M_PIのような数学定数や、MathArctanなどのユーティリティ関数を利用でき、パターン検出アルゴリズムで傾きや角度、平坦度の許容範囲を計算する際に役立ちます。これらのヘッダファイルの組み合わせにより、堅牢で読みやすく、保守しやすいコードを構築するための基盤が整います。

#include <Arrays\ArrayObj.mqh>       // For CArrayObj: dynamic arrays of objects 
#include <Indicators\Indicators.mqh> // For iATR, CopyHigh, CopyLow, CopyTime
#include <Math\Stat\Math.mqh>        // For M_PI, MathArctan, and other math utilities

コンテナクラス

GeometricPatternDetector.mqhヘッダファイルでは、まず2つのシンプルなコンテナクラス、SwingPointとPatternResultを定義します。どちらもMQL5の基底クラスであるCObjectを継承しています。SwingPointクラスは、タイムスタンプ、価格、そしてそのピボットが高値か安値かを示すブール値を保持します。この設計により、個々の市場ピボットを1つのオブジェクト配列でまとめて管理できます。

PatternResultクラスは、検出されたパターンを記述するために必要な情報をすべてカプセル化します。具体的には、銘柄、時間足、パターンの種類、3つの定義頂点、およびラベルを配置すべきポイントです。これらのデータ要素をオブジェクトとしてまとめることで、検出器のコードはクリーンで一貫性のあるものとなります。CArrayObjを用いてデータを格納するため、原始型の並列配列を手動で管理する必要もありません。

// SwingPoint: holds one market pivot
class SwingPoint : public CObject {
public:
   datetime time;
   double   price;
   bool     isHigh;
   SwingPoint(datetime t=0,double p=0.0,bool h=false)
     : time(t), price(p), isHigh(h) {}
};

// PatternResult: holds the details of one detected pattern
class PatternResult : public CObject {
public:
   string            symbol;
   ENUM_TIMEFRAMES   timeframe;
   ENUM_PATTERN_TYPE type;
   datetime          detectionTime;
   datetime          labelTime;
   double            labelPrice;
   datetime          vertex1Time;
   double            vertex1Price;
   datetime          vertex2Time;
   double            vertex2Price;
   datetime          vertex3Time;
   double            vertex3Price;
   PatternResult(const string _s,const ENUM_TIMEFRAMES _tf,const ENUM_PATTERN_TYPE _t,
                 datetime lt,double lp,
                 datetime v1t,double v1p,
                 datetime v2t,double v2p,
                 datetime v3t,double v3p)
     : symbol(_s), timeframe(_tf), type(_t), detectionTime(TimeCurrent()),
       labelTime(lt), labelPrice(lp),
       vertex1Time(v1t), vertex1Price(v1p),
       vertex2Time(v2t), vertex2Price(v2p),
       vertex3Time(v3t), vertex3Price(v3p) {}
};

検出器クラスの構造

ヘッダファイルの中核となるのがCGeometricPatternDetectorクラスです。privateセクションでは、ピボットオブジェクトを格納するメンバー変数や、スイングの過去遡り期間、ATR乗数、最低タッチポイント数などの設定パラメータ、そして重複描画を防ぐための状態（最後に検出された三角形および長方形の名前やハッシュ、検出時刻）が宣言されています。

また、privateで宣言される4つの補助メソッド、IsNewBar、UpdateSwingPoints、CalculateATR、GetSwingHashは、それぞれ新しいバーの判定、最近の高値・安値データからのスイングピボット抽出、ATRを用いた市場感度の計算、4つのピボットセットごとに一意の文字列キーを生成する処理を担います。これらのユーティリティは、2つの主要な公開検出ルーチンであるDetectTriangleおよびDetectRectangleをサポートします。さらに、これらを統合するUpdateメソッドや、検出結果を取得するGetLastPatternメソッド、リソースをクリアするClearPatternsメソッドも備えており、クラス全体の処理を円滑におこなえる構造になっています。

class CGeometricPatternDetector {
private:
   CArrayObj   m_swings;
   int         m_swingLookback;
   double      m_atrMultiplier;
   int         m_minTouchPoints;

   string      m_lastTriangle;
   string      m_lastSwingHash;
   datetime    m_lastTriangleTime;

   string      m_lastRectangle;
   string      m_lastRectangleHash;
   datetime    m_lastRectangleTime;

   bool    IsNewBar(const string sym,const ENUM_TIMEFRAMES tf);
   void    UpdateSwingPoints(const string sym,const ENUM_TIMEFRAMES tf);
   double  CalculateATR(const string sym,const ENUM_TIMEFRAMES tf,const int period=14);
   string  GetSwingHash(SwingPoint *p1,SwingPoint *p2,SwingPoint *p3,SwingPoint *p4);

public:
   CGeometricPatternDetector(int swingLookback=3,double atrMultiplier=1.5,int minTouchPoints=2);
   ~CGeometricPatternDetector();

   void Update(const string sym,const ENUM_TIMEFRAMES tf);
   void DetectTriangle(const string sym,const ENUM_TIMEFRAMES tf);
   void DetectRectangle(const string sym,const ENUM_TIMEFRAMES tf);
   ENUM_PATTERN_TYPE GetLastPattern();
   void ClearPatterns();

   CArrayObj m_currentPatterns;
};

スイングポイント抽出

スイングポイント抽出メソッドであるUpdateSwingPointsは、新しいバーが形成されるたびに呼び出されます。このメソッドでは、チャートから高値、安値、タイムスタンプのウィンドウをコピーし、そのウィンドウの中央のバーを評価します。中央バーの価格が両隣のバーよりも高ければスイング高値、低ければスイング安値として指定されます。確認された各ピボットはSwingPointオブジェクトにラップされ、m_swings配列に追加されます。

配列が設定された容量を超えると、最も古いエントリは削除されます。この移動リストとしてのピボットは、三角形および長方形の検出の基礎を形成し、最新かつ重要な市場の転換点のみを考慮できるようにします。

void CGeometricPatternDetector::UpdateSwingPoints(const string sym,const ENUM_TIMEFRAMES tf)
{
   int bars = m_swingLookback*2 + 1;
   double highs[], lows[];
   datetime times[];
   ArraySetAsSeries(highs,true);
   ArraySetAsSeries(lows,true);
   ArraySetAsSeries(times,true);

   if(CopyHigh(sym,tf,0,bars,highs)<bars ||
      CopyLow(sym,tf,0,bars,lows)<bars   ||
      CopyTime(sym,tf,0,bars,times)<bars)
   {
      Print("Error: Failed to copy price/time data");
      return;
   }

   int mid = m_swingLookback;
   datetime t = times[mid];
   double h = highs[mid], l = lows[mid];

   bool isH = true;
   for(int i=1; i<=m_swingLookback; i++)
      if(h<=highs[mid-i] || h<=highs[mid+i]) { isH=false; break; }
   if(isH) {
      m_swings.Add(new SwingPoint(t,h,true));
      Print("Swing High detected at ",TimeToString(t)," Price: ",h);
   }

   bool isL = true;
   for(int i=1; i<=m_swingLookback; i++)
      if(l>=lows[mid-i] || l>=lows[mid+i]) { isL=false; break; }
   if(isL) {
      m_swings.Add(new SwingPoint(t,l,false));
      Print("Swing Low detected at ",TimeToString(t)," Price: ",l);
   }

   while(m_swings.Total()>50) {
      delete (SwingPoint*)m_swings.At(0);
      m_swings.Delete(0);
   }
}

CalculateATRはMQL5に組み込まれたATRインジケーターをラップし、市場感度を反映した値幅の基準単位を提供します。一方、GetSwingHashは4つのピボットの時刻と価格を連結し、文字列キーを生成します。ATRの値は、三角形における「平坦さ」や長方形における整列の許容範囲をスケーリングするために使用されます。また、ハッシュ文字列によって、各ユニークなピボットセットがロックアウト期間中に一度だけ描画されるよう保証されます。

double CGeometricPatternDetector::CalculateATR(const string sym,const ENUM_TIMEFRAMES tf,const int period)
{
   int h = iATR(sym,tf,period);
   if(h==INVALID_HANDLE) { Print("ATR handle error"); return 0; }
   double buf[]; ArraySetAsSeries(buf,true);
   if(CopyBuffer(h,0,0,1,buf)!=1) { Print("ATR copy error"); return 0; }
   return buf[0];
}

string CGeometricPatternDetector::GetSwingHash(SwingPoint *p1,SwingPoint *p2,SwingPoint *p3,SwingPoint *p4)
{
   return TimeToString(p1.time)+"*"+DoubleToString(p1.price,8)+"*"
        + TimeToString(p2.time)+"*"+DoubleToString(p2.price,8)+"*"
        + TimeToString(p3.time)+"*"+DoubleToString(p3.price,8)+"*"
        + TimeToString(p4.time)+"_"+DoubleToString(p4.price,8);
}

三角形検出ロジック

三角形の検出ルーチンでは、安値から高値、安値から高値という順序で連続する4つのスイングを厳密に探します。各辺について最小バー間隔を満たすことを確認したうえで、価格差を時間差で割ることで上下両辺の傾きを計算します。ATRに基づく許容範囲を用いて、三角形の上辺または下辺が十分に水平であるかを判定し、該当する場合は下降型または上昇型として分類します。いずれの辺も水平と見なせない場合は、対称型として分類されます。

次に、両辺の直線を解析的に交差させることで、将来の時間における三角形の頂点を求めます。検出されたパターンは、2つのピボットポイントと計算された頂点を使って1つのOBJ_TRIANGLEオブジェクトとして描画され、同時にPatternResultオブジェクトが生成されて保存されます。描画のちらつきを防ぐために、検出器は4つのピボットから生成されたハッシュを直前のパターンと比較し、同じ形状が一定数のバーにわたって再描画されないようロックアウトをおこないます。

void CGeometricPatternDetector::DetectTriangle(const string sym,const ENUM_TIMEFRAMES tf)
{
   int tot = m_swings.Total();
   if(tot < 4) return;
   ulong barSec = PeriodSeconds(tf);
   ulong minSpan = (ulong)m_swingLookback * barSec;

   for(int i=0; i<=tot-4; i++)
   {
      SwingPoint *p1 = (SwingPoint*)m_swings.At(i);
      SwingPoint *p2 = (SwingPoint*)m_swings.At(i+1);
      SwingPoint *p3 = (SwingPoint*)m_swings.At(i+2);
      SwingPoint *p4 = (SwingPoint*)m_swings.At(i+3);

      if(!( !p1.isHigh && p2.isHigh && !p3.isHigh && p4.isHigh )) continue;
      if((ulong)(p2.time-p1.time)<minSpan ||
         (ulong)(p3.time-p2.time)<minSpan ||
         (ulong)(p4.time-p3.time)<minSpan) continue;

      double m_low  = (p3.price - p1.price) / double(p3.time - p1.time);
      double m_high = (p4.price - p2.price) / double(p4.time - p2.time);
      double tolFlat = CalculateATR(sym,tf,14) * m_atrMultiplier;

      bool lowerFlat = MathAbs(p3.price-p1.price) < tolFlat;
      bool upperFlat = MathAbs(p4.price-p2.price) < tolFlat;

      ENUM_PATTERN_TYPE type;
      if(lowerFlat && m_high < 0)             type = PATTERN_TRIANGLE_DESCENDING;
      else if(upperFlat && m_low > 0)         type = PATTERN_TRIANGLE_ASCENDING;
      else                                    type = PATTERN_TRIANGLE_SYMMETRICAL;

      double denom = m_low - m_high;
      if(MathAbs(denom)<1e-12) continue;
      double num = (p2.price - p1.price) + (m_low*p1.time - m_high*p2.time);
      double tx  = num/denom;
      double px  = p1.price + m_low*(tx-p1.time);

      datetime latest = MathMax(p1.time,p2.time);
      if(tx<=latest || tx>TimeCurrent()+barSec*50) continue;

      if(StringLen(m_lastTriangle)>0)
         ObjectDelete(0,m_lastTriangle);

      string base = "GPD_"+sym+"_"+EnumToString(tf)+"_"+TimeToString(TimeCurrent(),TIME_SECONDS);
      long cid    = ChartID();
      m_lastTriangle = base+"_T";

      ObjectCreate(cid,m_lastTriangle,OBJ_TRIANGLE,0,
                   p1.time,p1.price,
                   p2.time,p2.price,
                   tx,      px);
      ObjectSetInteger(cid,m_lastTriangle,OBJPROP_COLOR,clrOrange);
      ObjectSetInteger(cid,m_lastTriangle,OBJPROP_WIDTH,2);
      ObjectSetInteger(cid,m_lastTriangle,OBJPROP_FILL,false);

      m_lastSwingHash    = GetSwingHash(p1,p2,p3,p4);
      m_lastTriangleTime = TimeCurrent();
      m_currentPatterns.Add(new PatternResult(
         sym,tf,type,
         latest,(p2.price+p4.price)/2.0,
         p1.time,p1.price,
         p2.time,p2.price,
         (datetime)tx,px
      ));

      ChartRedraw(cid);
      break;
   }
}

長方形検出ロジック

長方形の検出は、三角形と同様のピボットシーケンスに従いますが、より厳格な制約が適用されます。まず、安値から高値、安値から高値という同じ順序で4つのスイングを特定し、それぞれのスイング（安値から高値、2つ目の安値から高値）が少なくとも5バー以上の幅を持ち、かつATRでスケーリングされた閾値を超えることを条件とします。長方形の下辺は、2つの安値がATRの許容範囲内に収まっている場合、その平均値に揃えられます。さらに、2つの高値も同様に許容範囲内で揃えば、その平均値を上辺に設定します。そうでない場合は、少なくとも1ATR分の高さを持たせることで、長方形が視認できるようにします。

長方形はOBJ_RECTANGLEオブジェクトとして描画され、最も早いピボット時刻からちょうど20バー先までを範囲とします。これにより、無制限に拡大することを防ぎます。ユニークなピボットハッシュによって、同じ長方形がロックアウト期間中に複数回描画されることを防止し、その詳細はPatternResultに記録されます。

void CGeometricPatternDetector::DetectRectangle(const string sym,const ENUM_TIMEFRAMES tf)
{
   int tot = m_swings.Total();
   if(tot < 4) return;

   ulong barSec    = PeriodSeconds(tf);
   ulong minSpan5  = 5 * barSec;                        
   double tolATR   = CalculateATR(sym,tf,14) * m_atrMultiplier;

   for(int i=0; i<=tot-4; i++)
   {
      SwingPoint *a = (SwingPoint*)m_swings.At(i);
      SwingPoint *b = (SwingPoint*)m_swings.At(i+1);
      SwingPoint *c = (SwingPoint*)m_swings.At(i+2);
      SwingPoint *d = (SwingPoint*)m_swings.At(i+3);

      if(!( !a.isHigh && b.isHigh && !c.isHigh && d.isHigh )) continue;
      if((ulong)(b.time - a.time) < minSpan5 ||
         (ulong)(d.time - c.time) < minSpan5) continue;
      if(MathAbs(b.price - a.price) < tolATR ||
         MathAbs(d.price - c.price) < tolATR) continue;
      if(MathAbs(a.price - c.price) > tolATR) continue;

      bool highAligned = MathAbs(b.price - d.price) < tolATR;
      double lowP  = (a.price + c.price) / 2.0;
      double highP = highAligned ? (b.price + d.price)/2.0 : lowP + tolATR;

      datetime leftT  = MathMin(a.time, c.time);
      datetime rightT = leftT + (datetime)(20 * barSec);

      string rh = TimeToString(leftT,TIME_SECONDS) + "_" +
                  DoubleToString(lowP,8) + "_" +
                  DoubleToString(highP,8);
      datetime lockT = m_lastRectangleTime + (datetime)(40 * barSec);
      if(rh == m_lastRectangleHash && TimeCurrent() < lockT) return;

      if(StringLen(m_lastRectangle) > 0)
         ObjectDelete(0,m_lastRectangle);

      string base = "GPD_"+sym+"_"+EnumToString(tf)+"_"+TimeToString(TimeCurrent(),TIME_SECONDS);
      long cid    = ChartID();
      m_lastRectangle = base+"_Rect";

      ObjectCreate(cid,m_lastRectangle,OBJ_RECTANGLE,0,
                   leftT,   highP,
                   rightT,  lowP);
      ObjectSetInteger(cid,m_lastRectangle,OBJPROP_COLOR, clrBlue);
      ObjectSetInteger(cid,m_lastRectangle,OBJPROP_WIDTH, 2);
      ObjectSetInteger(cid,m_lastRectangle,OBJPROP_FILL,  false);

      m_currentPatterns.Add(new PatternResult(
         sym,tf,PATTERN_RECTANGLE,
         leftT,(highP+lowP)/2.0,
         leftT,highP,
         leftT,lowP,
         rightT,lowP
      ));
      m_lastRectangleHash = rh;
      m_lastRectangleTime = TimeCurrent();

      ChartRedraw(cid);
      break;
   }
}

EAでのヘッダの使用

このヘッダファイルをEAに統合するのは非常に簡単です。ファイルをインクルードし、好みのパラメータでCGeometricPatternDetectorをインスタンス化し、OnTickイベントハンドラの中でUpdate(Symbol(), _Period)メソッドを呼び出すだけです。各更新の後、GetLastPatternを使えば新しい三角形または長方形が検出されたかどうかを確認でき、detector.m_currentPatternsを調べることで詳細情報を取得したり、アラートを発行したり、チャートにラベルを配置したりできます。

EAは、幾何学やピボットロジックの内部処理を知る必要はありません。ただ検出器を駆動し、上位レベルの結果に反応するだけです。この分離構造（宣言はヘッダファイルにまとめ、詳細な実装は同ファイルに収め、EA側ではシンプルに利用する）は、MQL5におけるオブジェクト指向設計が複雑さをカプセル化し、再利用性と保守性の高いコードを実現することを示しています。ここからは詳細な手順を確認していきます。

ヘッダのインクルードとグローバル状態

GeometryAnalyzerEA.mq5の冒頭で、まず検出器のヘッダファイルをインクルードし、EAがCGeometricPatternDetectorクラスおよび関連する型にアクセスできるようにします。その直後に、単一の検出器オブジェクトをインスタンス化します。ここでは、ピボット検出用に過去3バーの遡り、許容範囲として1.5倍のATR乗数、そしてパターン検出に必要な最低タッチポイント数を2と設定します。さらに、3つのグローバル変数を宣言します。lastAlertedは直近にアラートを出したパターンの種類を記録し、同じバー内で繰り返さないようにします。lastBarTimeは新しいバーが出現したタイミングを追跡し、lastLabelNameは配置したテキストラベルの名前を保持し、新しいパターンが現れた際に古いラベルを削除できるようにします。

#include <GeometricPatternDetector.mqh>

//–– detector instance & state
CGeometricPatternDetector  detector(3, 1.5, 2);
ENUM_PATTERN_TYPE          lastAlerted    = PATTERN_NONE;
datetime                   lastBarTime    = 0;
string                     lastLabelName  = "";

初期化とクリーンアップ

OnInit関数はEAの起動時に一度だけ実行されます。ここでは、初期化が完了したことを確認するメッセージを出力するだけですが、必要に応じてタイマーを開始したりリソースを確保したりすることも可能です。逆に、OnDeinitはEAが削除されたときやチャートが閉じられたときに実行されます。このルーチンでは、detector.ClearPatterns()を呼び出して描画されたすべてのパターンをクリアし、さらに残っているテキストラベルがあれば名前を指定して削除します。最後に、EAが停止した理由をログに記録することで、動作停止の原因を診断しやすくしています。

int OnInit()
{
   Print("GeometryAnalyzerEA initialized");
   return(INIT_SUCCEEDED);
}

void OnDeinit(const int reason)
{
   detector.ClearPatterns();
   if(StringLen(lastLabelName) > 0)
      ObjectDelete(0, lastLabelName);
   Print("GeometryAnalyzerEA deinitialized, reason=", reason);
}

新しいバーの検出

OnTick内で最初に行う処理は、受け取ったティックが新しく形成されたバーに属するかどうかを判定することです。現在のバーの開始時刻を取得し、それを保持しているlastBarTimeと比較します。バーが新しい場合は、lastAlertedをリセットしてパターンが再度トリガーされるようにし、さらに前回のテキストラベルを削除してチャートを整理します。バーが新しくなければ、そのまま処理を終了し、それ以上は何もおこないません。これにより、パターン検出は各バーにつき一度だけ実行されることが保証されます。

void OnTick()
{
   datetime curBar = iTime(Symbol(), _Period, 0);
   bool isNewBar  = (curBar != lastBarTime);
   if(isNewBar)
   {
      lastBarTime = curBar;
      lastAlerted = PATTERN_NONE;
      if(StringLen(lastLabelName) > 0)
      {
         ObjectDelete(0, lastLabelName);
         lastLabelName = "";
      }
   }
   if(!isNewBar)
      return;
   // …
}

検出器の実行

新しいバーであることを確認した後、検出器のUpdateメソッドを呼び出し、現在の銘柄と時間足を引数として渡します。この1回の呼び出しでスイングポイントが更新され、内部的に三角形と長方形の検出ルーチンが実行されます。Updateが戻った後にGetLastPattern()を照会し、そのバーで有効なパターンが見つかったかを確認します。新しいパターンが検出されなかった場合、あるいはすでにアラート済みのパターンと一致した場合には、そこで処理を終了します。

detector.Update(Symbol(), _Period);

ENUM_PATTERN_TYPE pattern = detector.GetLastPattern();
if(pattern == PATTERN_NONE || pattern == lastAlerted)
   return;
lastAlerted = pattern;

検出されたパターンの処理

新しいパターンが出現した場合、検出器のパターン配列から直近のPatternResultを取得します。次に、パターンの列挙型を人間が読める名前に変換し、その頂点をログ出力用に整形します。長方形については特別な処理をおこないます。これは3つの頂点しか供給されないためで、完全な座標セットを提示するために4つ目の頂点を近似的に補います。最後に、AlertによるポップアップとPrintによるログ出力を発行し、パターン名、時間、価格、および各頂点の座標を表示します。

int count = detector.m_currentPatterns.Total();
PatternResult *pr = (PatternResult*)detector.m_currentPatterns.At(count - 1);

string name = (pattern == PATTERN_RECTANGLE) ? "Rectangle" :
              (pattern == PATTERN_TRIANGLE_ASCENDING)   ? "Ascending Triangle" :
              (pattern == PATTERN_TRIANGLE_DESCENDING)  ? "Descending Triangle" :
                                                         "Symmetrical Triangle";

Alert("GeometryAnalyzerEA: Detected ", name, " on ", Symbol(), " ", EnumToString(_Period));
Print("GeometryAnalyzerEA: ", name,
      " @", TimeToString(pr.labelTime, TIME_SECONDS),
      " Price=", pr.labelPrice);

ラベルの描画

最後に、パターンで指定された時刻と価格にテキストラベルをチャート上に配置します。ラベルの一意なオブジェクト名は、パターン名とラベル時刻を組み合わせて生成されます。チャートオブジェクト関連の関数を用いてOBJ_TEXTを描画し、そのプロパティとしてテキスト内容、色、フォントサイズ、背景などを設定し、チャート上で明確に視認できるようにします。配置したラベルの名前は記録しておき、次の新しいバーで新たなラベルを描画する前に削除できるようにします。最後に、チャートの再描画を呼び出すことで、即座にレンダリングが反映されます。

   lastLabelName = name + "_" + TimeToString(pr.labelTime, TIME_SECONDS);
   long chartId = ChartID();
   if(ObjectCreate(chartId, lastLabelName, OBJ_TEXT, 0, pr.labelTime, pr.labelPrice))
   {
      ObjectSetString(chartId, lastLabelName, OBJPROP_TEXT,     name);
      ObjectSetInteger(chartId, lastLabelName, OBJPROP_COLOR,    clrOrangeRed);
      ObjectSetInteger(chartId, lastLabelName, OBJPROP_FONTSIZE, 12);
      ObjectSetInteger(chartId, lastLabelName, OBJPROP_BACK,     true);
   }
   ChartRedraw(chartId);
}

テストと結果

EAのパフォーマンスを素早く評価するために、ストラテジーテスターを使って過去データ上での挙動を確認しました。結果は良好で、パターンは正しく検出され、図形も期待どおりに描画されました。さらに、実際のチャート上でEAを稼働させる機会がありましたが、その動作は非常に優れていました。パターンシグナルはリアルタイムの図形描画とともにシームレスにトリガーされ、統合の堅牢さが確認できました。それでは、以下のプレゼンテーションをご覧ください。

ストラテジーテスターの可視化：GeometricAnalyzerEA

以下は、テスト中に上昇三角形が検出された際のログです。

2025.05.20 13:40:54.241 2025.01.14 18:45:00   Alert: GeometryAnalyzerEA: Detected Ascending Triangle on AUDJPY.0 PERIOD_M1
2025.05.20 13:40:54.241 2025.01.14 18:45:00   GeometryAnalyzerEA: Ascending Triangle @14:03:00 Price=97.45599999999999 → Vertices: (1736863200@97.381), (1736863380@97.448), (1736873819@97.912)
2025.05.20 13:40:54.242 2025.01.14 18:46:00   Swing High detected at 2025.01.14 18:43 Price: 97.789

結論

まとめとして、私たちはMQL5を用いて、三角形および長方形の市場構造を自動検出できるシステムを開発することに成功しました。これらの幾何学パターンは、テクニカル分析において長く認識されてきたものであり、特にトレンド継続や反転の可能性があるゾーンを特定する際に、意味のある市場洞察を提供します。上昇三角形や長方形のように明確に定義された形状に注目することで、価格の動きを視覚的かつアルゴリズム的な構造に変換し、実践的かつ信頼性の高い分析が可能であることを示しています。

今回実装したアプローチは、より複雑な分析システムを構築するための強固な基盤となります。GeometricPatternDetectorクラスはモジュール化され再利用可能であり、他のプロジェクトに統合したり、検出精度や柔軟性を向上させるために拡張したりすることが可能です。

本システムはチャート上で形状を正確に描画できますが、構造検出ロジックをさらに洗練させてエッジケースに対応し、パターン認識の精度を向上させる余地は残されています。このプロジェクトは、複雑な市場パターンの検出をアルゴリズム化することで、従来は非常に複雑な手作業を必要としたプロセスを効率化できることを示しています。

この取り組みは継続的な学習の過程でもありました。その中で、MQL5におけるクラスベースの開発が、モジュール性の向上だけでなくコードの再利用やインターフェース抽象化を促進することも実感しました。この設計により、他の開発者や最終ユーザーは低レベルの検出ロジックを理解する必要がなく、高レベルで整理されたインターフェースを使って作業できるようになります。

このようなシステムを構築する者にとって、内部実装を理解することは重要ですが、カプセル化された設計のおかげで、他の人も内部コードを知らなくても機能を利用できます。この構造が整ったことで、必要なクラスを設計するだけで、任意の市場パターンを検出するシステムを自信を持って開発・拡張できるようになりました。

次の論理的な進展としては、確定したパターンに基づく注文実行ロジックを統合することが考えられます。例えば、上昇三角形のブレイクアウト時に買い注文を実行し、直近のスイングポイントにストップロスを置き、パターンの高さを活用して動的に利確ポイントを設定することです。さらに高度な改善としては、出来高やオシレーター指標でパターンを確認したり、マルチタイムフレーム分析で検証したり、高品質なセットアップを優先するランキングシステムを実装したりすることも可能です。

添付ファイル

ファイル	説明
GeometricPatternDetector.mqh	このヘッダファイルには、幾何学パターン検出ロジックのクラスベース実装がすべて含まれています。スイングポイントやパターン結果を格納するデータ構造が定義されており、スイングポイントの検出、ATRを用いた市場感度の計算、三角形および長方形を特定するルーチンも含まれています。EAへのモジュール化統合を想定して設計されています。
GeometryAnalyzerEA.mq5	このEAは、パターン検出ヘッダの実践的な使用例を示します。新しいバーごとにCGeometricPatternDetectorクラスを初期化・更新し、パターン結果を取得して、検出されたパターンをチャート上に視覚的に注釈します。オブジェクト指向のパターン認識をトレーディング戦略に統合する、シンプルで実用的な例となっています。