
Atomic Orbital Search (AOS) algorithm
Contents
Introduction
Modern approaches to solving complex optimization problems increasingly draw inspiration from the principles of physics, especially from the field of quantum mechanics. In this article, we consider the Atomic Orbital Search (AOS) algorithm based on the concepts of the atomic orbital model. The algorithm was proposed by Mahdi Azizi in 2021. This algorithm is a new metaheuristic method. The model describes the behavior of electrons not as strictly defined trajectories, but as wave functions that create probability clouds around the atomic nucleus, thanks to the scientific developments of the outstanding physicist Erwin Schroeder.An atomic orbital, which is the result of a quantum description, is a region where the probability of finding an electron is maximum. In this model, electrons move in imaginary layers that are defined by radii and quantum numbers that reflect energy levels. Layers with higher n values correspond to larger radii and, accordingly, higher energy levels. This behavior of electrons, subject to excitations from interactions with other particles and the influence of photons, creates a dynamic and changing environment, in which electrons can emit or absorb energy as they move between different orbitals.
The AOS algorithm uses these physical principles to model the process of finding solutions to optimization problems. It takes into account probability distributions and interaction dynamics, which allows for efficient exploration of the solution space. In particular, the algorithm considers updates of the positions of candidate solutions (electrons) depending on their energies, which in turn affects the probability of being in certain layers. This allows AOS not only to find optimal solutions, but also to adapt to changes in the environment.
In this paper, we will examine in detail the mathematical model of AOS, including the steps for updating the positions of candidate solutions, as well as the mechanisms that regulate energy absorption and release. Thus, AOS not only represents an interesting approach to optimization, but also opens new horizons for applying quantum principles to computational problems.
Implementation of the algorithm
The AOS algorithm is based on the principles of the atomic orbital model, which considers the emission and absorption of energy by atoms, as well as the configuration of the electron density. At the beginning of the algorithm, several candidate solutions are specified, denoted as X, which are considered as electrons located around the nucleus of an atom. These candidates form a cloud of electrons, and the search space is represented as a spherical volume divided into concentric layers. The solution candidates can be written in general form as follows:
X = [x1, x2 ..., xj ..., xm], where xi is the i th solution candidate, while m is a total number of candidates.
The initial positions of the solution candidates are initialized randomly. Each electron has an energy level determined by an objective function that must be minimized. Thus, electrons with low energy levels correspond to candidates with the best objective function values, and electrons with high energy levels correspond to candidates with the worst values. The vector of values of the objective function is written as:
E = [E1, E2, ..., Ei, ..., Em], where Ei is the energy level of the i th candidate.
The imaginary layers around the core are modeled using a random integer n, which can be from 1 to the number of layers L. The layer with the smallest radius L0 represents the core, and the remaining Li layers are the location of electrons (in AOS, the "core" layer can also contain electrons). The distribution of solution candidates across layers is carried out using the probability density function (PDF), which determines the probability of finding the value of a variable in a given range. The algorithm uses a log-normal distribution, which allows it to simulate the real wave behavior of electrons. The solution candidates are distributed across different layers, where the Xk vector containing the candidates in n layers is set as:
Xk = [Xk1, Xk2, ..., Xki, ..., Xkp], where k is a layer index, p is a number of candidates in the layer.
According to the atomic orbital model, electrons are assumed to be in the ground state energy level. The binding state and binding energy for each layer are calculated as:
BS_k = (1/p) * Σ(Xki),
BE_k = (1/p) * Σ(Eki).
The overall energy level of an atom is defined as:
BS = (1/m) * Σ(Xi),
BE = (1/m) * Σ(Ei).
Electrons can change their position and move between layers under the influence of photons and other interactions. The update of the position of solution candidates in the AOS algorithm is based on the interaction probability, represented by a randomly generated ϕ number, which is distributed in the range [0,1]. If ϕ ≥ PR (photon velocity parameter), then emission or absorption of energy is possible.
If Eki ≥ BEk, then energy emission occurs: Xki[t+1] = Xkit + αi × (βi × LE − γi × BS) / k.
If Eki < BEk, then energy absorption occurs: Xki[t+1] = Xkit + αi × (βi × LEk − γi × BSk).
If ϕ < PR, then displacements into magnetic fields or interactions with other particles are considered: Xki[t+1] = Xkit + ri, where ri is a random increment in the range from min to max of the corresponding optimized parameter of the problem.
In simple terms, in AOS the population of candidate solutions can be figuratively represented as a molecule, where the atoms correspond to coordinates in the search space, and the electrons in these atoms correspond to specific solutions. Thus, if the population consists of 50 candidate solutions, then in each atom there will be 50 electrons distributed across the layers according to the log-normal distribution.
In the description of the algorithm, the author does not indicate how the diameter of the atom outer layer is determined, implying that the atom nucleus is located in the center in relation to the layers. This means that the atom, together with the layers, moves within the given boundaries of the problem. To give the algorithm greater flexibility, we agree that the diameter of the outer layer will correspond to the [min; max] range for the corresponding coordinate in the search space, and the center of the atomic nucleus will be located at the point of the best global solution for the given coordinate. Visually, the model of an atom in AOS can be represented in Figure 1.
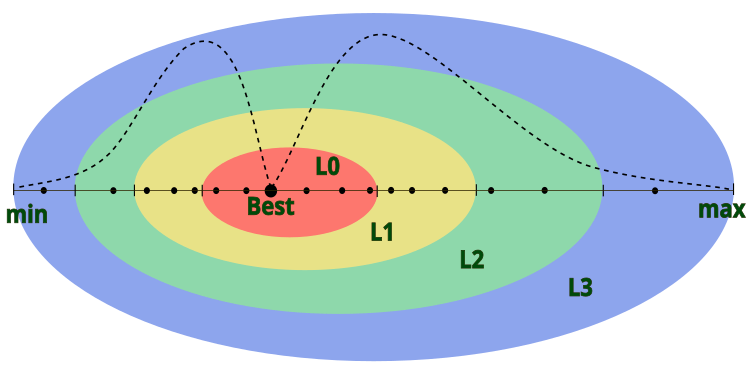
Figure 1. Model of an atom in the AOS algorithm, where the dots represent electrons and the dotted line represents the log-normal distribution of electrons
Pseudocode of the Atomic Orbital Search (AOS) algorithm:
1. Initialization
1.1 Initial positions (Xi)
A population of m candidate solutions is created
Each candidate is assigned a random position in the search space.
1.2 Calculating the initial fitness (Ei)
For each candidate, the value of the objective function is calculated
This value represents the energy of the particle.
The lower the energy, the better the solution.
1.3 Determining the atom parameters
BS (Binding State) is the state of the atom binding, represents the current average position of all particles
BE (Binding Energy) represents the average energy of all particles
LE (Lowest Energy) is a particle with the lowest energy (best solution)
2. Creating a layer structure
2.1 Generating a random number of layers [1; n] for each atom
The number of imaginary orbitals is determined
Each orbital represents a level of search with different intensity.
2.2 Particle distribution
Particles are distributed into layers according to the probability density function (PDF)
The inner layers usually contain the best solutions.
The outer layers are used to explore space.
2.3 Search process for each layer (k)
3.1 Layer parameters
BSk is the connection state for a specific layer
BEk - binding energy of the layer
LEk is the particle with the lowest energy in the layer
3.2 Updating particle positions
For each i particle in k layer:
3.3 Generating control parameters:
φ: define the movement type
α: scaling factor
β: coefficient of attraction to the best solution
γ: coefficient of repulsion from the mean state
PR: probability of photon movement
3.4 Select movement type:
if φ ≥ PR:
if Eki ≥ BEk:
// Global research
Xi[t+1] = Xit + αi × (βi × LE - γi × BS) / k
otherwise:
// Local research
Xi[t+1] = Xit + αi × (βi × LEk - γi × BSk)
otherwise:
// Random movement
Xki[t+1] = Xkit + ri
4. Fitness calculation (Ei)
5. Updating global settings
6. Repeat from 1.3 until the stop criterion is met
To calculate the probability of electron distribution around the nucleus (the best solution), one can use number generation for different distributions. The author prefers the log-normal distribution, which requires its implementation in the code. Let's write the generator code. For the algorithm, it is necessary to make not just a log-normal distribution, but one shifted asymmetrically relative to the center (core), as shown in Figure 1. We implement the LognormalDistribution function in the collection of functions library for optimization algorithms, which generates a random number distributed according to the log-normal law within the given boundaries with a bias.
The function takes the following parameters:
1. center - central value of the distribution.
2. min_value - minimum value that can be generated.
3. max_value - maximum value that can be generated.
4. peakDisplCoeff - coefficient of peak displacement relative to the distribution center (default is 0.2).
Function description:
1. Checking boundaries:
If min_value is greater than or equal to max_value, the function returns max_value.
If max_value is less than or equal to min_value, the function returns min_value.
2. The random number is generated in the range from 0 to 1.
3. Center adjustment:
If center is less than min_value, it is set to min_value, and random is set to 1.
If center exceeds max_value, it is set to max_value, and random is set to 0.
4. Calculate the peak_left and peak_right values, which determine the position of the distribution peaks.
5. Generating a value:
If random is less than 0.5, the calculation is performed for the left part of the distribution:
Calculate the mu_left and sigma_left parameters.
Generate random numbers u1 and u2 for the Box-Muller method.
Apply Box-Muller method to obtain a normally distributed z value.
The result for the left side is calculated.
If random is greater than or equal to 0.5, a similar process is performed for the right side of the distribution using the mu_right and sigma_right parameters.
6. If the generated result value goes beyond min_value and max_value, the RNDfromCI function is called to "throw" the value into the acceptable range, thereby preventing the accumulation of probabilities at the boundaries of the generated random numbers.
//------------------------------------------------------------------------------ //The lognormal distribution of the species: min|------P---C---P------|max double C_AO_Utilities :: LognormalDistribution (double center, double min_value, double max_value, double peakDisplCoeff = 0.2) { // Check the right border if (min_value >= max_value) { return max_value; } // Check the left border if (max_value <= min_value) { return min_value; } // Generate a random number from 0 to 1 double random = MathRand () / 32767.0; // Correction of the center if it goes beyond the boundaries if (center < min_value) { center = min_value; random = 1; } if (center > max_value) { center = max_value; random = 0; } // Calculate the position of the peaks double peak_left = center - (center - min_value) * peakDisplCoeff; double peak_right = center + (max_value - center) * peakDisplCoeff; double result = 0.0; if (random < 0.5) // Left side of the distribution { // Calculate parameters for the left side double diff_center_peak = MathMax (center - peak_left, DBL_EPSILON); double diff_center_min = MathMax (center - min_value, DBL_EPSILON); double mu_left = MathLog (diff_center_peak); double sigma_left = MathSqrt (2.0 * MathLog (MathMax (diff_center_min / diff_center_peak, DBL_EPSILON)) / 9.0); // Generate random numbers for the Box-Muller method double u1 = MathRand () / 32767.0; double u2 = MathRand () / 32767.0; // Protection against null values u1 = MathMax (u1, DBL_EPSILON); // Application of the Box-Muller method double z = MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2); // Calculate the result for the left side result = center - MathExp (mu_left + sigma_left * z); } else // Right side of the distribution { // Calculate parameters for the right side double diff_peak_center = MathMax (peak_right - center, DBL_EPSILON); double diff_max_center = MathMax (max_value - center, DBL_EPSILON); double mu_right = MathLog (diff_peak_center); double sigma_right = MathSqrt (2.0 * MathLog (MathMax (diff_max_center / diff_peak_center, DBL_EPSILON)) / 9.0); // Generate random numbers for the Box-Muller method double u1 = MathRand () / 32767.0; double u2 = MathRand () / 32767.0; // Protection against null values u1 = MathMax (u1, DBL_EPSILON); // Application of the Box-Muller method double z = MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2); // Calculate the result for the right side result = center + MathExp (mu_right + sigma_right * z); } // Check and correct the result if it goes beyond the limits if (result < min_value || result > max_value) return RNDfromCI (min_value, max_value); return result; }
Let's write a script to visually check the resulting distribution. This is what the test script does (we will not provide the rest of the code - the class on working with canvas for the test stand can be found in the article archive):
1. Create the Canvas object to draw graphics.
2. Initialize canvas parameters: W width, H height and O indents.
3. Create CountL and CountR arrays to count the values to the left and right of the Inp_P input initialized by zeros.
4. Create a graphical element (canvas) with specified dimensions and background color.
The log-normal distribution describes random variables whose logarithm has a normal distribution. In the code, it is used to generate values visualized on the graph.
5. In the for loop, generate N values using the U.LognormalDistribution() function. Each value is compared to Inp_P: if less, the CountL[i] counter is increased, if more - CountR[i].
6. Before generation, CountL and CountR are initialized by zeros.
7. The minimum and maximum values in the arrays are calculated to determine the range of the graphs.
8. Coordinates for drawing graphs are calculated, including the canvas center and the steps for the left and right parts.
9. Dots are drawn on the canvas representing the number of values in the ranges, with the color determined by the occurrence frequency.
10. The canvas is updated to reflect the changes.
// Function called at startup void OnStart () { CCanvas Canvas; // Object for handling graphics (canvas) // Canvas parameters int W = 750; // Canvas width int H = 400; // Canvas height int O = 10; // Margins from canvas borders // Arrays for storing count values int CountL []; // Count values to the left of the input int CountR []; // Count values to the right of the input // Initialize arrays ArrayResize (CountL, Size_P); // Resize the CountL array ArrayInitialize (CountL, 0); // Initialize the CountL array with zeros ArrayResize (CountR, Size_P); // Resize the CountR array ArrayInitialize (CountR, 0); // Initialize the CountR array with zeros // Create a canvas string canvasName = "Test_Probability_Distribution_Canvas"; // Canvas name if (!Canvas.CreateBitmapLabel(canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW)) { Print ("Error creating Canvas: ", GetLastError()); // Display an error if creation fails return; } // Set up canvas properties ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false); // Make canvas visible ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true); // Make canvas selectable // Clear the canvas and draw the border Canvas.Erase (COLOR2RGB(clrWhite)); // Fill with white color Canvas.Rectangle (1, 1, W - 1, H - 1, COLOR2RGB(clrBlack)); // Draw a black frame int ind = 0; // Index for counting double X = 0.0; // Variable for storing values // Main loop for generating values for (int i = 0; i < CNT_P; i++) { // Generate log-normal distribution X = U.LognormalDistribution (Inp_P, Min_P, Max_P, PeakDisplCoeff_P); // Determine which side of the input parameter the value falls on if (X < Inp_P) { // Calculate the index for the left part ind = (int) U.Scale(X, Min_P, Inp_P, 0, Size_P, true); if (ind >= Size_P) ind = Size_P - 1; // Limit the index if (ind < 0) ind = 0; // Limit the index CountL [ind] += 1; // Increment the counter for the left side } else { // Calculate the index for the right side ind = (int) U.Scale (X, Inp_P, Max_P, 0, Size_P, false); if (ind >= Size_P) ind = Size_P - 1; // Limit the index if (ind < 0) ind = 0; // Limit the index CountR [ind] += 1; // Increment the counter for the right side } } // Define minimum and maximum values for the graph int minCNT = CNT_P; // Initial value for the minimum counter int maxCNT = 0; // Initial value for the max counter // Finding minimum and maximum values in counters for (int i = 0; i < Size_P; i++) { if (CountL [i] > maxCNT) maxCNT = CountL [i]; // Update the max value for the left side if (CountR [i] > maxCNT) maxCNT = CountR [i]; // Update the max value for the right side if (CountL [i] < minCNT) minCNT = CountL [i]; // Update the min value for the left side if (CountR [i] < minCNT) minCNT = CountR [i]; // Update the minimum value for the right side } // Variables for drawing graphs int x = 0.0; // X coordinate int y = 0.0; // Y coordinate color clrF; // Color int centre = 0; // Canvas center int stepL = 0; // Left side step int stH_L = 0; // Left side height int stepR = 0; // Right side step int stH_R = 0; // Right side height // Determine the center of the canvas centre = (int) U.Scale(Inp_P, Min_P, Max_P, O, W - O - 1, false); // Calculate steps and heights for the left side stepL = (centre - O) / Size_P; stH_L = stepL / 2; if (stH_L == 0) stH_L = 1; // Make sure the height is not 0 // Calculate steps and heights for the right side stepR = (W - O - centre) / Size_P; stH_R = stepR / 2; if (stH_R == 0) stH_R = 1; // Make sure the height is not 0 // Draw graphs for left and right parts for (int i = 0; i < Size_P; i++) { // Draw for the left side x = (int) U.Scale (i, 0, Size_P - 1, O, centre - stH_L, true); // Calculate the X coordinate y = (int) U.Scale (CountL [i], 0, maxCNT, O, H - O - 1, true); // Calculate the Y coordinate clrF = DoubleToColor(CountL [i], minCNT, maxCNT, 0, 255); // Define color by value // Draw dots for the left side Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); // Draw a small circle Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); // Draw a larger circle // Draw for the right side x = (int) U.Scale (i, 0, Size_P - 1, centre + stH_R, W - O - 1, false); // Calculate the X coordinate y = (int) U.Scale (CountR[i], 0, maxCNT, O, H - O - 1, true); // Calculate the Y coordinate clrF = DoubleToColor (CountR [i], minCNT, maxCNT, 0, 255); // Define color by value // Draw dots for the right side Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); // Draw a small circle Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); // Draw a larger circle } Canvas.Update (); // Update the canvas to reflect the changes}
Let's run the script and get a picture on the chart as in Figure 2.
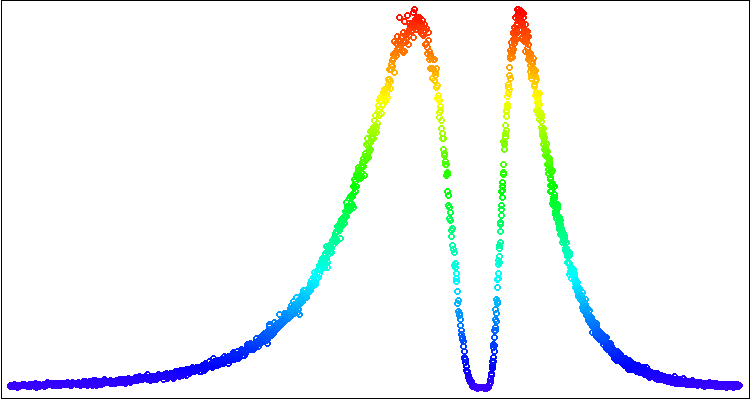
Figure 2. Visualizing asymmetric log-normal distribution plot using the standard Canvas library
After we have examined in detail the theory of all stages of the algorithm, let's move directly to the code implementation. While the AOS algorithm is a minimization method for the problem, we will adjust the logic so that it works for maximization. Let's implement the S_Layer structure, which will simulate the atomic layer and contain information about the number of particles located in this layer. It will include both the numeric characteristics and the method for initialization. Structure fields:
- pc — counter of particles located in a given layer of an atom, which allows you to track how many particles (electrons) are in a particular layer.
- BSk — state of connection in the layer, reflects the level of interaction between particles in the layer.
- BEk — binding energy in the layer, shows how strongly the particles in the layer are bound to each other.
- LEk — minimum energy in a layer used to determine the lowest energy level that can be achieved by particles in a given particular layer.
The Init method is intended to initialize the structure fields with default values and allows us to easily reset the layer state multiple times if necessary.
//—————————————————————————————————————————————————————————————————————————————— struct S_Layer { int pc; // particle counter double BSk; // connection state double BEk; // binding energy double LEk; // minimum energy void Init () { pc = 0; BSk = 0.0; BEk = 0.0; LEk = 0.0; } }; //——————————————————————————————————————————————————————————————————————————————
Next, let's look at the S_Atom structure and its Init method. S_Atom is a structure that represents an atom consisting of several layers. Each layer is simulated using the layers [] array of the S_Layer structure described earlier. Structure fields:
- Init — method for initializing an array of atomic layers, as well as initializing each layer in this array.
- layersNumb — integer parameter specifying the number of layers that will be created for a given atom.
//—————————————————————————————————————————————————————————————————————————————— struct S_Atom { S_Layer layers []; // array of atom layers void Init (int layersNumb) { ArrayResize (layers, layersNumb); for (int i = 0; i < layersNumb; i++) layers [i].Init (); } }; //——————————————————————————————————————————————————————————————————————————————
The next structure S_Electron and its Init method. The structure is an electron, a member of the solution population, which contains information about its position in the corresponding layer of the atom. layerID [] fields is an array of integers, which stores the IDs of the layers the electron belongs to. Each ID corresponds to a specific layer in the atom, allowing us to track what level the electron is on.
//—————————————————————————————————————————————————————————————————————————————— struct S_Electron { int layerID []; // array of layer IDs for the electron void Init (int coords) { ArrayResize (layerID, coords); } }; //——————————————————————————————————————————————————————————————————————————————
The C_AO_AOS AOS class algorithm inherits from the base C_AO class and implies the presence of a common functionality associated with atomic orbits.
Class parameters:
- popSize — population size in the algorithm.
- maxLayers — maximum number of layers that can be used in an atomic model.
- photonEmissions — number of photon emissions that will be used in the optimization process.
- PR — photon transition coefficient, determines the probability of transition between states.
- peakPosition — peak position in the log-normal distribution.
Class methods:
1. SetParams () — set the algorithm parameters by reading values from the params array.
2. Init () — initialize the algorithm with the given search parameters: minimum and maximum ranges, search step and number of epochs.
3. Moving () — method for moving particles in the search space.
4. Revision () — the method is responsible for revising the best solutions found during the optimization.
Class private fields:
- atomStage — current stage of the atom processes.
- currentLayers [] — current number of layers for each atom (at each epoch, the number of layers in each atom is a random number in the range [1; maxLayers]).
- S_Atom atoms [] — array of atoms whose size corresponds to the number of coordinates used in the algorithm.
- S_Electron electrons [] — array of electrons corresponding to the population size.
- BS [] — states of bindings between electrons throughout the population.
Private class methods:
1. GetOrbitBandID () — get the orbital band ID for the given parameters, such as number of layers and ranges.2. DistributeParticles() — method for distributing particles in the search space.
3. LayersGenerationInAtoms () — generate the number of layers in atoms.
4. UpdateElectronsIDs () — update layer IDs for electrons.
5. CalcLayerParams () — calculate the parameters of layers and includes the determination of energy levels and bonds.
6. UpdateElectrons () — update the position of electrons.
//—————————————————————————————————————————————————————————————————————————————— // Class implementing the atomic optimization algorithm (Atomic Orbital Search) class C_AO_AOS : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_AOS () { } C_AO_AOS () { ao_name = "AOS"; ao_desc = "Atomic Orbital Search"; ao_link = "https://www.mql5.com/en/articles/16276"; popSize = 50; // population size maxLayers = 5; // maximum number of layers photonEmissions = 1; // number of photon emissions PR = 0.1; // photon transition coefficient peakPosition = 0.05; // peak position in the log-normal distribution ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "maxLayers"; params [1].val = maxLayers; params [2].name = "photonEmissions"; params [2].val = photonEmissions; params [3].name = "photonRate"; params [3].val = PR; params [4].name = "peakPsition"; params [4].val = peakPosition; } // Setting algorithm parameters void SetParams () { popSize = (int)params [0].val; maxLayers = (int)params [1].val; photonEmissions = (int)params [2].val; PR = params [3].val; peakPosition = params [4].val; } // Initialization of the algorithm with the given search parameters bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Method of moving particles void Revision (); // Method of revising the best solutions //---------------------------------------------------------------------------- int maxLayers; // maximum number of layers int photonEmissions; // number of photon emissions double PR; // photon transition coefficient double peakPosition; // peak position in the log-normal distribution private: //------------------------------------------------------------------- int atomStage; // current stage of the atom int currentLayers []; // current number of layers for the corresponding atom (coordinates) S_Atom atoms []; // atoms with their size corresponding to the number of coordinates S_Electron electrons []; // electrons corresponding to the population size double BS []; // connection states // Get orbital band for given parameters int GetOrbitBandID (int layersNumb, double min, double max, double center, double p); // Distribution of particles in the search space void DistributeParticles (); // Generate layers in atoms void LayersGenerationInAtoms (); // Update electron IDs void UpdateElectronsIDs (); // Calculate layer parameters void CalcLayerParams (); // Update electron positions void UpdateElectrons (); }; //——————————————————————————————————————————————————————————————————————————————
Let's see what happens in the Init method of the AOS algorithm class.
1. Standard initialization: The method starts by calling StandardInit and performs common initialization steps such as setting ranges for coordinates.
2. Initialization of variables:
- atomStage — set to 0, which means that the algorithm starts from the initial stage.
- ArrayResize (currentLayers, coords) resizes the currentLayers array according to the number of coords coordinates.
- ArrayResize (atoms, coords) resizes the atoms array creating a separate object for each atom (coordinate). For each atom, the Init (maxLayers) method is called, which initializes it with the maximum number of layers.
- ArrayResize (electrons, popSize) resizes the electrons array according to the popSize population size. The layerID array is created for each electron. The array corresponds to the number of coordinates.
- ArrayResize (BS, coords) changes the BS array size, which stores states for each coordinate.
4. If all initialization operations are successful, the method returns true.
//—————————————————————————————————————————————————————————————————————————————— // Initialize the algorithm bool C_AO_AOS::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- atomStage = 0; ArrayResize (currentLayers, coords); ArrayResize (atoms, coords); for (int i = 0; i < coords; i++) atoms [i].Init (maxLayers); ArrayResize (electrons, popSize); for (int i = 0; i < popSize; i++) ArrayResize (electrons [i].layerID, coords); ArrayResize (BS, coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Particle displacement method. Let's describe the Moving method:
1. Initial random positioning:
- If the revision variable is equal to false, this means that the algorithm has not yet started its work. In this case, random positioning of particles occurs.
- Next, the nested for loop iterates over all the electrons (population size) and generates a random value using the u.RNDfromCI method for each coordinate. The method takes its value from the range specified by rangeMin and rangeMax. This value is then adjusted using the u.SeInDiSp, which sets the value according to the specified 'step'.
2. Execution of the corresponding stage of evolution of atoms:
- If revision is true, this means that the algorithm has already been initialized and its main stages can be executed. Depending on the current stage of atomStage, different methods are called:
- If atomStage is 0, DistributeParticles () is called. It is responsible for the distribution of particles in space in accordance with the asymmetric log-normal distribution.
- Otherwise, methods are called that generate layers in atoms, update electron IDs, calculate layer parameters, and update electron positions.
3. After completing all the necessary operations, atomStage is increased by 1. If atomStage exceeds the value of photonEmissions, it resets to 0, which allows the algorithm stages to be repeated cyclically.
//—————————————————————————————————————————————————————————————————————————————— // Particle displacement method void C_AO_AOS::Moving () { // Initial random positioning if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Execute the corresponding stage of the algorithm if (atomStage == 0) { DistributeParticles (); } else { LayersGenerationInAtoms (); UpdateElectronsIDs (); CalcLayerParams (); UpdateElectrons (); } // Proceed to the next stage atomStage++; if (atomStage > photonEmissions) atomStage = 0; } //——————————————————————————————————————————————————————————————————————————————
Let's move on to the analysis of specific methods. The GetOrbitBandID method of the C_AO_AOS class is designed to determine the orbital band for a particle based on its position relative to a given center. It takes the number of layers, the min and max values, the center and position of the p particle.
1. Calculates the width of the bands to the left and right of the center.
2. If the position of the p particle is less than the center, then search which of the left bands it is located in.
3. If there are more, it searches in the right bands.
4. If it is equal to the center, return the number of 0 (the center).
Thus, the function returns the index of the corresponding orbital band for the given position.
//—————————————————————————————————————————————————————————————————————————————— // Determining the orbital band for a particle int C_AO_AOS::GetOrbitBandID (int layersNumb, double min, double max, double center, double p) { // Calculate the width of the bands to the left and right of the center double leftWidth = (center - min) / layersNumb; double rightWidth = (max - center) / layersNumb; // Define the band index if (p < center) { // The object is located to the left of the center for (int i = 1; i <= layersNumb; i++) { if (p >= center - i * leftWidth) return i - 1; } return layersNumb - 1; // If the object is in the leftmost band } else if (p > center) { // The object is located to the right of the center for (int i = 1; i <= layersNumb; i++) { if (p <= center + i * rightWidth) return i - 1; } return layersNumb - 1; // If the object is in the far right band } else { // The object is in the center return 0; } } //——————————————————————————————————————————————————————————————————————————————
The DistributeParticles method of the C_AO_AOS class is responsible for the distribution of particles in the search space. The method distributes particles in the search space using a log-normal distribution.
For each particle (in a loop by popSize) and for each coordinate (in a loop by "coords"):
- Generates a particle position using a log-normal distribution given the parameters (cB, rangeMin, rangeMax, peakPosition).
- Applies the SeInDiSp function to adjust the particle position value within a given range taking into account the step.
//—————————————————————————————————————————————————————————————————————————————— // Distribution of particles in the search space void C_AO_AOS::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Use log-normal distribution to position particles a [i].c [c] = u.LognormalDistribution (cB [c], rangeMin [c], rangeMax [c], peakPosition); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
The UpdateElectronsIDs method of the C_AO_AOS class updates the layer IDs for electrons depending on their coordinates and specified parameters.
//—————————————————————————————————————————————————————————————————————————————— // Update layer IDs for each electron void C_AO_AOS::UpdateElectronsIDs () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { electrons [i].layerID [c] = GetOrbitBandID (currentLayers [c], rangeMin [c], rangeMax [c], cB [c], a [i].c [c]); } } } //——————————————————————————————————————————————————————————————————————————————
The CalcLayerParams method of the C_AO_AOS class is designed to calculate parameters for each layer of atoms in the system. The main components of the method:
1. Variable initialization: energy is a variable for storing the maximum energy that will be updated when handling the electron.
2. The loop goes through all atoms (coordinates) in the system. The c index points to the current atom.
3. For each atom, the Init method is called, which initializes the parameters for the maximum number of layers specified by the maxLayers variable.
4. Layer loop: the inner loop that iterates over all layers associated with the current atom, currentLayers [c] indicates the number of layers for the c atom.
5. Electron handling: Another internal loop iterates over all the e electrons in the population where we check whether the current electron belongs to the L layer for the c atom.
6. Updating layer parameters:
- If the electron belongs to a layer, the particle counter in the layer is incremented.
- BEk energy values and BSk states are updated for the layer depending on the electron properties.
- If the electron energy a [e].f exceeds the current maximum energy level, then the maximum energy values and LEk states are updates.
7. Calculating average values for a layer: if the pc particle counter is not equal to zero, average values for energy and state are calculated.
8. Calculation of the general state of bindings: The state of bonds for each atom is calculated similarly for each BS atom, but for the population of electrons as a whole.
//—————————————————————————————————————————————————————————————————————————————— // Calculate parameters for each layer void C_AO_AOS::CalcLayerParams () { double energy; // Handle each coordinate (atom) for (int c = 0; c < coords; c++) { atoms [c].Init (maxLayers); // Handle each layer for (int L = 0; L < currentLayers [c]; L++) { energy = -DBL_MAX; // Handle each electron for (int e = 0; e < popSize; e++) { if (electrons [e].layerID [c] == L) { atoms [c].layers [L].pc++; atoms [c].layers [L].BEk = a [e].f; atoms [c].layers [L].BSk = a [e].c [c]; if (a [e].f > energy) { energy = a [e].f; atoms [c].layers [L].LEk = a [e].c [c]; } } } // Calculate average values for the layer if (atoms [c].layers [L].pc != 0) { atoms [c].layers [L].BEk /= atoms [c].layers [L].pc; atoms [c].layers [L].BSk /= atoms [c].layers [L].pc; } } } // Calculate the general state of connections ArrayInitialize (BS, 0); for (int c = 0; c < coords; c++) { for (int e = 0; e < popSize; e++) { BS [c] += a [e].c [c]; } BS [c] /= popSize; } } //——————————————————————————————————————————————————————————————————————————————
The UpdateElectrons method of the C_AO_AOS class is responsible for updating the position of electrons in the system.
1. Initialization of parameters: the speed coefficients, the weights of the best solution, the weights of the average state and the transition probability are determined.
2. For each particle and each coordinate:
- A random probability φ is generated.
- If φ is less than the PR threshold value, a random scatter occurs and a new position is chosen randomly, within a given range.
- Otherwise:
- The lID layer ID is obtained for the current particle.
- Random values for the ratios are generated.
- If the current energy of a particle is less than the average energy of the layer, movement towards the global optimum occurs.
- If not, there is a movement towards the local optimum of the layer.
- At the end, the new position is limited within the specified range taking into account the step.
//—————————————————————————————————————————————————————————————————————————————— // Update electron positions void C_AO_AOS::UpdateElectrons () { double α; // speed coefficient double β; // best solution weight coefficient double γ; // average state weight coefficient double φ; // transition probability double newPos; // new position double LE; // best energy double BSk; // connection state int lID; // layer ID // Handle each particle for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Random scatter newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); β = u.RNDprobab (); γ = u.RNDprobab (); // If the current particle energy is less than the average layer energy if (a [p].f < atoms [c].layers [lID].BEk) { // Moving towards the global optimum---------------------------- LE = cB [c]; newPos = a [p].c [c]+ α * (β * LE - γ * BS [c]) / currentLayers [c]; } else { // Movement towards the local optimum of the layer LE = atoms [c].layers [lID].LEk; BSk = atoms [c].layers [lID].BSk; newPos = a [p].c [c] + α * (β * LE - γ * BSk); } } // Limiting the new position within the search range taking into account the step a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
The Revision method of the C_AO_AOS class is designed to review and update the best solutions (or optimal states) during the iteration. Method steps:
1. Initialization of the bestIndex variable, which will be used to store the index of the best solution.
2. Finding the best solution. Condition for checking whether the function value (or estimate) of the current a [i].f solution exceeds the current value of the fB global best solution. If this condition is true, then the value of the global best solution is updated to the current value and the index of the current solution is saved as the best.
3. If the best solution is found, then the coordinates of the a[bestIndex].c best solution are copied to the cB array.
//—————————————————————————————————————————————————————————————————————————————— // Method of revising the best solutions void C_AO_AOS::Revision () { int bestIndex = -1; // Find the best solution in the current iteration for (int i = 0; i < popSize; i++) { // Update the global best solution if (a [i].f > fB) { fB = a [i].f; bestIndex = i; } } // Update the best coordinates if a better solution is found if (bestIndex != -1) ArrayCopy (cB, a [bestIndex].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Test results
Let's run the test stand and get the following results of AOS operation:
AOS|Atomic Orbital Search|50.0|5.0|1.0|0.1|0.05|
=============================
5 Hilly's; Func runs: 10000; result: 0.6521321213930082
25 Hilly's; Func runs: 10000; result: 0.39883708808831186
500 Hilly's; Func runs: 10000; result: 0.2602779698842558
=============================
5 Forest's; Func runs: 10000; result: 0.5165008091396371
25 Forest's; Func runs: 10000; result: 0.30233740723010416
500 Forest's; Func runs: 10000; result: 0.1926906342754638
=============================
5 Megacity's; Func runs: 10000; result: 0.39384615384615385
25 Megacity's; Func runs: 10000; result: 0.1892307692307692
500 Megacity's; Func runs: 10000; result: 0.09903076923077013
=============================
All score: 3.00488 (33.39%)
In the visualization of the AOS algorithm, one can notice interesting behavior, characteristic areas of "clumping" in the orbitals of atoms, but the accuracy of convergence is not very high.
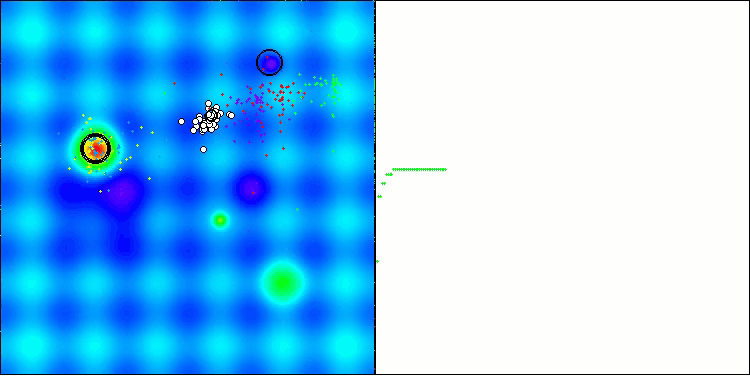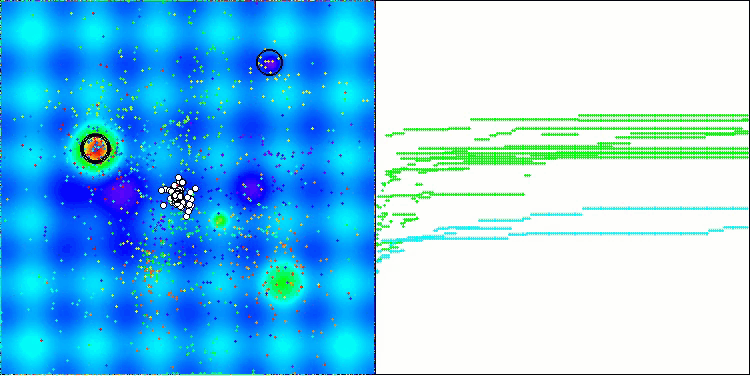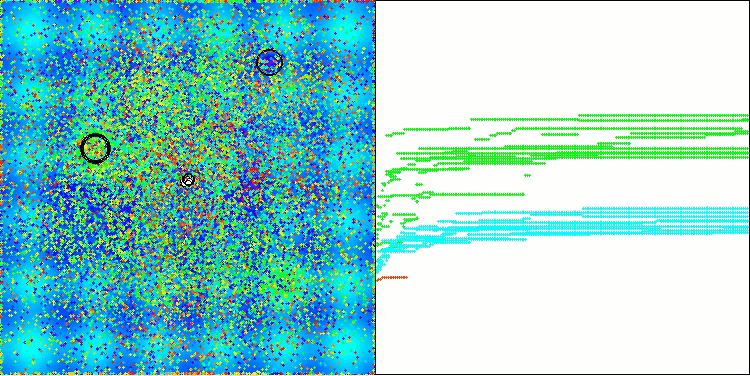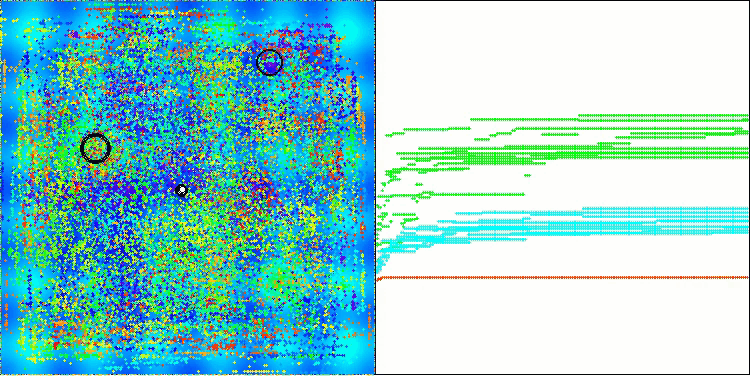
AOS on the Hilly test function
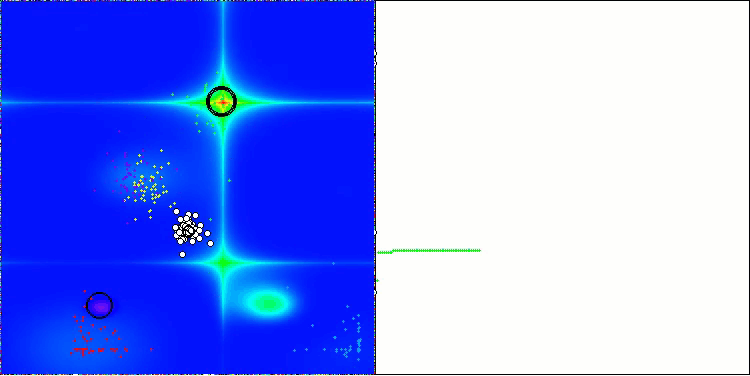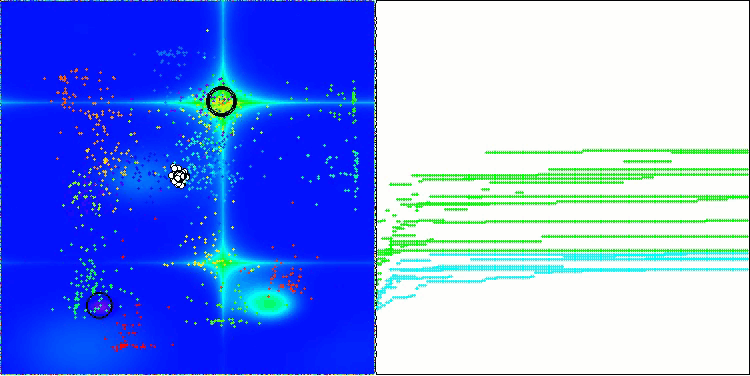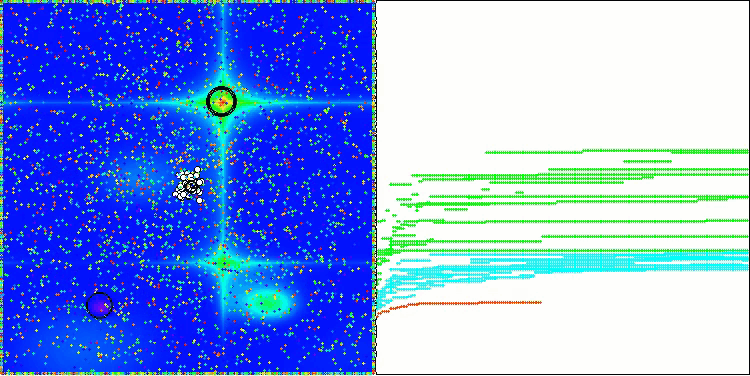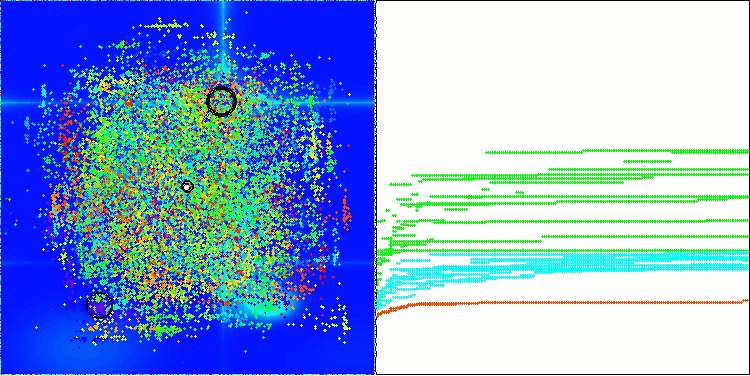
AOS on the Forest test function
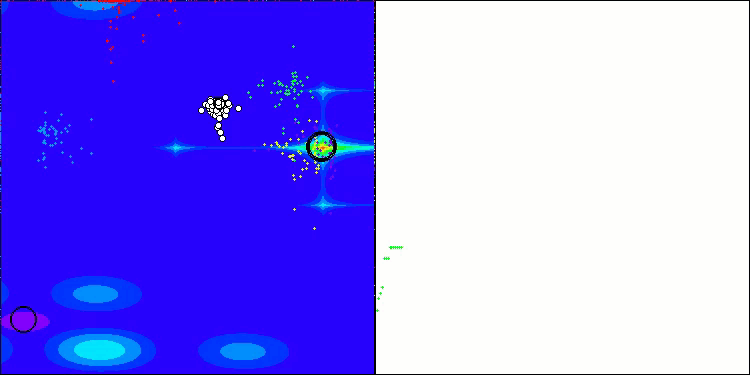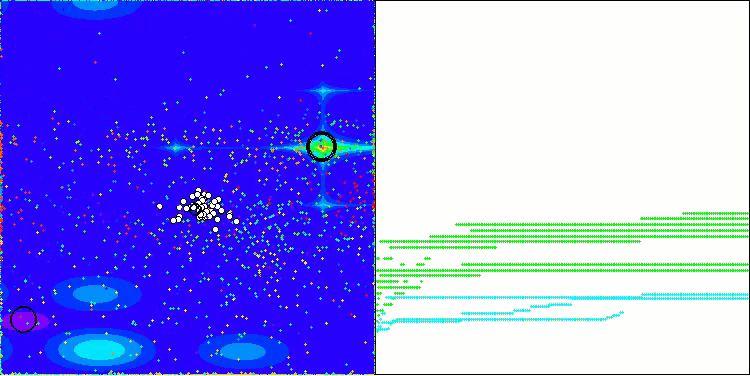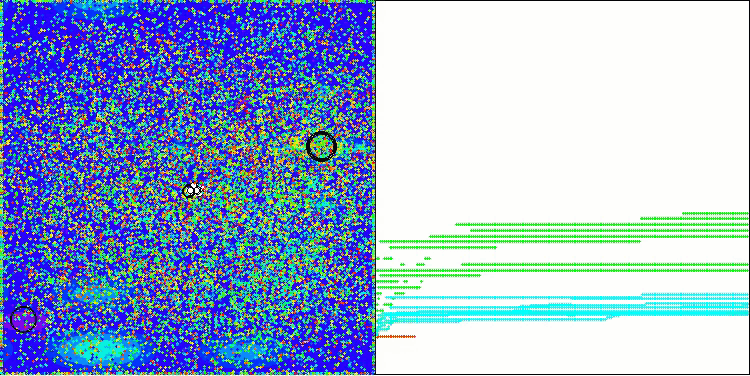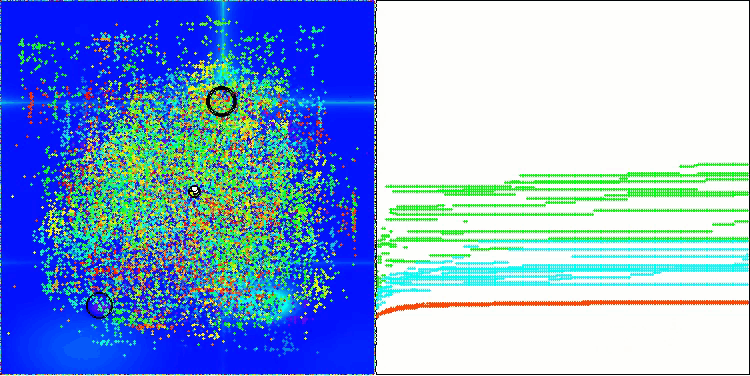
AOS on the Megacity test function
Based on the test results, the AOS algorithm was ranked 39 th in the rating table.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration ptimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 12 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 13 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 14 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 15 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 16 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 17 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 18 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 19 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 20 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 21 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 22 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 23 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 24 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 25 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 26 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 27 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 28 | ABHA | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 29 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 30 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 31 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 32 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 33 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 34 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 35 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 36 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 37 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 38 | FAm | firefly algorithm M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 39 | AOS | atomic orbital search | 0.65213 | 0.39884 | 0.26028 | 1.31125 | 0.51650 | 0.30234 | 0.19269 | 1.01153 | 0.39385 | 0.18923 | 0.09903 | 0.68211 | 3.005 | 33.39 |
| 40 | GSA | gravitational search algorithm | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 41 | BFO | bacterial foraging optimization | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 42 | ABC | artificial bee colony | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 43 | BA | bat algorithm | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 44 | AAA | algae adaptive algorithm | 0.50007 | 0.32040 | 0.25525 | 1.07572 | 0.37021 | 0.22284 | 0.16785 | 0.76089 | 0.27846 | 0.14800 | 0.09755 | 0.52402 | 2.361 | 26.23 |
| 45 | SA | simulated annealing | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
Summary
We have considered an interesting atomic orbital search algorithm that uses innovative approaches to global search and local refinement of results. Thanks to the dynamic orbital layers of atoms, electrons move in a balanced manner in search of a stable atomic state. The algorithm shows limited capabilities on smooth functions, but demonstrates good results when the problem dimension increases, even on the discrete Megacity function.
This algorithm is an example of a promising idea, but its efficiency suffers due to some small but significant nuances. In the next article, we will look at my modification of AOS and analyze what this wonderful orbital search concept is actually capable of.
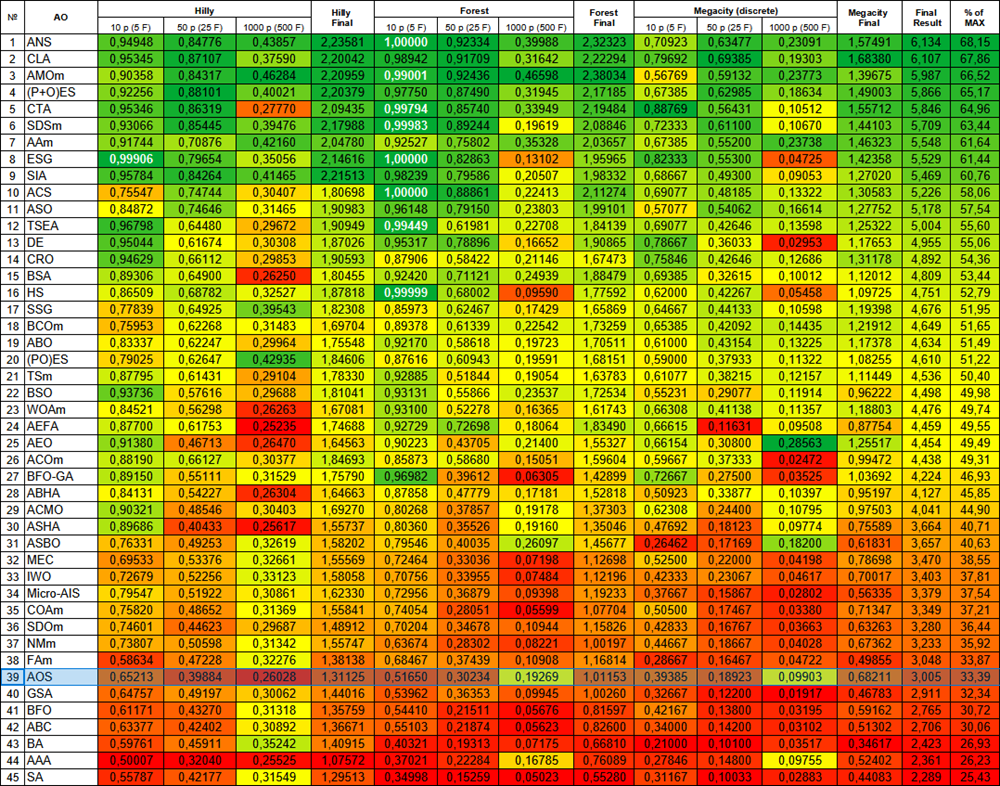
Figure 3. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white
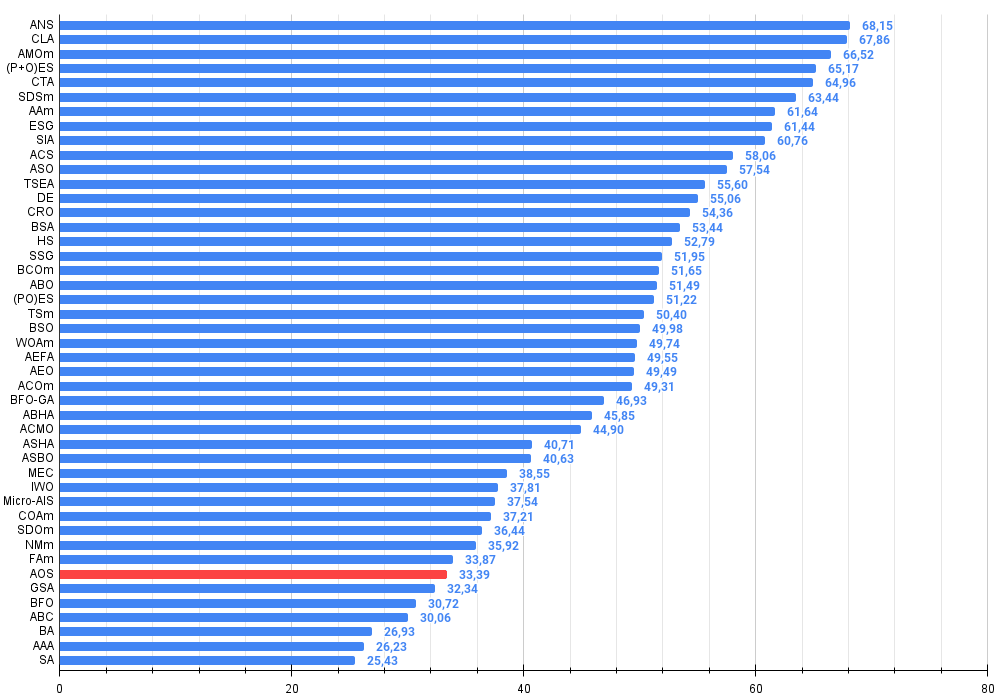
Figure 4. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,
where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)
AOS pros and cons:
Pros:
- A promising basis for algorithm improvements.
- A small number of external parameters.
Cons:
- Slow due to frequent random number generation.
- Quite a complex implementation.
- Low convergence accuracy.
The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.
Programs used in the article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Parent class of population optimization algorithms |
| 2 | #C_AO_enum.mqh | Include | Enumeration of population optimization algorithms |
| 3 | TestFunctions.mqh | Include | Library of test functions |
| 4 | TestStandFunctions.mqh | Include | Test stand function library |
| 5 | Utilities.mqh | Include | Library of auxiliary functions |
| 6 | CalculationTestResults.mqh | Include | Script for calculating results in the comparison table |
| 7 | Testing AOs.mq5 | Script | The unified test stand for all population optimization algorithms |
| 8 | AO_AOS_AtomicOrbitalSearch.mqh | Include | AOS algorithm class |
| 9 | Test_AO_AOS.mq5 | Script | AOS test stand |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/16276
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Installing MetaTrader 5 and Other MetaQuotes Apps on HarmonyOS NEXT
Installing MetaTrader 5 and Other MetaQuotes Apps on HarmonyOS NEXT
 Data Science and ML (Part 44): Forex OHLC Time series Forecasting using Vector Autoregression (VAR)
Data Science and ML (Part 44): Forex OHLC Time series Forecasting using Vector Autoregression (VAR)
 Developing Advanced ICT Trading Systems: Implementing Order Blocks in an Indicator
Developing Advanced ICT Trading Systems: Implementing Order Blocks in an Indicator
 Price Action Analysis Toolkit Development (Part 28): Opening Range Breakout Tool
Price Action Analysis Toolkit Development (Part 28): Opening Range Breakout Tool
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Atomic Orbital Search Algorithm - Atomic Orbital Search (AOS) has been published:
Author: Andrey Dik
This is the whole system, which includes physics, maths, chess, etc.