
Algoritmo de Busca Orbital Atômica — Atomic Orbital Search (AOS)
Conteúdo
Introdução
As abordagens modernas para resolver problemas complexos de otimização têm buscado cada vez mais inspiração nos princípios da física, especialmente na mecânica quântica. Neste artigo, apresentamos o algoritmo AOS (Atomic Orbital Search), que é baseado nos conceitos do modelo orbital atômico. O algoritmo foi proposto por Mahdi Azizi em 2021. Este é um novo método meta-heurístico. O modelo descreve o comportamento dos elétrons não como trajetórias rigidamente definidas, mas como funções de onda que formam nuvens de probabilidade ao redor do núcleo atômico, com base nas descobertas científicas do renomado físico Erwin Schrödinger.A orbital atômica, resultado da descrição quântica, representa a região onde a probabilidade de encontrar um elétron é máxima. Neste modelo, os elétrons se movem em camadas imaginárias, determinadas por raios e números quânticos que refletem os níveis de energia. Camadas com valores mais altos de n correspondem a raios maiores e, portanto, a níveis de energia mais elevados. Esse comportamento dos elétrons, que sofrem excitações devido a interações com outras partículas e ao impacto de fótons, cria um ambiente dinâmico e mutável, no qual os elétrons podem emitir ou absorver energia, movendo-se entre diferentes orbitais.
O algoritmo AOS usa esses princípios físicos para simular o processo de busca por soluções em problemas de otimização. Ele considera distribuições probabilísticas e a dinâmica das interações, o que permite explorar eficientemente o espaço de soluções. Em particular, o algoritmo trata das atualizações das posições dos candidatos a soluções (elétrons) com base em suas energias, o que por sua vez influencia a probabilidade de estarem em determinadas camadas. Isso permite ao AOS não apenas encontrar soluções ótimas, mas também se adaptar a mudanças no ambiente.
Neste artigo, analisamos detalhadamente o modelo matemático do AOS, incluindo as etapas de atualização das posições dos candidatos a soluções, bem como os mecanismos que regulam a absorção e a emissão de energia. Assim, o AOS não apenas representa uma abordagem interessante para a otimização, como também abre novos horizontes para a aplicação de princípios quânticos em tarefas computacionais.
Implementação do algoritmo
O algoritmo AOS é baseado nos princípios do modelo orbital atômico, que considera a emissão e absorção de energia pelos átomos, assim como a configuração da densidade eletrônica. No início da execução do algoritmo, são definidos vários candidatos a soluções, designados como X, que são tratados como elétrons posicionados ao redor do núcleo atômico. Esses candidatos formam uma nuvem eletrônica, e o espaço de busca é representado como um volume esférico dividido em camadas concêntricas. Os candidatos a soluções podem ser representados de forma geral como:
X = [x1, x2 ..., xj ..., xm], onde xi é o i-ésimo candidato a solução, e m é o número total de candidatos.
As posições iniciais dos candidatos a soluções são inicializadas aleatoriamente. Cada elétron possui um nível de energia determinado pela função objetivo, a qual deve ser minimizada. Assim, elétrons com níveis de energia mais baixos correspondem a candidatos com melhores valores da função objetivo, enquanto elétrons com altos níveis de energia estão associados a candidatos com piores valores. O vetor de valores da função objetivo é representado como:
E = [E1, E2, ..., Ei, ..., Em], onde Ei é o nível de energia do i-ésimo candidato.
As camadas imaginárias ao redor do núcleo são modeladas com um número inteiro aleatório n, que pode variar de 1 até o número total de camadas L. A camada com o menor raio, L0, representa o núcleo, e as demais camadas Li representam a localização dos elétrons (no AOS, até mesmo a camada “núcleo” pode conter elétrons). A distribuição dos candidatos a soluções entre as camadas é feita com o uso de uma função densidade de probabilidade (PDF), que determina a chance de um valor da variável estar dentro de um intervalo definido. O algoritmo utiliza uma distribuição lognormal, o que permite simular o comportamento ondulatório real dos elétrons. Os candidatos a soluções são distribuídos entre as diferentes camadas, e o vetor Xk, contendo os candidatos nas n camadas, é descrito como:
Xk = [Xk1, Xk2, ..., Xki, ..., Xkp], onde k é o número da camada, e p é a quantidade de candidatos na camada.
De acordo com o modelo orbital atômico, os elétrons são considerados em seu estado fundamental de nível de energia. O estado de ligação e a energia de ligação para cada camada são calculados como:
BS_k = (1/p) * Σ(Xki),
BE_k = (1/p) * Σ(Eki).
O nível total de energia do átomo é determinado como:
BS = (1/m) * Σ(Xi),
BE = (1/m) * Σ(Ei).
Os elétrons podem alterar sua posição e se mover entre camadas sob a influência de fótons e outras interações. A atualização da posição dos candidatos a soluções no algoritmo AOS ocorre com base na probabilidade de interação, representada por um número ϕ gerado aleatoriamente, distribuído no intervalo [0,1]. Se ϕ ≥ PR (parâmetro de velocidade dos fótons), então é possível ocorrer emissão ou absorção de energia.
Se Eki ≥ BEk, ocorre emissão de energia: Xki[t+1] = Xkit + αi × (βi × LE − γi × BS) / k.
Se Eki < BEk, ocorre absorção de energia: Xki[t+1] = Xkit + αi × (βi × LEk − γi × BSk).
Se ϕ < PR, são considerados deslocamentos em campos magnéticos ou interações com outras partículas: Xki[t+1] = Xkit + ri, onde ri é um incremento aleatório no intervalo de min até max do parâmetro otimizado da tarefa.
Simplificando, no AOS a população de candidatos a soluções pode ser imaginada como uma molécula, onde os átomos correspondem a coordenadas no espaço de busca, e os elétrons nesses átomos representam soluções específicas. Assim, se a população for composta por 50 candidatos a soluções, então em cada átomo haverá, distribuídos em camadas conforme uma distribuição lognormal, 50 elétrons.
Na descrição do algoritmo, o autor não especifica como é determinado o diâmetro da camada externa do átomo, presumindo que o núcleo atômico esteja posicionado no centro em relação às camadas. Isso significa que o átomo, junto com suas camadas, se move dentro dos limites definidos do problema. Para proporcionar maior flexibilidade ao algoritmo, convenciona-se que o diâmetro da camada externa corresponderá ao intervalo [min; max] para a coordenada correspondente no espaço de busca, e o centro do núcleo do átomo estará localizado no ponto da melhor solução global para essa coordenada. Visualmente, o modelo atômico no AOS pode ser representado conforme ilustrado na figura 1.
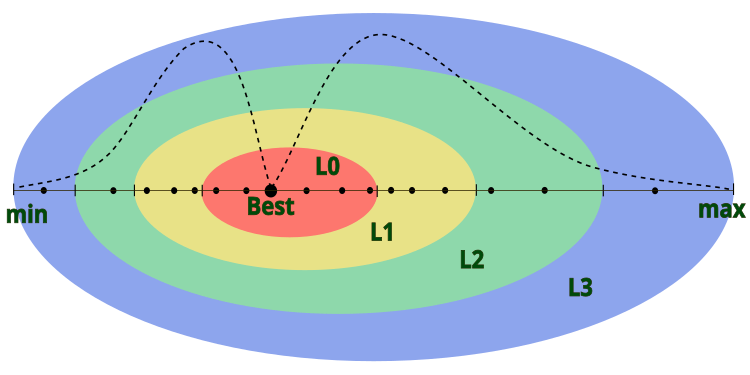
Figura 1. Modelo atômico no algoritmo AOS, onde os pontos representam elétrons e a linha pontilhada indica a distribuição lognormal dos elétrons
Pseudocódigo do algoritmo de busca orbital atômica (AOS):
1. Inicialização
1.1 Posições iniciais (Xi)
Cria-se uma população de m candidatos a soluções
Cada candidato recebe uma posição aleatória no espaço de busca
1.2 Cálculo da aptidão inicial (Ei)
Para cada candidato, calcula-se o valor da função objetivo
Esse valor representa a energia da partícula
Quanto menor a energia, melhor a solução
1.3 Definição dos parâmetros do átomo
BS (Binding State) estado de ligação do átomo, representa a posição média atual de todas as partículas
BE (Binding Energy) energia de ligação, representa a energia média de todas as partículas
LE (Lowest Energy) partícula com a menor energia (melhor solução)
2. Criação da estrutura de camadas
2.1 Geração de uma quantidade aleatória de camadas [1; n] para cada átomo
Define-se a quantidade de orbitais imaginários
Cada orbital representa um nível de busca com intensidade diferente
2.2 Distribuição das partículas
As partículas são distribuídas entre as camadas conforme a função densidade de probabilidade (PDF)
As camadas internas geralmente contêm as melhores soluções
As camadas externas são utilizadas para explorar o espaço
2.3 Processo de busca para cada camada (k)
3.1 Parâmetros da camada
BSk estado de ligação para a camada específica
BEk energia de ligação da camada
LEk partícula com o menor nível de energia na camada
3.2 Atualização das posições das partículas
Para cada partícula i na camada k:
3.3 Geração dos parâmetros de controle:
φ: determina o tipo de movimento
α: coeficiente de escalonamento
β: coeficiente de atração para a melhor solução
γ: coeficiente de repulsão do estado médio
PR: probabilidade de deslocamento por fótons
3.4 Escolha do tipo de movimento:
se φ ≥ PR:
se Eki ≥ BEk:
// Exploração global
Xi[t+1] = Xit + αi × (βi × LE - γi × BS) / k
senão:
// Exploração local
Xi[t+1] = Xit + αi × (βi × LEk - γi × BSk)
senão:
// Deslocamento aleatório
Xki[t+1] = Xkit + ri
4. Cálculo da aptidão (Ei)
5. Atualização dos parâmetros globais
6. Repetir a partir de 1.3 até que o critério de parada seja satisfeito
Para calcular a probabilidade da distribuição dos elétrons ao redor do núcleo (melhor solução), pode-se utilizar a geração de números com diferentes distribuições. O autor prefere a distribuição lognormal, o que exige sua implementação no código. Vamos escrever o código do gerador. Para o algoritmo, não é suficiente utilizar uma distribuição lognormal simples, mas sim uma com deslocamento assimétrico em relação ao centro (núcleo), como mostrado na figura 1. Vamos implementar a função "LognormalDistribution" na biblioteca de funções para algoritmos de otimização, que gera um número aleatório distribuído segundo a lei lognormal dentro de limites definidos com deslocamento.
A função recebe os seguintes parâmetros:
1. center – valor central da distribuição
2. min_value – valor mínimo que pode ser gerado
3. max_value – valor máximo que pode ser gerado
4. peakDisplCoeff – coeficiente de deslocamento do pico em relação ao centro da distribuição (por padrão igual a 0.2)
Descrição do funcionamento da função:
1. Verificação de limites:
Se "min_value" for maior ou igual a "max_value", a função retorna "max_value".
Se "max_value" for menor ou igual a "min_value", a função retorna "min_value".
2. Um número aleatório "random" é gerado no intervalo de 0 a 1.
3. Correção do centro:
Se "center" for menor que "min_value", ele é ajustado para "min_value", e "random" é definido como 1.
Se "center" for maior que "max_value", ele é ajustado para "max_value", e "random" é definido como 0.
4. Calculam-se os valores "peak_left" e "peak_right", que determinam a posição dos picos da distribuição.
5. Geração do valor:
Se "random" for menor que 0.5, executa-se o cálculo para a parte esquerda da distribuição:
Calculam-se os parâmetros "mu_left" e "sigma_left".
Geram-se números aleatórios "u1" e "u2" para o método de Box-Muller.
Aplica-se o método de Box-Muller para obter o valor "z" com distribuição normal.
Calcula-se o resultado para a parte esquerda.
Se "random" for maior ou igual a 0.5, o processo é análogo para a parte direita da distribuição, usando os parâmetros "mu_right" e "sigma_right".
6. Se o valor gerado "result" estiver fora dos limites de "min_value" e "max_value", é chamada a função "RNDfromCI" para “jogar” o valor de volta ao intervalo permitido, evitando assim o acúmulo de probabilidades nas extremidades dos números aleatórios gerados.
//------------------------------------------------------------------------------ //The lognormal distribution of the species: min|------P---C---P------|max double C_AO_Utilities :: LognormalDistribution (double center, double min_value, double max_value, double peakDisplCoeff = 0.2) { // Check the right border if (min_value >= max_value) { return max_value; } // Check the left border if (max_value <= min_value) { return min_value; } // Generate a random number from 0 to 1 double random = MathRand () / 32767.0; // Correction of the center if it goes beyond the boundaries if (center < min_value) { center = min_value; random = 1; } if (center > max_value) { center = max_value; random = 0; } // Calculate the position of the peaks double peak_left = center - (center - min_value) * peakDisplCoeff; double peak_right = center + (max_value - center) * peakDisplCoeff; double result = 0.0; if (random < 0.5) // Left side of the distribution { // Calculate parameters for the left side double diff_center_peak = MathMax (center - peak_left, DBL_EPSILON); double diff_center_min = MathMax (center - min_value, DBL_EPSILON); double mu_left = MathLog (diff_center_peak); double sigma_left = MathSqrt (2.0 * MathLog (MathMax (diff_center_min / diff_center_peak, DBL_EPSILON)) / 9.0); // Generate random numbers for the Box-Muller method double u1 = MathRand () / 32767.0; double u2 = MathRand () / 32767.0; // Protection against null values u1 = MathMax (u1, DBL_EPSILON); // Application of the Box-Muller method double z = MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2); // Calculate the result for the left side result = center - MathExp (mu_left + sigma_left * z); } else // Right side of the distribution { // Calculate parameters for the right side double diff_peak_center = MathMax (peak_right - center, DBL_EPSILON); double diff_max_center = MathMax (max_value - center, DBL_EPSILON); double mu_right = MathLog (diff_peak_center); double sigma_right = MathSqrt (2.0 * MathLog (MathMax (diff_max_center / diff_peak_center, DBL_EPSILON)) / 9.0); // Generate random numbers for the Box-Muller method double u1 = MathRand () / 32767.0; double u2 = MathRand () / 32767.0; // Protection against null values u1 = MathMax (u1, DBL_EPSILON); // Application of the Box-Muller method double z = MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2); // Calculate the result for the right side result = center + MathExp (mu_right + sigma_right * z); } // Check and correct the result if it goes beyond the limits if (result < min_value || result > max_value) return RNDfromCI (min_value, max_value); return result; }
Vamos escrever um script para verificação visual da distribuição obtida. Eis o que o script de verificação faz (o restante do código não será apresentado — a classe para trabalhar com o canvas do ambiente de teste pode ser encontrada no arquivo anexo ao artigo):
1. Cria-se um objeto "Canvas" para desenhar gráficos.
2. Inicializam-se os parâmetros do canvas: largura "W", altura "H" e margens "O".
3. Criam-se os arrays "CountL" e "CountR" para contar os valores à esquerda e à direita do parâmetro de entrada "Inp_P", iniciados com zeros.
4. Cria-se um elemento gráfico (canvas) com dimensões e cor de fundo definidas.
A distribuição lognormal descreve variáveis aleatórias cujo logaritmo possui distribuição normal. No código, ela é usada para gerar valores que são visualizados no gráfico.
5. No laço "for", são gerados "N" valores usando a função "U.LognormalDistribution()". Cada valor é comparado com "Inp_P": se for menor, incrementa-se o contador "CountL[i]", se for maior – "CountR[i]".
6. Antes da geração, os arrays "CountL" e "CountR" são inicializados com zeros.
7. Calculam-se os valores mínimos e máximos nos arrays para determinar a faixa dos gráficos.
8. Calculam-se as coordenadas para desenhar os gráficos, incluindo o centro do canvas e os passos para as partes esquerda e direita.
9. Pontos são desenhados no canvas, representando a quantidade de valores em cada faixa, com a cor determinada pela frequência de ocorrência.
10. O canvas é atualizado para exibir as alterações.
// Function called at startup void OnStart () { CCanvas Canvas; // Object for handling graphics (canvas) // Canvas parameters int W = 750; // Canvas width int H = 400; // Canvas height int O = 10; // Margins from canvas borders // Arrays for storing count values int CountL []; // Count values to the left of the input int CountR []; // Count values to the right of the input // Initialize arrays ArrayResize (CountL, Size_P); // Resize the CountL array ArrayInitialize (CountL, 0); // Initialize the CountL array with zeros ArrayResize (CountR, Size_P); // Resize the CountR array ArrayInitialize (CountR, 0); // Initialize the CountR array with zeros // Create a canvas string canvasName = "Test_Probability_Distribution_Canvas"; // Canvas name if (!Canvas.CreateBitmapLabel(canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW)) { Print ("Error creating Canvas: ", GetLastError()); // Display an error if creation fails return; } // Set up canvas properties ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false); // Make canvas visible ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true); // Make canvas selectable // Clear the canvas and draw the border Canvas.Erase (COLOR2RGB(clrWhite)); // Fill with white color Canvas.Rectangle (1, 1, W - 1, H - 1, COLOR2RGB(clrBlack)); // Draw a black frame int ind = 0; // Index for counting double X = 0.0; // Variable for storing values // Main loop for generating values for (int i = 0; i < CNT_P; i++) { // Generate log-normal distribution X = U.LognormalDistribution (Inp_P, Min_P, Max_P, PeakDisplCoeff_P); // Determine which side of the input parameter the value falls on if (X < Inp_P) { // Calculate the index for the left part ind = (int) U.Scale(X, Min_P, Inp_P, 0, Size_P, true); if (ind >= Size_P) ind = Size_P - 1; // Limit the index if (ind < 0) ind = 0; // Limit the index CountL [ind] += 1; // Increment the counter for the left side } else { // Calculate the index for the right side ind = (int) U.Scale (X, Inp_P, Max_P, 0, Size_P, false); if (ind >= Size_P) ind = Size_P - 1; // Limit the index if (ind < 0) ind = 0; // Limit the index CountR [ind] += 1; // Increment the counter for the right side } } // Define minimum and maximum values for the graph int minCNT = CNT_P; // Initial value for the minimum counter int maxCNT = 0; // Initial value for the max counter // Finding minimum and maximum values in counters for (int i = 0; i < Size_P; i++) { if (CountL [i] > maxCNT) maxCNT = CountL [i]; // Update the max value for the left side if (CountR [i] > maxCNT) maxCNT = CountR [i]; // Update the max value for the right side if (CountL [i] < minCNT) minCNT = CountL [i]; // Update the min value for the left side if (CountR [i] < minCNT) minCNT = CountR [i]; // Update the minimum value for the right side } // Variables for drawing graphs int x = 0.0; // X coordinate int y = 0.0; // Y coordinate color clrF; // Color int centre = 0; // Canvas center int stepL = 0; // Left side step int stH_L = 0; // Left side height int stepR = 0; // Right side step int stH_R = 0; // Right side height // Determine the center of the canvas centre = (int) U.Scale(Inp_P, Min_P, Max_P, O, W - O - 1, false); // Calculate steps and heights for the left side stepL = (centre - O) / Size_P; stH_L = stepL / 2; if (stH_L == 0) stH_L = 1; // Make sure the height is not 0 // Calculate steps and heights for the right side stepR = (W - O - centre) / Size_P; stH_R = stepR / 2; if (stH_R == 0) stH_R = 1; // Make sure the height is not 0 // Draw graphs for left and right parts for (int i = 0; i < Size_P; i++) { // Draw for the left side x = (int) U.Scale (i, 0, Size_P - 1, O, centre - stH_L, true); // Calculate the X coordinate y = (int) U.Scale (CountL [i], 0, maxCNT, O, H - O - 1, true); // Calculate the Y coordinate clrF = DoubleToColor(CountL [i], minCNT, maxCNT, 0, 255); // Define color by value // Draw dots for the left side Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); // Draw a small circle Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); // Draw a larger circle // Draw for the right side x = (int) U.Scale (i, 0, Size_P - 1, centre + stH_R, W - O - 1, false); // Calculate the X coordinate y = (int) U.Scale (CountR[i], 0, maxCNT, O, H - O - 1, true); // Calculate the Y coordinate clrF = DoubleToColor (CountR [i], minCNT, maxCNT, 0, 255); // Define color by value // Draw dots for the right side Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); // Draw a small circle Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); // Draw a larger circle } Canvas.Update (); // Update the canvas to reflect the changes}
Vamos executar o script e obter no gráfico uma imagem semelhante à da figura 2.
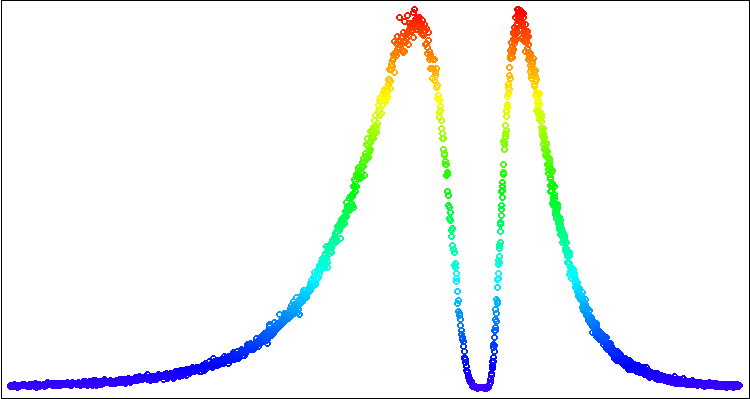
Figura 2. Visualização da construção de uma distribuição lognormal assimétrica com a biblioteca padrão Canvas
Depois de termos analisado detalhadamente a teoria de todas as etapas do algoritmo, passamos agora diretamente à implementação do código. Embora o algoritmo AOS tenha sido descrito como um método de minimização de problemas, vamos ajustar a lógica para que ele funcione com maximização. Vamos escrever a estrutura "S_Layer", que irá modelar uma camada do átomo e conter informações sobre a quantidade de partículas localizadas naquela camada. Ela incluirá tanto características numéricas quanto um método de inicialização. Os campos da estrutura são:
- pc — contador de partículas presentes na camada do átomo, permitindo acompanhar quantas partículas (elétrons) estão em determinada camada.
- BSk — estado de ligação da camada, reflete o nível de interação entre as partículas naquela camada.
- BEk — energia de ligação da camada, indica o quão fortemente as partículas na camada estão ligadas entre si.
- LEk — energia mínima na camada, usada para determinar o menor nível de energia que pode ser alcançado pelas partículas naquela camada específica.
O método "Init" é destinado à inicialização dos campos da estrutura com valores padrão, permitindo resetar facilmente o estado da camada sempre que necessário.
//—————————————————————————————————————————————————————————————————————————————— struct S_Layer { int pc; // particle counter double BSk; // connection state double BEk; // binding energy double LEk; // minimum energy void Init () { pc = 0; BSk = 0.0; BEk = 0.0; LEk = 0.0; } }; //——————————————————————————————————————————————————————————————————————————————
Em seguida, analisamos a estrutura "S_Atom" e seu método "Init". "S_Atom" é uma estrutura que representa o átomo, composto por várias camadas. Cada camada é modelada por meio do array "layers[]" da estrutura "S_Layer", descrita anteriormente. Os campos da estrutura são:
- Init — método de inicialização do array de camadas do átomo, bem como da inicialização de cada camada dentro desse array.
- layersNumb — parâmetro inteiro que indica o número de camadas que serão criadas para esse átomo.
//—————————————————————————————————————————————————————————————————————————————— struct S_Atom { S_Layer layers []; // array of atom layers void Init (int layersNumb) { ArrayResize (layers, layersNumb); for (int i = 0; i < layersNumb; i++) layers [i].Init (); } }; //——————————————————————————————————————————————————————————————————————————————
A estrutura seguinte é "S_Electron" e seu método "Init". Essa estrutura representa um elétron — um membro da população de soluções, que contém informações sobre sua posição na camada correspondente do átomo. O campo "layerID[]" — array de números inteiros que armazena os identificadores das camadas às quais o elétron pertence. Cada identificador corresponde a uma camada específica do átomo, permitindo acompanhar em qual nível o elétron se encontra.
//—————————————————————————————————————————————————————————————————————————————— struct S_Electron { int layerID []; // array of layer IDs for the electron void Init (int coords) { ArrayResize (layerID, coords); } }; //——————————————————————————————————————————————————————————————————————————————
A classe do algoritmo AOS, "C_AO_AOS", herda da classe base "C_AO" e pressupõe a existência de funcionalidades comuns relacionadas às órbitas atômicas.
Parâmetros da classe:
- popSize — tamanho da população no algoritmo.
- maxLayers — número máximo de camadas que pode ser utilizado no modelo atômico.
- photonEmissions — quantidade de emissões de fótons a serem utilizadas no processo de otimização.
- PR — coeficiente de transição dos fótons, determina a probabilidade de transição entre estados.
- peakPosition — posição do pico na distribuição lognormal.
Métodos da classe:
1. SetParams() — define os parâmetros do algoritmo, lendo os valores a partir do array "params".
2. Init() — inicializa o algoritmo com os parâmetros de busca especificados: intervalos mínimo e máximo, passo de busca e número de épocas.
3. Moving() — método responsável por mover as partículas no espaço de busca.
4. Revision() — método encarregado de revisar as melhores soluções encontradas durante o processo de otimização.
Campos privados da classe:
- atomStage — estágio atual do átomo, define em que etapa os processos atômicos se encontram.
- currentLayers[] — array que armazena a quantidade atual de camadas para cada átomo (em cada época, o número de camadas de cada átomo é um valor aleatório dentro do intervalo [1; maxLayers]).
- S_Atom atoms[] — array de átomos, cujo tamanho corresponde ao número de coordenadas utilizadas no algoritmo.
- S_Electron electrons[] — array de elétrons, com tamanho igual ao da população.
- BS[] — array que armazena os estados de ligação entre os elétrons em toda a população.
Métodos privados da classe:
1. GetOrbitBandID() — obtém o identificador da banda orbital para os parâmetros fornecidos, como quantidade de camadas e intervalos.2. DistributeParticles() — método para distribuir as partículas no espaço de busca.
3. LayersGenerationInAtoms() — gera a quantidade de camadas nos átomos.
4. UpdateElectronsIDs() — atualiza os identificadores de camada dos elétrons.
5. CalcLayerParams() — calcula os parâmetros das camadas, incluindo a determinação dos níveis energéticos e das ligações.
6. UpdateElectrons() — atualiza a posição dos elétrons.
//—————————————————————————————————————————————————————————————————————————————— // Class implementing the atomic optimization algorithm (Atomic Orbital Search) class C_AO_AOS : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_AOS () { } C_AO_AOS () { ao_name = "AOS"; ao_desc = "Atomic Orbital Search"; ao_link = "https://www.mql5.com/en/articles/16276"; popSize = 50; // population size maxLayers = 5; // maximum number of layers photonEmissions = 1; // number of photon emissions PR = 0.1; // photon transition coefficient peakPosition = 0.05; // peak position in the log-normal distribution ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "maxLayers"; params [1].val = maxLayers; params [2].name = "photonEmissions"; params [2].val = photonEmissions; params [3].name = "photonRate"; params [3].val = PR; params [4].name = "peakPsition"; params [4].val = peakPosition; } // Setting algorithm parameters void SetParams () { popSize = (int)params [0].val; maxLayers = (int)params [1].val; photonEmissions = (int)params [2].val; PR = params [3].val; peakPosition = params [4].val; } // Initialization of the algorithm with the given search parameters bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Method of moving particles void Revision (); // Method of revising the best solutions //---------------------------------------------------------------------------- int maxLayers; // maximum number of layers int photonEmissions; // number of photon emissions double PR; // photon transition coefficient double peakPosition; // peak position in the log-normal distribution private: //------------------------------------------------------------------- int atomStage; // current stage of the atom int currentLayers []; // current number of layers for the corresponding atom (coordinates) S_Atom atoms []; // atoms with their size corresponding to the number of coordinates S_Electron electrons []; // electrons corresponding to the population size double BS []; // connection states // Get orbital band for given parameters int GetOrbitBandID (int layersNumb, double min, double max, double center, double p); // Distribution of particles in the search space void DistributeParticles (); // Generate layers in atoms void LayersGenerationInAtoms (); // Update electron IDs void UpdateElectronsIDs (); // Calculate layer parameters void CalcLayerParams (); // Update electron positions void UpdateElectrons (); }; //——————————————————————————————————————————————————————————————————————————————
Vejamos o que ocorre no método "Init" da classe do algoritmo AOS.
1. Inicialização padrão: o método começa com a chamada de "StandardInit", que executa etapas comuns de inicialização, como a definição dos intervalos para as coordenadas.
2. Inicialização das variáveis:
- atomStage — é definido como "0", indicando que o algoritmo está na fase inicial.
- ArrayResize(currentLayers, coords) — redimensiona o array "currentLayers" de acordo com a quantidade de coordenadas "coords".
- ArrayResize(atoms, coords) — redimensiona o array "atoms", criando um objeto separado para cada átomo (coordenada). Para cada átomo, é chamado o método "Init(maxLayers)", que o inicializa com o número máximo de camadas.
- ArrayResize(electrons, popSize) — redimensiona o array "electrons" conforme o tamanho da população "popSize". Para cada elétron, é criado um array "layerID", que corresponde à quantidade de coordenadas.
- ArrayResize(BS, coords) — redimensiona o array "BS", que armazena os estados de ligação para cada coordenada.
4. Se todas as operações de inicialização forem concluídas com sucesso, o método retorna "true".
//—————————————————————————————————————————————————————————————————————————————— // Initialize the algorithm bool C_AO_AOS::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- atomStage = 0; ArrayResize (currentLayers, coords); ArrayResize (atoms, coords); for (int i = 0; i < coords; i++) atoms [i].Init (maxLayers); ArrayResize (electrons, popSize); for (int i = 0; i < popSize; i++) ArrayResize (electrons [i].layerID, coords); ArrayResize (BS, coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Método de movimentação das partículas. Vamos descrever o método "Moving":
1. Posicionamento inicial aleatório:
- Se a variável "revision" for igual a "false", isso indica que o algoritmo ainda não iniciou sua execução. Nesse caso, ocorre o posicionamento aleatório das partículas.
- Em seguida, um laço "for" aninhado percorre todos os elétrons (tamanho da população) e, para cada coordenada, gera um valor aleatório utilizando o método "u.RNDfromCI", que extrai um valor do intervalo definido por "rangeMin" e "rangeMax". Esse valor é então ajustado pelo método "u.SeInDiSp", que o adapta ao passo (step) especificado.
2. Execução da etapa correspondente da evolução dos átomos:
- Se "revision" for igual a "true", isso significa que o algoritmo já foi inicializado e pode executar suas etapas principais. Dependendo do estágio atual "atomStage", diferentes métodos são chamados:
- Se "atomStage" for igual a "0", chama-se "DistributeParticles()", responsável por distribuir as partículas no espaço de busca de acordo com a distribuição lognormal assimétrica.
- Caso contrário, são chamados métodos que geram as camadas nos átomos, atualizam os identificadores dos elétrons, calculam os parâmetros das camadas e atualizam a posição dos elétrons.
3. Após todas as operações necessárias, o valor de "atomStage" é incrementado em "1". Se "atomStage" exceder o valor de "photonEmissions", ele é redefinido para "0", permitindo que as etapas do algoritmo sejam repetidas ciclicamente.
//—————————————————————————————————————————————————————————————————————————————— // Particle displacement method void C_AO_AOS::Moving () { // Initial random positioning if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Execute the corresponding stage of the algorithm if (atomStage == 0) { DistributeParticles (); } else { LayersGenerationInAtoms (); UpdateElectronsIDs (); CalcLayerParams (); UpdateElectrons (); } // Proceed to the next stage atomStage++; if (atomStage > photonEmissions) atomStage = 0; } //——————————————————————————————————————————————————————————————————————————————
Agora passamos à análise de métodos específicos. O método "GetOrbitBandID" da classe "C_AO_AOS" é destinado a determinar a faixa orbital para uma partícula com base em sua posição em relação ao centro definido. Ele recebe como parâmetros a quantidade de camadas, os valores mínimo e máximo, o centro e a posição da partícula "p".
1. Calcula a largura das faixas à esquerda e à direita do centro.
2. Se a posição da partícula "p" for menor que o centro, verifica em qual das faixas à esquerda ela se encontra.
3. Se for maior, verifica em qual das faixas à direita ela está.
4. Se for igual ao centro, retorna o número 0 (centro).
Dessa forma, a função retorna o índice da faixa orbital correspondente à posição fornecida.
//—————————————————————————————————————————————————————————————————————————————— // Determining the orbital band for a particle int C_AO_AOS::GetOrbitBandID (int layersNumb, double min, double max, double center, double p) { // Calculate the width of the bands to the left and right of the center double leftWidth = (center - min) / layersNumb; double rightWidth = (max - center) / layersNumb; // Define the band index if (p < center) { // The object is located to the left of the center for (int i = 1; i <= layersNumb; i++) { if (p >= center - i * leftWidth) return i - 1; } return layersNumb - 1; // If the object is in the leftmost band } else if (p > center) { // The object is located to the right of the center for (int i = 1; i <= layersNumb; i++) { if (p <= center + i * rightWidth) return i - 1; } return layersNumb - 1; // If the object is in the far right band } else { // The object is in the center return 0; } } //——————————————————————————————————————————————————————————————————————————————
O método "DistributeParticles" da classe "C_AO_AOS" é responsável pela distribuição das partículas no espaço de busca. O método realiza essa distribuição utilizando uma distribuição lognormal.
Para cada partícula (no laço sobre "popSize") e para cada coordenada (no laço sobre "coords"):
- Gera-se a posição da partícula com base na distribuição lognormal, utilizando os parâmetros fornecidos ("cB", "rangeMin", "rangeMax", "peakPosition").
- Aplica-se a função "SeInDiSp" para ajustar o valor da posição da partícula dentro do intervalo especificado, respeitando o passo definido.
//—————————————————————————————————————————————————————————————————————————————— // Distribution of particles in the search space void C_AO_AOS::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Use log-normal distribution to position particles a [i].c [c] = u.LognormalDistribution (cB [c], rangeMin [c], rangeMax [c], peakPosition); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
O método "UpdateElectronsIDs" da classe "C_AO_AOS" atualiza os identificadores de camada para os elétrons, com base em suas coordenadas e nos parâmetros definidos.
//—————————————————————————————————————————————————————————————————————————————— // Update layer IDs for each electron void C_AO_AOS::UpdateElectronsIDs () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { electrons [i].layerID [c] = GetOrbitBandID (currentLayers [c], rangeMin [c], rangeMax [c], cB [c], a [i].c [c]); } } } //——————————————————————————————————————————————————————————————————————————————
O método "CalcLayerParams" da classe "C_AO_AOS" é responsável pelo cálculo dos parâmetros de cada camada dos átomos no sistema. Os principais componentes do método são:
1. Inicialização da variável: "energy" — variável usada para armazenar a energia máxima, que será atualizada durante o processamento dos elétrons.
2. Um laço percorre todos os átomos (coordenadas) do sistema. O índice "c" indica o átomo atual.
3. Para cada átomo, é chamado o método "Init", que inicializa os parâmetros com o número máximo de camadas definido pela variável "maxLayers".
4. Laço sobre as camadas: um laço interno percorre todas as camadas associadas ao átomo atual, sendo "currentLayers[c]" o número de camadas para o átomo "c".
5. Processamento dos elétrons: outro laço interno percorre todos os elétrons "e" da população, verificando se o elétron atual pertence à camada "L" do átomo "c".
6. Atualização dos parâmetros da camada:
- Se o elétron pertence à camada, o contador de partículas naquela camada é incrementado.
- Os valores de energia "BEk" e de estado "BSk" da camada são atualizados de acordo com as propriedades do elétron.
- Se a energia do elétron "a[e].f" for maior que a energia máxima atual "energy" da camada, então os valores da energia máxima "energy" e do estado "LEk" são atualizados.
7. Cálculo dos valores médios da camada: se o contador de partículas "pc" for diferente de zero, os valores médios de energia e estado são calculados.
8. Cálculo do estado geral de ligação: de maneira análoga, é calculado o estado de ligação "BS" para cada átomo, mas considerando toda a população de elétrons.
//—————————————————————————————————————————————————————————————————————————————— // Calculate parameters for each layer void C_AO_AOS::CalcLayerParams () { double energy; // Handle each coordinate (atom) for (int c = 0; c < coords; c++) { atoms [c].Init (maxLayers); // Handle each layer for (int L = 0; L < currentLayers [c]; L++) { energy = -DBL_MAX; // Handle each electron for (int e = 0; e < popSize; e++) { if (electrons [e].layerID [c] == L) { atoms [c].layers [L].pc++; atoms [c].layers [L].BEk = a [e].f; atoms [c].layers [L].BSk = a [e].c [c]; if (a [e].f > energy) { energy = a [e].f; atoms [c].layers [L].LEk = a [e].c [c]; } } } // Calculate average values for the layer if (atoms [c].layers [L].pc != 0) { atoms [c].layers [L].BEk /= atoms [c].layers [L].pc; atoms [c].layers [L].BSk /= atoms [c].layers [L].pc; } } } // Calculate the general state of connections ArrayInitialize (BS, 0); for (int c = 0; c < coords; c++) { for (int e = 0; e < popSize; e++) { BS [c] += a [e].c [c]; } BS [c] /= popSize; } } //——————————————————————————————————————————————————————————————————————————————
O método "UpdateElectrons" da classe "C_AO_AOS" é responsável por atualizar a posição dos elétrons no sistema.
1. Inicialização dos parâmetros: são definidos os coeficientes de velocidade, peso da melhor solução, peso do estado médio e a probabilidade de transição.
2. Para cada partícula e cada coordenada:
- Gera-se uma probabilidade aleatória "φ".
- Se "φ" for menor que o valor limiar "PR", ocorre dispersão aleatória, e uma nova posição é escolhida aleatoriamente dentro do intervalo especificado.
- Caso contrário:
- Obtém-se o identificador de camada "lID" para a partícula atual.
- Geram-se valores aleatórios para os coeficientes.
- Se a energia atual da partícula for menor que a energia média da camada, ocorre um movimento em direção ao ótimo global.
- Caso contrário, ocorre um movimento em direção ao ótimo local da camada.
- Ao final, a nova posição é limitada dentro do intervalo definido, respeitando o passo.
//—————————————————————————————————————————————————————————————————————————————— // Update electron positions void C_AO_AOS::UpdateElectrons () { double α; // speed coefficient double β; // best solution weight coefficient double γ; // average state weight coefficient double φ; // transition probability double newPos; // new position double LE; // best energy double BSk; // connection state int lID; // layer ID // Handle each particle for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Random scatter newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); β = u.RNDprobab (); γ = u.RNDprobab (); // If the current particle energy is less than the average layer energy if (a [p].f < atoms [c].layers [lID].BEk) { // Moving towards the global optimum---------------------------- LE = cB [c]; newPos = a [p].c [c]+ α * (β * LE - γ * BS [c]) / currentLayers [c]; } else { // Movement towards the local optimum of the layer LE = atoms [c].layers [lID].LEk; BSk = atoms [c].layers [lID].BSk; newPos = a [p].c [c] + α * (β * LE - γ * BSk); } } // Limiting the new position within the search range taking into account the step a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" da classe "C_AO_AOS" é destinado à revisão e atualização das melhores soluções (ou estados ótimos) durante a iteração. Etapas do método:
1. Inicialização da variável "bestIndex", que será usada para armazenar o índice da melhor solução.
2. Busca pela melhor solução. A condição verifica se o valor da função (ou avaliação) da solução atual "a[i].f" é maior que o valor do melhor resultado global "fB". Se essa condição for verdadeira, o valor do melhor resultado global é atualizado com o valor atual e o índice da solução atual é salvo como o melhor.
3. Se uma melhor solução for encontrada, suas coordenadas "a[bestIndex].c" são copiadas para o array "cB".
//—————————————————————————————————————————————————————————————————————————————— // Method of revising the best solutions void C_AO_AOS::Revision () { int bestIndex = -1; // Find the best solution in the current iteration for (int i = 0; i < popSize; i++) { // Update the global best solution if (a [i].f > fB) { fB = a [i].f; bestIndex = i; } } // Update the best coordinates if a better solution is found if (bestIndex != -1) ArrayCopy (cB, a [bestIndex].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Vamos rodar o ambiente de testes e obter os seguintes resultados de desempenho do AOS:
AOS|Atomic Orbital Search|50.0|5.0|1.0|0.1|0.05|
=============================
5 Hilly's; Func runs: 10000; result: 0.6521321213930082
25 Hilly's; Func runs: 10000; result: 0.39883708808831186
500 Hilly's; Func runs: 10000; result: 0.2602779698842558
=============================
5 Forest's; Func runs: 10000; result: 0.5165008091396371
25 Forest's; Func runs: 10000; result: 0.30233740723010416
500 Forest's; Func runs: 10000; result: 0.1926906342754638
=============================
5 Megacity's; Func runs: 10000; result: 0.39384615384615385
25 Megacity's; Func runs: 10000; result: 0.1892307692307692
500 Megacity's; Func runs: 10000; result: 0.09903076923077013
=============================
All score: 3.00488 (33.39%)
Na visualização do funcionamento do algoritmo AOS é possível notar um comportamento interessante, com regiões características de “aglomeração” nas orbitais dos átomos, mas a precisão de convergência não é muito alta.
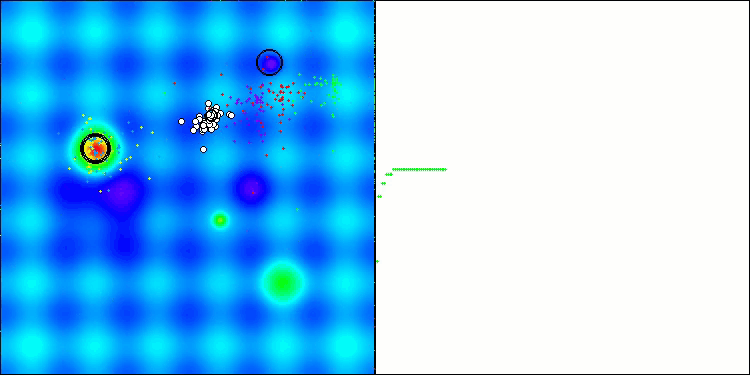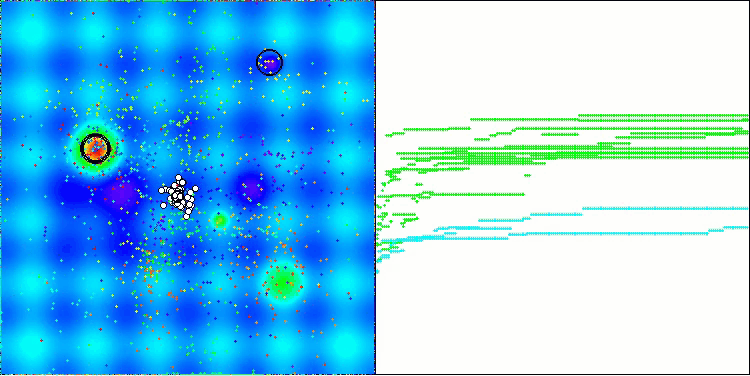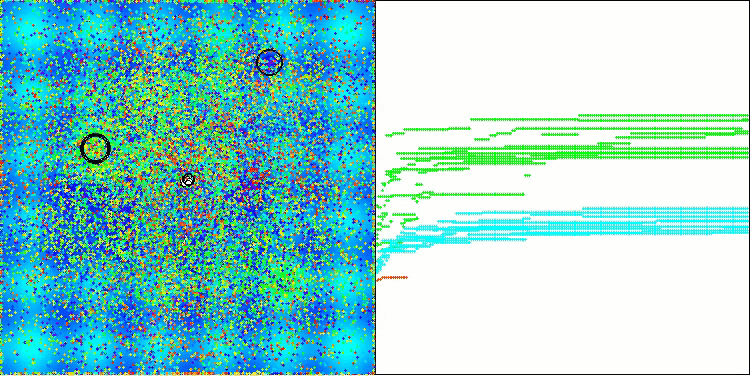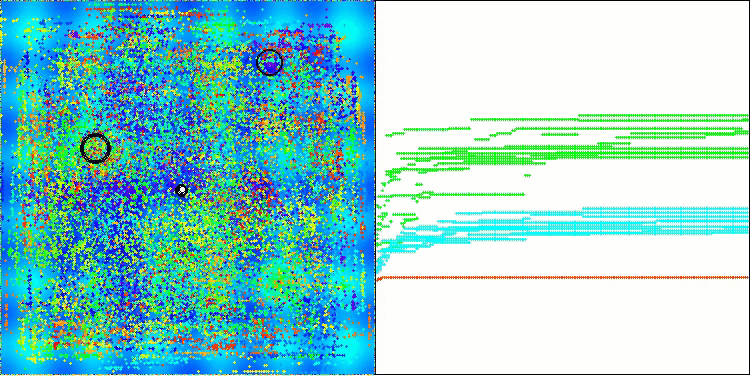
AOS na função de teste Hilly
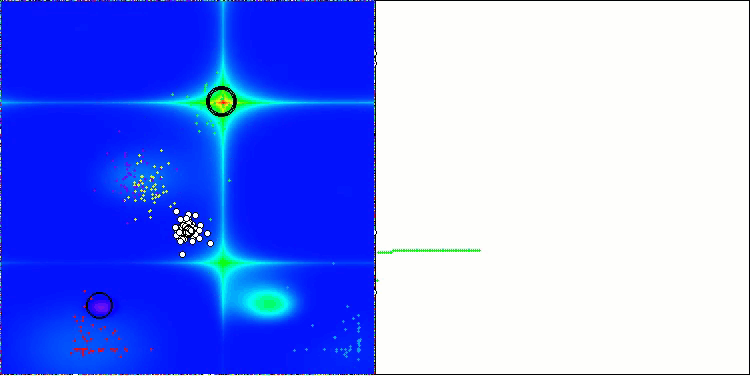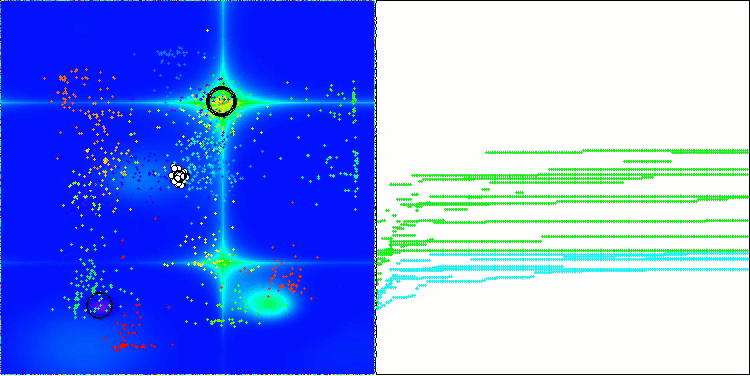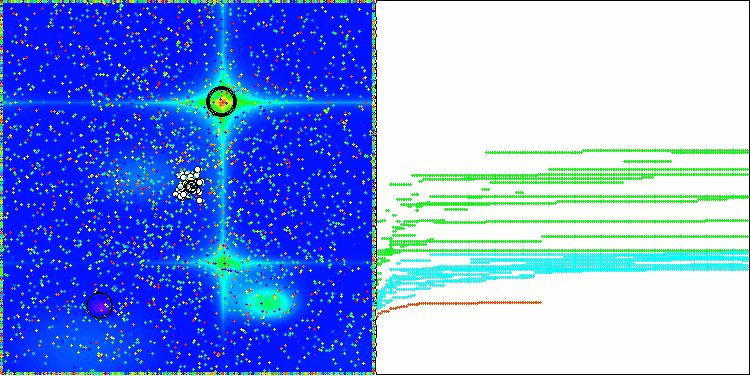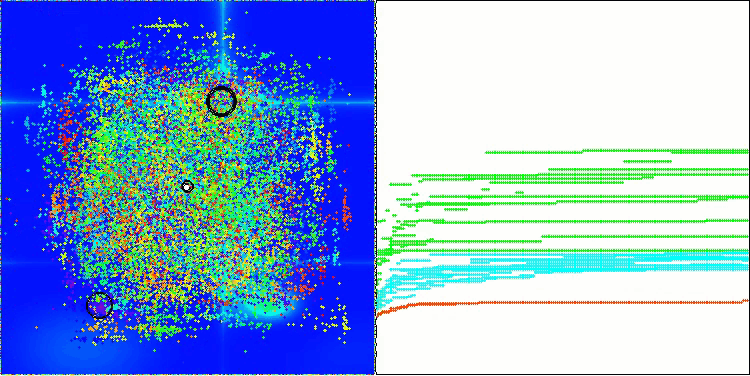
AOS na função de teste Forest

AOS na função de teste Megacity
Com base nos testes, o algoritmo AOS ficou na 39ª posição na tabela de classificação.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration ptimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 12 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 13 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 14 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 15 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 16 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 17 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 18 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 19 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 20 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 21 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 22 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 23 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 24 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 25 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 26 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 27 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 28 | ABHA | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 29 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 30 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 31 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 32 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 33 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 34 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 35 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 36 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 37 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 38 | FAm | firefly algorithm M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 39 | AOS | atomic orbital search | 0.65213 | 0.39884 | 0.26028 | 1.31125 | 0.51650 | 0.30234 | 0.19269 | 1.01153 | 0.39385 | 0.18923 | 0.09903 | 0.68211 | 3.005 | 33.39 |
| 40 | GSA | gravitational search algorithm | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 41 | BFO | bacterial foraging optimization | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 42 | ABC | artificial bee colony | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 43 | BA | bat algorithm | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 44 | AAA | algae adaptive algorithm | 0.50007 | 0.32040 | 0.25525 | 1.07572 | 0.37021 | 0.22284 | 0.16785 | 0.76089 | 0.27846 | 0.14800 | 0.09755 | 0.52402 | 2.361 | 26.23 |
| 45 | SA | simulated annealing | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
Considerações finais
Analisamos um algoritmo interessante de busca orbital atômica, que aplica abordagens inovadoras para a busca global e o refinamento local dos resultados. Graças às camadas orbitais dinâmicas dos átomos, os elétrons se movimentam de forma equilibrada na busca por um estado atômico estável. O algoritmo apresenta limitações em funções suaves, mas mostra resultados razoáveis com o aumento da dimensionalidade do problema, inclusive em função discreta como Megacity.
Este algoritmo é um exemplo de uma ideia promissora, no entanto, sua eficácia é prejudicada por alguns detalhes pequenos, mas significativos. No próximo artigo, vamos abordar minha modificação do AOS e analisar o que essa excelente concepção de busca orbital realmente pode alcançar.
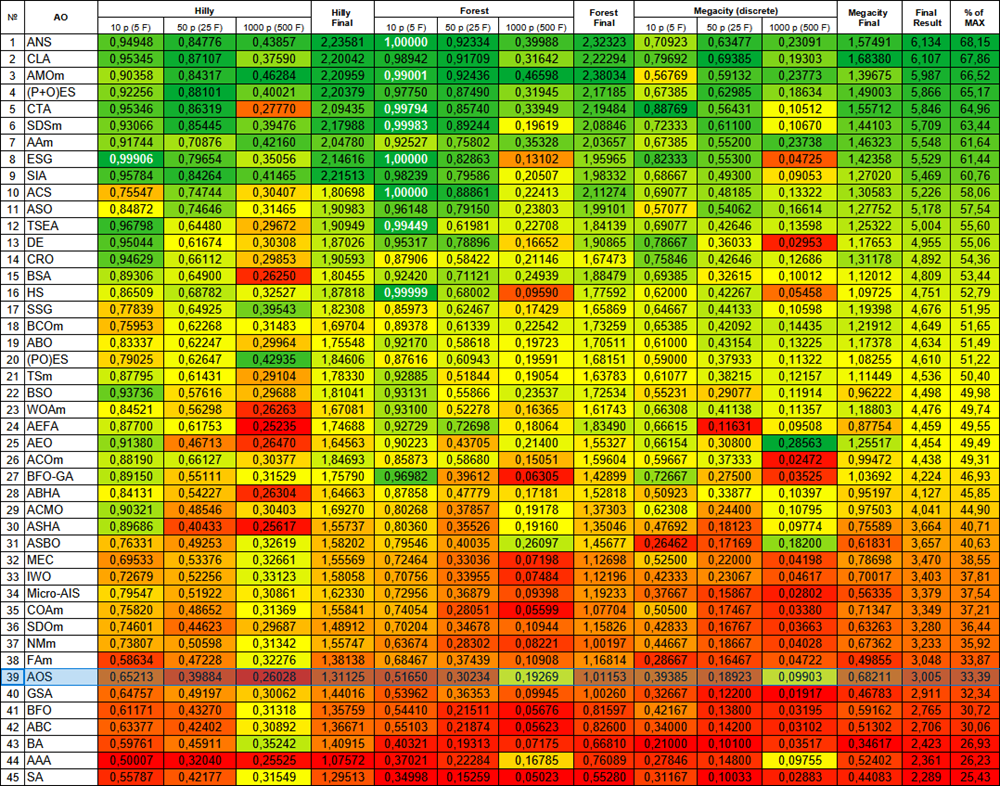
Figura 3. Graduação de cores dos algoritmos conforme os testes correspondentes. O branco destaca resultados maiores ou iguais a 0.99
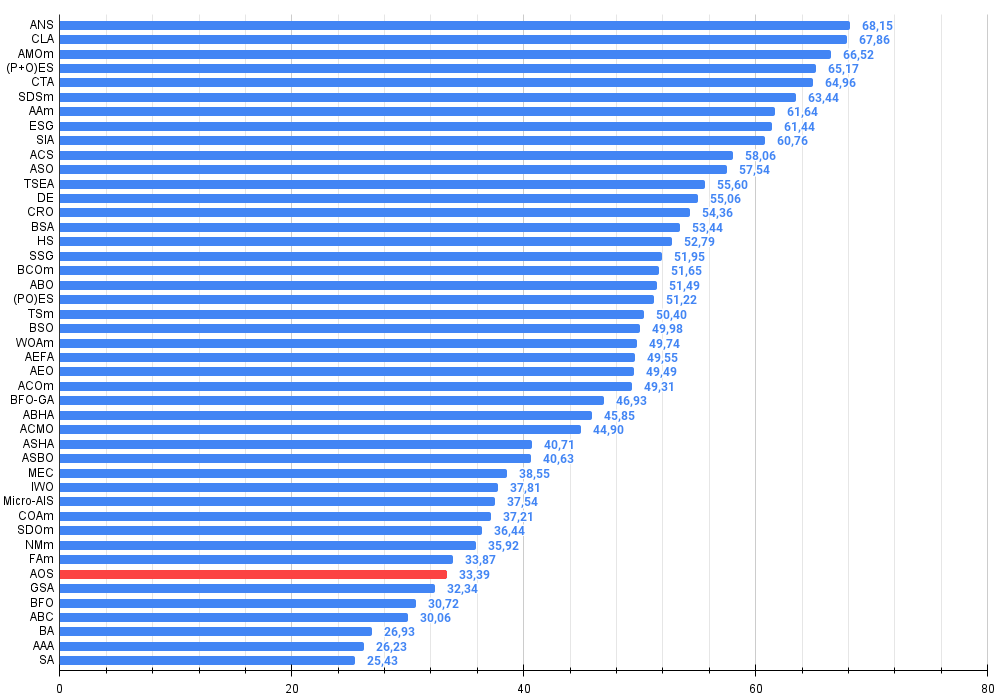
Figura 4. Histograma dos resultados de teste dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor,
onde 100 é o resultado teórico máximo possível, no arquivo anexo há o script para cálculo da tabela de classificação)
Vantagens e desvantagens do algoritmo AOS:
Vantagens:
- Base promissora para melhorias no algoritmo.
- Pequena quantidade de parâmetros externos.
Desvantagens:
- Lento devido à geração frequente de números aleatórios.
- Implementação relativamente complexa.
- Baixa precisão de convergência.
Está anexado ao artigo um arquivo compactado com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela exatidão absoluta na descrição dos algoritmos canônicos, pois muitas versões foram modificadas para melhorar a capacidade de busca. As conclusões e interpretações apresentadas nos artigos são baseadas nos resultados dos experimentos realizados.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | C_AO.mqh | Arquivo incluído | Classe base dos algoritmos populacionais de otimização |
| 2 | C_AO_enum.mqh | Arquivo incluído | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluído | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluído | Biblioteca de funções para o ambiente de teste |
| 5 | Utilities.mqh | Arquivo incluído | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluído | Script para cálculo de resultados na tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Ambiente de teste unificado para todos os algoritmos populacionais de otimização |
| 8 | AO_AOS_AtomicOrbitalSearch.mqh | Arquivo incluído | Classe do algoritmo AOS |
| 9 | Test_AO_AOS.mq5 | Script | Ambiente de teste específico para o AOS |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16276
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Simulação de mercado (Parte 17): Sockets (XI)
Simulação de mercado (Parte 17): Sockets (XI)
 Redes neurais em trading: Modelo hiperbólico de difusão latente (Conclusão)
Redes neurais em trading: Modelo hiperbólico de difusão latente (Conclusão)
 Do básico ao intermediário: Estruturas (V)
Do básico ao intermediário: Estruturas (V)
 Implementando uma Estratégia de Trading Rápido com Parabolic SAR e Média Móvel Simples (SMA) em MQL5
Implementando uma Estratégia de Trading Rápido com Parabolic SAR e Média Móvel Simples (SMA) em MQL5
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Algoritmo de busca orbital atômica - O Atomic Orbital Search (AOS) foi publicado:
Autor: Andrey Dik
Este é o sistema completo, que inclui física, matemática, xadrez, etc.