
Algoritmo de búsqueda orbital atómica - Atomic Orbital Search (AOS)
Contenido
Introducción
Los planteamientos modernos para resolver problemas complejos de optimización se inspiran cada vez más en los principios de la física, sobre todo en la mecánica cuántica. En este artículo, nos familiarizaremos con el algoritmo AOS (Atomic Orbital Search), basado en conceptos de modelos orbitales atómicos. El algoritmo fue propuesto por Mahdi Azizi en 2021, y supone un nuevo método metaheurístico. El modelo describe el comportamiento de los electrones no como trayectorias estrictamente definidas, sino como funciones de onda que crean nubes de probabilidad alrededor del núcleo atómico, tomando los avances científicos del eminente físico Erwin Schroeder.El orbital atómico, resultado de la descripción cuántica, es la región donde se maximiza la probabilidad de encontrar un electrón. En este modelo, los electrones se desplazan en capas imaginarias definidas por radios y números cuánticos que reflejan los niveles de energía. Las capas con valores más altos de n se corresponden con radios más grandes y, por tanto, con niveles de energía más altos. Este comportamiento de los electrones, sujeto a excitaciones por la interacción con otras partículas y la exposición a fotones, crea un entorno dinámico y variable en el que los electrones pueden emitir o absorber energía al moverse entre distintos orbitales.
El algoritmo AOS usa estos principios físicos para modelar el proceso de búsqueda de soluciones en problemas de optimización. El AOS tiene en cuenta las distribuciones de probabilidad y la dinámica de las interacciones, lo cual permite realizar una exploración eficaz del espacio de soluciones. En concreto, el algoritmo considera la actualización de las posiciones de las soluciones candidatas (electrones) según sus energías, lo que a su vez afecta a la probabilidad de encontrarse en determinadas capas. Esto permite al AOS no solo encontrar soluciones óptimas, sino también adaptarse a los cambios del entorno.
En este artículo, hablaremos con detalle del modelo matemático AOS, incluyendo los pasos para actualizar las posiciones de las soluciones candidatas y los mecanismos que rigen la absorción y liberación de energía. Así pues, el AOS no solo supone un enfoque interesante de la optimización, sino que también abre nuevos horizontes para la aplicación de los principios cuánticos a los problemas computacionales.
Implementación del algoritmo
El algoritmo AOS se basa en los principios del modelo orbital atómico, que tiene en cuenta la emisión y absorción de energía por los átomos, así como la configuración de la densidad de electrones. Al principio del algoritmo, se ofrecen varias soluciones candidatas, denotadas como X, que se tratan como electrones alrededor del núcleo del átomo. Estos candidatos forman una nube de electrones, mientras que el espacio de búsqueda se representa como un volumen esférico dividido en capas concéntricas. Las soluciones candidatas pueden escribirse de forma general como sigue:
X = [x1, x2 ..., xj ..., xm], donde xi es el i-ésimo candidato a la decisión, y m es el número total de candidatos.
Las posiciones iniciales de las soluciones candidatas se inicializan aleatoriamente. Cada electrón posee un nivel de energía definido por una función objetivo que debe minimizarse. Así, los electrones con niveles de energía bajos se corresponden con los candidatos con mejores valores de la función objetivo, mientras que los electrones con niveles de energía altos se corresponden con los candidatos con peores valores. El vector de valores de la función objetivo se escribe como:
E = [E1, E2, ..., Ei, ..., Em], donde Ei es el nivel de energía del i-ésimo candidato.
Las capas imaginarias alrededor del núcleo se modelan usando un número entero aleatorio n, que puede ser desde 1 hasta el número de capas L. La capa con el radio más pequeño L0 representa el núcleo, mientras que las capas Li restantes representan la ubicación de los electrones (en el AOS la capa "núcleo" también puede contener electrones). La distribución de las soluciones candidatas entre capas se realiza mediante una función de densidad de probabilidad (PDF) que determina la probabilidad de encontrar el valor de una variable dentro de un rango determinado. El algoritmo usa una distribución lognormal para simular el comportamiento ondulatorio real de los electrones. Las soluciones candidatas se distribuyen en diferentes capas, donde el vector Xk que contiene los candidatos en n capas se escribe como:
Xk = [Xk1, Xk2, ..., Xki, ..., Xkp], donde k es el número de capa, y p es el número de candidatos en la capa.
Según el modelo orbital atómico, se supone que los electrones se encuentran en el estado fundamental del nivel de energía. El estado de enlace y la energía de enlace de cada capa se calculan como vemos abajo:
BS_k = (1/p) * Σ(Xki),
BE_k = (1/p) * Σ(Eki).
El nivel de energía total de un átomo se define así:
BS = (1/m) * Σ(Xi),
BE = (1/m) * Σ(Ei).
Los electrones pueden cambiar su ubicación y desplazarse entre capas bajo la influencia de los fotones y otras interacciones. La posición de las soluciones candidatas en el algoritmo AOS se actualiza según la probabilidad de interacción representada por un número ϕ generado aleatoriamente, que se distribuye en el intervalo [0,1]. Si ϕ ≥ PR (parámetro de velocidad del fotón), entonces es posible la emisión o absorción de energía.
Si Eki ≥ BEk, entonces tiene lugar la emisión de energía: Xki[t+1] = Xkit + αi × (βi × LE − γi × BS) / k.
Si Eki < BEk, entonces se da la absorción de energía: Xki[t+1] = Xkit + αi × (βi × LEk − γi × BSk).
Si ϕ < PR, entonces se consideran los desplazamientos hacia campos magnéticos o las interacciones con otras partículas: Xki[t+1] = Xkit + ri, donde ri supone un incremento aleatorio en el rango de min a max del correspondiente parámetro optimizado del problema.
Por decirlo de forma sencilla, en el AOS, la población de soluciones candidatas puede representarse figurativamente como una molécula en la que los átomos se corresponden con coordenadas en el espacio de búsqueda, mientras que los electrones de estos átomos se corresponden con soluciones específicas. Así, si la población consta de 50 soluciones candidatas, cada átomo tendrá 50 electrones distribuidos en capas, según una distribución lognormal.
En la descripción del algoritmo, el autor no especifica cómo se determina el diámetro de la capa exterior del átomo, lo cual implica que el núcleo del átomo estará situado en el centro con respecto a las capas. Y esto significa que el átomo, junto con las capas, se moverá dentro de los límites dados del problema. Para ofrecer más flexibilidad al algoritmo, nos basaremos en la condición de que el diámetro de la capa exterior se corresponderá con el rango [min; max] para la coordenada correspondiente en el espacio de búsqueda, mientras que el centro del núcleo del átomo se situará en el punto de la mejor solución global en la coordenada dada. De manera visual, el modelo de un átomo en el AOS puede visualizarse en la figura 1.
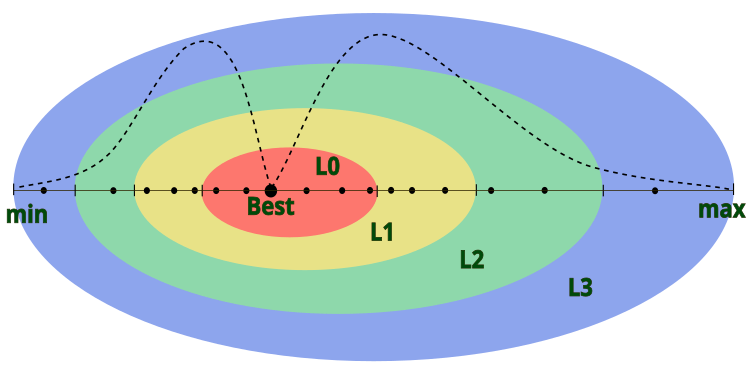
Figura 1. Modelo de un átomo en el algoritmo AOS, donde los puntos denotan electrones, mientras que la línea discontinua indica la distribución lognormal de electrones
Pseudocódigo del algoritmo de búsqueda orbital atómica (AOS):
1. Inicialización
1.1 Posiciones iniciales (Xi)
Se crea una población de m soluciones candidatas
A cada candidato se le asigna una posición aleatoria en el espacio de búsqueda
1.2 Cálculo de la aptitud inicial (Ei)
Para cada candidato se calcula el valor de la función objetivo
Este valor representa la energía de la partícula
Cuanto menor sea la energía, mejor resultará la solución
1.3 Determinación de los parámetros de los átomos
BS (Binding State) estado de enlace de un átomo; representa la posición media actual de todas las partículas
BE (Binding Energy) energía de enlace; representa la energía media de todas las partículas
LE (Lowest Energy) partícula de menor energía (mejor solución)
2. Creación de una estructura de capas
2.1 Generación de un número aleatorio de capas [1; n] para cada átomo
Determinación del número de orbitales imaginarios
Cada orbital representa un nivel de búsqueda con una intensidad distinta
2.2 Distribución de partículas
Las partículas se distribuyen en capas según la función de densidad de probabilidad (PDF)
Las capas internas suelen contener las mejores soluciones
Las capas exteriores se usan para explorar el espacio
2.3 Proceso de búsqueda para cada capa (k)
3.1 Parámetros de las capas
Estado de enlace BSk para una capa específica
BEk energía de enlace de la capa
LEk partícula con la energía más baja de la capa
3.2 Actualización de las posiciones de las partículas
Para cada partícula i en la capa k:
3.3 Generación de parámetros de control:
φ: determina el tipo de movimiento
α: factor de escalado
β: coeficiente de atracción hacia la mejor solución
γ: coeficiente de repulsión respecto al estado medio
PR: probabilidad de desplazamiento del fotón
3.4 Selección del tipo de movimiento:
si φ ≥ PR:
si Eki ≥ BEk:
// Investigación global
Xi[t+1] = Xit + αi × (βi × LE - γi × BS) / k
de lo contrario:
// Investigación local.
Xi[t+1] = Xit + αi × (βi × LEk - γi × BSk)
de lo contrario:
// Paseo aleatorio
Xki[t+1] = Xkit + ri
4. Cálculo de la aptitud (Ei)
5. Actualización de los parámetros globales
6. Repetimos desde 1.3 hasta que se cumpla el criterio de parada
Para calcular la probabilidad de la distribución de electrones alrededor del núcleo (la mejor solución), podemos usar la generación de números para diferentes distribuciones. El autor prefiere la distribución lognormal, que requiere su implementación en código. Ahora escribiremos el código del generador. Para el algoritmo, necesitaremos crear no solo una distribución lognormal, sino una distribución asimétricamente desplazada con respecto al centro (kernel), como se muestra en la figura 1. Implementaremos la función "LognormalDistribution" en la colección de bibliotecas de funciones para algoritmos de optimización, que genera un número aleatorio distribuido según la ley lognormal en los límites dados con un desplazamiento.
La función aceptará los siguientes parámetros:
1. center- valor central de la distribución.
2. min_value - valor mínimo que se puede generar.
3. max_value - valor máximo que se puede generar.
4. peakDisplCoeff - coeficiente de desplazamiento máximo relativo al centro de distribución (por defecto es igual a 0,2).
Descripción funcional:
1. Comprobación de límites:
Si "min_value" es mayor o igual a "max_value", la función retornará "max_value".
Si "max_value" es menor o igual a "min_value", la función retornará "min_value".
2. Se genera un número "random" en el rango de 0 a 1.
3. Corrección del centro:
Si "center" es menor que "min_value", se fijará en "min_value" y "random" se fijará en 1.
Si "center" es mayor que "max_value", se fijará en "max_value" y "random" se fijará en 0.
4. Se calculan los valores "peak_left" y "peak_right", que determinarán la posición de los picos de distribución.
5. Generación de valor:
Si "random" es inferior a 0,5, se realizará el cálculo para la parte izquierda de la distribución:
Se calculan los parámetros "mu_left" y "sigma_left".
Se generan números aleatorios "u1" y "u2" para el método Box-Muller.
Se aplica el método de Box-Muller para obtener un valor "z" con distribución normal.
Se calcula el resultado de la parte izquierda.
Si "random" es mayor o igual que 0,5, se realizará el mismo proceso para el lado derecho de la distribución, utilizando los parámetros "mu_right" y "sigma_right".
6. Si el valor "result" se sale de los límites "min_value" y "max_value", se llamará a la función "RNDfromCI" para "lanzar" el valor al rango aceptable, evitando así la acumulación de probabilidades en los límites de los números aleatorios generados.
//------------------------------------------------------------------------------ //The lognormal distribution of the species: min|------P---C---P------|max double C_AO_Utilities :: LognormalDistribution (double center, double min_value, double max_value, double peakDisplCoeff = 0.2) { // Check the right border if (min_value >= max_value) { return max_value; } // Check the left border if (max_value <= min_value) { return min_value; } // Generate a random number from 0 to 1 double random = MathRand () / 32767.0; // Correction of the center if it goes beyond the boundaries if (center < min_value) { center = min_value; random = 1; } if (center > max_value) { center = max_value; random = 0; } // Calculate the position of the peaks double peak_left = center - (center - min_value) * peakDisplCoeff; double peak_right = center + (max_value - center) * peakDisplCoeff; double result = 0.0; if (random < 0.5) // Left side of the distribution { // Calculate parameters for the left side double diff_center_peak = MathMax (center - peak_left, DBL_EPSILON); double diff_center_min = MathMax (center - min_value, DBL_EPSILON); double mu_left = MathLog (diff_center_peak); double sigma_left = MathSqrt (2.0 * MathLog (MathMax (diff_center_min / diff_center_peak, DBL_EPSILON)) / 9.0); // Generate random numbers for the Box-Muller method double u1 = MathRand () / 32767.0; double u2 = MathRand () / 32767.0; // Protection against null values u1 = MathMax (u1, DBL_EPSILON); // Application of the Box-Muller method double z = MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2); // Calculate the result for the left side result = center - MathExp (mu_left + sigma_left * z); } else // Right side of the distribution { // Calculate parameters for the right side double diff_peak_center = MathMax (peak_right - center, DBL_EPSILON); double diff_max_center = MathMax (max_value - center, DBL_EPSILON); double mu_right = MathLog (diff_peak_center); double sigma_right = MathSqrt (2.0 * MathLog (MathMax (diff_max_center / diff_peak_center, DBL_EPSILON)) / 9.0); // Generate random numbers for the Box-Muller method double u1 = MathRand () / 32767.0; double u2 = MathRand () / 32767.0; // Protection against null values u1 = MathMax (u1, DBL_EPSILON); // Application of the Box-Muller method double z = MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2); // Calculate the result for the right side result = center + MathExp (mu_right + sigma_right * z); } // Check and correct the result if it goes beyond the limits if (result < min_value || result > max_value) return RNDfromCI (min_value, max_value); return result; }
Vamos a escribir un script para comprobar visualmente la distribución resultante. Esto es lo que hará el script de prueba (no daremos el resto del código, la clase de trabajo con el lienzo para el banco de pruebas se puede encontrar en el archivo del artículo):
1. Se crea un objeto "Canvas" para dibujar gráficos.
2. Se inicializan los parámetros del lienzo: anchura "W", altura "H" y separaciones "O".
3. Se crean los arrays "CountL" y "CountR" para calcular los valores a la izquierda y a la derecha del parámetro de entrada "Inp_P", inicializados con ceros.
4. Se crea un elemento gráfico (lienzo) con las dimensiones y el color de fondo especificados.
La distribución lognormal describe las variables aleatorias cuyo logaritmo tiene una distribución normal. En el código, se usa para generar los valores visualizados en el gráfico.
5. El ciclo "for" genera "N" valores utilizando la función "U.LognormalDistribution()". Cada valor se compara con "Inp_P": si es menor, se incrementará el contador "CountL[i]", si es mayor, se incrementará "CountR[i]".
6. Se inicializan los arrays "CountL" y "CountR" con ceros antes de la generación.
7. Los valores mínimo y máximo de los arrays se calculan para determinar el rango de los gráficos.
8. Se calculan las coordenadas para dibujar los gráficos, incluido el centro del lienzo y los pasos para las partes izquierda y derecha.
9. Se dibujan puntos en el lienzo que representan el número de valores en los rangos, con el color definido por la frecuencia del ocurrencia.
10. El lienzo se actualiza para mostrar los cambios.
// Function called at startup void OnStart () { CCanvas Canvas; // Object for handling graphics (canvas) // Canvas parameters int W = 750; // Canvas width int H = 400; // Canvas height int O = 10; // Margins from canvas borders // Arrays for storing count values int CountL []; // Count values to the left of the input int CountR []; // Count values to the right of the input // Initialize arrays ArrayResize (CountL, Size_P); // Resize the CountL array ArrayInitialize (CountL, 0); // Initialize the CountL array with zeros ArrayResize (CountR, Size_P); // Resize the CountR array ArrayInitialize (CountR, 0); // Initialize the CountR array with zeros // Create a canvas string canvasName = "Test_Probability_Distribution_Canvas"; // Canvas name if (!Canvas.CreateBitmapLabel(canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW)) { Print ("Error creating Canvas: ", GetLastError()); // Display an error if creation fails return; } // Set up canvas properties ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false); // Make canvas visible ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true); // Make canvas selectable // Clear the canvas and draw the border Canvas.Erase (COLOR2RGB(clrWhite)); // Fill with white color Canvas.Rectangle (1, 1, W - 1, H - 1, COLOR2RGB(clrBlack)); // Draw a black frame int ind = 0; // Index for counting double X = 0.0; // Variable for storing values // Main loop for generating values for (int i = 0; i < CNT_P; i++) { // Generate log-normal distribution X = U.LognormalDistribution (Inp_P, Min_P, Max_P, PeakDisplCoeff_P); // Determine which side of the input parameter the value falls on if (X < Inp_P) { // Calculate the index for the left part ind = (int) U.Scale(X, Min_P, Inp_P, 0, Size_P, true); if (ind >= Size_P) ind = Size_P - 1; // Limit the index if (ind < 0) ind = 0; // Limit the index CountL [ind] += 1; // Increment the counter for the left side } else { // Calculate the index for the right side ind = (int) U.Scale (X, Inp_P, Max_P, 0, Size_P, false); if (ind >= Size_P) ind = Size_P - 1; // Limit the index if (ind < 0) ind = 0; // Limit the index CountR [ind] += 1; // Increment the counter for the right side } } // Define minimum and maximum values for the graph int minCNT = CNT_P; // Initial value for the minimum counter int maxCNT = 0; // Initial value for the max counter // Finding minimum and maximum values in counters for (int i = 0; i < Size_P; i++) { if (CountL [i] > maxCNT) maxCNT = CountL [i]; // Update the max value for the left side if (CountR [i] > maxCNT) maxCNT = CountR [i]; // Update the max value for the right side if (CountL [i] < minCNT) minCNT = CountL [i]; // Update the min value for the left side if (CountR [i] < minCNT) minCNT = CountR [i]; // Update the minimum value for the right side } // Variables for drawing graphs int x = 0.0; // X coordinate int y = 0.0; // Y coordinate color clrF; // Color int centre = 0; // Canvas center int stepL = 0; // Left side step int stH_L = 0; // Left side height int stepR = 0; // Right side step int stH_R = 0; // Right side height // Determine the center of the canvas centre = (int) U.Scale(Inp_P, Min_P, Max_P, O, W - O - 1, false); // Calculate steps and heights for the left side stepL = (centre - O) / Size_P; stH_L = stepL / 2; if (stH_L == 0) stH_L = 1; // Make sure the height is not 0 // Calculate steps and heights for the right side stepR = (W - O - centre) / Size_P; stH_R = stepR / 2; if (stH_R == 0) stH_R = 1; // Make sure the height is not 0 // Draw graphs for left and right parts for (int i = 0; i < Size_P; i++) { // Draw for the left side x = (int) U.Scale (i, 0, Size_P - 1, O, centre - stH_L, true); // Calculate the X coordinate y = (int) U.Scale (CountL [i], 0, maxCNT, O, H - O - 1, true); // Calculate the Y coordinate clrF = DoubleToColor(CountL [i], minCNT, maxCNT, 0, 255); // Define color by value // Draw dots for the left side Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); // Draw a small circle Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); // Draw a larger circle // Draw for the right side x = (int) U.Scale (i, 0, Size_P - 1, centre + stH_R, W - O - 1, false); // Calculate the X coordinate y = (int) U.Scale (CountR[i], 0, maxCNT, O, H - O - 1, true); // Calculate the Y coordinate clrF = DoubleToColor (CountR [i], minCNT, maxCNT, 0, 255); // Define color by value // Draw dots for the right side Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); // Draw a small circle Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); // Draw a larger circle } Canvas.Update (); // Update the canvas to reflect the changes}
Ejecutamos el script y obtenemos una imagen en el gráfico como en la figura 2.
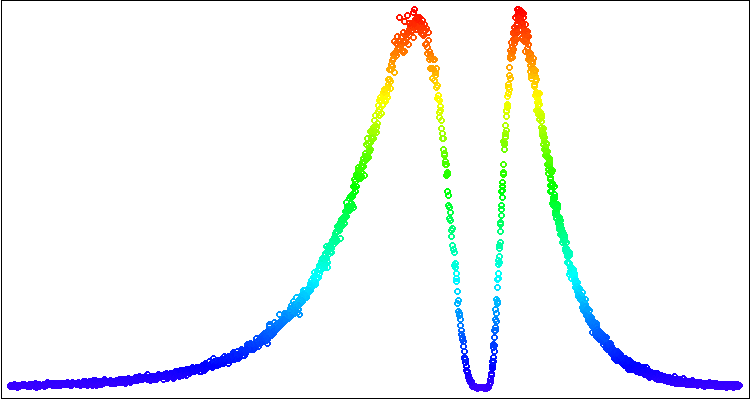
Figura 2. Visualización de la construcción de una distribución lognormal asimétrica usando la biblioteca estándar Canvas
Tras detallar la teoría de todos los pasos del algoritmo, pasaremos directamente a la implementación del código, al tiempo que en el AOS (como método de minimización para el problema), corregiremos su lógica para que funcione para la maximización. Ahora escribiremos una estructura "S_Layer", que modelará una capa de un átomo y contendrá información sobre el número de partículas de esa capa. Incluirá tanto las características numéricas como un método de inicialización. Campos de la estructura:
- pc - contador de partículas en una capa determinada del átomo, que permitirá llevar la cuenta de cuántas partículas (electrones) hay en una capa concreta.
- BSk - estado de enlace en la capa; refleja el nivel de interacción entre las partículas de la capa.
- BEk - energía de enlace en la capa; muestra la fuerza con la que las partículas de la capa están unidas entre sí.
- LEk - energía mínima en una capa; se utiliza para determinar el nivel de energía más bajo que pueden alcanzar las partículas en esa capa concreta.
El método "Init" está diseñado para inicializar los campos de la estructura con valores por defecto y permite restablecer fácilmente el estado de la capa varias veces si es necesario.
//—————————————————————————————————————————————————————————————————————————————— struct S_Layer { int pc; // particle counter double BSk; // connection state double BEk; // binding energy double LEk; // minimum energy void Init () { pc = 0; BSk = 0.0; BEk = 0.0; LEk = 0.0; } }; //——————————————————————————————————————————————————————————————————————————————
A continuación, analizaremos la estructura "S_Atom" y su método "Init". "S_Atom" es una estructura que supone un átomo compuesto de múltiples capas. Cada capa se modela utilizando el array "layers []" de la estructura "S_Layer", descrita anteriormente. Campos de la estructura:
- Init - método para inicializar un array de capas de átomos e inicializar cada capa en ese array.
- layersNumb - este parámetro entero indica el número de capas que se crearán para este átomo.
//—————————————————————————————————————————————————————————————————————————————— struct S_Atom { S_Layer layers []; // array of atom layers void Init (int layersNumb) { ArrayResize (layers, layersNumb); for (int i = 0; i < layersNumb; i++) layers [i].Init (); } }; //——————————————————————————————————————————————————————————————————————————————
A continuación, vendrá la siguiente estructura "S_Electron" y su método "Init". La estructura representa un electrón miembro de la población de la solución que contiene información sobre su posición en la capa correspondiente del átomo. Los campos "layerID []" suponen un array de números enteros que almacena los identificadores de las capas a las que pertenece el electrón. Cada identificador se corresponderá con una capa específica del átomo, lo cual nos permitirá saber en qué nivel se encuentra un electrón.
//—————————————————————————————————————————————————————————————————————————————— struct S_Electron { int layerID []; // array of layer IDs for the electron void Init (int coords) { ArrayResize (layerID, coords); } }; //——————————————————————————————————————————————————————————————————————————————
La clase de algoritmo AOS "C_AO_AOS" hereda de la clase básica "C_AO" e implica funcionalidad común relacionada con las órbitas atómicas.
Parámetros de la clase:
- popSize - tamaño de la población en el algoritmo.
- maxLayers - número máximo de capas que se pueden utilizar en el modelo atómico.
- photonEmissions - número de emisiones de fotones que se utilizarán en el proceso de optimización.
- PR - coeficiente de transición fotónica, determina la probabilidad de transición entre estados.
- peakPosition - posición del pico en la distribución lognormal.
Métodos de clase:
1. SetParams () - establece los parámetros del algoritmo leyendo los valores del array "params".
2. Init () - inicializa el algoritmo con los parámetros de búsqueda especificados: rangos mínimo y máximo, paso de búsqueda y número de épocas.
3. Moving () - método para mover partículas en el espacio de búsqueda.
4. Revision () - método se encarga de revisar las mejores soluciones encontradas durante el proceso de optimización.
Campos privados de la clase:
- atomStage - la etapa actual del átomo define en qué etapa se encuentran los procesos del átomo.
- currentLayers [] - el array almacena información sobre el número actual de capas para cada átomo (en cada época el número de capas en cada átomo será un número aleatorio en el rango [1; maxLayers].
- S_Atom atoms [] - array de átomos cuyo tamaño corresponde al número de coordenadas utilizadas en el algoritmo.
- S_Electron electrons [] - array de electrones correspondiente al tamaño de la población.
- BS [] - el array almacena los estados de enlace entre electrones a través de la población.
Métodos privados de clase:
1. GetOrbitBandID () - obtiene el ID de banda orbital para parámetros establecidos como el número de capas y rangos.2. DistributeParticles() - método para distribuir partículas en el espacio de búsqueda.
3. LayersGenerationInAtoms () - genera el número de capas en los átomos.
4. UpdateElectronsIDs () - actualiza los identificadores de capa de los electrones.
5. CalcLayerParams () - calcula los parámetros de la capa e incluye la definición de niveles de energía y enlaces.
6. ActualizarElectrones () - actualiza la posición de los electrones.
//—————————————————————————————————————————————————————————————————————————————— // Class implementing the atomic optimization algorithm (Atomic Orbital Search) class C_AO_AOS : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_AOS () { } C_AO_AOS () { ao_name = "AOS"; ao_desc = "Atomic Orbital Search"; ao_link = "https://www.mql5.com/es/articles/16276"; popSize = 50; // population size maxLayers = 5; // maximum number of layers photonEmissions = 1; // number of photon emissions PR = 0.1; // photon transition coefficient peakPosition = 0.05; // peak position in the log-normal distribution ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "maxLayers"; params [1].val = maxLayers; params [2].name = "photonEmissions"; params [2].val = photonEmissions; params [3].name = "photonRate"; params [3].val = PR; params [4].name = "peakPsition"; params [4].val = peakPosition; } // Setting algorithm parameters void SetParams () { popSize = (int)params [0].val; maxLayers = (int)params [1].val; photonEmissions = (int)params [2].val; PR = params [3].val; peakPosition = params [4].val; } // Initialization of the algorithm with the given search parameters bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Method of moving particles void Revision (); // Method of revising the best solutions //---------------------------------------------------------------------------- int maxLayers; // maximum number of layers int photonEmissions; // number of photon emissions double PR; // photon transition coefficient double peakPosition; // peak position in the log-normal distribution private: //------------------------------------------------------------------- int atomStage; // current stage of the atom int currentLayers []; // current number of layers for the corresponding atom (coordinates) S_Atom atoms []; // atoms with their size corresponding to the number of coordinates S_Electron electrons []; // electrons corresponding to the population size double BS []; // connection states // Get orbital band for given parameters int GetOrbitBandID (int layersNumb, double min, double max, double center, double p); // Distribution of particles in the search space void DistributeParticles (); // Generate layers in atoms void LayersGenerationInAtoms (); // Update electron IDs void UpdateElectronsIDs (); // Calculate layer parameters void CalcLayerParams (); // Update electron positions void UpdateElectrons (); }; //——————————————————————————————————————————————————————————————————————————————
Veamos qué ocurre en el método "Init" de la clase de algoritmo AOS.
1. Inicialización estándar: el método comienza con una llamada a "StandardInit" y ejecuta los pasos comunes de inicialización como el establecimiento de rangos para las coordenadas.
2. Inicialización de variables:
- atomStage - se establece en "0", lo cual significa que el algoritmo comienza desde la etapa inicial.
- ArrayResize (currentLayers, coords) - redimensiona el array "currentLayers" según el número de coordenadas "coords".
- ArrayResize (atoms, coords) - redimensiona el array "atoms", creando un objeto distinto para cada átomo (coordenadas). Para cada átomo, se llama al método "Init (maxLayers)" para inicializarlo con el número máximo de capas.
- ArrayResize (electrons, popSize) - redimensiona el array "electrons" según el tamaño de la población "popSize". Para cada electrón, se crea un array "layerID" que corresponde al número de coordenadas.
- ArrayResize (BS, coords) - redimensiona el array "BS", que almacena los estados de cada coordenada.
4. Si todas las operaciones de inicialización se han efectuado correctamente, el método retornará "true".
//—————————————————————————————————————————————————————————————————————————————— // Initialize the algorithm bool C_AO_AOS::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- atomStage = 0; ArrayResize (currentLayers, coords); ArrayResize (atoms, coords); for (int i = 0; i < coords; i++) atoms [i].Init (maxLayers); ArrayResize (electrons, popSize); for (int i = 0; i < popSize; i++) ArrayResize (electrons [i].layerID, coords); ArrayResize (BS, coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Método para mover las partículas. Vamos a describir el métodoMoving:
1. Posicionamiento aleatorio inicial:
- Si la variable "revision" es "false", significará que el algoritmo aún no ha comenzado su trabajo. En este caso, se producirá un posicionamiento aleatorio de las partículas.
- A continuación, el ciclo "for" anidado recorrerá todos los electrones (tamaño de la población) y para cada coordenada generará un valor aleatorio utilizando el método "u.RNDfromCI", que tomará un valor del rango dado por "rangeMin" y "rangeMax". A continuación, este valor se ajustará mediante el método "u.SeInDiSp", que fijará el valor según el paso especificado.
2. Ejecución de la etapa adecuada en la evolución de los átomos:
- Si "revision" es "true", significará que el algoritmo ya se ha inicializado y se pueden ejecutar los pasos básicos. Dependiendo de la etapa actual de "atomStage", se llamarán diferentes métodos:
- Si "atomStage" es "0", se llamará "DistributeParticles ()", que se encargará de distribuir las partículas en el espacio según una distribución lognormal asimétrica.
- En caso contrario, se llamarán los métodos que generan capas en los átomos, se actualizarán los identificadores de electrones, se calcularán los parámetros de las capas y se actualizarán las posiciones de los electrones.
3. Una vez realizadas todas las operaciones necesarias, "atomStage" se incrementará en "1". Si "atomStage" supera el valor de "photonEmissions", se restablecerá a "0", permitiendo que los pasos del algoritmo sean cíclicos.
//—————————————————————————————————————————————————————————————————————————————— // Particle displacement method void C_AO_AOS::Moving () { // Initial random positioning if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Execute the corresponding stage of the algorithm if (atomStage == 0) { DistributeParticles (); } else { LayersGenerationInAtoms (); UpdateElectronsIDs (); CalcLayerParams (); UpdateElectrons (); } // Proceed to the next stage atomStage++; if (atomStage > photonEmissions) atomStage = 0; } //——————————————————————————————————————————————————————————————————————————————
Vamos a desglosar los métodos específicos. El método "GetOrbitBandID" de la clase "C_AO_AOS" está diseñado para determinar la banda orbital para una partícula basándose en su posición relativa a un centro dado. Toma el número de capas, los valores mínimo y máximo, el centro y la posición de la partícula "p".
1. Calcula la anchura de las bandas a la izquierda y la derecha del centro.
2. Si la posición de la partícula "p" es inferior al centro, buscará en cuál de las bandas de la izquierda se encuentra.
3. Si es más grande, buscará en las bandas correctas.
4. Si es igual al centro, devolverá el número 0 (centro).
Así, la función devuelve el índice de la banda orbital correspondiente para una posición dada.
//—————————————————————————————————————————————————————————————————————————————— // Determining the orbital band for a particle int C_AO_AOS::GetOrbitBandID (int layersNumb, double min, double max, double center, double p) { // Calculate the width of the bands to the left and right of the center double leftWidth = (center - min) / layersNumb; double rightWidth = (max - center) / layersNumb; // Define the band index if (p < center) { // The object is located to the left of the center for (int i = 1; i <= layersNumb; i++) { if (p >= center - i * leftWidth) return i - 1; } return layersNumb - 1; // If the object is in the leftmost band } else if (p > center) { // The object is located to the right of the center for (int i = 1; i <= layersNumb; i++) { if (p <= center + i * rightWidth) return i - 1; } return layersNumb - 1; // If the object is in the far right band } else { // The object is in the center return 0; } } //——————————————————————————————————————————————————————————————————————————————
El método "DistributeParticles" de la clase "C_AO_AOS" se encarga de distribuir las partículas en el espacio de búsqueda. El método distribuye las partículas en el espacio de búsqueda usando una distribución lognormal.
Para cada partícula (en un ciclo por "popSize") y para cada coordenada (en un ciclo por "coords"):
- Genera la posición de la partícula mediante una distribución lognormal usando los parámetros dados ("cB", "rangeMin", "rangeMax", "peakPosition").
- Aplica la función "SeInDiSp" para ajustar el valor de la posición de la partícula dentro del rango especificado, teniendo en cuenta el paso.
//—————————————————————————————————————————————————————————————————————————————— // Distribution of particles in the search space void C_AO_AOS::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Use log-normal distribution to position particles a [i].c [c] = u.LognormalDistribution (cB [c], rangeMin [c], rangeMax [c], peakPosition); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
El método "UpdateElectronsIDs" de la clase "C_AO_AOS", que actualiza los identificadores de capa para los electrones dependiendo de sus coordenadas y parámetros dados.
//—————————————————————————————————————————————————————————————————————————————— // Update layer IDs for each electron void C_AO_AOS::UpdateElectronsIDs () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { electrons [i].layerID [c] = GetOrbitBandID (currentLayers [c], rangeMin [c], rangeMax [c], cB [c], a [i].c [c]); } } } //——————————————————————————————————————————————————————————————————————————————
El método "CalcLayerParams" de la clase "C_AO_AOS" se utiliza para calcular los parámetros de cada capa de átomos del sistema. Aquí tenemos los principales componentes del método:
1. Inicialización de la variable: "energy" es una variable para almacenar la energía máxima que se actualizará durante el procesamiento de los electrones.
2. El ciclo recorre todos los átomos (coordenadas) del sistema. El índice "c" indica el átomo actual.
3. Para cada átomo, se llama al método "Init", que inicializa los parámetros para el número máximo de capas especificado por la variable "maxLayers".
4. Ciclo de capas: ciclo interno que recorre todas las capas asociadas al átomo actual, "currentLayers [c]" indica el número de capas del átomo "c".
5. Procesamiento de electrones: otro ciclo interno recorre todos los electrones "e" de la población, donde se comprueba si el electrón actual pertenece a la capa "L" para el átomo "c".
6. Actualización de los parámetros de la capa:
- Si un electrón pertenece a una capa, aumentará el número de partículas en la capa.
- Los valores de energía "BEk" y de estado "BSk" se actualizan para la capa según las propiedades del electrón.
- Si la energía del electrón "a[e].f" es mayor que la energía máxima actual "energy" de la capa, se actualizarán los valores de la energía máxima "energy" y del estado "LEk".
7. Cálculo de los valores medios de la capa: si el contador de partículas "pc" no es igual a cero, se calcularán los valores medios de energía y estado.
8. Cálculo del estado de enlace total: de forma similar, el estado de enlace se calcula para cada átomo "BS", pero para la población de electrones en conjunto.
//—————————————————————————————————————————————————————————————————————————————— // Calculate parameters for each layer void C_AO_AOS::CalcLayerParams () { double energy; // Handle each coordinate (atom) for (int c = 0; c < coords; c++) { atoms [c].Init (maxLayers); // Handle each layer for (int L = 0; L < currentLayers [c]; L++) { energy = -DBL_MAX; // Handle each electron for (int e = 0; e < popSize; e++) { if (electrons [e].layerID [c] == L) { atoms [c].layers [L].pc++; atoms [c].layers [L].BEk = a [e].f; atoms [c].layers [L].BSk = a [e].c [c]; if (a [e].f > energy) { energy = a [e].f; atoms [c].layers [L].LEk = a [e].c [c]; } } } // Calculate average values for the layer if (atoms [c].layers [L].pc != 0) { atoms [c].layers [L].BEk /= atoms [c].layers [L].pc; atoms [c].layers [L].BSk /= atoms [c].layers [L].pc; } } } // Calculate the general state of connections ArrayInitialize (BS, 0); for (int c = 0; c < coords; c++) { for (int e = 0; e < popSize; e++) { BS [c] += a [e].c [c]; } BS [c] /= popSize; } } //——————————————————————————————————————————————————————————————————————————————
El método "UpdateElectrons" de la clase "C_AO_AOS" se ocupa de actualizar la posición de los electrones en el sistema.
1. Inicialización de los parámetros: se definen los coeficientes de velocidad, los pesos de la mejor solución, los pesos medios de los estados y la probabilidad de transición.
2. Para cada partícula y cada coordenada:
- Se genera una probabilidad aleatoria "φ".
- Si "φ" es inferior al valor umbral "PR", se producirá una dispersión aleatoria y se seleccionará aleatoriamente una nueva posición dentro del intervalo especificado.
- De lo contrario:
- Se obtendrá el identificador de capa "lID" de la partícula actual.
- Se generarán valores aleatorios para los coeficientes.
- Si la energía actual de una partícula es inferior a la energía media de la capa, se producirá un movimiento hacia el óptimo global.
- Si no, se producirá un movimiento hacia el óptimo local de la capa.
- Al final, la nueva posición se limitará dentro del rango especificado teniendo en cuenta el paso.
//—————————————————————————————————————————————————————————————————————————————— // Update electron positions void C_AO_AOS::UpdateElectrons () { double α; // speed coefficient double β; // best solution weight coefficient double γ; // average state weight coefficient double φ; // transition probability double newPos; // new position double LE; // best energy double BSk; // connection state int lID; // layer ID // Handle each particle for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Random scatter newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); β = u.RNDprobab (); γ = u.RNDprobab (); // If the current particle energy is less than the average layer energy if (a [p].f < atoms [c].layers [lID].BEk) { // Moving towards the global optimum---------------------------- LE = cB [c]; newPos = a [p].c [c]+ α * (β * LE - γ * BS [c]) / currentLayers [c]; } else { // Movement towards the local optimum of the layer LE = atoms [c].layers [lID].LEk; BSk = atoms [c].layers [lID].BSk; newPos = a [p].c [c] + α * (β * LE - γ * BSk); } } // Limiting the new position within the search range taking into account the step a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
El método "Revision" de la clase "C_AO_AOS" está diseñado para revisar y actualizar las mejores soluciones (o estados óptimos) durante la iteración. Pasos del método:
1. Inicialización de la variable "bestIndex", que se usará para almacenar el índice de la mejor solución.
2. Búsqueda de la mejor solución. Condición para comprobar si el valor de la función (o puntuación) de la solución actual "a[i].f" es mayor que el valor actual de la mejor solución global "fB". Si esta condición es verdadera, el valor de la mejor solución global se actualizará hasta el valor actual y el índice de la solución actual se almacenará como la mejor solución.
3. Si se encuentra la mejor solución, las coordenadas de la mejor solución "a[bestIndex].c" se copiarán en el array "cB".
//—————————————————————————————————————————————————————————————————————————————— // Method of revising the best solutions void C_AO_AOS::Revision () { int bestIndex = -1; // Find the best solution in the current iteration for (int i = 0; i < popSize; i++) { // Update the global best solution if (a [i].f > fB) { fB = a [i].f; bestIndex = i; } } // Update the best coordinates if a better solution is found if (bestIndex != -1) ArrayCopy (cB, a [bestIndex].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Resultados de las pruebas
Vamos a ejecutar el banco de pruebas y obtener estos resultados del AOS:
AOS|Atomic Orbital Search|50.0|5.0|1.0|0.1|0.05|
=============================
5 Hilly's; Func runs: 10000; result: 0.6521321213930082
25 Hilly's; Func runs: 10000; result: 0.39883708808831186
500 Hilly's; Func runs: 10000; result: 0.2602779698842558
=============================
5 Forest's; Func runs: 10000; result: 0.5165008091396371
25 Forest's; Func runs: 10000; result: 0.30233740723010416
500 Forest's; Func runs: 10000; result: 0.1926906342754638
=============================
5 Megacity's; Func runs: 10000; result: 0.39384615384615385
25 Megacity's; Func runs: 10000; result: 0.1892307692307692
500 Megacity's; Func runs: 10000; result: 0.09903076923077013
=============================
All score: 3.00488 (33.39%)
En la visualización del funcionamiento del algoritmo AOS, observamos un comportamiento interesante: regiones características de "aglomeración" en los orbitales atómicos, pero la precisión de convergencia no es muy alta.
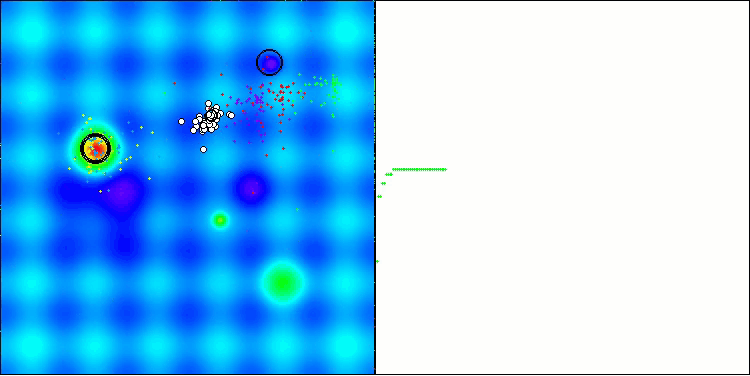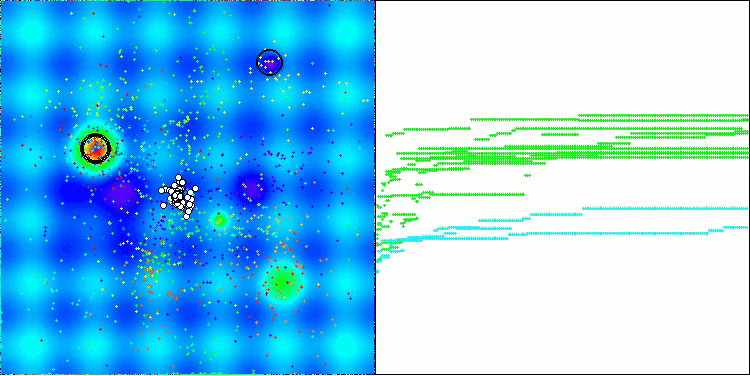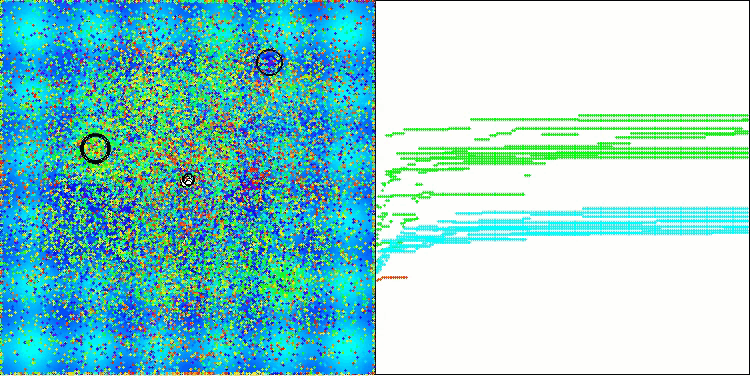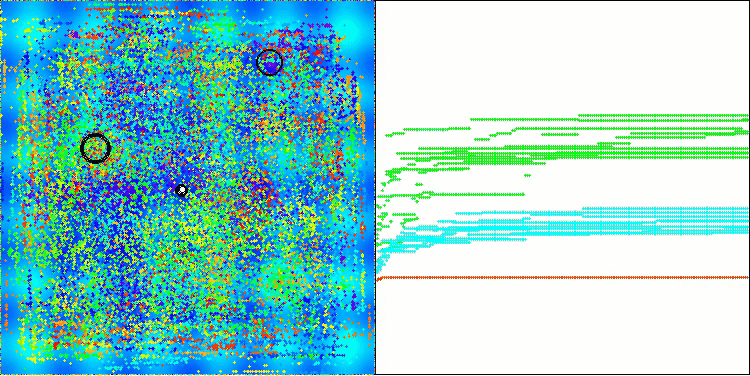
AOS en la función de prueba Hilly
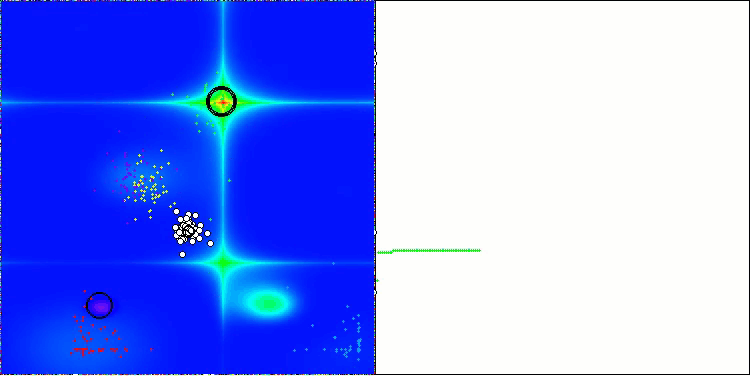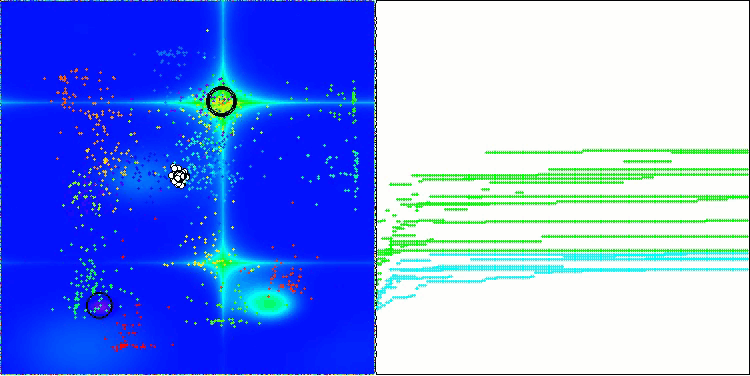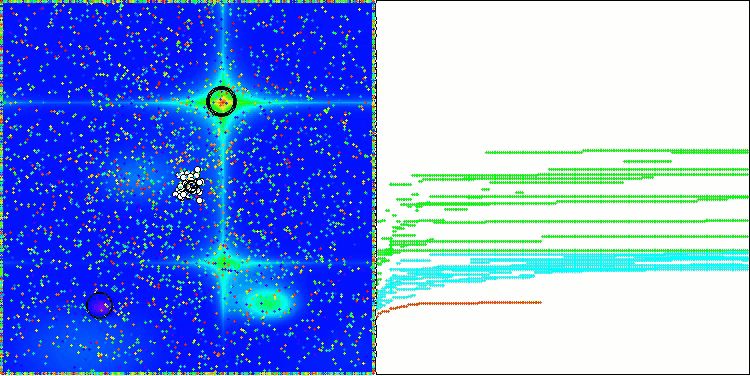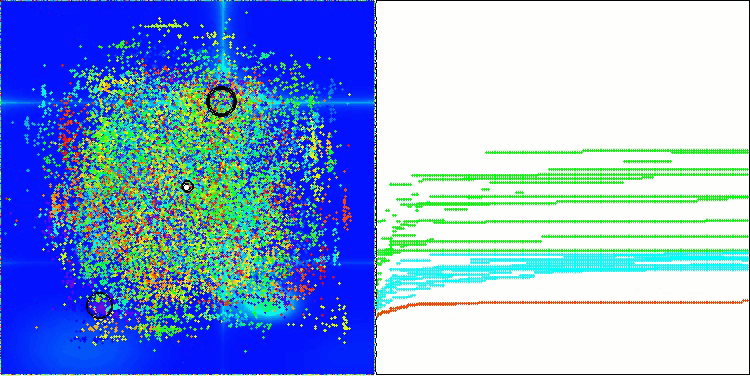
AOS en la función de prueba Forest
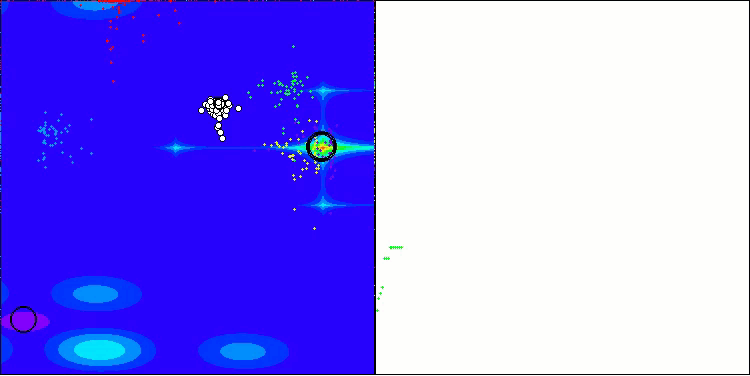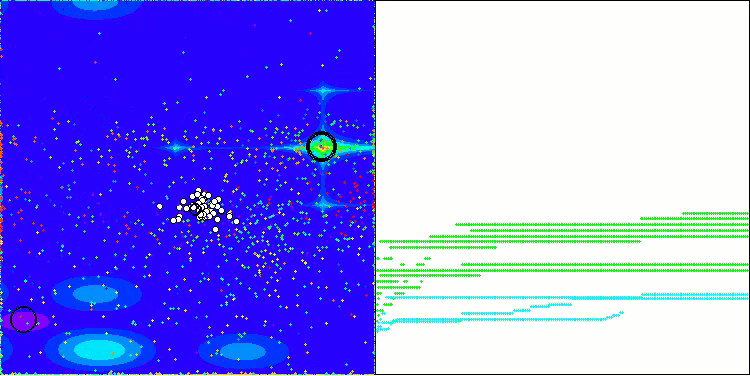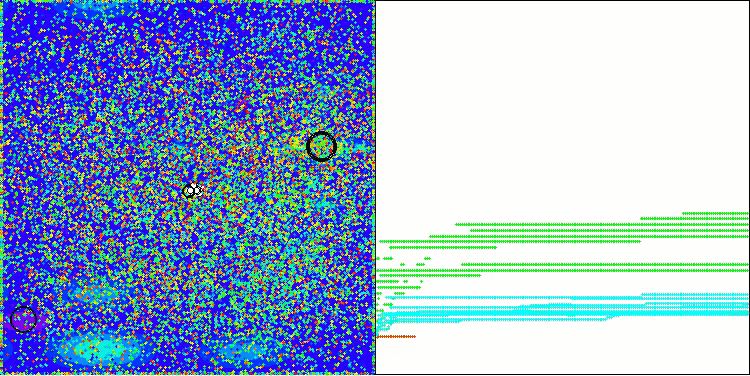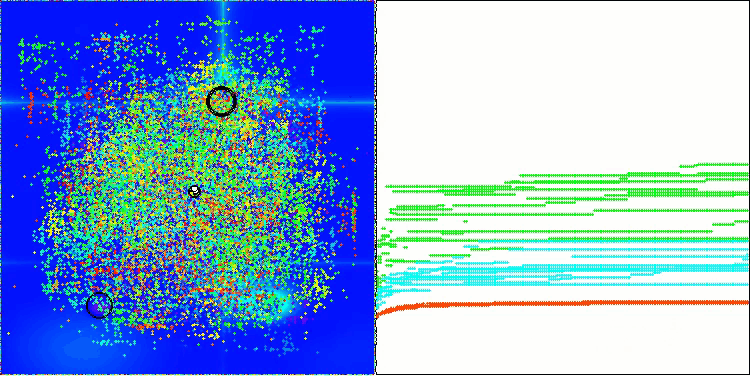
AOS en la función de prueba Megacity
Según los resultados de la prueba, el algoritmo del AOS se ha situado en el puesto 39 de la tabla de clasificación.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration optimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 12 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 13 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 14 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 15 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 16 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 17 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 18 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 19 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 20 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 21 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 22 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 23 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 24 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 25 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 26 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 27 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 28 | ABH | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 29 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 30 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 31 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 32 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 33 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 34 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 35 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 36 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 37 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 38 | FAm | firefly algorithm M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 39 | AOS | atomic orbital search | 0.65213 | 0.39884 | 0.26028 | 1.31125 | 0.51650 | 0.30234 | 0.19269 | 1.01153 | 0.39385 | 0.18923 | 0.09903 | 0.68211 | 3.005 | 33.39 |
| 40 | GSA | gravitational search algorithm | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 41 | BFO | bacterial foraging optimization | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 42 | ABC | artificial bee colony | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 43 | BA | bat algorithm | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 44 | AAA | algae adaptive algorithm | 0.50007 | 0.32040 | 0.25525 | 1.07572 | 0.37021 | 0.22284 | 0.16785 | 0.76089 | 0.27846 | 0.14800 | 0.09755 | 0.52402 | 2.361 | 26.23 |
| 45 | SA | simulated annealing | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
Conclusiones
Hoy hemos analizado un interesante algoritmo de búsqueda de orbitales atómicos que utiliza enfoques novedosos para la búsqueda global y el refinamiento local de los resultados. Gracias a las capas orbitales dinámicas de los átomos, los electrones se mueven de forma equilibrada en busca de un estado atómico estable. El algoritmo muestra un rendimiento limitado en funciones suaves, pero ofrece buenos resultados cuando se aumenta la dimensionalidad del problema, incluso en la función discreta Megacity.
Este algoritmo me parece un buen ejemplo de idea prometedora, pero su eficacia se resiente debido a algunos matices pequeños pero significativos. En el próximo artículo, veremos mi modificación del AOS y analizaremos de qué es capaz realmente este maravilloso concepto de búsqueda orbital.
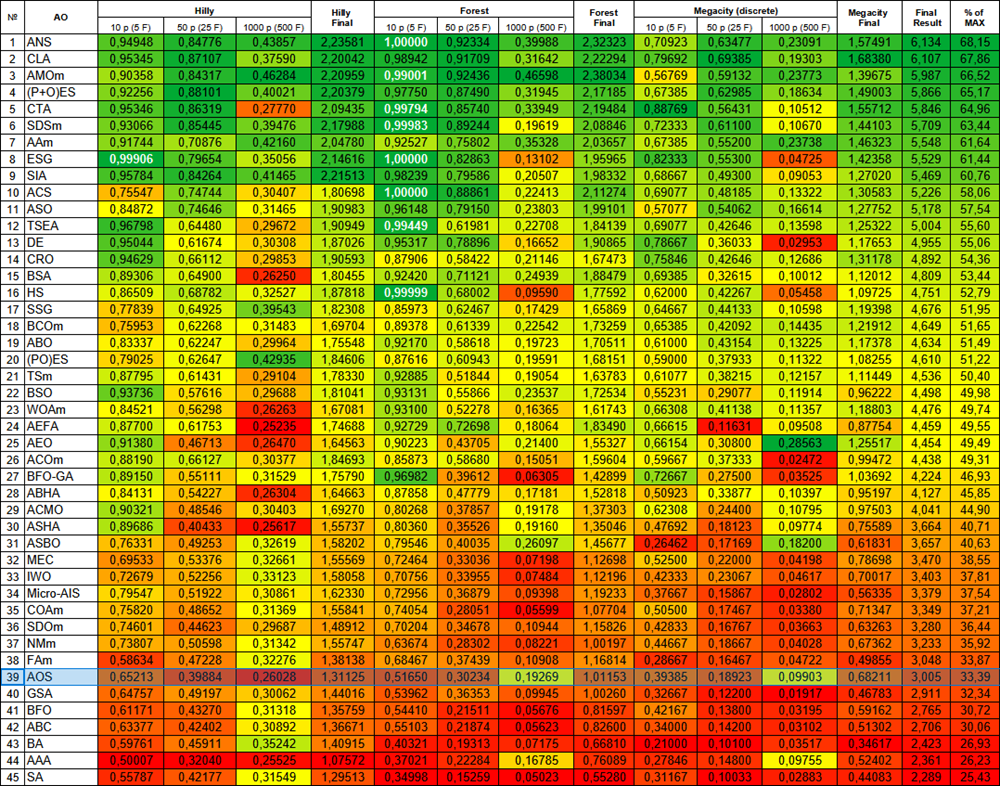
Figura 3. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0.99 se resaltan en blanco.
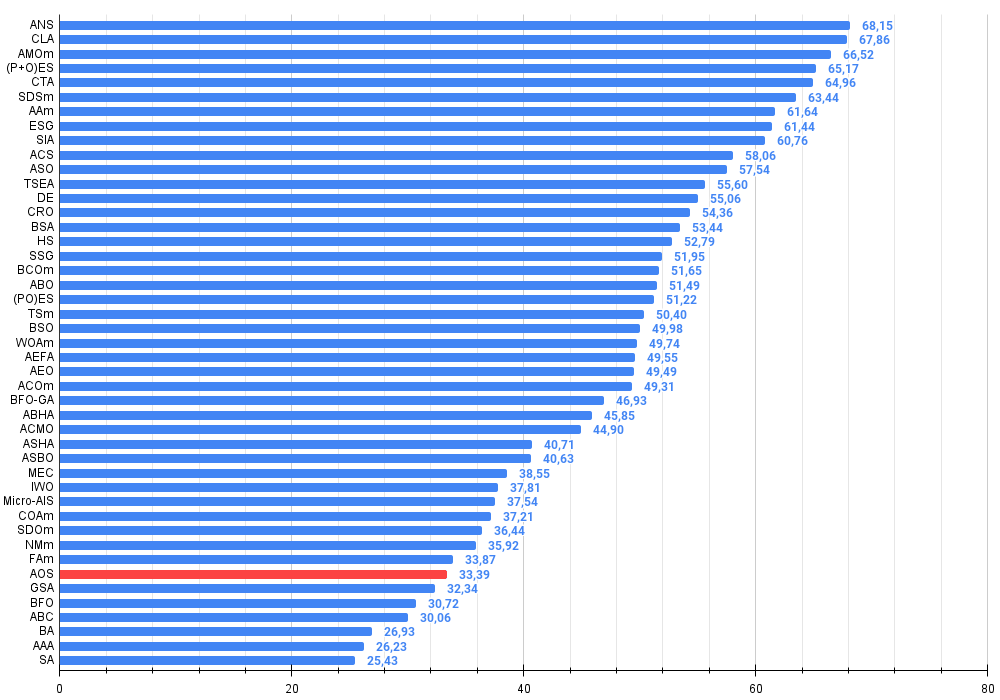
Figura 4. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor,
donde 100 es el máximo resultado teórico posible; el script para calcular la tabla de clasificación está en el archivo)
Ventajas e inconvenientes del algoritmo del AOS:
Ventajas:
- Una base prometedora para mejorar el algoritmo.
- Tiene un número reducido de parámetros externos.
Desventajas:
- La frecuente generación de números aleatorios lo hace lento.
- Aplicación bastante compleja.
- Baja precisión de convergencia.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | #C_AO.mqh | Archivo de inclusión | Clase padre de algoritmos de optimización basados en la población |
| 2 | #C_AO_enum.mqh | Archivo de inclusión | Enumeración de los algoritmos de optimización basados en la población |
| 3 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 4 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 5 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
| 6 | CalculationTestResults.mqh | Archivo de inclusión | Script para calcular los resultados en una tabla comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de pruebas único para todos los algoritmos de optimización basados en la población |
| 8 | AO_AOS_AtomicOrbitalSearch.mqh | Archivo de inclusión | Clase del algoritmo AOS |
| 9 | Test_AO_AOS.mq5 | Script | Banco de pruebas para el AOS |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16276
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Simulador rápido de estrategias comerciales en Python usando Numba
Simulador rápido de estrategias comerciales en Python usando Numba
 Reimaginando las estrategias clásicas en MQL5 (Parte IX): Análisis de múltiples marcos temporales (II)
Reimaginando las estrategias clásicas en MQL5 (Parte IX): Análisis de múltiples marcos temporales (II)
 Encabezado en Connexus (Parte 3): Dominando el uso de encabezado HTTP para solicitudes WebRequest
Encabezado en Connexus (Parte 3): Dominando el uso de encabezado HTTP para solicitudes WebRequest
 Redes neuronales en el trading: Modelo hiperbólico de difusión latente (Final)
Redes neuronales en el trading: Modelo hiperbólico de difusión latente (Final)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Algoritmo de búsqueda orbital atómica - Se ha publicado el algoritmo de búsqueda orbital atómica (AOS):
Autor: Andrey Dik
Este es el sistema completo, que incluye física, matemáticas, ajedrez, etc.