原子轨道搜索（AOS）算法

内容

1. 概述
2. 算法实现
3. 测试结果

概述

现如今，解决复杂优化问题的现代方法越来越多地从物理学原理中汲取灵感，尤其是量子力学领域。在本文中，我们将探讨基于原子轨道模型概念的原子轨道搜索（AOS）算法。该算法由马赫迪·阿齐兹（Mahdi Azizi）于2021年提出。这是一种新的元启发式方法。得益于杰出的物理学家Erwin Schroeder的科学成果，该模型将电子的行为描述为并非严格界定的轨迹，而是围绕原子核形成概率云的波函数。 

原子轨道是量子描述的结果，是电子出现概率最大的区域。在该模型中，电子在由半径和反映能量水平的量子数定义的假想电子层中运动。量子数n值越大的电子层，对应的半径越大，能量水平也越高。电子在与其他粒子相互作用及光子影响下发生激发，这种行为创造了一个动态多变的环境，在此环境中，电子在不同轨道间移动时会发射或吸收能量。

AOS算法利用这些物理原理来模拟寻找优化问题解的过程。它考虑了概率分布和相互作用动力学，从而能够高效地探索解空间。具体而言，该算法根据候选解（电子）的能量来更新其位置，而这反过来又会影响它们处于特定电子层的概率。这使得AOS不仅能够找到最优解，还能适应环境的变化。

在本文中，我们将详细研究AOS的数学模型，包括更新候选解位置的步骤，以及调节能量吸收和释放的机制。因此，AOS不仅代表了一种有趣的优化方法，还为将量子原理应用于计算问题开辟了新视野。

算法实现

AOS算法基于原子轨道模型原理，该模型考虑了原子的能量发射和吸收以及电子密度的配置。算法开始时，指定若干候选解，记为X，这些候选解被视为位于原子核周围的电子。这些候选解形成一个电子云，搜索空间被表示为一个划分为同心层的球体。候选解的通常形式如下：

X = [x₁, x₂, ..., xⱼ, ..., xₘ]，其中xᵢ是第i个候选解，m是候选解的总数。

通过随机初始化得到候选解的初始位置。每个电子都有一个由必须最小化的目标函数确定的能量水平。因此，能量水平低的电子对应于目标函数值的最优候选解，而能量水平高的电子对应于目标函数值的最差候选解。目标函数值向量可写为：

E = [E₁, E₂, ..., Eᵢ, ..., Eₘ]，其中Eᵢ是第i个候选解的能量水平。

原子核周围的假想电子层使用一个1到电子层数L之间的随机整数n来建模。半径最小的电子层L₀代表原子核，其余的Lᵢ层是电子所在的位置（在AOS中，“原子核”层也可能包含电子）。候选解在各电子层的分布是使用概率密度函数（PDF）进行的，该函数确定变量值在给定范围内的概率。该算法使用对数正态分布，使其能够模拟电子的真实波行为。候选解分布在不同的电子层中，其中包含n层候选解的向量Xₖ设置为：

Xₖ = [Xₖ₁, Xₖ₂, ..., Xₖᵢ, ..., Xₖₚ]，其中k是电子层索引，p是该层中的候选解数量。

根据原子轨道模型，假设电子处于基态能量水平。每层的束缚态和束缚能的计算方法如下：

BS_k = (1/p) * Σ(Xki),

BE_k = (1/p) * Σ(Eki).

原子的总能量水平定义为：

BS = (1/m) * Σ(Xi),

BE = (1/m) * Σ(Ei).

电子可以在光子和其他相互作用的影响下改变位置并在电子层间移动。AOS算法中候选解位置的更新是基于相互作用概率的，该概率由一个随机生成的ϕ数表示，ϕ数分布在[0,1]范围内。如果ϕ ≥ PR（光子速度参数），则可能发射或吸收能量。

如果Eₖᵢ ≥ BEₖ，则发射能量：Xₖᵢ[t+1] = Xₖᵢ[t] + αᵢ × (βᵢ × LE − γᵢ × BS) / k。

如果Eₖᵢ < BEₖ，则吸收能量：Xₖᵢ[t+1] = Xₖᵢ[t] + αᵢ × (βᵢ × LEₖ − γᵢ × BSₖ)。

如果ϕ < PR，则考虑进入磁场或与其他粒子相互作用：Xₖᵢ[t+1] = Xₖᵢ[t] + rᵢ，其中rᵢ是问题相应优化参数的最小值到最大值范围内的随机增量。

简单来说，在AOS中，候选解群体可以形象地表示为一个分子，其中原子对应于搜索空间中的坐标，而这些原子中的电子对应于特定的解。因此，如果群体由50个候选解组成，那么每个原子中将有50个电子，这些电子根据对数正态分布分布在各电子层中。

在算法描述中，作者未说明如何确定原子外层的直径，只是暗示原子核相对于各电子层位于中心。这意味着原子及其电子层在给定的问题边界内移动。为了使算法具有更多的灵活性，我们约定外层直径将对应于搜索空间中相应坐标的[最小值；最大值]范围，原子核的中心将位于给定坐标的全局最优解点。从视觉上看，AOS中的原子模型如图1所示。

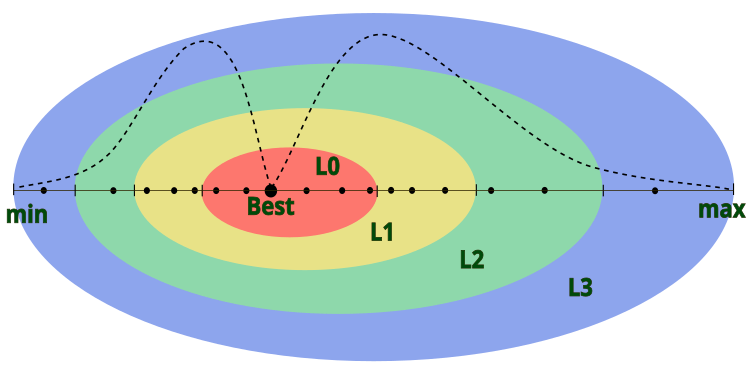
图例1. AOS算法中的原子模型，其中点代表电子，虚线代表电子的对数正态分布

AOS算法伪代码：

1. 初始化

1.1初始位置（Xi）

创建一个包含m个候选解的种群
为每个候选解在搜索空间中分配一个随机位置。

1.2计算初始适应度（Ei）

对于每个候选解，计算目标函数的值
该值代表粒子的能量。
能量越低，解越好。

1.3确定原子参数

BS（结合态）表示原子的结合状态，代表所有粒子的当前平均位置
BE（结合能）代表所有粒子的平均能量
LE（最低能量）是能量最低的粒子（最优解）

2. 创建层结构

2.1为每个原子生成一个 [1; n] 范围内的随机层数

确定想象轨道的数量
每个轨道代表一个不同强度的搜索级别。

2.2粒子分布

根据概率密度函数（PDF）将粒子分布到各层
内层通常包含最优解。
外层用于探索空间。

2.3对每一层（k）进行搜索过程

3.1层参数

BSk - 特定层的连接状态
BEk - 层的结合能
LEk - 该层中能量最低的粒子

3.2更新粒子位置

对于第k层中的每个第i个粒子：

3.3生成控制参数：

   φ：定义移动类型
α：缩放因子
β：吸引到最优解的系数
γ：排斥平均状态的系数
PR：光子移动概率

3.4选择移动类型：

   如果 φ ≥ PR：
如果 Eki ≥ BEk： // 全局搜索
           Xi[t+1] = Xit + αi × (βi × LE - γi × BS) / k
否则：
// 局部搜索
           Xi[t+1] = Xit + αi × (βi × LEk - γi × BSk)
否则：
// 随机移动
       Xki[t+1] = Xkit + ri

4. 适应度计算（Ei）  

5. 更新全局设置

6. 从1.3步骤开始重复，直至满足停止准则

要计算原子核（最优解）周围电子分布的概率，可以使用不同分布的随机数生成方法。作者倾向于使用对数正态分布，这需要在代码中实现该分布。让我们编写生成器代码。对于该算法，不仅要实现一个对数正态分布，还要实现一个相对于中心（核心）非对称偏移的分布，如图1所示。我们在优化算法函数库中实现LognormalDistribution函数，该函数在给定边界和偏移条件下，生成一个符合对数正态分布的随机数。

该函数接受以下参数：

1. center（中心） - 分布的中心值。
2. min_value（最小值） - 可生成的最小值。
3. max_value（最大值） - 可生成的最大值。4. peakDisplCoeff（峰值偏移系数） - 相对于分布中心的峰值偏移系数（默认值为0.2）。

函数描述：

1. 边界检查：
如果min_value大于或等于max_value，则函数返回max_value。
如果max_value小于或等于min_value，则函数返回min_value。

2. 生成一个0到1范围内的随机数。

3. 中心调整：
如果center小于min_value，则将其设置为min_value，并将随机数设置为1。
如果center 超过max_value，则将其设置为max_value，并将随机数设置为0。

4. 计算peak_left和peak_right值，这两个值决定分布峰值的位置。

5. 生成一个值：
如果随机数小于0.5，则对左侧的分布进行计算：
计算mu_left和sigma_left参数。
为Box-Muller方法生成随机数u1和u2。
应用Box-Muller方法得到一个正态分布的z值。
计算左侧的结果。
如果随机数大于或等于0.5，则使用mu_right和sigma_right参数对分布的右侧执行类似过程。

6. 如果生成的结果值超出min_value和max_value范围，则调用RNDfromCI函数将该值“投射”到可接受范围内，从而防止生成的随机数在边界处累积的概率性。

//------------------------------------------------------------------------------
//The lognormal distribution of the species:  min|------P---C---P------|max
double C_AO_Utilities :: LognormalDistribution (double center, double min_value, double max_value, double peakDisplCoeff = 0.2)
{
  // Check the right border
  if (min_value >= max_value)
  {
    return max_value;
  }

  // Check the left border
  if (max_value <= min_value)
  {
    return min_value;
  }

  // Generate a random number from 0 to 1
  double random = MathRand () / 32767.0;

  // Correction of the center if it goes beyond the boundaries
  if (center < min_value)
  {
    center = min_value;
    random = 1;
  }

  if (center > max_value)
  {
    center = max_value;
    random = 0;
  }

  // Calculate the position of the peaks
  double peak_left  = center - (center - min_value) * peakDisplCoeff;
  double peak_right = center + (max_value - center) * peakDisplCoeff;

  double result = 0.0;

  if (random < 0.5) // Left side of the distribution
  {
    // Calculate parameters for the left side
    double diff_center_peak = MathMax (center - peak_left, DBL_EPSILON);
    double diff_center_min  = MathMax (center - min_value, DBL_EPSILON);

    double mu_left = MathLog (diff_center_peak);
    double sigma_left = MathSqrt (2.0 * MathLog (MathMax (diff_center_min / diff_center_peak, DBL_EPSILON)) / 9.0);

    // Generate random numbers for the Box-Muller method
    double u1 = MathRand () / 32767.0;
    double u2 = MathRand () / 32767.0;

    // Protection against null values
    u1 = MathMax (u1, DBL_EPSILON);

    // Application of the Box-Muller method
    double z = MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2);

    // Calculate the result for the left side
    result = center - MathExp (mu_left + sigma_left * z);
  }
  else // Right side of the distribution
  {
    // Calculate parameters for the right side
    double diff_peak_center = MathMax (peak_right - center, DBL_EPSILON);
    double diff_max_center  = MathMax (max_value - center,  DBL_EPSILON);

    double mu_right    = MathLog  (diff_peak_center);
    double sigma_right = MathSqrt (2.0 * MathLog (MathMax (diff_max_center / diff_peak_center, DBL_EPSILON)) / 9.0);

    // Generate random numbers for the Box-Muller method
    double u1 = MathRand () / 32767.0;
    double u2 = MathRand () / 32767.0;

    // Protection against null values
    u1 = MathMax (u1, DBL_EPSILON);

    // Application of the Box-Muller method
    double z = MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2);

    // Calculate the result for the right side
    result = center + MathExp (mu_right + sigma_right * z);
  }

  // Check and correct the result if it goes beyond the limits
  if (result < min_value || result > max_value) return RNDfromCI (min_value, max_value);

  return result;
}

让我们编写一个脚本来对所得分布进行可视化检查。以下是测试脚本的功能（我们不会提供其余代码——测试平台中用于操作画布的类可在文章存档中找到）：

1. 创建Canvas对象以绘制图形。
2. 初始化画布参数：W（宽度）、H（高度）和O（边距）。
3. 创建CountL和CountR数组，用于统计输入值Inp_P左右两侧的值数量，并初始化为0。
4. 创建具有指定尺寸和背景颜色的图形元素（画布）。

对数正态分布描述的是其对数服从正态分布的随机变量。在代码中，它用于生成在图表中可视化的值。

5. 在for循环中，使用U.LognormalDistribution()函数生成N个值。将每个值与Inp_P进行比较：如果小于Inp_P，则增加CountL[i]计数器；如果大于，则增加CountR[i]计数器。
6. 在生成值之前，将CountL和CountR初始化为0。
7. 计算数组中的最小值和最大值，以确定图表的取值范围。
8. 计算绘制图表的坐标，包括画布中心以及左右两部分的步长。
9. 在画布上绘制点，这些点代表各取值范围内的值的数量，颜色由出现频率决定。
10. 更新画布以展示更改。

// Function called at startup
void OnStart ()
{
    CCanvas Canvas; // Object for handling graphics (canvas)

    // Canvas parameters
    int W = 750; // Canvas width
    int H = 400; // Canvas height
    int O = 10;  // Margins from canvas borders

    // Arrays for storing count values
    int CountL []; // Count values to the left of the input
    int CountR []; // Count values to the right of the input

    // Initialize arrays
    ArrayResize (CountL, Size_P);  // Resize the CountL array
    ArrayInitialize (CountL, 0);   // Initialize the CountL array with zeros

    ArrayResize (CountR, Size_P);  // Resize the CountR array
    ArrayInitialize (CountR, 0);   // Initialize the CountR array with zeros

    // Create a canvas
    string canvasName = "Test_Probability_Distribution_Canvas"; // Canvas name
    if (!Canvas.CreateBitmapLabel(canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW))
    {
        Print ("Error creating Canvas: ", GetLastError()); // Display an error if creation fails
        return;
    }

    // Set up canvas properties
    ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false);    // Make canvas visible
    ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true); // Make canvas selectable

    // Clear the canvas and draw the border
    Canvas.Erase (COLOR2RGB(clrWhite));                         // Fill with white color
    Canvas.Rectangle (1, 1, W - 1, H - 1, COLOR2RGB(clrBlack)); // Draw a black frame

    int    ind = 0;   // Index for counting
    double X   = 0.0; // Variable for storing values

    // Main loop for generating values
    for (int i = 0; i < CNT_P; i++)
    {
        // Generate log-normal distribution
        X = U.LognormalDistribution (Inp_P, Min_P, Max_P, PeakDisplCoeff_P);

        // Determine which side of the input parameter the value falls on
        if (X < Inp_P)
        {
            // Calculate the index for the left part
            ind = (int) U.Scale(X, Min_P, Inp_P, 0, Size_P, true);
            if (ind >= Size_P) ind = Size_P - 1; // Limit the index
            if (ind < 0) ind = 0;                // Limit the index
            CountL [ind] += 1;                   // Increment the counter for the left side
        }
        else
        {
            // Calculate the index for the right side
            ind = (int) U.Scale (X, Inp_P, Max_P, 0, Size_P, false);
            if (ind >= Size_P) ind = Size_P - 1; // Limit the index
            if (ind < 0) ind = 0;                // Limit the index
            CountR [ind] += 1;                   // Increment the counter for the right side
        }
    }

    // Define minimum and maximum values for the graph
    int minCNT = CNT_P; // Initial value for the minimum counter
    int maxCNT = 0;     // Initial value for the max counter

    // Finding minimum and maximum values in counters
    for (int i = 0; i < Size_P; i++)
    {
        if (CountL [i] > maxCNT) maxCNT = CountL [i]; // Update the max value for the left side
        if (CountR [i] > maxCNT) maxCNT = CountR [i]; // Update the max value for the right side

        if (CountL [i] < minCNT) minCNT = CountL [i]; // Update the min value for the left side
        if (CountR [i] < minCNT) minCNT = CountR [i]; // Update the minimum value for the right side
    }

    // Variables for drawing graphs
    int   x      = 0.0; // X coordinate
    int   y      = 0.0; // Y coordinate
    color clrF;         // Color
    int   centre = 0;   // Canvas center
    int   stepL  = 0;   // Left side step
    int   stH_L  = 0;   // Left side height
    int   stepR  = 0;   // Right side step
    int   stH_R  = 0;   // Right side height

    // Determine the center of the canvas
    centre = (int) U.Scale(Inp_P, Min_P, Max_P, O, W - O - 1, false);

    // Calculate steps and heights for the left side
    stepL = (centre - O) / Size_P;
    stH_L = stepL / 2;
    if (stH_L == 0) stH_L = 1; // Make sure the height is not 0

    // Calculate steps and heights for the right side
    stepR = (W - O - centre) / Size_P;
    stH_R = stepR / 2;
    if (stH_R == 0) stH_R = 1; // Make sure the height is not 0

    // Draw graphs for left and right parts
    for (int i = 0; i < Size_P; i++)
    {
        // Draw for the left side 
        x = (int) U.Scale (i, 0, Size_P - 1, O, centre - stH_L, true); // Calculate the X coordinate
        y = (int) U.Scale (CountL [i], 0, maxCNT, O, H - O - 1, true); // Calculate the Y coordinate

        clrF = DoubleToColor(CountL [i], minCNT, maxCNT, 0, 255); // Define color by value

        // Draw dots for the left side
        Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); // Draw a small circle
        Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); // Draw a larger circle

        // Draw for the right side
        x = (int) U.Scale (i, 0, Size_P - 1, centre + stH_R, W - O - 1, false); // Calculate the X coordinate
        y = (int) U.Scale (CountR[i], 0, maxCNT, O, H - O - 1, true);           // Calculate the Y coordinate

        clrF = DoubleToColor (CountR [i], minCNT, maxCNT, 0, 255); // Define color by value

        // Draw dots for the right side
        Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); // Draw a small circle
        Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); // Draw a larger circle
    }

    Canvas.Update (); // Update the canvas to reflect the changes}

让我们运行脚本，得到如图例2所示的图表画面。

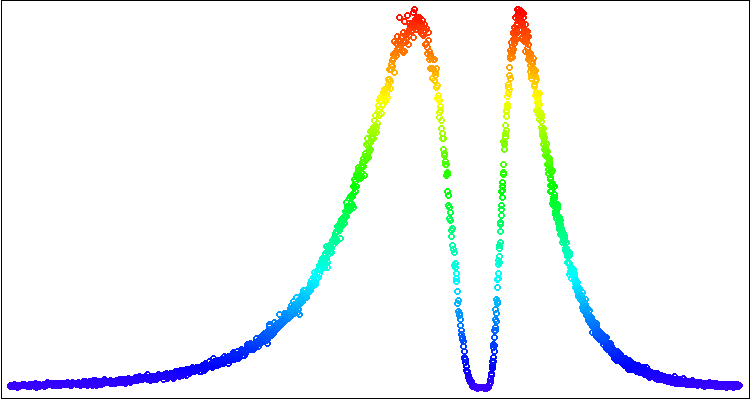
图例2. 使用标准Canvas库可视化非对称对数正态分布图

在详细研究算法各阶段的理论之后，让我们直接进入代码实现环节。虽然AOS算法是一种用于求解最小化问题的方法，但我们将调整其逻辑，使其适用于最大化问题。让我们实现S_Layer结构，该结构将模拟原子层，并包含有关该层中粒子数量的信息。它将包括数值特征和初始化方法。结构字段：

• pc — 位于原子某一给定层的粒子计数器，用于跟踪特定层中有多少粒子（电子）。 
• BSk — 层中的连接状态，反映层中粒子之间的相互作用水平。 
• BEk — 层中的结合能，显示层中粒子相互结合的紧密程度。
  
• LEk — 层中的最小能量，用于确定给定特定层中粒子能够达到的最低能级。 

Init方法旨在用默认值初始化结构字段，并允许我们在必要时轻松多次重置层状态。

//——————————————————————————————————————————————————————————————————————————————
struct S_Layer
{
    int    pc;  // particle counter
    double BSk; // connection state
    double BEk; // binding energy
    double LEk; // minimum energy

    void Init ()
    {
      pc  = 0;
      BSk = 0.0;
      BEk = 0.0;
      LEk = 0.0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

接下来，让我们看看S_Atom结构及其Init方法。S_Atom是一个表示原子的结构，该原子由多个层组成。每一层都使用前面描述的S_Layer结构数组layers []进行模拟。结构字段：

• Init — 用于初始化原子层数组的方法，同时初始化该数组中的每一层。
• layersNumb — 整数参数，用于指定为给定原子创建的层数。

//——————————————————————————————————————————————————————————————————————————————
struct S_Atom
{
    S_Layer layers [];  // array of atom layers

    void Init (int layersNumb)
    {
      ArrayResize (layers, layersNumb);
      for (int i = 0; i < layersNumb; i++) layers [i].Init ();
    }
};
//——————————————————————————————————————————————————————————————————————————————

接下来是S_Electron结构及其Init方法。该结构表示一个电子，是解群体（solution population）中的成员，包含其在原子对应层中的位置信息。layerID []字段是一个整数数组，用于存储该电子所属层的ID。每个ID对应原子中的特定层，从而可以追踪电子所处的能级。

//——————————————————————————————————————————————————————————————————————————————
struct S_Electron
{
    int layerID [];  // array of layer IDs for the electron

    void Init (int coords)
    {
      ArrayResize (layerID, coords);
    }
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_AOS 类算法继承自基础类 C_AO，并包含与原子轨道相关的通用功能。

类参数：

• popSize — 算法中的种群规模（粒子数量）。
• maxLayers — 原子模型中可使用的最大层数。
• photonEmissions — 优化过程中使用的光子发射次数。
• PR — 光子跃迁系数，决定状态间跃迁的概率。
• peakPosition — 对数正态分布中的峰值位置。

类方法：

1. SetParams () — 通过从params数组读取值来设置算法参数。
2. Init () — 使用给定的搜索参数初始化算法：最小和最大范围、搜索步长以及迭代次数（epochs）。
3. Moving () — 在搜索空间中移动粒子的方法。
4. Revision () — 负责修订优化过程中找到的最优解的方法。

类私有字段：

• atomStage — 原子过程的当前阶段。
• currentLayers [] — 每个原子当前的层数（在每次迭代中，每个原子的层数是 [1; maxLayers] 范围内的随机数）。
  
• S_Atom atoms [] — 原子数组，其大小对应于算法中使用的坐标数量。
• S_Electron electrons [] — 电子数组，对应于种群规模。
• BS [] — 整个种群中电子间的结合状态。

私有类方法：

1. GetOrbitBandID () — 根据给定参数（如层数和范围）获取轨道带ID。
2. DistributeParticles() — 在搜索空间中分配粒子的方法。
3. LayersGenerationInAtoms () — 生成原子中的层数。
4. UpdateElectronsIDs () — 更新电子的层ID。
5. CalcLayerParams () — 计算层参数，包括确定能级和键合。
6. UpdateElectrons () — 更新电子的位置。

//——————————————————————————————————————————————————————————————————————————————
// Class implementing the atomic optimization algorithm (Atomic Orbital Search)
class C_AO_AOS : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AOS () { }
  C_AO_AOS ()
  {
    ao_name = "AOS";
    ao_desc = "Atomic Orbital Search";
    ao_link = "https://www.mql5.com/en/articles/16276";

    popSize         = 50;      // population size

    maxLayers       = 5;       // maximum number of layers
    photonEmissions = 1;       // number of photon emissions
    PR              = 0.1;     // photon transition coefficient
    peakPosition    = 0.05;    // peak position in the log-normal distribution

    ArrayResize (params, 5);

    params [0].name = "popSize";         params [0].val = popSize;
    params [1].name = "maxLayers";       params [1].val = maxLayers;
    params [2].name = "photonEmissions"; params [2].val = photonEmissions;
    params [3].name = "photonRate";      params [3].val = PR;
    params [4].name = "peakPsition";     params [4].val = peakPosition;
  }

  // Setting algorithm parameters
  void SetParams ()
  {
    popSize         = (int)params [0].val;
    maxLayers       = (int)params [1].val;
    photonEmissions = (int)params [2].val;
    PR              = params      [3].val;
    peakPosition    = params      [4].val;
  }

  // Initialization of the algorithm with the given search parameters
  bool Init (const double &rangeMinP  [], // minimum search range
             const double &rangeMaxP  [], // maximum search range
             const double &rangeStepP [], // search step
             const int     epochsP = 0);  // number of epochs

  void Moving   (); // Method of moving particles
  void Revision (); // Method of revising the best solutions

  //----------------------------------------------------------------------------
  int    maxLayers;       // maximum number of layers
  int    photonEmissions; // number of photon emissions
  double PR;              // photon transition coefficient
  double peakPosition;    // peak position in the log-normal distribution

  private: //-------------------------------------------------------------------
  int        atomStage;        // current stage of the atom
  int        currentLayers []; // current number of layers for the corresponding atom (coordinates)
  S_Atom     atoms         []; // atoms with their size corresponding to the number of coordinates
  S_Electron electrons     []; // electrons corresponding to the population size
  double     BS            []; // connection states

  // Get orbital band for given parameters
  int  GetOrbitBandID          (int layersNumb, double min, double max, double center, double p);

  // Distribution of particles in the search space
  void DistributeParticles     ();

  // Generate layers in atoms
  void LayersGenerationInAtoms ();

  // Update electron IDs
  void UpdateElectronsIDs      ();

  // Calculate layer parameters 
  void CalcLayerParams         ();

  // Update electron positions
  void UpdateElectrons         ();
};
//——————————————————————————————————————————————————————————————————————————————

让我们看一下AOS算法类中的Init方法的作用。

1. 标准初始化：该方法首先调用StandardInit，执行常见的初始化步骤，例如设置坐标范围。 

2. 变量初始化：

• atomStage  — 设置为0，表示算法从初始阶段开始。
• ArrayResize (currentLayers, coords)根据coords坐标数量调整currentLayers组大小。
• ArrayResize (atoms, coords)调整atoms数组大小，为每个原子（坐标）创建单独的对象。对每个原子调用Init (maxLayers)方法，用最大层数进行初始化。
• ArrayResize (electrons, popSize)根据popSize种群规模调整electrons数组大小。为每个电子创建layerID数组。数组大小与坐标数量对应
• ArrayResize (BS, coords)调整BS数组大小，用于存储每个坐标的状态。

4. 如果所有初始化操作均成功，该方法返回true。

//——————————————————————————————————————————————————————————————————————————————
// Initialize the algorithm
bool C_AO_AOS::Init (const double &rangeMinP [],
                     const double &rangeMaxP [],
                     const double &rangeStepP [],
                     const int epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  atomStage = 0;

  ArrayResize (currentLayers, coords);

  ArrayResize (atoms, coords);
  for (int i = 0; i < coords; i++) atoms [i].Init (maxLayers);

  ArrayResize (electrons,   popSize);
  for (int i = 0; i < popSize; i++) ArrayResize (electrons [i].layerID, coords);

  ArrayResize (BS, coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

粒子位移方法以下是对Moving方法的描述：

1. 初始随机定位：

• 如果revision变量等于false，表示算法尚未开始运行。此时，粒子会进行随机定位。
•  接下来，嵌套的for循环遍历所有电子（种群规模），并使用 u.RNDfromCI方法为每个坐标生成一个随机值。该方法从rangeMin和rangeMax指定的范围内取值。然后，使用u.SeInDiSp对该值进行调整，使其符合指定的“步长”（step）。

2. 执行原子演化的相应阶段：

• 如果revision为true，表示算法已完成初始化，可以执行其主要阶段。根据atomStage的当前阶段，调用不同的方法：
• 如果atomStage为0，调用DistributeParticles ()。该方法负责按照非对称对数正态分布在空间中分布粒子。
• 否则，调用以下方法：生成原子中的层（LayersGenerationInAtoms()）、更新电子的层ID（UpdateElectronsIDs()）、计算层参数（CalcLayerParams()）和更新电子位置（UpdateElectrons()）。

3. 完成所有必要操作后，atomStage增加1。如果atomStage超过photonEmissions的值，则重置为0，使算法阶段可以循环重复执行。

//——————————————————————————————————————————————————————————————————————————————
// Particle displacement method
void C_AO_AOS::Moving ()
{
  // Initial random positioning
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  // Execute the corresponding stage of the algorithm
  if (atomStage == 0)
  {
    DistributeParticles ();
  }
  else
  {
    LayersGenerationInAtoms ();
    UpdateElectronsIDs      ();
    CalcLayerParams         ();
    UpdateElectrons         ();
  }

  // Proceed to the next stage
  atomStage++;
  if (atomStage > photonEmissions) atomStage = 0;
}
//——————————————————————————————————————————————————————————————————————————————

让我们继续特定方法分析。C_AO_AOS类中的GetOrbitBandID方法旨在根据粒子相对于给定中心的位置，确定其所属的轨道带（orbital band）。它接受层数、最小值和最大值、中心以及粒子p的位置作为输入。

1. 计算中心左侧和右侧轨道带的宽度。
2. 如果粒子p的位置小于中心，则查找它位于左侧的哪个轨道带中。
3. 如果粒子位置大于中心，则在右侧轨道带中进行查找。
4. 如果粒子位置等于中心，则返回 0（中心）。

因此，该函数返回给定位置对应的轨道带索引。

//——————————————————————————————————————————————————————————————————————————————
// Determining the orbital band for a particle
int C_AO_AOS::GetOrbitBandID (int layersNumb, double min, double max, double center, double p)
{
  // Calculate the width of the bands to the left and right of the center
  double leftWidth  = (center - min) / layersNumb;
  double rightWidth = (max - center) / layersNumb;

  // Define the band index
  if (p < center)
  {
    // The object is located to the left of the center
    for (int i = 1; i <= layersNumb; i++)
    {
      if (p >= center - i * leftWidth) return i - 1;
    }
    return layersNumb - 1; // If the object is in the leftmost band
  }
  else
    if (p > center)
    {
      // The object is located to the right of the center
      for (int i = 1; i <= layersNumb; i++)
      {
        if (p <= center + i * rightWidth) return i - 1;
      }
      return layersNumb - 1; // If the object is in the far right band
    }
    else
    {
      // The object is in the center
      return 0;
    }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AOS类的DistributeParticles方法负责在搜索空间中分配粒子。该方法使用对数正态分布将粒子分布在搜索空间中。

对于每个粒子（在popSize的循环中）以及每个坐标（在coords的循环中）：

• 根据参数（cB、rangeMin、rangeMax、peakPosition）使用对数正态分布生成粒子位置。
• 应用SeInDiSp函数，根据给定的步长调整粒子位置值，使其保持在指定范围内。

//——————————————————————————————————————————————————————————————————————————————
// Distribution of particles in the search space
void C_AO_AOS::DistributeParticles ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Use log-normal distribution to position particles
      a [i].c [c] = u.LognormalDistribution (cB [c], rangeMin [c], rangeMax [c], peakPosition);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AOS类的UpdateElectronsIDs方法根据电子的坐标和指定的参数更新电子的层ID。

//——————————————————————————————————————————————————————————————————————————————
//  Update layer IDs for each electron
void C_AO_AOS::UpdateElectronsIDs ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      electrons [i].layerID [c] = GetOrbitBandID (currentLayers [c], rangeMin [c], rangeMax [c], cB [c], a [i].c [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AOS类的CalcLayerParams方法旨在计算系统中每一层原子的参数。该方法的主要组成部分：

1. 变量初始化：energy是一个用于存储最大能量的变量，在处理电子时会对其进行更新。

2. 循环遍历系统中的所有原子（坐标）。c索引指向当前原子。

3. 对于每个原子，调用Init方法，该方法根据maxLayers变量指定的最大层数来初始化参数。

4. 层循环：内部循环遍历与当前原子相关的所有层，currentLayers [c]表示c原子的层数。

5. 电子处理：另一个内部循环遍历种群中的所有电子e ，检查当前电子是否属于c原子的L层。

6. 更新层参数：

• 如果电子属于某一层，则该层的粒子计数器递增。
• 根据电子属性，更新该层的BEk能量值和BSk状态。
• 如果电子能量a [e].f超过当前最大能量水平energy，则更新最大energy值和LEk状态。

7. 计算层的平均值：如pc粒子计数器不为0，则计算能量和状态的平均值。

8. 计算结合态的总体状态：对于每个BS原子，类似于为每个原子计算键的状态，但这里是针对所有电子的总体。

//——————————————————————————————————————————————————————————————————————————————
// Calculate parameters for each layer
void C_AO_AOS::CalcLayerParams ()
{
  double energy;

  // Handle each coordinate (atom)
  for (int c = 0; c < coords; c++)
  {
    atoms [c].Init (maxLayers);

    // Handle each layer
    for (int L = 0; L < currentLayers [c]; L++)
    {
      energy = -DBL_MAX;

      // Handle each electron
      for (int e = 0; e < popSize; e++)
      {
        if (electrons [e].layerID [c] == L)
        {
          atoms [c].layers [L].pc++;
          atoms [c].layers [L].BEk = a [e].f;
          atoms [c].layers [L].BSk = a [e].c [c];

          if (a [e].f > energy)
          {
            energy = a [e].f;
            atoms [c].layers [L].LEk = a [e].c [c];
          }
        }
      }

      // Calculate average values for the layer
      if (atoms [c].layers [L].pc != 0)
      {
        atoms [c].layers [L].BEk /= atoms [c].layers [L].pc;
        atoms [c].layers [L].BSk /= atoms [c].layers [L].pc;
      }
    }
  }

  // Calculate the general state of connections
  ArrayInitialize (BS, 0);

  for (int c = 0; c < coords; c++)
  {
    for (int e = 0; e < popSize; e++)
    {
      BS [c] += a [e].c [c];
    }

    BS [c] /= popSize;
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AOS类的UpdateElectrons方法负责更新系统中电子的位置。

1. 参数初始化：确定速度系数、最优解权重、平均状态权重以及转移概率。

2. 针对每个粒子和每个坐标：

• 生成一个随机概率φ。
• 如果φ小于PR阈值，则发生随机散射，并在给定范围内随机选择一个新位置。
• 否则：

• 获取当前粒子的lID层ID。
• 生成用于比例的随机值。
• 如果当前粒子的能量小于该层的平均能量，则向全局最优位置移动。
• 否则，向该层的局部最优位置移动。

• 最后，在考虑步长的情况下，将新位置限制在指定范围内。

//——————————————————————————————————————————————————————————————————————————————
// Update electron positions
void C_AO_AOS::UpdateElectrons ()
{
  double α;      // speed coefficient
  double β;      // best solution weight coefficient
  double γ;      // average state weight coefficient
  double φ;      // transition probability
  double newPos; // new position
  double LE;     // best energy
  double BSk;    // connection state
  int    lID;    // layer ID

  // Handle each particle
  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      φ = u.RNDprobab ();

      if (φ < PR)
      {
        // Random scatter
        newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      }
      else
      {
        lID = electrons [p].layerID [c];

        α = u.RNDfromCI (-1.0, 1.0);
        β = u.RNDprobab ();
        γ = u.RNDprobab ();

        // If the current particle energy is less than the average layer energy
        if (a [p].f < atoms [c].layers [lID].BEk)
        {
          // Moving towards the global optimum----------------------------
          LE = cB [c];

          newPos = a [p].c [c]+ α * (β * LE - γ * BS [c]) / currentLayers [c];
        }
        else
        {
          // Movement towards the local optimum of the layer
          LE  = atoms [c].layers [lID].LEk;
          BSk = atoms [c].layers [lID].BSk;

          newPos = a [p].c [c] + α * (β * LE - γ * BSk);
        }
      }

      // Limiting the new position within the search range taking into account the step
      a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AOS类的Revision方法旨在迭代过程中对最优解（或最优状态）进行审查与更新。方法步骤：

1. 初始化bestIndex变量，该变量将用于存储最优解的索引。

2. 寻找最优解。检查当前解a [i].f的函数值（或评估值）是否超过全局最优解fB的当前值。若此条件成立，则将全局最优解的值更新为当前值，并将当前解的索引保存为最优解索引。

3. 若找到最优解，则将最优解a[bestIndex].c的坐标复制到 cB数组中。

//——————————————————————————————————————————————————————————————————————————————
// Method of revising the best solutions
void C_AO_AOS::Revision ()
{
  int bestIndex = -1;

  // Find the best solution in the current iteration
  for (int i = 0; i < popSize; i++)
  {
    // Update the global best solution
    if (a [i].f > fB)
    {
      fB = a [i].f;
      bestIndex = i;
    }
  }

  // Update the best coordinates if a better solution is found 
  if (bestIndex != -1) ArrayCopy (cB, a [bestIndex].c, 0, 0, WHOLE_ARRAY);
}
//——————————————————————————————————————————————————————————————————————————————

测试结果

让我们运行测试平台，获取到的AOS运行结果如下：

AOS|Atomic Orbital Search|50.0|5.0|1.0|0.1|0.05|
=============================
5 Hilly's; Func runs: 10000; result: 0.6521321213930082
25 Hilly's; Func runs: 10000; result: 0.39883708808831186
500 Hilly's; Func runs: 10000; result: 0.2602779698842558
=============================
5 Forest's; Func runs: 10000; result: 0.5165008091396371
25 Forest's; Func runs: 10000; result: 0.30233740723010416
500 Forest's; Func runs: 10000; result: 0.1926906342754638
=============================
5 Megacity's; Func runs: 10000; result: 0.39384615384615385
25 Megacity's; Func runs: 10000; result: 0.1892307692307692
500 Megacity's; Func runs: 10000; result: 0.09903076923077013
=============================
总分：3.00488 (33.39%)

在AOS算法的可视化过程中，可以观察到一种有趣的现象：原子轨道上存在特征性的“聚集”区域，但算法的收敛精度并不高。

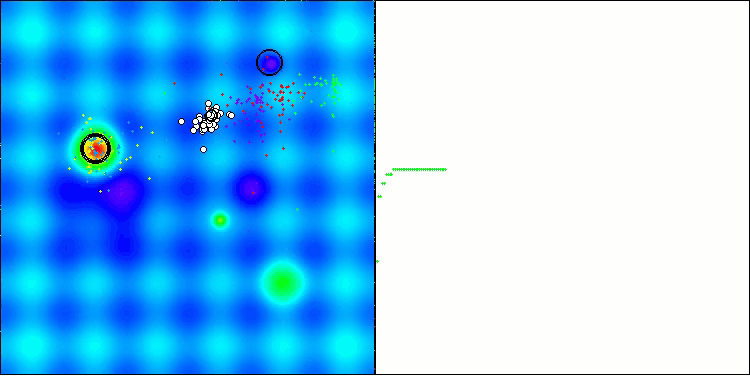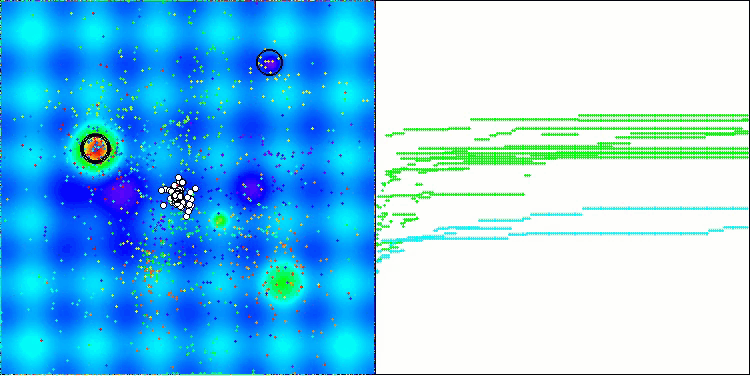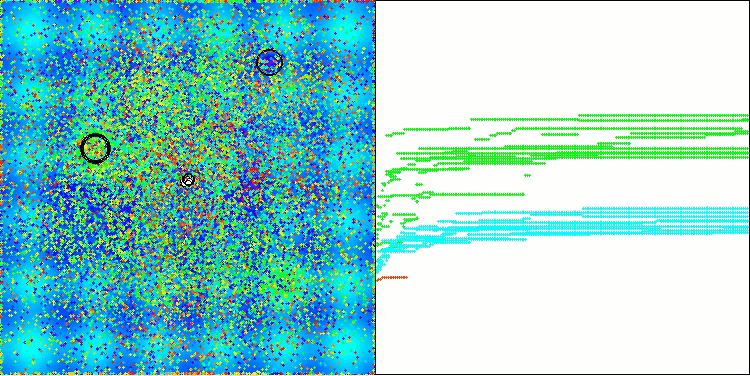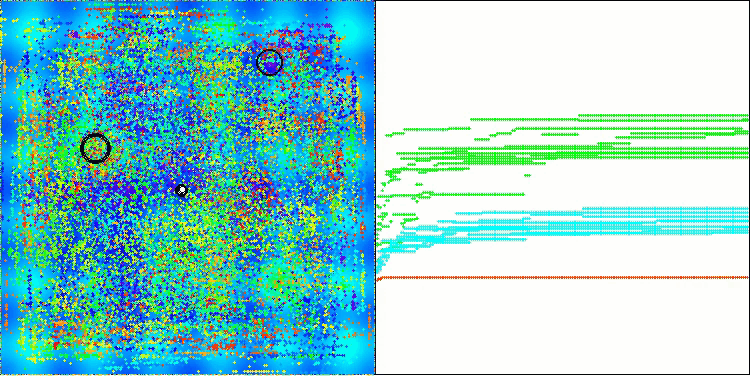
AOS在Hilly测试函数上

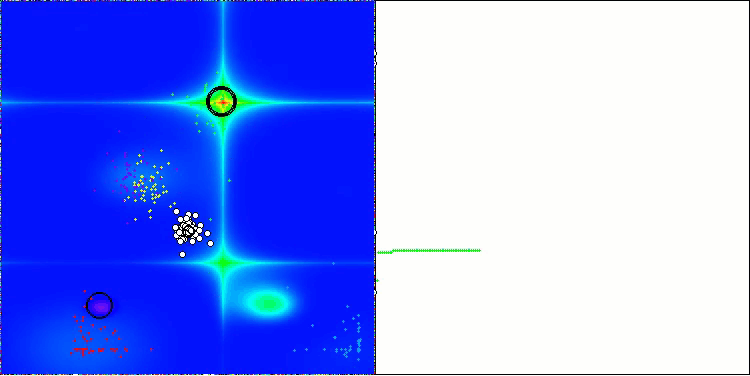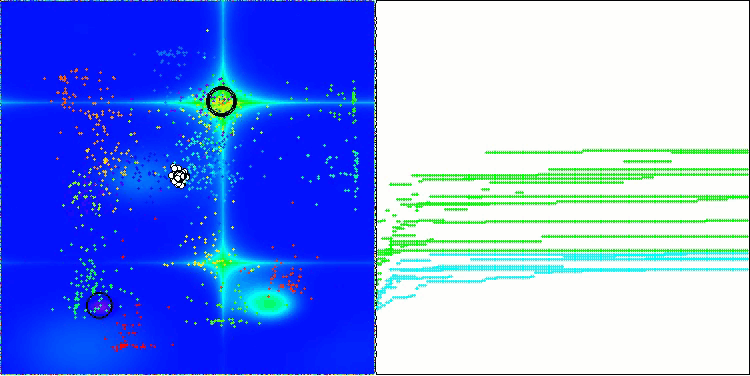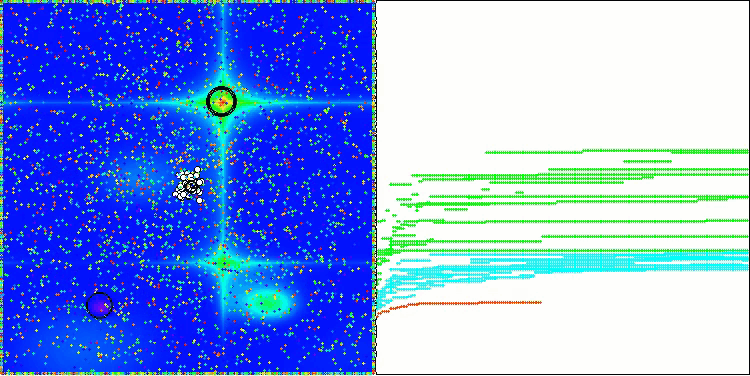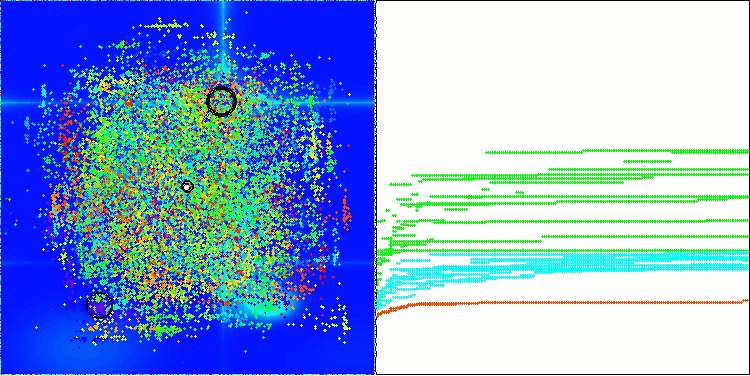
AOS在Forest测试函数上

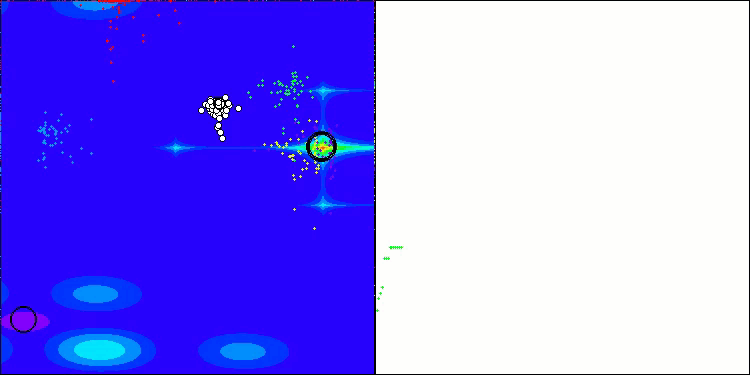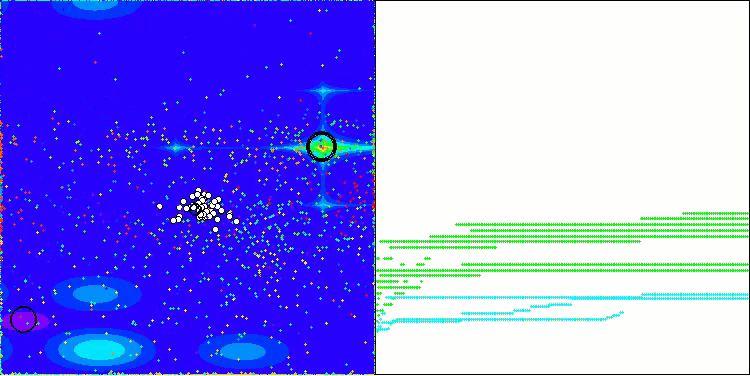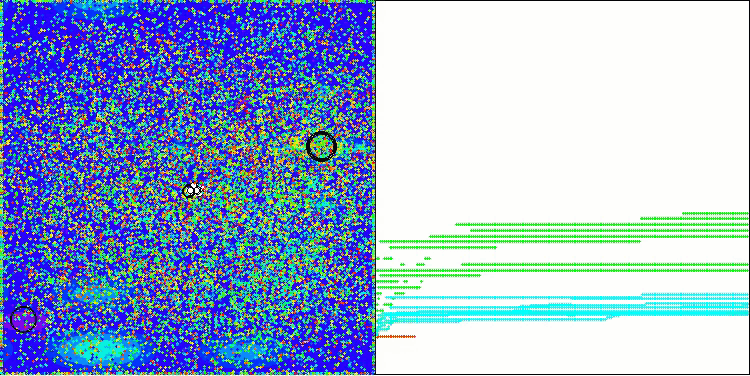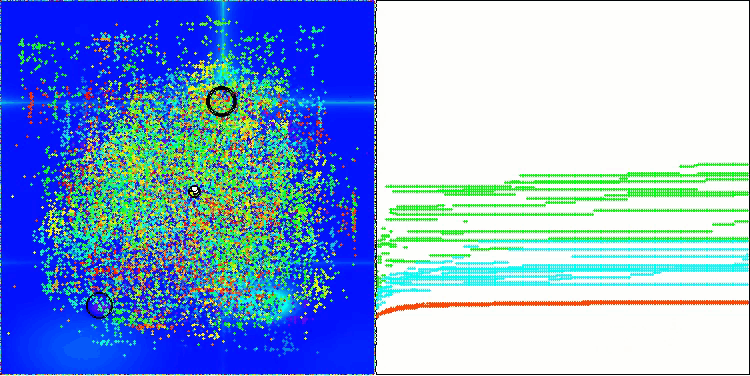
AOS在Megacity测试函数上

根据测试结果，AOS算法在排名表中位列第39名。

#	AO	描述	Hilly值			Hilly最终值	Forest值			Forest最终值	Megacity (离散)			Megacity最终值	最终结果	最大百分比
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	跨邻域搜索	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	密码锁算法（joo）	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	动物迁徙优化M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O) 进化策略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	彗星尾算法（joo）	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	随机扩散搜索 M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	AAm	射箭算法M	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
8	ESG	社会群体的进化（joo）	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
9	SIA	模拟各向同性退火（joo）	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
10	ACS	人工协同搜索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
11	ASO	无序社会优化	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
12	TSEA	龟壳演化算法（joo）	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
13	DE	差分进化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
14	CRO	化学反应优化	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
15	BSA	鸟群算法	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
16	HS	和声搜索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
17	SSG	树苗播种和生长	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
18	BCOm	细菌趋化性优化算法M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
19	ABO	非洲水牛优化	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
20	(PO)ES	(PO) 进化策略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
21	TSm	禁忌搜索M	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
22	BSO	头脑风暴优化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
23	WOAm	鲸鱼优化算法M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
24	AEFA	人工电场算法	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
25	AEO	基于人工生态系统的优化算法	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
26	ACOm	蚁群优化 M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
27	BFO-GA	细菌觅食优化 - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
28	ABHA	人工蜂巢算法	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
29	ACMO	大气云模型优化	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
30	ASHA	人工淋浴算法	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
31	ASBO	适应性社会行为优化	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
32	MEC	思维进化计算	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
33	IWO	入侵杂草优化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
34	Micro-AIS	微型人工免疫系统	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
35	COAm	布谷鸟优化算法 M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
36	SDOm	螺旋动力学优化 M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
37	NMm	Nelder-Mead方法 M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
38	FAm	萤火虫算法 M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
39	AOS	原子轨道搜索	0.65213	0.39884	0.26028	1.31125	0.51650	0.30234	0.19269	1.01153	0.39385	0.18923	0.09903	0.68211	3.005	33.39
40	GSA	引力搜索算法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
41	BFO	细菌觅食优化	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
42	ABC	人工蜂群	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
43	BA	蝙蝠算法	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
44	AAA	人工藻类算法	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23
45	SA	模拟退火	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43

总结

我们探讨了一种颇具趣味的原子轨道搜索算法，该算法采用创新方法实现全局搜索与结果的局部优化。得益于原子的动态轨道层设计，电子能够以平衡的方式移动，以探寻稳定的原子状态。该算法在处理平滑函数时能力有限，但随着问题维度的增加，即便面对离散型的“Megacity”函数，也能展现出良好的效果。

这一算法虽蕴含着极具前景的创意，但其效率却因一些细微却关键的因素而受到影响。在下一篇文章中，我们将介绍我对AOS算法的改进版本，并深入分析这一卓越的轨道搜索理念究竟具备怎样的实际能力。

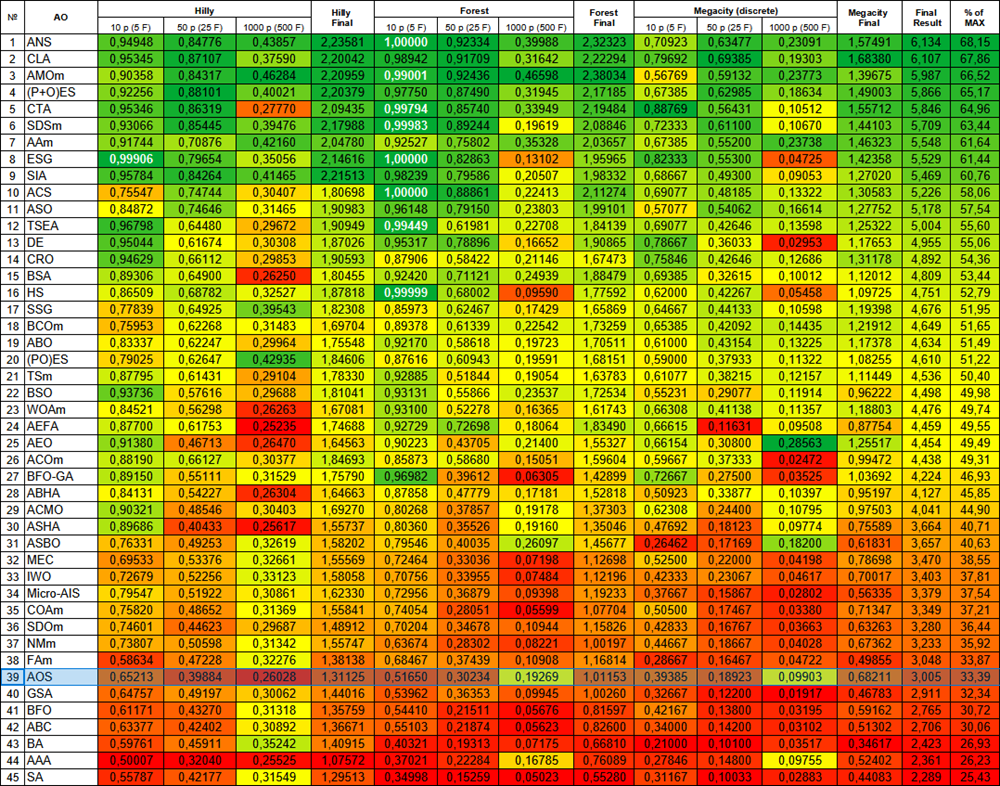
图例3. 根据相关测试，将算法的颜色等级大于或等于0.99的结果以白色突出显示。

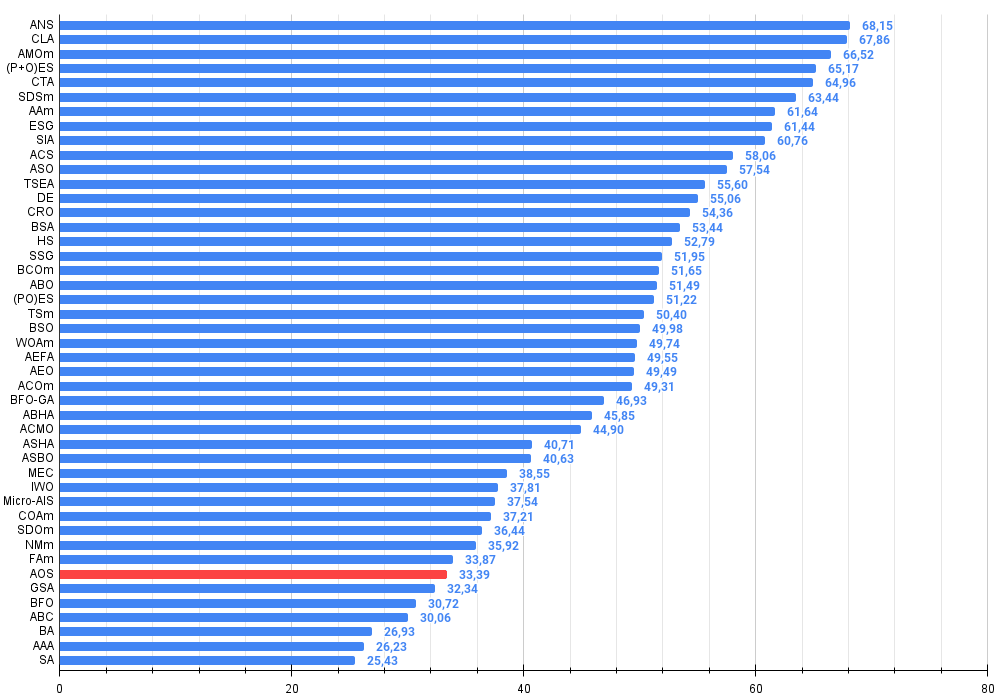
图例 4. 算法测试结果的直方图（标尺从 0 到 100，数字越大结果越好，

其中 100 是理论上的最大可能结果，将计算评级表格的脚本存档）

AOS的优缺点：

优点：

1. 为算法改进提供了基础。
2. 少量外部参数。
   

缺点：

1. 因频繁生成随机数而导致运行速度缓慢。
   
2. 实现过程相当复杂。
3. 收敛精度较低。

文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。

文中所用的程序

#	名称	类型	描述
1	#C_AO.mqh	库	种群优化算法的基类
2	#C_AO_enum.mqh	库	种群优化算法的枚举说明
3	TestFunctions.mqh	库	测试函数库
4	TestStandFunctions.mqh	库	测试台函数库
5	Utilities.mqh	库	辅助函数库
6	CalculationTestResults.mqh	库	用于计算比较表结果的脚本
7	Testing AOs.mq5	脚本	面向所有种群优化算法的统一测试平台
8	AO_AOS_AtomicOrbitalSearch.mqh	库	AOS algorithm class
9	Test_AO_AOS.mq5	脚本	AOS测试