MetaTrader 5 / トレーディングシステム
English Русский Español Português
preview
取引におけるニューラルネットワーク：双曲潜在拡散モデル(HypDiff)

取引におけるニューラルネットワーク：双曲潜在拡散モデル(HypDiff)

MetaTrader 5 — トレーディングシステム |
20 0
Dmitriy Gizlyk
Dmitriy Gizlyk

はじめに

グラフは、生データに含まれる多様性やトポロジー構造の重要性を表現しています。これらのトポロジー的特徴は、しばしば基礎となる物理的法則や発展パターンを反映しています。古典的なグラフ理論に基づく従来のランダムグラフモデルは、特定のトポロジーに対応したアルゴリズムを人工的なヒューリスティックに依存して設計しており、多様で複雑なグラフ構造を効果的にモデル化する柔軟性に欠けています。この制約に対応するため、多くのグラフ生成のための深層学習モデルが開発されています。特に、ノイズ除去機能を持つ確率的拡散モデルは、可視化タスクにおいて高い性能と可能性を示しています。

しかし、グラフ構造の非ユークリッド的かつ不規則な性質により、拡散モデルをこの文脈で適用するには2つの大きな制約があります。

  1. 計算コストの高さグラフ生成には本質的に、離散的で疎な、そして非ユークリッド的なトポロジー的特徴の処理が伴います。従来の拡散モデルで用いられるガウスノイズの摂動は、離散データには適していません。このため、離散的なグラフ拡散モデルは構造の疎性によって時間的・空間的な計算コストが非常に高くなります。また、これらのモデルは連続ガウスノイズプロセスに依存して完全連結されたノイジーなグラフを生成するため、構造情報やその背後にあるトポロジー的特性が失われることがあります。
  2. 非ユークリッド構造における異方性：規則的な構造を持つデータとは異なり、非ユークリッド空間におけるグラフノードの埋め込みは、潜在空間内で異方性を示します。ノード埋め込みがユークリッド空間にマッピングされると、特定方向に対して顕著な異方性を示します。潜在空間における等方的な拡散プロセスでは、こうした異方的構造情報がノイズとして扱われ、除去の過程で失われてしまいます。

双曲空間は、離散的な木構造や階層構造を連続的に表現するための理想的な多様体として広く認識されており、さまざまなグラフ学習タスクにおいて使用されています。論文「Hyperbolic Geometric Latent Diffusion Model for Graph Generation」の著者らは、非ユークリッド構造における異方性の問題を解決する手段として、双曲幾何学が有効であると主張しています。双曲空間では、ノードの埋め込み分布は大局的には等方的になりやすく、局所的には異方性が保持されます。さらに、双曲幾何学は極座標における角度と半径の測定を統一し、物理的意味や解釈可能性を持った幾何学的な次元を提供します。これは、グラフの本質的構造を反映する幾何学的事前知識を潜在空間に与えることができます。

これらの知見をもとに、著者らは双曲幾何学に基づいた潜在空間を設計し、非ユークリッド構造上での効率的な拡散プロセスを可能にし、トポロジーの整合性を保持したグラフ生成を実現しようとしています。その目的の中核となるのが、以下の2つの課題です。

  1. 双曲潜在空間では、連続ガウス分布の加法性が定義できない
  2. 非ユークリッド構造に適応した異方性拡散プロセスの設計

これらの課題を克服するために、著者らは双曲潜在拡散モデル(HypDiff: Hyperbolic Latent Diffusion Model)を提案します。双曲空間におけるガウス分布の加法性の問題に対しては、放射方向に基づいた拡散プロセスを導入しています。また、角度方向の制約を加えることで異方的ノイズを制限し、構造的な事前知識を保持しながら、拡散モデルがグラフ内のより細かな構造情報に収束するよう誘導します。

1. HypDiffアルゴリズム

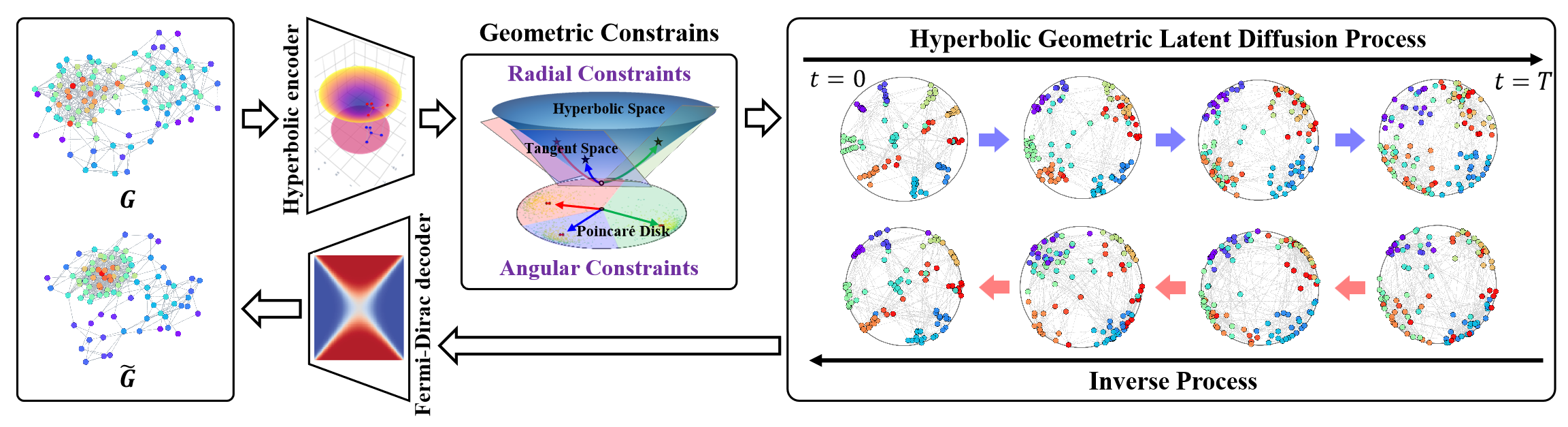
双曲潜在拡散モデル(HypDiff: Hyperbolic Latent Diffusion Model)は、グラフ生成における2つの主要な課題に対応するために設計されたモデルです。本手法では、双曲幾何学を活用してグラフノード間に内在する階層構造を抽象化し、重要なトポロジー的特性を保持するために2つの幾何学的制約を導入しています。著者らは2段階の学習戦略を採用しています。まず双曲オートエンコーダを用いてノードの事前埋め込みを学習し、次に双曲空間上の潜在拡散プロセスを訓練します。

初期ステップでは、グラフデータ𝒢 = (𝐗, A)を低次元の双曲空間に埋め込むことで、拡散処理の効率を高め、より適切な潜在表現を得られるようにします。

提案された双曲オートエンコーダは、双曲幾何エンコーダとフェルミ・ディラックデコーダから構成されており、前者はグラフ𝒢 = (𝐗, A)を双曲空間にマッピングして適切な双曲表現を抽出し、後者はそれを元のグラフデータドメインに再構成します。双曲空間の指数写像および対数写像を用いて、双曲多様体 ℍᵈ H dとその接空間 𝒯xを相互に変換可能です。これらの写像後の表現に対して、多層パーセプトロン(MLP)やグラフニューラルネットワーク(GNN)といった手法を適用することが可能です。実装では、著者らは双曲グラフ畳み込みネットワーク(HGCN: Hyperbolic Graph Convolutional Network)を双曲幾何エンコーダとして使用しています。

双曲空間ではガウス分布の加法性が定義されないため、従来のリーマン正規分布やラップド正規分布をそのまま適用することはできません。そこで著者らは、埋め込みを直接双曲空間上で拡散させるのではなく、複数の多様体の積空間を用いる方法を提案しています。この問題を解決するため、HypDiffでは双曲空間における新たな拡散プロセスを導入し、計算効率の向上を図っています。具体的には、双曲空間の正規分布を接平面𝒯μ上のガウス分布で近似しています。

ユークリッド空間のように線形加算が可能な空間とは異なり、双曲空間ではメビウス加算が用いられます。これにより、多様体（マニフォールド）上での拡散計算には特有の課題が生じます。さらに、等方性ノイズをそのまま適用するとSNR（信号対雑音比）が急速に低下し、トポロジー情報の保持が困難になる問題もあります。

潜在空間におけるグラフの異方性は、グラフ構造に関する帰納的バイアスを本質的に含んでいます。ここでの中心的課題は、この異方性の主要な方向性を特定することです。これに対処するため、HypDiffの著者らは双曲幾何学に基づく異方性拡散の枠組みを提案しています。核となる考え方は、ノードの類似性に基づいてクラスタリングをおこない、そこから主要な拡散方向（すなわち角度）を選択することで、双曲潜在空間を効果的に複数のセクターに分割することです。各クラスタのノードは、それぞれのクラスタセントロイドの接平面上に射影されます。

これらのクラスタは、前処理段階で任意の類似性ベースのクラスタリングアルゴリズムを用いて形成できます。

双曲幾何学におけるクラスタリングパラメータk ∈ [1, n]は、双曲空間を分割するセクターの数を定義します。双曲異方性拡散は、複数の曲率Ci ∈|k|を持つクラインモデル𝕂c,n内における有向拡散として表され、これはクラスタセントロイドOi∈{|k|}における接平面の集合𝒯𝐨i∈{|k|}への射影として近似されます。

この特性により、HypDiffの著者らが提案した近似アルゴリズムは、多曲率クラインモデルとの関連性を巧みに示しています。

提案されたアルゴリズムの挙動は、kの値によって変化します。これにより、双曲幾何学の異方性をより柔軟かつ細かく表現でき、ノイズの注入やモデルの学習における精度と効率が向上します。

双曲幾何学は、グラフの成長プロセスにおけるノード間の接続性を自然かつ幾何学的に記述することができます。ノードの人気度は放射座標によって抽象化され、類似性は双曲空間内の角度距離によって表現されます。

本モデルの主な目的は、双曲空間の固有の特性に即した幾何学的な放射状成長を伴う拡散プロセスをモデリングすることにあります。

標準的な拡散モデルがグラフ上で性能を発揮しにくい根本的な理由は、SNRが急激に低下することです。HypDiffでは、各クラスタの中心から極点Oへの測地線方向を拡散の目標方向として設定し、この幾何学的制約のもとで順方向拡散プロセスを制御します。

また、標準的なノイズ除去および逆拡散モデリングの手順に従い、著者らはUNetをベースとしたノイズ除去拡散モデル(DDM)を採用し、元データX0の予測をおこないます。

さらに、HypDiffの著者らは、効率化のために複数のクラスタ中心の接線空間をまたぐのではなく、単一の接線空間内で共同サンプリングをおこなう手法を提案し、これが実際に可能であることを示しています。

著者らは、以下の図でHypDiffフレームワークの全体像を示しています。


2.MQL5での実装

HypDiff手法の理論的側面を確認した後、この記事の実践的な部分に進み、MQL5を使用して提案されたアプローチの解釈を実装します。最初に注意しておきたいのは、この実装はかなり長く、難易度も高いという点です。したがって、相応の作業量に備えておいてください。

2.1 OpenCLプログラムの拡張

実践的な実装は、既存のOpenCLプログラムの修正から始まります。最初のステップは、入力データを双曲空間に射影することです。この変換の際には、双曲空間がユークリッド的な空間パラメータと時間的側面を組み合わせているため、シーケンス内の各要素の位置を考慮することが重要です。元の手法に従い、ローレンツモデルを適用します。この射影は、HyperProjectionHyperProjectionカーネル内で実装されています。

__kernel void HyperProjection(__global const float *inputs,
                              __global float *outputs
                             )
  {
   const size_t pos = get_global_id(0);
   const size_t d = get_local_id(1);
   const size_t total = get_global_size(0);
   const size_t dimension = get_local_size(1);

このカーネルは、解析対象のシーケンスと変換結果を格納するデータバッファへのポインタをパラメータとして受け取ります。これらのデータバッファの特性は、ワークロードスペースによって定義されます。第一の次元はシーケンスの長さに対応し、第二の次元はシーケンス内の各要素を記述する特徴ベクトルのサイズを表します。ワークアイテムは最終次元に基づいてワークグループに分割されます。 

なお、シーケンスの各要素に対する特徴ベクトルには、1つの追加コンポーネントが含まれる点に注意してください。

続いて、ワークグループ内のスレッド間でデータを交換するためのローカル配列を宣言します。

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);

データバッファ内のオフセット定数を定義します。

   const int shift_in = pos * dimension + d;
   const int shift_out = pos * (dimension + 1) + d + 1;

グローバルバッファからの入力データを対応するワークフローのローカル要素に読み込み、二次値を計算してみましょう。操作実行結果も必ず確認する必要があります。

   float v = inputs[shift_in];
   if(isinf(v) || isnan(v))
      v = 0;
//---
   float v2 = v * v;
   if(isinf(v2) || isnan(v2))
      v2 = 0;

次に、入力データベクトルのノルムを計算する必要があります。これを実行するには、ローカル配列を使用してその値の二乗を合計します。これは、各ワークグループスレッドに1つの要素が含まれているためです。

//---
   if(d < ls)
      temp[d] = v2;
   barrier(CLK_LOCAL_MEM_FENCE);
   for(int i = ls; i < (int)dimension; i += ls)
     {
      if(d >= i && d < (i + ls))
         temp[d % ls] += v2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   int count = min(ls, (int)dimension);
//---
   do
     {
      count = (count + 1) / 2;
      if(d < count)
         temp[d] += ((d + count) < dimension ? temp[d + count] : 0);
      if(d + count < dimension)
         temp[d + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

ここで注意すべき点は、シーケンス要素の双曲座標を表すベクトルにおいて、最初の要素の値を計算するためにのみベクトルノルムが必要であるということです。その他の要素は、位置のシフトを伴ってそのままの値で移動させますが、値自体は変更しません。

   outputs[shift_out] = v;

余分な演算を避けるため、双曲ベクトルの最初の要素の値は、各ワークグループの最初のスレッドのみで計算します。

まず、元のシーケンス内で解析対象の要素がどの程度オフセットされているかの割合を計算します。次に、先ほど計算した初期表現ベクトルのノルム値の二乗を減算します。最後に、その結果から平方根を求めます。

   if(d == 0)
     {
      v = ((float)pos) / ((float)total);
      if(isinf(v) || isnan(v))
         v = 0;
      outputs[shift_out - 1] = sqrt(fmax(temp[0] - v * v, 1.2e-07f));
     }
  }

平方根を抽出する際には、値がゼロより大きい場合にのみ計算をおこなうよう明示的に制御します。これにより、実行時エラーや計算中の無効な結果を防ぐことができます。

バックプロパゲーション（誤差逆伝播法）アルゴリズムを実装するために、ここでHyperProjectionGradカーネルを作成します。これは、先に定義したフィードフォワード処理を通じた誤差勾配の伝播を実装するものです。以下の2点に注意してください。第一に、シーケンス内の要素の位置は静的かつ非パラメトリックであるため、そこには勾配は伝播しません。

第二に、残りの要素に対する勾配は、2つの独立した情報経路を通じて伝播します。1つは直接的な勾配伝播です。同時に、元の特徴ベクトルのすべての成分はベクトルノルムの計算に使用されており、このノルムが双曲表現ベクトルの最初の要素を決定します。したがって、各特徴成分は、双曲ベクトルの最初の要素からの誤差勾配を比例的に受け取る必要があります。

それでは、これらのアプローチがコード内でどのように実装されているかを見ていきましょう。HyperProjectionGradカーネルは、3つのデータバッファポインタを引数として受け取ります。新たに入力勾配バッファ(inputs_gr)が導入され、元のシーケンスの双曲表現を格納していたバッファは、対応する誤差勾配バッファ(outputs_gr)に置き換えられます。

__kernel void HyperProjectionGrad(__global const float *inputs,
                                  __global float *inputs_gr,
                                  __global const float *outputs_gr
                                 )
  {
   const size_t pos = get_global_id(0);
   const size_t d = get_global_id(1);
   const size_t total = get_global_size(0);
   const size_t dimension = get_global_size(1);

カーネルのタスクスペースはフィードフォワード時と同じに保ちますが、スレッドをワークグループにまとめることはおこないません。カーネル本体では、まず現在のスレッドがタスクスペース内のどこに属しているかを特定します。その取得した値に基づいて、データバッファ内のオフセットを決定します。

   const int shift_in = pos * dimension + d;
   const int shift_start_out = pos * (dimension + 1);
   const int shift_out = shift_start_out + d + 1;

グローバルバッファからデータを読み込むブロックでは、元の表現から解析対象の要素の値と、それに対応する双曲表現レベルでの誤差勾配の値を計算します。

   float v = inputs[shift_in];
   if(isinf(v) || isnan(v))
      v = 0;
   float grad = outputs_gr[shift_out];
   if(isinf(grad) || isnan(grad))
      grad = 0;

次に、双曲表現の最初の要素からの誤差勾配の一部を計算します。これは、その要素の誤差勾配と、解析対象の入力値との積として定義されます。

   v = v * outputs_gr[shift_start_out];
   if(isinf(v) || isnan(v))
      v = 0;

また、各段階でプロセスを管理することも忘れてはなりません。

合計された誤差勾配を対応するグローバルデータバッファに保存します。

//---
   inputs_gr[shift_in] = v + grad;
  }

この段階で、入力データを双曲空間に射影する処理を実装しました。しかし、HypDiff手法の著者たちは、拡散プロセスは双曲空間の射影を接平面におこなった上で実施すべきだと提案しています。

一見すると、データをまず平坦な空間から双曲空間へ射影し、ノイズを加えるためだけに再び元に戻すのは不思議に思えるかもしれません。しかし、重要な点は、元の平坦な表現が最終的な射影と大きく異なる可能性が高いということです。なぜなら、元のデータ平面と双曲表現を射影するために使われる接平面は、同じ平面ではないからです。

この概念は、写真から技術図面を作成する過程に例えられます。まず、写真に写っている物体の3次元表現を経験や知識に基づいて頭の中で再構築し、その後、そのイメージを側面図、正面図、上面図を含む2次元の技術図面に変換します。同様に、HypDiffはデータを複数の接平面に射影し、それぞれ異なる双曲空間の点を中心としています。

この機能を実装するために、LogMapカーネルを作成します。このカーネルは7つのデータバッファポインタをパラメータとして受け取ります。確かに数は多いですが、その中には3つの入力データバッファが含まれています。

  1. featuresバッファは、入力データを表す双曲埋め込みテンソルを格納します。 
  2. 「centroids」バッファは、接平面の基準点となるセントロイドの座標を保持します。
  3. curvaturesバッファは、それぞれのセントロイドに関連する曲率パラメータを定義します。

outputsバッファは射影処理の結果を格納します。さらに、3つのバッファが中間結果を保存し、これらはバックプロパゲーション計算時に使用されます。

ここで一点、実装において元のフレームワークから若干逸脱したことを述べておきます。元のHypDiff手法では、データ前処理段階でシーケンス要素を事前にクラスタリングし、各グループのメンバーのみを接平面に射影していました。しかし私たちのアプローチでは、シーケンス要素を事前にグルーピングせず、すべての要素を各接平面にすべて射影します。当然ながら、処理量は増加しますが、その分モデルの解析対象シーケンスの理解はより深まることになります。

__kernel void LogMap(__global const float *features,
                     __global const float *centroids,
                     __global const float *curvatures,
                     __global float *outputs,
                     __global float *product,
                     __global float *distance,
                     __global float *norma
                    )
  {
//--- identify
   const size_t f = get_global_id(0);
   const size_t cent = get_global_id(1);
   const size_t d = get_local_id(2);
   const size_t total_f = get_global_size(0);
   const size_t total_cent = get_global_size(1);
   const size_t dimension = get_local_size(2);

メソッド本体では、3次元のタスク空間内で現在の処理スレッドを特定します。第一の次元は元のシーケンスの要素を指し、第二の次元はセントロイドを示します。第三の次元は解析対象シーケンス要素の記述ベクトル内の位置を示します。この場合、スレッドは最後の次元に基づいてワークグループにまとめられます。

次に、ワークグループ内でローカルデータ交換配列を宣言します。

//--- create local array
   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);

データバッファ内のオフセット定数を定義します。

//--- calc shifts
   const int shift_f = f * dimension + d;
   const int shift_out = (f * total_cent + cent) * dimension + d;
   const int shift_cent = cent * dimension + d;
   const int shift_temporal = f * total_cent + cent;

その後、グローバルバッファから入力データをロードし、取得した値の有効性を確認します。

//--- load inputs
   float feature = features[shift_f];
   if(isinf(feature) || isnan(feature))
      feature = 0;
   float centroid = centroids[shift_cent];
   if(isinf(centroid) || isnan(centroid))
      centroid = 0;
   float curv = curvatures[cent];
   if(isinf(curv) || isnan(curv))
      curv = 1.2e-7;

次に、入力データのテンソルとセントロイドのテンソルの積を計算する必要があります。ただし、双曲表現を扱っているため、ミンコフスキー積を使用します。その計算には、まず対応するスカラー値同士の乗算をおこないます。

//--- dot(features, centroids)
   float fc = feature * centroid;
   if(isnan(fc) || isinf(fc))
      fc = 0;

次に、得られた値をワーキンググループ内で合計します。

//---
   if(d < ls)
      temp[d] = (d > 0 ? fc : -fc);
   barrier(CLK_LOCAL_MEM_FENCE);
   for(int i = ls; i < (int)dimension; i += ls)
     {
      if(d >= i && d < (i + ls))
         temp[d % ls] += fc;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   int count = min(ls, (int)dimension);
//---
   do
     {
      count = (count + 1) / 2;
      if(d < count)
         temp[d] += ((d + count) < dimension ? temp[d + count] : 0);
      if(d + count < dimension)
         temp[d + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);
   float prod = temp[0];
   if(isinf(prod) || isnan(prod))
      prod = 0;

通常のユークリッド空間でのベクトルの積とは異なり、ベクトルの最初の要素同士は符号を反転させて積を取る点に注意してください。

計算結果の妥当性を確認した上で、得られた値を対応するグローバル一時データストレージバッファの要素に保存します。この値はバックプロパゲーションの際に必要となります。

   product[shift_temporal] = prod;

これにより、解析対象の要素がセントロイドからどの程度、どの方向にずれているかを判定できます。

//--- project
   float u = feature + prod * centroid * curv;
   if(isinf(u) || isnan(u))
      u = 0;

得られたシフトベクトルのミンコフスキーノルムを求めます。前と同様に、各要素の平方を取ります。

//--- norm(u)
   float u2 = u * u;
   if(isinf(u2) || isnan(u2))
      u2 = 0;

そして、ワークグループ内で得られた値を合計し、反対符号の最初の要素の平方をとります。

   if(d < ls)
      temp[d] = (d > 0 ? u2 : -u2);
   barrier(CLK_LOCAL_MEM_FENCE);
   for(int i = ls; i < (int)dimension; i += ls)
     {
      if(d >= i && d < (i + ls))
         temp[d % ls] += u2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   count = min(ls, (int)dimension);
//---
   do
     {
      count = (count + 1) / 2;
      if(d < count)
         temp[d] += ((d + count) < dimension ? temp[d + count] : 0);
      if(d + count < dimension)
         temp[d + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);
   float normu = temp[0];
   if(isinf(normu) || isnan(normu) || normu <= 0)
      normu = 1.0e-7f;
   normu = sqrt(normu);

この値もバックプロパゲーションで使用するため、一時データストレージバッファに保存します。

   norma[shift_temporal] = normu;

次に、解析対象の点からセントロイドまでの双曲空間上の距離を、セントロイドの曲率パラメータを用いて求めます。この場合、ベクトルの積を再計算するのではなく、先に得られた値を使用します。 

//--- distance features to centroid
   float theta = -prod * curv;
   if(isinf(theta) || isnan(theta))
      theta = 0;
   theta = fmax(theta, 1.0f + 1.2e-07f);
   float dist = sqrt(clamp(pow(acosh(theta), 2.0f) / curv, 0.0f, 50.0f));
   if(isinf(dist) || isnan(dist))
      dist = 0;

得られた値の妥当性を確認し、結果をグローバル一時データストレージバッファに保存します。

   distance[shift_temporal] = dist;

オフセットベクトルの値を調整します。

   float proj_u = dist * u / normu;

そして最後に、得られた値を接平面に射影するだけです。ここでも、上記のローレンツ射影と同様に、射影ベクトルの最初の要素を調整する必要があります。そのために、射影ベクトルとセントロイドベクトルの最初の要素を除いた部分の積を計算します。

   if(d < ls)
      temp[d] = (d > 0 ? proj_u * centroid : 0);
   barrier(CLK_LOCAL_MEM_FENCE);
   for(int i = ls; i < (int)dimension; i += ls)
     {
      if(d >= i && d < (i + ls))
         temp[d % ls] += proj_u * centroid;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   count = min(ls, (int)dimension);
//---
   do
     {
      count = (count + 1) / 2;
      if(d < count)
         temp[d] += ((d + count) < dimension ? temp[d + count] : 0);
      if(d + count < dimension)
         temp[d + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

最初の投射要素の値を調整します。

//---
   if(d == 0)
     {
      proj_u = temp[0] / centroid;
      if(isinf(proj_u) || isnan(proj_u))
         proj_u = 0;
      proj_u = fmax(u, 1.2e-7f);
     }

結果を保存します。

//---
   outputs[shift_out] = proj_u;
  }

ご覧の通り、このカーネルのアルゴリズムは複雑な結びつきが多く、非常に煩雑です。そのため、バックプロパゲーションの際に誤差勾配がどのように伝播しているかを理解するのは非常に困難です。しかし、この絡み合いを解きほぐす必要があります。細部に非常に注意してください。バックプロパゲーションのアルゴリズムはLogMapGradカーネルで実装されています。

__kernel void LogMapGrad(__global const float *features, __global float *features_gr,
                         __global const float *centroids, __global float *centroids_gr,
                         __global const float *curvatures, __global float *curvatures_gr,
                         __global const float *outputs, __global const float *outputs_gr,
                         __global const float *product,
                         __global const float *distance,
                         __global const float *norma
                        )
  {
//--- identify
   const size_t f = get_local_id(0);
   const size_t cent = get_global_id(1);
   const size_t d = get_local_id(2);
   const size_t total_f = get_local_size(0);
   const size_t total_cent = get_global_size(1);
   const size_t dimension = get_local_size(2);

カーネルのパラメータには、入力および出力レベルでの誤差勾配バッファを追加しました。これにより、4つの追加データバッファが増えました。

カーネルのタスク空間はフィードフォワードパスとほぼ同じにしましたが、ワークグループへのまとめ方の原則は変更しました。なぜなら、今やシーケンス内の個々の要素のベクトル内だけでなく、セントロイドに対する勾配も収集しなければならないためです。各セントロイドは解析対象シーケンスのすべての要素と連携して動作します。そのため、各要素から誤差勾配を受け取る必要があります。

カーネル本体では、タスク空間のすべての次元において現在の処理スレッドを特定します。その後、ワークグループ内の要素間でデータ交換をおこなうためのローカル配列を作成します。

//--- create local array
   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);

グローバルデータバッファにオフセット定数を定義します。

//--- calc shifts
   const int shift_f = f * dimension + d;
   const int shift_out = (f * total_cent + cent) * dimension + d;
   const int shift_cent = cent * dimension + d;
   const int shift_temporal = f * total_cent + cent;

その後、グローバルバッファからデータをロードします。まず、入力データと中間値を抽出します。 

//--- load inputs
   float feature = features[shift_f];
   if(isinf(feature) || isnan(feature))
      feature = 0;
   float centroid = centroids[shift_cent];
   if(isinf(centroid) || isnan(centroid))
      centroid = 0;
   float centroid0 = (d > 0 ? centroids[shift_cent - d] : centroid);
   if(isinf(centroid0) || isnan(centroid0) || centroid0 == 0)
      centroid0 = 1.2e-7f;
   float curv = curvatures[cent];
   if(isinf(curv) || isnan(curv))
      curv = 1.2e-7;
   float prod = product[shift_temporal];
   float dist = distance[shift_temporal];
   float normu = norma[shift_temporal];

次に、解析対象のシーケンス要素がセントロイドからずれているベクトルの値を計算します。フィードフォワードの処理とは異なり、ここではすでに必要なすべてのデータが揃っています。

   float u = feature + prod * centroid * curv;
   if(isinf(u) || isnan(u))
      u = 0;

既存の誤差勾配を結果レベルで読み込みます。

   float grad = outputs_gr[shift_out];
   if(isinf(grad) || isnan(grad))
      grad = 0;
   float grad0 = (d>0 ? outputs_gr[shift_out - d] : grad);
   if(isinf(grad0) || isnan(grad0))
      grad0 = 0;

解析対象の要素の誤差勾配だけでなく、解析対象シーケンス要素の記述ベクトルの最初の要素の誤差勾配も読み込む点に注意してください。この理由は、先に述べたHyperProjectionGradカーネルの場合と同様です。

次に、誤差勾配の累積用のローカル変数を初期化します。

   float feature_gr = 0;
   float centroid_gr = 0;
   float curv_gr = 0;
   float prod_gr = 0;
   float normu_gr = 0;
   float dist_gr = 0;

まず、データの接平面への射影からオフセットベクトルへ誤差勾配を伝播させます。

   float proj_u_gr = (d > 0 ? grad + grad0 / centroid0 * centroid : 0);

ここで注意すべきは、オフセットベクトルの最初の要素は結果に影響を与えていないため、その勾配は「0」となることです。その他の要素は、直接的な誤差勾配と、結果の最初の要素からの勾配の一部の両方を受け取ります。

次に、セントロイドに対する誤差勾配の最初の値を決定します。これはループ内で計算し、シーケンスの全要素から値を集めます。

   for(int id = 0; id < dimension; id += ls)
     {
      if(d >= id && d < (id + ls))
        {
         int t = d % ls;
         for(int ifeat = 0; ifeat < total_f; ifeat++)
           {
            if(f == ifeat)
              {
               if(d == 0)
                  temp[t] = (f > 0 ? temp[t] : 0) + outputs[shift_out] / centroid * grad;
               else
                  temp[t] = (f > 0 ? temp[t] : 0) + grad0 / centroid0 * outputs[shift_out];
              }
            barrier(CLK_LOCAL_MEM_FENCE);
           }

シーケンスのすべての要素から誤差勾配をローカル配列内に集めた後、1つのスレッドを使って集約した値をローカル変数に転送します。

         if(f == 0)
           {
            if(isnan(temp[t]) || isinf(temp[t]))
               temp[t] = 0;
            centroid_gr += temp[0];
           }
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }

すべての処理スレッドが例外なくバリアに到達することを確認する必要があります。

次に、距離ベクトル、ノルム、およびオフセットベクトルに対する誤差勾配を計算します。

   dist_gr = u / normu * proj_u_gr;
   float u_gr = dist / normu * proj_u_gr;
   normu_gr = dist * u / (normu * normu) * proj_u_gr;

オフセットベクトルの要素は各スレッドで個別に扱われますが、ベクトルノルムと距離は離散的な値です。そのため、解析対象シーケンスの各要素ごとに対応する誤差勾配を合計する必要があります。まず、距離に対する誤差勾配を集めます。値の合計はローカル配列を通じておこないます。

   for(int ifeat = 0; ifeat < total_f; ifeat++)
     {
      if(d < ls && f == ifeat)
         temp[d] = dist_gr;
      barrier(CLK_LOCAL_MEM_FENCE);
      for(int id = ls; id < (int)dimension; id += ls)
        {
         if(d >= id && d < (id + ls) && f == ifeat)
            temp[d % ls] += dist_gr;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      int count = min(ls, (int)dimension);
      //---
      do
        {
         count = (count + 1) / 2;
         if(f == ifeat)
           {
            if(d < count)
               temp[d] += ((d + count) < dimension ? temp[d + count] : 0);
            if(d + count < dimension)
               temp[d + count] = 0;
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      if(f == ifeat)
        {
         if(isinf(temp[0]) || isnan(temp[0]))
            temp[0] = 0;
         dist_gr = temp[0];

続いて、対応するセントロイドの曲率パラメータおよびベクトルの積に対する誤差勾配を求めます。

         if(d == 0)
           {
            float theta = -prod * curv;
            float theta_gr = 1.0f / sqrt(curv * (theta * theta - 1)) * dist_gr;
            if(isinf(theta_gr) || isnan(theta_gr))
               theta_gr = 0;
            curv_gr += -pow(acosh(theta), 2.0f) / (2 * sqrt(pow(curv, 3.0f))) * dist_gr;
            if(isinf(curv_gr) || isnan(curv_gr))
               curv_gr = 0;
            temp[0] = -curv * theta_gr;
            if(isinf(temp[0]) || isnan(temp[0]))
               temp[0] = 0;
            curv_gr += -prod * theta_gr;
            if(isinf(curv_gr) || isnan(curv_gr))
               curv_gr = 0;
           }
        }
      barrier(CLK_LOCAL_MEM_FENCE);

ただし、曲率パラメータの誤差勾配はグローバルデータバッファに保存するためにのみ累積されることに注意してください。一方で、ベクトル積の誤差勾配は後続の影響要素間での分配のための中間値です。そのため、ワークグループ内で同期させることが重要となります。したがって、この段階ではローカル配列の要素に保存し、後でローカル変数に移動します。

      if(f == ifeat)
         prod_gr += temp[0];
      barrier(CLK_LOCAL_MEM_FENCE);

多くの繰り返しチェックがあることにお気づきかと思います。これはコードを複雑にしますが、ワークグループ内のスレッドが同期バリアを正しく通過するために必要な処理です。

次に、同様にオフセットベクトルのノルムに対する誤差勾配を合計します。

      if(d < ls && f == ifeat)
         temp[d] = normu_gr;
      barrier(CLK_LOCAL_MEM_FENCE);
      for(int id = ls; id < (int)dimension; id += ls)
        {
         if(d >= id && d < (id + ls) && f == ifeat)
            temp[d % ls] += normu_gr;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      count = min(ls, (int)dimension);
      //---
      do
        {
         count = (count + 1) / 2;
         if(f == ifeat)
           {
            if(d < count)
               temp[d] += ((d + count) < dimension ? temp[d + count] : 0);
            if(d + count < dimension)
               temp[d + count] = 0;
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      if(f == ifeat)
        {
         normu_gr = temp[0];
         if(isinf(normu_gr) || isnan(normu_gr))
            normu_gr = 1.2e-7;

次に、オフセットベクトルの誤差勾配を調整します。

         u_gr += u / normu * normu_gr;
         if(isnan(u_gr) || isinf(u_gr))
            u_gr = 0;

そして、それを入力データとセントロイドに分配します。

         feature_gr += u_gr;
         centroid_gr += prod * curv * u_gr;
        }
      barrier(CLK_LOCAL_MEM_FENCE);

ここで重要なのは、オフセットベクトルの誤差勾配がベクトル積のレベルと曲率パラメータの両方に分配されなければならないということです。ただし、これらはスカラー値であるため、解析対象シーケンスの各要素内で値を集約する必要があります。この段階では、オフセットベクトルの対応する誤差勾配とセントロイドの各要素との積の和を計算します。実質的に、この操作はこれらのベクトルの内積を計算することに相当します。

      //--- dot (u_gr * centroid)
      if(d < ls && f == ifeat)
         temp[d] = u_gr * centroid;
      barrier(CLK_LOCAL_MEM_FENCE);
      for(int id = ls; id < (int)dimension; id += ls)
        {
         if(d >= id && d < (id + ls) && f == ifeat)
            temp[d % ls] += u_gr * centroid;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      count = min(ls, (int)dimension);
      //---
      do
        {
         count = (count + 1) / 2;
         if(f == ifeat)
           {
            if(d < count)
               temp[d] += ((d + count) < dimension ? temp[d + count] : 0);
            if(d + count < dimension)
               temp[d + count] = 0;
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);

得られた値を用いて、誤差勾配を対応する各要素に分配します。

      if(f == ifeat && d == 0)
        {
         if(isinf(temp[0]) || isnan(temp[0]))
            temp[0] = 0;
         prod_gr += temp[0] * curv;
         if(isinf(prod_gr) || isnan(prod_gr))
            prod_gr = 0;
         curv_gr += temp[0] * prod;
         if(isinf(curv_gr) || isnan(curv_gr))
            curv_gr = 0;
         temp[0] = prod_gr;
        }
      barrier(CLK_LOCAL_MEM_FENCE);

次に、ワークグループ内でベクトル積レベルの誤差勾配の値を同期させます。

      if(f == ifeat)
        {
         prod_gr = temp[0];

そして、得られた値を入力データ全体に分配します。

         feature_gr += prod_gr * centroid * (d > 0 ? 1 : -1);
         centroid_gr += prod_gr * feature * (d > 0 ? 1 : -1);
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }

すべての処理が正常に完了し、誤差勾配がローカル変数に完全に集約された後、得られた値をグローバルデータバッファへ伝播させます。

//--- result
   features_gr[shift_f] = feature_gr;
   centroids_gr[shift_cent] = centroid_gr;
   if(f == 0 && d == 0)
      curvatures_gr[cent] = curv;
  }

これでカーネルの実装は完了です。

ご覧のとおり、アルゴリズムは非常に複雑ですが、とても興味深いものです。理解するには細部に注意を払う必要があります。

前述のとおり、HypDiffフレームワークの実装には膨大な作業が伴います。本記事では、OpenCLプログラム内のアルゴリズム実装に限定して解説しました。完全なソースコードは添付資料にて提供しています。しかし、記事の分量がほぼ限界に達しているため、次回の記事ではメインプログラム側でのフレームワークアルゴリズム実装の解説を続けることを提案します。このように作業を論理的に二つの部分に分割することが可能です。


結論

双曲幾何学の利用は、離散グラフデータと連続的な拡散モデルとの不整合による課題に効果的に対処します。HypDiffフレームワークは、双曲空間内でのガウス分布の加法的失敗問題に対応するための高度な双曲ガウスノイズ生成手法を導入しています。局所的なグラフ構造を保持するために、角度類似性に基づく幾何学的制約を異方拡散過程に適用しています。

本記事の実践部分では、提案手法のMQL5による実装を開始しましたが、作業範囲は一記事に収まるものではありません。次回の記事で、提案フレームワークのさらなる開発を続けていきます。


参照文献


記事で使用されているプログラム

# 名前 種類 詳細
1 Research.mq5 EA 事例収集のためのEA
2 ResearchRealORL.mq5
 EA
 Real-ORL法による事例収集のためのEA
3 Study.mq5 EA モデル訓練EA
4 Test.mq5 EA モデルテストEA
5 Trajectory.mqh クラスライブラリ システム状態記述の構造体
6 NeuroNet.mqh クラスライブラリ ニューラルネットワークを作成するためのクラスのライブラリ
7 NeuroNet.cl ライブラリ OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16306

添付されたファイル |
ZIPをダウンロード
MQL5.zip (2101.86 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
取引におけるニューラルネットワーク：双曲潜在拡散モデル（最終回） 取引におけるニューラルネットワーク：双曲潜在拡散モデル（最終回）
HypDiffフレームワークで提案されているように、双曲潜在空間における初期データのエンコーディングに異方性拡散プロセスを用いることで、現在の市場状況におけるトポロジー的特徴を保持しやすくなり、分析の質を向上させることができます。前回の記事では、提案されたアプローチの実装をMQL5を用いて開始しました。今回はその作業を継続し、論理的な完結に向けて進めていきます。
レーベンバーグ・マルカートアルゴリズムを用いた多層パーセプトロンのトレーニング レーベンバーグ・マルカートアルゴリズムを用いた多層パーセプトロンのトレーニング
この記事では、順伝播型（フィードフォワード）ニューラルネットワークの学習におけるレーベンバーグ・マルカートアルゴリズムの実装を紹介します。また、scikit-learn Pythonライブラリのアルゴリズムと性能比較もおこなっています。まずは、勾配降下法、モーメンタム付き勾配降下法、確率的勾配降下法などのより単純な学習法について簡単に触れます。
原子軌道探索(AOS)アルゴリズム 原子軌道探索(AOS)アルゴリズム
この記事では、原子軌道モデルの概念を利用して解を探索する原子軌道検索(AOS:Atomic Orbital Search)アルゴリズムについて考えます。AOSは、原子内における確率分布や相互作用のダイナミクスに基づいており、解の探索プロセスをシミュレートするアルゴリズムです。この記事では、候補解の位置更新やエネルギーの吸収・放出のメカニズムを含めたAOSの数学的な側面について詳しく説明します。AOSは、量子力学の原理を計算問題に応用する新たな可能性を切り開く、革新的な最適化手法です。
Pythonによる農業国通貨への天候影響分析 Pythonによる農業国通貨への天候影響分析
天候と外国為替にはどのような関係があるのでしょうか。古典的な経済理論は、天候のような要因が市場の動きに与える影響を長い間無視してきました。しかし、すべてが変わりました。天候条件と農業通貨の市場でのポジションとの間に、どのようなつながりがあるのかを探ってみましょう。