MetaTrader 5 / トレーディングシステム
English Русский 中文 Español Deutsch Português
preview
取引におけるニューラルネットワーク：双曲潜在拡散モデル（最終回）

取引におけるニューラルネットワーク：双曲潜在拡散モデル（最終回）

MetaTrader 5 — トレーディングシステム |
77 1
Dmitriy Gizlyk
Dmitriy Gizlyk

はじめに

双曲幾何空間は、離散的な木構造や階層構造を表現するのに適しており、さまざまなグラフ学習タスクに応用することが可能です。また、非ユークリッド空間における構造的異方性の問題に対しても、潜在グラフ拡散プロセスの中で有効な手段となります。双曲幾何学は、極座標の角度成分と半径成分を統合し、物理的意味や解釈可能性を備えた幾何学的測定を可能にします。

このような背景のもと、HypDiffフレームワークは、双曲空間内での加法的ガウス摂動の問題を効果的に解決するための、双曲ガウスノイズ生成の高度な手法を提示しています。フレームワークの著者らは、角度類似性に基づいた幾何学的制約を導入し、それを異方性拡散のプロセスに適用することで、グラフの局所構造を保持することを目指しています。

フレームワークのオリジナルの視覚化を以下に示します。

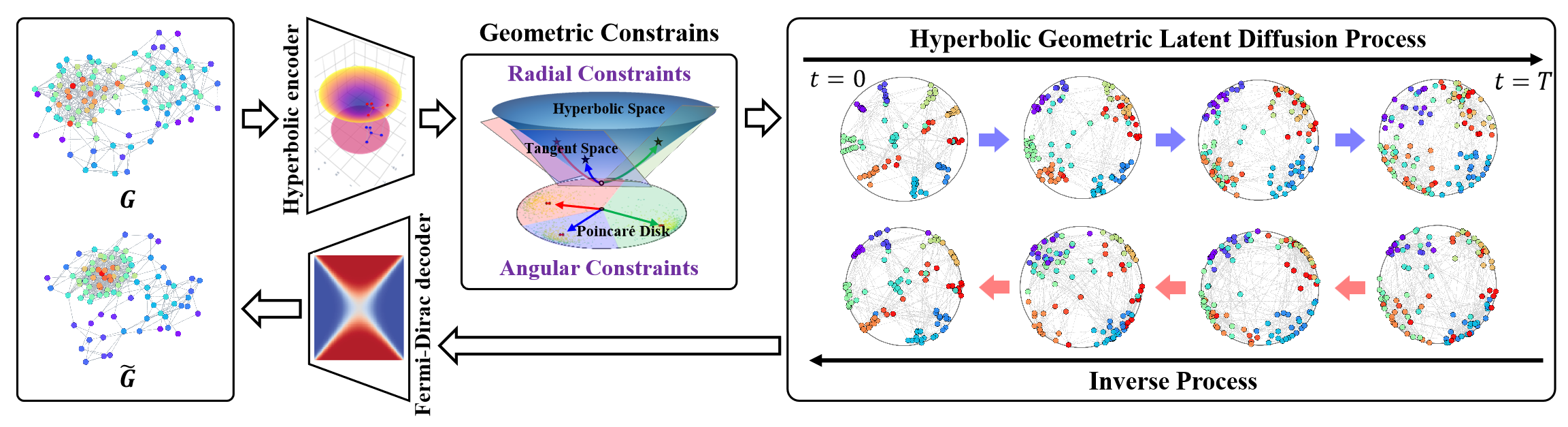
前回の記事では、提案されたアプローチをMQL5で実装し始めました。しかし、作業の範囲は非常に広く、OpenCLプログラム側の実装ブロックのみにとどまりました。この記事では、前回の作業の続きをおこない、HypDiffフレームワークの実装を論理的な結論へと導きます。ただし、私たちの実装では、元のアルゴリズムからいくつかの逸脱を導入しており、それらについてはアルゴリズムの開発プロセス全体を通して説明していきます。



1. 双曲空間へのデータ射影

OpenCLプログラム側の作業は、元のデータを双曲空間へ射影する順伝播および逆伝播（バックプロパゲーション）の各パスに対応したカーネル（それぞれHyperProjectionおよびHyperProjectionGrad）の開発から始まりました。同様に、メインプログラム側におけるHypDiffフレームワークの実装も、この機能に関するアルゴリズムの構築から始めます。これを実現するために、新しいクラスCNeuronHyperProjectionを作成します。その構造は以下のとおりです。

class CNeuronHyperProjection   :  public CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iUnits;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)   { return true; }

public:
                     CNeuronHyperProjection(void) : iWindow(-1), iUnits(-1) {};
                    ~CNeuronHyperProjection(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint units_count, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronHyperProjection;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
  };

提示された構造体では、オブジェクトの構成を定義する定数を格納するための2つの内部変数の宣言と、よく知られたオーバーライド可能なメソッド群が見られます。ただし、モデルのパラメータ更新メソッドであるupdateInputWeightsは、意図的に常に成功を返す「スタブ」として実装されている点に注意してください。これは意図的です。私たちが開発した順伝播および逆伝播の射影カーネルは、明確に定義されたアルゴリズムを実装しており、学習可能なパラメータを含みません。それにもかかわらず、モデルの正しい動作にはパラメータ更新メソッドの存在が必要なため、このメソッドを必ず成功を返す形でオーバーライドせざるを得ません。

新たに宣言された内部オブジェクトが存在しないため、クラスのコンストラクタおよびデストラクタは空のままで問題ありません。継承されたオブジェクトや内部変数の初期化は、Initメソッド内で処理されます。

初期化メソッドのアルゴリズムは比較的単純です。通常どおり、作成されるオブジェクトの構造を一意に特定するために必要な主要な定数をパラメータとして受け取ります。

bool CNeuronHyperProjection::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                  uint window, uint units_count, 
                                  ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, (window + 1)*units_count, optimization_type, batch))
      return false;
   iWindow = window;
   iUnits = units_count;
//---
   return true;
  }

メソッドの本体では、まず同名の親クラスのメソッドを呼び出し、受け取ったパラメータの該当部分を引数として渡します。ご存知のように、親クラスはこれらのパラメータの検証および継承オブジェクトの初期化のロジックをすでに実装しています。私たちがおこなううべきは、親メソッドの実行結果を論理的に確認することだけです。その後、外部プログラムから受け取った構造定数を内部変数に保存します。

これで完了です。新たに内部オブジェクトを宣言しておらず、継承オブジェクトの初期化は親クラスのメソッド内でおこなわれています。後は、処理結果を呼び出し元プログラムに返してメソッドを終了するだけです。

このクラスの順伝播および逆伝播のメソッドについては、各自で確認していただくことをお勧めします。両者とも、OpenCLプログラムの対応するカーネルを呼び出すシンプルな「ラッパー」になっています。これらのメソッドは、当連載の中でも何度も説明していますので、実装のロジックはご理解いただけると思います。このクラスおよびそのすべてのメソッドの完全なコードは、添付ファイルにて確認できます。



2. 接平面への射影

元のデータを双曲空間に射影した後、HypDiffフレームワークでは、双曲ノード埋め込みを生成するエンコーダの構築が求められます。私たちは、この機能を既存のライブラリのコンポーネントを活用して実装する予定です。得られた埋め込みは、k個のセントロイドに対応する接平面へ射影されます。すでにOpenCL側では、接線写像の射影アルゴリズムと対応する勾配の逆伝播を、それぞれLogMapおよびLogMapGradカーネルとして実装済みです。ただし、セントロイドの問題は未解決のままです。

なお、HypDiffフレームワークの著者らは、データ準備段階で学習データセットからセントロイドを定義しています。しかしながら、このアプローチは私たちの目的には適していません。その理由は単なる労力の多さだけではありません。この方法は、動的な金融市場の文脈での分析には不向きです。価格変動のテクニカル分析においては、特定の価格値よりも新たに現れるパターンが優先されることが多いためです。異なる時間区間で観測される類似の市場状況に対しては、異なるセントロイドが関連する可能性があります。これらを踏まえ、セントロイドとそのパラメータを適応・生成する動的モデルの構築が必要であると結論づけました。そこで私たちの実装では、元データの埋め込みに基づくセントロイド生成モデルを採用することにしました。その結果、セントロイド生成と対応する接平面へのデータ射影のプロセスを1つのクラス、CNeuronHyperboloidsに統合する方針としました。その構造を以下に示します。

class CNeuronHyperboloids  :  public CNeuronBaseOCL
  {
protected:
   uint              iWindows;
   uint              iUnits;
   uint              iCentroids;
   //---
   CLayer            cHyperCentroids;
   CLayer            cHyperCurvatures;
   //---
   int               iProducts;
   int               iDistances;
   int               iNormes;
   //---
   virtual bool      LogMap(CNeuronBaseOCL *featers, CNeuronBaseOCL *centroids, 
                            CNeuronBaseOCL *curvatures, CNeuronBaseOCL *outputs);
   virtual bool      LogMapGrad(CNeuronBaseOCL *featers, CNeuronBaseOCL *centroids, 
                                CNeuronBaseOCL *curvatures, CNeuronBaseOCL *outputs);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronHyperboloids(void) : iWindows(0), iUnits(0), iCentroids(0), 
                                                 iProducts(-1), iDistances(-1), iNormes(-1) {};
                    ~CNeuronHyperboloids(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint units_count, uint centroids, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronHyperboloids;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   virtual void      TrainMode(bool flag);
  };

新しいクラスの構造体では、2つの動的配列と6つの変数が、2つのグループに分けて宣言されていることが確認できます。

動的配列は、2つの入れ子モデルのニューラル層オブジェクトへのポインタを格納するために用いられます。実際、私たちの実装では、セントロイドパラメータの生成機能を2つの別々のモデルに分割することにしました。1つ目のモデルは、双曲空間におけるセントロイドの座標を生成します。2つ目のモデルは、対応する点における空間の曲率パラメータを返します。

内部変数のグループ分けにも論理的な理由があります。1つのグループは、外部プログラムから受け取る作成中オブジェクトの構造パラメータを含みます。もう1つのグループは、OpenCLコンテキスト内でのみ作成され、システムのメインメモリへのデータコピーなしに使用される中間値用バッファのポインタを格納する変数群です。

すべての内部オブジェクトは静的に宣言されているため、クラスのコンストラクタおよびデストラクタは空のままで問題ありません。継承および宣言された全オブジェクトの初期化は、Initメソッド内で実装されています。

bool CNeuronHyperboloids::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                               uint window, uint units_count, uint centroids,
                               ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window*units_count*centroids, optimization_type, batch))
      return false;

通常どおり、メソッドのパラメータには、作成されるオブジェクトの構造を一意に定義するいくつかの定数が含まれています。これらは以下の通りです。

  • units_count：解析対象のシーケンス内の要素数
  • window：解析対象シーケンスの単一要素に対応する埋め込みベクトルのサイズ
  • centroids：元データの包括的な解析のためにモデルが生成するセントロイドの数

メソッド本体では、これまでの手法に従い、親クラスの同名メソッドを呼び出して、継承されたオブジェクトと変数の初期化をおこないます。ここで注目すべき点は、元のHypDiffアルゴリズムとは異なり、私たちの実装では入力シーケンスの各要素を特定のセントロイドに割り当てていないことです。代わりに、モデルに最大限の情報を提供するため、シーケンス全体をすべての接平面に射影しています。このため、生成されるテンソルのサイズは、生成されたセントロイドの数に比例して大きくなります。したがって、親クラスの初期化メソッドを呼び出す際には、外部から渡された3つの定数の積を作成する層のサイズとして指定しています。

親メソッドが成功し、ブール値で示される論理的な戻り値が返された後、受け取った定数を内部変数に保存します。

   iWindows = window;
   iUnits = units_count;
   iCentroids = centroids;

次のステップでは、セントロイドパラメータ生成モデルのオブジェクトへのポインタを格納するために、動的配列の準備をおこないます。

   cHyperCentroids.Clear();
   cHyperCurvatures.Clear();
   cHyperCentroids.SetOpenCL(OpenCL);
   cHyperCurvatures.SetOpenCL(OpenCL);

次に、モデルオブジェクトの初期化に直接移ります。まず、セントロイドの座標を生成するモデルを初期化します。

ここでは、入力データを解析した後に該当するセントロイドの座標バッチを返す線形モデルを構築することを目指しています。しかし、この目的で全結合層を用いると、学習可能なパラメータが膨大になり、計算負荷も増大します。そこで、畳み込み層を用いることで、学習パラメータ数と計算量の両方を削減できます。さらに、単変量のシーケンスそれぞれに畳み込み層を適用することは、理にかなったアプローチと考えられます。この実装のために、まず入力データを適切に転置する必要があります。

   CNeuronTransposeOCL *transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, 0, OpenCL, iUnits, iWindows, optimization, iBatch) ||
      !cHyperCentroids.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction(None);

次に、単変量シーケンスの次元を削減するための畳み込み層を追加します。

   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 1, OpenCL, iUnits, iUnits, iCentroids, iWindows, 1, optimization, iBatch) ||
      !cHyperCentroids.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(TANH);

この層では、すべての単変量シーケンスに共通のパラメータセットを使用します。層の出力には、非線形性を導入するため活性化関数として双曲線正接関数を適用します。

次に、活性化関数を用いず、かつ単変量シーケンスごとに異なる学習可能なパラメータを持つ別の畳み込み層を追加します。

   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 2, OpenCL, iCentroids, iCentroids, iCentroids, 1, iWindows, optimization, iBatch) ||
      !cHyperCentroids.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

結果として、これら2つの連続した畳み込み層は、入力シーケンス内の各単変量系列に対して固有のMLP（多層パーセプトロン）を形成しています。各MLPは、必要セントロイド数に応じた1つの座標を生成します。つまり、座標空間の各次元ごとにMLPを構築し、それらが連携して指定された重心の全座標セットを生成していることになります。

あとは、生成されたセントロイド座標を元の表現形式に戻すだけです。そのために、さらにデータの転置層を追加します。

   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, 3, OpenCL, iWindows, iCentroids, optimization, iBatch) ||
      !cHyperCentroids.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

次に、セントロイドの位置における双曲空間の曲率パラメータを決定する第二のモデルのオブジェクト構築に移ります。曲率パラメータは、生成された重心座標に基づいて導出されます。曲率パラメータは特定の座標のみに依存すると考えるのが妥当です。なぜなら、モデルは訓練過程で双曲空間の内部表現を形成し、それを学習済みパラメータに反映させることが期待されるからです。したがって、曲率パラメータモデルでは転置層を用いず、代わりに2つの連続した畳み込み層で構成される、各重心ごとに固有のMLPを単純に作成します。

   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 4, OpenCL, iWindows, iWindows, iWindows, iCentroids, 1, optimization, iBatch) ||
      !cHyperCurvatures.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(TANH);
//---
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 5, OpenCL, iWindows, iWindows, 1, 1, iCentroids, optimization, iBatch) ||
      !cHyperCurvatures.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

ここでも、モデルの層間に非線形性を導入するために双曲線正接関数を使用します。

この段階で、セントロイドパラメータを生成するモデルオブジェクトの初期化は完了です。あとは、データを接平面に射影し、勾配誤差を分配するためのカーネルをサポートするオブジェクトを準備するだけとなります。ここで改めてお伝えしたいのは、前述のカーネル開発時に、中間結果を格納するための一時バッファの作成について議論したことです。これらは3つのデータバッファであり、それぞれが「セントロイド-シーケンス要素」のペアごとに1要素を含みます。

これらのバッファは、順伝播のカーネルから勾配分配カーネルへ情報を受け渡すためだけに使用されます。したがって、それらの作成はOpenCLコンテキスト内でのみ正当化されます。言い換えれば、これらのバッファをシステムメモリ上に確保し、OpenCLコンテキストとメインメモリ間でデータをコピーするのは冗長です。同様に、これらのバッファは各順伝播パスで更新されるため、モデルパラメータの保存時に保持する必要もありません。したがって、メインプログラム側では、これらのデータバッファのポインタを保持する変数のみを宣言します。

とはいえ、OpenCLコンテキスト内でバッファを作成する必要は依然としてあります。そのため、まずデータバッファの必要サイズを決定します。前述の通り、3つのバッファはすべて同じサイズを共有しています。

   uint size = iCentroids * iUnits * sizeof(float);
   iProducts = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE);
   if(iProducts < 0)
      return false;
   iDistances = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE);
   if(iDistances < 0)
      return false;
   iNormes = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE);
   if(iNormes < 0)
      return false;
//---
   return true;
  }

次に、OpenCLメモリ上にデータバッファを作成し、生成されたポインタを対応する変数に格納します。いつも通り、受け取ったポインタの有効性を確認します。

すべてのオブジェクトの初期化が完了したら、操作の論理結果を呼び出し元に返し、メソッドの実行を終了します。

次の作業段階は、CNeuronHyperboloidsクラスの順伝播アルゴリズムの開発です。ここで触れておくべき点として、LogMapおよびLogMapGradメソッドは対応するOpenCLカーネルを呼び出すためのラッパーであり、それらの詳細はご自身でご確認いただくこととします。

feedForwardメソッドを見てみましょう。このメソッドのパラメータでは、元のデータのテンソルを含むニューラル層オブジェクトへのポインタを受け取ります。

bool CNeuronHyperboloids::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *prev = NeuronOCL;
   CNeuronBaseOCL *centroids = NULL;
   CNeuronBaseOCL *curvatures = NULL;

メソッド本体では、まず準備作業として、内部ニューラル層オブジェクトへのポインタを一時的に格納するためのローカル変数を宣言します。そのうちの1つには、受け取った入力データオブジェクトへのポインタを割り当てます。残りの2つは、現時点では空のままにしておきます。

ここで注意すべき点は、この時点では受け取った入力データポインタの有効性をチェックしないことです。メソッドの実行中にこのオブジェクトのデータバッファへ直接アクセスするわけではないため、そのようなチェックは不要だからです。

次に、現在の入力データセットに対するセントロイド座標の生成処理へ進みます。これをおこなうために、対応する内部モデルのオブジェクト群をループ処理します。

//--- Centroids
   for(int i = 0; i < cHyperCentroids.Total(); i++)
     {
      centroids = cHyperCentroids[i];
      if(!centroids ||
         !centroids.FeedForward(prev))
         return false;
      prev = centroids;
     }

ループの本体では、内部のニューラル層オブジェクトへのポインタを順に取得し、その有効性を確認します。次に、取得した内部オブジェクトのfeedForwardメソッドを呼び出し、対応するローカル変数に格納されている適切な入力データポインタを渡します。内部層の順伝播が正常に実行されると、そのオブジェクトがモデル内の次の層への入力データのソースとなるため、そのポインタをローカルの入力データ変数に保存します。したがって、そのポインタをローカル入力データ変数に格納します。

このローカル変数は、初期状態では外部プログラムから受け取った入力データオブジェクトのポインタを保持していました。したがって、ループの最初の反復では、この変数を入力データとして使用しています。つまり、外部からのデータポインタの有効性チェックは内部モデルの各層のfeedForwardメソッド内でおこなわれており、すべてのチェックポイントが確保され、入力オブジェクトからのデータフローが維持されています。

同様のループ構造を用いて、セントロイド座標生成モデルの最終層オブジェクトを基に、セントロイド位置における双曲空間の曲率パラメータを決定します。前述のループ終了後、ローカル変数prevとcentroidsは共にセントロイド座標生成モデルの最終層オブジェクトを指しています。曲率パラメータはセントロイド座標に基づいて決定されるため、このprev変数を用いて安心して処理を進めることができます。

//--- Curvatures
   for(int i = 0; i < cHyperCurvatures.Total(); i++)
     {
      curvatures = cHyperCurvatures[i];
      if(!curvatures ||
         !curvatures.FeedForward(prev))
         return false;
      prev = curvatures;
     }

すべての必要なセントロイドパラメータの取得が正常に完了したら、入力データを対応する接平面上に射影する処理を実行できます。そのために、前回の記事で紹介したLogMapカーネルのラッパーメソッドを呼び出します。

   if(!LogMap(NeuronOCL, centroids, curvatures, AsObject()))
      return false;
//---
   return true;
  }

現在のオブジェクトへのポインタを、結果受取用のエンティティとして渡している点にご注目ください。これにより、演算結果を本クラスのインターフェイスバッファ内に保存することができ、モデルの後続のニューラル層がそれにアクセス可能となります。

あとは、処理結果の論理値を呼び出し元に返し、順伝播パスメソッドを終了するだけです。

順伝播メソッドの実装が完了したので、次は逆伝播アルゴリズムの開発に移ります。ここでは、勾配の伝播を処理するcalcInputGradientsメソッドに注目することを提案します。updateInputWeightsメソッドについては、ご自身での確認にお任せします。

通常どおり、calcInputGradientsメソッドは前段層のオブジェクトへのポインタを受け取ります。このオブジェクトのバッファに対して、入力データがモデルの最終出力に与えた影響に基づいて計算された誤差勾配を伝達することになります。

bool CNeuronHyperboloids::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

今回は、受け取ったポインタの正当性をすぐにチェックします。なぜなら、もし不正なポインタが渡されていた場合、それ以降のすべての処理が無意味になってしまうからです。

順伝播パスのときと同様に、内部モデルオブジェクトのポインタを一時的に保持するためのローカル変数を宣言します。ただし、今回は内部モデルの最終層へのポインタを即座に取得します。  

   CObject *next = NULL;
   CNeuronBaseOCL *centroids = cHyperCentroids[-1];
   CNeuronBaseOCL *curvatures = cHyperCurvatures[-1];

その後、元のデータを接空間へ射影する操作を通じて、勾配分配カーネルのラッパーメソッドを呼び出します。

   if(!LogMapGrad(prevLayer, centroids, curvatures, AsObject()))
      return false;

次に、セントロイドにおける双曲空間の曲率を決定する内部モデルに従って、誤差勾配を分配します。その際、モデル内のニューラル層を逆順に列挙するループを作成します。

//--- Curvatures
   for(int i = cHyperCurvatures.Total() - 2; i >= 0; i--)
     {
      next = curvatures;
      curvatures = cHyperCurvatures[i];
      if(!curvatures ||
         !curvatures.calcHiddenGradients(next))
         return false;
     }

そして次に、曲率決定モデルからセントロイド座標生成モデルへ誤差勾配を渡す必要があります。しかしここで、セントロイド座標生成モデルの最終層のバッファには、すでにデータを接平面へ射影する処理からの誤差勾配が含まれていることに気づきます。私たちはこれらの値を保持したいと考えています。このような場合には、データバッファへのポインタの差し替えをおこなう手法を用います。まず、セントロイド座標生成モデルの最終層における誤差勾配バッファへの現在のポインタをローカル変数に保存し、必要であれば、ニューラル層の活性化関数の導関数に基づいて値を調整します。

   CBufferFloat *temp = centroids.getGradient();
   if(centroids.Activation()!=None)
      if(!DeActivation(centroids.getOutput(),temp,temp,centroids.Activation()))
        return false;
   if(!centroids.SetGradient(centroids.getPrevOutput(), false) ||
      !centroids.calcHiddenGradients(curvatures.AsObject()) ||
      !SumAndNormilize(temp, centroids.getGradient(), temp, iWindows, false, 0, 0, 0, 1) ||
      !centroids.SetGradient(temp, false)
     )
      return false;

次に、適切なサイズの未使用バッファと一時的に差し替えます。そして、セントロイド座標生成モデルの最終層に対して誤差勾配の伝播メソッドを呼び出し、その次のオブジェクトとして、セントロイド上における超空間の曲率決定モデルの最初の層を渡します。2つのデータバッファの値を加算し、それぞれのポインタを元の状態に戻します。操作の実行を制御することを忘れないでください。

これで、セントロイド座標決定モデルの最終層のバッファに合算された誤差勾配が格納されたことになります。したがって、このモデルの各ニューラル層を逆方向にたどるループを構築できます。このループ内では、最終的な結果への寄与に応じて、各層に誤差勾配を分配していきます。

//--- Centroids
   for(int i = cHyperCentroids.Total() - 2; i >= 0; i--)
     {
      next = centroids;
      centroids = cHyperCentroids[i];
      if(!centroids ||
         !centroids.calcHiddenGradients(next))
         return false;
     }

最後に、蓄積された誤差勾配を入力データレベルへ伝播させます。しかしここでも、すでに蓄積された誤差勾配を保持する必要があるという問題に直面します。そのため、入力データオブジェクトのデータバッファを差し替える処理をおこないます。

   temp = prevLayer.getGradient();
   if(prevLayer.Activation()!=None)
      if(!DeActivation(prevLayer.getOutput(),temp,temp,prevLayer.Activation()))
        return false;
   if(!prevLayer.SetGradient(prevLayer.getPrevOutput(), false) ||
      !prevLayer.calcHiddenGradients(centroids.AsObject()) ||
      !SumAndNormilize(temp, prevLayer.getGradient(), temp, iWindows, false, 0, 0, 0, 1) ||
      !prevLayer.SetGradient(temp, false)
     )
      return false;
//---
   return true;
  }

その後、すべての処理結果を呼び出し元に返し、メソッドを終了します。

これで、新しく作成したクラスCNeuronHyperboloidsにおける各メソッドの実装に関する解説は完了です。このクラスの完全なコードとすべてのメソッドは添付ファイルにあります。



3.HypDiffフレームワークの構築

HypDiffフレームワークの個々の新しいコンポーネントの開発を完了し、いよいよフレームワークの最上位実装を表す統合オブジェクトの構築段階に入りました。この目的のために、新しいクラスCNeuronHypDiffを作成します。その構造は以下のとおりです。

class CNeuronHypDiff :  public CNeuronRMAT
  {
public:
                     CNeuronHypDiff(void) {};
                    ~CNeuronHypDiff(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint layers, uint centroids,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronHypDiff; }
   //---
   virtual uint      GetWindow(void) const override
     {
      CNeuronRMAT* neuron = cLayers[1];
      return (!neuron ? 0 : neuron.GetWindow() - 1);
     }
   virtual uint      GetUnits(void) const override
     {
      CNeuronRMAT* neuron = cLayers[1];
      return (!neuron ? 0 : neuron.GetUnits());
     }
  };

新しいクラスの構造から分かるように、そのコア機能はCNeuronRMATオブジェクトから継承されています。この基底オブジェクトは、小規模な線形モデルの動作を組織する機能を提供しており、HypDiffフレームワークの実装に十分な機能を備えています。したがって、この段階では、埋め込みモデルの正しいアーキテクチャを指定してオブジェクトの初期化メソッドをオーバーライドするだけで十分です。その他の処理はすでに親クラスのメソッドでカバーされています。

初期化メソッドのパラメータには、作成されるオブジェクトのアーキテクチャを一意に解釈するための主要な定数が渡されます。

bool CNeuronHypDiff::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint units_count, 
                          uint heads, uint layers, uint centroids, 
                          ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

メソッド本体内では、まず基底のニューラルレイヤーオブジェクトの対応するメソッドを呼び出します。ここでコアインターフェースの初期化が実装されています。この段階で直接の親クラスの初期化メソッドを呼び出さないのは、私たちが作成している埋め込みモデルのアーキテクチャが大きく異なるため、意図的に避けています。

次に、継承された動的配列を準備し、内部オブジェクトへのポインタを格納できるようにします。

   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);
   int layer = 0;

次に、HypDiffフレームワークの内部アーキテクチャの構築に直接進みます。

モデルに渡される入力データはまず双曲空間に射影されます。そのために、先に作成したCNeuronHyperProjectionクラスのインスタンスを追加します。

//--- Projection
   CNeuronHyperProjection *lorenz = new CNeuronHyperProjection();
   if(!lorenz ||
      !lorenz.Init(0, layer, OpenCL, window, units_count, optimization, iBatch) ||
      !cLayers.Add(lorenz))
     {
      delete lorenz;
      return false;
     }
   layer++;

次に、HypDiffフレームワークでは、解析対象グラフのノードの埋め込みを生成するための双曲エンコーダが必要です。元のフレームワークの著者はこの段階でグラフニューラルネットワークと畳み込み層を組み合わせたモデルを使用していましたが、私たちの実装では、グラフニューラルネットワークの代わりに相対位置エンコーディングを用いたTransformerを採用します。

//--- Encoder
   CNeuronRMAT *rmat = new CNeuronRMAT();
   if(!rmat ||
      !rmat.Init(0, layer, OpenCL, window + 1, window_key, units_count, heads, layers, optimization, iBatch) ||
      !cLayers.Add(rmat))
     {
      delete rmat;
      return false;
     }
   layer++;
//---
   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, layer, OpenCL, window + 1, window + 1, 2 * window, units_count, 1, optimization, iBatch) ||
      !cLayers.Add(conv))
     {
      delete conv;
      return false;
     }
   layer++;
   conv.SetActivationFunction(TANH);
//---
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, layer, OpenCL, 2 * window, 2 * window, 3, units_count, 1, optimization, iBatch) ||
      !cLayers.Add(conv))
     {
      delete conv;
      return false;
     }
   layer++;

得られた埋め込みを接平面に射影する際、データ全体を用いてすべての接平面に射影をおこなうため、処理する情報量が大幅に増加することに注意が必要です。この影響を部分的に緩和するために、各ノードの埋め込みの次元数を削減しています。

その後、生成されたデータ埋め込みは、セントロイドの接平面へ投影されます。セントロイドの生成および入力データの対応する接平面への射影機能は、既にCNeuronHyperboloidsクラスで実装済みです。ここでは、そのオブジェクトのインスタンスを線形モデルに追加するだけで十分です。

//--- LogMap projecction
   CNeuronHyperboloids *logmap = new CNeuronHyperboloids();
   if(!logmap ||
      !logmap.Init(0, layer, OpenCL, 3, units_count, centroids, optimization, iBatch) ||
      !cLayers.Add(logmap))
     {
      delete logmap;
      return false;
     }
   layer++;

出力として、入力データが複数の接平面上に射影された結果が得られます。これらは、もともとユークリッドモデル向けに開発された指向性拡散アルゴリズムを用いて処理可能です。私たちの実装では、この目的のためにCNeuronDiffusionオブジェクトを使用しています。

//--- Diffusion model
  CNeuronDiffusion *diff = new CNeuronDiffusion();
  if(!diff ||
     !diff.Init(0, layer, OpenCL, 3, window_key, heads, units_count*centroids, 2, layers, optimization, iBatch) ||
     !cLayers.Add(diff))
    {
     delete diff;
     return false;
    }
  layer++;

ここで特に注目すべき点の1つは、単一の系列要素に対する複数の射影を1つの統合された実体にまとめていないことです。むしろ、私たちの拡散モデルは各射影を独立したオブジェクトとして扱います。これにより、同じ系列の異なる射影間の相関関係をモデルが学習し、基礎データの立体的な表現を形成できるようにしています。

もう1つの暗黙のポイントとして、ノイズの注入方法があります。同じ系列要素の複数の射影間でノイズを合わせようとすることでモデルを複雑にすることは避けました。ノイズの付加は、もとの入力がある程度の範囲でぼやけることを意味します。異なる射影に異なるノイズを入れることで、立体的なぼかし効果を実現しています。

拡散モデルの出力としては、複数の射影にわたってノイズ除去された入力データの表現を期待しています。ここが私たちの実装とオリジナルのHypDiffフレームワークとの最も大きな相違点です。オリジナルでは、著者らは逆射影によって再び双曲空間に戻し、フェルミ・ディラックデコーダを用いて元のグラフ表現を復元していました。一方、私たちの目的は入力データの有益な潜在表現を得ることであり、それをエージェントの行動に対する利益最大化方策を学習するActorモデルに渡すことです。したがって、デコードの代わりに依存関係に基づくプーリング層を適用し、各系列要素の統一された表現を導出しています。

//--- Pooling
   CNeuronMHAttentionPooling *pooling = new CNeuronMHAttentionPooling();
   if(!pooling ||
      !pooling.Init(0, layer, OpenCL, 3, units_count, centroids, optimization, iBatch) ||
      !cLayers.Add(pooling))
     {
      delete pooling;
      return false;
     }
   layer++;

結果テンソルのサイズを入力データのレベルに変更します。

//--- Resize to source size
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, layer, OpenCL, 3, 3, window, units_count, 1, optimization, iBatch) ||
      !cLayers.Add(conv))
     {
      delete conv;
      return false;
     }

あとは、インターフェイス用データバッファのポインタを、モデルの最終層に対応するバッファのポインタに差し替えるだけです。これで、クラスの初期化メソッドの処理が完了します。

//---
   if(!SetOutput(conv.getOutput(), true) ||
      !SetGradient(conv.getGradient(), true))
      return false;
//---
   return true;
  }

これにて、MQL5によるHypDiffフレームワークの独自解釈の実装を完了します。本記事で解説した全クラスおよびメソッドの完全なソースコードは添付ファイルにてご覧いただけます。また、環境とのインタラクションやモデル学習プログラムのコードも、これまでの作品から変更なく引き継いで収録しています。

最後に、学習可能なモデルのアーキテクチャについていくつか補足します。ActorモデルおよびCriticモデルの構造に変更はありませんが、環境状態のエンコーダモデルには若干の改良を加えています。こちらのモデルの入力データは、従来通りバッチ正規化層による初期前処理を経て処理されます。

bool CreateEncoderDescriptions(CArrayObj *&encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

その後、それらはすぐに双曲潜在拡散モデルに渡されます。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronHypDiff;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.window_out = BarDescr;
   descr.layers=2;
   descr.step=10;                                        // centroids
   {
      int temp[] = {4};                                  // Heads
      if(ArrayCopy(descr.heads, temp) < (int)temp.Size())
         return false;
   }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

上述の双曲潜在拡散モデルのアルゴリズムは非常に複雑かつ包括的なプロセスです。そこで、以降のデータ処理は割愛しました。データの次元をActorモデルに入力可能なテンソルサイズに縮小するために、全結合層を1層のみ使用しています。

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

ここで、HypDiffフレームワークの実装は一旦完了とし、次に最も期待される段階である実際の過去データを用いた結果の評価に移ります。



4.テスト

MQL5を用いてHypDiffフレームワークの実装を完了し、現在は最終段階であるモデルの訓練と得られたActor方策の評価に移っています。訓練はこれまでの研究で説明したアルゴリズムに従い、State Encoder、Actor、Criticの3モデルを同時に訓練します。Encoderは市場環境を分析します。Actorは学習した方策に基づいて取引判断をおこない、CriticはActorの行動を評価し、方策の改善を導きます。

訓練は2023年の1年間のEURUSD（H1時間足）の実データを用いて反復的におこない、すべてのインジケーターのパラメータはデフォルト値のままとしています。

訓練過程では訓練データセットの定期的な更新も含まれます。

学習済み方策の有効性を検証するために、2024年の第1四半期の過去データを用いてテストを実施しました。以下にそのテスト結果を示します。

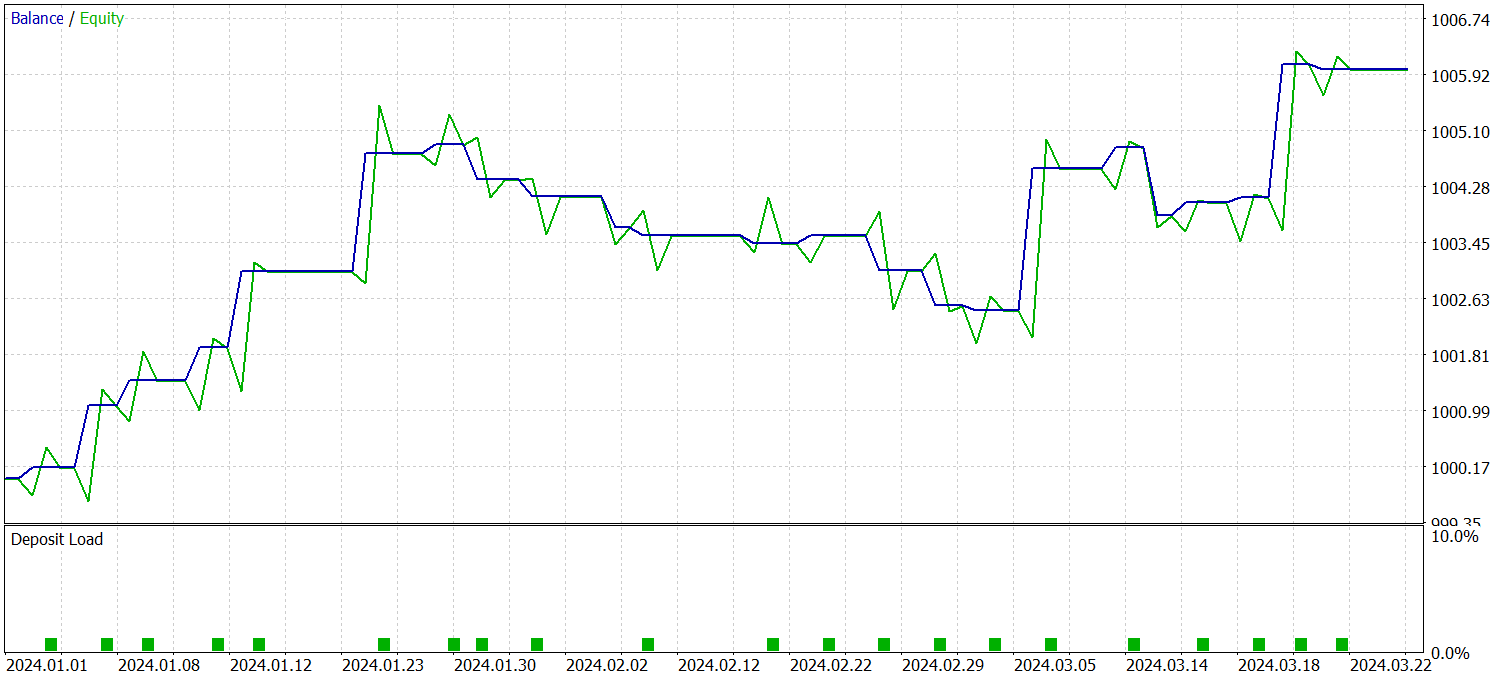
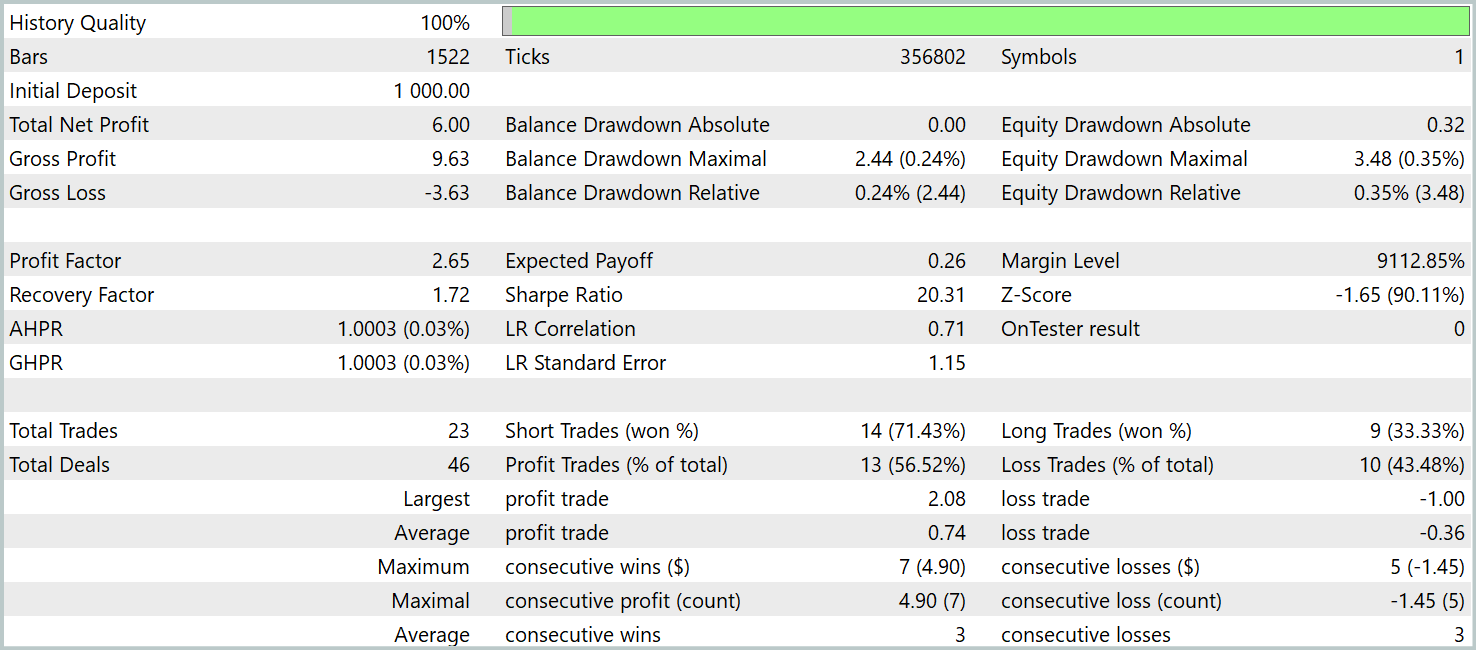
データが示す通り、モデルはテスト期間中に利益を上げることに成功しました。3か月間で合計23回の取引がおこなわれ、比較的少ない回数となっています。取引のうち56％以上が利益確定であり、1回あたりの最大利益および平均利益は損失の約2倍に達しています。

しかし、より興味深い洞察は取引の詳細な内訳から得られます。テスト期間の3か月のうち、モデルが利益を上げたのは2か月間だけであり、2月は全く利益が出ませんでした。2024年1月では8回の取引中7回が利益を出し、唯一の損失は月末の最後の取引でした。この結果は、1年間の訓練サンプルがモデルの最初の1か月以降の実運用において代表性が限定的であるという、先に述べた仮説を支持しています。

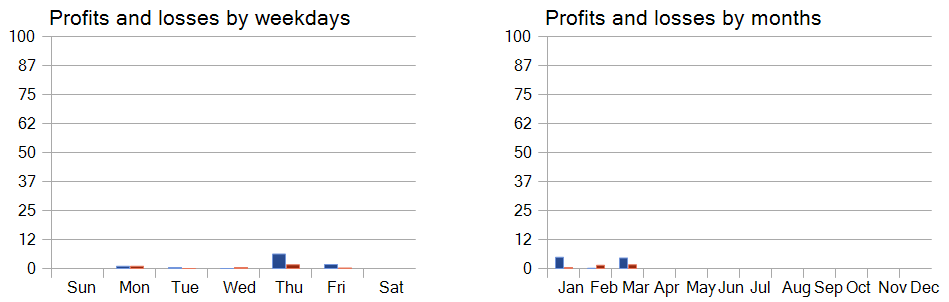
曜日別のパフォーマンス分析では、木曜日と金曜日に取引が集中している傾向も明らかになりました。



結論

双曲幾何学の応用は、離散的なグラフ構造データと連続的な拡散モデルとの根本的な矛盾に起因する課題の解決に役立ちます。HypDiffフレームワークは、双曲空間におけるガウス分布の加法的一貫性の問題を解消する高度な双曲ガウスノイズ生成手法を導入しました。異方性拡散の過程で局所構造を保持するために、角度の類似性に基づく幾何学的制約が課されています。

実践的な部分では、提案手法をMQL5で実装し、実際の過去データを用いてモデルの学習をおこないました。さらに、学習済みのActor方策を訓練セット外のデータで評価し、提案手法の可能性を示すとともに、モデル性能向上のための今後の課題を示唆しました。


参照文献

記事で使用されているプログラム

# 名前 種類 詳細
1 Research.mq5 EA 事例収集のためのEA
2 ResearchRealORL.mq5
 EA
 Real-ORL法による事例収集のためのEA
3 Study.mq5 EA モデル訓練EA
4 Test.mq5 EA モデルテストEA
5 Trajectory.mqh クラスライブラリ システム状態記述の構造体
6 NeuroNet.mqh クラスライブラリ ニューラルネットワークを作成するためのクラスのライブラリ
7 NeuroNet.cl ライブラリ OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16323

添付されたファイル |
ZIPをダウンロード
MQL5.zip (2101.97 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

最後のコメント | ディスカッションに移動 (1)
Mulukas
Mulukas | 9 7月 2025 において 07:43
MetaQuotes:

新しい記事をご覧ください：トレーディングにおけるニューラルネットワーク：ハイパーボリック潜在拡散モデル（最終回）。

著者ドミトリー・ギズリク

技術的には印象的だが、実用的な成果はかなり控えめである。
原子軌道探索(AOS)アルゴリズム 原子軌道探索(AOS)アルゴリズム
この記事では、原子軌道モデルの概念を利用して解を探索する原子軌道検索(AOS:Atomic Orbital Search)アルゴリズムについて考えます。AOSは、原子内における確率分布や相互作用のダイナミクスに基づいており、解の探索プロセスをシミュレートするアルゴリズムです。この記事では、候補解の位置更新やエネルギーの吸収・放出のメカニズムを含めたAOSの数学的な側面について詳しく説明します。AOSは、量子力学の原理を計算問題に応用する新たな可能性を切り開く、革新的な最適化手法です。
取引におけるニューラルネットワーク：双曲潜在拡散モデル(HypDiff) 取引におけるニューラルネットワーク：双曲潜在拡散モデル(HypDiff)
この記事では、異方性拡散プロセスを用いた双曲潜在空間における初期データのエンコーディング手法について検討します。これにより、現在の市場状況におけるトポロジー的特徴をより正確に保持でき、分析の質が向上します。
Numbaを使用したPythonの高速取引ストラテジーテスター Numbaを使用したPythonの高速取引ストラテジーテスター
この記事では、Numbaを使った機械学習モデルのための高速ストラテジーテスターを実装しています。純粋なPythonのストラテジーテスターと比べて50倍速く動作します。このライブラリを使って特にループを含む数学計算を高速化することを推奨しています
レーベンバーグ・マルカートアルゴリズムを用いた多層パーセプトロンのトレーニング レーベンバーグ・マルカートアルゴリズムを用いた多層パーセプトロンのトレーニング
この記事では、順伝播型（フィードフォワード）ニューラルネットワークの学習におけるレーベンバーグ・マルカートアルゴリズムの実装を紹介します。また、scikit-learn Pythonライブラリのアルゴリズムと性能比較もおこなっています。まずは、勾配降下法、モーメンタム付き勾配降下法、確率的勾配降下法などのより単純な学習法について簡単に触れます。