
Algorithmus der Atomic Orbital Search (AOS)
Inhalt
Einführung
Moderne Ansätze zur Lösung komplexer Optimierungsprobleme lassen sich zunehmend von den Prinzipien der Physik, insbesondere der Quantenmechanik, inspirieren. In diesem Artikel betrachten wir den Algorithmus Atomic Orbital Search (AOS), der auf den Konzepten des atomaren Orbitalmodells basiert. Der Algorithmus wurde von Mahdi Azizi im Jahr 2021 vorgeschlagen. Dieser Algorithmus ist eine neue metaheuristische Methode. Das Modell beschreibt das Verhalten der Elektronen nicht als streng definierte Flugbahnen, sondern als Wellenfunktionen, die Wahrscheinlichkeitswolken um den Atomkern herum bilden, dank der wissenschaftlichen Entwicklungen des herausragenden Physikers Erwin Schroeder.Ein Atomorbital, das das Ergebnis einer Quantenbeschreibung ist, ist ein Bereich, in dem die Wahrscheinlichkeit, ein Elektron zu finden, maximal ist. In diesem Modell bewegen sich die Elektronen in imaginären Schichten, die durch Radien und Quantenzahlen definiert sind, die Energieniveaus widerspiegeln. Schichten mit höheren n-Werten entsprechen größeren Radien und dementsprechend höheren Energieniveaus. Dieses Verhalten der Elektronen, das durch die Wechselwirkung mit anderen Teilchen und den Einfluss von Photonen angeregt wird, schafft eine dynamische und sich verändernde Umgebung, in der Elektronen Energie abgeben oder aufnehmen können, wenn sie sich zwischen verschiedenen Orbitalen bewegen.
Der AOS-Algorithmus nutzt diese physikalischen Prinzipien, um den Prozess der Lösungsfindung für Optimierungsprobleme zu modellieren. Es berücksichtigt Wahrscheinlichkeitsverteilungen und Interaktionsdynamik, was eine effiziente Erkundung des Lösungsraums ermöglicht. Insbesondere berücksichtigt der Algorithmus Aktualisierungen der Positionen der Lösungsvorschläge (Elektronen) in Abhängigkeit von ihren Energien, was sich wiederum auf die Wahrscheinlichkeit auswirkt, sich in bestimmten Schichten zu befinden. Dadurch kann AOS nicht nur optimale Lösungen finden, sondern sich auch an Veränderungen in der Umgebung anpassen.
In diesem Beitrag werden wir das mathematische Modell von AOS im Detail untersuchen, einschließlich der Schritte zur Aktualisierung der Positionen der Lösungsvorschläge sowie der Mechanismen, die die Energieaufnahme und -abgabe regeln. AOS ist also nicht nur ein interessanter Ansatz für die Optimierung, sondern eröffnet auch neue Horizonte für die Anwendung von Quantenprinzipien auf Berechnungsprobleme.
Implementierung des Algorithmus
Der AOS-Algorithmus basiert auf den Prinzipien des Atomorbitalmodells, das die Emission und Absorption von Energie durch Atome sowie die Konfiguration der Elektronendichte berücksichtigt. Zu Beginn des Algorithmus werden mehrere Lösungsvorschläge mit der Bezeichnung X angegeben, die als Elektronen um den Kern eines Atoms betrachtet werden. Diese Kandidaten bilden eine Elektronenwolke, und der Suchraum wird als ein kugelförmiges Volumen dargestellt, das in konzentrische Schichten unterteilt ist. Die Lösungskandidaten können in allgemeiner Form wie folgt geschrieben werden:
X = [x1, x2 ..., xj ..., xm], wobei xi der i-te Lösungskandidat ist, während m die Gesamtzahl der Kandidaten ist.
Die Anfangspositionen der Lösungskandidaten werden nach dem Zufallsprinzip initialisiert. Jedes Elektron hat ein Energieniveau, das durch eine Zielfunktion bestimmt wird, die es zu minimieren gilt. So entsprechen Elektronen mit niedrigen Energieniveaus den Kandidaten mit den besten Zielfunktionswerten, und Elektronen mit hohen Energieniveaus entsprechen den Kandidaten mit den schlechtesten Werten. Der Vektor der Werte der Zielfunktion wird wie folgt geschrieben:
E = [E1, E2, ..., Ei, ..., Em], wobei Ei das Energieniveau des i-ten Kandidaten ist.
Die imaginären Schichten um den Kern herum werden mit einer zufälligen ganzen Zahl n modelliert, die von 1 bis zur Anzahl der Schichten L reichen kann. Die Schicht mit dem kleinsten Radius L0 stellt den Kern dar, und die übrigen Li-Schichten sind der Ort, an dem sich die Elektronen befinden (bei AOS kann die „Kern“-Schicht auch Elektronen enthalten). Die Verteilung der Lösungskandidaten auf die verschiedenen Schichten erfolgt mithilfe der Wahrscheinlichkeitsdichtefunktion (PDF), die die Wahrscheinlichkeit bestimmt, den Wert einer Variablen in einem bestimmten Bereich zu finden. Der Algorithmus verwendet eine Log-Normal-Verteilung, die es ihm ermöglicht, das reale Wellenverhalten von Elektronen zu simulieren. Die Lösungskandidaten werden auf verschiedene Schichten verteilt, wobei der Vektor Xk, der die Kandidaten in n Schichten enthält, wie folgt festgelegt wird:
Xk = [Xk1, Xk2, ..., Xki, ..., Xkp], wobei k ein Schichtindex und p die Anzahl der Kandidaten in der Schicht ist.
Nach dem atomaren Orbitalmodell wird davon ausgegangen, dass sich die Elektronen im Grundzustand befinden. Der Bindungszustand und die Bindungsenergie für jede Schicht werden wie folgt berechnet:
BS_k = (1/p) * Σ(Xki),
BE_k = (1/p) * Σ(Eki).
Das Gesamtenergieniveau eines Atoms ist definiert als:
BS = (1/m) * Σ(Xi),
BE = (1/m) * Σ(Ei).
Unter dem Einfluss von Photonen und anderen Wechselwirkungen können Elektronen ihre Position verändern und sich zwischen Schichten bewegen. Die Aktualisierung der Position der Lösungskandidaten im AOS-Algorithmus basiert auf der Interaktionswahrscheinlichkeit, die durch eine zufällig erzeugte ϕ-Zahl dargestellt wird, die im Bereich [0,1] verteilt ist. Wenn ϕ ≥ PR (Photonengeschwindigkeitsparameter), dann ist eine Emission oder Absorption von Energie möglich.
Wenn Eki ≥ BEk ist, kommt es zur Energieabgabe: Xki[t+1] = Xkit + αi × (βi × LE − γi × BS) / k.
Wenn Eki < BEk ist, erfolgt eine Energieabsorption: Xki[t+1] = Xkit + αi × (βi × LEk − γi × BSk).
Ist ϕ < PR, so werden Verschiebungen in Magnetfeldern oder Wechselwirkungen mit anderen Teilchen berücksichtigt: Xki[t+1] = Xkit + ri, wobei ri ein zufälliges Inkrement im Bereich von min bis max des entsprechenden optimierten Parameters des Problems ist.
Vereinfacht ausgedrückt, kann die Population der Lösungsvorschläge in AOS als Molekül dargestellt werden, wobei die Atome den Koordinaten im Suchraum und die Elektronen in diesen Atomen den spezifischen Lösungen entsprechen. Wenn also die Population aus 50 Lösungsansätzen besteht, dann gibt es in jedem Atom 50 Elektronen, die gemäß der Log-Normal-Verteilung über die Schichten verteilt sind.
In der Beschreibung des Algorithmus gibt der Autor nicht an, wie der Durchmesser der äußeren Atomschicht bestimmt wird, was bedeutet, dass sich der Atomkern im Verhältnis zu den Schichten in der Mitte befindet. Das bedeutet, dass sich das Atom zusammen mit den Schichten innerhalb der vorgegebenen Grenzen des Problems bewegt. Um dem Algorithmus mehr Flexibilität zu geben, vereinbaren wir, dass der Durchmesser der äußeren Schicht dem [min; max]-Bereich für die entsprechende Koordinate im Suchraum entspricht und der Mittelpunkt des Atomkerns am Punkt der besten globalen Lösung für die gegebene Koordinate liegt. Das Modell eines Atoms in AOS kann in Abbildung 1 dargestellt werden.
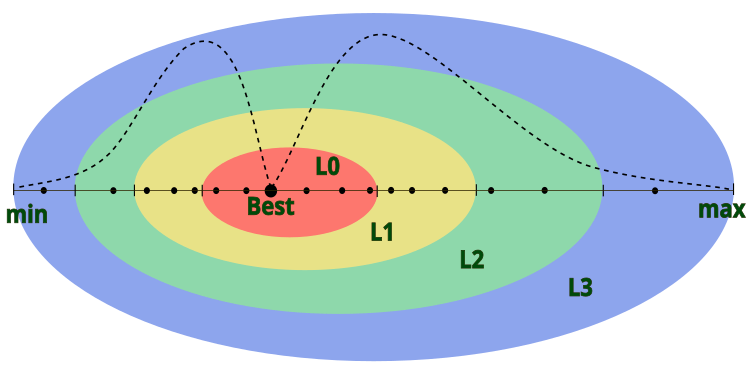
Abbildung 1. Modell eines Atoms im AOS-Algorithmus, wobei die Punkte Elektronen darstellen und die gestrichelte Linie die lognormale Verteilung der Elektronen repräsentiert
Pseudocode des Atomic Orbital Search (AOS)-Algorithmus:
1. Initialisierung
1.1 Ausgangspositionen (Xi)
Es wird eine Population von m Lösungsvorschlägen erstellt
Jedem Kandidaten wird eine zufällige Position im Suchraum zugewiesen.
1.2 Berechnung der anfänglichen Fitness (Ei)
Für jeden Kandidaten wird der Wert der Zielfunktion berechnet
Dieser Wert stellt die Energie des Teilchens dar.
Je niedriger die Energie, desto besser die Lösung.
1.3 Bestimmung der Atomparameter
BS (Binding State) ist der Bindungszustand des Atoms, der die aktuelle Durchschnittsposition aller Teilchen darstellt
BE (Binding Energy) steht für die durchschnittliche Energie aller Teilchen
LE (Lowest Energy) ist ein Teilchen mit der niedrigsten Energie (beste Lösung)
2. Erstellen einer Schicht-Struktur
2.1 Generierung einer zufälligen Anzahl von Schichten [1; n] für jedes Atom
Die Anzahl der imaginären Orbitale wird bestimmt
Jedes Orbital stellt eine Schicht der Suche mit unterschiedlicher Intensität dar.
2.2 Partikelverteilung
Die Partikel werden gemäß der Wahrscheinlichkeitsdichtefunktion (PDF) in Schichten verteilt
Die inneren Schichten enthalten in der Regel die besten Lösungen.
Die äußeren Schichten werden zur Erforschung des Raumes verwendet.
2.3 Suchprozess für jede Schicht (k)
3.1 Schicht-Parameter
BSk ist der Verbindungsstatus für eine bestimmte Schicht
BEk - Bindungsenergie der Schicht
LEk ist das Teilchen mit der niedrigsten Energie in der Schicht
3.2 Aktualisierung der Partikelpositionen
Für jedes Partikel i in der Schicht k:
3.3 Generierung von Steuerungsparametern:
φ: Definition der Bewegungsart
α: Skalierungsfaktor
β: Koeffizient der Anziehungskraft auf die beste Lösung
γ: Koeffizient der Abstoßung vom mittleren Zustand
PR: Wahrscheinlichkeit der Photonenbewegung
3.4 Bewegungsart auswählen:
wenn φ ≥ PR:
wenn Eki ≥ BEk:
// Globale Forschung
Xi[t+1] = Xit + αi × (βi × LE - γi × BS) / k
sonst:
// Lokale Forschung
Xi[t+1] = Xit + αi × (βi × LEk - γi × BSk)
sonst:
// Zufällige Bewegung
Xki[t+1] = Xkit + ri
4. Berechnung der Fitness (Ei)
5. Aktualisierung der globalen Einstellungen
6. Wiederholen des Vorgang ab 1.3, bis das Stoppkriterium erfüllt ist.
Um die Wahrscheinlichkeit der Elektronenverteilung um den Kern (die beste Lösung) zu berechnen, kann man die Zahlenbildung für verschiedene Verteilungen verwenden. Der Autor bevorzugt die Log-Normal-Verteilung, was ihre Implementierung im Code erfordert. Schreiben wir nun den Generatorcode. Für den Algorithmus ist es notwendig, nicht nur eine lognormale Verteilung zu erstellen, sondern eine, die asymmetrisch zum Zentrum (Kern) verschoben ist, wie in Abbildung 1 dargestellt. Wir implementieren die Funktion LognormalDistribution in der Funktionssammlungsbibliothek für Optimierungsalgorithmen, die eine Zufallszahl erzeugt, die nach dem Lognormalgesetz innerhalb der vorgegebenen Grenzen mit einer Vorspannung verteilt ist.
Die Funktion benötigt die folgenden Parameter:
1. center - Zentralwert der Verteilung.
2. min_value - Mindestwert, der erzeugt werden kann.
3. max_value - maximaler Wert, der erzeugt werden kann.
4. peakDisplCoeff - Koeffizient der Spitzenverschiebung relativ zum Verteilungszentrum (Standardwert ist 0,2).
Beschreibung der Funktion:
1. Kontrolle der Grenzen:
Wenn min_value größer oder gleich max_value ist, gibt die Funktion max_value zurück.
Wenn max_value kleiner oder gleich min_value ist, gibt die Funktion min_value zurück.
2. Die Zufallszahl wird im Bereich von 0 bis 1 erzeugt.
3. Einstellung der Mitte:
Wenn center kleiner als min_value ist, wird es auf min_value und random wird auf 0 gesetzt.
Wenn center größer als max_value ist, wird es auf max_value und random wird auf 0 gesetzt.
4. Berechnen der Werte peak_left und peak_right, die die Position der Verteilungsspitzen bestimmen.
5. Erzeugen eines Wertes:
Wenn random kleiner als 0,5 ist, wird die Berechnung für den linken Teil der Verteilung durchgeführt:
Berechnen der Parameter mu_left und sigma_left.
Erzeugen von Zufallszahlen u1 und u2 für das Box-Muller-Verfahren.
Anwenden der Box-Muller-Methode, um einen normalverteilten Wert z zu erhalten.
Das Ergebnis für die linke Seite wird berechnet.
Wenn random größer oder gleich 0,5 ist, wird ein ähnlicher Prozess für die rechte Seite der Verteilung unter Verwendung der Parameter mu_right und sigma_right durchgeführt.
6. Wenn der generierte Ergebniswert über min_value und max_value hinausgeht, wird die Funktion RNDfromCI aufgerufen, um den Wert in den akzeptablen Bereich zu „werfen“ und so die Akkumulation von Wahrscheinlichkeiten an den Grenzen der generierten Zufallszahlen zu verhindern.
//------------------------------------------------------------------------------ //The lognormal distribution of the species: min|------P---C---P------|max double C_AO_Utilities :: LognormalDistribution (double center, double min_value, double max_value, double peakDisplCoeff = 0.2) { // Check the right border if (min_value >= max_value) { return max_value; } // Check the left border if (max_value <= min_value) { return min_value; } // Generate a random number from 0 to 1 double random = MathRand () / 32767.0; // Correction of the center if it goes beyond the boundaries if (center < min_value) { center = min_value; random = 1; } if (center > max_value) { center = max_value; random = 0; } // Calculate the position of the peaks double peak_left = center - (center - min_value) * peakDisplCoeff; double peak_right = center + (max_value - center) * peakDisplCoeff; double result = 0.0; if (random < 0.5) // Left side of the distribution { // Calculate parameters for the left side double diff_center_peak = MathMax (center - peak_left, DBL_EPSILON); double diff_center_min = MathMax (center - min_value, DBL_EPSILON); double mu_left = MathLog (diff_center_peak); double sigma_left = MathSqrt (2.0 * MathLog (MathMax (diff_center_min / diff_center_peak, DBL_EPSILON)) / 9.0); // Generate random numbers for the Box-Muller method double u1 = MathRand () / 32767.0; double u2 = MathRand () / 32767.0; // Protection against null values u1 = MathMax (u1, DBL_EPSILON); // Application of the Box-Muller method double z = MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2); // Calculate the result for the left side result = center - MathExp (mu_left + sigma_left * z); } else // Right side of the distribution { // Calculate parameters for the right side double diff_peak_center = MathMax (peak_right - center, DBL_EPSILON); double diff_max_center = MathMax (max_value - center, DBL_EPSILON); double mu_right = MathLog (diff_peak_center); double sigma_right = MathSqrt (2.0 * MathLog (MathMax (diff_max_center / diff_peak_center, DBL_EPSILON)) / 9.0); // Generate random numbers for the Box-Muller method double u1 = MathRand () / 32767.0; double u2 = MathRand () / 32767.0; // Protection against null values u1 = MathMax (u1, DBL_EPSILON); // Application of the Box-Muller method double z = MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2); // Calculate the result for the right side result = center + MathExp (mu_right + sigma_right * z); } // Check and correct the result if it goes beyond the limits if (result < min_value || result > max_value) return RNDfromCI (min_value, max_value); return result; }
Schreiben wir ein Skript, um die resultierende Verteilung visuell zu überprüfen. Das ist es, was das Testskript tut (wir werden den Rest des Codes nicht zur Verfügung stellen - die Klasse für die Arbeit mit dem Hintergrund „Canvas“ für den Test kann im Artikelarchiv gefunden werden):
1. Erstellen des Objekts Canvas zum Zeichnen von Grafiken.
2. Initialisierung der Canvas-Parameter: B Breite, H Höhe und O Abstände.
3. Erstellen der Arrays CountL und CountR, um die Werte links und rechts der mit Nullen initialisierten Eingabe Inp_P zu zählen.
4. Erstellen eines grafischen Elements (Canvas) mit bestimmten Abmessungen und Hintergrundfarben.
Die Log-Normalverteilung beschreibt Zufallsvariablen, deren Logarithmus normalverteilt ist. Im Code wird er verwendet, um Werte zu erzeugen, die im Diagramm angezeigt werden.
5. In der for-Schleife werden N Werte mit der Funktion U.LognormalDistribution() erzeugt. Jeder Wert wird mit Inp_P verglichen: Wenn er kleiner ist, wird der Zähler CountL[i] erhöht, wenn er größer ist - CountR[i].
6. Vor der Erzeugung werden CountL und CountR mit Nullen initialisiert.
7. Die Minimal- und Maximalwerte in den Feldern werden berechnet, um den Bereich der Diagramme zu bestimmen.
8. Die Koordinaten für das Zeichnen von Diagrammen werden berechnet, einschließlich der Mitte des Hintergrunds und der Schritte für den linken und rechten Teil.
9. Auf dem Hintergrund werden Punkte gezeichnet, die die Anzahl der Werte in den Bereichen darstellen, wobei die Farbe durch die Häufigkeit des Auftretens bestimmt wird.
10. Der Hintergrund wird aktualisiert, um die Änderungen widerzuspiegeln.
// Function called at startup void OnStart () { CCanvas Canvas; // Object for handling graphics (canvas) // Canvas parameters int W = 750; // Canvas width int H = 400; // Canvas height int O = 10; // Margins from canvas borders // Arrays for storing count values int CountL []; // Count values to the left of the input int CountR []; // Count values to the right of the input // Initialize arrays ArrayResize (CountL, Size_P); // Resize the CountL array ArrayInitialize (CountL, 0); // Initialize the CountL array with zeros ArrayResize (CountR, Size_P); // Resize the CountR array ArrayInitialize (CountR, 0); // Initialize the CountR array with zeros // Create a canvas string canvasName = "Test_Probability_Distribution_Canvas"; // Canvas name if (!Canvas.CreateBitmapLabel(canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW)) { Print ("Error creating Canvas: ", GetLastError()); // Display an error if creation fails return; } // Set up canvas properties ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false); // Make canvas visible ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true); // Make canvas selectable // Clear the canvas and draw the border Canvas.Erase (COLOR2RGB(clrWhite)); // Fill with white color Canvas.Rectangle (1, 1, W - 1, H - 1, COLOR2RGB(clrBlack)); // Draw a black frame int ind = 0; // Index for counting double X = 0.0; // Variable for storing values // Main loop for generating values for (int i = 0; i < CNT_P; i++) { // Generate log-normal distribution X = U.LognormalDistribution (Inp_P, Min_P, Max_P, PeakDisplCoeff_P); // Determine which side of the input parameter the value falls on if (X < Inp_P) { // Calculate the index for the left part ind = (int) U.Scale(X, Min_P, Inp_P, 0, Size_P, true); if (ind >= Size_P) ind = Size_P - 1; // Limit the index if (ind < 0) ind = 0; // Limit the index CountL [ind] += 1; // Increment the counter for the left side } else { // Calculate the index for the right side ind = (int) U.Scale (X, Inp_P, Max_P, 0, Size_P, false); if (ind >= Size_P) ind = Size_P - 1; // Limit the index if (ind < 0) ind = 0; // Limit the index CountR [ind] += 1; // Increment the counter for the right side } } // Define minimum and maximum values for the graph int minCNT = CNT_P; // Initial value for the minimum counter int maxCNT = 0; // Initial value for the max counter // Finding minimum and maximum values in counters for (int i = 0; i < Size_P; i++) { if (CountL [i] > maxCNT) maxCNT = CountL [i]; // Update the max value for the left side if (CountR [i] > maxCNT) maxCNT = CountR [i]; // Update the max value for the right side if (CountL [i] < minCNT) minCNT = CountL [i]; // Update the min value for the left side if (CountR [i] < minCNT) minCNT = CountR [i]; // Update the minimum value for the right side } // Variables for drawing graphs int x = 0.0; // X coordinate int y = 0.0; // Y coordinate color clrF; // Color int centre = 0; // Canvas center int stepL = 0; // Left side step int stH_L = 0; // Left side height int stepR = 0; // Right side step int stH_R = 0; // Right side height // Determine the center of the canvas centre = (int) U.Scale(Inp_P, Min_P, Max_P, O, W - O - 1, false); // Calculate steps and heights for the left side stepL = (centre - O) / Size_P; stH_L = stepL / 2; if (stH_L == 0) stH_L = 1; // Make sure the height is not 0 // Calculate steps and heights for the right side stepR = (W - O - centre) / Size_P; stH_R = stepR / 2; if (stH_R == 0) stH_R = 1; // Make sure the height is not 0 // Draw graphs for left and right parts for (int i = 0; i < Size_P; i++) { // Draw for the left side x = (int) U.Scale (i, 0, Size_P - 1, O, centre - stH_L, true); // Calculate the X coordinate y = (int) U.Scale (CountL [i], 0, maxCNT, O, H - O - 1, true); // Calculate the Y coordinate clrF = DoubleToColor(CountL [i], minCNT, maxCNT, 0, 255); // Define color by value // Draw dots for the left side Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); // Draw a small circle Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); // Draw a larger circle // Draw for the right side x = (int) U.Scale (i, 0, Size_P - 1, centre + stH_R, W - O - 1, false); // Calculate the X coordinate y = (int) U.Scale (CountR[i], 0, maxCNT, O, H - O - 1, true); // Calculate the Y coordinate clrF = DoubleToColor (CountR [i], minCNT, maxCNT, 0, 255); // Define color by value // Draw dots for the right side Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); // Draw a small circle Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); // Draw a larger circle } Canvas.Update (); // Update the canvas to reflect the changes}
Führen wir das Skript aus und erhalten wir ein Bild auf dem Chart wie in Abbildung 2.
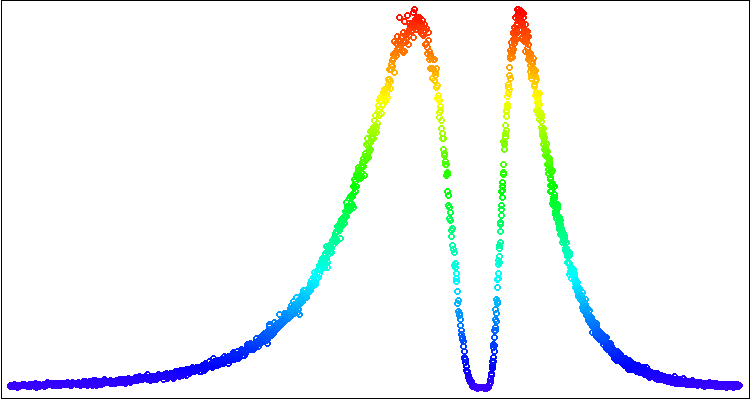
Abbildung 2. Visualisierung einer asymmetrischen Log-Normal-Verteilung mit der Standardbibliothek Canvas
Nachdem wir die Theorie aller Stufen des Algorithmus eingehend untersucht haben, wollen wir uns nun direkt der Code-Implementierung zuwenden. Während der AOS-Algorithmus eine Minimierungsmethode für das Problem ist, werden wir die Logik so anpassen, dass sie für die Maximierung funktioniert. Implementieren wir die Struktur S_Layer, die die atomare Schicht simuliert und Informationen über die Anzahl der in dieser Schicht befindlichen Teilchen enthält. Sie enthält sowohl die numerischen Merkmale als auch die Methode zur Initialisierung. Die Felder der Struktur:
- pc - Zähler der Teilchen, die sich in einer bestimmten Schicht eines Atoms befinden, mit dem man verfolgen kann, wie viele Teilchen (Elektronen) sich in einer bestimmten Schicht befinden.
- BSk - Zustand der Verbindung in der Schicht, spiegelt den Grad der Interaktion zwischen den Teilchen in der Schicht wider.
- BEk - Bindungsenergie in der Schicht, zeigt an, wie stark die Teilchen in der Schicht aneinander gebunden sind.
- LEk - Mindestenergie in einer Schicht zur Bestimmung des niedrigsten Energieniveaus, das von Teilchen in einer bestimmten Schicht erreicht werden kann.
Die Methode Init dient dazu, die Strukturfelder mit Standardwerten zu initialisieren und ermöglicht es uns, den Zustand der Schicht bei Bedarf mehrfach zurückzusetzen.
//—————————————————————————————————————————————————————————————————————————————— struct S_Layer { int pc; // particle counter double BSk; // connection state double BEk; // binding energy double LEk; // minimum energy void Init () { pc = 0; BSk = 0.0; BEk = 0.0; LEk = 0.0; } }; //——————————————————————————————————————————————————————————————————————————————
Als Nächstes wollen wir uns die Struktur S_Atom und ihre Methode Init ansehen. S_Atom ist eine Struktur, die ein aus mehreren Schichten bestehendes Atom darstellt. Jede Schicht wird mit dem Array layers[] der zuvor beschriebenen S_Layer-Struktur simuliert. Die Felder der Struktur:
- Init - Methode zur Initialisierung eines Arrays von atomaren Schichten sowie zur Initialisierung jeder Schicht in diesem Array.
- layersNumb - ganzzahliger Parameter, der die Anzahl der Schichten angibt, die für ein bestimmtes Atom erstellt werden.
//—————————————————————————————————————————————————————————————————————————————— struct S_Atom { S_Layer layers []; // array of atom layers void Init (int layersNumb) { ArrayResize (layers, layersNumb); for (int i = 0; i < layersNumb; i++) layers [i].Init (); } }; //——————————————————————————————————————————————————————————————————————————————
Die nächste Struktur S_Electron und ihre Methode Init. Die Struktur ist ein Elektron, ein Mitglied der Lösungspopulation, das Informationen über seine Position in der entsprechenden Schicht des Atoms enthält. Die Felder von layerID[] stellen ein Array aus Ganzzahlen dar, das die IDs der Schichten speichert, zu denen das Elektron gehört. Jede ID entspricht einer bestimmten Schicht im Atom, sodass wir verfolgen können, auf welcher Schicht sich das Elektron befindet.
//—————————————————————————————————————————————————————————————————————————————— struct S_Electron { int layerID []; // array of layer IDs for the electron void Init (int coords) { ArrayResize (layerID, coords); } }; //——————————————————————————————————————————————————————————————————————————————
Der Algorithmus der Klasse C_AO_AOS AOS erbt von der Basisklasse C_AO und impliziert das Vorhandensein einer gemeinsamen Funktionalität im Zusammenhang mit Atomumlaufbahnen.
Parameter der Klasse:
- popSize - Größe der Population im Algorithmus.
- maxLayers - maximale Anzahl von Schichten, die in einem atomaren Modell verwendet werden können.
- photonEmissions - Anzahl der Photonenemissionen, die für den Optimierungsprozess verwendet werden.
- PR - Photonenübergangskoeffizient, bestimmt die Wahrscheinlichkeit des Übergangs zwischen Zuständen.
- peakPosition - Spitzenposition in der Log-Normal-Verteilung.
Methoden der Klasse:
1. SetParams() - setzt die Algorithmusparameter durch Lesen von Werten aus dem Array params.
2. Init() - initialisiert den Algorithmus mit den angegebenen Suchparametern: minimaler und maximaler Bereich, Suchschritt und Anzahl der Epochen.
3. Moving() - Methode zum Verschieben von Partikeln im Suchraum.
4. Überarbeitung() - die Methode ist für die Überarbeitung der besten Lösungen zuständig, die während der Optimierung gefunden wurden.
Private Felder der Klasse:
- atomStage - aktueller Stand des Atomprozesses.
- currentLayers[] - aktuelle Anzahl der Schichten für jedes Atom (zu jeder Epoche ist die Anzahl der Schichten in jedem Atom eine Zufallszahl im Bereich [1; maxLayers]).
- S_Atom atoms[] - Array von Atomen, deren Größe der Anzahl der im Algorithmus verwendeten Koordinaten entspricht.
- S_Electron electrons[] - Array von Elektronen, die der Populationsgröße entsprechen.
- BS[] - Zustände von Bindungen zwischen Elektronen in der gesamten Population.
Private Methoden der Klasse:
1. GetOrbitBandID() - ermittelt die Orbitalband-ID für die angegebenen Parameter wie Anzahl der Schichten und Bereiche.2. DistributeParticles() - Methode zum Verteilen von Partikeln im Suchraum.
3. LayersGenerationInAtoms() - erzeugt die Anzahl der Schichten in Atomen.
4. UpdateElectronsIDs() - Aktualisierung der Schicht-IDs für Elektronen.
5. CalcLayerParams() - berechnet die Parameter von Schichten und umfasst die Bestimmung von Energieniveaus und Bindungen.
6. UpdateElectrons() - aktualisiert die Position der Elektronen.
//—————————————————————————————————————————————————————————————————————————————— // Class implementing the atomic optimization algorithm (Atomic Orbital Search) class C_AO_AOS : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_AOS () { } C_AO_AOS () { ao_name = "AOS"; ao_desc = "Atomic Orbital Search"; ao_link = "https://www.mql5.com/en/articles/16276"; popSize = 50; // population size maxLayers = 5; // maximum number of layers photonEmissions = 1; // number of photon emissions PR = 0.1; // photon transition coefficient peakPosition = 0.05; // peak position in the log-normal distribution ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "maxLayers"; params [1].val = maxLayers; params [2].name = "photonEmissions"; params [2].val = photonEmissions; params [3].name = "photonRate"; params [3].val = PR; params [4].name = "peakPsition"; params [4].val = peakPosition; } // Setting algorithm parameters void SetParams () { popSize = (int)params [0].val; maxLayers = (int)params [1].val; photonEmissions = (int)params [2].val; PR = params [3].val; peakPosition = params [4].val; } // Initialization of the algorithm with the given search parameters bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Method of moving particles void Revision (); // Method of revising the best solutions //---------------------------------------------------------------------------- int maxLayers; // maximum number of layers int photonEmissions; // number of photon emissions double PR; // photon transition coefficient double peakPosition; // peak position in the log-normal distribution private: //------------------------------------------------------------------- int atomStage; // current stage of the atom int currentLayers []; // current number of layers for the corresponding atom (coordinates) S_Atom atoms []; // atoms with their size corresponding to the number of coordinates S_Electron electrons []; // electrons corresponding to the population size double BS []; // connection states // Get orbital band for given parameters int GetOrbitBandID (int layersNumb, double min, double max, double center, double p); // Distribution of particles in the search space void DistributeParticles (); // Generate layers in atoms void LayersGenerationInAtoms (); // Update electron IDs void UpdateElectronsIDs (); // Calculate layer parameters void CalcLayerParams (); // Update electron positions void UpdateElectrons (); }; //——————————————————————————————————————————————————————————————————————————————
Schauen wir uns an, was in der Methode Init der AOS-Algorithmusklasse passiert.
1. Standard-Initialisierung: Die Methode beginnt mit dem Aufruf von StandardInit und führt allgemeine Initialisierungsschritte durch, wie z. B. das Festlegen von Bereichen für Koordinaten.
2. Initialisierung von Variablen:
- atomStage - auf 0 gesetzt, was bedeutet, dass der Algorithmus mit der Anfangsphase beginnt.
- ArrayResize(currentLayers, coords) ändert die Größe des Arrays currentLayers entsprechend der Anzahl der Koordinatenanzahl coords.
- ArrayResize(atoms, coords) ändert die Größe des Arrays atoms und erstellt für jedes Atom (Koordinate) ein eigenes Objekt. Für jedes Atom wird die Methode Init(maxLayers) aufgerufen, die es mit der maximalen Anzahl von Schichten initialisiert.
- ArrayResize(electrons, popSize) ändert die Größe des Elektronen-Arrays entsprechend der Populationsgröße popSize. Das Array layerID wird für jedes Elektron erstellt. Das Feld entspricht der Anzahl der Koordinaten.
- ArrayResize(BS, coords) ändert die Größe des BS-Arrays, in dem Zustände für jede Koordinate gespeichert werden.
4. Wenn alle Initialisierungsvorgänge erfolgreich sind, gibt die Methode true zurück.
//—————————————————————————————————————————————————————————————————————————————— // Initialize the algorithm bool C_AO_AOS::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- atomStage = 0; ArrayResize (currentLayers, coords); ArrayResize (atoms, coords); for (int i = 0; i < coords; i++) atoms [i].Init (maxLayers); ArrayResize (electrons, popSize); for (int i = 0; i < popSize; i++) ArrayResize (electrons [i].layerID, coords); ArrayResize (BS, coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Methode der Partikelverschiebung Beschreiben wir die Methode Moving:
1. Erste zufällige Positionierung:
- Ist die Revisionsvariable gleich false, bedeutet dies, dass der Algorithmus noch nicht mit seiner Arbeit begonnen hat. In diesem Fall kommt es zu einer zufälligen Positionierung der Partikel.
- Als Nächstes durchläuft die verschachtelte for-Schleife alle Elektronen (Populationsgröße) und erzeugt mit der Methode u.RNDfromCI für jede Koordinate einen Zufallswert. Die Methode nimmt ihren Wert aus dem durch rangeMin und rangeMax angegebenen Bereich. Dieser Wert wird dann mit Hilfe der u.SeInDiSp angepasst, die den Wert entsprechend dem angegebenen „Schritt“ einstellt.
2. Ausführung der entsprechenden Evolutionsstufe der Atome:
- Wenn Revision wahr ist, bedeutet dies, dass der Algorithmus bereits initialisiert wurde und seine Hauptphasen ausgeführt werden können. Je nachdem, in welchem Stadium sich atomStage befindet, werden unterschiedliche Methoden aufgerufen:
- Wenn atomStage 0 ist, wird DistributeParticles() aufgerufen. Sie ist für die Verteilung der Teilchen im Raum gemäß der asymmetrischen Log-Normal-Verteilung verantwortlich.
- Ansonsten werden Methoden aufgerufen, die Schichten in Atomen erzeugen, Elektronen-IDs aktualisieren, Schichtparameter berechnen und Elektronenpositionen aktualisieren.
3. Nach Abschluss aller notwendigen Operationen wird atomStage um 1 erhöht. Wenn atomStage den Wert von photonEmissions überschreitet, wird es auf 0 zurückgesetzt, sodass die Algorithmusphasen zyklisch wiederholt werden können.
//—————————————————————————————————————————————————————————————————————————————— // Particle displacement method void C_AO_AOS::Moving () { // Initial random positioning if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Execute the corresponding stage of the algorithm if (atomStage == 0) { DistributeParticles (); } else { LayersGenerationInAtoms (); UpdateElectronsIDs (); CalcLayerParams (); UpdateElectrons (); } // Proceed to the next stage atomStage++; if (atomStage > photonEmissions) atomStage = 0; } //——————————————————————————————————————————————————————————————————————————————
Kommen wir nun zur Analyse der einzelnen Methoden. Die Methode GetOrbitBandID der Klasse C_AO_AOS dient der Bestimmung des Orbitalbandes für ein Teilchen auf der Grundlage seiner Position relativ zu einem bestimmten Zentrum. Es nimmt die Anzahl der Schichten, die Minimal- und Maximalwerte, den Mittelpunkt und die Position des p-Partikel.
1. Berechnet die Breite der Bänder links und rechts der Mitte.
2. Wenn die Position des Teilchens p kleiner als die Mitte ist, dann wird gesucht, in welchem der linken Bänder es sich befindet.
3. Wenn es mehr sind, wird es es in den richtigen Bändern gesucht.
4. Wenn sie gleich dem Mittelpunkt ist, wird die Zahl 0 (der Mittelpunkt) zurückgegeben.
Die Funktion gibt also den Index des entsprechenden Orbitalbandes für die angegebene Position zurück.
//—————————————————————————————————————————————————————————————————————————————— // Determining the orbital band for a particle int C_AO_AOS::GetOrbitBandID (int layersNumb, double min, double max, double center, double p) { // Calculate the width of the bands to the left and right of the center double leftWidth = (center - min) / layersNumb; double rightWidth = (max - center) / layersNumb; // Define the band index if (p < center) { // The object is located to the left of the center for (int i = 1; i <= layersNumb; i++) { if (p >= center - i * leftWidth) return i - 1; } return layersNumb - 1; // If the object is in the leftmost band } else if (p > center) { // The object is located to the right of the center for (int i = 1; i <= layersNumb; i++) { if (p <= center + i * rightWidth) return i - 1; } return layersNumb - 1; // If the object is in the far right band } else { // The object is in the center return 0; } } //——————————————————————————————————————————————————————————————————————————————
Die Methode DistributeParticles der Klasse C_AO_AOS ist für die Verteilung der Partikel im Suchraum zuständig. Die Methode verteilt die Partikel im Suchraum anhand einer Log-Normal-Verteilung.
Für jedes Partikel (in einer Schleife durch popSize) und für jede Koordinate (in einer Schleife durch „coords“):
- Erzeugt eine Partikelposition unter Verwendung einer Log-Normal-Verteilung unter Angabe der Parameter (cB, rangeMin, rangeMax, peakPosition).
- Wendet die Funktion SeInDiSp an, um den Partikelpositionswert innerhalb eines bestimmten Bereichs unter Berücksichtigung der Stufe anzupassen.
//—————————————————————————————————————————————————————————————————————————————— // Distribution of particles in the search space void C_AO_AOS::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Use log-normal distribution to position particles a [i].c [c] = u.LognormalDistribution (cB [c], rangeMin [c], rangeMax [c], peakPosition); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode UpdateElectronsIDs der Klasse C_AO_AOS aktualisiert die Schicht-IDs für Elektronen in Abhängigkeit von ihren Koordinaten und den angegebenen Parametern.
//—————————————————————————————————————————————————————————————————————————————— // Update layer IDs for each electron void C_AO_AOS::UpdateElectronsIDs () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { electrons [i].layerID [c] = GetOrbitBandID (currentLayers [c], rangeMin [c], rangeMax [c], cB [c], a [i].c [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode CalcLayerParams der Klasse C_AO_AOS dient der Berechnung von Parametern für jede Schicht von Atomen im System. Die wichtigsten Bestandteile der Methode:
1. Variableninitialisierung: energy ist eine Variable zur Speicherung der maximalen Energie, die beim Umgang mit dem Elektron aktualisiert wird.
2. Die Schleife durchläuft alle Atome (Koordinaten) des Systems. Der Index c zeigt auf das aktuelle Atom.
3. Für jedes Atom wird die Methode Init aufgerufen, die die Parameter für die durch die Variable maxLayers festgelegte maximale Anzahl von Schichten initialisiert.
4. Schichtenschleife: die innere Schleife, die alle mit dem aktuellen Atom verbundenen Schichten durchläuft; currentLayers[c] gibt die Anzahl der Schichten für das Atom c an.
5. Handhabung von Elektronen: Eine weitere interne Schleife durchläuft alle e-Elektronen in der Population, wobei geprüft wird, ob das aktuelle Elektron zur Schicht L für das Atom c gehört.
6. Aktualisierung der Schicht-Parameter:
- Wenn das Elektron zu einer Schicht gehört, wird der Partikelzähler in der Schicht erhöht.
- Die Energiewerte BEk und die Zustände BSk werden für die Schicht in Abhängigkeit von den Elektroneneigenschaften aktualisiert.
- Wenn die Elektronenenergie a[e].f das aktuelle maximale Energieniveau überschreitet, werden die maximalen Energiewerte und die Zustände LEk aktualisiert.
7. Berechnung von Durchschnittswerten für eine Schicht: Wenn der Partikelzähler pc ungleich Null ist, werden Durchschnittswerte für Energie und Zustand berechnet.
8. Berechnung des allgemeinen Zustands der Bindungen: Der Bindungszustand jedes Atoms wird in ähnlicher Weise für jedes Atom BS, aber für die Gesamtheit der Elektronen berechnet.
//—————————————————————————————————————————————————————————————————————————————— // Calculate parameters for each layer void C_AO_AOS::CalcLayerParams () { double energy; // Handle each coordinate (atom) for (int c = 0; c < coords; c++) { atoms [c].Init (maxLayers); // Handle each layer for (int L = 0; L < currentLayers [c]; L++) { energy = -DBL_MAX; // Handle each electron for (int e = 0; e < popSize; e++) { if (electrons [e].layerID [c] == L) { atoms [c].layers [L].pc++; atoms [c].layers [L].BEk = a [e].f; atoms [c].layers [L].BSk = a [e].c [c]; if (a [e].f > energy) { energy = a [e].f; atoms [c].layers [L].LEk = a [e].c [c]; } } } // Calculate average values for the layer if (atoms [c].layers [L].pc != 0) { atoms [c].layers [L].BEk /= atoms [c].layers [L].pc; atoms [c].layers [L].BSk /= atoms [c].layers [L].pc; } } } // Calculate the general state of connections ArrayInitialize (BS, 0); for (int c = 0; c < coords; c++) { for (int e = 0; e < popSize; e++) { BS [c] += a [e].c [c]; } BS [c] /= popSize; } } //——————————————————————————————————————————————————————————————————————————————
Die Methode UpdateElectrons der Klasse C_AO_AOS ist für die Aktualisierung der Position der Elektronen im System zuständig.
1. Initialisierung der Parameter: Die Geschwindigkeitskoeffizienten, die Gewichte der besten Lösung, die Gewichte des Durchschnittszustands und die Übergangswahrscheinlichkeit werden bestimmt.
2. Für jedes Teilchen und jede Koordinate:
- Es wird eine Zufallswahrscheinlichkeit φ erzeugt.
- Ist φ kleiner als der Schwellenwert PR, wird eine zufällige Streuung vorgenommen und eine neue Position innerhalb eines bestimmten Bereichs zufällig gewählt.
- Andernfalls:
- Die Schicht-ID lID wird für das aktuelle Partikel ermittelt.
- Es werden zufällige Werte für die Verhältnisse erzeugt.
- Wenn die aktuelle Energie eines Teilchens geringer ist als die durchschnittliche Energie der Schicht, kommt es zu einer Bewegung in Richtung des globalen Optimums.
- Ist dies nicht der Fall, kommt es zu einer Bewegung in Richtung des lokalen Optimums der Schicht.
- Am Ende wird die neue Position innerhalb des angegebenen Bereichs unter Berücksichtigung des Schritts begrenzt.
//—————————————————————————————————————————————————————————————————————————————— // Update electron positions void C_AO_AOS::UpdateElectrons () { double α; // speed coefficient double β; // best solution weight coefficient double γ; // average state weight coefficient double φ; // transition probability double newPos; // new position double LE; // best energy double BSk; // connection state int lID; // layer ID // Handle each particle for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Random scatter newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); β = u.RNDprobab (); γ = u.RNDprobab (); // If the current particle energy is less than the average layer energy if (a [p].f < atoms [c].layers [lID].BEk) { // Moving towards the global optimum---------------------------- LE = cB [c]; newPos = a [p].c [c]+ α * (β * LE - γ * BS [c]) / currentLayers [c]; } else { // Movement towards the local optimum of the layer LE = atoms [c].layers [lID].LEk; BSk = atoms [c].layers [lID].BSk; newPos = a [p].c [c] + α * (β * LE - γ * BSk); } } // Limiting the new position within the search range taking into account the step a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode Revision der Klasse C_AO_AOS dient der Überprüfung und Aktualisierung der besten Lösungen (oder optimalen Zustände) während der Iteration. Schritte der Methode:
1. Initialisierung der Variablen bestIndex, die zum Speichern des Index der besten Lösung verwendet wird.
2. Die Suche nach der besten Lösung. Bedingung für die Prüfung, ob der Funktionswert (oder die Schätzung) der aktuellen Lösung a[i].f den aktuellen Wert der global besten Lösung fB übersteigt. Wenn diese Bedingung erfüllt ist, wird der Wert der global besten Lösung auf den aktuellen Wert aktualisiert und der Index der aktuellen Lösung wird als beste Lösung gespeichert.
3. Wird die beste Lösung gefunden, so werden die Koordinaten der besten Lösung a[bestIndex].c in das Array cB kopiert.
//—————————————————————————————————————————————————————————————————————————————— // Method of revising the best solutions void C_AO_AOS::Revision () { int bestIndex = -1; // Find the best solution in the current iteration for (int i = 0; i < popSize; i++) { // Update the global best solution if (a [i].f > fB) { fB = a [i].f; bestIndex = i; } } // Update the best coordinates if a better solution is found if (bestIndex != -1) ArrayCopy (cB, a [bestIndex].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Testergebnisse
Führen wir den Test aus und erhalten die folgenden Ergebnisse des AOS-Betriebs:
AOS|Atomic Orbital Search|50.0|5.0|1.0|0.1|0.05|
=============================
5 Hilly's; Func runs: 10000; result: 0.6521321213930082
25 Hilly's; Func runs: 10000; result: 0.39883708808831186
500 Hilly's; Func runs: 10000; result: 0.2602779698842558
=============================
5 Forest's; Func runs: 10000; result: 0.5165008091396371
25 Forest's; Func runs: 10000; result: 0.30233740723010416
500 Forest's; Func runs: 10000; result: 0.1926906342754638
=============================
5 Megacity's; Func runs: 10000; result: 0.39384615384615385
25 Megacity's; Func runs: 10000; result: 0.1892307692307692
500 Megacity's; Func runs: 10000; result: 0.09903076923077013
=============================
All score: 3.00488 (33.39%)
Bei der Visualisierung des AOS-Algorithmus kann man ein interessantes Verhalten feststellen, charakteristische Bereiche der „Verklumpung“ in den Orbitalen der Atome, aber die Genauigkeit der Konvergenz ist nicht sehr hoch.
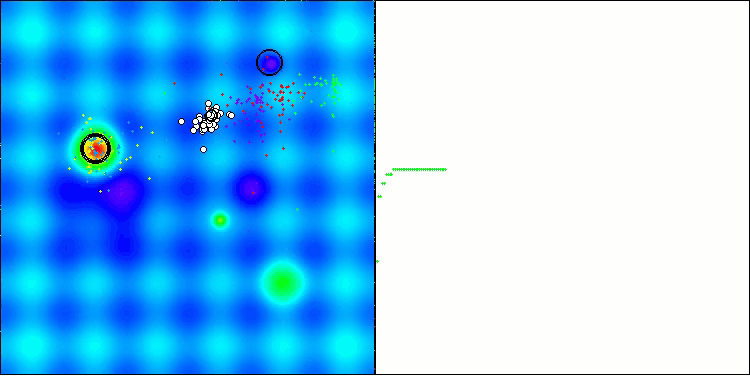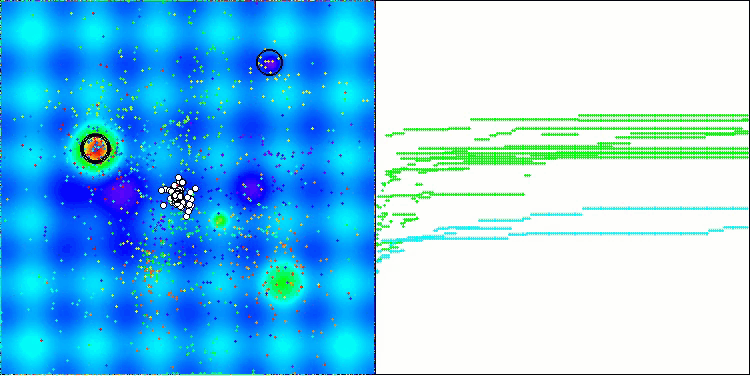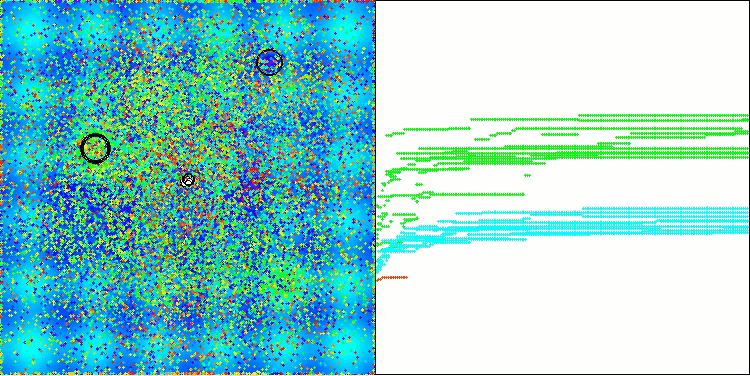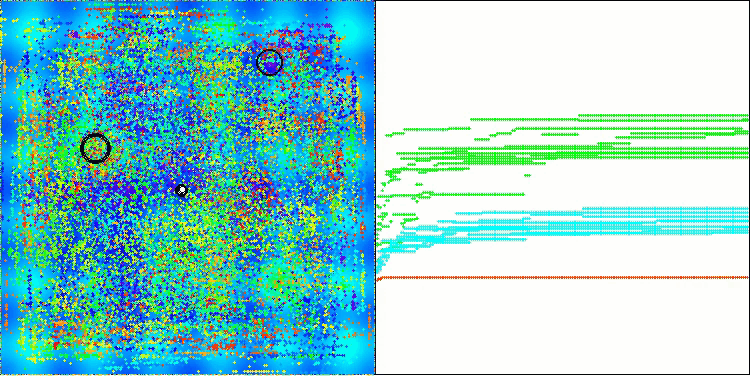
AOS mit der Testfunktion Hilly
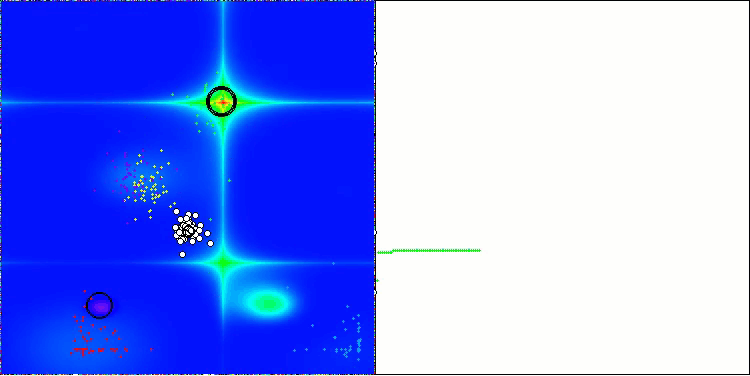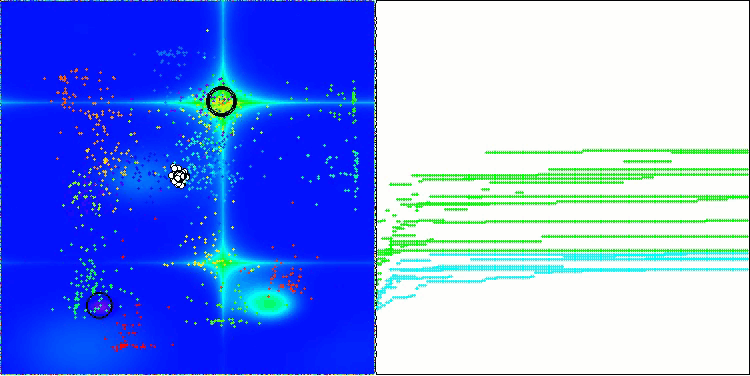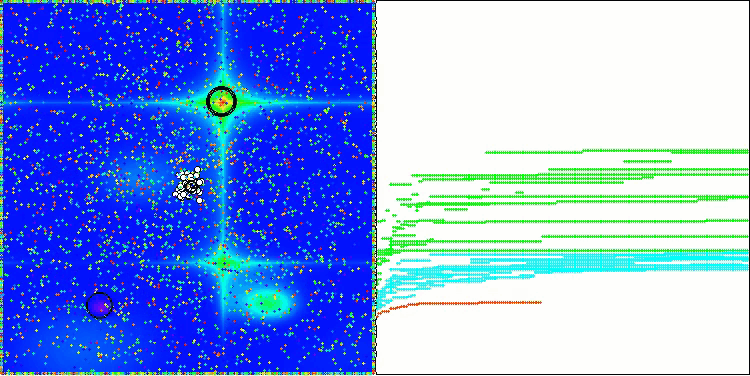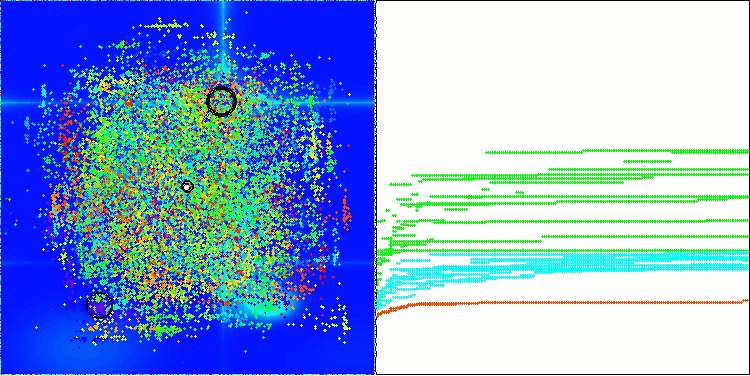
AOS mit der Testfunktion Forest
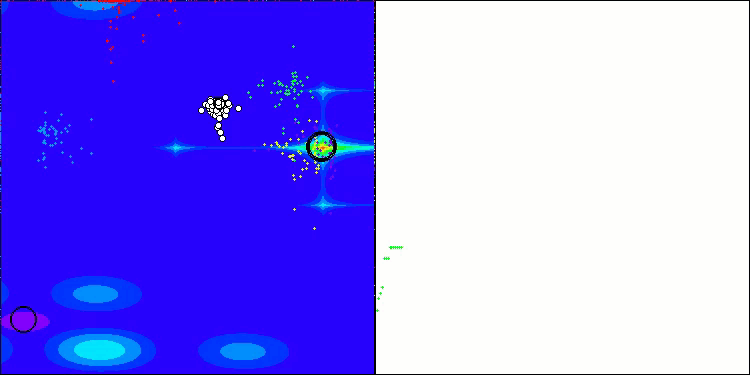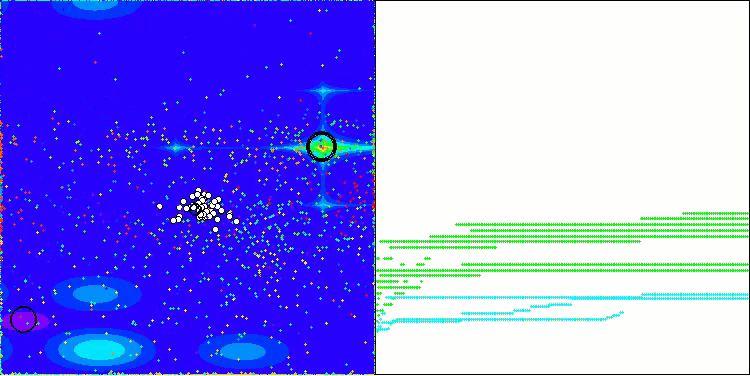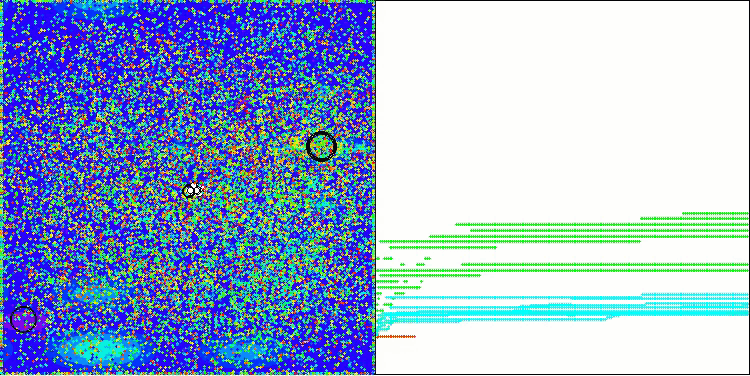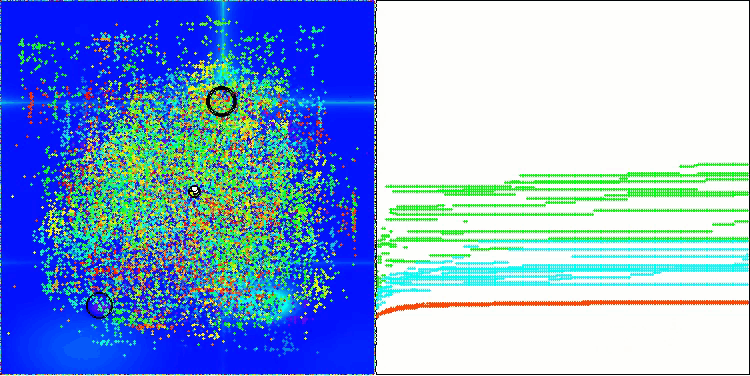
AOS mit der Testfunktion Megacity
Auf der Grundlage der Testergebnisse wurde der AOS-Algorithmus in der Bewertungstabelle auf Platz 39 eingestuft.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Code-Sperr-Algorithmus (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | Entwicklung sozialer Gruppen (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | Simuliertes isotropes Glühen (Joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 12 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 13 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 14 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 15 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 16 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 17 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 18 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 19 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 20 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 21 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 22 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 23 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 24 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 25 | AEO | Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 26 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 27 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 28 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 29 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 30 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 31 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 32 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 33 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 34 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 35 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 36 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 37 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 38 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 39 | AOS | Suche nach atomaren Orbitalen | 0.65213 | 0.39884 | 0.26028 | 1.31125 | 0.51650 | 0.30234 | 0.19269 | 1.01153 | 0.39385 | 0.18923 | 0.09903 | 0.68211 | 3.005 | 33.39 |
| 40 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 41 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 42 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 43 | BA | Fledermaus-Algorithmus | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 44 | AAA | Künstlicher Algenalgorithmus (AAA) | 0.50007 | 0.32040 | 0.25525 | 1.07572 | 0.37021 | 0.22284 | 0.16785 | 0.76089 | 0.27846 | 0.14800 | 0.09755 | 0.52402 | 2.361 | 26.23 |
| 45 | SA | Simuliertes Abkühlen | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
Zusammenfassung
Wir haben einen interessanten Algorithmus für die Suche nach Atomorbitalen untersucht, der innovative Ansätze für die globale Suche und die lokale Verfeinerung der Ergebnisse verwendet. Dank der dynamischen Orbitalschichten der Atome bewegen sich die Elektronen auf der Suche nach einem stabilen Atomzustand im Gleichgewicht. Der Algorithmus zeigt begrenzte Fähigkeiten bei glatten Funktionen, zeigt aber gute Ergebnisse, wenn die Problemdimension zunimmt, sogar bei der diskreten Megacity-Funktion.
Dieser Algorithmus ist ein Beispiel für eine vielversprechende Idee, aber seine Effizienz leidet unter einigen kleinen, aber wichtigen Nuancen. Im nächsten Artikel werden wir uns meine Modifikation von AOS ansehen und analysieren, wozu dieses wunderbare Konzept der orbitalen Suche tatsächlich in der Lage ist.
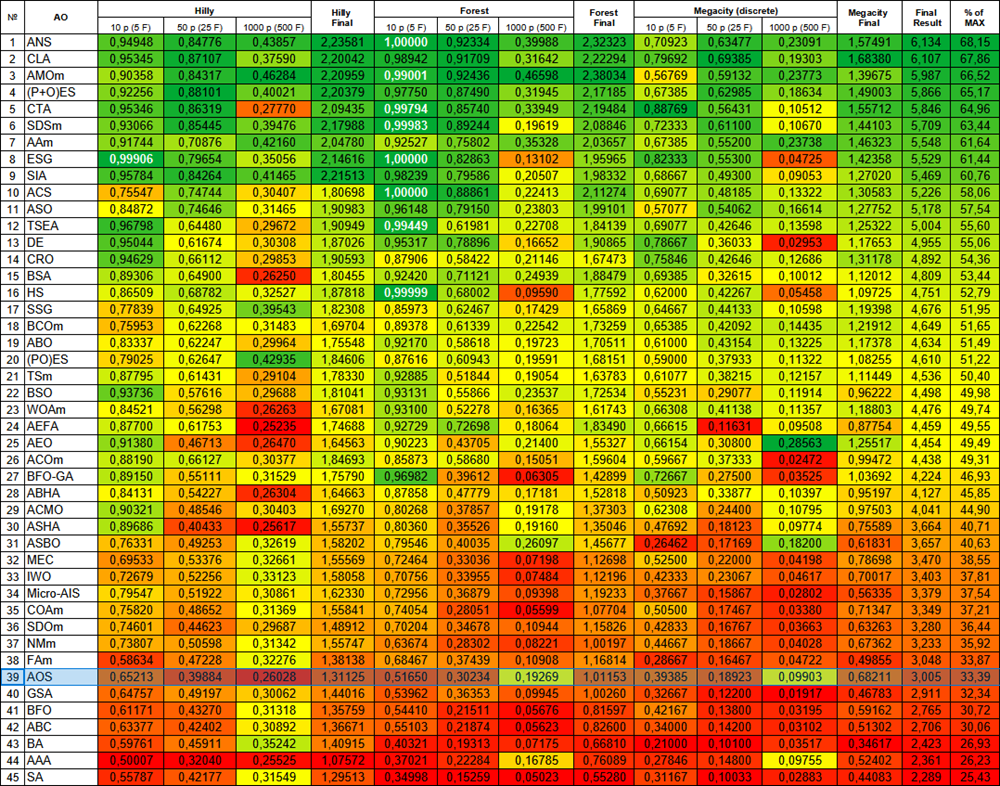
Abbildung 3. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben
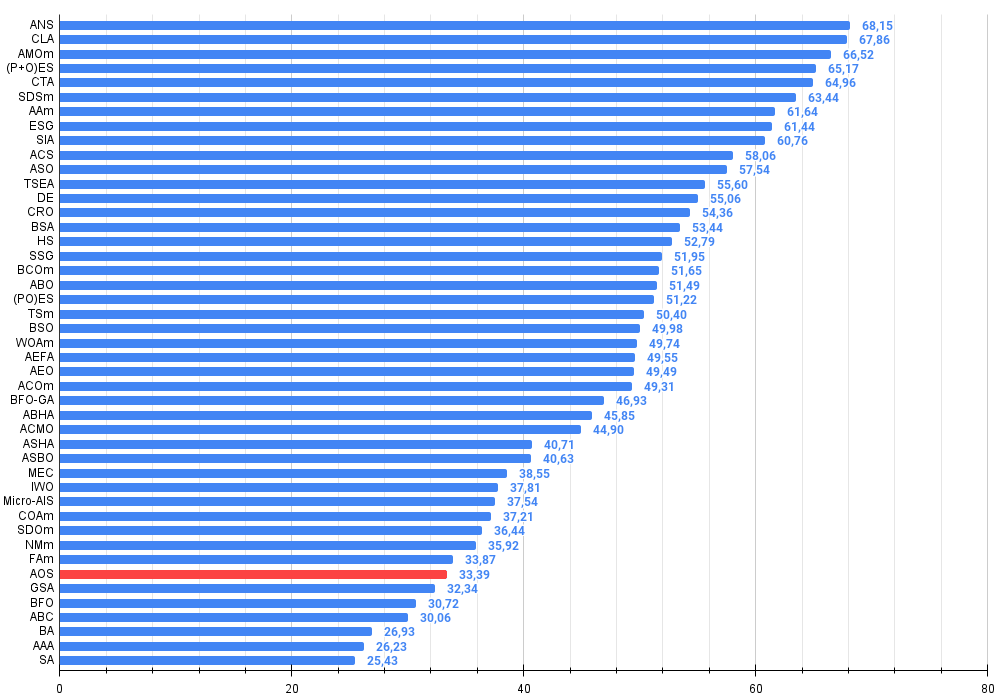
Abbildung 4. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Wertungstabelle)
Vor- und Nachteile von AOS:
Vorteile:
- Eine vielversprechende Grundlage für die Verbesserung von Algorithmen.
- Eine kleine Anzahl externer Parameter.
Nachteile
- Langsam aufgrund der häufigen Erzeugung von Zufallszahlen.
- Eine recht komplexe Umsetzung.
- Geringe Konvergenzgenauigkeit.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Übergeordnete Klasse von Populationsoptimierungsalgorithmen |
| 2 | #C_AO_enum.mqh | Include | Enumeration von Algorithmen zur Bevölkerungsoptimierung |
| 3 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 4 | TestStandFunctions.mqh | Include | Bibliothek der Testfunktionen |
| 5 | Utilities.mqh | Include | Bibliothek der Hilfsfunktionen |
| 6 | CalculationTestResults.mqh | Include | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 7 | Testing AOs.mq5 | Skript | Die einheitlichen Tests für alle Algorithmen zur Bevölkerungsoptimierung |
| 8 | AO_AOS_AtomicOrbitalSearch.mqh | Include | AOS-Algorithmus-Klasse |
| 9 | Test_AO_AOS.mq5 | Skript | AOS-Test |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16276
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Entwicklung eines Replay-Systems (Teil 75): Neuer Chart-Handel (II)
Entwicklung eines Replay-Systems (Teil 75): Neuer Chart-Handel (II)
 Entwicklung eines Replay-Systems (Teil 74): Neuer Chart-Handel (I)
Entwicklung eines Replay-Systems (Teil 74): Neuer Chart-Handel (I)
 Die Verwendung von Assoziationsregeln in der Forex-Datenanalyse
Die Verwendung von Assoziationsregeln in der Forex-Datenanalyse
 Analyse der Auswirkungen des Wetters auf die Währungen der Agrarländer mit Python
Analyse der Auswirkungen des Wetters auf die Währungen der Agrarländer mit Python
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Atomic Orbital Search Algorithm - Atomic Orbital Search (AOS) ist veröffentlicht worden:
Autor: Andrey Dik
Dies ist das gesamte System, das Physik, Mathematik, Schach, etc. umfasst.