Artificial Ecosystem-based Optimization (AEO) algorithm

Contents

1. Introduction
2. Implementation of the algorithm
3. Test results

Introduction

In the world of optimization and artificial intelligence, there is a constant search for new, more efficient methods to solve complex problems. One such innovative approach is the Artificial Ecosystem-based Optimization (AEO) algorithm, which was developed and presented in 2019. This method draws inspiration from natural ecosystems, mimicking the complex interactions and processes that occur in the natural environment.

The AEO algorithm is based on several key principles observed in nature. Just as ecosystems contain many species, each adapted to its own ecological niche, AEO uses a population of diverse solutions. In this context, each solution can be viewed as a separate "species" with unique characteristics and adaptive capabilities.

In nature, energy is transferred from one organism to another through food chains. In AEO this is modeled through the interaction of different types of "agents" - from "grass" to "omnivores". Here, information, similar to energy, is transferred between solutions, which helps improve the overall quality of the population. Ecosystems are characterized by both competition for resources and symbiotic relationships. The AEO algorithm reflects these processes through decision updating strategies, where agents can "compete" for better positions or "cooperate" by exchanging information.

Natural ecosystems are subject to cyclical changes, which is also reflected in AEO. The iterative optimization process involves alternating consumption and decomposition phases, which allows the algorithm to adapt to the dynamics of the problem. In nature, random events such as mutations and natural disasters coexist with deterministic processes such as natural selection. AEO uses both stochastic elements (such as the Levy distribution) and deterministic rules to update solutions, striking a balance between exploring new areas and exploiting those already found.

To better understand how natural processes are reflected in the AEO algorithm, let's look at some specific examples. In the African savannah, energy moves from grass to zebras (herbivores), then to lions (predators), and finally to hyenas (scavengers). In AEO, information about the best solutions is passed from the "grass" (the worst solution) to the "herbivores" (average solutions) and "carnivores" (the best solutions), which helps improve the overall quality of the population.

When organisms die, they decompose, returning nutrients to the ecosystem. For example, fallen leaves in the forest decompose, enriching the soil and feeding new plants. In AEO, the decomposition stage of the algorithm mimics this process. After the consumption (updating decisions) phase comes the decomposition phase, where information from the current decisions is "decomposed" and distributed throughout the search space. This allows the algorithm to explore new areas and avoid getting stuck in local optima. In the algorithm, this is implemented by applying a Gaussian distribution to the current solutions relative to the best one (the global best solution acts as a decomposer), which can be seen as a "decomposition" and "redistribution" of information in the search space.

Thus, the AEO algorithm is an elegant synthesis of natural principles and mathematical optimization. Not only does it offer an effective method for solving complex problems, it also opens up a new perspective on the relationship between natural processes and artificial intelligence. Next, we will take a detailed look at the structure and working mechanisms of this algorithm to better understand its potential and application.

Implementation of the algorithm

To better understand the idea of the authors of the AEO algorithm, let us turn to the Figure 1, which shows the hierarchy of organisms in an artificial ecosystem. The entire ecosystem consists of organisms conventionally numbered from 1 to Xn. Number 1 is the "grass" that has the maximum energy (minimum fitness function value), while Xn represents the saprophyte that performs the decomposition function (minimum energy, maximum fitness function value).

In the figure, the arrows indicate the directions of feeding: grass (number 1) can only use the waste products of saprophytes, herbivores (number 2) feed on grass, and organisms numbered 2, 4, and 5 can be herbivores (eat only grass), carnivores (organisms can only eat creatures whose energy is lower than their own), and omnivores (can eat both grass and organisms with higher energy). The top of the ecosystem is occupied by saprophytes, which decompose all organisms at the end of their life cycle.

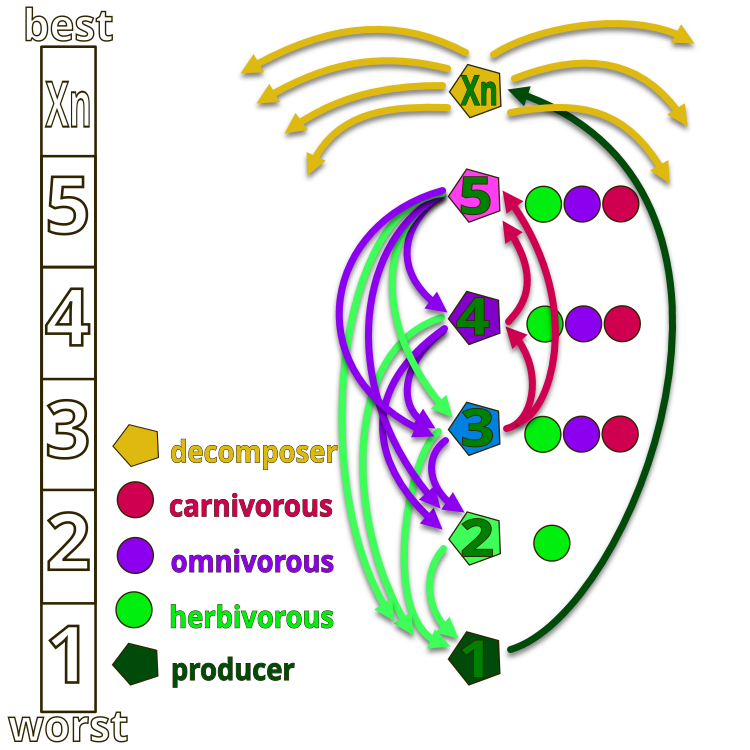
Figure 1. Hierarchy of organisms in the artificial ecosystem of the AEO algorithm

The main idea of the algorithm is to model interactions between ecosystem components to solve optimization problems. The algorithm is based on three key principles observed in nature:

1. Production - in nature, producers (such as plants) transform solar energy into organic compounds.
2. Consumption - consumers (herbivores, carnivores, omnivores) use energy produced by others, particularly plants.
3. Decomposition - saprophytes decompose complex organic substances into simple ones, which is modeled in the algorithm as a decomposition of solutions.

Algorithm principles:

1. Initialization - an initial population of solutions is created, representing the ecosystem.
2. Production - at each iteration, the worst solution is updated taking into account the best one and a random factor.
3. Consumption - the remaining decisions are updated using three strategies:

• Herbivores: Updated based on the producer.
• Predators: Updated based on a randomly selected best solution.
• Omnivores: Update based on both the producer and a random decision.

4. Decomposition - all solutions undergo a "decomposition", which improves global search.
5. Selection - only improved solutions are retained, ensuring a gradual improvement of the population.

Thus, the algorithm relies on the mechanism of energy transfer between living organisms, which helps maintain the stability of species using three operators: production, consumption and decomposition.

1. Production - the worst individual in the X1 population updated relative to the best Xn with the addition of a randomly generated coordinate Xrand in a given range, creating a new individual through the production operator. Mathematical representation: X1 (t + 1) = (1 - a) * Xn (t) + a * Xrand (t), where a = (1 - t / T) * r1 (t - current epoch, T - total epochs), r1 - random number [0; 1]. In this case, the r1 component can be omitted, since we already use a random coordinate in the equation.

2. Consumption - a randomly selected consumer can "eat" the producer to obtain energy. C consumption factor is defined as: C = 1/2 * (v1 / |v2|), where v1 and v2 - uniformly distributed random numbers in the range [0; 1].

• Herbivores: Xi (t + 1) = Xi (t) + C * (Xi (t) - X1 (t)).
• Carnivores: Xi (t + 1) = Xi (t) + C * (Xi (t) - Xj (t)).
• Omnivores: Xi (t + 1) = Xi (t) + C * (r2 * Xi (t) + (1 - r2) * Xj (t)).

3. Decomposition - the saprophyte decomposes the remains of dead individuals, providing nutrients for the producers. The update of the position of individuals after the work of the saprophyte is described as:

Xi (t + 1) = Xn (t) + D * (e * Xn (t) - h * Xi (t)), where D = 3u, u ~ N (0, 1), e = r3 * rand (i), h = 2 * r3 - 1 (r3, a random number in the [0; 1] range).

So, at the beginning a random population is generated, and at each iteration the position of the first individual is updated using the p.1 equation. The positions of other individuals are updated by choosing among the p.2 equations with equal probability. In the decomposition stage, each individual updates its position using the p.3 equation. The process continues until a satisfactory termination criterion is reached. The final step returns the best individual found so far.

Now we can write the pseudocode for the AEO algorithm:

AEO (Artificial Ecosystem-based Optimization) algorithm

Initialization:
    Set population size (popSize)
    Set the number of epochs (epochs)
    Set the Levy distribution parameter (levisPower)
    Initialize the population with random solutions in a given range
    Evaluate the fitness function for each solution
    Find the best global solution cB

For each epoch from 1 to 'epochs':
    // Consumption phase
    For each agent i in the population:
        If i == 0:
            Apply Gaussian distribution to current solution
        Otherwise if i == popSize - 1:
            Apply grass behavior (GrassBehavior)
        Otherwise:
            Select behavior randomly:
                - Herbivore behavior (HerbivoreBehavior)
                - Carnivore behavior (CarnivoreBehavior)
                - Omnivore behavior (OmnivoreBehavior)
    
    // Decomposition phase
    For each agent i in the population:
        For each c coordinate:
            Select a random agent j
            Calculate the D distance between cB [c] and a [j].c [c]
            Update a [i].c [c] using Gaussian distribution

    // Revision
    Evaluate the fitness function for each agent
    Update the best personal solution for each agent
    Update the cB best global solution
    Sort population by fitness function value

Return the cB best solution found

Subprocedures:

GrassBehavior (agent):
    α = (1 - current_epoch / total_number_of_epochs)
    For each c coordinate:
        Xr = random value in the range [min [c], max [c]]
        Xn = cB [c]
        X1 = Xn + α * (Xn - Xr)
        agent.c [c] = X1 (considering limitations)

HerbivoreBehavior (agent, coordinate_index):
    Xi = agent.cB [coordinate_index]
    X1 = worst solution in the population for a given coordinate
    C = random number from Levy distribution (levisPower)
    Xi = Xi + C * (Xi - X1)
    agent.c [coordinate_index] = Xi (considering limitations)

CarnivoreBehavior (agent, agent_index, coordinate_index):
    Xi = agent.cB [coordinate]
    j = random index < agent_index
    Xj = a [j].cB [coordinate_index]
    C = random number from Levy distribution (levisPower)
    Xi = Xi + C * (Xj - Xi)
    agent.c [coordinate_index] = Xi (considering limitations)

OmnivoreBehavior (agent, agent_index, coordinate_index):
    Xi = agent.cB [coordinate]
    X1 = worst solution in the population for a given coordinate
    j = random index > agent_index
    Xj = a [j].cB [coordinate_index]
    C = random number from Levy distribution (levisPower)
    r = random number from 0 to 1
    Xi = Xi + C * r * (Xi - X1) + (1 - r) * (Xi - Xj)
    agent.c [coordinate_index] = Xi (considering limitations)

After a detailed description and analysis of the algorithm, let's move on to writing the code.

The algorithm uses the Levy distribution to generate extremely distant but rare jumps in the search space. We have used this random number distribution before, for example in the Cuckoo Search algorithm, but we have not gone into detail about its features. The point is that correctly generating the Levy distribution requires using four random uniformly distributed numbers, which is expensive in itself. In addition, the Levy distribution has an infinitely long tail (it is asymmetric, with one tail), which makes it difficult to use in practical optimization algorithms, especially in the presence of boundary conditions. It is also necessary to check boundary conditions during generation, such as checking for 0 before calculating the natural logarithm, and also to avoid division by 0.

Below is the code for generating random numbers with the Levy distribution, which lacks the above-described checks and without explaining the logic of the code:

double LevyFlight()
{
    const double epsilon = 1e-10; // Small value to avoid division by zero
    const double maxValue = 1e10; // Maximum allowed value

    double log1 = MathMax (RNDprobab(), epsilon);
    double log2 = MathMax (RNDprobab(), epsilon);

    double cos1 = MathCos (2 * M_PI * RNDprobab());
    double cos2 = MathCos (2 * M_PI * RNDprobab());

    double U = MathSqrt (-2.0 * MathLog (log1)) * cos1;
    double v = MathSqrt (-2.0 * MathLog (log2)) * cos2;

    double l = 0.5 * MathAbs(U) / MathMax(MathAbs(v), epsilon);

    return l;
}

To get rid of the shortcomings of generating numbers with the Levy distribution, let's implement our own function LevyFlightDistribution with a close distribution and place it in our standard set of functions C_AO_Utilities for use in optimization algorithms. Let's break it down:

1. The levisPower parameter is a power that determines the shape of the distribution. The higher the value of levisPower, the more "sparse" the distribution will be.
2. The function calculates the minimum value that will be used for scaling. It depends on levisPower and is calculated as 20^levisPower.
3. Generating the "r" random number using the RNDfromCI function in the range from 1 to 20.
4. Applying a power - the generated number "r" is raised to the power of "-levisPower", which changes its distribution.
5. Scaling the result - the obtained value of "r" is scaled to the range [0, 1]. This is done by subtracting the minimum value and dividing by the difference between 1 and the minimum value. Thus, the result will always be within the range [0, 1].
6. Returning result - the function returns the generated "r" value, which now has a distribution close to the Levy distribution, biased towards 0.

As we can see, the function generates random numbers strictly in the range [0, 1], which is very convenient in practical application. The range can always be expanded to any values by applying the appropriate ratio. This function is much faster and provides a distribution very close to the desired one (the right side of the distribution relative to the maximum).

//------------------------------------------------------------------------------
//A distribution function close to the Levy Flight distribution.
//The function generates numbers in the range [0.0;1.0], with the distribution shifted to 0.0.
double C_AO_Utilities :: LevyFlightDistribution (double levisPower)
{
  double min = pow (20, -levisPower); //calculate the minimum possible value
  double r = RNDfromCI (1.0, 20);     //generating a number in the range [1; 20]

  r = pow (r, -levisPower);           //we raise the number r to a power
  r = (r - min) / (1 - min);          //we scale the resulting number to [0; 1]

  return r;
}

Let's proceed to the description of the main code of the algorithm. The C_AO_AEO class is derived from the C_AO class and implements the algorithm. Let's take a closer look at its structure, members and methods.

Constructor:

• Set default values for population size and Levy degree.
• Create the params array of parameters and initializes it with values.

Methods:

• Set popSize and levisPower parameters from the params array.
• Init ()initializes the algorithm with the specified search ranges and number of epochs. The method returns bool, which implies the possibility of checking the success of initialization.
• Moving () handles the movement of agents in the current era, updating their coordinates.
• Revision () updates information about agents and their best decisions.

Private members and variables:

• levisPower - parameter used in the Levy distribution.
• epochs - total number of epochs.
• epochNow - current era.
• consModel - stage (consumption or decomposition).

S_AO_Agent aT [] — temporary array of agents used to sort the population.

Private methods:

• GrassBehavior () - handle the behavior of the "grass" agent.
• HerbivoreBehavior () - handle the behavior of a herbivorous agent that "eats" grass (the worst agent).
• CarnivoreBehavior () - handle the behavior of a carnivorous agent that "eats" agents with a higher fitness function value.
• OmnivoreBehavior () - handle the behavior of an omnivorous agent, which combines the behavior of a herbivore and an eater of anything with a lower fitness.

The C_AO_AEO class provides an implementation of an optimization algorithm based on an artificial ecosystem, using different types of agents and their interactions to find optimal solutions. Each method is responsible for certain aspects of the algorithm, including initialization, movement of agents, and updating their state.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AEO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AEO () { }
  C_AO_AEO ()
  {
    ao_name = "AEOm";
    ao_desc = "Artificial Ecosystem-based Optimization Algorithm";
    ao_link = "https://www.mql5.com/en/articles/16058";


    popSize    = 50;       // population size
    levisPower = 2;

    ArrayResize (params, 2);

    params [0].name = "popSize";    params [0].val = popSize;
    params [1].name = "levisPower"; params [1].val = levisPower;
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;
    levisPower = params      [1].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum search range
             const double &rangeMaxP  [],  // maximum search range
             const double &rangeStepP [],  // step search
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double levisPower;


  private: //-------------------------------------------------------------------
  int  epochs;
  int  epochNow;
  int  consModel; // consumption model;
  S_AO_Agent aT [];

  void GrassBehavior     (S_AO_Agent &animal);
  void HerbivoreBehavior (S_AO_Agent &animal, int indCoord);
  void CarnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord);
  void OmnivoreBehavior  (S_AO_Agent &animal, int indAnimal, int indCoord);
};
//——————————————————————————————————————————————————————————————————————————————

Let's take a closer look at the code of the Init method of the C_AO_AEO class. The Init method returns the value of bool type, which allows us to determine whether the initialization was successful. Standard initialization check: The StandardInit method is called here, which performs basic initialization of the parameters passed to the method. If StandardInit returns false, this means that the initialization failed and the Init method also returns false.

Setting up the variables:

• epochs - set the total number of epochs obtained from the epochsP parameter.
• epochNow - initialize the current epoch to 0, indicating that the algorithm has just started.
• consModel - set the value for the model to 0, so that it can subsequently move from one stage to another.
  

Resizing the aT temporary agent array to popSize.

Return result: If all previous operations are successful, the method returns true, which indicates that the initialization was successful.

The Init method of the C_AO_AEO class is responsible for the initial setup of the algorithm. It checks the default parameters, sets the values for the epochs and the initial stage, and prepares the array of agents to work with. If all stages are successfully completed, the method returns true, indicating that the algorithm is ready to be executed.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AEO::Init (const double &rangeMinP [],
                     const double &rangeMaxP [],
                     const double &rangeStepP [],
                     const int epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs    = epochsP;
  epochNow  = 0;
  consModel = 0;
  ArrayResize (aT, popSize);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Let's analyze the code of the Moving method of the C_AO_AEO class. The general structure of the method: Moving is responsible for updating the state of the population of agents (individuals) depending on the current epoch and consumption model. It is divided into several logical blocks:

1. Increasing the epoch: epochNow++ increases the current epoch counter.

2. First initialization:

• If revision is false, the first initialization of the coordinates of agents in the population occurs. The coordinates are selected randomly from a given range and then rounded to the nearest value that corresponds to the step.
• After that, revision is set to true, and the method completes execution.

3. Consumption model:

• If consModel is 0, the coordinates of agents are updated based on their behavior. 
• For the first agent (index 0), Gaussian distributions are used to initialize coordinates.
• For the remaining agents, the behavior depends on their index: the last agent (index popSize - 1) calls the GrassBehavior function. For the penultimate and subsequent agents (indices popSize - 2 and below), behavior is determined randomly: either herbivorous, carnivorous, or omnivorous.

4. Decomposition: if consModel is not equal to 0, a decomposition occurs, where its coordinates are updated based on random values and a Gaussian distribution for each agent. For each coordinate, a random index of another agent is selected, and based on this value, new coordinates are calculated taking into account the minimum and maximum boundaries.

The Moving method implements the logic associated with changing the coordinates of agents depending on their behavior and the current era. It includes both the first initialization and updating the state of agents based on their consumption pattern.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  // Consumption ---------------------------------------------------------------
  if (consModel == 0)
  {
    double r = 0.0;

    for (int i = 0; i < popSize; i++)
    {
      if (i == 0)
      {
        for (int c = 0; c < coords; c++)
        {
          a [i].c [c] = u.GaussDistribution (a [i].c [c], rangeMin [c], rangeMax [c], 8);
          a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }

        continue;
      }

      if (i == popSize - 1) GrassBehavior (a [i]);
      else
      {
        if (i >= popSize - 2)
        {
          for (int c = 0; c < coords; c++)
          {
            r = u.RNDprobab ();

            if (r < 0.333) HerbivoreBehavior (a [i], c);
            else
            {
              if (r < 0.667)
              {
                CarnivoreBehavior (a [i], i, c);
              }
              else
              {
                OmnivoreBehavior (a [i], i, c);
              }
            }
          }
        }
        else
        {
          for (int c = 0; c < coords; c++)
          {
            r = u.RNDprobab ();

            if (r < 0.5) CarnivoreBehavior (a [i], i, c);
            else         OmnivoreBehavior  (a [i], i, c);
          }
        }
      }
    }

    consModel++;
    return;
  }

  // Decomposition -------------------------------------------------------------
  int    j   = 0;
  double D   = 0.0;
  double min = 0.0;
  double max = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      j = u.RNDminusOne (popSize);
      D = 3.0 * (cB [c] - a [j].c [c]); // * u.RNDprobab ();
      min = cB [c] - D;
      max = cB [c] + D;

      if (min < rangeMin [c]) min = u.RNDfromCI (rangeMin [c], cB [c]);
      if (max > rangeMax [c]) min = u.RNDfromCI (cB [c], rangeMax [c]);

      a [i].c [c] = u.GaussDistribution (cB [c], min, max, 1);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  consModel = 0;
}
//——————————————————————————————————————————————————————————————————————————————

The Revision method in the C_AO_AEO class is responsible for updating information about the best agents in the population. It implements logic that allows tracking and storing the best solutions found during the execution of the algorithm. The structure of the method:

1. Finding the best agent:

• Iterate over all agents in the population.
• Compare their fitness (f value) with the current best fitness of fB.
• If an agent with better fitness is found, update fB and remember its index.

2. Copying the coordinates of the best agent: if the best agent was found (index not equal to -1), copy its coordinates to the cB array, which stores the current best coordinates.

3. Updating agents' personal best fitnesses: loop through all agents again and check if their current fitness exceeds their personal best fitness (fB). If so, update their personal best fitness and copy their current coordinates to cB.

4. Sorting agents: At the end, we call the sorting function to order the agents by their personal best fitness value.

The Revision method is an important element of the algorithm, as it ensures that the best solutions found during the work are tracked and saved.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

The GrassBehavior method in the C_AO_AEO class implements the behavior of agents based on the concept of "herbivores", which symbolizes the search for new solutions in space. Method structure:

1. Calculation of the α ratio is defined as (1.0 - (double) epochNow / epochs), which means that it decreases as the epoch number increases. This allows the algorithm to explore the space more actively at the beginning and then focus on improving the solutions it finds.

2. Initialization of variables:

• X1 - current coordinate of the herbivorous agent.
• Xn - current coordinate of the saprophyte.
• Xr - random coordinate selected from a given range.

3. Cycle by coordinates. For each agent coordinate:

• The Xr random value is generated within the specified range [Xmin, Xmax].
• The current coordinate Xn is taken from the cB array, which stores the current global best coordinates (the position of the saprophyte in space).
• The new coordinate of X1 is calculated according to the equation X1 = Xn + α * (Xn - Xr), which allows the current value to be mixed with a random value, reducing the influence of randomness as the number of epochs increases.
• Finally, the new coordinate is constrained within the given range using the SeInDiSp function.

//——————————————————————————————————————————————————————————————————————————————
// Grass
// (Worst) X1 X2 X3 ...... Xn (Best)
// X1(t+1) = (1 - α) * Xn(t) + α * Xrnd (t)
// α = (1 - t / T) * rnd [0.0; 1.0]
// Xrnd = rnd [Xmin; Xmax]

void C_AO_AEO::GrassBehavior (S_AO_Agent &animal)
{
  //0) (1 - α) * Xn + α * Xrnd
  //1) Xn - α * Xn + α * Xrnd
  //2) Xn + α * (Xrnd - Xn)

  double α = (1.0 - (double)epochNow / epochs);

  double X1 = 0.0;
  double Xn = 0.0;
  double Xr = 0.0;

  for (int c = 0; c < coords; c++)
  {
    Xr = u.RNDfromCI (rangeMin [c], rangeMax [c]);
    Xn = cB [c];

    //X1 = Xn + α * (Xr - Xn);
    X1 = Xn + α * (Xn - Xr);

    animal.c [c] = u.SeInDiSp (X1, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

The HerbivoreBehavior method in the C_AO_AEO class implements the behavior of a herbivorous agent. Method structure:

1. Initialization of variables:

• Xi - current coordinate of the agent that will be updated.
• X1 - coordinate of the worst agent in the population, which corresponds to the maximum energy (or the lowest fitness).
• C - random value generated using the Levy distribution.

2. Coordinate update: Xi coordinate is updated according to the equation: Xi (t+1)=Xi (t)+C ⋅ (Xi (t)−X1 (t)). This equation means that the agent changes its coordinate based on the difference between its current coordinate and the coordinate of the worst agent. This allows the herbivore to "feed" on the worst agent, that is, to explore even unpromising search areas.

3. Coordinate limit: After updating the Xi coordinate, it is limited within a given range using the SeInDiSp function, which takes the new value, the minimum and maximum limits, and the step as arguments.

The HerbivoreBehavior method demonstrates how herbivorous agents can adapt by "feeding" on the worst members of the population.

//——————————————————————————————————————————————————————————————————————————————
// Herbivore
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * (Xi(t) - X1(t)) for i ∈ [2, n]
// Herbivore eats only the one with the highest energy (eats the one with the worst FF)
void C_AO_AEO::HerbivoreBehavior (S_AO_Agent &animal, int indCoord)
{
  double Xi = animal.c [indCoord];
  double X1 = a [popSize - 1].c [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);

  Xi = Xi + C * (Xi - X1);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

The CarnivoreBehavior method in the C_AO_AEO class implements the behavior of a carnivorous agent within the framework of the algorithm. Method structure:

1. Initialization of variables:

• Xi - current coordinate of the carnivorous agent that will be updated.
• j - index of a randomly selected sacrificial agent (the carnivore "eats" agents with less energy but better fitness).
• Xj - coordinate of the victim, which will be used to update the coordinate of the carnivore.
• C - random value generated using the Levy distribution.
  

2. Coordinate update: Xi coordinate is updated according to the equation: Xi (t+1) = Xi (t) + C * (Xj (t) - Xi (t)). This equation means that the carnivorous agent changes its coordinate based on the difference between the coordinate of the prey and its current coordinate. This allows the carnivore to "feed" on the victim, improving its characteristics.

3. Coordinate limit: After updating the Xi coordinate, it is limited within a given range using the SeInDiSp function.

The CarnivoreBehavior method demonstrates how carnivorous agents can adapt by "feeding" on prey with less energy. This allows them to improve their performance, striving for more optimal solutions. 

//——————————————————————————————————————————————————————————————————————————————
// Carnivorous
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * (Xi(t) - Xj(t)) for i ∈ [3, n]
// Carnivore eats those with less energy (eats those with higher FF)
void C_AO_AEO::CarnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord)
{
  //double Xi = animal.c [indCoord];
  double Xi = animal.cB [indCoord];
  int    j  = u.RNDminusOne (indAnimal);
  //double Xj = a [j].c [indCoord];
  double Xj = a [j].cB [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);

  //Xi = Xi + C * (Xi - Xj);
  Xi = Xi + C * (Xj - Xi);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

The OmnivoreBehavior method in the C_AO_AEO class describes the behavior of an omnivorous agent in the context of an evolutionary algorithm. Method structure:

1. Initialization of variables:

• Xi - current coordinate of the omnivorous agent that needs to be updated.
• X1 - worst agent coordinate (the agent with the highest energy).
  
• j - random index of another agent selected from the population that will be used to update the coordinate.
• Xj - coordinate of another selected agent.
• C - random value generated using the Levy distribution.
• r - random probability that will be used to mix the coordinate update.

2. Coordinate update: Xi coordinate is updated according to the equation: Xi (t+1) = Xi (t) + C * r * (Xi (t) - X1 (t)) + (1 - r)  (Xi (t) - Xj (t)). This equation allows the omnivorous agent to adapt by "feeding" both from the worst agent (with the highest energy) and from another random agent with lower fitness, making its behavior more flexible.

3. Coordinate limit: after updating the Xi coordinate, it is limited within the specified constraints using the SeInDiSp function.

The OmnivoreBehavior method demonstrates how omnivorous agents can adapt and benefit from different energy sources, including worse agents and randomly selected other agents with lower fitness.

//——————————————————————————————————————————————————————————————————————————————
// Omnivorous
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * r2 * (Xi(t) - X1(t)) + (1 - r2) * (Xi(t) - Xj(t)) for i ∈ [3, n]
// An omnivore eats everyone who has more energy (grass and small animals, that is, those who have worse FF)
void C_AO_AEO::OmnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord)
{
  //double Xi = animal.c [indCoord];
  double Xi = animal.cB [indCoord];
  //double X1 = a [popSize - 1].c [indCoord];
  double X1 = a [popSize - 1].cB [indCoord];
  int    j  = u.RNDintInRange (indAnimal + 1, popSize - 1);
  //double Xj = a [j].c [indCoord];
  double Xj = a [j].cB [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);
  double r  = u.RNDprobab ();

  Xi = Xi + C * r * (Xi - X1) + (1.0 - r) * (Xi - Xj);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

Now that we have implemented the code for the algorithm, we can finally start testing it on our test functions.

AEO|Artificial Ecosystem-based Optimization Algorithm|50.0|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.6991675795357223
25 Hilly's; Func runs: 10000; result: 0.34855292688850514
500 Hilly's; Func runs: 10000; result: 0.253085011547826
=============================
5 Forest's; Func runs: 10000; result: 0.6907505745478882
25 Forest's; Func runs: 10000; result: 0.23365521509528495
500 Forest's; Func runs: 10000; result: 0.1558073538195803
=============================
5 Megacity's; Func runs: 10000; result: 0.5430769230769231
25 Megacity's; Func runs: 10000; result: 0.20676923076923082
500 Megacity's; Func runs: 10000; result: 0.1004461538461546
=============================
All score: 3.23131 (35.90%)

The algorithm scored about 36% during testing. This is an average result. For this algorithm, I decided to revise the Moving method, and here is what I got:

Modified logic of agent movement taking into account different behavior models (production, consumption and decomposition) in the Moving method:

1. The initial population initialization remains unchanged.

2. Update α ratio is calculated as a function of the current epoch, decreasing as epochNow increases. This ratio is moved outside of a separate private method.

3. Production (consModel == 0) - in this part, agents update their coordinates using an equation based on the previous state and a random value. This allows them to "produce" new states.

4. Consumption (consModel == 1). Here we divide agents into three groups depending on the random value:

• Herbivores.
• Carnivores.
• Omnivores.

5. Decomposition: In this stage, agents interact with each other, changing their coordinates based on random values and interactions with other agents.

6. Resetting the consumption model: At the end of the consModel, set to 0 to start a new loop.

As you can see, the main change in the logic of the algorithm is the allocation of Production into a separate stage. A separate era is allocated for this, which allows for a serious shake-up of the population of organisms. This is also reflected in the behavior of the AEO during visualization: we can see "blinking", that is, individual stages of the artificial ecosystem can be noticed even visually.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double α = (1.0 - (double)epochNow / epochs);

  double Xi   = 0.0;
  double Xb   = 0.0;
  double Xr   = 0.0;
  double Xj   = 0.0;
  double C    = 0.0;
  int    j    = 0;
  double r    = 0.0;

  // Production --------------------------------------------------------------
  // X(t + 1) = (1 - α) * Xb(t) + α * Xrnd (t)
  // α = (1 - t / T) * rnd [0.0; 1.0]
  // Xrnd = rnd [Xmin; Xmax]
  if (consModel == 0)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        Xb = cB [c];
        Xr = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        //Xi = Xb + α * (Xr - Xb);
        Xi = Xb + α * (Xb - Xr);

        a [i].c [c] = u.SeInDiSp (Xi, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    consModel++;
    return;
  }

  // Consumption --------------------------------------------------------------- 
  if (consModel == 1)
  {
    for (int i = 0; i < popSize; i++)
    {
      if (i > 1)
      {
        for (int c = 0; c < coords; c++)
        {
          r = u.RNDprobab ();

          // Herbivore behavior ------------------------------------------------ 
          //Xi (t + 1) = Xi (t) + C * (Xi (t) - Xb (t));
          if (r < 0.333)
          {
            C  = u.LevyFlightDistribution (levisPower);
            Xb = cB [c];
            //Xi = a [i].c [c];
            Xi = a [i].cB [c];

            //Xi = Xi + C * (Xi - Xb);
            Xi = Xi + C * (Xb - Xi);
          }
          else
          {
            // Carnivore behavior ---------------------------------------------- 
            //Xi (t + 1) = Xi (t) + C * (Xi (t) - Xj (t));
            if (r < 0.667)
            {
              C  = u.LevyFlightDistribution (levisPower);
              j  = u.RNDminusOne (i);
              //Xj = a [j].c [c];
              Xj = a [j].cB [c];
              //Xi = a [i].c [c];
              Xi = a [i].cB [c];

              //Xi = Xi + C * (Xi - Xj);
              Xi = Xi + C * (Xj - Xi);
            }
            // Omnivore behavior ----------------------------------------------- 
            //Xi (t + 1) = Xi (t) + C * r2 * (Xi (t) - Xb (t)) +
            //                    (1 - r2) * (Xi (t) - Xj (t));
            else
            {
              C  = u.LevyFlightDistribution (levisPower);
              Xb = cB [c];
              j  = u.RNDminusOne (i);
              //Xj = a [j].c [c];
              Xj = a [j].cB [c];
              //Xi = a [i].c [c];
              Xi = a [i].cB [c];
              r = u.RNDprobab ();

              //Xi = Xi + C * r * (Xi - Xb) +
              //     (1 - r) * (Xi - Xj);
              Xi = Xi + C * r * (Xb - Xi) +
                   (1 - r) * (Xj - Xi);
            }
          }

          a [i].c [c] = u.SeInDiSp (Xi, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }
    }

    consModel++;
    return;
  }

  // Decomposition -------------------------------------------------------------
  double D = 0.0;
  double h = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    D = 3 * u.RNDprobab ();
    h = u.RNDprobab () * (u.RNDprobab () < 0.5 ? 1 : -1);
    C = u.LevyFlightDistribution (levisPower);
    j = u.RNDminusOne (popSize);

    for (int c = 0; c < coords; c++)
    {
      double x = a [i].cB [c] + D * (C * a [i].cB [c] - h * a [j].c [c]);
      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  consModel = 0;
}
//——————————————————————————————————————————————————————————————————————————————

Test results

Now we can test the algorithm again with my changes in logic. 

AEO|Artificial Ecosystem-based Optimization Algorithm|50.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9137986747745103
25 Hilly's; Func runs: 10000; result: 0.4671288391599192
500 Hilly's; Func runs: 10000; result: 0.2647022528159094
=============================
5 Forest's; Func runs: 10000; result: 0.9022293417142482
25 Forest's; Func runs: 10000; result: 0.4370486099190667
500 Forest's; Func runs: 10000; result: 0.2139965996985526
=============================
5 Megacity's; Func runs: 10000; result: 0.6615384615384616
25 Megacity's; Func runs: 10000; result: 0.30799999999999994
500 Megacity's; Func runs: 10000; result: 0.28563076923076974
=============================
All score: 4.45407 (49.49%)

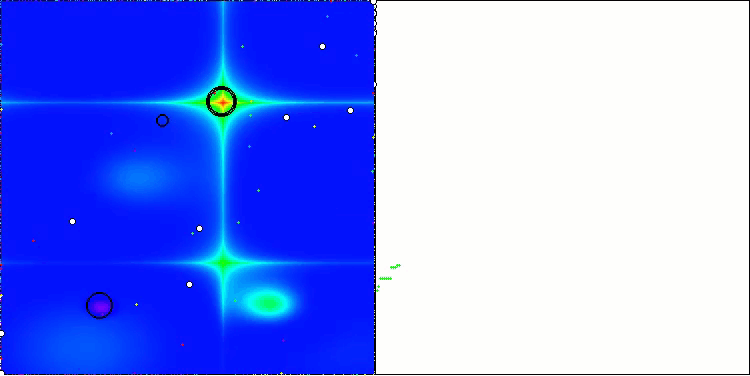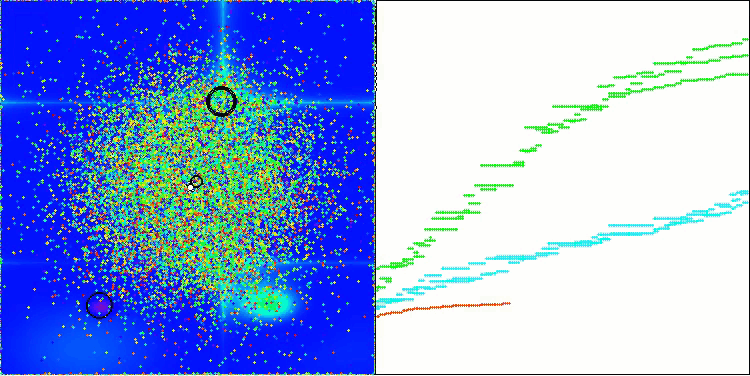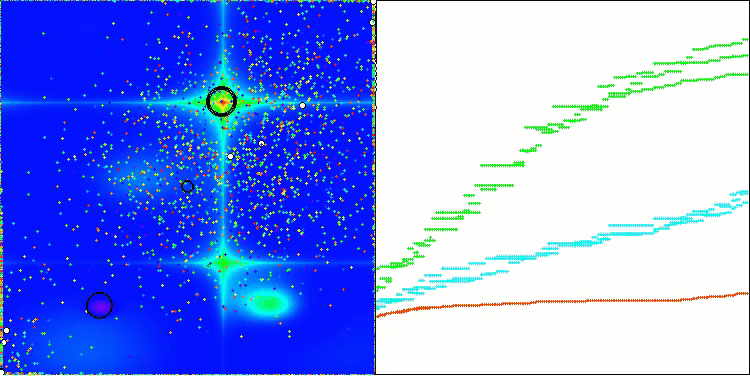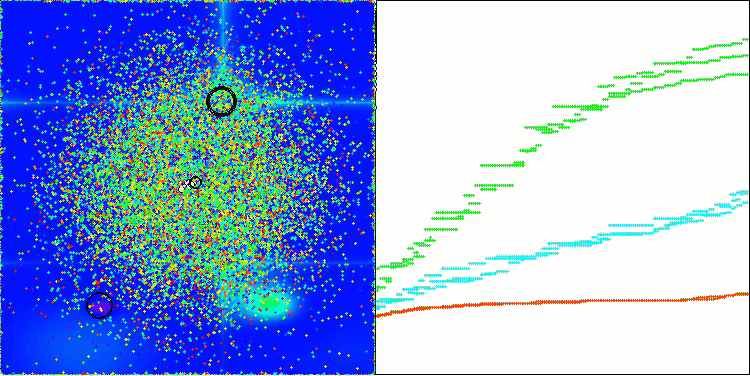
It is noteworthy that there is no significant spread in the results. The algorithm successfully avoids local traps, although the convergence accuracy is average. Also we can notice the already mentioned "blinking" when switching stages. The algorithm demonstrates the most unusual behavior on the discrete Megacity function, separating groups of coordinates into separate vertical and diagonal lines passing through significant areas of the surface. This is also reflected in the results of working with this discrete function - they are the best in the rating table for a discrete function with 1000 variables.

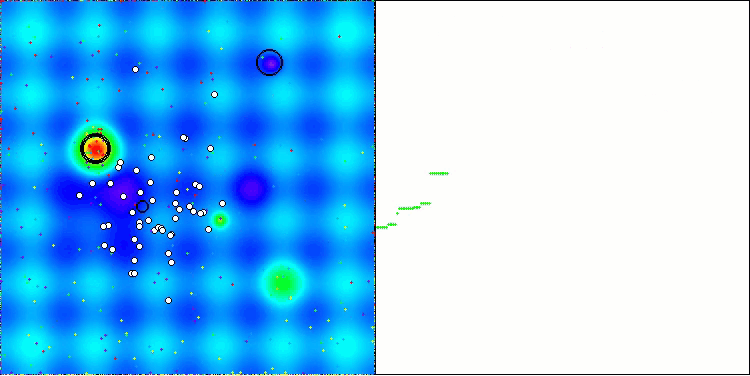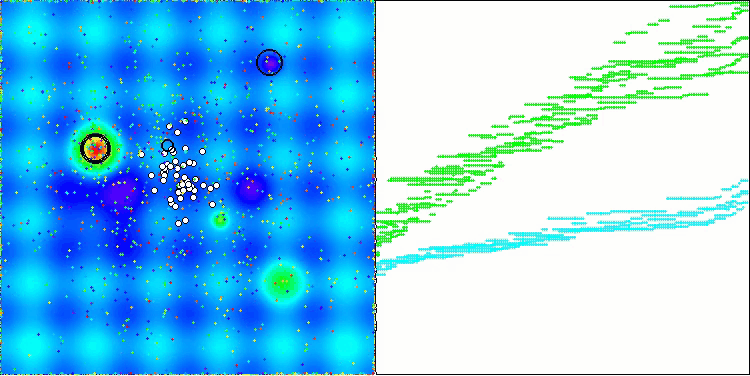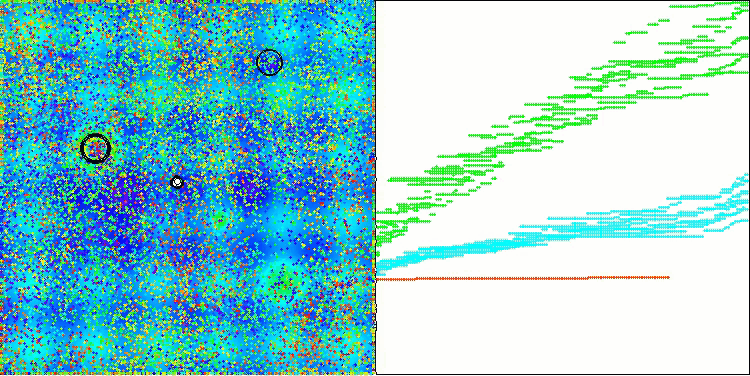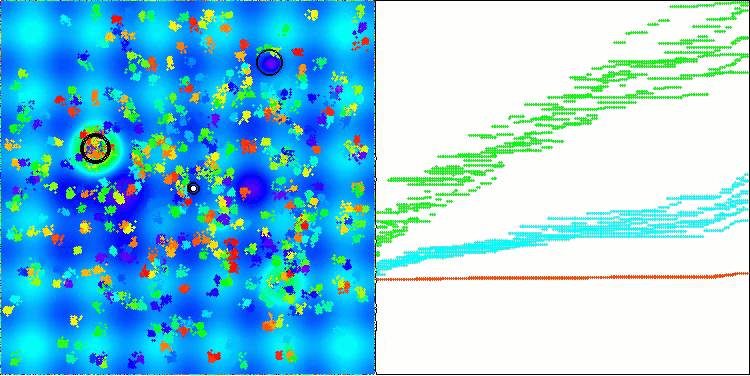
AEO on the Hilly test function

AEO on the Forest test function

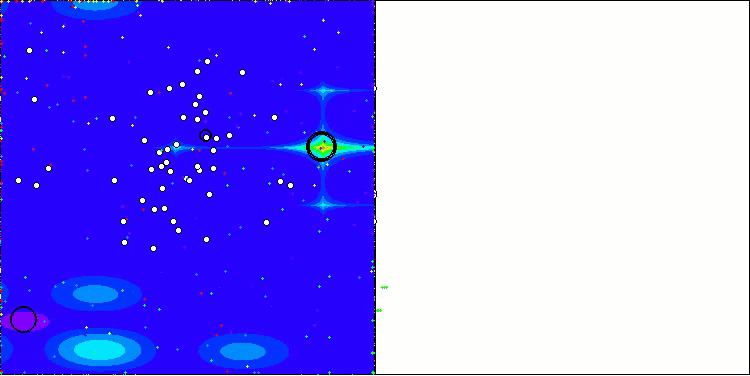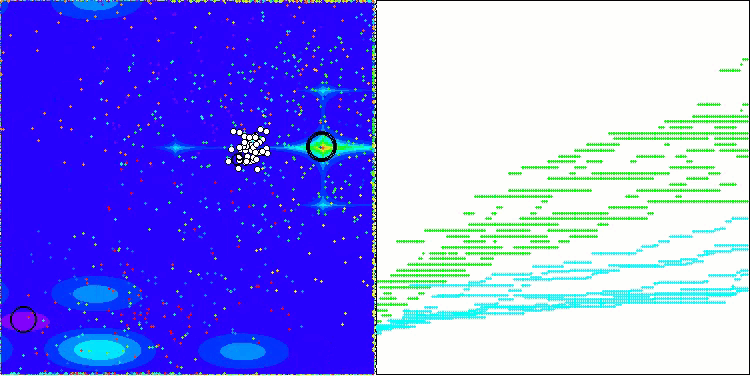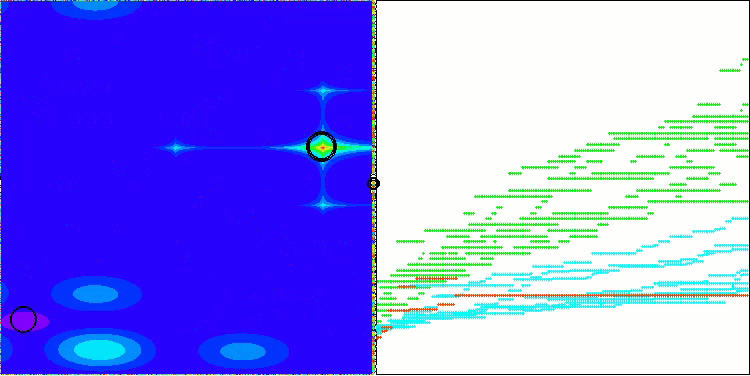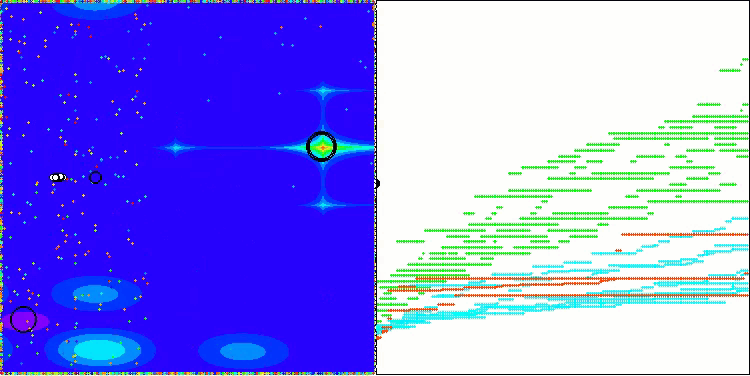
AEO on the Megacity test function

As you can see, the algorithm has significantly improved its performance compared to the original version and now reaches about 50% of the maximum possible. This is a truly impressive result! In the rating table, the algorithm occupies 25 th place, which is also quite notable. What is particularly impressive is that AEO set a new record on the Megacity discrete function, improving the 1000-parameter result by a whopping 5%!

#	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	code lock algorithm (joo)	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	animal migration optimization M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O) evolution strategies	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	comet tail algorithm (joo)	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	stochastic diffusion search M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	AAm	archery algorithm M	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
8	ESG	evolution of social groups (joo)	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
9	SIA	simulated isotropic annealing (joo)	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
10	ACS	artificial cooperative search	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
11	ASO	anarchy society optimization	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
12	TSEA	turtle shell evolution algorithm (joo)	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
13	DE	differential evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
14	CRO	chemical reaction optimization	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
15	BSA	bird swarm algorithm	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
16	HS	harmony search	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
17	SSG	saplings sowing and growing	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
18	BCOm	bacterial chemotaxis optimization M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
19	ABO	african buffalo optimization	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
20	(PO)ES	(PO) evolution strategies	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
21	TSm	tabu search M	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
22	BSO	brain storm optimization	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
23	WOAm	wale optimization algorithm M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
24	AEFA	artificial electric field algorithm	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
25	AEO	artificial ecosystem-based optimization algorithm	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
26	ACOm	ant colony optimization M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
27	BFO-GA	bacterial foraging optimization - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
28	ABHA	artificial bee hive algorithm	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
29	ACMO	atmospheric cloud model optimization	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
30	ASHA	artificial showering algorithm	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
31	ASBO	adaptive social behavior optimization	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
32	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
33	IWO	invasive weed optimization	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
34	Micro-AIS	micro artificial immune system	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
35	COAm	cuckoo optimization algorithm M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
36	SDOm	spiral dynamics optimization M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
37	NMm	Nelder-Mead method M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
38	FAm	firefly algorithm M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
39	GSA	gravitational search algorithm	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
40	BFO	bacterial foraging optimization	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
41	ABC	artificial bee colony	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
42	BA	bat algorithm	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
43	AAA	algae adaptive algorithm	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23
44	SA	simulated annealing	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
45	IWDm	intelligent water drops M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06

Summary

The algorithm features and advantages:

1. Balance between exploration and exploitation. AEO provides a good balance between global exploration of the solution space (through production and consumption) and local exploitation (through decomposition).

2. Adaptability. The algorithm adapts to the problem landscape through different solution updating strategies.

3. Simplicity. Despite the biological metaphor, the algorithm is relatively simple to implement and understand.

4. Excellent results on discrete functions of large dimensions.

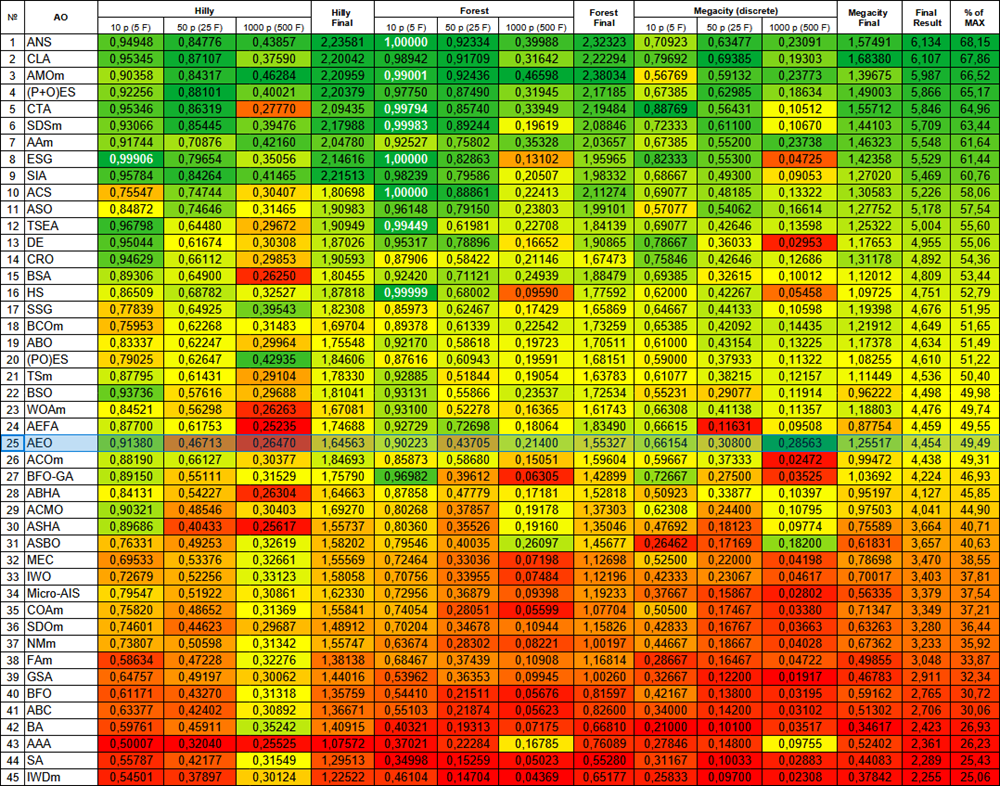
Figure 2. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white

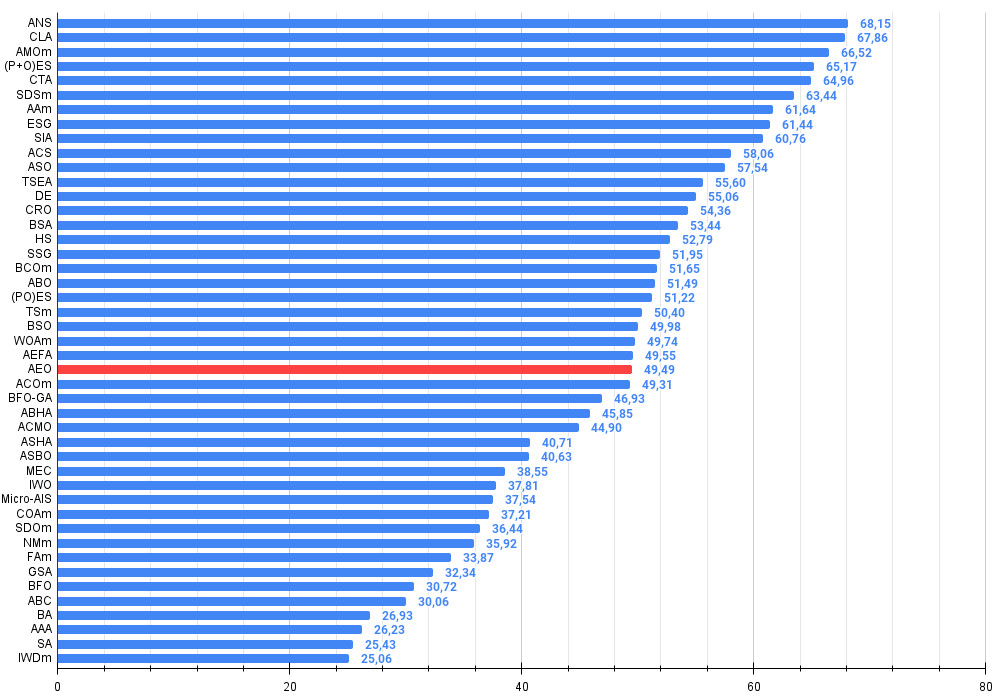
Figure 3. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,

where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)

AEO pros and cons:

Pros:

1. Only one external parameter (besides population size).
   
2. Performed well on the discrete function.

Cons:

1. Not the highest convergence accuracy.
   

The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5