
Алгоритм оптимизации на основе искусственной экосистемы — Artificial Ecosystem-based Optimization (AEO)
Содержание
Введение
В мире оптимизации и искусственного интеллекта постоянно ведется поиск новых, более эффективных методов решения сложных задач. Одним из таких инновационных подходов является алгоритм оптимизации на основе искусственной экосистемы (Artificial Ecosystem-based Optimization, AEO), был разработан и представлен в 2019 году. Этот метод черпает вдохновение из природных экосистем, имитируя сложные взаимодействия и процессы, происходящие в естественной среде.
Алгоритм AEO основан на нескольких ключевых принципах, наблюдаемых в природе. Подобно тому, как в экосистемах существует множество видов, каждый из которых адаптирован к своей экологической нише, AEO использует популяцию разнообразных решений. В этом контексте каждое решение можно рассматривать как отдельный "вид", обладающий уникальными характеристиками и способностями к адаптации.
В природе энергия передается от одного организма к другому через пищевые цепи. В AEO это моделируется через взаимодействие различных типов "агентов" – от "травы" до "всеядных". Здесь информация, аналогичная энергии, передается между решениями, что способствует улучшению общего качества популяции. Экосистемы характеризуются как конкуренцией за ресурсы, так и симбиотическими отношениями. Алгоритм AEO отражает эти процессы через стратегии обновления решений, где агенты могут "конкурировать" за лучшие позиции или "сотрудничать", обмениваясь информацией.
Природные экосистемы подвержены циклическим изменениям, что также находит отражение в AEO. Итеративный процесс оптимизации включает чередующиеся фазы потребления и разложения, что позволяет алгоритму адаптироваться к динамике задачи. В природе случайные события, такие как мутации и природные катаклизмы, сосуществуют с детерминированными процессами, например, естественным отбором. AEO использует как стохастические элементы (например, распределение Леви), так и детерминированные правила для обновления решений, обеспечивая баланс между исследованием новых областей и эксплуатацией уже найденных.
Чтобы лучше понять, как природные процессы отражены в алгоритме AEO, рассмотрим несколько конкретных примеров. В африканской саванне энергия перемещается от травы к зебрам (травоядные), затем к львам (хищники) и, наконец, к гиенам (падальщики). В AEO информация о лучших решениях передается от "травы" (самое худшее решение) к "травоядным" (средние решения) и "хищникам" (лучшие решения), что способствует улучшению общего качества популяции.
Когда организмы умирают, они разлагаются, возвращая питательные вещества в экосистему. Например, опавшие листья в лесу разлагаются, обогащая почву и питая новые растения. В AEO стадия разложения в алгоритме имитирует этот процесс. После фазы потребления (обновления решений) следует фаза разложения, где информация из текущих решений "разлагается" и распространяется по всему пространству поиска. Это позволяет алгоритму исследовать новые области и избегать застревания в локальных оптимумах. В алгоритме это реализовано через применение гауссова распределения к текущим решениям относительно самого лучшего (глобальное лучшее решение выступает в роли декомпозитора), что можно рассматривать как "разложение" и "перераспределение" информации в пространстве поиска.
Таким образом, алгоритм AEO представляет собой элегантный синтез природных принципов и математической оптимизации. Он не только предлагает эффективный метод решения сложных задач, но и открывает новый взгляд на связь между природными процессами и искусственным интеллектом. Далее мы подробно рассмотрим структуру и механизмы работы этого алгоритма, чтобы глубже понять его потенциал и применение.
Реализация алгоритма
Чтобы лучше понять идею авторов алгоритма AEO, обратимся к иллюстрации на рисунке 1, где представлена иерархия организмов в искусственной экосистеме. Вся экосистема состоит из организмов, условно пронумерованных от 1 до Xn. Под номером 1 находится "трава", обладающая максимальной энергией (минимальное значение фитнес-функции), в то время как Xn представляет собой сапрофита, выполняющего функцию декомпозиции (минимальная энергия, максимальное значение фитнес-функции).
На рисунке стрелками обозначены направления питания: трава (номер 1) может использовать только продукты жизнедеятельности сапрофитов, травоядные (номер 2) питаются травой, а организмы под номерами 2, 4 и 5 могут быть травоядными (употребляют только траву), плотоядными (организмы могут питаться лишь теми существами, чья энергия ниже их собственной), и всеядные (могут употреблять как траву, так и организмы с более высокой энергией). Вершину экосистемы занимают сапрофиты, которые разлагают все организмы в конце их жизненного цикла.
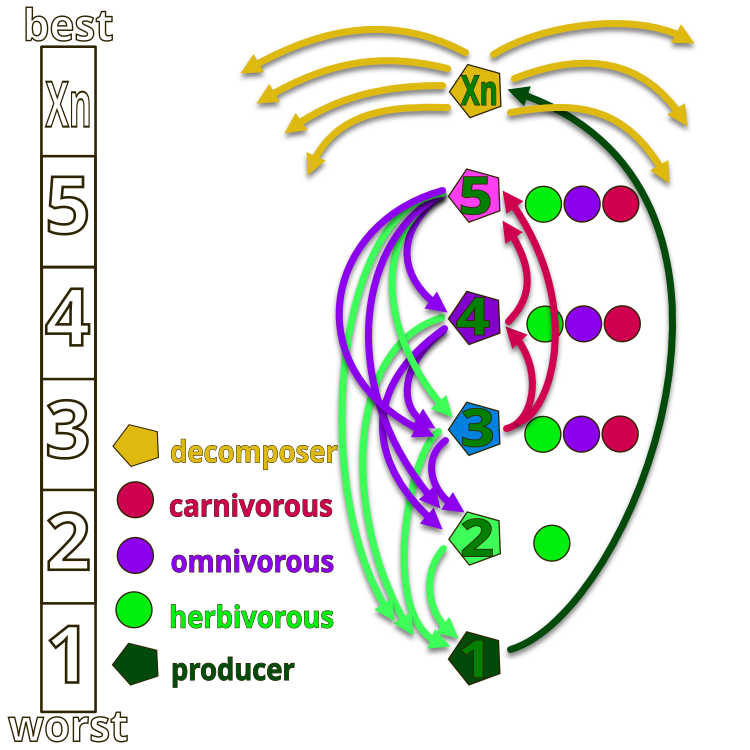
Рисунок 1. Иерархия организмов в искусственной экосистеме алгоритма AEO
Основная идея алгоритма заключается в моделировании взаимодействий между компонентами экосистемы для решения оптимизационных задач. Алгоритм опирается на три ключевых принципа, наблюдаемых в природе:
1. Производство - в природе производители, например растения, трансформируют солнечную энергию в органические соединения.
2. Потребление - потребители (травоядные, хищники, всеядные) используют энергию, произведенную другими, в частности растениями.
3. Разложение - сапрофиты разлагают сложные органические вещества на простые, что моделируется в алгоритме как декомпозиция решений.
Принципы работы алгоритма:
1. Инициализация - создается начальная популяция решений, представляющая экосистему.
2. Производство - на каждой итерации худшее решение обновляется с учетом лучшего и случайного фактора.
3. Потребление - остальные решения обновляются с использованием трех стратегий:
- Травоядные: обновляются на основе производителя.
- Хищники: обновляются на основе случайно выбранного лучшего решения.
- Всеядные: обновляются на основе как производителя, так и случайного решения.
4. Разложение - все решения проходят процесс "разложения", что улучшает глобальный поиск.
5. Отбор - сохраняются только улучшенные решения, обеспечивая постепенное улучшение популяции.
Таким образом, алгоритм опирается на механизм передачи энергии между живыми организмами, что помогает поддерживать стабильность видов с использованием трех операторов: производство, потребление и разложение.
1. Производство - худший индивид популяции "X1" обновляется относительно лучшего "Xn" с добавлением случайно сгенерированной координаты "Xrand" в заданном диапазоне, создавая новый индивид через оператор производства. Математическое представление: X1 (t + 1) = (1 - a) * Xn (t) + a * Xrand (t), где a = (1 - t / T) * r1 (t - текущая эпоха, T - всего эпох), r1 - случайное число [0; 1]. В данном случае компонент "r1" можно не применять, так как и так мы используем случайную координату в формуле.
2. Потребление - случайно выбранный потребитель может "съесть" производителя для получения энергии. Фактор потребления C определяется как: C = 1/2 * (v1 / |v2|), где v1 и v2 - равномерно распределённые случайные числа в диапазоне [0; 1].
- Травоядные: Xi (t + 1) = Xi (t) + C * (Xi (t) - X1 (t)).
- Хищники: Xi (t + 1) = Xi (t) + C * (Xi (t) - Xj (t)).
- Всеядные: Xi (t + 1) = Xi (t) + C * (r2 * Xi (t) + (1 - r2) * Xj (t)).
3. Разложение - сапрофит разлагает останки погибших индивидов, обеспечивая питательные вещества для производителей. Обновление позиции индивидов после работы сапрофита описывается как:
Xi (t + 1) = Xn (t) + D * (e * Xn (t) - h * Xi (t)), где D = 3u, u ~ N (0, 1), e = r3 * rand (i), h = 2 * r3 - 1 (r3, случайное число в диапазоне [0; 1]).
Итак, в начале генерируется случайная популяция, и на каждой итерации позиция первого индивида обновляется с использованием уравнения п.1. Позиции других индивидов обновляются, выбирая среди уравнений п.2 с одинаковой вероятностью. На стадии разложения каждый индивид обновляет свою позицию с использованием уравнения п.3. Этот процесс продолжается, пока не будет достигнут удовлетворительный критерий завершения. Последний шаг возвращает лучшего индивида, найденного на данный момент.
Теперь мы можем составить псевдокод алгоритма AEO:
Алгоритм AEO (Artificial Ecosystem-based Optimization)
Инициализация:
Задать размер популяции (popSize)
Задать количество эпох (epochs)
Задать параметр распределения Леви (levisPower)
Инициализировать популяцию случайными решениями в заданном диапазоне
Оценить фитнес-функцию для каждого решения
Найти лучшее глобальное решение cB
Для каждой эпохи от 1 до epochs:
// Фаза потребления
Для каждого агента i в популяции:
Если i == 0:
Применить гауссово распределение к текущему решению
Иначе если i == popSize - 1:
Применить поведение травы (GrassBehavior)
Иначе:
Случайно выбрать поведение:
- Поведение травоядного (HerbivoreBehavior)
- Поведение хищника (CarnivoreBehavior)
- Поведение всеядного (OmnivoreBehavior)
// Фаза разложения
Для каждого агента i в популяции:
Для каждой координаты c:
Выбрать случайного агента j
Рассчитать расстояние D между cB [c] и a [j].c [c]
Обновить a [i].c [c] с использованием гауссова распределения
// Ревизия
Оценить фитнес-функцию для каждого агента
Обновить лучшее персональное решение для каждого агента
Обновить лучшее глобальное решение cB
Отсортировать популяцию по значению фитнес-функции
Вернуть лучшее найденное решение cB
Подпроцедуры:
GrassBehavior (агент):
α = (1 - текущая_эпоха / общее_число_эпох)
Для каждой координаты c:
Xr = случайное значение в диапазоне [min [c], max [c]]
Xn = cB [c]
X1 = Xn + α * (Xn - Xr)
агент.c [c] = X1 (с учетом ограничений)
HerbivoreBehavior (агент, индекс_координаты):
Xi = агент.cB [индекс_координаты]
X1 = худшее решение в популяции для данной координаты
C = случайное число из распределения Леви (levisPower)
Xi = Xi + C * (Xi - X1)
агент.c [индекс_координаты] = Xi (с учетом ограничений)
CarnivoreBehavior (агент, индекс_агента, индекс_координаты):
Xi = агент.cB [координата]
j = случайный индекс < индекс_агента
Xj = a [j].cB [индекс_координаты]
C = случайное число из распределения Леви (levisPower)
Xi = Xi + C * (Xj - Xi)
агент.c [индекс_координаты] = Xi (с учетом ограничений)
OmnivoreBehavior (агент, индекс_агента, индекс_координаты):
Xi = агент.cB [координата]
X1 = худшее решение в популяции для данной координаты
j = случайный индекс > индекс_агента
Xj = a [j].cB [индекс_координаты]
C = случайное число из распределения Леви (levisPower)
r = случайное число от 0 до 1
Xi = Xi + C * r * (Xi - X1) + (1 - r) * (Xi - Xj)
агент.c [индекс_координаты] = Xi (с учетом ограничений)
После подробного описания и разбора алгоритма переходим к написанию кода.
В алгоритме используется распределение Леви для генерации экстремально далеких, но редких скачков в пространстве поиска. Ранее мы уже применяли это распределение случайных чисел, например, в алгоритме «Поиск с кукушкой», но не вдавались в подробности его особенностей. Дело в том, что корректная генерация распределения Леви подразумевает использование четырёх случайных равномерно распределённых чисел, что само по себе затратно. Кроме того, распределение Леви имеет бесконечно длинный хвост (оно ассиметрично, с одним хвостом), что затрудняет его практическое использование в алгоритмах оптимизации, особенно при наличии граничных условий. Также необходимо проверять граничные условия при генерации, такие как проверка на 0 перед вычислением натурального логарифма, а также, чтобы избежать деления на 0.
Привожу код генерации случайных чисел с распределением Леви, в котором отсутствуют вышеописанные проверки и без объяснения логики кода:
double LevyFlight() { const double epsilon = 1e-10; // Малое значение для избежания деления на ноль const double maxValue = 1e10; // Максимальное допустимое значение double log1 = MathMax (RNDprobab(), epsilon); double log2 = MathMax (RNDprobab(), epsilon); double cos1 = MathCos (2 * M_PI * RNDprobab()); double cos2 = MathCos (2 * M_PI * RNDprobab()); double U = MathSqrt (-2.0 * MathLog (log1)) * cos1; double v = MathSqrt (-2.0 * MathLog (log2)) * cos2; double l = 0.5 * MathAbs(U) / MathMax(MathAbs(v), epsilon); return l; }
Чтобы избавится от недостатков генерации чисел с распределением Леви, напишем свою функцию "LevyFlightDistribution" с близким распределением и разместим в нашем стандартном наборе функций "C_AO_Utilities" для применения в алгоритмах оптимизации. Давайте разберем ее:
1. Параметр "levisPower"- это степень, которая определяет форму распределения. Чем больше значение "levisPower", тем более "разреженным" будет распределение.
2. Расчет минимального значения - вычисляется минимальное значение, которое будет использоваться для масштабирования. Оно зависит от "levisPower" и вычисляется как 20^levisPower.
3. Генерация случайного числа "r" с помощью функции "RNDfromCI" в диапазоне от 1 до 20.
4. Применение степени - сгенерированное число "r" возводится в степень "-levisPower", что изменяет его распределение.
5. Масштабирование результата - полученное значение "r" масштабируется в диапазон [0, 1]. Это делается путем вычитания минимального значения и деления на разницу между 1 и минимальным значением. Таким образом, результат всегда будет находиться в пределах [0, 1].
6. Возврат результата - функция возвращает сгенерированное значение "r", которое теперь имеет распределение, близкое к распределению Леви, смещенное к 0.
Как видим, функция генерирует случайные числа строго в диапазоне [0, 1], что очень удобно в практическом применении, этот диапазон всегда можно расширить до любых значений применив соответствующий коэффициент. Эта функция гораздо быстрее и обеспечивает распределение очень близкое к искомому (правая часть распределения относительно максимума).
//------------------------------------------------------------------------------ //A distribution function close to the Levy Flight distribution. //The function generates numbers in the range [0.0;1.0], with the distribution shifted to 0.0. double C_AO_Utilities :: LevyFlightDistribution (double levisPower) { double min = pow (20, -levisPower); //calculate the minimum possible value double r = RNDfromCI (1.0, 20); //generating a number in the range [1; 20] r = pow (r, -levisPower); //we raise the number r to a power r = (r - min) / (1 - min); //we scale the resulting number to [0; 1] return r; }
Приступим к описанию основного кода алгоритма. Класс "C_AO_AEO" является производным от класса "C_AO" и реализует алгоритм. Давайте подробно рассмотрим его структуру, члены и методы.
Конструктор:
- Устанавливает значения по умолчанию для размера популяции и степени Леви.
- Создает массив параметров "params" и инициализирует его значениями.
Методы:
- Устанавливает параметры "popSize" и "levisPower" из массива "params".
- Init () - инициализирует алгоритм с заданными диапазонами поиска и количеством эпох. Метод возвращает "bool", что предполагает возможность проверки успешности инициализации.
- Moving () - обрабатывает движение агентов в текущую эпоху, обновляя их координаты.
- Revision () - обновляет информацию об агентах и их лучших решениях.
Приватные члены и переменные:
- levisPower - параметр, используемый в распределении Леви.
- epochs - общее количество эпох.
- epochNow - текущая эпоха.
- consModel - стадия (потребление или разложение).
S_AO_Agent aT [] — временный массив агентов, используемый для сортировки популяции.
Приватные методы:
- GrassBehavior () - обрабатывает поведение агента "трава".
- HerbivoreBehavior () - обрабатывает поведение травоядного агента, который "ест" траву (наихудшего агента).
- CarnivoreBehavior () - обрабатывает поведение плотоядного агента, который "ест" агентов с более высоким значением фитнес-функции.
- OmnivoreBehavior () - обрабатывает поведение всеядного агента, который комбинирует поведение травоядного и поедающего любого с приспособленностью ниже.
Класс "C_AO_AEO" предоставляет реализацию алгоритма оптимизации на основе искусственной экосистемы, используя различные типы агентов и их взаимодействия для нахождения оптимальных решений. Каждый метод отвечает за определенные аспекты алгоритма, включая инициализацию, движение агентов и обновление их состояния.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_AEO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_AEO () { } C_AO_AEO () { ao_name = "AEOm"; ao_desc = "Artificial Ecosystem-based Optimization Algorithm"; ao_link = "https://www.mql5.com/ru/articles/16058"; popSize = 50; // population size levisPower = 2; ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "levisPower"; params [1].val = levisPower; } void SetParams () { popSize = (int)params [0].val; levisPower = params [1].val; } bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // step search const int epochsP = 0); // number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double levisPower; private: //------------------------------------------------------------------- int epochs; int epochNow; int consModel; // consumption model; S_AO_Agent aT []; void GrassBehavior (S_AO_Agent &animal); void HerbivoreBehavior (S_AO_Agent &animal, int indCoord); void CarnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord); void OmnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord); }; //——————————————————————————————————————————————————————————————————————————————
Давайте подробно разберем код метода "Init" класса "C_AO_AEO". Метод "Init" возвращает значение типа "bool", что позволяет определить успешность выполнения инициализации. Проверка стандартной инициализации: в этом блоке происходит вызов метода "StandardInit", который выполняет базовую инициализацию параметров, переданных в метод. Если "StandardInit" возвращает "false", это означает, что инициализация не удалась, и метод "Init" также возвращает "false".
Настройка переменных:
- epochs - устанавливает общее количество эпох, полученное из параметра "epochsP".
- epochNow - инициализирует текущую эпоху значением 0, что указывает на то, что алгоритм только что начался.
- consModel - устанавливает значение для модели в 0, чтобы в дальнейшем поочерёдно переходить из одной стадии к другой.
Изменение размера временного массива агентов "aT" до значения "popSize".
Возврат результата: если все предыдущие операции выполнены успешно, метод возвращает "true", что сигнализирует о том, что инициализация прошла успешно.
Метод "Init" класса "C_AO_AEO" отвечает за начальную настройку алгоритма. Он проверяет стандартные параметры, устанавливает значения для эпох и начальную стадию, а также подготавливает массив агентов для работы. Если все этапы успешно завершены, метод возвращает "true", указывая на готовность алгоритма к выполнению.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_AEO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; consModel = 0; ArrayResize (aT, popSize); return true; } //——————————————————————————————————————————————————————————————————————————————
Разберем код метода "Moving" класса "C_AO_AEO". Общая структура метода: "Moving" отвечает за обновление состояния популяции агентов (особей) в зависимости от текущей эпохи и модели потребления. Он делится на несколько логических блоков:
1. Увеличение эпохи: "epochNow++" увеличивает счетчик текущей эпохи.
2. Первоначальная инициализация:
- Если "revision" равно "false", происходит начальная инициализация координат агентов в популяции. Координаты выбираются случайным образом из заданного диапазона и затем округляются до ближайшего значения, которое соответствует шагу.
- После этого "revision" устанавливается в "true", и метод завершает выполнение.
3. Модель потребления:
- Если "consModel" равно "0", происходит обновление координат агентов на основе их поведения.
- Для первого агента (индекс 0) используются гауссовы распределения для инициализации координат.
- Для остальных агентов поведение зависит от их индекса: последний агент (индекс "popSize - 1") вызывает функцию "GrassBehavior". Для предпоследнего и последующих агентов (индексы "popSize - 2" и ниже) поведение определяется случайным образом: либо травоядное, либо плотоядное, либо всеядное.
4. Декомпозиция: если "consModel" не равен "0", происходит декомпозиция, где для каждого агента обновляются его координаты на основе случайных значений и гауссового распределения. Для каждой координаты выбирается случайный индекс другого агента, и на основе этого значения вычисляются новые координаты с учетом минимальных и максимальных границ.
Метод "Moving" реализует логику, связанную с изменением координат агентов в зависимости от их поведения и текущей эпохи. Он включает в себя как первоначальную инициализацию, так и обновление состояния агентов с учетом их модели потребления.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEO::Moving () { epochNow++; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } // Consumption --------------------------------------------------------------- if (consModel == 0) { double r = 0.0; for (int i = 0; i < popSize; i++) { if (i == 0) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.GaussDistribution (a [i].c [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } continue; } if (i == popSize - 1) GrassBehavior (a [i]); else { if (i >= popSize - 2) { for (int c = 0; c < coords; c++) { r = u.RNDprobab (); if (r < 0.333) HerbivoreBehavior (a [i], c); else { if (r < 0.667) { CarnivoreBehavior (a [i], i, c); } else { OmnivoreBehavior (a [i], i, c); } } } } else { for (int c = 0; c < coords; c++) { r = u.RNDprobab (); if (r < 0.5) CarnivoreBehavior (a [i], i, c); else OmnivoreBehavior (a [i], i, c); } } } } consModel++; return; } // Decomposition ------------------------------------------------------------- int j = 0; double D = 0.0; double min = 0.0; double max = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { j = u.RNDminusOne (popSize); D = 3.0 * (cB [c] - a [j].c [c]); // * u.RNDprobab (); min = cB [c] - D; max = cB [c] + D; if (min < rangeMin [c]) min = u.RNDfromCI (rangeMin [c], cB [c]); if (max > rangeMax [c]) min = u.RNDfromCI (cB [c], rangeMax [c]); a [i].c [c] = u.GaussDistribution (cB [c], min, max, 1); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } consModel = 0; } //——————————————————————————————————————————————————————————————————————————————
Метод "Revision" в классе "C_AO_AEO" отвечает за обновление информации о лучших агентах в популяции. Он реализует логику, которая позволяет отслеживать и сохранять лучшие найденные решения в процессе выполнения алгоритма. Структура метода:
1. Поиск лучшего агента:
- Перебираем всех агентов в популяции.
- Сравниваем их фитнес (значение "f") с текущим наилучшим фитнесом "fB".
- Если найден агент с лучшим фитнесом, обновляем "fB" и запоминаем его индекс.
2. Копирование координат лучшего агента: если был найден лучший агент (индекс не равен -1), копируем его координаты в массив "cB", который хранит текущие лучшие координаты.
3. Обновление личных лучших фитнесов агентов: перебираем всех агентов снова и проверяем, если их текущий фитнес превышает их личный лучший фитнес ("fB"). Если да, обновляем их личный лучший фитнес и копируем их текущие координаты в "cB".
4. Сортировка агентов: в конце вызываем функцию сортировки, чтобы упорядочить агентов по их личному лучшему значению приспособленности.
Метод "Revision" является важным элементом алгоритма, так как он обеспечивает отслеживание и сохранение лучших решений, найденных в ходе работы.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEO::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Метод "GrassBehavior" в классе "C_AO_AEO" реализует поведение агентов, основанное на концепции "травоядных", что символизирует поиск новых решений в пространстве. Структура метода:
1. Вычисление коэффициента "α", определяется как "(1.0 - (double) epochNow / epochs)", что означает, что он уменьшается по мере увеличения номера эпохи. Это позволяет алгоритму более активно исследовать пространство в начале, а затем сосредоточиться на улучшении найденных решений.
2. Инициализация переменных:
- X1 - текущая координата травоядного агента .
- Xn - текущая координата сапрофита.
- Xr - случайная координата, выбранная из заданного диапазона.
3. Цикл по координатам. Для каждой координаты агента:
- Генерируется случайное значение "Xr" в пределах заданного диапазона "[Xmin, Xmax]".
- Текущая координата "Xn" берется из массива "cB", который хранит текущие глобальные лучшие координаты (положение сапрофита в пространстве).
- Вычисляется новая координата "X1" по формуле "X1 = Xn + α * (Xn - Xr)", что позволяет смешать текущее значение со случайным значением, уменьшая влияние случайности по мере увеличения количества эпох.
- Наконец, новая координата ограничивается в пределах заданного диапазона с помощью функции "SeInDiSp".
//—————————————————————————————————————————————————————————————————————————————— // Трава // (Худший) X1 X2 X3 ...... Xn (Лучший) // X1(t+1) = (1 - α) * Xn(t) + α * Xrnd (t) // α = (1 - t / T) * rnd [0.0; 1.0] // Xrnd = rnd [Xmin; Xmax] void C_AO_AEO::GrassBehavior (S_AO_Agent &animal) { //0) (1 - α) * Xn + α * Xrnd //1) Xn - α * Xn + α * Xrnd //2) Xn + α * (Xrnd - Xn) double α = (1.0 - (double)epochNow / epochs); double X1 = 0.0; double Xn = 0.0; double Xr = 0.0; for (int c = 0; c < coords; c++) { Xr = u.RNDfromCI (rangeMin [c], rangeMax [c]); Xn = cB [c]; //X1 = Xn + α * (Xr - Xn); X1 = Xn + α * (Xn - Xr); animal.c [c] = u.SeInDiSp (X1, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Метод "HerbivoreBehavior" в классе "C_AO_AEO" реализует поведение травоядного агента. Структура метода:
1. Инициализация переменных:
- Xi - текущая координата агента, которая будет обновлена.
- X1 - координата самого худшего агента в популяции, что соответствует максимальной энергии (или наименьшему фитнесу).
- C - случайное значение, генерируемое с использованием распределения Леви.
2. Обновление координаты: координата "Xi" обновляется по формуле: Xi (t+1)=Xi (t)+C ⋅ (Xi (t)−X1 (t)). Эта формула означает, что агент изменяет свою координату, основываясь на разнице между своей текущей координатой и координатой худшего агента. Это позволяет травоядному "питаться" от худшего агента, то есть исследовать даже бесперспективные области поиска.
3. Ограничение координаты: после обновления координаты "Xi", она ограничивается в пределах заданного диапазона с помощью функции "SeInDiSp", которая принимает в качестве аргументов новое значение, минимальные и максимальные пределы, а также шаг.
Метод "HerbivoreBehavior" демонстрирует, как травоядные агенты могут адаптироваться, "питаясь" от худших представителей популяции.
//—————————————————————————————————————————————————————————————————————————————— // Травоядный // (Худший) X1 X2 X3 ...... Xn (Лучший) // Xi(t+1) = Xi(t) + C * (Xi(t) - X1(t)) для i ∈ [2, n] // Травоядный ест только того, у кого энергия максимальна (ест того, у кого самый худший ФФ) void C_AO_AEO::HerbivoreBehavior (S_AO_Agent &animal, int indCoord) { double Xi = animal.c [indCoord]; double X1 = a [popSize - 1].c [indCoord]; double C = u.LevyFlightDistribution (levisPower); Xi = Xi + C * (Xi - X1); animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]); } //——————————————————————————————————————————————————————————————————————————————
Метод "CarnivoreBehavior " в классе "C_AO_AEO " реализует поведение плотоядного агента в рамках алгоритма. Структура метода:
1. Инициализация переменных:
- Xi - текущая координата плотоядного агента, которая будет обновлена.
- j - индекс случайно выбранного жертвенного агента (плотоядный "ест" агентов с меньшей энергией, но лучшим фитнесом).
- Xj - координата жертвы, которая будет использоваться для обновления координаты плотоядного.
- C - случайное значение, генерируемое с использованием распределения Леви.
2. Обновление координаты: координата "Xi" обновляется по формуле: Xi (t+1) = Xi (t) + C * (Xj (t) - Xi (t)). Эта формула означает, что плотоядный агент изменяет свою координату, основываясь на разнице между координатой жертвы и своей текущей координатой. Это позволяет плотоядному "питаться" за счет жертвы, улучшая свои характеристики.
3. Ограничение координаты: после обновления координаты "Xi", она ограничивается в пределах заданного диапазона с помощью функции "SeInDiSp ".
Метод "CarnivoreBehavior " демонстрирует, как плотоядные агенты могут адаптироваться, "питаясь" от жертв с меньшей энергией. Это позволяет им улучшать свои характеристики, стремясь к более оптимальным решениям.
//—————————————————————————————————————————————————————————————————————————————— // Плотоядный // (Худший) X1 X2 X3 ...... Xn (Лучший) // Xi(t+1) = Xi(t) + C * (Xi(t) - Xj(t)) для i ∈ [3, n] // Плотоядный ест тех, у кого энергии меньше (ест того, у кого выше ФФ) void C_AO_AEO::CarnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord) { //double Xi = animal.c [indCoord]; double Xi = animal.cB [indCoord]; int j = u.RNDminusOne (indAnimal); //double Xj = a [j].c [indCoord]; double Xj = a [j].cB [indCoord]; double C = u.LevyFlightDistribution (levisPower); //Xi = Xi + C * (Xi - Xj); Xi = Xi + C * (Xj - Xi); animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]); } //——————————————————————————————————————————————————————————————————————————————
Метод "OmnivoreBehavior" в классе "C_AO_AEO" описывает поведение всеядного агента в контексте эволюционного алгоритма. Структура метода:
1. Инициализация переменных:
- Xi - текущая координата всеядного агента, которую необходимо обновить.
- X1 - координата худшего агента (агента с наибольшей энергией).
- j - случайный индекс другого агента, выбранного из популяции, который будет использоваться для обновления координаты.
- Xj - координата выбранного другого агента.
- C - случайное значение, генерируемое с использованием распределения Леви.
- r - случайная вероятность, которая будет использоваться для смешивания обновления координат.
2. Обновление координаты: координата "Xi" обновляется по формуле: Xi (t+1) = Xi (t) + C * r * (Xi (t) - X1 (t)) + (1 - r) (Xi (t) - Xj (t)). Эта формула позволяет всеядному агенту адаптироваться, "питаясь" как от худшего агента (с наибольшей энергией), так и от случайного другого агента с меньшей приспособленностью, что делает его поведение более гибким.
3. Ограничение координаты: после обновления координаты "Xi", она ограничивается в заданных пределах с помощью функции "SeInDiSp".
Метод "OmnivoreBehavior" демонстрирует, как всеядные агенты могут адаптироваться и извлекать выгоду из различных источников энергии, включая худших агентов и случайно выбранных других агентов с меньшей приспособленностью.
//—————————————————————————————————————————————————————————————————————————————— // Всеядный // (Худший) X1 X2 X3 ...... Xn (Лучший) // Xi(t+1) = Xi(t) + C * r2 * (Xi(t) - X1(t)) + (1 - r2) * (Xi(t) - Xj(t)) для i ∈ [3, n] // Всеядный есть всех, у кого энергии больше (траву и мелких животных, тоесть тех, у кого ФФ хуже) void C_AO_AEO::OmnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord) { //double Xi = animal.c [indCoord]; double Xi = animal.cB [indCoord]; //double X1 = a [popSize - 1].c [indCoord]; double X1 = a [popSize - 1].cB [indCoord]; int j = u.RNDintInRange (indAnimal + 1, popSize - 1); //double Xj = a [j].c [indCoord]; double Xj = a [j].cB [indCoord]; double C = u.LevyFlightDistribution (levisPower); double r = u.RNDprobab (); Xi = Xi + C * r * (Xi - X1) + (1.0 - r) * (Xi - Xj); animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]); } //——————————————————————————————————————————————————————————————————————————————
Теперь, когда мы написали код алгоритма, можем наконец приступить к его тестированию на наших тестовых функциях.
AEO|Artificial Ecosystem-based Optimization Algorithm|50.0|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.6991675795357223
25 Hilly's; Func runs: 10000; result: 0.34855292688850514
500 Hilly's; Func runs: 10000; result: 0.253085011547826
=============================
5 Forest's; Func runs: 10000; result: 0.6907505745478882
25 Forest's; Func runs: 10000; result: 0.23365521509528495
500 Forest's; Func runs: 10000; result: 0.1558073538195803
=============================
5 Megacity's; Func runs: 10000; result: 0.5430769230769231
25 Megacity's; Func runs: 10000; result: 0.20676923076923082
500 Megacity's; Func runs: 10000; result: 0.1004461538461546
=============================
All score: 3.23131 (35.90%)
Алгоритм набрал при тестировании около 36%, однако, это средний результат. Для данного алгоритма я решил пересмотреть метод "Moving", и вот что получилось:
Измененная логика перемещения агентов с учетом различных моделей поведения (производство, потребление и разложение) в методе "Moving":
1. Начальная инициализация популяции осталась без изменений.
2. Обновление коэффициента "α", вычисляется как функция текущей эпохи, уменьшаясь по мере увеличения "epochNow". Этот коэффициент вынесен наружу из отдельного приватного метода.
3. Производство (consModel == 0) - в этой части агенты обновляют свои координаты, используя формулу, основанную на предыдущем состоянии и случайном значении. Это позволяет им "производить" новые состояния.
4. Потребление (consModel == 1). Здесь агентов разделяем на три группы в зависимости от случайного значения:
- Травоядные.
- Плотоядные.
- Всеядные.
5. Разложение: на этом этапе агенты взаимодействуют друг с другом, изменяя свои координаты на основе случайных значений и взаимодействий с другими агентами.
6. Сброс модели потребления: в конце метода "consModel" сбрасывается в "0", чтобы начать новый цикл.
Как видно, основное изменение в логике алгоритма заключается в выделении "Производства" в отдельную стадию. Для этого отведена отдельная эпоха, что позволяет серьезно перетряхивать популяцию организмов. Это также отразилось на поведении AEO на визуализации: наблюдаются "мигания", то есть отдельные стадии искусственной экосистемы можно заметить даже визуально.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEO::Moving () { epochNow++; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double α = (1.0 - (double)epochNow / epochs); double Xi = 0.0; double Xb = 0.0; double Xr = 0.0; double Xj = 0.0; double C = 0.0; int j = 0; double r = 0.0; // Production ---------------------------------------------------------------- Производство // X(t + 1) = (1 - α) * Xb(t) + α * Xrnd (t) // α = (1 - t / T) * rnd [0.0; 1.0] // Xrnd = rnd [Xmin; Xmax] if (consModel == 0) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { Xb = cB [c]; Xr = u.RNDfromCI (rangeMin [c], rangeMax [c]); //Xi = Xb + α * (Xr - Xb); Xi = Xb + α * (Xb - Xr); a [i].c [c] = u.SeInDiSp (Xi, rangeMin [c], rangeMax [c], rangeStep [c]); } } consModel++; return; } // Consumption --------------------------------------------------------------- Потребление if (consModel == 1) { for (int i = 0; i < popSize; i++) { if (i > 1) { for (int c = 0; c < coords; c++) { r = u.RNDprobab (); // Herbivore behavior ------------------------------------------------ Травоядный //Xi (t + 1) = Xi (t) + C * (Xi (t) - Xb (t)); if (r < 0.333) { C = u.LevyFlightDistribution (levisPower); Xb = cB [c]; //Xi = a [i].c [c]; Xi = a [i].cB [c]; //Xi = Xi + C * (Xi - Xb); Xi = Xi + C * (Xb - Xi); } else { // Carnivore behavior ---------------------------------------------- Плотоядный //Xi (t + 1) = Xi (t) + C * (Xi (t) - Xj (t)); if (r < 0.667) { C = u.LevyFlightDistribution (levisPower); j = u.RNDminusOne (i); //Xj = a [j].c [c]; Xj = a [j].cB [c]; //Xi = a [i].c [c]; Xi = a [i].cB [c]; //Xi = Xi + C * (Xi - Xj); Xi = Xi + C * (Xj - Xi); } // Omnivore behavior ----------------------------------------------- Всеядный //Xi (t + 1) = Xi (t) + C * r2 * (Xi (t) - Xb (t)) + // (1 - r2) * (Xi (t) - Xj (t)); else { C = u.LevyFlightDistribution (levisPower); Xb = cB [c]; j = u.RNDminusOne (i); //Xj = a [j].c [c]; Xj = a [j].cB [c]; //Xi = a [i].c [c]; Xi = a [i].cB [c]; r = u.RNDprobab (); //Xi = Xi + C * r * (Xi - Xb) + // (1 - r) * (Xi - Xj); Xi = Xi + C * r * (Xb - Xi) + (1 - r) * (Xj - Xi); } } a [i].c [c] = u.SeInDiSp (Xi, rangeMin [c], rangeMax [c], rangeStep [c]); } } } consModel++; return; } // Decomposition ------------------------------------------------------------- double D = 0.0; double h = 0.0; for (int i = 0; i < popSize; i++) { D = 3 * u.RNDprobab (); h = u.RNDprobab () * (u.RNDprobab () < 0.5 ? 1 : -1); C = u.LevyFlightDistribution (levisPower); j = u.RNDminusOne (popSize); for (int c = 0; c < coords; c++) { double x = a [i].cB [c] + D * (C * a [i].cB [c] - h * a [j].c [c]); a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } consModel = 0; } //——————————————————————————————————————————————————————————————————————————————
Результаты тестов
Теперь можем снова протестировать алгоритм с моими изменениями в логике.
AEO|Artificial Ecosystem-based Optimization Algorithm|50.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9137986747745103
25 Hilly's; Func runs: 10000; result: 0.4671288391599192
500 Hilly's; Func runs: 10000; result: 0.2647022528159094
=============================
5 Forest's; Func runs: 10000; result: 0.9022293417142482
25 Forest's; Func runs: 10000; result: 0.4370486099190667
500 Forest's; Func runs: 10000; result: 0.2139965996985526
=============================
5 Megacity's; Func runs: 10000; result: 0.6615384615384616
25 Megacity's; Func runs: 10000; result: 0.30799999999999994
500 Megacity's; Func runs: 10000; result: 0.28563076923076974
=============================
All score: 4.45407 (49.49%)
Обращает на себя внимание отсутствие значительного разброса результатов. Алгоритм успешно обходит локальные ловушки, хотя точность сходимости имеет средние значения. Также заметно "мигание" при переключении стадий, о котором мы говорили выше. Особенно необычно алгоритм ведет себя на дискретной функции Megacity, выделяя группы координат в отдельные вертикальные и диагональные линии, проходящие через значимые участки поверхности. Это отразилось и на результатах работы с этой дискретной функцией — они лучшие по рейтинговой таблице для дискретной функции с 1000 переменными.
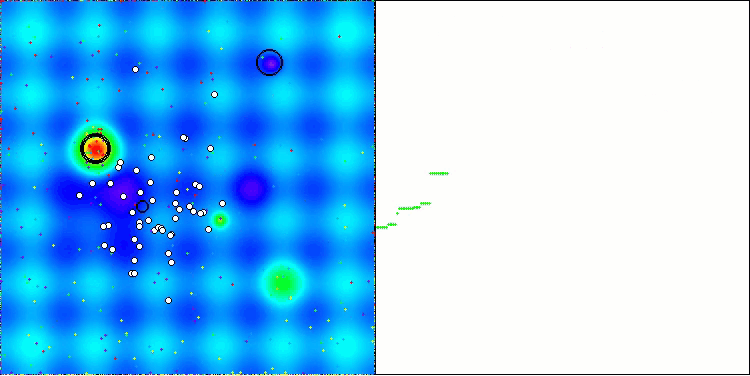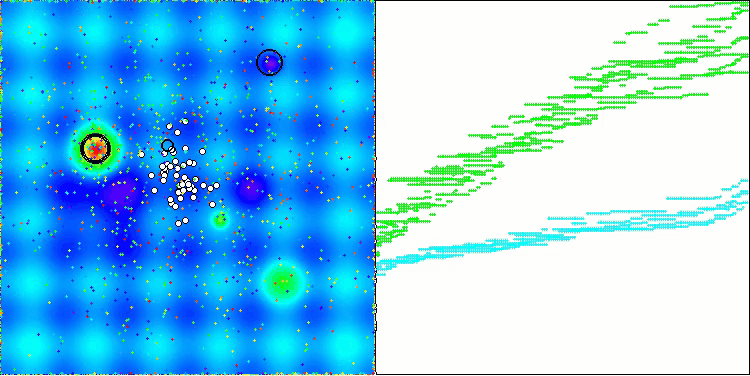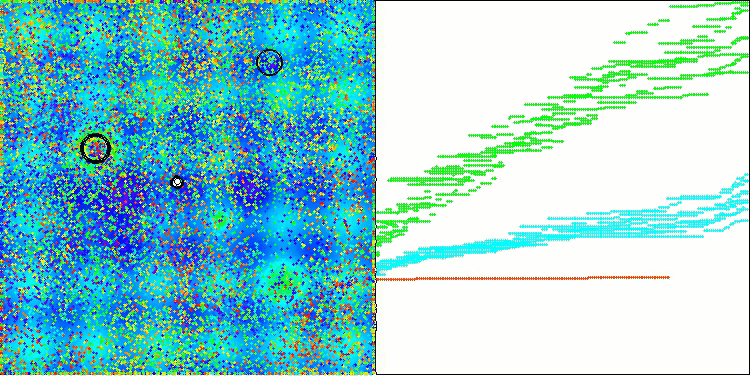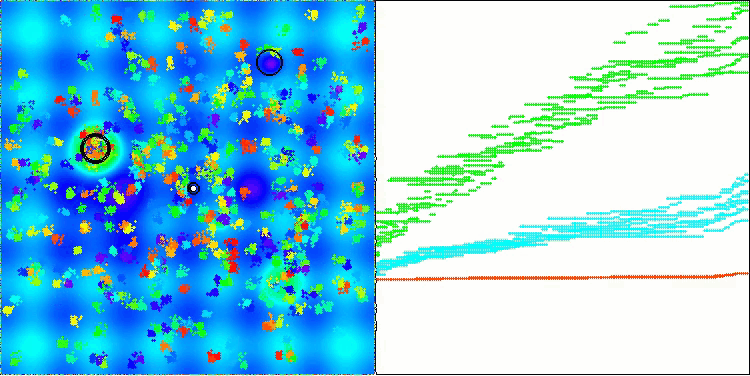
AEO на тестовой функции Hilly
AEO на тестовой функции Forest
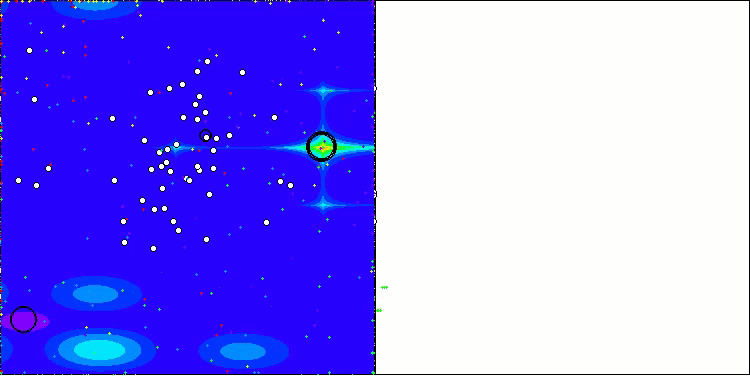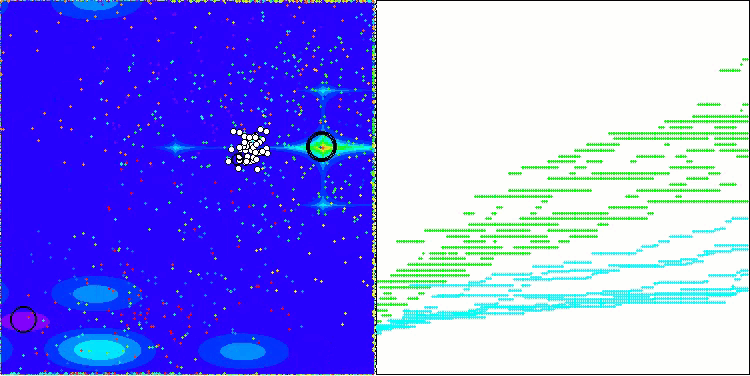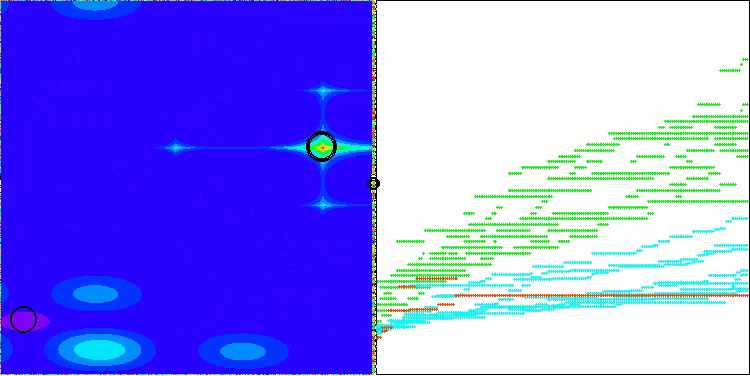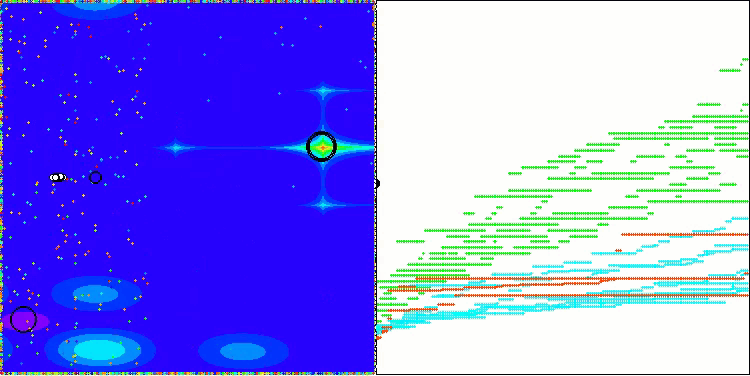
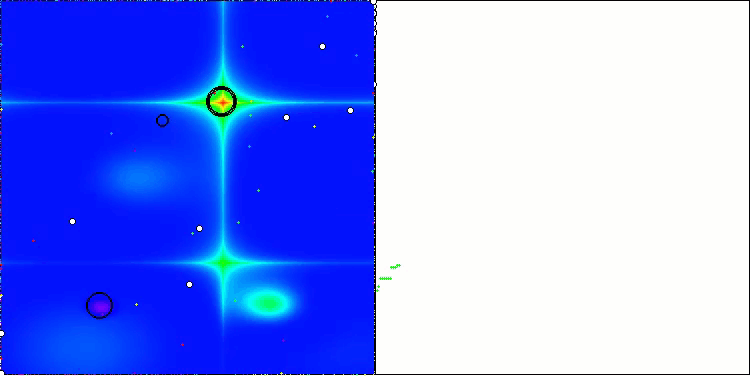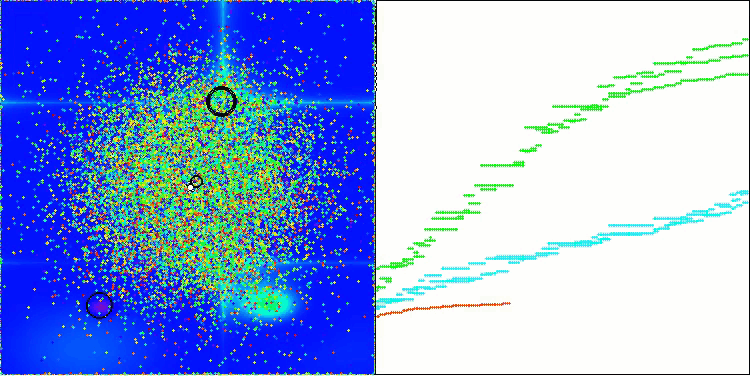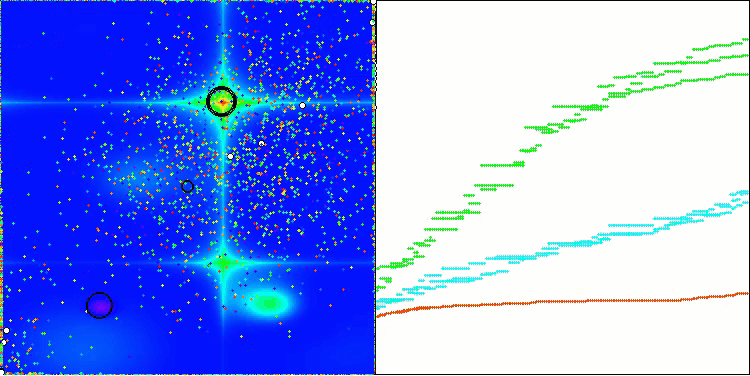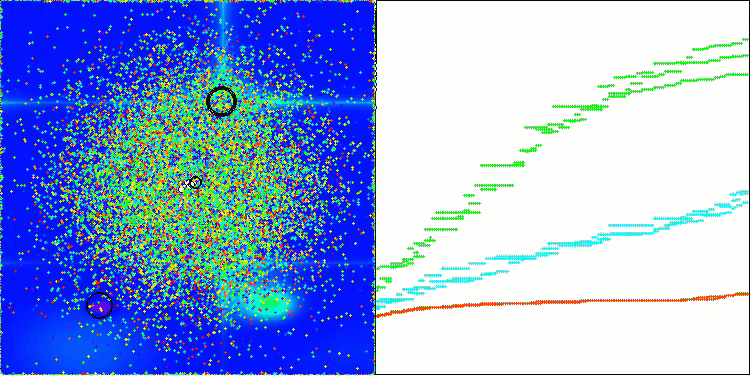
AEO на тестовой функции Megacity
Как можно заметить, алгоритм значительно улучшил свои показатели по сравнению с оригинальной версией и теперь достигает около 50% от максимально возможного. Это действительно впечатляющий результат! В рейтинговой таблице алгоритм занимает 25-е место, что тоже весьма достойно. Особенно впечатляет, что AEO установил новый рекорд по таблице на дискретной функции Megacity, улучшив результат с 1000 параметрами на целых 5%!
№ | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration optimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 12 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 13 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 14 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 15 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 16 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 17 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 18 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 19 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 20 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 21 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 22 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 23 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 24 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 25 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 26 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 27 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 28 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 29 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 30 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 31 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 32 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 33 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 34 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 35 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 36 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 37 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 38 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 39 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 40 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 41 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 42 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 43 | AAA | algae adaptive algorithm | 0,50007 | 0,32040 | 0,25525 | 1,07572 | 0,37021 | 0,22284 | 0,16785 | 0,76089 | 0,27846 | 0,14800 | 0,09755 | 0,52402 | 2,361 | 26,23 |
| 44 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 45 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
Выводы
Особенности и преимущества алгоритма:
1. Баланс между исследованием и эксплуатацией. AEO обеспечивает хороший баланс между глобальным исследованием пространства решений (через производство и потребление) и локальной эксплуатацией (через разложение).
2. Адаптивность. Алгоритм адаптируется к ландшафту задачи благодаря различным стратегиям обновления решений.
3. Простота. Несмотря на биологическую метафору, алгоритм относительно прост в реализации и понимании.
4. Отличные результаты работы на дискретных функциях большой размерности.
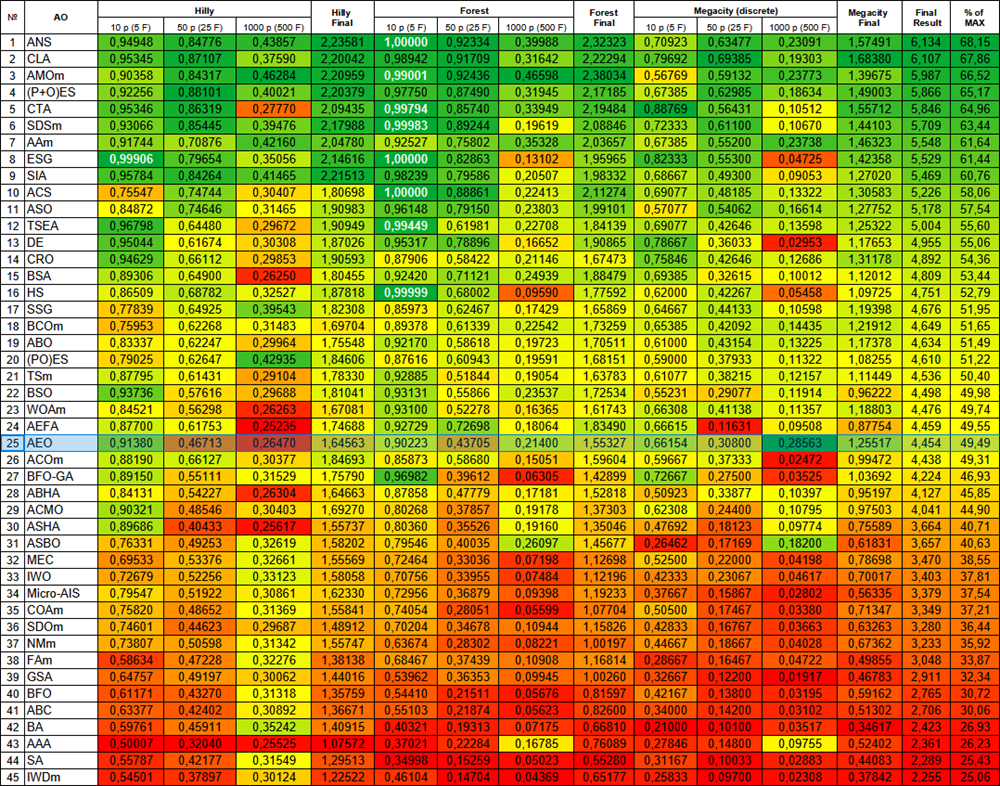
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам. Белым цветом подсвечены результаты больше или равные 0.99
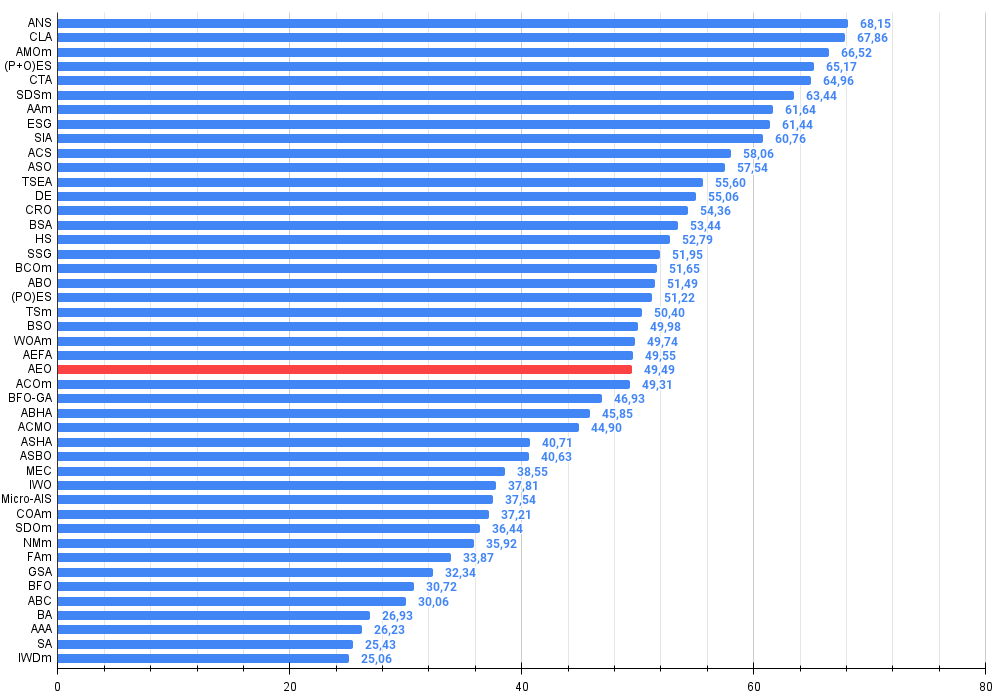
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,
где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма AEO:
Плюсы:
- Всего один внешний параметр (помимо размера популяции).
- Хорошо показал себя на дискретной функции.
Минусы:
- Не самая высокая точность сходимости.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Как опередить любой рынок (Часть II): Прогнозирование технических индикаторов
Как опередить любой рынок (Часть II): Прогнозирование технических индикаторов
 Нейронная сеть на практике: Псевдообратная (II)
Нейронная сеть на практике: Псевдообратная (II)
 Нейронная сеть на практике: Зарисовка нейрона
Нейронная сеть на практике: Зарисовка нейрона
 Стратегия Билла Вильямса с индикаторами и прогнозами и без них
Стратегия Билла Вильямса с индикаторами и прогнозами и без них
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования