MetaTrader 5 / 测试者
English Русский Español Deutsch 日本語 Português
preview
基于人工生态系统的优化（AEO）算法

基于人工生态系统的优化（AEO）算法

MetaTrader 5 — 测试者 | 2 六月 2025, 09:29
103 0
Andrey Dik
Andrey Dik


内容

  1. 概述
  2. 算法实现
  3. 测试结果


概述

在优化与人工智能（AI）领域，人们始终在不断探寻新颖且更高效的方法，以解决复杂问题。其中一种创新方法便是基于人工生态系统的优化算法（Artificial Ecosystem-based Optimization, AEO），该算法于2019年被提出并发展完善。该方法从自然生态系统中汲取灵感，模拟自然环境中发生的复杂相互作用与过程。

AEO算法基于自然界中观察到的若干关键原则。正如生态系统包含众多物种，每个物种都适应其特定的生态位一样，AEO算法也采用了一组多样化的解。在此背景下，每个解都可被视为一个具有独特特征和适应能力的独立“物种”。

在自然界中，能量通过食物链从一个生物体传递到另一个生物体。在AEO算法中，这是通过不同类型“智能体”（从“草”到“杂食动物”）之间的相互作用来模拟的。这里，信息如同能量一样，在解之间传递，这样有助于提升整个种群的质量。生态系统既存在资源竞争，也存在共生关系。AEO算法通过更新策略来体现这些过程，在此过程中，智能体可以通过“竞争”以获取更优的位置，或者通过交换信息来“合作”。

自然生态系统会经历周期性变化，这一点在AEO算法中也有所体现。迭代优化过程涉及消耗阶段与分解阶段的交替进行，这使得算法能够适应问题的动态变化。在自然界中，随机事件（如突变和自然灾害）与确定性过程（如自然选择）并存。AEO算法同时采用随机元素（如莱维分布）和确定性规则来更新解，在探索新区域与利用已发现区域之间取得平衡。

为了更好地理解自然过程如何在AEO算法中得到体现，让我们来看一些具体例子。在非洲大草原上，能量从草传递到斑马（草食动物），再传递到狮子（捕食者），最后传递到鬣狗（食腐动物）。在AEO算法中，关于最优解的信息从“草”（最差解）传递到“草食动物”（平均解）和“肉食动物”（最优解），这样有助于提升整个种群的质量。

当生物体死亡时，它们会分解，将营养物质返还给生态系统。例如，森林中的落叶会分解，使土壤肥沃，滋养新植物。在AEO算法中，分解阶段模拟了这一过程。在消耗（更新决策）阶段之后，是分解阶段，当前决策中的信息被“分解”并分布于整个搜索空间中。这使得算法能够探索新区域，并避免陷入局部最优解。在该算法中，这是通过对当前解相对于最优解（全局最优解作为分解者）应用高斯分布来实现的，这一点可以看作是搜索空间中信息的“分解”和“重新分配”。

因此，AEO算法是自然原理与数学优化的巧妙融合。它不仅为解决复杂问题提供了一种有效的方法，还为自然过程与人工智能之间的关系开辟了新的视角。接下来，我们将详细探讨该算法的结构和工作原理，以便更好地理解其潜力和应用。


算法实现

为了更好地理解AEO算法设计者的思路，请看图1，它展示了人工生态系统中生物体的层级结构。整个生态系统由生物体组成，这些生物体按惯例编号为1到Xn。编号为1的是“草”，它具有最大的能量（适应度函数值最小），而Xn则代表执行分解功能的腐生生物（能量最小，适应度函数值最大）。

在图中，箭头表示了摄食方向：草（编号为1）只能利用腐生生物的废弃物，草食动物（编号为2）以草为食，而编号为2、4和5的生物体可以是草食动物（仅吃草）、肉食动物（这些生物体只能捕食能量低于自身的生物）以及杂食动物（既可以吃草，也可以吃能量高于自身的生物）。生态系统的顶端由腐生生物占据，它们会在生物体生命周期结束时分解所有的生物体。

AEO

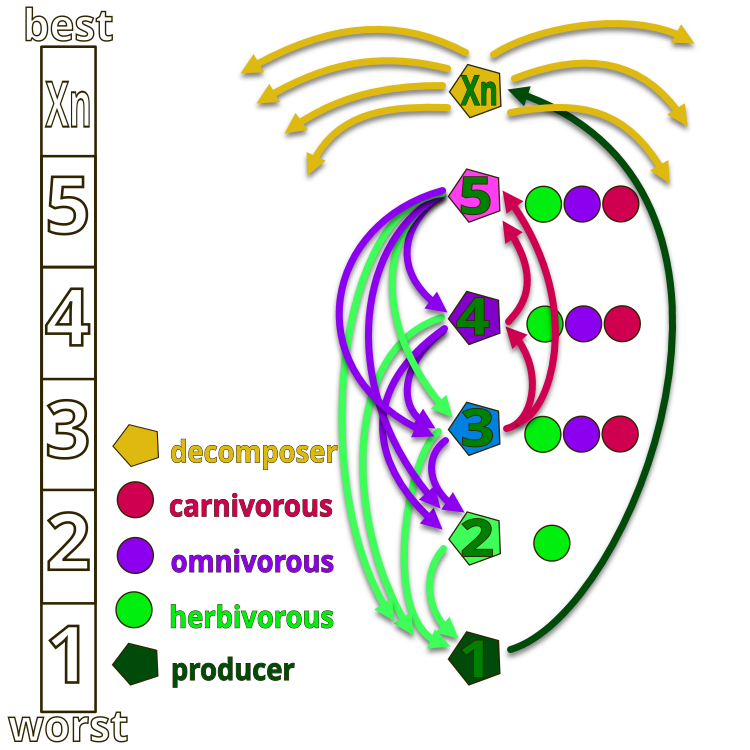
图例1. AEO算法中人工生态系统中生物的层级结构


该算法的主要思想是模拟生态系统组成部分之间的相互作用以解决优化问题。算法基于自然界中观察到的三个关键原则：

1. 生产——在自然界中，生产者（如植物）将太阳能转化为有机化合物。
2. 消费——消费者（食草动物、食肉动物、杂食动物）利用他人产生的能量，尤其是植物产生的能量。
3. 分解——腐生生物将复杂的有机物质分解为简单的物质，在算法中被建模为解的分解。

算法原理

1. 初始化——创建一个初始解的种群，代表生态系统。
2. 生产——在每次迭代中，通过考虑最优解和随机因素来更新最差解。
3. 消费——使用三种策略更新剩余的解：

  • 食草动物：基于生产者进行更新。
  • 食肉动物：基于随机选择的最佳解进行更新。
  • 杂食动物：基于生产者和随机解进行更新。

4. 分解——所有解都经历“分解”，这有助于改善全局搜索。
5. 选择——只有改进的解被保留，以确保种群的逐渐优化。

因此，该算法依赖于生物之间能量传递的机制，通过三个操作符——生产、消费和分解——帮助维持物种的稳定性。

1. 生产——种群中最差的个体X1通过在给定范围内添加随机生成的坐标Xrand ，相对于最优个体Xn进行更新，通过生产操作符创建一个新个体。数学表示：X1(t + 1) = (1 - a) * Xn(t) + a * Xrand(t)，其中a = (1 - t / T) * r1（t——当前迭代次数，T——总迭代次数），r1——[0; 1]范围内的随机数。在此情况下，可以省略r1这一部分，因为我们已经在方程中使用了随机坐标。

2. 消费——随机选择的消费者可以“吃掉”生产者以获取能量。定义消费因子C：C = 1/2 * (v1 / |v2|)，其中v1和v2是在[0; 1]范围内均匀分布的随机数。

  • 食草动物：Xi (t + 1) = Xi (t) + C * (Xi (t) - X1 (t))。
  • 食肉动物：Xi (t + 1) = Xi (t) + C * (Xi (t) - Xj (t))。
  • 杂食动物：Xi (t + 1) = Xi (t) + C * (r2 * Xi (t) + (1 - r2) * Xj (t))。

3. 分解——腐生生物分解死亡个体的残骸，为生产者提供养分。在腐生生物作用后个体位置的更新描述为：

Xi(t + 1) = Xn(t) + D * (e * Xn(t) - h * Xi(t))，其中 D = 3u，u ~ N(0, 1)，e = r3 * rand(i)，h = 2 * r3 - 1（r3，[0; 1]范围内的随机数）。

因此，在开始时生成一个随机种群，并且在每次迭代中，使用方程p.1更新第一个个体的位置。通过在方程p.2中以相等的概率选择，更新其他个体的位置。在分解阶段，每个个体使用方程p.3更新其位置。该过程一直持续至达到满意的终止条件为止。最后一步返回到目前为止找到的最优个体。

现在我们可以编写AEO算法的伪代码：

AEO（基于人工生态系统的优化）算法

初始化：
设置种群大小（popSize）
设置迭代次数（epochs）
设置莱维分布参数（levisPower）
在给定的范围内用随机解初始化种群
对每个解评估适应度函数
找到全局最优解cB。

对于从1到epochs的每个迭代：
// 消费阶段
对于种群中的每个智能体i：
如果i =0：
对当前解应用高斯分布。
否则，如果i = popSize - 1： 应用草的行为（GrassBehavior）
除此之外：
随机选择行为：
- 食草动物行为（HerbivoreBehavior）
- 食肉动物行为（CarnivoreBehavior）
- 杂食动物行为（OmnivoreBehavior）
    
// 分解阶段
对于种群中的每个智能体i：
对于每个c坐标：
选择一个随机智能体j
计算cB[c]和a[j].c[c]之间的距离D
使用高斯分布更新a[i].c[c]

//修订
对每个智能体评估适应度函数
更新每个智能体的最优个体解
更新全局最优解cB
按适应度函数值对种群进行排序

返回找到的全局最优解cB

子程序：

GrassBehavior (agent):
    α = (1 - current_epoch / total_number_of_epochs)
对于每个c坐标：
Xr = [min[c], max[c]]范围内的随机值。
        Xn = cB [c]
        X1 = Xn + α * (Xn - Xr)
agent.c[c] = X1（考虑限制条件）

HerbivoreBehavior (agent, coordinate_index):
    Xi = agent.cB [coordinate_index]
X1 =种群中给定坐标的最差解。
C =莱维分布的随机数（levisPower）
    Xi = Xi + C * (Xi - X1)
agent.c [coordinate_index] = Xi (考虑限制条件)

CarnivoreBehavior (agent, agent_index, coordinate_index):
    Xi = agent.cB [coordinate]
j = 随机索引 < agent_index
    Xj = a [j].cB [coordinate_index]
C =莱维分布的随机数（levisPower）
    Xi = Xi + C * (Xj - Xi)
agent.c [coordinate_index] = Xi (考虑限制条件)

OmnivoreBehavior (agent, agent_index, coordinate_index):
    Xi = agent.cB [coordinate]
X1 =种群中给定坐标的最差解。
j = 随机索引 > agent_index
    Xj = a [j].cB [coordinate_index]
C =莱维分布的随机数（levisPower）
r =0到1的随机数。
    Xi = Xi + C * r * (Xi - X1) + (1 - r) * (Xi - Xj)
agent.c [coordinate_index] = Xi (考虑限制条件)

在对算法进行了详细的描述和分析之后，让我们继续编写代码。

该算法使用莱维分布来在搜索空间中生成极为遥远但极为罕见的跳跃。我们以前也使用过这种随机数分布，例如在布谷鸟搜索算法中，但我们没有深入探讨其特性。关键在于，正确生成莱维分布需要使用四个均匀分布的随机数，这样本身代价就很大。此外，莱维分布具有无限长的尾部（它是不对称的，有一个尾部），这使得它在实际优化算法中难以使用，尤其是在存在边界条件的情况下。在生成过程中还需要检查边界条件，例如在计算自然对数之前检查是否为0，以及避免除以0。

以下是生成莱维分布随机数的代码，其缺少对于上述描述的检查，并且没有解释代码的逻辑：

double LevyFlight()
{
    const double epsilon = 1e-10; // Small value to avoid division by zero
    const double maxValue = 1e10; // Maximum allowed value

    double log1 = MathMax (RNDprobab(), epsilon);
    double log2 = MathMax (RNDprobab(), epsilon);

    double cos1 = MathCos (2 * M_PI * RNDprobab());
    double cos2 = MathCos (2 * M_PI * RNDprobab());

    double U = MathSqrt (-2.0 * MathLog (log1)) * cos1;
    double v = MathSqrt (-2.0 * MathLog (log2)) * cos2;

    double l = 0.5 * MathAbs(U) / MathMax(MathAbs(v), epsilon);

    return l;
}

为了消除生成莱维分布数字的缺点，我们来实现自己的函数LevyFlightDistribution，它具有接近莱维分布的特性，并将其放入标准函数集C_AO_Utilities中，以便在优化算法中使用。我们来将其分解：

1. levisPower参数是一个决定分布形状的指数。levisPower的值越高，分布就越“稀疏”。
2. 该函数负责计算将用于缩放的最小值。其取决于levisPower，计算为20^levisPower。3. 使用RNDfromCI函数在1到20的范围内生成“r”随机数。4. 应用指数——生成的数字“r”被提升到“-levisPower”的幂，从而改变其分布。5. 缩放结果——得到的“r”值被缩放到[0, 1]范围内。通过减去最小值并除以1与最小值之间的差值来实现。因此，结果将始终在[0, 1]范围内。6. 返回结果——函数返回生成的“r”值，该值的分布现在已接近莱维分布，偏向于0。

正如我们所见，该函数严格地限制在[0, 1]范围内生成随机数，这在实际应用中非常方便。通过应用适当的比率，此范围可以扩展到任何值。该函数速度更快，并且提供了非常接近所需分布的分布（相对于最大值的右侧）。 

//------------------------------------------------------------------------------
//A distribution function close to the Levy Flight distribution.
//The function generates numbers in the range [0.0;1.0], with the distribution shifted to 0.0.
double C_AO_Utilities :: LevyFlightDistribution (double levisPower)
{
  double min = pow (20, -levisPower); //calculate the minimum possible value
  double r = RNDfromCI (1.0, 20);     //generating a number in the range [1; 20]

  r = pow (r, -levisPower);           //we raise the number r to a power
  r = (r - min) / (1 - min);          //we scale the resulting number to [0; 1]

  return r;
}

让我们继续描述算法的主要代码。C_AO_AEO类是从C_AO派生的，并实现了该算法。让我们更详细地看一下它的结构、成员和方法。

构造函数：

  • 为种群大小和莱维指数设置默认值。
  • 创建参数数组params并初始化其值。

方法：

  • 从params 数组中设置popSize和levisPower参数。
  • Init()通过设置指定的搜索范围和迭代次数来初始化算法。该方法返回bool类型，这意味着要检查初始化是否成功。
  • Moving ()方法处理当前迭代中智能体的移动，同时更新它们的坐标。
  • Revision ()方法更新有关智能体及其最优决策的信息。

私有成员和变量：

  • levisPower——在莱维分布中使用的参数。
  • epochs——总迭代次数。
  • epochNow——当前迭代。
  • consModel ——阶段（消费或分解）。

S_AO_Agent aT []——用于对种群进行排序的智能体临时数组。

私有方法：

  • GrassBehavior ()——处理“草”智能体的行为。
  • HerbivoreBehavior()——处理“吃草”（最差智能体）的食草动物智能体的行为。
  • CarnivoreBehavior ()——处理“吃掉”具有更高适应度函数值智能体的食肉动物智能体的行为。
  • OmnivoreBehavior ()——处理杂食动物智能体的行为，结合了食草动物的行为和“吃掉”任何适应度较低的智能体的行为。

C_AO_AEO类提供了基于人工生态系统的优化算法的实现，使用不同类型的智能体及其相互作用来寻找最优解。每个方法都负责算法的某些方面，包括初始化、智能体的移动以及更新它们的状态。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AEO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AEO () { }
  C_AO_AEO ()
  {
    ao_name = "AEOm";
    ao_desc = "Artificial Ecosystem-based Optimization Algorithm";
    ao_link = "https://www.mql5.com/en/articles/16058";


    popSize    = 50;       // population size
    levisPower = 2;

    ArrayResize (params, 2);

    params [0].name = "popSize";    params [0].val = popSize;
    params [1].name = "levisPower"; params [1].val = levisPower;
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;
    levisPower = params      [1].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum search range
             const double &rangeMaxP  [],  // maximum search range
             const double &rangeStepP [],  // step search
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double levisPower;


  private: //-------------------------------------------------------------------
  int  epochs;
  int  epochNow;
  int  consModel; // consumption model;
  S_AO_Agent aT [];

  void GrassBehavior     (S_AO_Agent &animal);
  void HerbivoreBehavior (S_AO_Agent &animal, int indCoord);
  void CarnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord);
  void OmnivoreBehavior  (S_AO_Agent &animal, int indAnimal, int indCoord);
};
//——————————————————————————————————————————————————————————————————————————————

让我们更详细地看看C_AO_AEO类的Init方法代码。Init方法返回bool类型的值，使我们能够确定初始化是否成功。标准初始化检查：这里调用了StandardInit方法，其执行传递给该方法参数的基本初始化。如果StandardInit返回false，这意味着初始化失败，Init方法也返回false。

设置变量：

  • epochs ——设置从epochsP参数获得的总迭代次数。
  • epochNow——将当前迭代初始化为0，表示算法刚刚开始。
  • consModel ——将模型的值设置为0，以便后续可以从一个阶段移动到另一个阶段。

将临时智能体数组aT的大小调整为popSize。

返回结果：如果所有前面的操作都成功，该方法返回true，表示初始化成功。

C_AO_AEO类的Init方法负责算法的初始设置。它检查默认参数，设置迭代次数和初始阶段的值，并准备智能体数组以供使用。如果所有的阶段都成功完结，该方法返回true，表示算法已准备好执行。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AEO::Init (const double &rangeMinP [],
                     const double &rangeMaxP [],
                     const double &rangeStepP [],
                     const int epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs    = epochsP;
  epochNow  = 0;
  consModel = 0;
  ArrayResize (aT, popSize);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

让我们分析C_AO_AEO类的Moving方法代码。该方法的总体结构：Moving负责根据当前迭代和消费模型更新智能体（个体）种群的状态。其分为几个逻辑块：

1. 增加迭代次数：epochNow++增加当前迭代计数器。

2. 首次初始化：

  • 如果revision为false，则对种群中智能体的坐标进行首次初始化。坐标从给定范围内随机选择，然后四舍五入到最接近的值，该值对应于步长。
  • 之后，将revision设置为true，方法执行完成。

3. 消费模型：

  • 如果consModel为0，则根据智能体的行为更新其坐标。 
  • 对于第一个智能体（索引0），使用高斯分布初始化坐标。
  • 对于其余智能体，其行为取决于它们的索引：最后一个智能体（索引popSize - 1）调用GrassBehavior函数。对于倒数第二个及之前的智能体（索引popSize - 2及以下），其行为随机确定：可能是食草动物、食肉动物或杂食动物。

4. 分解：如果 consModel不等于0，则发生分解，其中每个智能体的坐标根据随机值和高斯分布进行更新。对于每个坐标，选择另一个智能体的随机索引，并基于此值计算新的坐标，同时考虑最小值和最大值边界。

Moving方法实现了与智能体坐标变化相关的逻辑，这些变化取决于它们的行为和当前迭代。包括首次初始化以及根据其消费模式更新智能体的状态。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  // Consumption ---------------------------------------------------------------
  if (consModel == 0)
  {
    double r = 0.0;

    for (int i = 0; i < popSize; i++)
    {
      if (i == 0)
      {
        for (int c = 0; c < coords; c++)
        {
          a [i].c [c] = u.GaussDistribution (a [i].c [c], rangeMin [c], rangeMax [c], 8);
          a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }

        continue;
      }

      if (i == popSize - 1) GrassBehavior (a [i]);
      else
      {
        if (i >= popSize - 2)
        {
          for (int c = 0; c < coords; c++)
          {
            r = u.RNDprobab ();

            if (r < 0.333) HerbivoreBehavior (a [i], c);
            else
            {
              if (r < 0.667)
              {
                CarnivoreBehavior (a [i], i, c);
              }
              else
              {
                OmnivoreBehavior (a [i], i, c);
              }
            }
          }
        }
        else
        {
          for (int c = 0; c < coords; c++)
          {
            r = u.RNDprobab ();

            if (r < 0.5) CarnivoreBehavior (a [i], i, c);
            else         OmnivoreBehavior  (a [i], i, c);
          }
        }
      }
    }

    consModel++;
    return;
  }

  // Decomposition -------------------------------------------------------------
  int    j   = 0;
  double D   = 0.0;
  double min = 0.0;
  double max = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      j = u.RNDminusOne (popSize);
      D = 3.0 * (cB [c] - a [j].c [c]); // * u.RNDprobab ();
      min = cB [c] - D;
      max = cB [c] + D;

      if (min < rangeMin [c]) min = u.RNDfromCI (rangeMin [c], cB [c]);
      if (max > rangeMax [c]) min = u.RNDfromCI (cB [c], rangeMax [c]);

      a [i].c [c] = u.GaussDistribution (cB [c], min, max, 1);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  consModel = 0;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEO类中的Revision方法负责更新种群中最优智能体的信息。其实现了允许在算法执行过程中跟踪和存储找到的最优解决方案的逻辑。该方法的结构如下：

1. 寻找最优智能体：

  • 遍历种群中的所有智能体。
  • 将它们的适应度（f值）与当前最佳适应度fB进行比较。
  • 如果找到适应度更好的智能体，则更新fB并记住其索引。

2. 复制最优智能体的坐标：如果找到了最优智能体（索引不等于-1），将其坐标复制到存储当前最佳坐标的cB数组中。

3. 更新智能体的个人最优适应度：再次遍历所有智能体，检查它们的当前适应度是否超过了其个人的最优适应度（fB）。如果是这样，更新它们的个人最优适应度，并将其当前坐标复制到cB中。

4. 对智能体进行排序：最后，我们调用排序函数，根据它们的个人最优适应度值对智能体进行排序。

Revision方法是算法的一个重要组成部分，因为它确保在工作过程中找到的最优解决方案被跟踪和保存。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEO类中的GrassBehavior方法实现了基于“食草动物”概念的智能体行为，象征着在空间中寻找新的解决方案。方法结构：

1. 计算α比率的公式为(1.0 - (double) epochNow / epochs)，这意味着随着迭代次数的增加，α会逐渐减小。这样使得算法在开始时更积极地探索空间，然后专注于改进它找到的解。

2. 变量初始化：

  • X1 ——食草动物智能体的当前坐标。
  • Xn ——腐生生物的当前坐标。
  • Xr ——从给定范围内选择的随机坐标。

3. 按坐标循环：对于每个智能体的坐标：

  • 在指定范围[Xmin, Xmax]内生成Xr随机值。
  • 从存储当前全局最优坐标（腐生生物在空间中的位置）的cB数组中取出当前坐标Xn。
  • 根据公式X1 = Xn + α * (Xn - Xr)计算X1的新坐标，使得当前值与随机值混合，并随着迭代次数的增加而减少随机性的影响。
  • 最后，使用SeInDiSp函数将新坐标限制在给定范围内。

//——————————————————————————————————————————————————————————————————————————————
// Grass
// (Worst) X1 X2 X3 ...... Xn (Best)
// X1(t+1) = (1 - α) * Xn(t) + α * Xrnd (t)
// α = (1 - t / T) * rnd [0.0; 1.0]
// Xrnd = rnd [Xmin; Xmax]

void C_AO_AEO::GrassBehavior (S_AO_Agent &animal)
{
  //0) (1 - α) * Xn + α * Xrnd
  //1) Xn - α * Xn + α * Xrnd
  //2) Xn + α * (Xrnd - Xn)

  double α = (1.0 - (double)epochNow / epochs);

  double X1 = 0.0;
  double Xn = 0.0;
  double Xr = 0.0;

  for (int c = 0; c < coords; c++)
  {
    Xr = u.RNDfromCI (rangeMin [c], rangeMax [c]);
    Xn = cB [c];

    //X1 = Xn + α * (Xr - Xn);
    X1 = Xn + α * (Xn - Xr);

    animal.c [c] = u.SeInDiSp (X1, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEO类中的HerbivoreBehavior方法实现了食草动物智能体的行为。方法结构：

1. 变量初始化：

  • Xi ——将要更新的智能体的当前坐标。
  • X1 ——种群中最差智能体的坐标，对应于最大能量（或最低适应度）。
  • C ——使用莱维分布生成的随机值。

2. 坐标更新：Xi坐标根据以下方程更新：Xi(t+1) = Xi(t) + C ⋅ (Xi(t) - X1(t))。该方程意味着智能体根据其当前坐标与最差智能体坐标之间的差异来改变其坐标。这使得食草动物可以“食用”最差的智能体，即探索甚至不那么有希望的搜索区域。

3. 坐标限制：更新Xi坐标后，使用SeInDiSp函数将其限制在给定范围内，该函数以新值、最小值和最大值限制以及步长作为参数。

HerbivoreBehavior方法展示了食草动物智能体如何通过“食用”种群中最差的成员来适应。

//——————————————————————————————————————————————————————————————————————————————
// Herbivore
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * (Xi(t) - X1(t)) for i ∈ [2, n]
// Herbivore eats only the one with the highest energy (eats the one with the worst FF)
void C_AO_AEO::HerbivoreBehavior (S_AO_Agent &animal, int indCoord)
{
  double Xi = animal.c [indCoord];
  double X1 = a [popSize - 1].c [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);

  Xi = Xi + C * (Xi - X1);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEO 类中的CarnivoreBehavior 方法实现了算法框架内的食肉动物智能体的行为。方法结构：

1. 变量初始化：

  • Xi ——将要更新的食肉动物智能体的当前坐标。
  • j ——随机选择的牺牲智能体的索引（食肉动物“吃掉”能量较少但适应度更好的智能体）。
  • Xj ——猎物的坐标，将用于更新食肉动物的坐标。
  • C ——使用莱维分布生成的随机值。

2. 坐标更新：Xi坐标根据以下方程更新：Xi(t+1) = Xi(t) + C * (Xj(t) - Xi(t))。该方程意味着食肉动物智能体根据猎物坐标与其当前坐标之间的差异来改变其坐标。这使得食肉动物可以“吃掉”猎物，从而改善其特性。

3. 坐标限制：更新Xi坐标后，使用SeInDiSp函数将其限制在给定范围内。

CarnivoreBehavior方法展示了食肉动物智能体如何通过“吃掉”能量较少的猎物来适应。这使它们能够改善其表现，努力追求更优的解决方案。 

//——————————————————————————————————————————————————————————————————————————————
// Carnivorous
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * (Xi(t) - Xj(t)) for i ∈ [3, n]
// Carnivore eats those with less energy (eats those with higher FF)
void C_AO_AEO::CarnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord)
{
  //double Xi = animal.c [indCoord];
  double Xi = animal.cB [indCoord];
  int    j  = u.RNDminusOne (indAnimal);
  //double Xj = a [j].c [indCoord];
  double Xj = a [j].cB [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);

  //Xi = Xi + C * (Xi - Xj);
  Xi = Xi + C * (Xj - Xi);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEO类中的OmnivoreBehavior方法描述了在进化算法背景下杂食动物智能体的行为。方法结构：

1. 变量初始化：

  • Xi ——需要更新的杂食动物智能体的当前坐标。
  • X1——最差智能体的坐标（能量最高的智能体）。
  • j ——从种群中随机选择的另一个智能体的索引，将用于更新坐标。
  • Xj ——另一个选定的智能体的坐标。
  • C ——使用莱维分布生成的随机值。
  • r ——将用于混合坐标更新的随机概率。

2. 坐标更新：Xi坐标根据以下方程更新：Xi(t+1) = Xi(t) + C * r * (Xi(t) - X1(t)) + (1 - r) * (Xi(t) - Xj(t))。该方程允许杂食动物智能体通过“食用”最差智能体（能量最高）和另一个适应度较低的随机智能体来适应，使其行为更加灵活。

3. 坐标限制：更新Xi坐标后，使用SeInDiSp函数将其限制在指定的约束范围内。

OmnivoreBehavior方法展示了杂食动物智能体如何通过利用不同的能量来源（包括最差的智能体和适应度较低的随机选择的其他智能体）来适应并受益。

//——————————————————————————————————————————————————————————————————————————————
// Omnivorous
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * r2 * (Xi(t) - X1(t)) + (1 - r2) * (Xi(t) - Xj(t)) for i ∈ [3, n]
// An omnivore eats everyone who has more energy (grass and small animals, that is, those who have worse FF)
void C_AO_AEO::OmnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord)
{
  //double Xi = animal.c [indCoord];
  double Xi = animal.cB [indCoord];
  //double X1 = a [popSize - 1].c [indCoord];
  double X1 = a [popSize - 1].cB [indCoord];
  int    j  = u.RNDintInRange (indAnimal + 1, popSize - 1);
  //double Xj = a [j].c [indCoord];
  double Xj = a [j].cB [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);
  double r  = u.RNDprobab ();

  Xi = Xi + C * r * (Xi - X1) + (1.0 - r) * (Xi - Xj);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

现在我们已经实现了算法的代码，终于可以开始在测试函数上进行测试了。

AEO|Artificial Ecosystem-based Optimization Algorithm|50.0|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.6991675795357223
25 Hilly's; Func runs: 10000; result: 0.34855292688850514
500 Hilly's; Func runs: 10000; result: 0.253085011547826
=============================
5 Forest's; Func runs: 10000; result: 0.6907505745478882
25 Forest's; Func runs: 10000; result: 0.23365521509528495
500 Forest's; Func runs: 10000; result: 0.1558073538195803
=============================
5 Megacity's; Func runs: 10000; result: 0.5430769230769231
25 Megacity's; Func runs: 10000; result: 0.20676923076923082
500 Megacity's; Func runs: 10000; result: 0.1004461538461546
=============================
总分：3.23131 (35.90%)

在测试过程中，该算法的得分为大约36%。这是一个平均结果。对于该算法，我决定修改Moving方法中的智能体移动逻辑，以下是修改后的内容：

在Moving方法中考虑不同行为模型（生产、消费和分解）的智能体移动逻辑，修改如下：

1. 原始种群的初始化保持不变。

2. 更新α比率的计算方式为当前迭代次数的函数，随着epochNow的增加而减小。该比率被移至一个单独的私有方法之外。

3. 生产（consModel = 0）——在这个部分中，智能体使用基于前一个状态和随机值的方程更新它们的坐标。这使它们能够“生产”新的状态。

4. 消费（consModel =1）。这里，我们根据随机值将智能体分为三组：

  • 食草动物。
  • 食肉动物。
  • 杂食动物。

5. 分解：在此阶段，智能体相互交互，根据随机值和与其他智能体的交互改变其坐标。

6. 重置消费模型：在consModel结束时，将其设置为0 以开始一个新的循环。

正如您所看到的，算法逻辑的主要变化是将生产分配到一个单独的阶段。为此分配了一个单独的迭代，使得生物种群发生了严重的动荡。这也反映在AEO可视化过程中的行为上：我们可以看到“闪烁”，也就是说，即使从视觉上也能注意到人工生态系统中的各个阶段。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double α = (1.0 - (double)epochNow / epochs);

  double Xi   = 0.0;
  double Xb   = 0.0;
  double Xr   = 0.0;
  double Xj   = 0.0;
  double C    = 0.0;
  int    j    = 0;
  double r    = 0.0;

  // Production --------------------------------------------------------------
  // X(t + 1) = (1 - α) * Xb(t) + α * Xrnd (t)
  // α = (1 - t / T) * rnd [0.0; 1.0]
  // Xrnd = rnd [Xmin; Xmax]
  if (consModel == 0)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        Xb = cB [c];
        Xr = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        //Xi = Xb + α * (Xr - Xb);
        Xi = Xb + α * (Xb - Xr);

        a [i].c [c] = u.SeInDiSp (Xi, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    consModel++;
    return;
  }

  // Consumption --------------------------------------------------------------- 
  if (consModel == 1)
  {
    for (int i = 0; i < popSize; i++)
    {
      if (i > 1)
      {
        for (int c = 0; c < coords; c++)
        {
          r = u.RNDprobab ();

          // Herbivore behavior ------------------------------------------------ 
          //Xi (t + 1) = Xi (t) + C * (Xi (t) - Xb (t));
          if (r < 0.333)
          {
            C  = u.LevyFlightDistribution (levisPower);
            Xb = cB [c];
            //Xi = a [i].c [c];
            Xi = a [i].cB [c];

            //Xi = Xi + C * (Xi - Xb);
            Xi = Xi + C * (Xb - Xi);
          }
          else
          {
            // Carnivore behavior ---------------------------------------------- 
            //Xi (t + 1) = Xi (t) + C * (Xi (t) - Xj (t));
            if (r < 0.667)
            {
              C  = u.LevyFlightDistribution (levisPower);
              j  = u.RNDminusOne (i);
              //Xj = a [j].c [c];
              Xj = a [j].cB [c];
              //Xi = a [i].c [c];
              Xi = a [i].cB [c];

              //Xi = Xi + C * (Xi - Xj);
              Xi = Xi + C * (Xj - Xi);
            }
            // Omnivore behavior ----------------------------------------------- 
            //Xi (t + 1) = Xi (t) + C * r2 * (Xi (t) - Xb (t)) +
            //                    (1 - r2) * (Xi (t) - Xj (t));
            else
            {
              C  = u.LevyFlightDistribution (levisPower);
              Xb = cB [c];
              j  = u.RNDminusOne (i);
              //Xj = a [j].c [c];
              Xj = a [j].cB [c];
              //Xi = a [i].c [c];
              Xi = a [i].cB [c];
              r = u.RNDprobab ();

              //Xi = Xi + C * r * (Xi - Xb) +
              //     (1 - r) * (Xi - Xj);
              Xi = Xi + C * r * (Xb - Xi) +
                   (1 - r) * (Xj - Xi);
            }
          }

          a [i].c [c] = u.SeInDiSp (Xi, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }
    }

    consModel++;
    return;
  }

  // Decomposition -------------------------------------------------------------
  double D = 0.0;
  double h = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    D = 3 * u.RNDprobab ();
    h = u.RNDprobab () * (u.RNDprobab () < 0.5 ? 1 : -1);
    C = u.LevyFlightDistribution (levisPower);
    j = u.RNDminusOne (popSize);

    for (int c = 0; c < coords; c++)
    {
      double x = a [i].cB [c] + D * (C * a [i].cB [c] - h * a [j].c [c]);
      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  consModel = 0;
}
//——————————————————————————————————————————————————————————————————————————————


测试结果

现在我们可以再次测试算法，看看我对逻辑的修改是否有效。 

AEO|Artificial Ecosystem-based Optimization Algorithm|50.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9137986747745103
25 Hilly's; Func runs: 10000; result: 0.4671288391599192
500 Hilly's; Func runs: 10000; result: 0.2647022528159094
=============================
5 Forest's; Func runs: 10000; result: 0.9022293417142482
25 Forest's; Func runs: 10000; result: 0.4370486099190667
500 Forest's; Func runs: 10000; result: 0.2139965996985526
=============================
5 Megacity's; Func runs: 10000; result: 0.6615384615384616
25 Megacity's; Func runs: 10000; result: 0.30799999999999994
500 Megacity's; Func runs: 10000; result: 0.28563076923076974
=============================
总分：4.45407 (49.49%)

值得注意的是，结果没有显著的分散。该算法成功地避免了局部陷阱，尽管其收敛精度是平均的。我们还可以注意到在阶段切换时已经提到的“闪烁”。该算法在离散的Megacity函数上展示出最不寻常的行为，将坐标组分离成通过表面重要区域的单独垂直和对角线。这也在处理这个离散函数的结果中得到反映——它们在1000个变量的离散函数的排名表中是最好的。

Hilly值

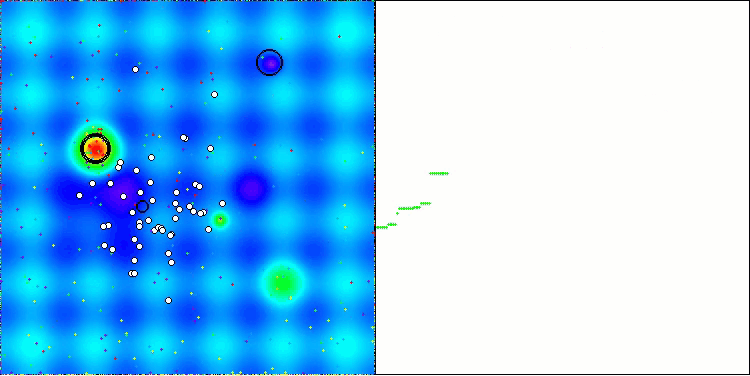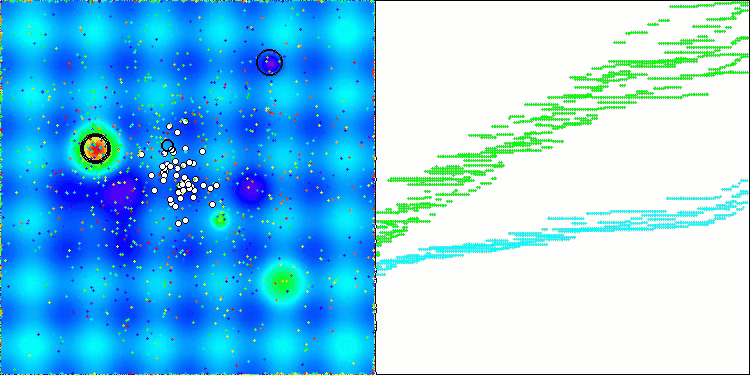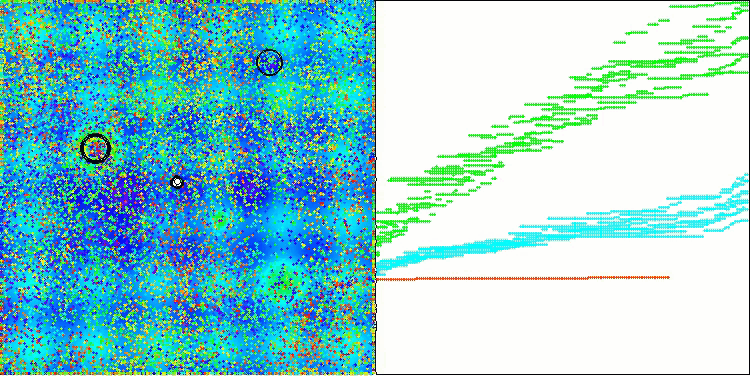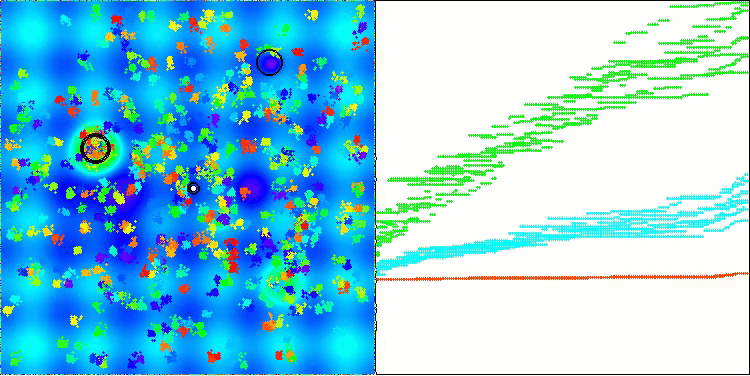
AEO在Hilly测试函数上

Forest值

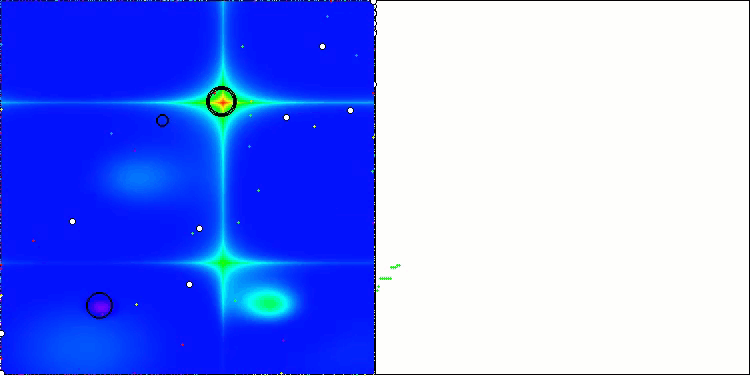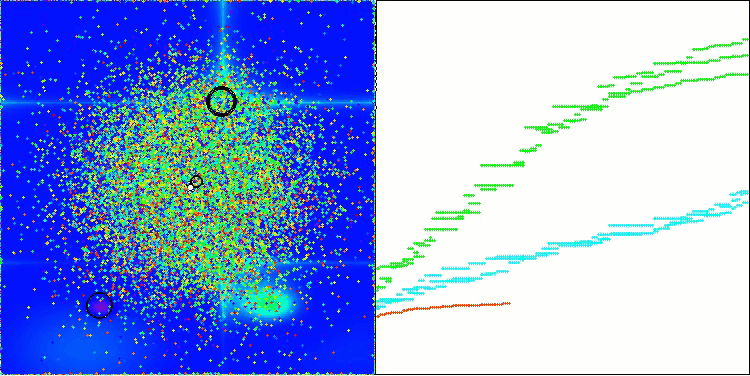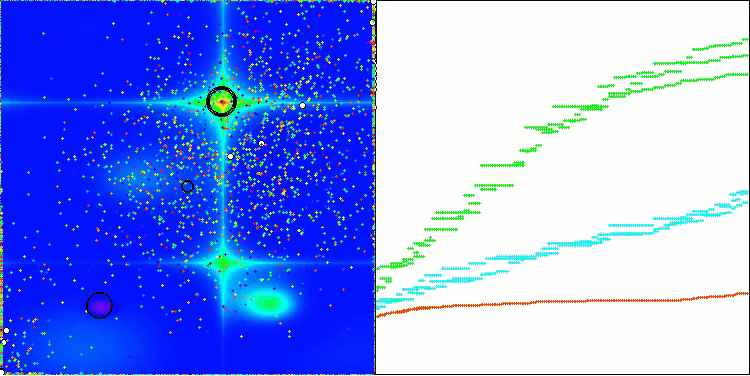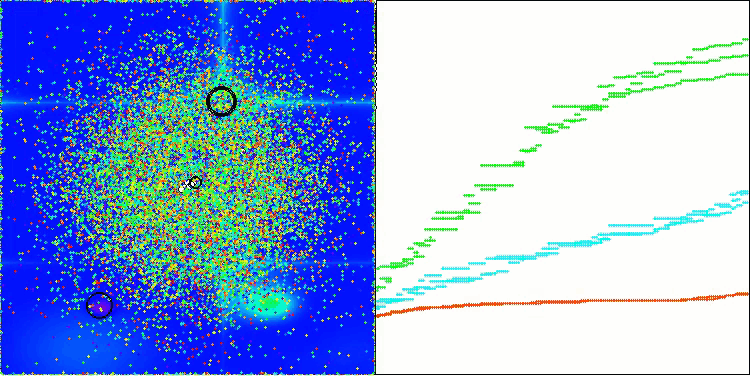
AEO在Forest测试函数上

Megacity

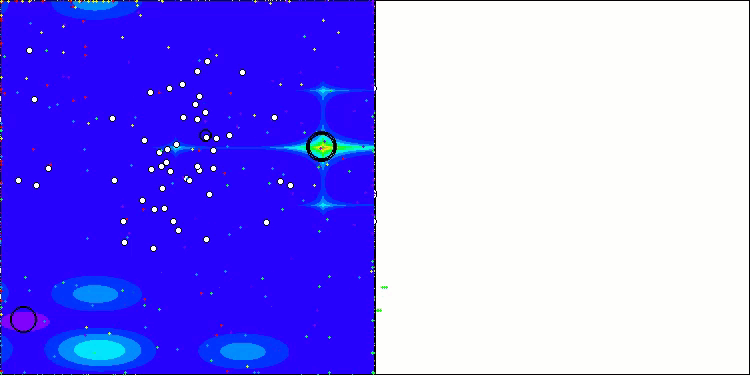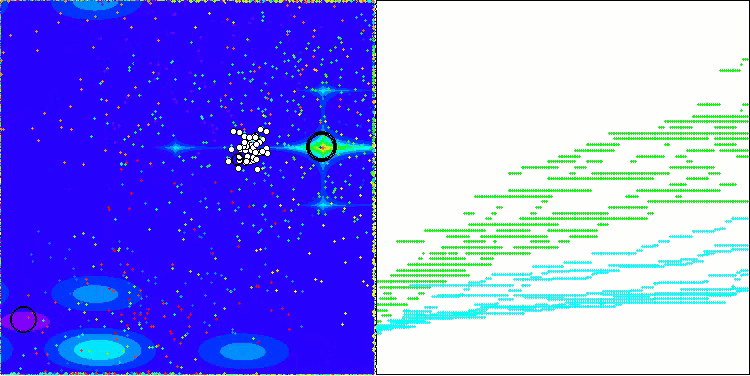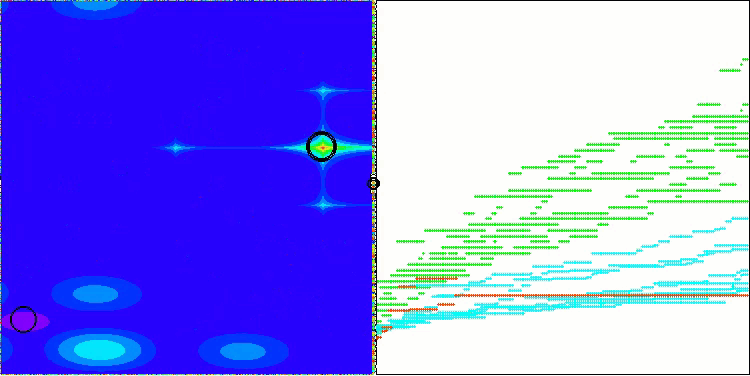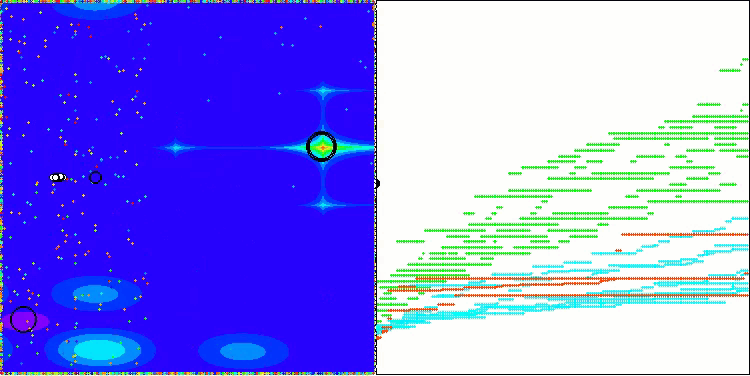
AEO在Megacity测试函数上

正如您所见，与原始版本相比，该算法的性能有了显著提升，现在达到了最大可能值的约50%。这真是一个令人鼓舞的结果！在排名表中，该算法位列第25位，这也是相当值得肯定的。特别令人印象深刻的是，AEO在Megacity离散函数上创下了新的纪录，将1000个参数的结果提高了惊人的5%！

#
AO
说明
Hilly值
Hilly最终值
Forest值
Forest最终值
Megacity (离散)
Megacity最终值
最终结果
最大百分比
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 ANS 跨邻域搜索 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
2 CLA 密码锁算法 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
3 AMOm 动物迁徙优化M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
4 (P+O)ES (P+O) 进化策略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA 彗星尾算法 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 AAm 射箭算法M 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
8 ESG 社会群体的进化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
9 SIA 模拟各向同性退火 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
10 ACS 人工协同搜索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
11 ASO 无序社会优化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
12 TSEA 龟壳演化算法 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
13 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
14 CRO 化学反应优化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
15 BSA 鸟群算法 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
16 HS 和声搜索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
17 SSG 树苗播种和生长 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
18 BCOm 细菌趋化性优化算法M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
19 ABO 非洲水牛优化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
20 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
21 TSm 禁忌搜索M 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
22 BSO 头脑风暴优化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
23 WOAm 鲸鱼优化算法M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
24 AEFA 人工电场算法 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
25 AEO 人工生态系统的优化算法 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
26 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
27 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
28 ABHA 人工蜂巢算法 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
29 ACMO 大气云模型优化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
30 ASHA 人工淋浴算法 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
31 ASBO 适应性社会行为优化 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
32 MEC 思维进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
33 IWO 入侵杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
34 Micro-AIS 微型人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
35 COAm 布谷鸟优化算法 M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
36 SDOm 螺旋动力学优化 M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
37 NMm Nelder-Mead方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
38 FAm 萤火虫算法 M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
39 GSA 引力搜索算法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
40 BFO 细菌觅食优化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
41 ABC 人工蜂群 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
42 BA 蝙蝠算法 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
43 AAA 人工藻类算法 0.50007 0.32040 0.25525 1.07572 0.37021 0.22284 0.16785 0.76089 0.27846 0.14800 0.09755 0.52402 2.361 26.23
44 SA 模拟退火 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
45 IWDm 智能水滴 M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06


总结

算法的特点和优势：

1. 探索与利用的平衡。AEO在全局探索解空间（通过生产和消费）与局部利用（通过分解）之间提供了良好的平衡。

2. 适应性。该算法通过不同的解更新策略来适应问题特性。

3. 简单性。尽管使用了生物学上的类比，但该算法相对容易实现和理解。

4. 在大维度离散函数上表现出色。

tab

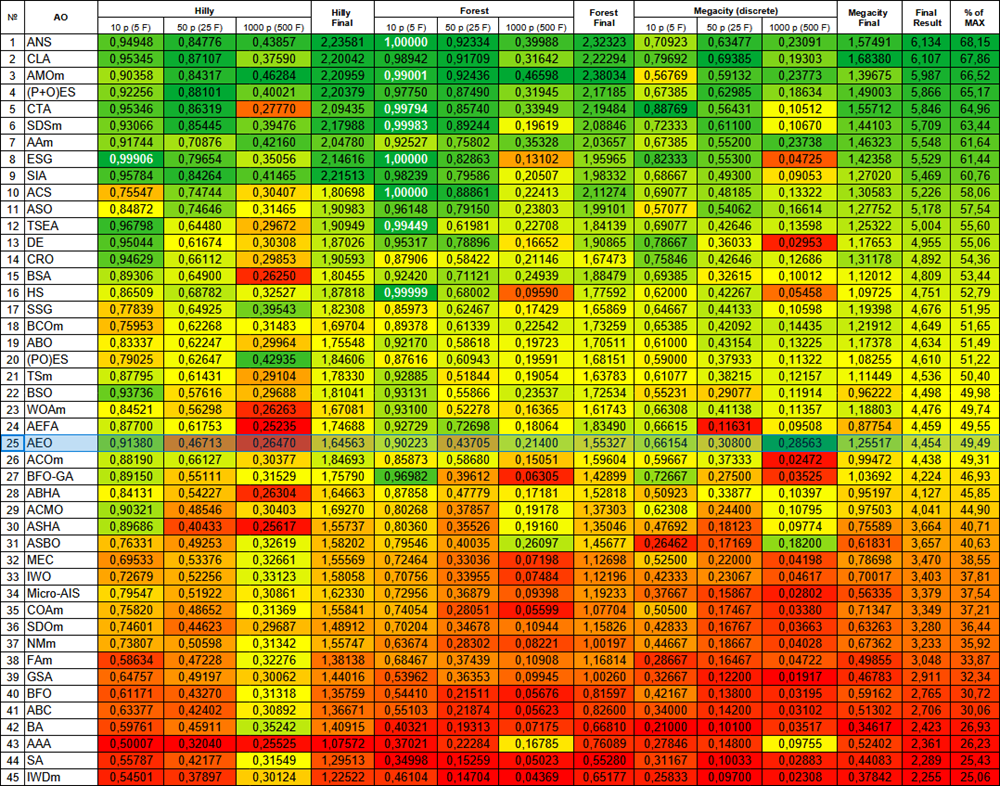
图例2. 根据相关测试，将算法的颜色等级大于或等于0.99的结果以白色突出显示。

图表

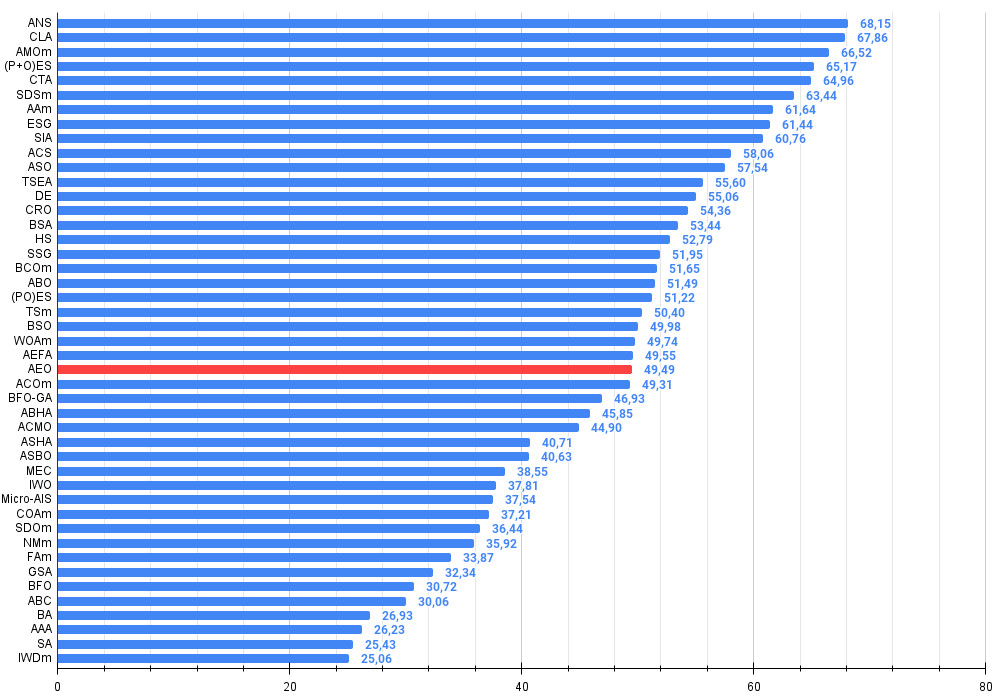
图例 3. 算法测试结果的直方图（标尺从 0 到 100，数字越大结果越好，

其中 100 是理论上的最大可能结果，将计算评级表格的脚本存档）

AEO的优缺点：

优点：

  1. 只有一个外部参数（除种群大小）。
  2. 在离散函数上表现良好。

缺点：

  1. 收敛精度不是最高的。

文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/16058

附加的文件 |
下载ZIP
AEO.zip (36.96 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
Connexus中的正文（第四部分）：添加HTTP请求正文 Connexus中的正文（第四部分）：添加HTTP请求正文
在本文中，我们探讨了HTTP请求中的正文概念，这对于发送诸如JSON和纯文本之类的数据至关重要。我们讨论并解释了如何正确地使用正文，并结合适当的头部信息。此外，我们还介绍了Connexus库中的ChttpBody类，它将简化对请求正文的处理。
开发基于订单簿的交易系统（第一部分）：指标 开发基于订单簿的交易系统（第一部分）：指标
市场深度无疑是执行快速交易的一个非常重要的因素，特别是在高频交易（HFT）算法中。在本系列文章中，我们将探讨这种类型的交易事件，这些事件可以通过经纪商在许多可交易的交易品种上获得。我们将从一个指标开始，您可以在其中自定义直接显示在图表上的直方图的调色板、位置和大小。我们还将研究如何生成 BookEvent 事件，以在特定条件下测试指标。未来文章的其他可能主题包括如何存储价格分布数据以及如何在策略测试器中使用它。
交易中的神经网络：点云的层次化特征学习 交易中的神经网络：点云的层次化特征学习
我们继续研究从点云提取特征的算法。在本文中，我们将领略提升 PointNet 方法效率的机制。
您应当知道的 MQL5 向导技术（第 37 部分）：配以线性和 Matérn 内核的高斯过程回归 您应当知道的 MQL5 向导技术（第 37 部分）：配以线性和 Matérn 内核的高斯过程回归
线性内核是机器学习中，针对线性回归和支持向量机所用的同类中最简单的矩阵。另一方面，Matérn 内核是我们在之前的文章中讲述的径向基函数的更普遍版本，它擅长映射不如 RBF 假设那样平滑的函数。我们构建了一个自定义信号类，即利用两个内核来预测做多和做空条件。