MetaTrader 5 / 例
English Русский Español Deutsch Português
preview
母集団最適化アルゴリズム：Intelligent Water Drops (IWD)アルゴリズム

母集団最適化アルゴリズム：Intelligent Water Drops (IWD)アルゴリズム

MetaTrader 5 — 例 | 2 4月 2024, 11:34
66 0
Andrey Dik
Andrey Dik

内容

1. はじめに
2.アルゴリズム
3.SDSmの修正版
4.テスト結果


1. はじめに

川底は自然が作り出した最も優美な創造物の1つであり、一滴一滴の水が生命のユニークなダンスの一翼を担っています。1キロメートル進むごとに、川は新たな境界線を形成し、そのエネルギーと知恵を雄大に放ちます。この自然現象のように、IWD最適化アルゴリズムは、自己組織化と粒子間の相互作用の原理を利用して、その機能において調和と完璧さを達成しようと努めています。このアルゴリズムは、自然の壮大さと、バランスを創造し維持する能力を反映しており、複雑な問題を最適化し解決するための重要なツールとなっています。

どんな川にも谷があり、地表水と地下水の影響下にある浸食プロセスによって形成されます。この谷の最も低い部分は、川の流れによって地面に切り込まれ、川底と呼ばれます。川の流れの主要な部分と底質がそれに沿って移動します。

川底の起伏は常に変化しています。水によって取り込まれた石や砂は、海底を鋭角に横切る尾根や裂け目を形成します。カーブでは、河川が新しい道を切り開き、三日月湖を形成することがあります。古い水路の一部が徐々に湖となり、独自の生態系を持つようになり、やがて干上がったり湿地帯になったりするのです。

自然界の川を観察していると、その流れに沿って多くの曲がり角があることに気づきます。なぜこのようなねじれが生じたのか、その背景には何か論理や理由があるのかという疑問が生じます。もしあるならば、河川で発生するメカニズムを利用し、その結果、それに基づいてインテリジェントなアルゴリズムを設計開発することができるのでしょうか。IWDアルゴリズムは、自然の河川で発生するプロセスのいくつかをモデル化し、それをアルゴリズムとして実装する試みです。

IWDは、群知能の分野では比較的新しいアルゴリズムの1つです。これは河川システムの力学をシミュレーションします。IWDは母集団ベースのアルゴリズムで、各水滴が解を表し、探索中に水滴を共有することでより良い解が得られます。

2007年、イランの科学者Hamed Shah-Hosseiniは、IWDの挙動アルゴリズムを開発しました。IWDアルゴリズムは、複数の人工的な水滴を特徴としており、相互作用の結果、最も抵抗の少ない経路に沿って最適な道を見つけるように環境を変化させることができます。IWDアルゴリズムは、構成的な集団指向の最適化アルゴリズムです。


2.アルゴリズム

IWDは、水滴が川の流れを変えることによって目的地までの最適な経路を見つけるモデルです。これは、3つの重要なパラメータによって促進されます。落下速度によって、川底の土壌も捕らえることができます。速度が速いほど、各滴が運べる土壌の量は多くなり、それぞれ後続のエージェントにとって自由な経路となります。土壌がないところでは流量が増えます。最適な経路とは、最高速度に到達できる土壌の量が最も少ない経路のことです。IWDの助けを借りて、最適化戦略を実行することが可能です。無作為なエージェントが、川の流れを変え、土壌が全くなく、エージェントの流量が可能な限り最大になるような最適な経路を作るように、インテリジェントに相互作用します。

基本原則

  • 水滴は土壌の少ない道を好む
  • 水滴は、水源から目的地までの道のりで、複数の経路の中から選択することを強いられた場合、より短い経路を好みます。
  • 道の難易度は土壌の量によって決まります。土壌が多い道は難しく、土壌が少ない道は簡単とみなされます。

自然界では、川でたくさんの水滴が巨大な塊（水滴の群れ）を形成しているのが観察されます。自然の川が流れる道は、水滴の群れによって作られました。水滴の群れ（川）は、群れによって大きく変化した環境の一部であり、将来も変化する可能性があります。さらに、環境そのものが水滴の通り道に大きな影響を与えます。それらは河岸の抵抗に直面しています。例えば、水滴の大群は、柔らかい土壌を構成する部分よりも、硬い土壌を構成する部分によって抵抗されます。川の自然な流れは、水滴とその動きに抵抗する環境との競争の結果です。

川に流れ込む水滴の特徴の1つは、その速度です。もう1つの特徴は土壌で、それぞれの川が運べる土壌の量は決まっています。このように、一滴の水はある場所から別の場所へ、ある程度の量の土壌を運ぶことができます。この土壌は速い粒子から遅い粒子に移動します。つまり、速い流れとともに川によって運ばれた土壌は、流れの緩やかな場所に落ち着きます。

この移行期には3つの明らかな変化が起こります。

  • 水滴の速度が上がる
  • 水滴の土壌飽和度が高まる
  • この2点の間で、川底の土壌の量は減少する（グラフ点）

水滴にはそれぞれ速度があることは前述しました。この速度は、川底の土壌の収集に直接的な役割を果たしています。高速の水滴は、低速の水滴よりも多くの土壌を拾います。速速の水滴は、低速の水滴よりも多くの土壌を川底から除去します。したがって、土壌の除去は水滴の速度に関係します。

水滴の速度は、土壌のレベルが低い道では、土壌のレベルが高い道よりも速くなります。したがって、土壌の量が少ない経路では、流れる水滴はより多くの土壌を集め、より大きな速度を得ることができますが、土壌の量が多い経路では速度が低下します。

つまり、IWDアルゴリズムでは、水滴は主に2つの特性によって特徴づけられます。

  • 速度
  • 土壌

これらの特性はどちらも、アルゴリズム動作中に変化する可能性があります。IWDにおける水滴は、供給源から目的地へと移動し、初速とゼロ地面から旅を始めます。水滴はその旅の間に、土壌が取り除かれた環境を移動し、ある程度の速度を得ることができます。IWDは反復的におこなわれるものとします。液滴速度は、現在の位置から次の位置まで、2つの位置間の土壌の逆数に非線形に比例する量だけ増加します。

vel = vel (t-1) + Av / [Bv + Cv * soil^2(i,j)]

ここでAv、Bv、Cvは速度比（入力）であり、soil (i,j)はグラフ頂点間の土壌量です。

したがって、土壌が少ない経路の方が、土壌が多い経路よりもIWD液滴の移動速度が速くなります。

IWDの水滴は、環境中を移動する際に土壌を集めます。この土壌は、2つの場所を結ぶ道から取り除かれます。IWDの液滴に加えられる土壌の量は、IWDを現在の位置から次の位置まで移動させるのに必要な時間に非線形に比例します。この時間間隔は、直線運動に関する単純な物理法則を使って計算されます。

time(i,j,vel) = R / vel

ここでRは2点間の距離です。

水滴に加えられた土壌の量：

dSoil(i,j) = As / [Bs + Cs * time(i,j,vel)]

ここでAs、Bs、Csは土壌の洗浄水比です。

点間の経路上の新しい土壌の量は次のようになります。

soil (i+1,j+1) = Po * soil(i,j) + Pn * dSoil(i,j)

ここで、PoとPnは土壌の量を変えたときの比率です。

したがって、移動に費やす時間は移動速度に反比例し、2点間の距離に正比例します。言い換えれば、土壌は環境に関する情報の定量的な指標です。これらの方程式は、水滴がプライミングレベルの高い経路よりも低い経路を選択することを決定します。この経路選択は、利用可能な経路に一様な無作為分布を適用することで達成されます。次の経路を選択する確率は、利用可能な経路の土壌レベルに反比例します。したがって、プライミングレベルの低い経路は、IWDの水滴によって選択される確率が高くなります。

IWDアルゴリズムの原型は、グラフ探索問題や巡回セールスマン問題などの最適経路問題を解くために著者によって開発されました。しかし、このアルゴリズムは、ここでのテストで検討している問題を解くには適していません。従って、IWDアルゴリズムを我々の最適化問題を解くために適応させる必要があります。対照的に、人口最適化アルゴリズムの記事で説明されているアルゴリズムは、グラフ探索問題を含むあらゆるタイプの問題を解くことができます。以前の記事で、改訂を必要とする同様の高度に専門化されたアルゴリズム、すなわち「蟻コロニー(ACO)」をすでに紹介しました。

IWDをあらゆる最適化問題を解く能力に適応させ、IWDが集団アルゴリズム競技に出場するためには、まず土壌の堆積と移動のプロセスをどのように適用するかを決定する必要があります。フェロモンが適応度関数の値と等価であるACOアルゴリズムで使用されているアプローチには従えません。IWDの場合、土壌は動的なパラメータであり、適応度に比例するわけではありません。

そこで、川の谷を同じ面積の区間に分けるように、座標を区間に分けるというアイデアが生まれました。この考え方は、もし水滴（エージェント）の位置が改善されれば、すべての座標に沿って対応するセクタの土壌の量が減少するというものです。土壌の量的変化は、すべての水滴で正規化された過去2回の反復における適応度関数の変化の差によって、適応度の変化の最大値と最小値の差によって決定されます。

水滴の移動挙動は、土壌の量が最も少ないセクタを無作為に選択することに基づいています。ここで、確率は対応するセクタの土壌の量に比例します。すべての領域の最良のコーディネートを、グローバルな「川底」ストレージに収納します。水滴がセクタを選択した後、新しい座標の確率が二次法則に従うように、ストレージに保存された座標を改善する試みがおこなわれます。これに応じて、新しい座標は前の座標から離れるよりも高い確率で近くなります。新しい座標が位置する領域の幅は、外部パラメータによって決定され、セクタサイズの部分で表されます。座標のセクタへの分解と新しい座標の確率分布を図1に示します。

iwd

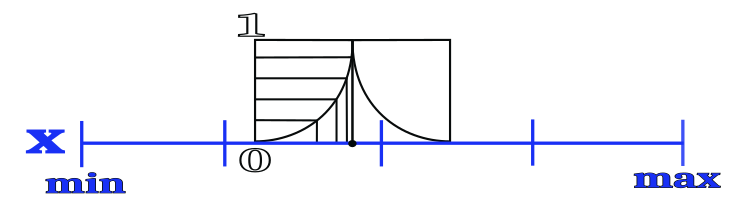
図1：座標をセクタに分割し、最もよく知られている座標の近傍で新しい座標を選択する確率分布

上記の規定とIWDアルゴリズムの概念に基づいて、以下のステップに分かれた擬似コードを作成することができます。

  1. 無作為な水滴を生成する（最初の反復）
  2. FFを計算する
  3. グローバル最良結果を更新する
  4. 無作為な水滴を生成する（2回目の反復）
  5. FFを計算する
  6. グローバル最良結果を更新する
  7. 各水滴の高さの変化を計算する（現在の高さと以前の高さ）
  8. セクタ別に高さを更新する
  9. 新しい水滴（確率的にセクタを選ぶ、既知のホールの近くの水滴）
  10. FFを計算する
  11. グローバル最良結果を更新する
  12. 7から繰り返す

コード分析に移りましょう。

「水滴」検索エージェントを、以下のフィールドを含むS_Drop構造体として表現します。

  • Init (int coords)：この関数は、coords座標の数を引数として、構造体オブジェクトを初期化します。関数内部では、c配列とrSection配列のサイズが、指定された座標数まで変更されます。f、fPrev、altChange変数も初期化されます。
  • c：座標を格納する配列
  • rSection： 河川のセクションを格納する配列
  • f：与えられた水滴の適応度指標
  • fPrev：前回の適応度の値
  • altChange：高さの変更
struct S_Drop
{
  void Init (int coords)
  {
    ArrayResize (c,            coords);
    ArrayResize (rSection,     coords);
    f         = -DBL_MAX;
    fPrev     = -DBL_MAX;
    altChange = 0.0;
  }
  double c            []; //coordinates
  int    rSection     []; //river section          (number of cells: number of coordinates, cell value: sector index on the coordinate)
  double f;               //fitness
  double fPrev;           //previous fitness
  double altChange;       //change in altitude
};

川の説明（水深の最適な座標と、実際には水深そのもの）を格納するストレージが必要なので、構造体をS_Riverbedと呼ぶことにします。

  • riverbedDepth：川床深度を格納する配列。配列のセル数は、座標のセクタ数に対応し、各セルの値は、対応するセクタの川床深度です。
  • coordOnSector：セクタ上の最も深い場所の特定の座標を格納するための配列で、配列のセル数は座標上のセクタ数に対応し、各セルの値は対応するセクタ上の座標です。
//——————————————————————————————————————————————————————————————————————————————
struct S_Riverbed //riverbed
{
  double riverbedDepth []; //riverbed depth 
  double coordOnSector []; //coordinate on the sector
};
//——————————————————————————————————————————————————————————————————————————————

水滴に基づく人工最適化アルゴリズムを実装したC_AO_IWDmクラス（m - modified）を宣言します。以下は各クラス要素の説明である：

クラスのプロパティ

  • cB：最適な座標を格納する配列
  • fB：最良の座標に対するターゲット関数の値
  • p：粒子（水滴）用の配列
  • rangeMax、rangeMin、rangeStep各配列は、検索範囲を定義するために使用

クラスのメソッド

  • Init：C_AO_IWDmクラスオブジェクトを、与えられたパラメータ（coordsP：座標の数、popSizeP：母集団のサイズ、sectsNumberP：セクタの数、waterViscosityP：水の粘度）で初期化
  • Moving：水滴を移動
  • Revision：水滴の状態を修正
privateクラスプロパティ
  • coords：座標の数
  • popSize：水滴数
  • sectorsNumbe：セクタ数
  • waterViscosity：セクタサイズに対する水の粘性率
  • sectorSpace：セクタサイズ
  • rb：川床を表す座標の配列
  • iterationCounter
  • revision：改訂の必要性を示すフラグ
privateクラスメソッド
  • SeInDiSp：指定された範囲内の新 し い座標値を、 指定されたステップで算出
  • RNDfromCI：指定された間隔で乱数を生成
  • Scale：数値を指定範囲に拡大縮小 
//——————————————————————————————————————————————————————————————————————————————
class C_AO_IWDm
{
  //----------------------------------------------------------------------------
  public: double cB  [];       //best coordinates
  public: double fB;           //FF of the best coordinates
  public: S_Drop p   [];       //particles (drops)

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,          //coordinates number
                     const int    popSizeP,         //population size
                     const int    sectorsNumberP,   //sectors number
                     const double waterViscosityP); //water viscosity (>= 1)

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;           //coordinates number
  private: int    popSize;          //population size

  private: int    sectorsNumber;    //sectors number
  private: double waterViscosity;   //water viscosity
  private: double sectorSpace [];   //sector space
  private: S_Riverbed      rb [];   //riverbed

  private: int    iterationCounter;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

InitメソッドはC_AO_IWDmクラスオブジェクトを指定されたパラメータ（座標数、滴数、セクタ数、水粘度）で初期化します。

この方法は次のようなものです。

1. 乱数発生器をリセットする。
2.ターゲット関数fBの値を「-DBL_MAX」の値で初期化する。
3.反復カウンターをゼロに設定する。
4.coords座標数とpopSize母集団サイズを指定された値に設定する。
5.sectorsNumberとwaterViscosityを指定された値に設定する。
6.sectorSpace配列サイズをcoordに変更する。
7.p配列サイズをpopSizeに変更し、p配列の各水滴を初期化する。
8.rangeMax、rangeMin、rangeStep、cBの各配列サイズをcoordsに変更する。
9.rb配列のサイズをcordsに変更し、riverbedDepth配列とcoordOnSector配列を含むrb配列の各要素を初期化する。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_IWDm::Init (const int    coordsP,          //coordinates number
                      const int    popSizeP,         //population size
                      const int    sectorsNumberP,   //sectors number
                      const double waterViscosityP)  //water viscosity (>= 1)
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB               = -DBL_MAX;
  iterationCounter = 0;

  coords  = coordsP;
  popSize = popSizeP;

  sectorsNumber  = sectorsNumberP;
  waterViscosity = waterViscosityP;
  ArrayResize (sectorSpace, coords);

  ArrayResize (p, popSize);
  for (int i = 0; i < popSize; i++) p [i].Init (coords);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);

  ArrayResize (rb,        coords);
  for (int i = 0; i < coords; i++)
  {
    ArrayResize     (rb [i].riverbedDepth, sectorsNumber);
    ArrayResize     (rb [i].coordOnSector, sectorsNumber);
    ArrayInitialize (rb [i].riverbedDepth, 0.0);
    ArrayInitialize (rb [i].coordOnSector, -DBL_MAX);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Moving()メソッドを部分的に見てみましょう。

このコードブロックは、1回目と2回目の繰り返しでのみ実行されます。各座標のsectorSpaceセクタのサイズを計算し、設定します。セクタサイズは、「rangeMax - rangeMin」値の範囲をsectorNumberセクタ数で割ることによって決定されます。

次に、一様分布で指定された範囲の無作為な値に基づく初期値で水滴を初期化します。

//----------------------------------------------------------------------------
  if (iterationCounter == 0)
  {
    for (int i = 0; i < coords; i++) sectorSpace [i] = (rangeMax [i] - rangeMin [i]) / sectorsNumber;
  }

  //1,4-------------------------------------------------------------------------
  if (iterationCounter == 0 || iterationCounter == 1)
  {
    double min = 0.0;
    double max = 0.0;
    int    s   = 0;

    for (int i = 0; i < popSize; i++)
    {
      p [i].fPrev = p [i].f;

      for (int c = 0; c < coords; c++)
      {
        s = (int)(RNDfromCI (0, sectorsNumber));
        if (s >= sectorsNumber) s = sectorsNumber - 1;

        p [i].rSection [c] = s;

        min = rangeMin [c] + sectorSpace [c] * s;
        max = min + sectorSpace [c];

        p [i].c [c] =  SeInDiSp (RNDfromCI (min, max), rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    for (int i = 0; i < popSize; i++) p [i].fPrev = p [i].f;

    return;
  }

次に、このコードスニペットは、母集団内の各水滴のaltChangeを計算し、正規化します。このコードにおける唯一の微妙な点は、0 による除算を避けるために、高さの変化の最大値と最小値が等しいかどうかを確認することです。この場合、水滴の高さに変化はなかったと仮定します。

各水滴のaltChange値は、0から1の範囲になるように正規化された値として計算されます。正規化は、altChangeからminAltChangeを引き、その結果をmaxAltChangeとminAltChangeの差で割ることによっておこなわれます。

//7---------------------------------------------------------------------------
double maxAltChange = -DBL_MAX;
double minAltChange =  DBL_MAX;
double altChange    = 0.0;
double randSC       = 0.0; //random selection component
double maxRC        = 0.0;
double nowRC        = 0.0;
int    indSector    = 0;

for (int i = 0; i < popSize; i++)
{
  altChange = fabs (p [i].f - p [i].fPrev);
  p [i].altChange = altChange;
  if (altChange < minAltChange) minAltChange = altChange;
  if (altChange > maxAltChange) maxAltChange = altChange;
}

if (minAltChange == maxAltChange)
{
  for (int i = 0; i < popSize; i++)
  {
    p [i].altChange = 0.0;
  }
}
else
{
  for (int i = 0; i < popSize; i++)
  {
    altChange = p [i].altChange;
    p [i].altChange = (altChange - minAltChange) / (maxAltChange - minAltChange);
  }
}

次のコード片は、適応度関数の現在の値が、対応する水滴の前の値よりも大きい場合に、各座標の川底の深さを更新します。これにより、高さの変化を考慮し、川床の形状に影響を与えることができます。したがって、水滴の位置が改善されるたびに、川底が変化したと考えられます。

//8---------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (p [i].f > p [i].fPrev)
    {
      for (int c = 0; c < coords; c++)
      {
        rb [c].riverbedDepth [p [i].rSection [c]] += p [i].altChange;
      }
    }
  }

以下のコードスニペットは、検索戦略を提供するエージェントの座標を変更するために、2つの基本的なアクションを実行します。

  • 水滴が母集団から別の水滴を無作為に選択し、その水滴からセクタ番号を借りることで、アルゴリズムの組み合わせ論的特性が保証されます。
  • 水滴は、各セクタの既知の深さに比例して、川のセクタを無作為に選択します。

セクタが選択されるとすぐに、そのセクタが別の水滴から取られたものであれば一様分布で、川底に保存された情報から選択されたものであれば二次関数分布で、水滴の新しい座標を生成します。その結果、各座標の値が許容範囲に収まります。

//9---------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      n = (int)(RNDfromCI (0, popSize));
      if (n >= popSize) n = popSize - 1;

      if (p [n].f > p [i].f)
      {
        p [i].rSection [c] = p [n].rSection [c];

        min = rangeMin [c] + sectorSpace [c] * p [i].rSection [c];
        max = min + sectorSpace [c];

        p [i].c [c] = SeInDiSp (RNDfromCI (min, max), rangeMin [c], rangeMax [c], rangeStep [c]);
      }
      else
      {
        randSC = RNDfromCI (0.0, 1.0);

        nowRC = rb [c].riverbedDepth [0] * randSC;
        maxRC = nowRC;
        indSector = 0;

        for (int r = 1; r < sectorsNumber; r++)
        {
          nowRC = rb [c].riverbedDepth [r] * randSC;
          if (nowRC > maxRC)
          {
            maxRC     = nowRC;
            indSector = r;
          }
        }

        if (rb [c].coordOnSector [indSector] == -DBL_MAX)
        {
          min = rangeMin [c] + sectorSpace [c] * indSector;
          max = min + sectorSpace [c];

          p [i].c [c] = RNDfromCI (min, max);
        }
        else
        {
          double x = RNDfromCI (-1.0, 1.0);
          double y = x * x;
          double pit = 0.0;

          double dif = Scale (y, 0.0, 1.0, 0.0, sectorSpace [c] * waterViscosity, false);

          pit = rb [c].coordOnSector [indSector];
          pit += x > 0.0 ? dif : -dif;

          p [i].c [c] = pit;
        }

        min = rangeMin [c] + sectorSpace [c] * indSector;
        max = min + sectorSpace [c];

        p [i].c [c] = SeInDiSp (p [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        p [i].rSection [c] = indSector;
      }
    }
  }

次に、目的関数fの現在の値が前の値より大きい場合、各水滴について前の適応度値fPrevを更新します。これにより、目的関数の変化を追跡することができ、この情報をアルゴリズムで使用して、次のステップを選択する決定を下すことができます。

for (int i = 0; i < popSize; i++)
  {
    if (p [i].f > p [i].fPrev)
    p [i].fPrev = p [i].f;
  }

最後に、Revisionメソッドについて考えてみましょう。これは、最適解cBとそれに対応する適応度関数値を更新するように設計されています。現在の反復でより良い解が見つかった場合、対応するセクタの座標を保存します。このように、川床は各座標の各セクタで最も深い場所を記憶しています。このメソッドでは、反復カウンタ iterationCounterを1つ増やし、Movomgメソッドで反復に対応するアクションを実行できるようにしています。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_IWDm::Revision ()
{
  //3,6,11----------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (p [i].f > fB)
    {
      fB = p [i].f;
      ArrayCopy (cB, p [i].c, 0, 0, WHOLE_ARRAY);

      for (int c = 0; c < coords; c++)
      {
        rb [c].coordOnSector [p [i].rSection [c]] = p [i].c [c];
      }
    }
    else
    {
      for (int c = 0; c < coords; c++)
      {
        if (rb [c].coordOnSector [p [i].rSection [c]] == -DBL_MAX)
        {
          rb [c].coordOnSector [p [i].rSection [c]] = p [i].c [c];
        }
      }
    }
  }

  iterationCounter++;
}
//——————————————————————————————————————————————————————————————————————————————


3.SDSmの修正版

IWDmアルゴリズムの結果については後で検討しますが、IWDmとSDSの両方が似たようなエンティティ（それぞれセクタとレストラン）を使用しているため、この結果は、格付けで最高である別のアルゴリズム、SDSの改善を試みるというアイデアを促しました。IWDで使用された方法、すなわち4元確率分布を使用した位置精密化の使用は、SDSをさらに優れたものにするのに役立った。最良の位置精密化方法は、最終的なテスト結果に大きな影響を与えました。唯一の違いは、SDSmでは、分布が近隣のレストランに行くと切り捨てられることです。

SDSアルゴリズムの修正方法に変更が加えられ、レストラン内の新しい座標の分布（以前は一様だった）とテスト結果に大きな変化があったため、このアルゴリズムにはmインデックスが割り当てられました。

コードでは、Research関数が確率変数の分布を担当していることがわかります。この関数は、分布の幅の比率、レストランの住所、レストランのサイズ、座標に沿った可能な最小値、座標に沿ったステップ、前のステップでの適応度、改善しようとしている座標を引数として取ります。

SDSmアルゴリズムでは、3種類の座標（レストランの料理）の改善を試みます。

  1. 対話者候補座標
  2. 無作為に選択されたレストランの最良の座標（IWDmの河川敷のように、SDSmではすべてのレストランの最良座標を保存。これは、市内のすべてのレストランの最高の料理のリストを保存するのと同様）
  3. 対応するレストランの独自座標

確率分布の幅の比率を外部パラメータに含めることもできますが、私見では、最適な値を設定することはしませんでした。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDSm::Revision ()
{
  /*
  here is the old code, no changes
  */

  for (int i = 0; i < populationSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      n = (int)(RNDfromCI (0, populationSize));
      if (n >= populationSize) n = populationSize - 1;

      if (cands [n].fPrev > cands [i].fPrev)
      {
        cands [i].raddr [c] = cands [n].raddrPrev [c];

        Research (0.25,
                  cands     [i].raddr [c],
                  restSpace [c],
                  rangeMin  [c],
                  rangeStep [c],
                  cands     [n].cPrev [c],
                  cands     [i].c     [c]);
      }
      else
      {
        rnd = RNDfromCI (0.0, 1.0);

        if (rnd < probabRest)
        {
          n = (int)(RNDfromCI (0, restNumb));
          if (n >= restNumb) n = restNumb - 1;
          cands [i].raddr [c] = n;

          Research (1.0,
                    cands     [i].raddr         [c],
                    restSpace [c],
                    rangeMin  [c],
                    rangeStep [c],
                    rb        [c].coordOnSector [n],
                    cands     [i].c             [c]);
        }
        else
        {
          cands [i].raddr [c] = cands [i].raddrPrev [c];

          Research (0.25,
                    cands     [i].raddr [c],
                    restSpace [c],
                    rangeMin  [c],
                    rangeStep [c],
                    cands     [i].cPrev [c],
                    cands     [i].c     [c]);
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

これが、前回のテストリーダーを12％以上向上させることを可能にした「魔法の」Research関数です。

この関数は以下のことをおこないます。

  • [-1.0;1.0]の範囲で乱数を生成する 
  • その結果得られる値を、分布のスケールファクターでレストランのサイズに対応する増分でスケーリングする
  • 現在のアップグレード座標に追加する
  • レストランの境界が決まる
  • レストランの境界に沿ってトリミングされた最適化されたパラメータのステップに従って、数が許容値に変換されます。
//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDSm::Research (const double  ko,
                          const int     raddr,
                          const double  restSpaceI,
                          const double  rangeMinI,
                          const double  rangeStepI,
                          const double  pitOld,
                          double       &pitNew)
{
  double x = RNDfromCI(-1.0, 1.0);
  double y = x * x;
  double pit = pitOld;
  double min = 0.0;
  double max = 0.0;

  double dif = Scale(y, 0.0, 1.0, 0.0, restSpaceI * ko, false);

  pit += x > 0.0 ? dif : -dif;

  min = rangeMinI + restSpaceI * raddr;
  max = min + restSpaceI;

  pitNew = SeInDiSp (pit, min, max, rangeStepI);
}
//——————————————————————————————————————————————————————————————————————————————


4.テスト結果

IWDテストスタンドの結果：

C_AO_IWDm:50;10;3.0
=============================
5 Rastrigin's; Func runs 10000 result:63.304838882364926
Score:0.78438
25 Rastrigin's; Func runs 10000 result:49.20424466627239
Score:0.60967
500 Rastrigin's; Func runs 10000 result:39.68464591598694
Score:0.49172
=============================
5 Forest's; Func runs 10000 result:0.6975685023058024
Score:0.39458
25 Forest's; Func runs 10000 result:0.19878497533879688
Score:0.11244
500 Forest's; Func runs 10000 result:0.0569274044494088
Score:0.03220
=============================
5 Megacity's; Func runs 10000 result:3.44
Score:0.28667
25 Megacity's; Func runs 10000 result:1.088
Score:0.09067
500 Megacity's; Func runs 10000 result:0.28480000000000005
Score:0.02373
=============================
All score:2.82606

控えめに言っても、比較表の結果は平均以下です。

SDSmテストスタンドの結果：

C_AO_SDSm:100;100;0.05
=============================
5 Rastrigin's; Func runs 10000 result:80.65976429448276
Score:0.99942
25 Rastrigin's; Func runs 10000 result:79.95659847225565
Score:0.99071
500 Rastrigin's; Func runs 10000 result:57.23107170601535
Score:0.70913
=============================
5 Forest's; Func runs 10000 result:1.7241883676504082
Score:0.97529
25 Forest's; Func runs 10000 result:1.497160007591401
Score:0.84687
500 Forest's; Func runs 10000 result:0.29481739063639945
Score:0.16676
=============================
5 Megacity's; Func runs 10000 result:10.559999999999999
Score:0.88000
25 Megacity's; Func runs 10000 result:6.824000000000001
Score:0.56867
500 Megacity's; Func runs 10000 result:1.2384
Score:0.10320
=============================
All score:6.24004

SDSmの結果は本当に印象的です。

IWDmアルゴリズムのアニメーションによる可視化は、潜在的に良い探索領域をクラスタリングする能力をある程度示しており、特にRastrigin関数において顕著です。しかし、収束グラフの長く平坦な部分は、アルゴリズムが顕著に行き詰まった場所を示しています。

rastrigin

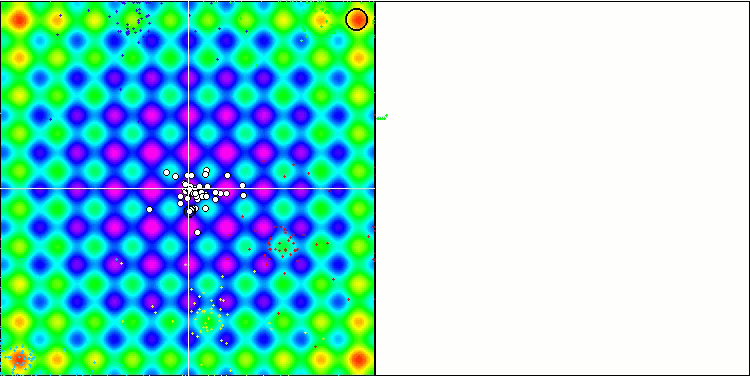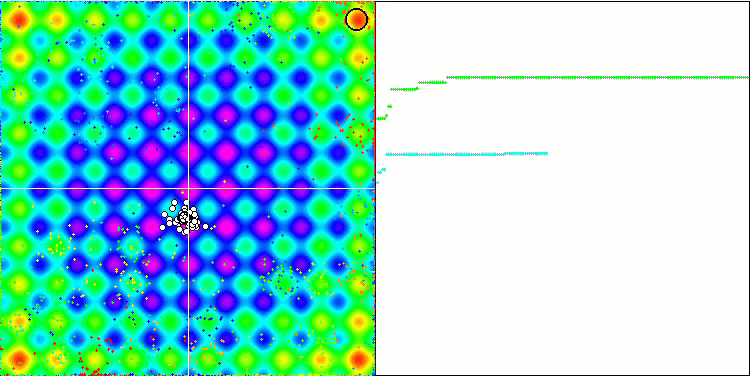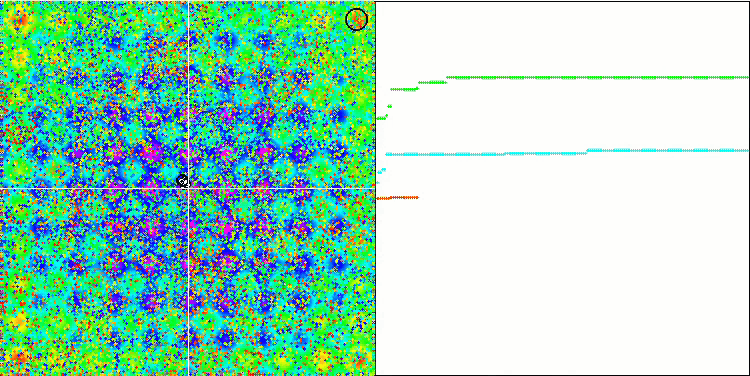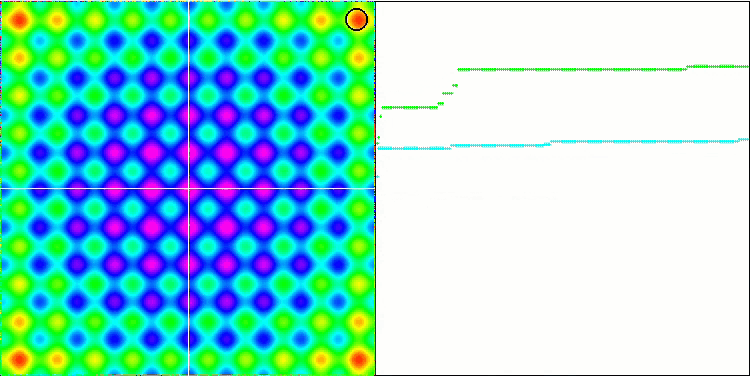
  Rastriginテスト関数のIWDm

forest

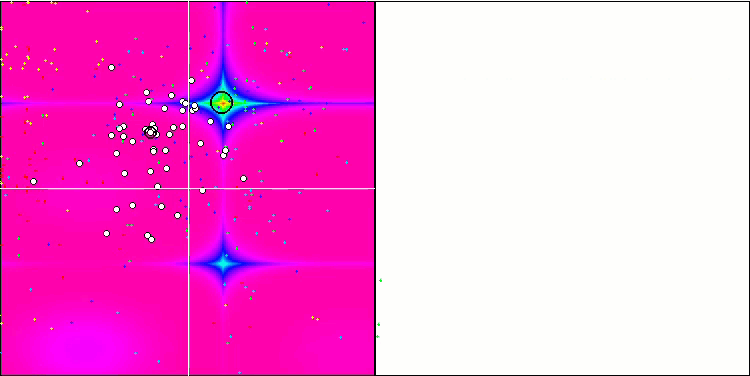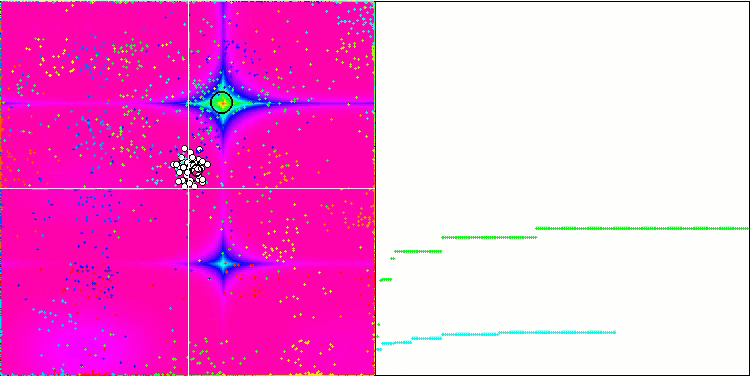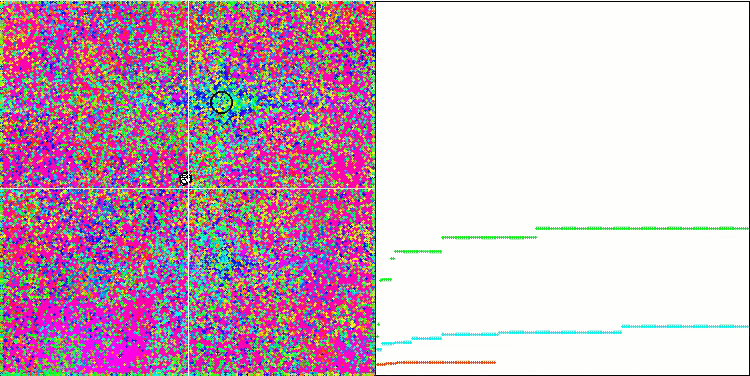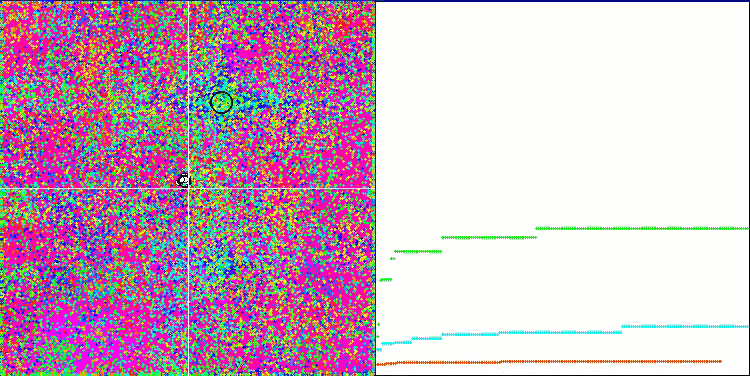
  Forestテスト関数のIWDm

Megacity

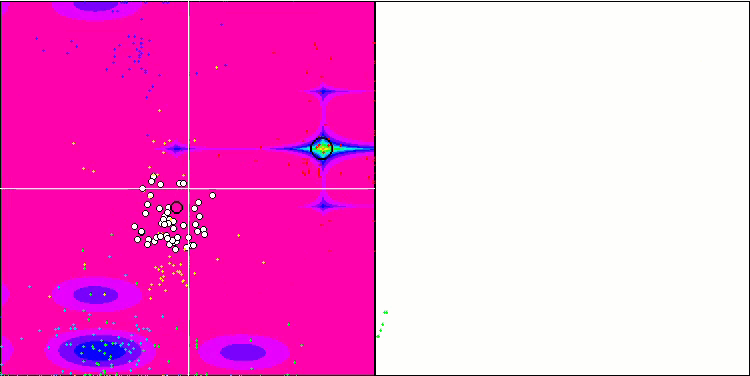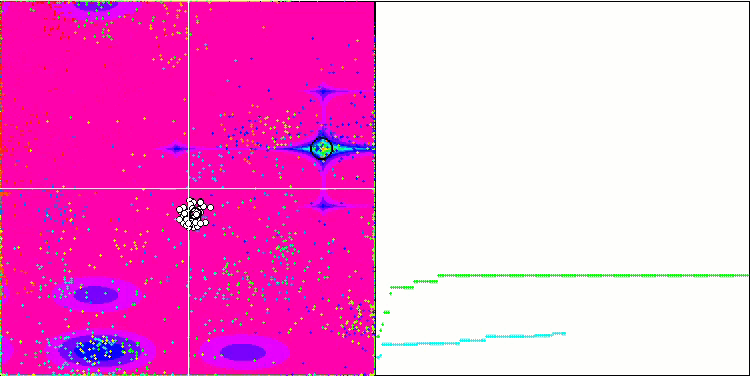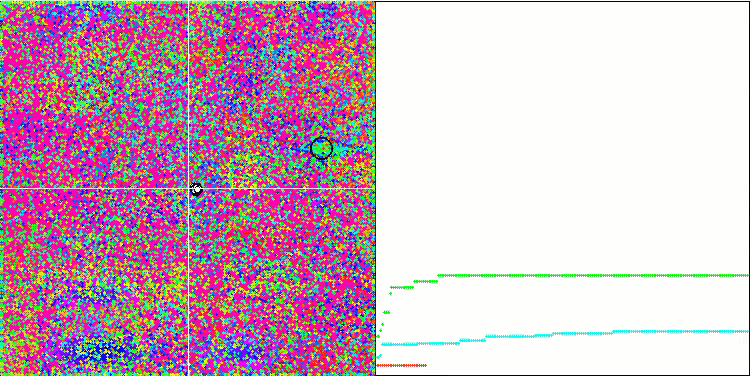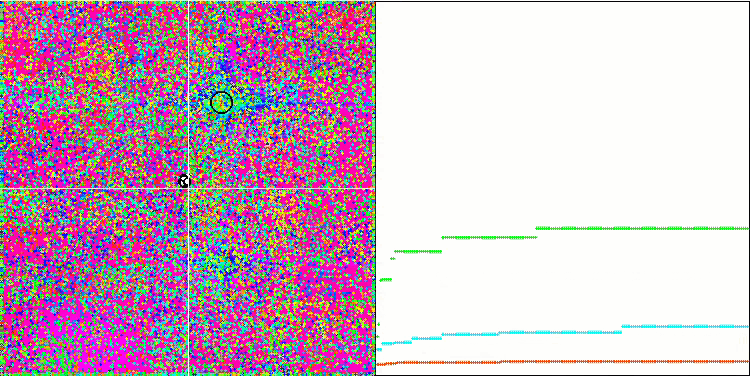
  Megacityテスト関数のIWDm


IWDmアルゴリズムは、22のアルゴリズムの中で19位（下から4番目）となり、有名で人気のあるPSOアルゴリズムを抜きました。IWDmは平滑関数で最高の結果を示しました。3つのテスト関数の収束グラフが一貫して改善されていることから、反復回数を増やせばアルゴリズムが収束し続けるという希望が持てるが、そうなると実用的な意味や使用上の便宜性はなくなってしまいます。テスト条件は厳しく、1万回の反復です。それを上回ることも下回ることもありません。

加えて、9つ可能な1位を7つ獲得した修正SDSmアルゴリズムも注目に値します。このアルゴリズムは、最適化アルゴリズムの中でもまさに「オールラウンダー」です。シャープなForest関数と複雑な離散Megacity関数において、従来のSDSと比較したSDSmの結果の改善は特に顕著です（後者の関数では、1000個のパラメータでほぼ30％の改善）。このように、記事のメインテーマであるIWDに加えて、私たちはSDSmという新たな素晴らしいゲストを目にすることになります。SDSの作動アニメーションはこちらからご覧いただけます。SDSmの動作を確認するには、SDSのあるフォルダにあるアーカイブからテストスクリプトを実行してください。

#

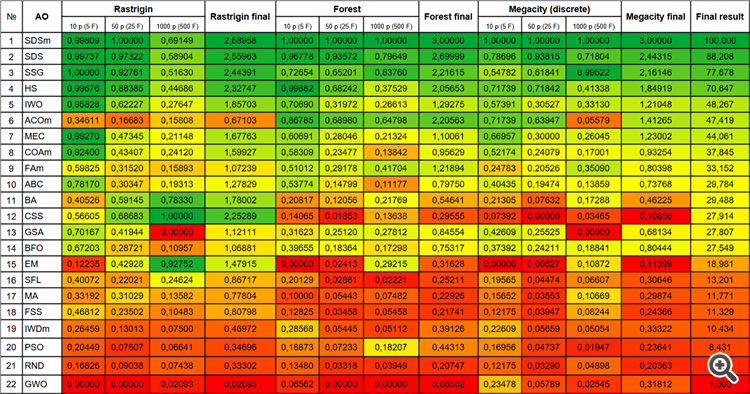
AO

詳細

Rastrigin

Rastrigin最終

Forest

Forest最終

Megacity（離散）

Megacity最終

最終結果

10 p (5 F)

50 p (25 F)

1000 p (500 F)

10 p (5 F)

50 p (25 F)

1000 p (500 F)

10 p (5 F)

50 p (25 F)

1000 p (500 F)

1

SDSm

確率的拡散探索M

0.99809

1.00000

0.69149

2.68958

1.00000

1.00000

1.00000

3.00000

1.00000

1.00000

1.00000

3.00000

100.000

2

SDS

Stochastic Diffusion Search

0.99737

0.97322

0.58904

2.55963

0.96778

0.93572

0.79649

2.69999

0.78696

0.93815

0.71804

2.44315

88.208

3

SSG

苗木の播種と育成

1.00000

0.92761

0.51630

2.44391

0.72654

0.65201

0.83760

2.21615

0.54782

0.61841

0.99522

2.16146

77.678

4

HS

ハーモニー検索

0.99676

0.88385

0.44686

2.32747

0.99882

0.68242

0.37529

2.05653

0.71739

0.71842

0.41338

1.84919

70.647

5

IWO

侵入雑草最適化

0.95828

0.62227

0.27647

1.85703

0.70690

0.31972

0.26613

1.29275

0.57391

0.30527

0.33130

1.21048

48.267

6

ACOm

蟻コロニー最適化M

0.34611

0.16683

0.15808

0.67103

0.86785

0.68980

0.64798

2.20563

0.71739

0.63947

0.05579

1.41265

47.419

7

MEC

Mind Evolutionary Computation

0.99270

0.47345

0.21148

1.67763

0.60691

0.28046

0.21324

1.10061

0.66957

0.30000

0.26045

1.23002

44.061

8

COAm

カッコウ最適化アルゴリズムM

0.92400

0.43407

0.24120

1.59927

0.58309

0.23477

0.13842

0.95629

0.52174

0.24079

0.17001

0.93254

37.845

9

FAm

ホタルアルゴリズムM

0.59825

0.31520

0.15893

1.07239

0.51012

0.29178

0.41704

1.21894

0.24783

0.20526

0.35090

0.80398

33.152

10

ABC

人工蜂コロニー

0.78170

0.30347

0.19313

1.27829

0.53774

0.14799

0.11177

0.79750

0.40435

0.19474

0.13859

0.73768

29.784

11

BA

コウモリアルゴリズム

0.40526

0.59145

0.78330

1.78002

0.20817

0.12056

0.21769

0.54641

0.21305

0.07632

0.17288

0.46225

29.488

12

CSS

荷電系探索

0.56605

0.68683

1.00000

2.25289

0.14065

0.01853

0.13638

0.29555

0.07392

0.00000

0.03465

0.10856

27.914

13

GSA

重力探索法

0.70167

0.41944

0.00000

1.12111

0.31623

0.25120

0.27812

0.84554

0.42609

0.25525

0.00000

0.68134

27.807

14

BFO

細菌採餌の最適化

0.67203

0.28721

0.10957

1.06881

0.39655

0.18364

0.17298

0.75317

0.37392

0.24211

0.18841

0.80444

27.549

15

EM

電磁気学的アルゴリズム

0.12235

0.42928

0.92752

1.47915

0.00000

0.02413

0.29215

0.31628

0.00000

0.00527

0.10872

0.11399

18.981

16

SFL

ShuffledFrog-Leaping

0.40072

0.22021

0.24624

0.86717

0.20129

0.02861

0.02221

0.25211

0.19565

0.04474

0.06607

0.30646

13.201

17

MA

モンキーアルゴリズム

0.33192

0.31029

0.13582

0.77804

0.10000

0.05443

0.07482

0.22926

0.15652

0.03553

0.10669

0.29874

11.771

18

FSS

魚群検索

0.46812

0.23502

0.10483

0.80798

0.12825

0.03458

0.05458

0.21741

0.12175

0.03947

0.08244

0.24366

11.329

19

IWDm

インテリジェント水滴M

0.26459

0.13013

0.07500

0.46972

0.28568

0.05445

0.05112

0.39126

0.22609

0.05659

0.05054

0.33322

10.434

20

PSO

粒子群最適化

0.20449

0.07607

0.06641

0.34696

0.18873

0.07233

0.18207

0.44313

0.16956

0.04737

0.01947

0.23641

8.431

21

RND

ランダム

0.16826

0.09038

0.07438

0.33302

0.13480

0.03318

0.03949

0.20747

0.12175

0.03290

0.04898

0.20363

5.056

22

GWO

灰色オオカミオプティマイザ

0.00000

0.00000

0.02093

0.02093

0.06562

0.00000

0.00000

0.06562

0.23478

0.05789

0.02545

0.31812

1.000


まとめ

元のIWDアルゴリズムは、輸送ロジスティクス、ネットワークルーティング、地理情報システムにおける最適経路の発見など、最短経路を見つける問題を解決するために著者によって開発されました。この記事では、これらの特定のタスクにおけるIWDmの能力と性能を検証しておらず、普遍的なものとして提示された新しい修正IWDmアルゴリズムは、印象的な結果を示すことができませんでした。セクタ数を増やしても、残念ながらアルゴリズムの効率向上にはつながらませんでした。

ただし、IWDmアルゴリズムの動作は、このエレガントなアルゴリズムの可能性がまだ完全に発揮されていないことを感じさせた。川底の土壌の動きをモデル化した上で、探索空間をセクタに分割し、そのレーティングを考慮するというアイデアは非常に興味深いものです。その結果、各レストランで最もおいしい料理を保存し、おそらく前の点の近傍に新しい点がある確率にバイアスをかけるなどのアプローチにより、SDSアルゴリズムの性能が大幅に向上することが示されました。

新しいSDSmのレストランの数を増やし（デフォルトのパラメータは100）、座標をより小さなエリアに分割すると（SDSパラメータは1000）、結果は悪くなります。つまり、このアプローチでは、個々のレストランの選択がより重要になり、その近辺の特定の点は重要でなくなります（アルゴリズムは通常のSDSに変わる）。これは、2次確率分布が座標上のある大きさのセクタに対して最大の影響力を持つことを意味します。これは、アルゴリズムに存在する、目的が異なる手法の間の一種のバランスです。

この記事から得られる最も重要なことは、個々の検索戦略で使われるどの方法が最良か最悪かを明確に言うことは不可能だということです。異なる方法を使うことで、あるアルゴリズムを悪化させることもあれば、他のアルゴリズムを大幅に改善することもあります。重要なのは、最適化アルゴリズムで使われる手法の組み合わせであって、手法そのものではありません。


格付け表

図2：関連テストによるアルゴリズムのカラーグラデーション


アルゴリズムのテスト結果のヒストグラムを以下に示します（0から100までのスケールで、多ければ多いほど良い。アーカイブには、この記事で説明した方法で格付け表を計算するスクリプトがある）。

チャート

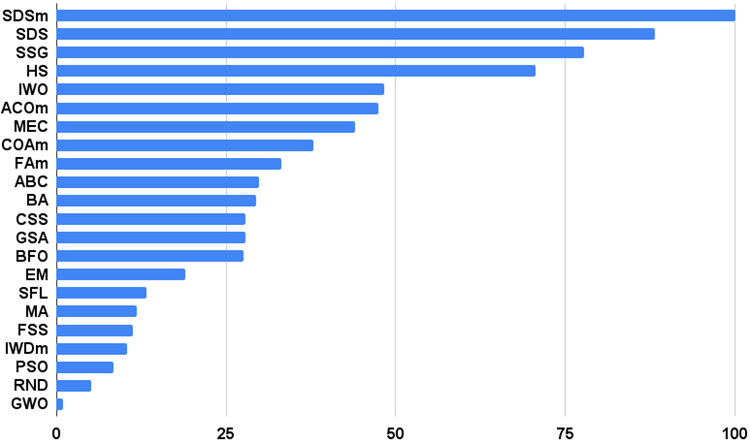
図3：テストアルゴリズムの最終結果のヒストグラム


Intelligent Water Drops改良(IWDm)アルゴリズムの長所と短所

長所
1. 外部パラメータが少ない

短所
1. 平滑離散的な関数に関する悪い結果
2.収束性が低い
3.局所的な極端な状況に陥る傾向

この記事には、過去の記事で説明したアルゴリズムコードの最新版を更新したアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/13730

添付されたファイル |
ZIPをダウンロード
21_The_world_of_AO_IWD.zip (491.81 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
母集団最適化アルゴリズム：Spiral Dynamics Optimization (SDO)アルゴリズム 母集団最適化アルゴリズム：Spiral Dynamics Optimization (SDO)アルゴリズム
本稿では、軟体動物の殻など自然界における螺旋軌道の構築パターンに基づく最適化アルゴリズム、Spiral Dynamics Optimization（SDO、螺旋ダイナミクス最適化）アルゴリズムを紹介します。著者らが提案したアルゴリズムを徹底的に修正し、改変しました。この記事では、こうした変更の必要性について考えてみたいと思います。
母集団最適化アルゴリズム：荷電系探索（Charged System Search、CSS）アルゴリズム 母集団最適化アルゴリズム：荷電系探索（Charged System Search、CSS）アルゴリズム
この記事では、無生物の自然にヒントを得た別の最適化アルゴリズムである荷電系探索(CSS)アルゴリズムについて検討します。この記事の目的は、物理学と力学の原理に基づいた新しい最適化アルゴリズムを提示することです。
母集団最適化アルゴリズム：差分進化(DE) 母集団最適化アルゴリズム：差分進化(DE)
この記事では、これまでに取り上げたアルゴリズムの中で最も議論の的となっているアルゴリズム、差分進化(DE)アルゴリズムについて考察します。
リプレイシステムの開発（第32回）：受注システム(I) リプレイシステムの開発（第32回）：受注システム(I)
これまで開発してきたものの中で、このシステムが最も複雑であることは、おそらく皆さんもお気づきでしょうし、最終的にはご納得いただけると思います。あとは非常に単純なことですが、取引サーバーの動作をシミュレーションするシステムを作る必要があります。取引サーバーの操作方法を正確に実装する必要性は、当然のことのように思えます。少なくとも言葉ではです。ただし、リプレイ/シミュレーションシステムのユーザーにとって、すべてがシームレスで透明なものとなるようにする必要があります。