Algorithmus für eine auf künstlichen Ökosystemen basierende Optimierung (AEO)

Inhalt

1. Einführung
2. Implementierung des Algorithmus
3. Testergebnisse

Einführung

In der Welt der Optimierung und der künstlichen Intelligenz ist man ständig auf der Suche nach neuen, effizienteren Methoden zur Lösung komplexer Probleme. Ein solcher innovativer Ansatz ist der AEO-Algorithmus (Artificial Ecosystem-based Optimization), der im Jahr 2019 entwickelt und vorgestellt wurde. Diese Methode lehnt sich an natürliche Ökosysteme an und ahmt die komplexen Interaktionen und Prozesse nach, die in der natürlichen Umwelt ablaufen.

Der AEO-Algorithmus basiert auf mehreren in der Natur beobachteten Schlüsselprinzipien. So wie Ökosysteme viele Arten enthalten, von denen jede an ihre eigene ökologische Nische angepasst ist, nutzt AEO eine Population verschiedener Lösungen. In diesem Zusammenhang kann jede Lösung als eine eigene „Spezies“ mit einzigartigen Merkmalen und Anpassungsfähigkeiten betrachtet werden.

In der Natur wird die Energie über Nahrungsketten von einem Organismus auf einen anderen übertragen. AEO moduliert dies durch die Interaktion verschiedener Arten von „Agenten“ - vom „Gras“ bis zum „Allesfresser“. Hier werden Informationen, ähnlich wie Energie, zwischen den Lösungen übertragen, was zur Verbesserung der Gesamtqualität der Bevölkerung beiträgt. Ökosysteme sind sowohl durch den Wettbewerb um Ressourcen als auch durch symbiotische Beziehungen gekennzeichnet. Der AEO-Algorithmus spiegelt diese Prozesse durch Entscheidungsaktualisierungsstrategien wider, bei denen die Agenten um bessere Positionen „konkurrieren“ oder durch den Austausch von Informationen „kooperieren“ können.

Natürliche Ökosysteme sind zyklischen Veränderungen unterworfen, was sich auch im AEO widerspiegelt. Der iterative Optimierungsprozess umfasst abwechselnde Verbrauchs- und Zerlegungsphasen, wodurch sich der Algorithmus an die Dynamik des Problems anpassen kann. In der Natur koexistieren zufällige Ereignisse wie Mutationen und Naturkatastrophen mit deterministischen Prozessen wie der natürlichen Selektion. AEO verwendet sowohl stochastische Elemente (wie die Levy-Verteilung) als auch deterministische Regeln, um Lösungen zu aktualisieren, wobei ein Gleichgewicht zwischen der Erkundung neuer Gebiete und der Nutzung bereits gefundener Gebiete hergestellt wird.

Um besser zu verstehen, wie sich natürliche Prozesse im AEO-Algorithmus widerspiegeln, wollen wir uns einige konkrete Beispiele ansehen. In der afrikanischen Savanne wandert die Energie vom Gras zu den Zebras (Pflanzenfresser), dann zu den Löwen (Raubtiere) und schließlich zu den Hyänen (Aasfresser). Bei AEO werden die Informationen über die besten Lösungen vom „Gras“ (die schlechteste Lösung) an die „Pflanzenfresser“ (durchschnittliche Lösung) und „Fleischfresser“ (die besten Lösung) weitergegeben, was zur Verbesserung der Gesamtqualität der Population beiträgt.

Wenn Organismen sterben, zersetzen sie sich und führen dem Ökosystem Nährstoffe zu. So zersetzt sich beispielsweise das Laub im Wald, reichert den Boden an und nährt neue Pflanzen. In AEO wird dieser Prozess durch die Zerlegungsphase des Algorithmus nachgeahmt. Nach der Verbrauchsphase (Aktualisierung der Entscheidungen) folgt die Zerlegungsphase, in der die Informationen aus den aktuellen Entscheidungen „zerlegt“ und über den Suchraum verteilt werden. Auf diese Weise kann der Algorithmus neue Bereiche erkunden und vermeiden, dass er in lokalen Optima stecken bleibt. Im Algorithmus wird dies durch die Anwendung einer Gauß-Verteilung auf die aktuellen Lösungen im Verhältnis zur besten Lösung umgesetzt (die global beste Lösung fungiert als Zersetzer), was als „Zersetzung“ und „Umverteilung“ von Informationen im Suchraum angesehen werden kann.

Der AEO-Algorithmus ist also eine elegante Synthese aus natürlichen Prinzipien und mathematischer Optimierung. Sie bietet nicht nur eine effektive Methode zur Lösung komplexer Probleme, sondern eröffnet auch eine neue Perspektive auf die Beziehung zwischen natürlichen Prozessen und künstlicher Intelligenz. Als Nächstes werden wir einen detaillierten Blick auf die Struktur und die Funktionsmechanismen dieses Algorithmus werfen, um sein Potenzial und seine Anwendung besser zu verstehen.

Implementierung des Algorithmus

Um die Idee der Autoren des AEO-Algorithmus besser zu verstehen, schauen wir uns die Abbildung 1 an, die die Hierarchie der Organismen in einem künstlichen Ökosystem zeigt. Das gesamte Ökosystem besteht aus Organismen, die üblicherweise von 1 bis Xn nummeriert werden. Nummer 1 ist das „Gras“, das die maximale Energie hat (minimaler Wert der Fitnessfunktion), während Xn den Zersetzer (Saprophyt) darstellt, der die Zersetzungsfunktion ausführt (minimale Energie, maximaler Wert der Fitnessfunktion).

In der Abbildung geben die Pfeile die Ernährungsrichtung an: Gras (Nummer 1) kann nur die Abfallprodukte von Saprophyten verwerten, Pflanzenfresser (Nummer 2) ernähren sich von Gras, und die Organismen mit den Nummern 2, 4 und 5 können Pflanzenfresser (fressen nur Gras), Fleischfresser (Organismen können nur Lebewesen fressen, deren Energie niedriger ist als ihre eigene) und Allesfresser (können sowohl Gras als auch Organismen mit höherer Energie fressen) sein. Die Spitze des Ökosystems wird von den Saprophyten eingenommen, die alle Organismen am Ende ihres Lebenszyklus zersetzen.

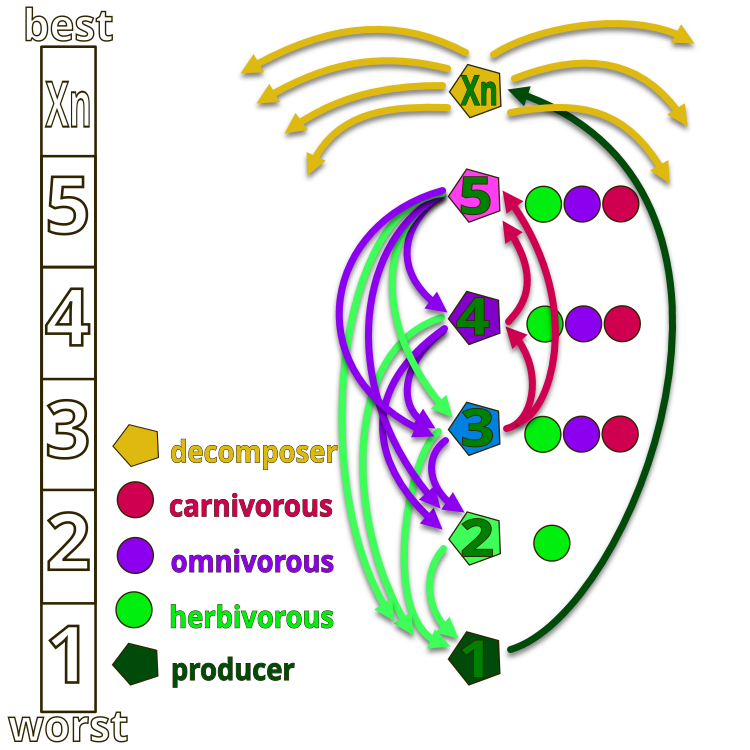
Abbildung 1. Hierarchie der Organismen im künstlichen Ökosystem des AEO-Algorithmus

Die Hauptidee des Algorithmus ist die Modellierung von Interaktionen zwischen Ökosystemkomponenten, um Optimierungsprobleme zu lösen. Der Algorithmus basiert auf drei in der Natur beobachteten Grundprinzipien:

1. Produktion - in der Natur wandeln Produzenten (z. B. Pflanzen) Sonnenenergie in organische Verbindungen um.
2. Verbrauch - Verbraucher (Pflanzenfresser, Fleischfresser, Allesfresser) nutzen die von anderen, insbesondere von Pflanzen, erzeugte Energie.
3. Zersetzung - Saprophyten zersetzen komplexe organische Substanzen in einfache. Im Algorithmus wird das als Zersetzung von Lösungen modelliert.

Grundsätze des Algorithmus:

1. Initialisierung - es wird eine Anfangspopulation von Lösungen erstellt, die das Ökosystem repräsentiert.
2. Produktion - bei jeder Iteration wird die schlechteste Lösung unter Berücksichtigung der besten Lösung und eines Zufallsfaktors aktualisiert.
3. Verbrauch - die übrigen Entscheidungen werden anhand von drei Strategien aktualisiert:

• Pflanzenfresser: Aktualisiert nach Angaben der Produktion.
• Raubtiere: Aktualisiert auf der Grundlage einer zufällig ausgewählten, besten Lösung.
• Allesfresser: Aktualisierung auf der Grundlage des Erzeugers und einer Zufallsentscheidung.

4. Dekomposition - alle Lösungen werden einer „Dekomposition“ unterzogen, die die globale Suche verbessert.
5. Selektion - nur verbesserte Lösungen werden beibehalten, wodurch eine allmähliche Verbesserung der Population gewährleistet wird.

Der Algorithmus beruht also auf dem Mechanismus des Energietransfers zwischen lebenden Organismen, der mit Hilfe von drei Operatoren - Produktion, Verbrauch und Zersetzung - zur Stabilität der Arten beiträgt.

1. Produktion - das schlechteste Individuum in der Population X1 wird im Verhältnis zum besten Xn durch Hinzufügen einer zufällig erzeugten Koordinate Xrand in einem bestimmten Bereich aktualisiert, wobei ein neues Individuum durch den Produktionsoperator geschaffen wird. Mathematische Darstellung: X1 (t + 1) = (1 - a) * Xn (t) + a * Xrand (t), wobei a = (1 - t / T) * r1 (t - aktuelle Epoche, T - Epochen insgesamt), r1 - Zufallszahl [0; 1]. In diesem Fall kann die Komponente r1 weggelassen werden, da wir bereits eine Zufallskoordinate in der Gleichung verwenden.

2. Verbrauch - ein zufällig ausgewählter Verbraucher kann den Erzeuger „essen“, um Energie zu erhalten. Der Konsumfaktor C ist definiert als: C = 1/2 * (v1 / |v2|), wobei v1 und v2 gleichmäßig verteilte Zufallszahlen im Bereich [0; 1] sind.

• Pflanzenfresser: Xi (t + 1) = Xi (t) + C * (Xi (t) - X1 (t)).
• Fleischfresser: Xi (t + 1) = Xi (t) + C * (Xi (t) - Xj (t)).
• Allesfresser: Xi (t + 1) = Xi (t) + C * (r2 * Xi (t) + (1 - r2) * Xj (t)).

3. Zersetzung - der Saprophyt zersetzt die Überreste toter Individuen und liefert so Nährstoffe für die Produzenten. Die Aktualisierung der Position von Einzelpersonen nach der Arbeit des Saprophyten wird wie folgt beschrieben:

Xi (t + 1) = Xn (t) + D * (e * Xn (t) - h * Xi (t)), wobei D = 3u, u ~ N (0, 1), e = r3 * rand (i), h = 2 * r3 - 1 (r3, eine Zufallszahl im Bereich [0; 1]).

Zu Beginn wird also eine zufällige Population erzeugt, und bei jeder Iteration wird die Position des ersten Individuums anhand der Gleichung p.1 aktualisiert. Die Positionen der anderen Individuen werden aktualisiert, indem aus den p.2 Gleichungen mit gleicher Wahrscheinlichkeit gewählt wird. In der Zersetzungsphase aktualisiert jedes Individuum seine Position anhand der Gleichung p.3. Der Prozess wird fortgesetzt, bis ein zufriedenstellendes Abbruchkriterium erreicht ist. Der letzte Schritt liefert das beste bisher gefundene Individuum.

Jetzt können wir den Pseudocode für den AEO-Algorithmus schreiben:

Der Algorithmus AEO (Artificial Ecosystem-based Optimization)

Initialisierung:
    Populationsgröße festlegen (popSize)
    Einstellen der Anzahl der Epochen (Epochs)
    Einstellen des Parameters für die Levy-Verteilung (levisPower)
    Initialisieren der Population mit Zufallslösungen in einem bestimmten Bereich
    Bewerten der Fitnessfunktion für jede Lösung
    Finden der besten globalen Lösung cB

Für jede Epoche von 1 bis „Epochs“:
    // Konsumphase
    Für jeden Agenten i in der Population:
        Wenn i == 0:
            Anwenden der Gaußschen Verteilung auf die aktuelle Lösung
        Ansonsten wenn i == popSize - 1:
            Anwenden des Grasverhaltens (GrassBehavior)
        Andernfalls:
            Auswahl eines zufälligen Verhaltens:
                - Verhalten der Pflanzenfresser (HerbivoreBehavior)
                - Verhalten der Fleischfresser (CarnivoreBehavior)
                - Verhalten der Allesfresser (OmnivoreBehavior)
    
    // Zersetzungsphase
    Für jeden Agenten i in der Population:
        Für jede Koordinate c:
            Wählen eines zufälligen Agenten j
            Berechnen des Abstands D zwischen cB [c] und a [j].c [c]
            Aktualisierung von a [i].c [c] unter Verwendung der Gaußschen Verteilung

    // Revision
    Bewerten der Fitnessfunktion für jeden Agenten
    Aktualisieren der besten persönlichen Lösung für jeden Agenten
    Aktualisieren der besten globalen Lösung von CB
    Sortieren der Population nach dem Wert der Fitnessfunktion

Rückgabe der besten gefundenen Lösung cB

Unterprozeduren:

GrassBehavior (Agent):
    α = (1 - current_epoch / total_number_of_epochs)
    Für jede Koordinate c:
        Xr = Zufallswert im Bereich [min [c], max [c]]
        Xn = cB [c]
        X1 = Xn + α * (Xn - Xr)
        agent.c [c] = X1 (unter Berücksichtigung von Einschränkungen)

HerbivoreBehavior (Agent, coordinate_index):
    Xi = agent.cB [coordinate_index]
    X1 = schlechteste Lösung in der Grundgesamtheit für eine bestimmte Koordinate
    C = Zufallszahl aus der Levy-Verteilung (levisPower)
    Xi = Xi + C * (Xi - X1)
    agent.c [coordinate_index] = Xi (unter Berücksichtigung der Einschränkungen)

CarnivoreBehavior (agent, agent_index, coordinate_index):
    Xi = agent.cB [coordinate]
    j = Zufallsindex < agent_index
    Xj = a [j].cB [coordinate_index]
    C = Zufallszahl aus der Levy-Verteilung (levisPower)
    Xi = Xi + C * (Xj - Xi)
    agent.c [coordinate_index] = Xi (unter Berücksichtigung der Einschränkungen)

OmnivoreBehavior (agent, agent_index, coordinate_index):
    Xi = agent.cB [coordinate]
    X1 = schlechteste Lösung in der Grundgesamtheit für eine bestimmte Koordinate
    j = Zufallsindex > agent_index
    Xj = a [j].cB [coordinate_index]
    C = Zufallszahl aus der Levy-Verteilung (levisPower)
    r = Zufallszahl von 0 bis 1
    Xi = Xi + C * r * (Xi - X1) + (1 - r) * (Xi - Xj)
    agent.c [coordinate_index] = Xi (unter Berücksichtigung der Einschränkungen)

Nach einer ausführlichen Beschreibung und Analyse des Algorithmus gehen wir nun zum Schreiben des Codes über.

Der Algorithmus verwendet die Levy-Verteilung, um extrem weit entfernte, aber seltene Sprünge im Suchraum zu erzeugen. Wir haben diese Zufallszahlenverteilung schon früher verwendet, z. B. im Suchalgorithmus des Kuckucks, aber wir sind nicht näher auf ihre Eigenschaften eingegangen. Der Punkt ist, dass die korrekte Generierung der Levy-Verteilung die Verwendung von vier gleichmäßig verteilten Zufallszahlen erfordert, was an sich schon teuer ist. Darüber hinaus hat die Levy-Verteilung einen unendlich langen Rand (sie ist asymmetrisch, mit nur einem Rand), was ihre Verwendung in praktischen Optimierungsalgorithmen erschwert, insbesondere bei Vorliegen von Randbedingungen. Es ist auch notwendig, die Randbedingungen während der Generierung zu überprüfen, wie z.B. die Prüfung auf 0 vor der Berechnung des natürlichen Logarithmus, und auch die Division durch 0 zu vermeiden.

Nachfolgend finden Sie den Code zur Erzeugung von Zufallszahlen mit der Levy-Verteilung, ohne die oben beschriebenen Prüfungen und ohne die Logik des Codes zu erklären:

double LevyFlight()
{
    const double epsilon = 1e-10; // Small value to avoid division by zero
    const double maxValue = 1e10; // Maximum allowed value

    double log1 = MathMax (RNDprobab(), epsilon);
    double log2 = MathMax (RNDprobab(), epsilon);

    double cos1 = MathCos (2 * M_PI * RNDprobab());
    double cos2 = MathCos (2 * M_PI * RNDprobab());

    double U = MathSqrt (-2.0 * MathLog (log1)) * cos1;
    double v = MathSqrt (-2.0 * MathLog (log2)) * cos2;

    double l = 0.5 * MathAbs(U) / MathMax(MathAbs(v), epsilon);

    return l;
}

Um die Unzulänglichkeiten der Zahlengenerierung mit der Levy-Verteilung zu beseitigen, implementieren wir unsere eigene Funktion LevyFlightDistribution mit einer nahen Verteilung und fügen sie in unseren Standard-Funktionssatz C_AO_Utilities zur Verwendung in Optimierungsalgorithmen ein. Schauen wir uns das mal an:

1. Der Parameter levisPower ist eine Potenz, die die Form der Verteilung bestimmt. Je höher der Wert von levisPower ist, desto „spärlicher“ wird die Verteilung sein.
2. Die Funktion berechnet den Mindestwert, der für die Skalierung verwendet wird. Sie hängt von levisPower ab und wird als 20^levisPower berechnet.
3. Generierung der Zufallszahl „r“ mit der Funktion RNDfromCI im Bereich von 1 bis 20.
4. Anwendung einer Potenz - die erzeugte Zahl „r“ wird mit der Potenz von „-levisPower“ erhöht, wodurch sich ihre Verteilung ändert.
5. Skalierung des Ergebnisses - der erhaltene Wert von „r“ wird auf den Bereich [0, 1] skaliert. Dazu wird der Minimalwert subtrahiert und durch die Differenz zwischen 1 und dem Minimalwert dividiert. Das Ergebnis wird also immer im Bereich [0, 1] liegen.
6. Rückgabe des Ergebnisses - Die Funktion gibt den generierten „r“-Wert zurück, der nun eine Verteilung nahe der Levy-Verteilung mit einer Tendenz zu 0 aufweist.

Wie wir sehen können, erzeugt die Funktion Zufallszahlen streng im Bereich [0, 1], was in der praktischen Anwendung sehr praktisch ist. Der Bereich kann jederzeit durch Anwendung des entsprechenden Verhältnisses auf beliebige Werte erweitert werden. Diese Funktion ist viel schneller und liefert eine Verteilung, die der gewünschten sehr nahe kommt (die rechte Seite der Verteilung relativ zum Maximum).

//------------------------------------------------------------------------------
//A distribution function close to the Levy Flight distribution.
//The function generates numbers in the range [0.0;1.0], with the distribution shifted to 0.0.
double C_AO_Utilities :: LevyFlightDistribution (double levisPower)
{
  double min = pow (20, -levisPower); //calculate the minimum possible value
  double r = RNDfromCI (1.0, 20);     //generating a number in the range [1; 20]

  r = pow (r, -levisPower);           //we raise the number r to a power
  r = (r - min) / (1 - min);          //we scale the resulting number to [0; 1]

  return r;
}

Fahren wir nun mit der Beschreibung des Hauptcodes des Algorithmus fort. Die Klasse C_AO_AEO ist von der Klasse C_AO abgeleitet und implementiert den Algorithmus. Schauen wir uns seine Struktur, Mitglieder und Methoden genauer an.

Konstruktor:

• Legen Sie Standardwerte für die Bevölkerungsgröße und den Levy-Grad fest.
• Erstellt das Array params mit Parametern und initialisiert es mit Werten.

Methoden:

• Setzen der Parameter popSize und levisPower aus dem Array params.
• Init ()initialisiert den Algorithmus mit den angegebenen Suchbereichen und der Anzahl der Epochen. Die Methode gibt bool zurück, was die Möglichkeit bietet, den Erfolg der Initialisierung zu überprüfen.
• Moving () führt die Bewegung der Agenten in der aktuellen Ära durch und aktualisiert ihre Koordinaten.
• Revision () aktualisiert Informationen über Bearbeiter und ihre besten Entscheidungen.

Private Mitglieder und Variablen:

• levisPower - in der Levy-Verteilung verwendeter Parameter.
• epochs - Gesamtzahl der Epochen.
• epochNow - aktuelle Epoche.
• consModel - Stufe (Verbrauch oder Zersetzung).

S_AO_Agent aT [] - temporäres Array von Agenten, die zum Sortieren der Population verwendet werden.

Private Methoden:

• GrassBehavior () - behandelt das Verhalten des Agenten „Gras“.
• HerbivoreBehavior () - behandelt das Verhalten eines pflanzenfressenden Agenten, der Gras „frisst“ (der schlechteste Agent).
• CarnivoreBehavior () - behandelt das Verhalten eines fleischfressenden Agenten, der Agenten mit einem höheren Fitnessfunktionswert „frisst“.
• OmnivoreBehavior () - behandelt das Verhalten eines omnivoren (allesfressenden) Agenten, der das Verhalten eines Pflanzenfressers und eines Fressers mit geringerer Fitness kombiniert.

Die Klasse C_AO_AEO bietet eine Implementierung eines Optimierungsalgorithmus, der auf einem künstlichen Ökosystem basiert und verschiedene Arten von Agenten und deren Interaktionen verwendet, um optimale Lösungen zu finden. Jede Methode ist für bestimmte Aspekte des Algorithmus verantwortlich, einschließlich der Initialisierung, der Bewegung von Agenten und der Aktualisierung ihres Zustands.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AEO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AEO () { }
  C_AO_AEO ()
  {
    ao_name = "AEOm";
    ao_desc = "Artificial Ecosystem-based Optimization Algorithm";
    ao_link = "https://www.mql5.com/de/articles/16058";


    popSize    = 50;       // population size
    levisPower = 2;

    ArrayResize (params, 2);

    params [0].name = "popSize";    params [0].val = popSize;
    params [1].name = "levisPower"; params [1].val = levisPower;
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;
    levisPower = params      [1].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum search range
             const double &rangeMaxP  [],  // maximum search range
             const double &rangeStepP [],  // step search
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double levisPower;


  private: //-------------------------------------------------------------------
  int  epochs;
  int  epochNow;
  int  consModel; // consumption model;
  S_AO_Agent aT [];

  void GrassBehavior     (S_AO_Agent &animal);
  void HerbivoreBehavior (S_AO_Agent &animal, int indCoord);
  void CarnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord);
  void OmnivoreBehavior  (S_AO_Agent &animal, int indAnimal, int indCoord);
};
//——————————————————————————————————————————————————————————————————————————————

Schauen wir uns den Code der Methode Init der Klasse C_AO_AEO genauer an. Init gibt den Wert vom Typ bool zurück, mit dem wir feststellen können, ob die Initialisierung erfolgreich war. Standard-Initialisierungsprüfung: Hier wird die Methode StandardInit aufgerufen, die eine grundlegende Initialisierung der an die Methode übergebenen Parameter vornimmt. Wenn StandardInit false zurückgibt, bedeutet dies, dass die Initialisierung fehlgeschlagen ist und die Methode Init ebenfalls false zurückgibt.

Einrichten der Variablen:

• epochs - legt die Gesamtzahl der Epochen fest, die sich aus dem Parameter epochsP ergibt.
• epochNow - initialisiert die aktuelle Epoche auf 0, was anzeigt, dass der Algorithmus gerade erst begonnen hat.
• consModel - setzt den Wert für das Modell auf 0, damit es anschließend von einer Stufe zur nächsten wechseln kann.
  

Ändern der Größe des temporären Agentenarrays aT auf popSize.

Zurückgegebenes Ergebnis: Wenn alle vorherigen Operationen erfolgreich waren, gibt die Methode true zurück, was bedeutet, dass die Initialisierung erfolgreich war.

Die Methode Init der Klasse C_AO_AEO ist für die Ersteinrichtung des Algorithmus zuständig. Es prüft die Standardparameter, setzt die Werte für die Epochen und die Anfangsphase und bereitet das Array der Agenten für die Arbeit vor. Wenn alle Phasen erfolgreich abgeschlossen sind, gibt die Methode true zurück und zeigt damit an, dass der Algorithmus zur Ausführung bereit ist.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AEO::Init (const double &rangeMinP [],
                     const double &rangeMaxP [],
                     const double &rangeStepP [],
                     const int epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs    = epochsP;
  epochNow  = 0;
  consModel = 0;
  ArrayResize (aT, popSize);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Analysieren wir nun den Code der Methode Moving der Klasse C_AO_AEO. Die allgemeine Struktur der Methode: Moving ist für die Aktualisierung des Zustands der Agentenpopulation (Individuen) in Abhängigkeit von der aktuellen Epoche und dem Verbrauchsmodell zuständig. Sie ist in mehrere logische Blöcke unterteilt:

1. Erhöhen der Epoche: epochNow++ erhöht den aktuellen Epochenzähler.

2. Erste Initialisierung:

• Wenn revision false ist, erfolgt die erste Initialisierung der Koordinaten der Agenten in der Population. Die Koordinaten werden nach dem Zufallsprinzip aus einem bestimmten Bereich ausgewählt und dann auf den nächsten Wert gerundet, der der Stufe entspricht.
• Danach wird revision auf true gesetzt, und die Methode wird ausgeführt.

3. Verbrauchsmodell:

• Wenn consModel 0 ist, werden die Koordinaten der Agenten auf der Grundlage ihres Verhaltens aktualisiert. 
• Für den ersten Agenten (Index 0) werden Gaußsche Verteilungen zur Initialisierung der Koordinaten verwendet.
• Bei den übrigen Agenten hängt das Verhalten von ihrem Index ab: Der letzte Agent (Index popSize - 1) ruft die Funktion GrassBehavior auf. Für den vorletzten und die folgenden Agenten (Indizes popSize - 2 und darunter) wird das Verhalten zufällig bestimmt: entweder pflanzenfressend, fleischfressend oder allesfressend.

4. Dekomposition: Wenn consModel ungleich 0 ist, erfolgt eine Dekomposition, bei der die Koordinaten auf der Grundlage von Zufallswerten und einer Gauß-Verteilung für jeden Agenten aktualisiert werden. Für jede Koordinate wird ein zufälliger Index eines anderen Agenten ausgewählt, und auf der Grundlage dieses Wertes werden neue Koordinaten berechnet, wobei die minimalen und maximalen Grenzen berücksichtigt werden.

Die Methode Moving implementiert die Logik, die mit der Änderung der Koordinaten der Agenten in Abhängigkeit von ihrem Verhalten und der aktuellen Zeit verbunden ist. Es umfasst sowohl die erste Initialisierung als auch die Aktualisierung des Zustands der Agenten auf der Grundlage ihres Verbrauchsmusters.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  // Consumption ---------------------------------------------------------------
  if (consModel == 0)
  {
    double r = 0.0;

    for (int i = 0; i < popSize; i++)
    {
      if (i == 0)
      {
        for (int c = 0; c < coords; c++)
        {
          a [i].c [c] = u.GaussDistribution (a [i].c [c], rangeMin [c], rangeMax [c], 8);
          a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }

        continue;
      }

      if (i == popSize - 1) GrassBehavior (a [i]);
      else
      {
        if (i >= popSize - 2)
        {
          for (int c = 0; c < coords; c++)
          {
            r = u.RNDprobab ();

            if (r < 0.333) HerbivoreBehavior (a [i], c);
            else
            {
              if (r < 0.667)
              {
                CarnivoreBehavior (a [i], i, c);
              }
              else
              {
                OmnivoreBehavior (a [i], i, c);
              }
            }
          }
        }
        else
        {
          for (int c = 0; c < coords; c++)
          {
            r = u.RNDprobab ();

            if (r < 0.5) CarnivoreBehavior (a [i], i, c);
            else         OmnivoreBehavior  (a [i], i, c);
          }
        }
      }
    }

    consModel++;
    return;
  }

  // Decomposition -------------------------------------------------------------
  int    j   = 0;
  double D   = 0.0;
  double min = 0.0;
  double max = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      j = u.RNDminusOne (popSize);
      D = 3.0 * (cB [c] - a [j].c [c]); // * u.RNDprobab ();
      min = cB [c] - D;
      max = cB [c] + D;

      if (min < rangeMin [c]) min = u.RNDfromCI (rangeMin [c], cB [c]);
      if (max > rangeMax [c]) min = u.RNDfromCI (cB [c], rangeMax [c]);

      a [i].c [c] = u.GaussDistribution (cB [c], min, max, 1);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  consModel = 0;
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Revision in der Klasse C_AO_AEO ist für die Aktualisierung der Informationen über die besten Agenten in der Population zuständig. Es implementiert eine Logik, die es ermöglicht, die besten Lösungen, die während der Ausführung des Algorithmus gefunden werden, zu verfolgen und zu speichern. Die Struktur der Methode:

1. Die Suche nach dem besten Agenten:

• Iterieren über alle Agenten in der Population.
• Vergleich ihrer Fitnesswerte (f) mit dem aktuellen, besten Fitnesswert fB.
• Wenn ein Agent mit einem besseren Fitnesswert gefunden wird, wird fB aktualisiert und sich seinen Index gespeichert.

2. Kopieren der Koordinaten des besten Agenten: Wenn der beste Agent gefunden wurde (Index ungleich -1), werden seine Koordinaten in das Array cB kopiert, in dem die aktuellen besten Koordinaten gespeichert sind.

3. Aktualisierung der persönlichen besten Fitnesswerte der Agenten: Alle Agenten werden erneut in einer Schleife durchlaufen und geprüft, ob ihr aktueller Fitnesswert ihre persönliche beste Fitnesswerte (fB) übersteigt. Wenn ja, werden ihre persönlichen besten Fitnesswerte und ihre aktuellen Koordinaten in cB kopiert.

4. Sortieren der Agenten: Am Ende rufen wir die Sortierfunktion auf, um die Agenten nach ihrem persönlich besten Fitnesswert zu reihen.

Die Methode Revision ist ein wichtiges Element des Algorithmus, da sie sicherstellt, dass die besten Lösungen, die während der Arbeit gefunden werden, verfolgt und gespeichert werden.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode GrassBehavior in der Klasse C_AO_AEO implementiert das Verhalten von Agenten auf der Grundlage des Konzepts der „Pflanzenfresser“, das nach neuen Lösungen im Raum sucht. Struktur der Methode:

1. Die Berechnung des Verhältnisses α ist definiert als (1,0 - (double) epochNow / epochs), was bedeutet, dass es mit steigender Epochenzahl abnimmt. Dadurch kann der Algorithmus den Raum zu Beginn aktiver erkunden und sich dann auf die Verbesserung der gefundenen Lösungen konzentrieren.

2. Initialisierung von Variablen:

• X1 - aktuelle Koordinate des Pflanzenfressers.
• Xn - aktuelle Koordinate des Saprophyten.
• Xr - zufällige Koordinate, die aus einem bestimmten Bereich ausgewählt wird.

3. Zyklus nach Koordinaten. Für jeden Agenten koordinieren:

• Der Zufallswert Xr wird innerhalb des angegebenen Bereichs [Xmin, Xmax] erzeugt.
• Die aktuelle Koordinate Xn wird dem Array cB entnommen, in dem die aktuell besten globalen Koordinaten (die Position des Saprophyten im Raum) gespeichert sind.
• Die neue Koordinate von X1 wird nach der Gleichung X1 = Xn + α * (Xn - Xr) berechnet, die es ermöglicht, den aktuellen Wert mit einem Zufallswert zu mischen, wodurch der Einfluss des Zufalls mit zunehmender Anzahl der Epochen verringert wird.
• Schließlich wird die neue Koordinate mit Hilfe der Funktion SeInDiSp in den vorgegebenen Bereich eingegrenzt.

//——————————————————————————————————————————————————————————————————————————————
// Grass
// (Worst) X1 X2 X3 ...... Xn (Best)
// X1(t+1) = (1 - α) * Xn(t) + α * Xrnd (t)
// α = (1 - t / T) * rnd [0.0; 1.0]
// Xrnd = rnd [Xmin; Xmax]

void C_AO_AEO::GrassBehavior (S_AO_Agent &animal)
{
  //0) (1 - α) * Xn + α * Xrnd
  //1) Xn - α * Xn + α * Xrnd
  //2) Xn + α * (Xrnd - Xn)

  double α = (1.0 - (double)epochNow / epochs);

  double X1 = 0.0;
  double Xn = 0.0;
  double Xr = 0.0;

  for (int c = 0; c < coords; c++)
  {
    Xr = u.RNDfromCI (rangeMin [c], rangeMax [c]);
    Xn = cB [c];

    //X1 = Xn + α * (Xr - Xn);
    X1 = Xn + α * (Xn - Xr);

    animal.c [c] = u.SeInDiSp (X1, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode HerbivoreBehavior in der Klasse C_AO_AEO implementiert das Verhalten eines pflanzenfressenden Agenten. Struktur der Methode:

1. Initialisierung von Variablen:

• Xi - aktuelle Koordinate des Agenten, der aktualisiert werden soll.
• X1 - Koordinate des schlechtesten Agenten in der Population, der die höchste Energie (oder die geringste Fitness) aufweist.
• C - Zufallswert, der mit Hilfe der Levy-Verteilung erzeugt wurde.

2. Aktualisierung koordinieren: Die Koordinate Xi wird gemäß der Gleichung aktualisiert: Xi (t+1)=Xi (t)+C ⋅ (Xi (t)−X1 (t)). Diese Gleichung bedeutet, dass der Agent seine Koordinate auf der Grundlage der Differenz zwischen seiner aktuellen Koordinate und der Koordinate des schlechtesten Agenten ändert. So kann sich der Pflanzenfresser vom schlechtesten Agenten „ernähren“, d. h. auch wenig aussichtsreiche Suchgebiete erkunden.

3. Koordinatengrenze: Nach der Aktualisierung der Koordinate Xi wird diese mit Hilfe der Funktion SeInDiSp, die den neuen Wert, die Mindest- und Höchstgrenze und den Schritt als Argumente erhält, innerhalb eines bestimmten Bereichs begrenzt.

Die Mitgliedern HerbivoreBehavior zeigt, wie sich Pflanzenfresser anpassen können, indem sie sich von den schlechtesten Mitgliedern der Population „ernähren“.

//——————————————————————————————————————————————————————————————————————————————
// Herbivore
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * (Xi(t) - X1(t)) for i ∈ [2, n]
// Herbivore eats only the one with the highest energy (eats the one with the worst FF)
void C_AO_AEO::HerbivoreBehavior (S_AO_Agent &animal, int indCoord)
{
  double Xi = animal.c [indCoord];
  double X1 = a [popSize - 1].c [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);

  Xi = Xi + C * (Xi - X1);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode CarnivoreBehavior in der Klasse C_AO_AEO implementiert das Verhalten eines fleischfressenden Agenten im Rahmen des Algorithmus. Struktur der Methode:

1. Initialisierung von Variablen:

• Xi - aktuelle Koordinate des fleischfressenden Mittels, das aktualisiert wird.
• j - Index eines zufällig ausgewählten Opfers (der Fleischfresser „frisst“ Agenten mit weniger Energie, aber besserer Fitness).
• Xj - Koordinate des Opfers, die zur Aktualisierung der Koordinate des Raubtiers verwendet wird.
• C - Zufallswert, der mit Hilfe der Levy-Verteilung erzeugt wurde.
  

2. Aktualisierung koordinieren: Die Koordinate Xi wird gemäß der Gleichung aktualisiert: Xi (t+1) = Xi (t) + C * (Xj (t) - Xi (t)). Diese Gleichung bedeutet, dass der fleischfressende Agent seine Koordinate auf der Grundlage der Differenz zwischen der Koordinate der Beute und seiner aktuellen Koordinate ändert. So kann sich das Raubtier von seinem Opfer „ernähren“ und dessen Eigenschaften verbessern.

3. Koordinatengrenze: Nach der Aktualisierung der Koordinate Xi wird diese mit der Funktion SeInDiSp auf einen bestimmten Bereich begrenzt.

Die Methode CarnivoreBehavior zeigt, wie sich fleischfressende Agenten anpassen können, indem sie sich von Beute mit weniger Energie „ernähren“. Auf diese Weise können sie ihre Leistung verbessern und optimale Lösungen anstreben. 

//——————————————————————————————————————————————————————————————————————————————
// Carnivorous
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * (Xi(t) - Xj(t)) for i ∈ [3, n]
// Carnivore eats those with less energy (eats those with higher FF)
void C_AO_AEO::CarnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord)
{
  //double Xi = animal.c [indCoord];
  double Xi = animal.cB [indCoord];
  int    j  = u.RNDminusOne (indAnimal);
  //double Xj = a [j].c [indCoord];
  double Xj = a [j].cB [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);

  //Xi = Xi + C * (Xi - Xj);
  Xi = Xi + C * (Xj - Xi);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode OmnivoreBehavior in der Klasse C_AO_AEO beschreibt das Verhalten eines omnivoren Agenten im Kontext eines evolutionären Algorithmus. Struktur der Methode:

1. Initialisierung von Variablen:

• Xi - aktuelle Koordinate des Allesfressers, die aktualisiert werden muss.
• X1 - Koordinate des schlechtesten Agenten (der Agent mit der höchsten Energie).
  
• j - Zufallsindex eines anderen Agenten aus der Population, der zur Aktualisierung der Koordinate verwendet wird.
• Xj - Koordinate eines anderen ausgewählten Agenten.
• C - Zufallswert, der mit Hilfe der Levy-Verteilung erzeugt wurde.
• r - Zufallswahrscheinlichkeit, die zur Mischung der Koordinatenaktualisierung verwendet wird.

2. Aktualisierung koordinieren: Die Koordinate Xi wird gemäß der Gleichung aktualisiert: Xi (t+1) = Xi (t) + C * r * (Xi (t) - X1 (t)) + (1 - r)  (Xi (t) - Xj (t)). Diese Gleichung ermöglicht es dem allesfressenden Agenten, sich anzupassen, indem er sich sowohl von dem schlechtesten Agenten (mit der höchsten Energie) als auch von einem anderen zufälligen Agenten mit geringerer Fitness „ernährt“, was sein Verhalten flexibler macht.

3. Koordinatenbegrenzung: Nach der Aktualisierung der Xi-Koordinate wird diese mit Hilfe der Funktion SeInDiSp innerhalb der angegebenen Grenzen begrenzt.

Die Methode OmnivoreBehavior zeigt, wie sich omnivore Agenten anpassen und von verschiedenen Energiequellen profitieren können, einschließlich schlechterer Agenten und zufällig ausgewählter anderer Agenten mit geringerer Fitness.

//——————————————————————————————————————————————————————————————————————————————
// Omnivorous
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * r2 * (Xi(t) - X1(t)) + (1 - r2) * (Xi(t) - Xj(t)) for i ∈ [3, n]
// An omnivore eats everyone who has more energy (grass and small animals, that is, those who have worse FF)
void C_AO_AEO::OmnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord)
{
  //double Xi = animal.c [indCoord];
  double Xi = animal.cB [indCoord];
  //double X1 = a [popSize - 1].c [indCoord];
  double X1 = a [popSize - 1].cB [indCoord];
  int    j  = u.RNDintInRange (indAnimal + 1, popSize - 1);
  //double Xj = a [j].c [indCoord];
  double Xj = a [j].cB [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);
  double r  = u.RNDprobab ();

  Xi = Xi + C * r * (Xi - X1) + (1.0 - r) * (Xi - Xj);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

Nun, da wir den Code für den Algorithmus implementiert haben, können wir endlich damit beginnen, ihn mit unseren Testfunktionen zu testen.

AEO|Artificial Ecosystem-based Optimization Algorithm|50.0|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.6991675795357223
25 Hilly's; Func runs: 10000; result: 0.34855292688850514
500 Hilly's; Func runs: 10000; result: 0.253085011547826
=============================
5 Forest's; Func runs: 10000; result: 0.6907505745478882
25 Forest's; Func runs: 10000; result: 0.23365521509528495
500 Forest's; Func runs: 10000; result: 0.1558073538195803
=============================
5 Megacity's; Func runs: 10000; result: 0.5430769230769231
25 Megacity's; Func runs: 10000; result: 0.20676923076923082
500 Megacity's; Func runs: 10000; result: 0.1004461538461546
=============================
All score: 3.23131 (35.90%)

Bei den Tests erreichte der Algorithmus etwa 36 %. Dies ist ein durchschnittliches Ergebnis. Für diesen Algorithmus habe ich beschlossen, die Methode Moving zu überarbeiten, und das Ergebnis sieht folgendermaßen aus:

Modifizierte Logik der Agentenbewegung unter Berücksichtigung verschiedener Verhaltensmodelle (Produktion, Verbrauch und Zersetzung) in der Methode Moving:

1. Die anfängliche Initialisierung der Population bleibt unverändert.

2. Das Aktualisierungsverhältnis α wird in Abhängigkeit von der aktuellen Epoche berechnet und nimmt mit zunehmender EpocheNow ab. Dieses Verhältnis wird außerhalb einer separaten privaten Methode verschoben.

3. Produktion (consModel == 0) - in diesem Teil aktualisieren die Agenten ihre Koordinaten anhand einer Gleichung, die auf dem vorherigen Zustand und einem Zufallswert basiert. Dadurch können sie neue Zustände „produzieren“.

4. Verbrauch (consModel == 1). Hier teilen wir die Agenten je nach Zufallswert in drei Gruppen ein:

• Pflanzenfresser.
• Fleischfresser.
• Allesfresser.

5. Zersetzung: In dieser Phase interagieren die Agenten miteinander und ändern ihre Koordinaten auf der Grundlage von Zufallswerten und Interaktionen mit anderen Agenten.

6. Rückstellung des Verbrauchsmodells: Am Ende des consModel auf 0 setzen, um eine neue Schleife zu beginnen.

Wie Sie sehen können, besteht die wichtigste Änderung in der Logik des Algorithmus darin, dass die Produktion in eine separate Phase eingeteilt wird. Hierfür ist eine eigene Ära vorgesehen, die eine erhebliche Umwälzung der Organismenpopulation ermöglicht. Dies spiegelt sich auch im Verhalten des AEO während der Visualisierung wider: Wir sehen ein „Blinken“, d.h. einzelne Stadien des künstlichen Ökosystems können auch visuell wahrgenommen werden.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double α = (1.0 - (double)epochNow / epochs);

  double Xi   = 0.0;
  double Xb   = 0.0;
  double Xr   = 0.0;
  double Xj   = 0.0;
  double C    = 0.0;
  int    j    = 0;
  double r    = 0.0;

  // Production --------------------------------------------------------------
  // X(t + 1) = (1 - α) * Xb(t) + α * Xrnd (t)
  // α = (1 - t / T) * rnd [0.0; 1.0]
  // Xrnd = rnd [Xmin; Xmax]
  if (consModel == 0)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        Xb = cB [c];
        Xr = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        //Xi = Xb + α * (Xr - Xb);
        Xi = Xb + α * (Xb - Xr);

        a [i].c [c] = u.SeInDiSp (Xi, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    consModel++;
    return;
  }

  // Consumption --------------------------------------------------------------- 
  if (consModel == 1)
  {
    for (int i = 0; i < popSize; i++)
    {
      if (i > 1)
      {
        for (int c = 0; c < coords; c++)
        {
          r = u.RNDprobab ();

          // Herbivore behavior ------------------------------------------------ 
          //Xi (t + 1) = Xi (t) + C * (Xi (t) - Xb (t));
          if (r < 0.333)
          {
            C  = u.LevyFlightDistribution (levisPower);
            Xb = cB [c];
            //Xi = a [i].c [c];
            Xi = a [i].cB [c];

            //Xi = Xi + C * (Xi - Xb);
            Xi = Xi + C * (Xb - Xi);
          }
          else
          {
            // Carnivore behavior ---------------------------------------------- 
            //Xi (t + 1) = Xi (t) + C * (Xi (t) - Xj (t));
            if (r < 0.667)
            {
              C  = u.LevyFlightDistribution (levisPower);
              j  = u.RNDminusOne (i);
              //Xj = a [j].c [c];
              Xj = a [j].cB [c];
              //Xi = a [i].c [c];
              Xi = a [i].cB [c];

              //Xi = Xi + C * (Xi - Xj);
              Xi = Xi + C * (Xj - Xi);
            }
            // Omnivore behavior ----------------------------------------------- 
            //Xi (t + 1) = Xi (t) + C * r2 * (Xi (t) - Xb (t)) +
            //                    (1 - r2) * (Xi (t) - Xj (t));
            else
            {
              C  = u.LevyFlightDistribution (levisPower);
              Xb = cB [c];
              j  = u.RNDminusOne (i);
              //Xj = a [j].c [c];
              Xj = a [j].cB [c];
              //Xi = a [i].c [c];
              Xi = a [i].cB [c];
              r = u.RNDprobab ();

              //Xi = Xi + C * r * (Xi - Xb) +
              //     (1 - r) * (Xi - Xj);
              Xi = Xi + C * r * (Xb - Xi) +
                   (1 - r) * (Xj - Xi);
            }
          }

          a [i].c [c] = u.SeInDiSp (Xi, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }
    }

    consModel++;
    return;
  }

  // Decomposition -------------------------------------------------------------
  double D = 0.0;
  double h = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    D = 3 * u.RNDprobab ();
    h = u.RNDprobab () * (u.RNDprobab () < 0.5 ? 1 : -1);
    C = u.LevyFlightDistribution (levisPower);
    j = u.RNDminusOne (popSize);

    for (int c = 0; c < coords; c++)
    {
      double x = a [i].cB [c] + D * (C * a [i].cB [c] - h * a [j].c [c]);
      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  consModel = 0;
}
//——————————————————————————————————————————————————————————————————————————————

Testergebnisse

Jetzt können wir den Algorithmus mit meinen Änderungen in der Logik erneut testen. 

AEO|Artificial Ecosystem-based Optimization Algorithm|50.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9137986747745103
25 Hilly's; Func runs: 10000; result: 0.4671288391599192
500 Hilly's; Func runs: 10000; result: 0.2647022528159094
=============================
5 Forest's; Func runs: 10000; result: 0.9022293417142482
25 Forest's; Func runs: 10000; result: 0.4370486099190667
500 Forest's; Func runs: 10000; result: 0.2139965996985526
=============================
5 Megacity's; Func runs: 10000; result: 0.6615384615384616
25 Megacity's; Func runs: 10000; result: 0.30799999999999994
500 Megacity's; Func runs: 10000; result: 0.28563076923076974
=============================
All score: 4.45407 (49.49%)

Es ist bemerkenswert, dass es keine signifikante Streuung in den Ergebnissen gibt. Der Algorithmus vermeidet erfolgreich lokale Fallen, obwohl die Konvergenzgenauigkeit durchschnittlich ist. Auch das bereits erwähnte „Blinken“ beim Umschalten der Stufen ist zu beobachten. Der Algorithmus zeigt das ungewöhnlichste Verhalten bei der diskreten Megacity-Funktion, indem er Koordinatengruppen in separate vertikale und diagonale Linien aufteilt, die durch wichtige Bereiche der Oberfläche verlaufen. Dies spiegelt sich auch in den Ergebnissen der Arbeit mit dieser diskreten Funktion wider - sie sind die besten in der Bewertungstabelle für eine diskrete Funktion mit 1000 Variablen.

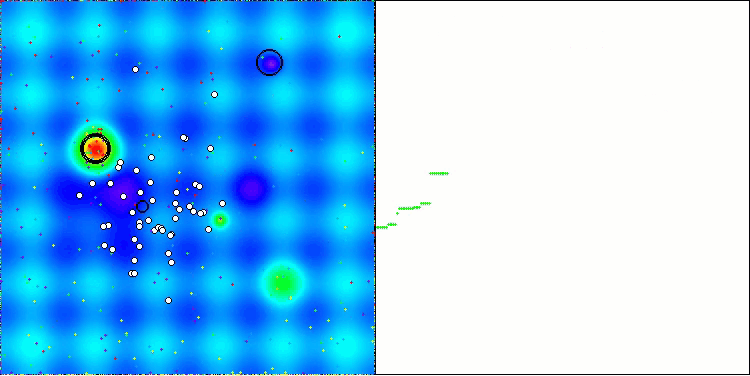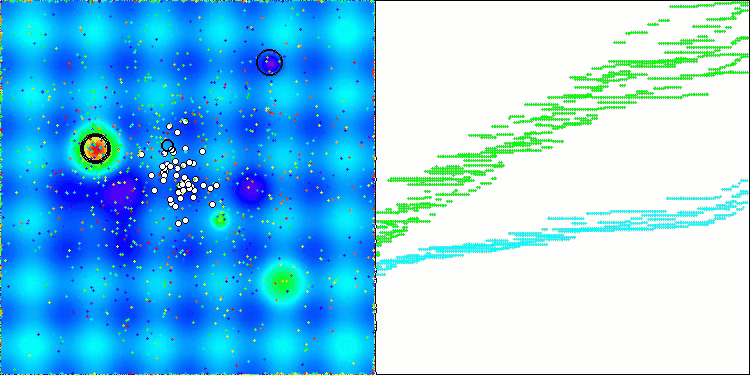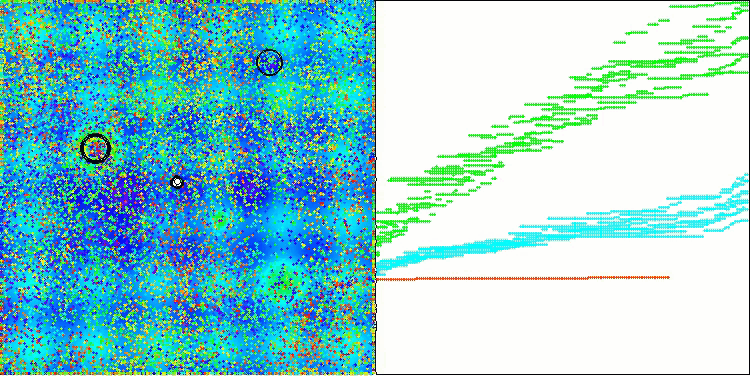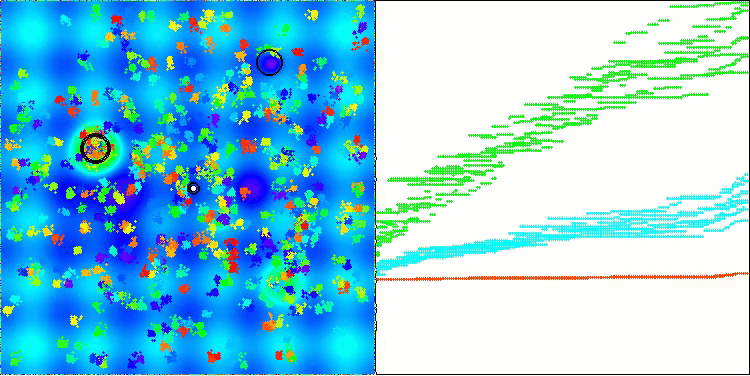
AEO mit der Testfunktion Hilly

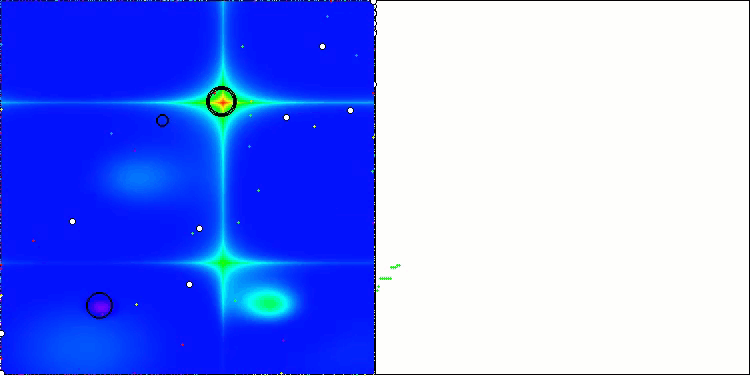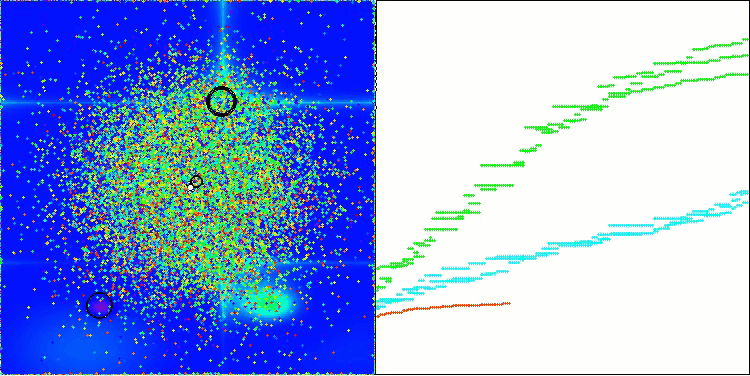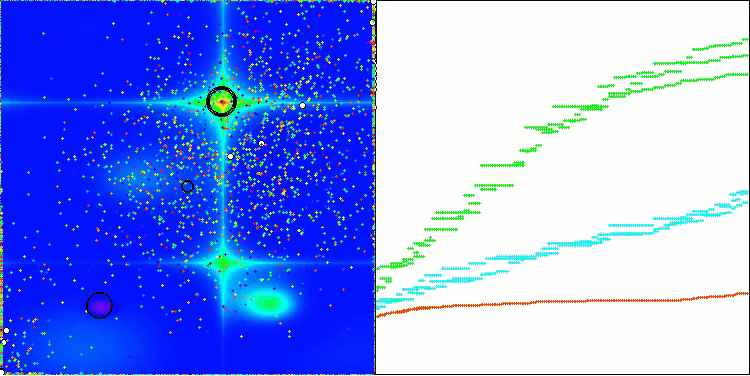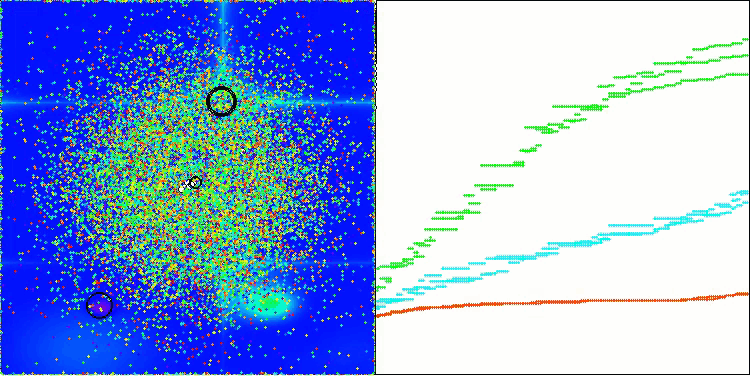
AEO mit der Testfunktion Forest

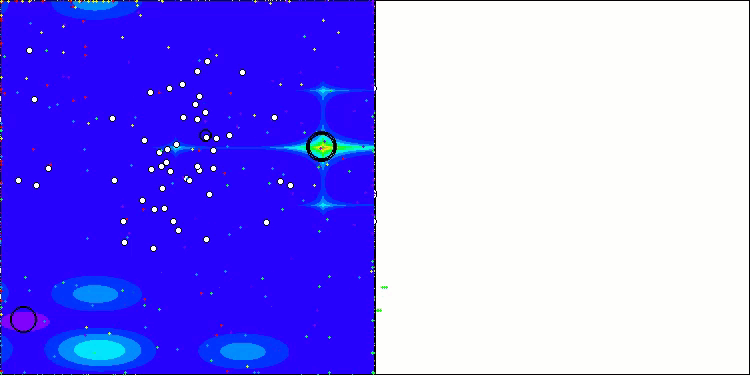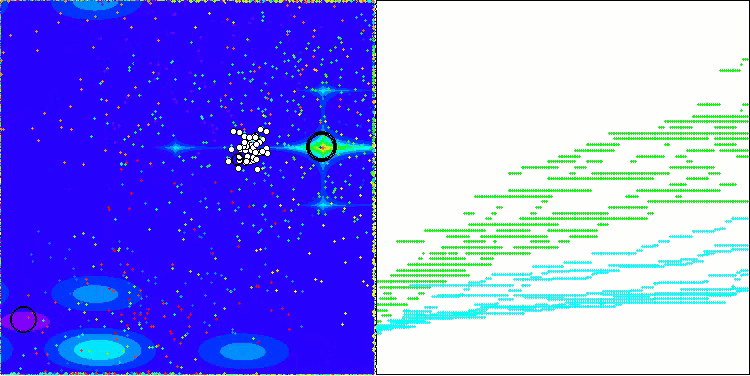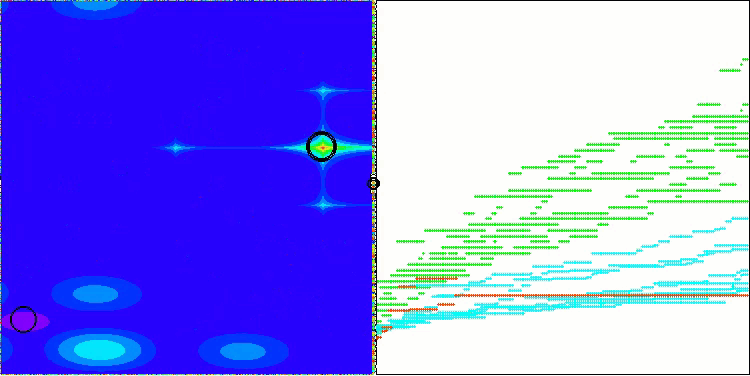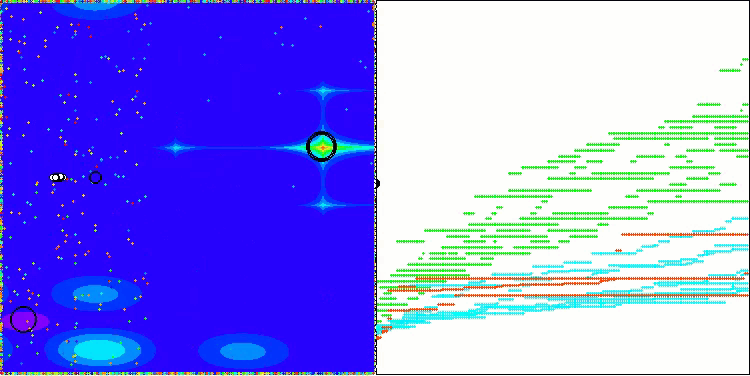
AEO mit der Testfunktion Megacity

Wie Sie sehen können, hat der Algorithmus seine Leistung im Vergleich zur ursprünglichen Version erheblich verbessert und erreicht nun etwa 50 % des maximal möglichen Wertes. Das ist ein wirklich beeindruckendes Ergebnis! In der Bewertungstabelle nimmt der Algorithmus den 25. Platz ein, was ebenfalls bemerkenswert ist. Besonders beeindruckend ist, dass AEO bei der diskreten Funktion Megacity einen neuen Rekord aufstellte und das Ergebnis für 1000 Parameter um satte 5% verbesserte!

#	AO	Beschreibung	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	Suche über die gesamte Nachbarschaft	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	Zahlenschloss-Algorithmus (joo)	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	Optimierung der Tierwanderung M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5.987	66,52
4	(P+O)ES	(P+O) Entwicklungsstrategien	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	Kometenschweif-Algorithmus (joo)	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	stochastische Diffusionssuche M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	AAm	Algorithmus für das Bogenschießen M	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
8	ESG	Entwicklung sozialer Gruppen (joo)	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
9	SIA	Simuliertes isotropes Abkühlen (Joo)	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
10	ACS	künstliche kooperative Suche	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
11	ASO	Optimierung einer anarchischen Gesellschaft	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5.178	57,54
12	TSEA	Schildkrötenpanzer-Evolutionsalgorithmus (joo)	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
13	DE	differentielle Evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
14	CRO	Optimierung chemischer Reaktionen	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
15	BSA	Vogelschwarm-Algorithmus	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
16	HS	Harmoniesuche	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
17	SSG	Setzlinge säen und wachsen	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
18	BCOm	Optimierung der bakteriellen Chemotaxis M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
19	ABO	Optimierung nach afrikanischen Büffeln	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
20	(PO)ES	(PO) Evolutionsstrategien	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
21	TSm	Tabu-Suche M	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
22	BSO	Brainstorming-Optimierung	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
23	WOAm	Wal-Optimierungsalgorithmus M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
24	AEFA	Algorithmus für künstliche elektrische Felder	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
25	AEO	Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
26	ACOm	Ameisen-Kolonie-Optimierung M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
27	BFO-GA	Optimierung der bakteriellen Nahrungssuche - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
28	ABHA	Algorithmus für künstliche Bienenstöcke	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
29	ACMO	Optimierung atmosphärischer Wolkenmodelle	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
30	ASHA	Algorithmus für künstliches Duschen	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
31	ASBO	Optimierung des adaptiven Sozialverhaltens	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
32	MEC	Evolutionäre Berechnung des Geistes	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
33	IWO	Optimierung invasiver Unkräuter	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
34	Micro-AIS	Künstliches Mikro-Immunsystem	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
35	COAm	Optimierungsalgorithmus des Kuckucks M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
36	SDOm	Optimierung der Spiraldynamik M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
37	NMm	Nelder-Mead-Verfahren M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
38	FAm	Firefly-Algorithmus M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
39	GSA	Algorithmus für die Gravitationssuche	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
40	BFO	Optimierung der bakteriellen Futtersuche	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
41	ABC	künstliches Bienenvolk	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
42	BA	Fledermaus-Algorithmus	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
43	AAA	adaptiver Algorithmus für Algen	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23
44	SA	simuliertes Abkühlen	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
45	IWDm	intelligente Wassertropfen M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06

Zusammenfassung

Die Merkmale und Vorteile des Algorithmus:

1. Gleichgewicht zwischen Erkundung und Ausbeutung. AEO bietet ein gutes Gleichgewicht zwischen der globalen Erkundung des Lösungsraums (durch Produktion und Verbrauch) und der lokalen Nutzung (durch Zerlegung).

2. Anpassungsfähigkeit. Der Algorithmus passt sich durch verschiedene Lösungsaktualisierungsstrategien an die Problemlandschaft an.

3. Einfachheit. Trotz der biologischen Metapher ist der Algorithmus relativ einfach zu implementieren und zu verstehen.

4. Hervorragende Ergebnisse zu diskreten Funktionen mit großen Dimensionen.

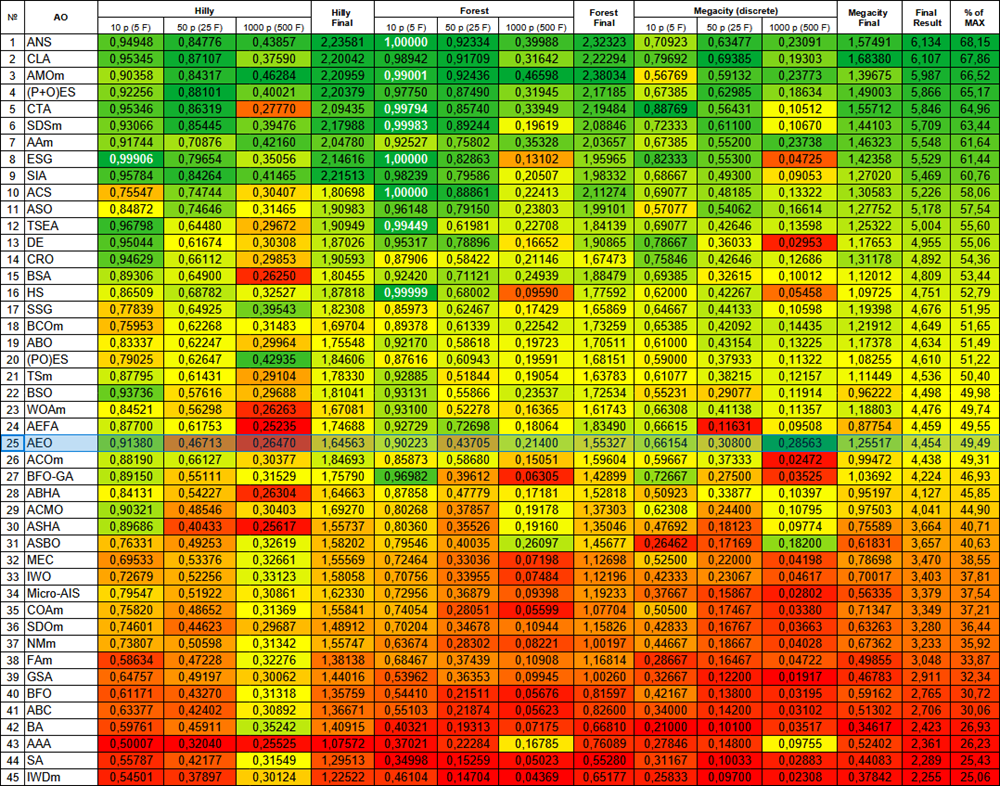
Abbildung 2. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben

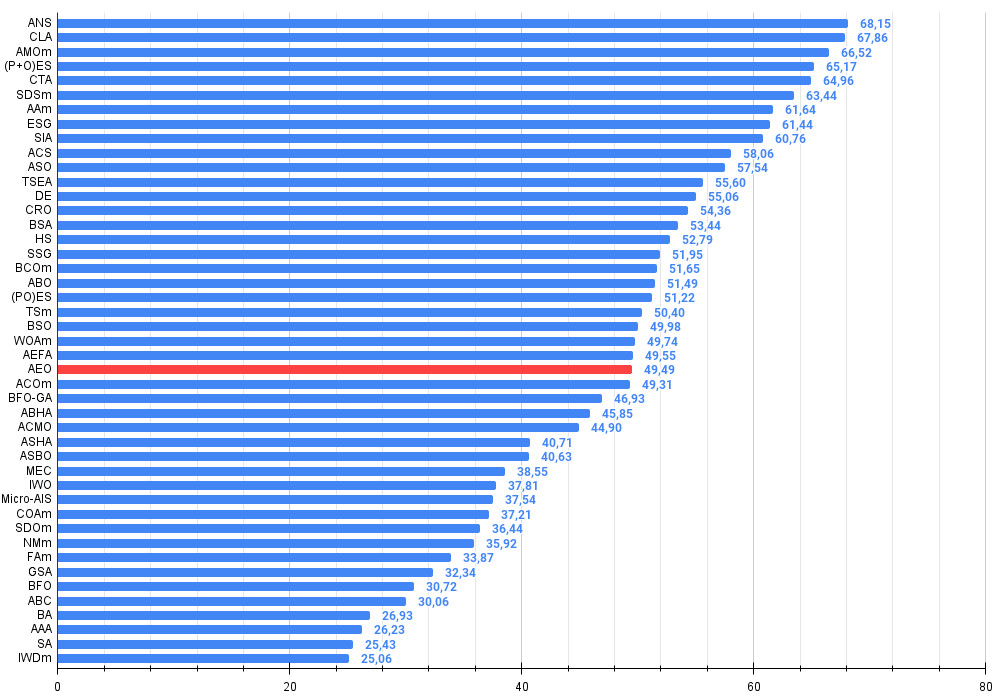
Abbildung 3. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,

wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Wertungstabelle)

Vor- und Nachteile des AEO:

Vorteile:

1. Nur ein externer Parameter (neben der Populationsgröße).
   
2. Gute Leistungen bei der diskreten Funktion.

Nachteile

1. Nicht die höchste Konvergenzgenauigkeit.
   

Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5