Оптимизация африканскими буйволами — African Buffalo Optimization (ABO)
625
5
Содержание
Введение
Алгоритм оптимизации африканских буйволов (African Buffalo Optimization, ABO) представляет собой метаэвристический подход, вдохновлённый удивительным поведением этих животных в дикой природе. Основываясь на социальном взаимодействии и стратегиях выживания африканских буйволов, алгоритм ABO был разработан в 2015 году учеными Джулиусом Бенеолучи Одили и Мохдом Низамом Кахаром.
Африканские буйволы известны своей способностью к коллективной защите и слаженной координации при поиске пищи и воды. Эти животные живут в крупных стадах, что обеспечивает им защиту от хищников и способствует формированию плотных групп, где взрослые особи заботятся о молодых и слабых. При нападении хищников буйволы демонстрируют впечатляющую способность к координации: они могут образовывать круг вокруг уязвимых членов стада, или атаковать врага совместными усилиями.
Основные принципы алгоритма ABO отражают ключевые аспекты поведения буйволов. Во-первых, общение: буйволы используют звуковые сигналы для координации своих действий, что в алгоритме соответствует обмену информацией между агентами. Во-вторых, обучение: буйволы учатся на собственном опыте и опыте других членов стада, что в алгоритме реализуется через обновление позиций агентов на основе собранной информации.
Уникальность поведения африканских буйволов делает их интересным источником вдохновения для алгоритмов оптимизации. Эти животные способны адаптироваться к изменениям в окружающей среде, совершая сезонные миграции в поисках пищи и воды, и преодолевая большие расстояния в поисках благоприятных условий. Во время миграций буйволы применяют стратегии поиска, которые позволяют им эффективно находить ресурсы и избегать опасностей.
Таким образом, поведение африканских буйволов, отличающееся высокой степенью координации, коллективной защиты и адаптации, служит мощным стимулом для разработки алгоритмов оптимизации, таких как ABO. Эти аспекты делают алгоритм эффективным инструментом для решения сложных задач, вдохновляясь природными механизмами, которые обеспечивают выживание и процветание этих удивительных животных в дикой природе.
Реализация алгоритма
Алгоритм African Buffalo Optimization (ABO) использует инстинкты поведения африканских буйволов, такие как сотрудничество и социальное взаимодействие, для решения задач оптимизации. Принципы его работы заключаются в следующем:
1. Алгоритм начинается с инициализации популяции буйволов, где каждый буйвол представляет собой потенциальное решение в пространстве решений. Позиции буйволов инициализируются случайным образом в данном пространстве.
2. Каждое решение (положение буйвола) оценивается с помощью функции фитнеса. Если фитнес текущего буйвола лучше, чем его лучший предыдущий фитнес "bp_max", то его позиция сохраняется. Аналогично, если фитнес лучше, чем лучший фитнес по всей стае "bg_max", то эта позиция также сохраняется.
3. Алгоритм обновляет позиции буйволов на основе двух основных сигналов — "maaa" (остаться и эксплуатировать) и "waaa" (двигаться и исследовать). Эти сигналы помогают буйволам оптимизировать поиск источников пищи.
4.W.k + 1 = W.k + lp * r1 * (bgmaxt.k - m.k) + lp * r2 * (bpmax.k - m.k): Это уравнение обновляет перемещение буйвола. W.k представляет собой перемещение для исследования, а m.k — текущее положение буйвола для эксплуатации. lp1 и lp2 — это факторы обучения, а r1 и r2 — случайные числа в интервале [0,1]. bgmax — это лучшее положение среди всей стаи, а bpmax — лучшее положение конкретного буйвола.
В этом уравнении (bgmaxt.k - m.k) представляет собой сигнал "maaa", а (bpmax.k - m.k) — сигнал "waaa".
5. Далее обновляется положение буйвола k относительно его личного текущего положения и рассчитанного в предыдущей формуле перемещения, с использованием следующего уравнения: m.k + 1 = λ * (W.k + m.k). Это уравнение определяет новое местоположение буйвола, где λ — коэффициент движения.
6. Если критерии остановки не выполнены, возвращаемся к шагу 2 для повторного обновления значений фитнеса.
7. Когда достигнут критерий остановки, алгоритм завершает работу и выводит вектор положения, представляющий лучшее найденное решение для данной задачи.
Опишем структуру "S_Buffalo" и класс "C_AO_ABO", реализующие основу алгоритма.
- S_Buffalo — структура, представляющая буйвола. Она содержит массив "w", который описывает вектор перемещения агента в алгоритме.
- В конструкторе класса устанавливаются параметры, такие как размер популяции "popSize", факторы обучения "lp1", "lp2" и значение "lambda", которые используются в алгоритме.
- Метод "SetParams" позволяет устанавливать параметры алгоритма на основе значений, хранящихся в массиве "params".
- Метод "Init" — предназначен для инициализации алгоритма. Он принимает минимальные и максимальные границы поиска, шаг поиска и количество эпох.
- Методы "Moving" и "Revision" реализуют основные шаги алгоритма оптимизации: перемещение (поиск нового решения) и ревизию (проверка и обновление решений).
- Поля класса "lp1", "lp2" и "lambda" используются для управления поведением алгоритма.
- Массив "b" типа "S_Buffalo" хранит экземпляры буйволов, которые участвуют в процессе оптимизации.
//—————————————————————————————————————————————————————————————————————————————— struct S_Buffalo { double w []; }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— class C_AO_ABO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ABO () { } C_AO_ABO () { ao_name = "ABO"; ao_desc = "African Buffalo Optimization"; ao_link = "https://www.mql5.com/ru/articles/16024"; popSize = 50; // размер популяции lp1 = 0.7; // фактор обучения 1 lp2 = 0.5; // фактор обучения 2 lambda = 0.3; // лямбда для уравнения движения ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "lp1"; params [1].val = lp1; params [2].name = "lp2"; params [2].val = lp2; params [3].name = "lambda"; params [3].val = lambda; } void SetParams () { popSize = (int)params [0].val; lp1 = params [1].val; lp2 = params [2].val; lambda = params [3].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double lp1; // фактор обучения 1 double lp2; // фактор обучения 2 double lambda; // лямбда для уравнения движения private: //------------------------------------------------------------------- S_Buffalo b []; }; //——————————————————————————————————————————————————————————————————————————————
Метод "Init" класса "C_AO_ABO" отвечает за инициализацию параметров для алгоритма. Параметры метода:
- rangeMinP [] — массив задает минимальные значения для диапазонов параметров.
- rangeMaxP [] — массив задает максимальные значения для диапазонов параметров.
- rangeStepP [] — массив задает шаги для изменения значений параметров.
- epochsP — количество эпох (итераций), по умолчанию равное 0. Этот параметр используется для определения количества итераций в процессе оптимизации.
Логика работы метода:
1. Стандартная инициализация: метод сначала вызывает "StandardInit" с переданными массивами "rangeMinP", "rangeMaxP" и "rangeStepP". Если эта инициализация не удалась, то возвращает "false".
2. Инициализация популяции:
- Метод изменяет размер массива "b" до значения "popSize", что соответствует количеству поисковых агентов в популяции.
- Для каждого агента в популяции (в цикле от 0 до "popSize"): изменяется размер массива "b [i].w" до значения "coords", что соответствует количеству координат (оптимизируемых параметров задачи) для каждого индивидуума.
- Массив "b [i].w" инициализируется нулями с помощью "ArrayInitialize".
3. Если все операции выполнены успешно, метод возвращает "true", что сигнализирует об успешной инициализации.
Метод "Init" отвечает за подготовку необходимых структур данных для алгоритма, обеспечивая корректную инициализацию параметров и популяции. Это важный шаг перед выполнением основного алгоритма, который будет использовать эти данные для оптимизации.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ABO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (b, popSize); for (int i = 0; i < popSize; i++) { ArrayResize(b [i].w, coords); ArrayInitialize (b [i].w, 0.0); } return true; } //——————————————————————————————————————————————————————————————————————————————
Метод "Moving" класса "C_AO_ABO" отвечает за перемещение буйволов популяции по пространству поиска в процессе оптимизации. Ниже приведено подробное описание его работы:
1. Метод сначала проверяет, была ли выполнена ревизия "if (!revision)", если ревизия еще не была проведена, он инициализирует популяцию случайными значениями:
- Внешний цикл проходит по всем индивидуумам в популяции "popSize".
- Внутренний цикл проходит по всем координатам "coords".
Для каждого параметра:
- Сначала генерируется случайное значение в диапазоне от "rangeMin [c]" до "rangeMax [c]" с помощью метода "u.RNDfromCI".
- Затем это значение проходит проверку и корректировку с помощью метода "u.SeInDiSp", который ограничивает значение в заданном диапазоне с учетом шага "rangeStep [c]".
- После завершения инициализации "revision" устанавливается в "true", и метод завершает выполнение.
2. Основная логика перемещения буйволов. Если ревизия уже была выполнена, метод переходит к обновлению положения буйволов в пространстве:
- Инициализируются переменные "w", "m", "r1", "r2", "bg", и "bp" для дальнейших вычислений.
- Внешний цикл проходит по всем индивидуумам в популяции "popSize".
- Внутренний цикл проходит по всем координатам "coords":
- Генерируются два случайных значения "r1" и "r2" для использования в обновлении положения буйволов, внося элемент случайности в их поведении.
- "bg" и "bp" получают значения из соответствующих массивов: "cB [c]" (глобальные лучшие координаты стада) и "a [i].cB [c]" (индивидуальные лучшие координаты буйвола).
- "m" получает значение элемента вектора текущего положения "a [i].c [c]", а "w" — значение элемента вектора текущего перемещения "b [i].w [c]" буйвола по соответствующей координате.
- Обновляется значение вектора перемещения "b [i].w [c]" по формуле, которая учитывает как глобальное, так и локальное лучшее положение буйвола: b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m).
- Затем положение по соответствующей координате "m" обновляется с учетом коэффициента "lambda".
- Наконец, новое значение координаты поискового агента "a [i].c [c]" вычисляется и корректируется с помощью "u.SeInDiSp".
Метод "Moving" отвечает за инициализацию и обновление положения и осуществляет перемещение членов популяции в процессе оптимизации. Он использует случайные значения для инициализации и обновление положения буйволов так же с применением случайных чисел на основе как глобальных, так и локальных лучших известных положений животных в стаде.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Метод "Revision" класса "C_AO_ABO" отвечает за обновление лучших значений функции и параметров в популяции. Описание метода:
1. Переменная "ind" инициализируется значением "-1". Она будет использоваться для хранения индекса индивидуумов с наилучшей функцией.
2. Поиск глобального лучшего индивидуума:
- Цикл "for" проходит по всем агентам в популяции "popSize":
- Для каждого агента проверяется, превышает ли его значение функции приспособленности "a [i].f" текущее глобальное лучшее значение "fB".
- Если это так, обновляется "fB" и сохраняется индекс этого агента в переменной "ind".
- После завершения цикла, если был найден лучший агент (т.е. "ind" не равен "-1"), вызывается функция "ArrayCopy", которая копирует параметры "c" этого агента в глобальный лучший массив параметров "cB".
3. Обновление локальных лучших значений:
- Второй цикл "for" снова проходит по всем агентам в популяции.
- Для каждого агента проверяется, превышает ли его значение функции приспособленности "a [i].f" его локальное лучшее значение "a [i].fB".
- Если это так, локальное лучшее значение "a [i].fB" обновляется, и координаты этого агента копируются в его локальный лучший массив координат "cB".
Метод "Revision" выполняет две основные задачи:
- Находит и обновляет глобальное лучшее значение функции приспособленности и соответствующие параметры.
- Обновляет локальные лучшие значения функции приспособленности и параметры для каждого агента в популяции.
Эта логика характерна для тех оптимизационных алгоритмов, для которых важно отслеживать как глобальные, так и локальные оптимумы для улучшения поиска решения.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Собственно, мы разобрали всю реализацию алгоритма, она достаточно проста, теперь можем перейти к этапу тестирования.
Посмотрим, как работает версия авторов алгоритма ABO:
=============================
5 Hilly's; Func runs: 10000; result: 0.8495807203797128
25 Hilly's; Func runs: 10000; result: 0.5186057937632769
500 Hilly's; Func runs: 10000; result: 0.2642792490546295
=============================
5 Forest's; Func runs: 10000; result: 0.6554510234450559
25 Forest's; Func runs: 10000; result: 0.41662244493546935
500 Forest's; Func runs: 10000; result: 0.21044033116304034
=============================
5 Megacity's; Func runs: 10000; result: 0.6015384615384616
25 Megacity's; Func runs: 10000; result: 0.26430769230769224
500 Megacity's; Func runs: 10000; result: 0.11120000000000112
=============================
All score: 3.89203 (43.24%)
Скажем так — результат неплохой. Однако я не был бы собой, если бы не попытался улучшить алгоритм. В авторской версии новое местоположение буйволов рассчитывается на основе предварительного вычисления вектора перемещения (приращения к текущему положению), основываясь на информации о глобальном лучшем положении в стаде, лучшем положении рассматриваемого буйвола и его текущем местоположении. Этот вектор перемещения выполняет роль своеобразной инерции в движении.
Мне пришла в голову идея отказаться от инерции и использовать информацию о лучших позициях как своего, так и стада напрямую, применяя расчёт к текущему положению. Мы закомментируем авторский участок кода и напишем новый, более простой, при этом избавившись от одного внешнего параметра — лямбды. Новый код выделен зелёным цветом.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { /* r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); */ r1 = u.RNDfromCI (-lp1, lp1); r2 = u.RNDfromCI (-lp2, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; m = m + r1 * (bg - m) + r2 * (bp - m); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Вот какие результаты получились после модификации логики перемещения буйволов:
=============================
5 Hilly's; Func runs: 10000; result: 0.833371781687727
25 Hilly's; Func runs: 10000; result: 0.6224659624836805
500 Hilly's; Func runs: 10000; result: 0.2996410968574058
=============================
5 Forest's; Func runs: 10000; result: 0.9217022975045926
25 Forest's; Func runs: 10000; result: 0.5861755787948962
500 Forest's; Func runs: 10000; result: 0.19722782275756043
=============================
5 Megacity's; Func runs: 10000; result: 0.6100000000000001
25 Megacity's; Func runs: 10000; result: 0.4315384615384614
500 Megacity's; Func runs: 10000; result: 0.13224615384615512
=============================
All score: 4.63437 (51.49%)
Результаты улучшились почти на 10%: 51.49% против 43.24%. Особенно заметны улучшения на функциях с 50 и 1000 параметрами, тогда как на функциях с 10 параметрами изменения почти неуловимы. Это свидетельствует о повышении способности алгоритма к масштабированию на задачах большой размерности.
Теперь осталось проверить ещё одну идею: что если в формуле использовать не лучшее положение быка, а лучшее положение случайно выбранного быка из стада, при этом смещая вероятность к началу списка особей в популяции? Это легко проверить, и для этого нужно будет внести всего несколько изменений в код. Смещение вероятности к началу списка популяции обеспечивает возведение случайного числа [0.0;1.0] в степень и отбрасывание дробной части полученного числа. В данном случае используется степень "4".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { /* r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); */ r1 = u.RNDfromCI (-lp1, lp1); r2 = u.RNDfromCI (-lp2, lp2); bg = cB [c]; //bp = a [i].cB [c]; double r = u.RNDprobab (); int ind = (int)pow (r - 1, 4); bp = a [ind].cB [c]; m = a [i].c [c]; m = m + r1 * (bg - m) + r2 * (bp - m); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Для применения вероятностного выбора особей в популяции со смещением в сторону лучших быков, нам потребуется сортировка по уровню приспособленности отдельных особей в методе "Revision". К счастью, соответствующий метод "Sorting_fB" уже был добавлен в одной из предыдущих статей.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Посмотрим на результаты применения вероятностного выбора лучшей позиции быков в стаде для использования в формуле расчета новой позиции в алгоритме ABO:
ABO|African Buffalo Optimization|50.0|0.1|0.8|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.841272551476775
25 Hilly's; Func runs: 10000; result: 0.5701677694693293
500 Hilly's; Func runs: 10000; result: 0.28850644933225034
=============================
5 Forest's; Func runs: 10000; result: 0.9015705858486595
25 Forest's; Func runs: 10000; result: 0.49493378365495344
500 Forest's; Func runs: 10000; result: 0.1919604395333699
=============================
5 Megacity's; Func runs: 10000; result: 0.5692307692307692
25 Megacity's; Func runs: 10000; result: 0.35261538461538455
500 Megacity's; Func runs: 10000; result: 0.12010769230769343
=============================
All score: 4.33037 (48.12%)
Общая результативность алгоритма ухудшилась, однако всё еще остается выше, чем у "чистого" авторского варианта. В связи с этим зафиксируем результаты первого эксперимента по модификации алгоритма и внесем их в рейтинговую таблицу. Хочу отметить, что для каждой версии алгоритма подбирались внешние параметры с целью обеспечения максимальной производительности по всем тестам, поскольку изменение логики алгоритма приводит к изменению его поведения в пространстве поиска.
Результаты тестов
На визуализации работы алгоритма ABO можно отметить достаточно хорошую проработку значимых участков гиперпространства, что говорит о высокой способности к исследованию поверхности оптимизируемой функции. К сожалению, небольшая модификация, улучшая масштабируемость алгоритма, увеличивает вероятность застревания на задачах малой размерности, что можно заметить по разбросу результатов (зеленые линии графика сходимости на визуализации).
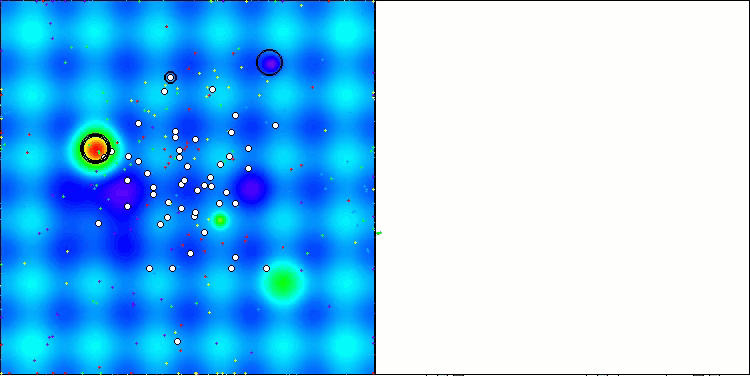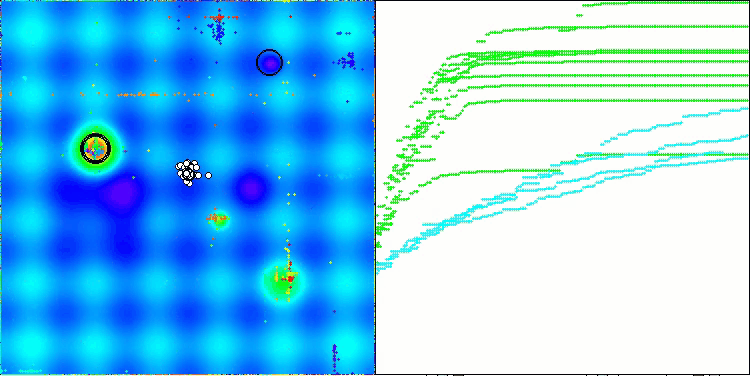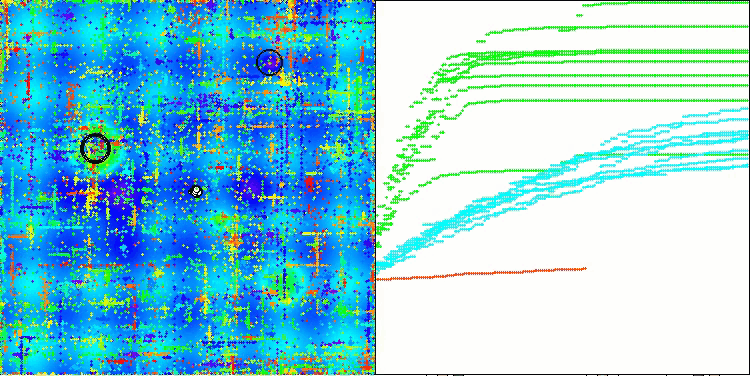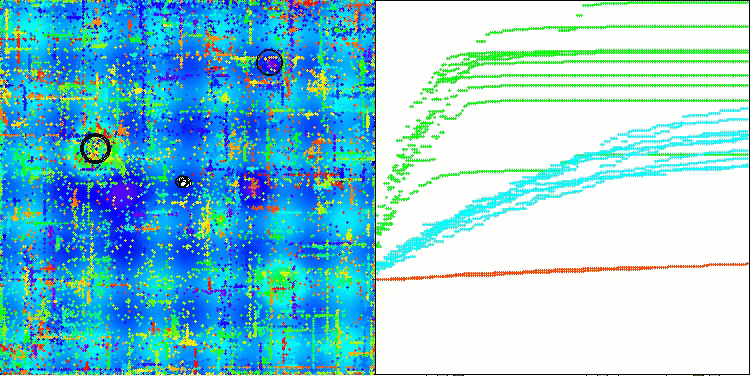
ABO на тестовой функции Hilly
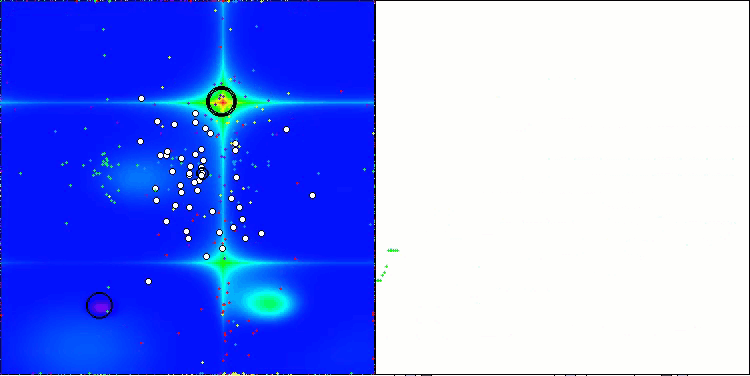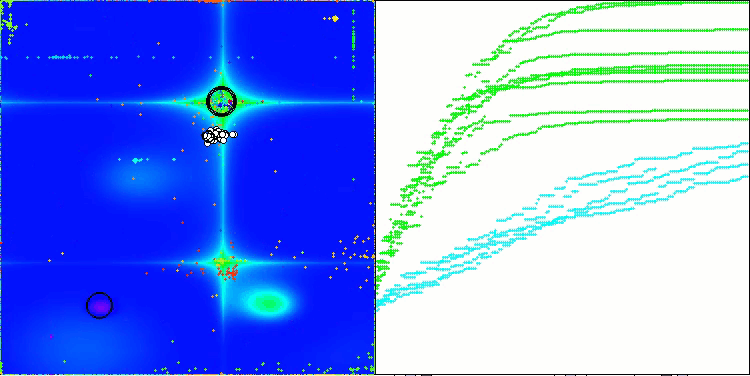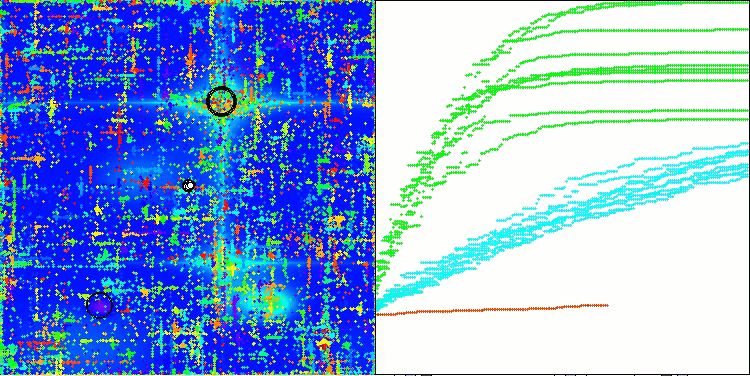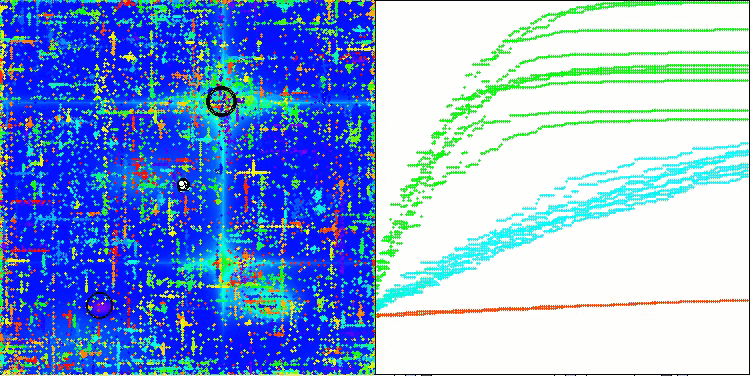
ABO на тестовой функции Forest
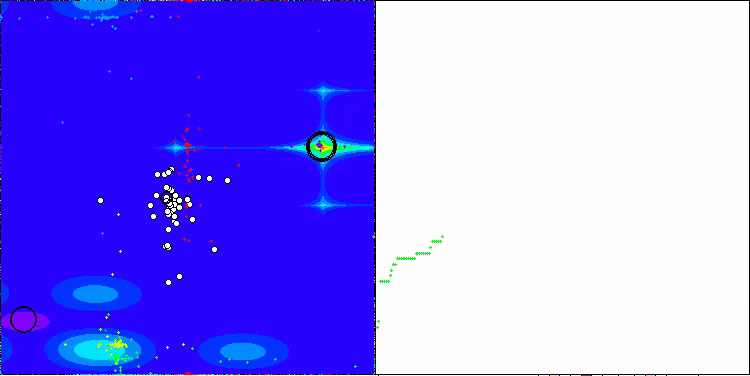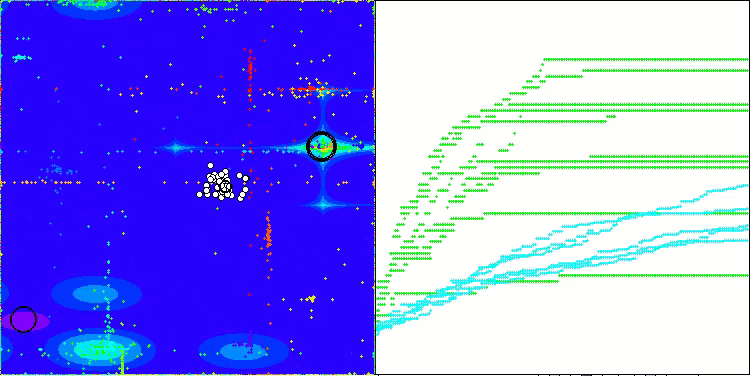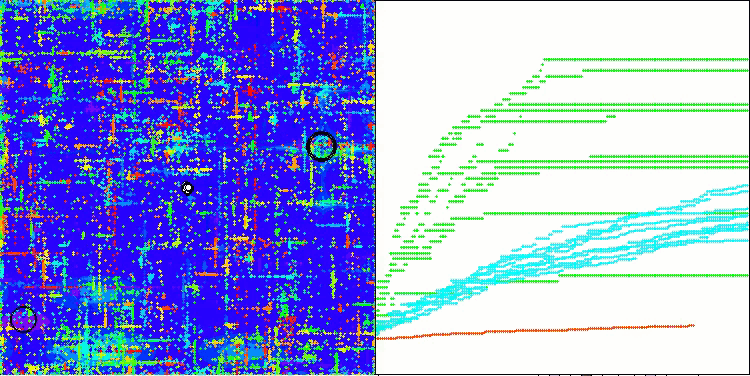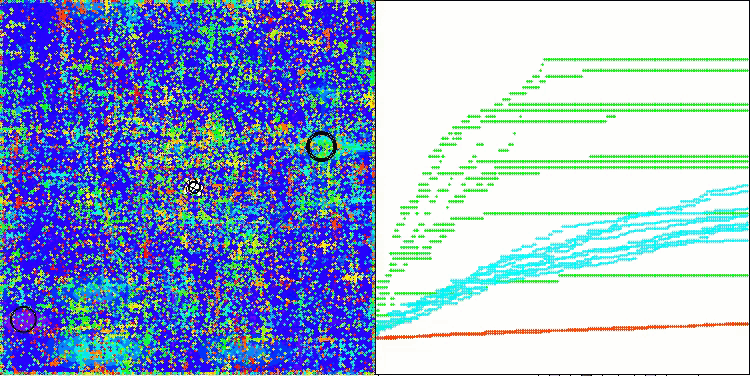
ABO на тестовой функции Megacity
Алгоритм по итогам тестирования занял стабильное 19 место в общем рейтинге алгоритмов оптимизации.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 12 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 13 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 14 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 15 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 16 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 17 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 18 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 19 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 20 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 21 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 22 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 23 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 24 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 25 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 26 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 27 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 28 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 29 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 30 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 31 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 32 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 33 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 34 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 35 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 36 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 37 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 38 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 39 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 40 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 41 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 42 | AAA | algae adaptive algorithm | 0,50007 | 0,32040 | 0,25525 | 1,07572 | 0,37021 | 0,22284 | 0,16785 | 0,76089 | 0,27846 | 0,14800 | 0,09755 | 0,52402 | 2,361 | 26,23 |
| 43 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 44 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 45 | PSO | particle swarm optimisation | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
Выводы
Вашему вниманию были представлены версии алгоритма ABO — оригинальная и с небольшими модификациями. Изменения в логике алгоритма привели к упрощению в вычислениях на каждом шаге оптимизации и уменьшению внешних параметров с трех до двух (не считая параметр, отвечающий за размер популяции), что положительно сказалось на общих результатах. Новый алгоритм также по-другому балансирует между исследованием нового пространства решений и эксплуатацией уже найденных хороших решений.
Несмотря на склонность алгоритма к застреванию на задачах малой размерности, он демонстрирует высокую эффективность в практическом применении. Визуализация работы алгоритма показала его способность к глубокому исследованию значимых участков гиперпространства, что так же свидетельствует об его улучшенных исследовательских способностях. В итоге, новая версия алгоритма оказалась более мощной и эффективной в сравнении с оригиналом, демонстрируя хорошую масштабируемость на всех типах тестовых функций, включая дискретные.
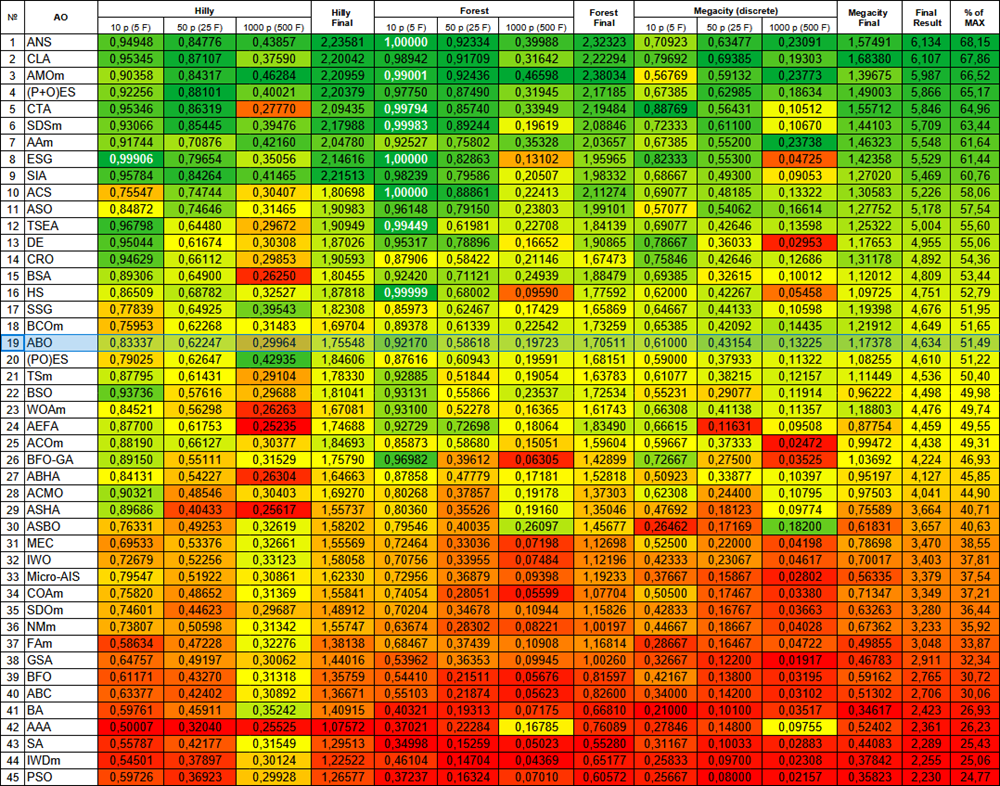
Рисунок 1. Цветовая градация алгоритмов по соответствующим тестам. Белым цветом подсвечены результаты больше или равные 0.99
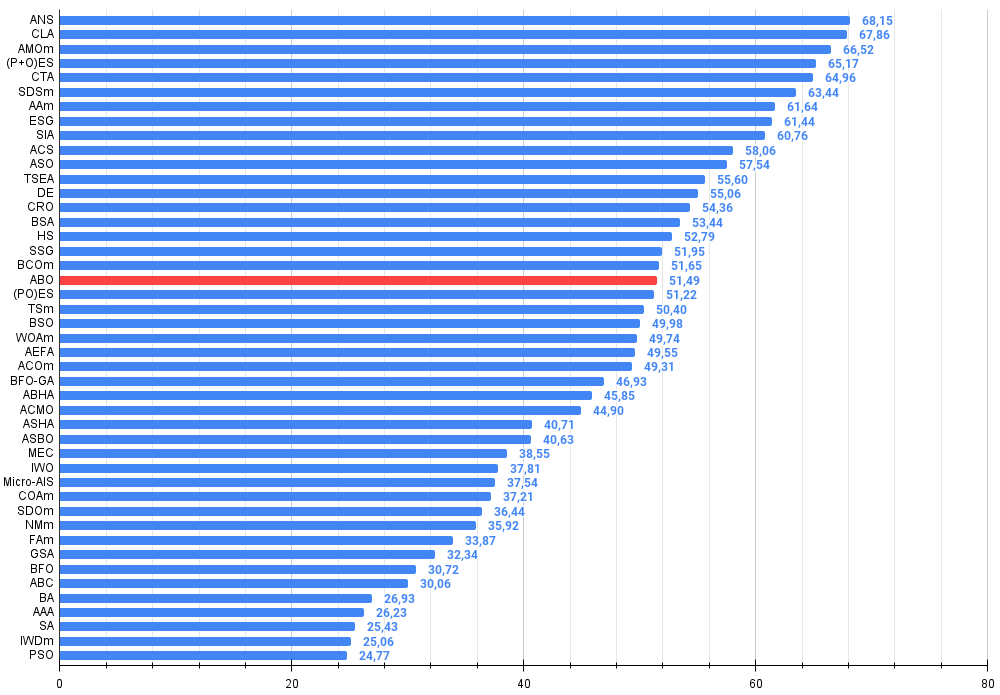
Рисунок 2. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,
где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма ABO:
Плюсы:
- Быстрый.
- Очень простая реализация.
- Хорошая масштабируемость.
- Мало внешних параметров.
Минусы:
- Высокий разброс результатов на функциях малой размерности.
- Отсутствие механизмов борьбы с застреванием.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Добавляем пользовательскую LLM в торгового робота (Часть 3): Обучение собственной LLM с помощью CPU
Нейронная сеть на практике: Функция прямой линии
Нейронная сеть на практике: Псевдообратная (I)
Нейронная сеть на практике: Метод наименьших квадратов
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Автор жуткий молодец! Я как абсолютный "чайник" в данной теме просто диву даюсь, сколько разных есть методов оптимизации. Наверное с перламутровыми пуговицами тоже есть? ))
Андрей, подскажите пож-ста, в каком ПО была проведена визуализация (к примеру ABO на тестовой функции Forest) ??? Может где-то упоминалось, да я пропустил мимо ушей...
Следующая статья про индийских слонов или мексиканских тушканов? ))
Очень интересная статья.
Спасибо, Николай, за добрые слова.
Об алгоритме Прыгающих Кузнечиков ничего не слышал, а вот на тему кошачьих, похоже, существуют такие: Panther Optimization Algorithm (POA) и Mountain Lion Algorithm (MLA). Возможно, будут рассмотрены мной, если смогу найти описание, достаточное для воспроизведения логики этих стратегий поиска.
Автор жуткий молодец! Я как абсолютный "чайник" в данной теме просто диву даюсь, сколько разных есть методов оптимизации. Наверное с перламутровыми пуговицами тоже есть? ))
Андрей, подскажите пож-ста, в каком ПО была проведена визуализация (к примеру ABO на тестовой функции Forest) ??? Может где-то упоминалось, да я пропустил мимо ушей...
Следующая статья про индийских слонов или мексиканских тушканов? ))
Спасибо, Денис.
Использую в статьях на mql5.com только язык MQL5, визуализация построена в MT5 штатными средствами. Все исходные коды доступны в прикрепе к статье и можете воспроизвести мои результаты.