
African Buffalo Optimierung (ABO)
Inhalt
Einführung
Der Algorithmus der Afrikanische Büffel-Optimierung (African Buffalo Optimization, ABO) ist ein metaheuristischer Ansatz, der durch das bemerkenswerte Verhalten dieser Tiere in freier Wildbahn inspiriert wurde. Der ABO-Algorithmus wurde 2015 von den Wissenschaftlern Julius Beneoluchi Odili und Mohd Nizam Kahar auf der Grundlage der sozialen Interaktionen und Überlebensstrategien von afrikanischen Büffeln entwickelt.
Afrikanische Büffel sind bekannt für ihre Fähigkeit, sich in Gruppen zu verteidigen und für ihre Koordination bei der Suche nach Nahrung und Wasser. Diese Tiere leben in großen Herden, was ihnen Schutz vor Raubtieren bietet und ihnen hilft, enge Gruppen zu bilden, in denen sich die Erwachsenen um die Jungen und Schwachen kümmern. Wenn sie von Raubtieren angegriffen werden, zeigen Büffel beeindruckende Koordinationsfähigkeiten: Sie können einen Kreis um die gefährdeten Mitglieder der Herde bilden oder den Feind mit vereinten Kräften angreifen.
Die Grundprinzipien des ABO-Algorithmus spiegeln wichtige Aspekte des Verhaltens von Büffeln wider. Erstens, die Kommunikation: Die Büffel verwenden Schallsignale, um ihre Aktionen zu koordinieren, was im Algorithmus dem Informationsaustausch zwischen den Agenten entspricht. Zweitens, Lernen: Büffel lernen aus ihren eigenen Erfahrungen und den Erfahrungen anderer Herdenmitglieder, was im Algorithmus umgesetzt wird, indem die Positionen der Agenten auf der Grundlage der gesammelten Informationen aktualisiert werden.
Das einzigartige Verhalten der afrikanischen Büffel macht sie zu einer interessanten Inspirationsquelle für Optimierungsalgorithmen. Diese Tiere sind in der Lage, sich an Veränderungen in der Umwelt anzupassen, indem sie auf der Suche nach Nahrung und Wasser saisonale Wanderungen unternehmen und auf der Suche nach günstigen Bedingungen weite Strecken zurücklegen. Während ihrer Wanderungen wenden Büffel Suchstrategien an, die es ihnen ermöglichen, effizient nach Ressourcen zu suchen und Gefahren zu vermeiden.
Das hochgradig koordinierte, kooperative und anpassungsfähige Verhalten afrikanischer Büffel bietet somit einen starken Anreiz für die Entwicklung von Optimierungsalgorithmen wie ABO. Diese Aspekte machen den Algorithmus zu einem effektiven Werkzeug für die Lösung komplexer Probleme, inspiriert von den natürlichen Mechanismen, die das Überleben und Gedeihen dieser erstaunlichen Tiere in freier Wildbahn gewährleisten.
Implementierung des Algorithmus
Die Optimierung nach den afrikanischen Büffeln (ABO) nutzt die Verhaltensinstinkte afrikanischer Büffel, wie Kooperation und soziale Interaktion, um Optimierungsprobleme zu lösen. Die Funktionsweise des Systems ist wie folgt:
1. Der Algorithmus beginnt mit der Initialisierung einer Population von Büffeln, wobei jeder Büffel eine potenzielle Lösung im Lösungsraum darstellt. Die Positionen der Büffel werden in diesem Raum zufällig initialisiert.
2. Jede Lösung (Büffelposition) wird anhand einer Fitnessfunktion bewertet. Wenn die Fitness des aktuellen Büffels besser ist als seine beste vorherige Fitness bp_max, wird seine Position beibehalten. Ähnlich verhält es sich, wenn die Fitness besser ist als die beste Fitness im gesamten Rudel bg_max, dann bleibt auch diese Position erhalten.
3. Der Algorithmus aktualisiert die Büffelpositionen auf der Grundlage von zwei Hauptsignalen — „maaa“ (bleiben und nutzen) und „waaa“ (bewegen und erkunden). Diese Signale helfen den Büffeln, ihre Suche nach Nahrungsquellen zu optimieren.
4.W.k + 1 = W.k + lp * r1 * (bgmaxt.k - m.k) + lp * r2 * (bpmax.k - m.k): Diese Gleichung aktualisiert die Bewegung des Büffels. W.k stellt eine Bewegung zur Erkundung dar, während m.k die aktuelle Position des Büffels zur Nutzung markiert. lp1 und lp2 sind Trainingsfaktoren, während r1 und r2 Zufallszahlen im Intervall [0,1] sind. bgmax ist die beste Position im gesamten Rudel, während bpmax die beste Position für einen bestimmten Büffel ist.
In der Gleichung steht (bgmaxt.k — m.k) für das Signal „maaa“, während (bpmax.k — m.k) das „waaa“-Signal ist.
5. Als Nächstes wird die Position von Büffel k im Verhältnis zu seiner persönlichen aktuellen Position und der in der vorherigen Gleichung berechneten Bewegung mit Hilfe der folgenden Gleichung aktualisiert: m.k + 1 = λ * (W.k + m.k). Diese Gleichung bestimmt den neuen Standort des Büffels, wobei λ ein Bewegungsverhältnis ist.
6. Wenn die Stoppkriterien nicht erfüllt sind, kehren wir zu Schritt 2 zurück, um die Fitnesswerte erneut zu aktualisieren.
7. Wenn das Stoppkriterium erreicht ist, wird der Algorithmus beendet und ein Positionsvektor ausgegeben, der die beste Lösung für das gegebene Problem darstellt.
Beschreiben wir die Struktur S_Buffalo und die Klasse C_AO_ABO, die die Grundlage des Algorithmus bilden.
- S_Buffalo — Struktur, die einen Büffel darstellt. Sie enthält das Array w, das den Bewegungsvektor des Agenten im Algorithmus beschreibt.
- Die folgenden Parameter werden im Klassenkonstruktor festgelegt: popSize (Populationsgröße), lp1 und lp2 (Lernfaktoren) sowie das im Algorithmus verwendete lambda.
- Die Methode SetParams ermöglicht die Einstellung von Algorithmusparametern auf der Grundlage der im Array params gespeicherten Werte.
- Die Methode Init initialisiert den Algorithmus. Er akzeptiert minimale und maximale Suchgrenzen, Suchschritte und die Anzahl der Epochen.
- Die Methoden Moving und Revision implementieren die Hauptschritte des Optimierungsalgorithmus: Bewegen (Suche nach einer neuen Lösung) und Überarbeiten (Überprüfung und Aktualisierung der Lösungen).
- Die Felder der Klassen lp1, lp2 und lambda werden zur Verwaltung des Algorithmusverhaltens verwendet.
- Das Array b vom Typ S_Buffalo speichert die Büffelinstanzen, die an der Optimierung teilnehmen.
//—————————————————————————————————————————————————————————————————————————————— struct S_Buffalo { double w []; }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— class C_AO_ABO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ABO () { } C_AO_ABO () { ao_name = "ABO"; ao_desc = "African Buffalo Optimization"; ao_link = "https://www.mql5.com/en/articles/16024"; popSize = 50; // population size lp1 = 0.7; // learning factor 1 lp2 = 0.5; // learning factor 2 lambda = 0.3; // lambda for the movement equation ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "lp1"; params [1].val = lp1; params [2].name = "lp2"; params [2].val = lp2; params [3].name = "lambda"; params [3].val = lambda; } void SetParams () { popSize = (int)params [0].val; lp1 = params [1].val; lp2 = params [2].val; lambda = params [3].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double lp1; // learning factor 1 double lp2; // learning factor 2 double lambda; // lambda for the movement equation private: //------------------------------------------------------------------- S_Buffalo b []; }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Init der Klasse C_AO_ABO ist für die Initialisierung der Algorithmusparameter zuständig. Parameter der Methode:
- rangeMinP [] — Array gibt die Mindestwerte für die Parameterbereiche an.
- rangeMaxP [] — Array gibt die Höchstwerte für die Parameterbereiche an.
- rangeStepP [] — Array gibt die Schritte zur Änderung der Parameterwerte an.
- epochsP — Anzahl der Epochen (Iterationen), Standardwert ist 0. Mit diesem Parameter wird die Anzahl der Iterationen im Optimierungsprozess bestimmt.
Die Logik der Methode:
1. Standardinitialisierung: Die Methode ruft zunächst StandardInit mit den übergebenen Arrays rangeMinP, rangeMaxP und rangeStepP auf. Wenn die Initialisierung fehlgeschlagen ist, wird false zurückgegeben.
2. Initialisierung der Population:
- Die Methode ändert die Größe des Arrays b bis zu popSize, was der Anzahl der Suchagenten in der Population entspricht.
- Für jeden Agenten in der Population (in einer Schleife von 0 bis popSize): Ändere die Größe des Arrays b [i].w auf coords, was der Anzahl der Koordinaten (optimierte Parameter des Problems) für jedes Individuum entspricht.
- Dem Array b [i].w wird mithilfe von ArrayInitialize Nullen zugewiesen.
3. Wenn alle Vorgänge erfolgreich waren, gibt die Methode true zurück, was auf eine erfolgreiche Initialisierung hinweist.
Die Methode Init ist für die Vorbereitung der erforderlichen Datenstrukturen für den Algorithmus zuständig und gewährleistet die korrekte Initialisierung der Parameter und der Population. Dies ist ein wichtiger Schritt vor der Ausführung des Hauptalgorithmus, der diese Daten für die Optimierung verwenden wird.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ABO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (b, popSize); for (int i = 0; i < popSize; i++) { ArrayResize(b [i].w, coords); ArrayInitialize (b [i].w, 0.0); } return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving der Klasse C_AO_ABO ist für die Bewegung der Büffel in der Population über den Suchraum während der Optimierung verantwortlich. Nachstehend finden Sie eine ausführliche Beschreibung der Funktionsweise:
1. Die Methode prüft zunächst, ob die Überprüfung if (!revision) durchgeführt wurde. Wurde die Revision noch nicht durchgeführt, wird die Population mit Zufallswerten initialisiert:
- Die äußere Schleife durchläuft alle Individuen in der Population popSize.
- Die innere Schleife durchläuft alle Koordinaten.
Für jeden Parameter:
- Zunächst wird mit der Methode u.RNDfromCI ein Zufallswert im Bereich von rangeMin [c] bis rangeMax [c] erzeugt.
- Dieser Wert wird dann mit Hilfe von u.SeInDiSp überprüft und angepasst, wodurch der Wert auf einen bestimmten Bereich begrenzt wird, wobei der Schritt rangeStep [c] berücksichtigt wird.
- Nachdem die Initialisierung abgeschlossen ist, wird revision auf true gesetzt, und die Methode wird zu Ende ausgeführt.
2. Die grundlegende Logik der Büffelbewegung. Wurde die Überprüfung bereits durchgeführt, fährt die Methode mit der Aktualisierung der Position der Büffel im Raum fort:
- Die Variablen w, m, r1, r2, bg und bp werden für weitere Berechnungen initialisiert.
- Die äußere Schleife durchläuft alle Individuen in der Population popSize.
- Die innere Schleife durchläuft alle Koordinaten:
- Für die Aktualisierung der Position der Büffel werden zwei Zufallswerte r1 und r2 generiert, die ein Zufallselement in das Verhalten der Büffel einbringen.
- bg und bp erhalten Werte aus den entsprechenden Feldern: cB [c] (beste globale Herdenkoordinaten) und a [i].cB [c] (beste individuelle Büffelkoordinaten).
- m erhält den Wert des aktuellen Positionsvektorelements a [i].c [c], während w den Wert des aktuellen Bewegungsvektorelements b [i].w [c] des Büffels an der entsprechenden Koordinate erhält.
- Der Wert des Bewegungsvektors b [i].w [c] wird gemäß der Gleichung aktualisiert, die sowohl die globale als auch die lokale beste Position des Büffels berücksichtigt: b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m).
- Dann wird die Position durch die entsprechende Koordinate m unter Verwendung des Verhältnisses lambda aktualisiert.
- Schließlich wird der neue Wert der Suchagenten-Koordinate a [i].c [c] berechnet und mit u.SeInDiSp angepasst.
Die Methode Moving ist für die Initialisierung und Aktualisierung der Position zuständig und führt die Bewegung der Populationsmitglieder während der Optimierung durch. Sie verwendet Zufallswerte, um die Positionen der Büffel zu initialisieren und zu aktualisieren. Dabei werden Zufallszahlen verwendet, die sowohl auf den globalen als auch auf den lokalen, besten, bekannten Positionen der Tiere in der Herde basieren.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode Revision der Klasse C_AO_ABO ist für die Aktualisierung der besten Werte der Funktion und der Parameter in der Population zuständig. Beschreibung der Methode:
1. Die Variable ind wird mit dem Wert -1 initialisiert. Es wird verwendet, um einen Index von Personen mit der besten Funktion zu speichern.
2. Suche nach dem global besten Individuum:
- Die for-Schleife durchläuft alle Agenten in der Population mit der Größe popSize:
- Für jeden Agenten wird geprüft, ob sein Fitnessfunktionswert von a [i].f den aktuellen globalen Bestwert von fB übersteigt.
- Wenn ja, wird fB aktualisiert und der Index dieses Agentens wird in der Variablen ind gespeichert.
- Nach Abschluss der Schleife wird, wenn ein besserer Agent gefunden wurde (ind ist ungleich -1), die Funktion ArrayCopy aufgerufen. Sie kopiert die c Parameter des Agenten in das Array der global besten Parameter cB.
3. Aktualisierung der lokalen Bestwerte:
- Die zweite for-Schleife durchläuft wieder alle Agenten in der Grundgesamtheit.
- Für jeden Agenten wird geprüft, ob sein Fitnessfunktionswert a [i].f seinen lokalen Bestwert a [i].fB übersteigt.
- Wenn ja, wird der beste lokale Wert von a [i].fB aktualisiert und die Koordinaten des Agenten werden in sein Feld für die besten lokalen Koordinaten cB kopiert.
Die Methode Revision erfüllt zwei Hauptaufgaben:
- Es findet und aktualisiert den besten Wert der globalen Fitnessfunktion und die zugehörigen Parameter.
- Außerdem werden für jeden Agenten in der Population die Werte der besten lokalen Fitnessfunktionen und Parameter aktualisiert.
Diese Logik ist typisch für jene Optimierungsalgorithmen, bei denen es wichtig ist, sowohl globale als auch lokale Optima zu verfolgen, um die Suche nach einer Lösung zu verbessern.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Wir haben die gesamte Implementierung des Algorithmus berücksichtigt. Es ist ganz einfach. Jetzt können wir zur Testphase übergehen.
Prüfen wir die Leistung der ursprünglichen ABO-Version:
=============================
5 Hilly's; Func runs: 10000; result: 0.8495807203797128
25 Hilly's; Func runs: 10000; result: 0.5186057937632769
500 Hilly's; Func runs: 10000; result: 0.2642792490546295
=============================
5 Forest's; Func runs: 10000; result: 0.6554510234450559
25 Forest's; Func runs: 10000; result: 0.41662244493546935
500 Forest's; Func runs: 10000; result: 0.21044033116304034
=============================
5 Megacity's; Func runs: 10000; result: 0.6015384615384616
25 Megacity's; Func runs: 10000; result: 0.26430769230769224
500 Megacity's; Func runs: 10000; result: 0.11120000000000112
=============================
All score: 3.89203 (43.24%)
Nicht schlecht. Aber ich wäre nicht ich selbst, wenn ich nicht versuchen würde, den Algorithmus zu verbessern. In der ursprünglichen Version wird der neue Standort der Büffel auf der Grundlage einer vorläufigen Berechnung des Verschiebungsvektors (Inkrement zur aktuellen Position) berechnet, die auf Informationen über die beste globale Position in der Herde, die beste Position des betreffenden Büffels und seinen aktuellen Standort beruht. Dieser Bewegungsvektor wirkt wie eine Art Trägheit in der Bewegung.
Ich kam auf die Idee, die Trägheit aufzugeben und die Informationen über die besten Positionen von mir und der Herde direkt zu nutzen und die Berechnung auf die aktuelle Situation anzuwenden. Wir werden den Codeabschnitt des Autors auskommentieren und einen neuen, einfacheren Code schreiben, wobei wir einen externen Parameter - lambda - loswerden. Der neue Code ist grün hervorgehoben.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { /* r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); */ r1 = u.RNDfromCI (-lp1, lp1); r2 = u.RNDfromCI (-lp2, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; m = m + r1 * (bg - m) + r2 * (bp - m); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Hier sind die Ergebnisse, die nach der Änderung der Logik der Büffelbewegung erzielt wurden:
=============================
5 Hilly's; Func runs: 10000; result: 0.833371781687727
25 Hilly's; Func runs: 10000; result: 0.6224659624836805
500 Hilly's; Func runs: 10000; result: 0.2996410968574058
=============================
5 Forest's; Func runs: 10000; result: 0.9217022975045926
25 Forest's; Func runs: 10000; result: 0.5861755787948962
500 Forest's; Func runs: 10000; result: 0.19722782275756043
=============================
5 Megacity's; Func runs: 10000; result: 0.6100000000000001
25 Megacity's; Func runs: 10000; result: 0.4315384615384614
500 Megacity's; Func runs: 10000; result: 0.13224615384615512
=============================
All score: 4.63437 (51.49%)
Die Ergebnisse verbesserten sich um fast 10 %: 51,49% gegenüber 43,24%. Besonders deutlich sind die Verbesserungen bei Funktionen mit 50 und 1000 Parametern, während bei Funktionen mit 10 Parametern die Veränderungen kaum wahrnehmbar sind. Dies beweist die bessere Skalierbarkeit des Algorithmus für große Probleme.
Jetzt gibt es noch eine weitere Idee zu testen: Was wäre, wenn die Gleichung nicht die beste Position des Büffels, sondern die beste Position eines zufällig ausgewählten Büffels aus der Herde verwendet, wobei die Wahrscheinlichkeit an den Anfang der Liste der Individuen in der Population verschoben wird? Dies ist leicht zu testen und erfordert nur wenige Änderungen am Code. Durch die Verschiebung der Wahrscheinlichkeit an den Anfang der Bevölkerungsliste wird sichergestellt, dass die Zufallszahl [0,0;1,0] auf eine Potenz erhöht und der Bruchteil der resultierenden Zahl verworfen wird. In diesem Fall wird die Potenz „4“ verwendet.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { /* r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); */ r1 = u.RNDfromCI (-lp1, lp1); r2 = u.RNDfromCI (-lp2, lp2); bg = cB [c]; //bp = a [i].cB [c]; double r = u.RNDprobab (); int ind = (int)pow (r - 1, 4); bp = a [ind].cB [c]; m = a [i].c [c]; m = m + r1 * (bg - m) + r2 * (bp - m); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Um die probabilistische Auswahl von Individuen in einer Population mit einer Tendenz zu den besten Büffeln anzuwenden, müssen wir in der Methode Revision nach dem Fitnessniveau der Individuen sortieren. Glücklicherweise wurde die entsprechende Methode Sorting_fB bereits in einem der früheren Artikel hinzugefügt.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Betrachten wir nun die Ergebnisse der Anwendung der probabilistischen Auswahl der besten Position der Büffel in der Herde zur Verwendung in der Gleichung zur Berechnung der neuen Position im ABO-Algorithmus:
ABO|African Buffalo Optimization|50.0|0.1|0.8|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.841272551476775
25 Hilly's; Func runs: 10000; result: 0.5701677694693293
500 Hilly's; Func runs: 10000; result: 0.28850644933225034
=============================
5 Forest's; Func runs: 10000; result: 0.9015705858486595
25 Forest's; Func runs: 10000; result: 0.49493378365495344
500 Forest's; Func runs: 10000; result: 0.1919604395333699
=============================
5 Megacity's; Func runs: 10000; result: 0.5692307692307692
25 Megacity's; Func runs: 10000; result: 0.35261538461538455
500 Megacity's; Func runs: 10000; result: 0.12010769230769343
=============================
All score: 4.33037 (48.12%)
Die Gesamtleistung des Algorithmus hat sich zwar verschlechtert, ist aber immer noch besser als die der „reinen“ Originalversion. In diesem Zusammenhang werden wir die Ergebnisse des ersten Experiments zur Änderung des Algorithmus festhalten und in die Bewertungstabelle eintragen. Ich möchte anmerken, dass für jede Version des Algorithmus externe Parameter gewählt wurden, um eine maximale Leistung für alle Tests zu gewährleisten, da eine Änderung der Logik des Algorithmus zu einer Änderung seines Verhaltens im Suchraum führt.
Testergebnisse
In der Visualisierung des ABO-Algorithmus können wir die gute Ausarbeitung von signifikanten Abschnitten des Hyperraums sehen, was auf eine hohe Fähigkeit zur Untersuchung der Oberfläche der optimierten Funktion hinweist. Leider erhöht diese kleine Änderung, die zwar die Skalierbarkeit des Algorithmus verbessert, die Wahrscheinlichkeit, bei kleindimensionalen Problemen stecken zu bleiben, was an der Streuung der Ergebnisse zu erkennen ist (grüne Linien der Konvergenzkurve in der Visualisierung).
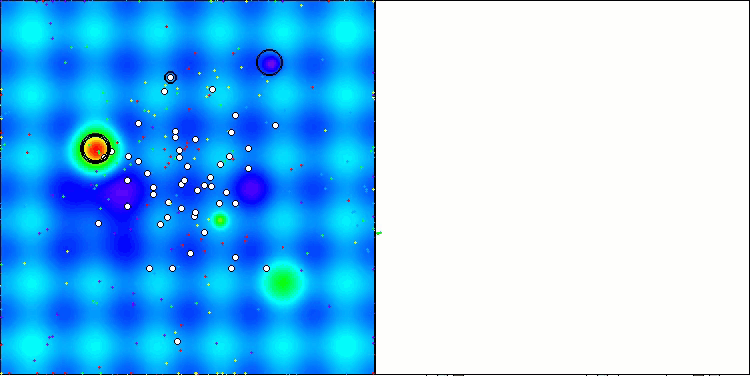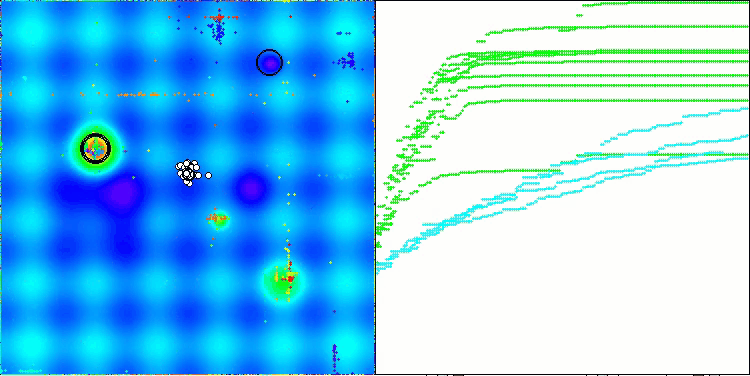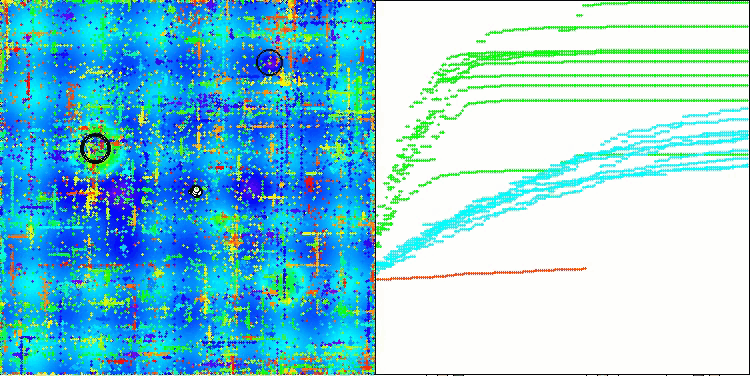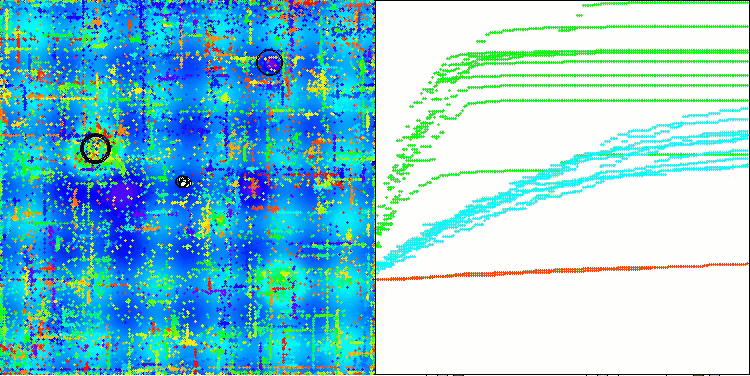
ABO mit der Testfunktion Hilly
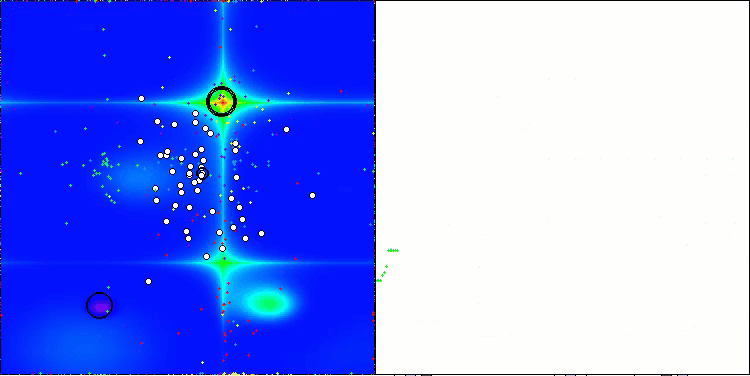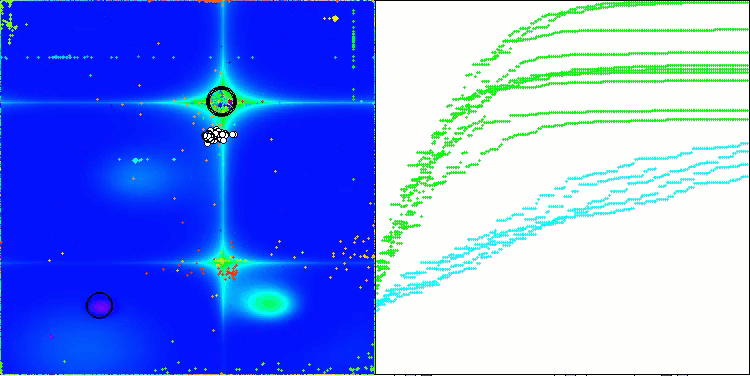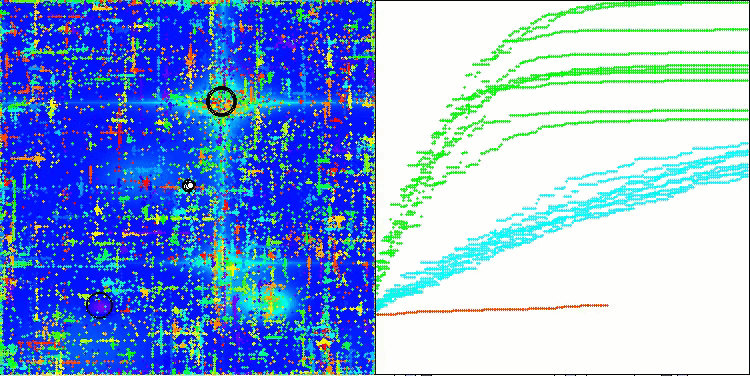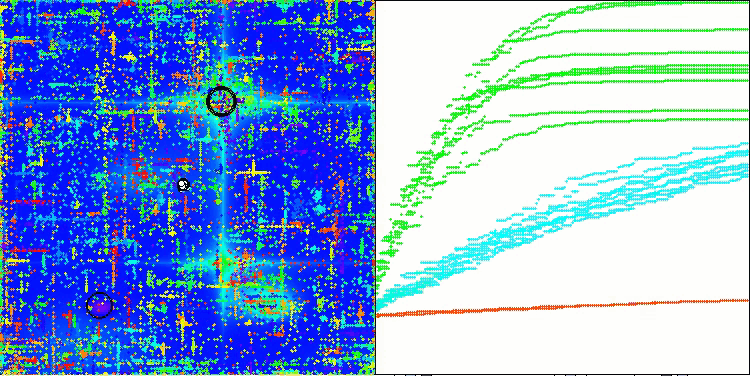
ABO mit der Testfunktion Forest
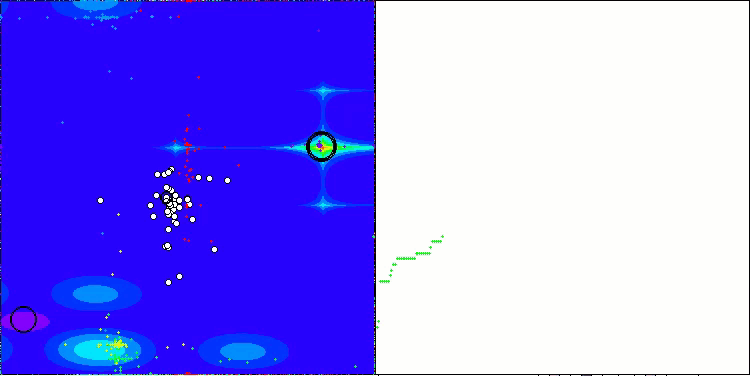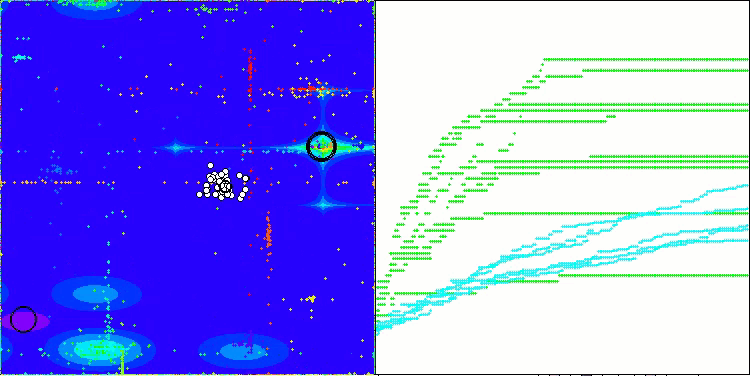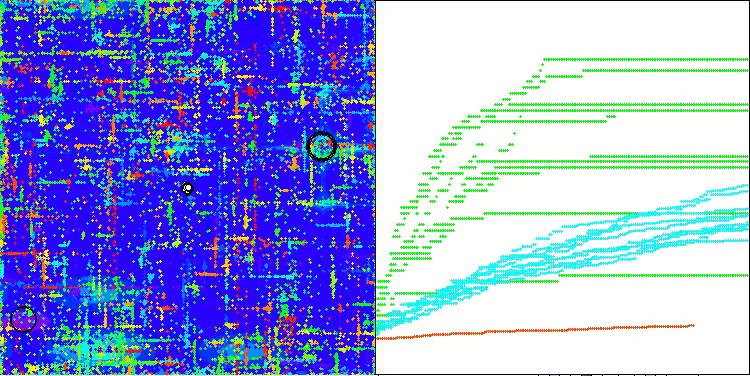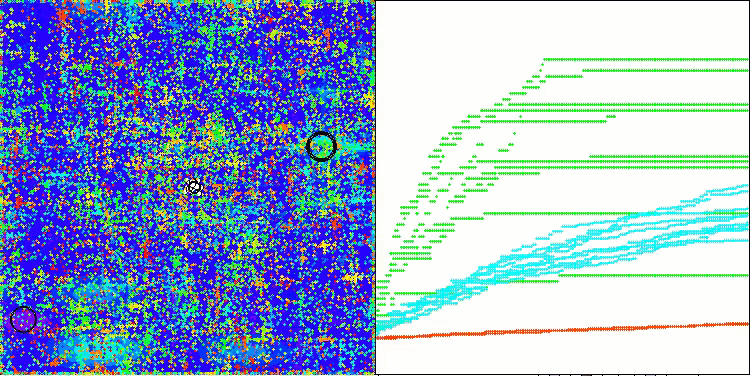
ABO mit der Testfunktion Megacity
Aufgrund der Testergebnisse belegte der Algorithmus einen stabilen 19. Platz in der Gesamtwertung der Optimierungsalgorithmen.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Сode Lock Algorithmus | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | Entwicklung der sozialen Gruppen | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | Simuliertes isotropes Abkühlen | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 12 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 13 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 14 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 15 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 16 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 17 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 18 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 19 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 20 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 21 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 22 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 23 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 24 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 25 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 26 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 27 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 28 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 29 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 30 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 31 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 32 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 33 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 34 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 35 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 36 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 37 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 38 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 39 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 40 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 41 | BA | Fledermaus-Algorithmus | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 42 | AAA | Künstlicher Algenalgorithmus (AAA) | 0.50007 | 0.32040 | 0.25525 | 1.07572 | 0.37021 | 0.22284 | 0.16785 | 0.76089 | 0.27846 | 0.14800 | 0.09755 | 0.52402 | 2.361 | 26.23 |
| 43 | SA | simuliertes Abkühlen | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 44 | IWDm | intelligente Wassertropfen M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 45 | PSO | Partikelschwarmoptimierung | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
Zusammenfassung
Ich habe die Versionen des ABO-Algorithmus vorgestellt — die ursprüngliche und die mit geringfügigen Änderungen. Änderungen in der Logik des Algorithmus führten zu einer Vereinfachung der Berechnungen bei jedem Optimierungsschritt und zu einer Reduzierung der externen Parameter von drei auf zwei (ohne den für die Populationsgröße verantwortlichen Parameter), was sich positiv auf die Gesamtergebnisse auswirkte. Der neue Algorithmus wägt außerdem zwischen der Erkundung eines neuen Lösungsraums und der Nutzung bereits gefundener guter Lösungen ab.
Trotz der Tendenz des Algorithmus, bei niedrigdimensionalen Problemen stecken zu bleiben, zeigt er in praktischen Anwendungen eine hohe Effizienz. Die Visualisierung der Funktionsweise des Algorithmus zeigte, dass er in der Lage ist, wichtige Bereiche des Hyperraums zu erforschen, was auch auf seine verbesserten Forschungsmöglichkeiten hinweist. Im Ergebnis erwies sich die neue Version des Algorithmus im Vergleich zum Original als leistungsfähiger und effizienter und zeigte eine gute Skalierbarkeit für alle Arten von Testfunktionen, einschließlich diskreter Funktionen.
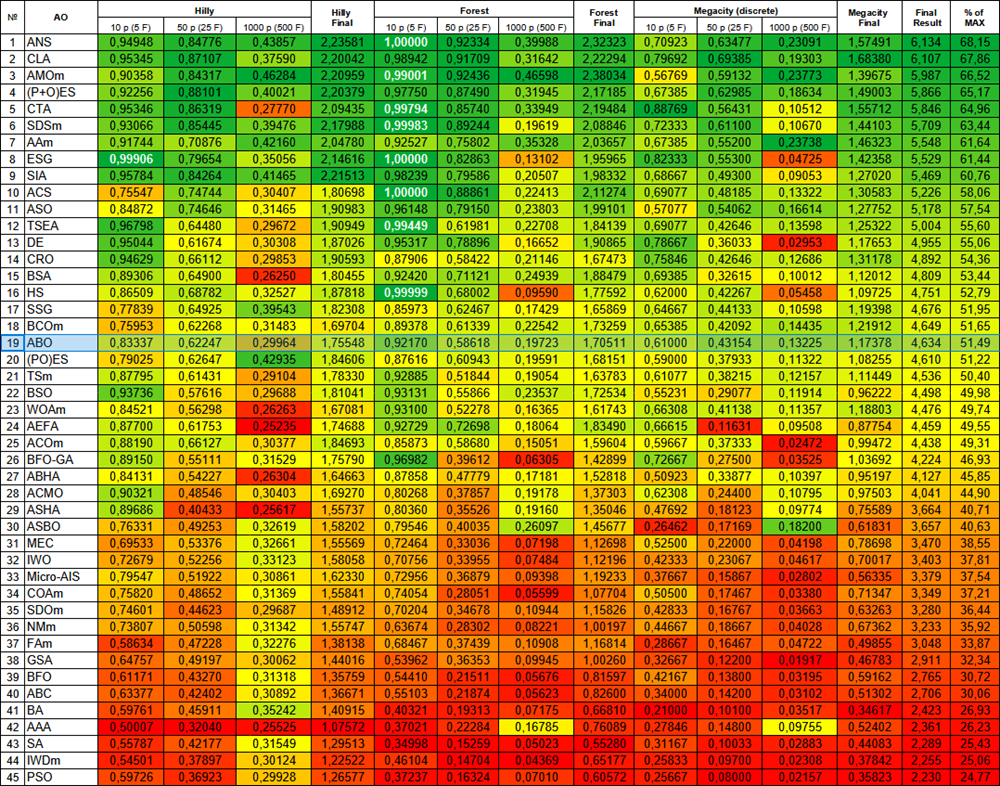
Abbildung 1. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben
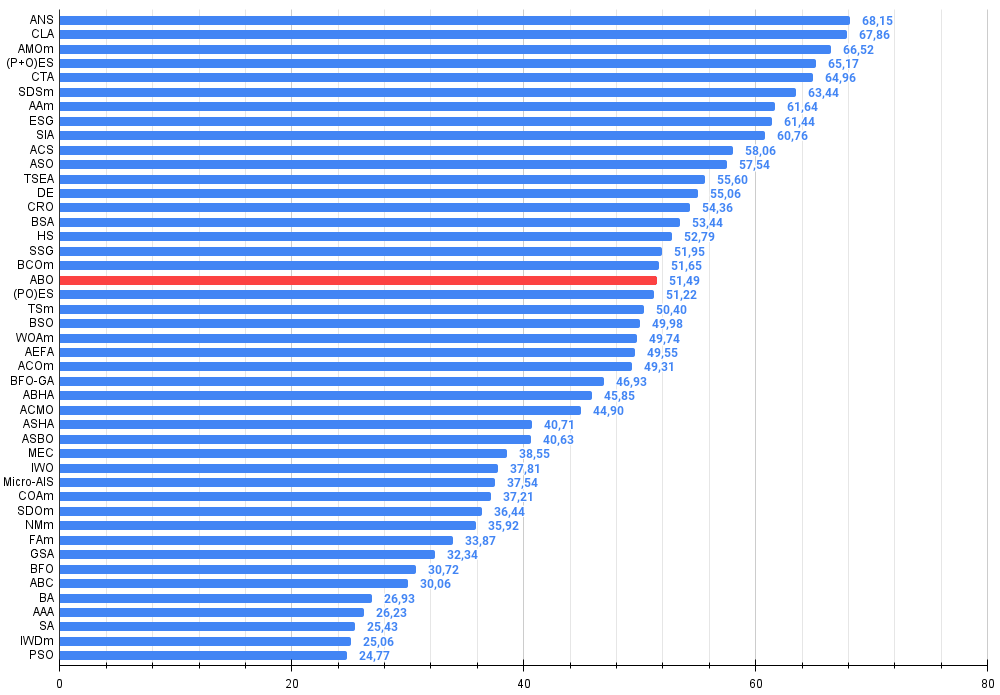
Abbildung 2. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Wertungstabelle)
ABO Pro und Kontra:
Vorteile:
- Schnell.
- Sehr einfache Umsetzung.
- Gute Skalierbarkeit.
- Geringe Anzahl von externen Parametern.
Nachteile
- Große Streuung der Ergebnisse bei niedrigdimensionalen Funktionen.
- Fehlende Mechanismen gegen das Hängenbleiben.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16024
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Von der Grundstufe bis zur Mittelstufe: Arrays und Zeichenketten (I)
Von der Grundstufe bis zur Mittelstufe: Arrays und Zeichenketten (I)
 Entwicklung eines Replay-Systems (Teil 66): Abspielen des Dienstes (VII)
Entwicklung eines Replay-Systems (Teil 66): Abspielen des Dienstes (VII)
 Neuronale Netze im Handel: Superpoint Transformer (SPFormer)
Neuronale Netze im Handel: Superpoint Transformer (SPFormer)
 Neuronale Netze im Handel: Erforschen lokaler Datenstrukturen
Neuronale Netze im Handel: Erforschen lokaler Datenstrukturen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Der Autor ist sehr gut! Als absoluter "Dummy" in diesem Thema bin ich einfach nur erstaunt, wie viele verschiedene Methoden der Optimierung es gibt. Wahrscheinlich auch mit Perlenknöpfen? ))
Andrei, bitte sag mir, in welcher Software die Visualisierung gemacht wurde (z.B. ABO auf der Forest-Testfunktion) ???? Vielleicht wurde es irgendwo erwähnt, aber ich habe es verpasst.....
Nächster Artikel über indische Elefanten oder mexikanische Tushkans? ))
Sehr interessanter Artikel.
Vielen Dank, Nikolay, für deine freundlichen Worte.
Ich habe noch nichts über den Jumping Grasshoppers Algorithmus gehört, aber es scheint einige zum Thema Katzen zu geben: Panther Optimisation Algorithm (POA) und Mountain Lion Algorithm (MLA). Ich könnte sie in Betracht ziehen, wenn ich eine Beschreibung finde, die ausreicht, um die Logik dieser Suchstrategien nachzuvollziehen.
Der Autor ist sehr gut! Als absoluter "Dummy" in diesem Thema bin ich einfach nur erstaunt, wie viele verschiedene Methoden der Optimierung es gibt. Wahrscheinlich auch mit Perlenknöpfen? ))
Andrei, bitte sag mir, in welcher Software die Visualisierung gemacht wurde (z.B. ABO auf der Forest-Testfunktion) ???? Vielleicht wurde es irgendwo erwähnt, aber ich habe es verpasst....
Nächster Artikel über indische Elefanten oder mexikanische Tushkans? ))
Danke, Denis.
Ich verwende in meinen Artikeln auf mql5.com nur die Sprache MQL5, die Visualisierung wird in MT5 mit Standardwerkzeugen erstellt. Alle Quellcodes sind im Anhang des Artikels verfügbar und Sie können meine Ergebnisse nachvollziehen.