African Buffalo Optimization (ABO)
462
5
Contents
Introduction
The African Buffalo Optimization (ABO) algorithm is a metaheuristic approach inspired by the remarkable behavior of these animals in the wild. The ABO algorithm was developed in 2015 by scientists Julius Beneoluchi Odili and Mohd Nizam Kahar based on the social interactions and survival strategies of African buffaloes.
African buffalo are known for their ability to defend themselves in groups and for their coordination in finding food and water. These animals live in large herds, which provides them with protection from predators and helps them form tight groups where adults take care of the young and weak. When attacked by predators, buffalo demonstrate impressive coordination skills: they can form a circle around vulnerable members of the herd, or attack the enemy with a joint effort.
The basic principles of the ABO algorithm reflect key aspects of buffalo behavior. First, communication: the buffaloes use sound signals to coordinate their actions, which in the algorithm corresponds to the exchange of information between agents. Second, learning: buffaloes learn from their own experiences and the experiences of other herd members, which is implemented in the algorithm by updating the agents' positions based on the information collected.
The unique behavior of African buffaloes makes them an interesting source of inspiration for optimization algorithms. These animals are able to adapt to changes in the environment, making seasonal migrations in search of food and water, and covering long distances in search of favorable conditions. During migrations, buffaloes employ search strategies that allow them to efficiently locate resources and avoid danger.
Thus, the highly coordinated, cooperative, and adaptive behavior of African buffalo provides a powerful incentive for the development of optimization algorithms such as ABO. These aspects make the algorithm an effective tool for solving complex problems, inspired by the natural mechanisms that ensure the survival and prosperity of these amazing animals in the wild.
Implementation of the algorithm
African Buffalo Optimization (ABO) algorithm exploits the behavioral instincts of African buffaloes, such as cooperation and social interaction, to solve optimization problems. The principles of its operation are as follows:
1. The algorithm starts by initializing a population of buffaloes, where each buffalo represents a potential solution in the solution space. The positions of the buffalo's are initialized randomly in this space.
2. Each solution (buffalo position) is evaluated using a fitness function. If the current buffalo's fitness is better than its best previous fitness bp_max, then its position is maintained. Similarly, if fitness is better than the best fitness in the entire pack bg_max, then this position also remains.
3. The algorithm updates the buffalo positions based on two main signals — "maaa" (stay and exploit) and "waaa" (move and explore). These signals help buffaloes optimize their search for food sources.
4.W.k + 1 = W.k + lp * r1 * (bgmaxt.k - m.k) + lp * r2 * (bpmax.k - m.k): This equation updates the buffalo's movement. W.k represents a movement for exploration, while m.k marks the current position of the buffalo for exploitation. lp1 and lp2 are training factors, while r1 and r2 are random numbers in the interval [0,1]. bgmax is the best position among the whole pack, while bpmax is the best position for a particular buffalo.
In the equation, (bgmaxt.k - m.k) represents the "maaa" signal, while (bpmax.k - m.k) is the "waaa" signal.
5. Next, the position of k buffalo is updated relative to its personal current position and the movement calculated in the previous equation, using the following equation: m.k + 1 = λ * (W.k + m.k). This equation determines the new location of the buffalo, where λ is a movement ratio.
6. If the stop criteria are not met, we return to step 2 to update the fitness values again.
7. When the stop criterion is reached, the algorithm terminates and outputs a position vector representing the best solution found for the given problem.
Describe the S_Buffalo structure and C_AO_ABO class implementing the basis of the algorithm.
- S_Buffalo — structure representing a buffalo. It contains the w array, which describes the agent's movement vector in the algorithm.
- The following parameters are set in the class constructor: popSize (population size), lp1 and lp2 (learning factors), as well as lambda used in the algorithm.
- The SetParams method allows setting algorithm parameters based on the values stored in the params array.
- The Init method is intended to initialize the algorithm. It accepts minimum and maximum search bounds, search step and number of epochs.
- The Moving and Revision methods implement the main steps of the optimization algorithm: movement (search for a new solution) and revision (checking and updating solutions).
- lp1, lp2 and lambda class fields are used to manage the algorithm behavior.
- The b array of the S_Buffalo type stores the buffalo instances that participate in the optimization.
//—————————————————————————————————————————————————————————————————————————————— struct S_Buffalo { double w []; }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— class C_AO_ABO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ABO () { } C_AO_ABO () { ao_name = "ABO"; ao_desc = "African Buffalo Optimization"; ao_link = "https://www.mql5.com/en/articles/16024"; popSize = 50; // population size lp1 = 0.7; // learning factor 1 lp2 = 0.5; // learning factor 2 lambda = 0.3; // lambda for the movement equation ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "lp1"; params [1].val = lp1; params [2].name = "lp2"; params [2].val = lp2; params [3].name = "lambda"; params [3].val = lambda; } void SetParams () { popSize = (int)params [0].val; lp1 = params [1].val; lp2 = params [2].val; lambda = params [3].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double lp1; // learning factor 1 double lp2; // learning factor 2 double lambda; // lambda for the movement equation private: //------------------------------------------------------------------- S_Buffalo b []; }; //——————————————————————————————————————————————————————————————————————————————
The Init method of the C_AO_ABO class is responsible for initializing the algorithm parameters. Method parameters:
- rangeMinP [] — array specifies the minimum values for the parameter ranges.
- rangeMaxP [] — array specifies the maximum values for the parameter ranges.
- rangeStepP [] — array specifies the steps for changing the parameter values.
- epochsP — number of epochs (iterations), default is 0. This parameter is used to determine the number of iterations in the optimization process.
The method logic:
1. Standard initialization: the method first calls StandardInit with passed arrays rangeMinP, rangeMaxP and rangeStepP. If initialization failed, return false.
2. Initialization of the population:
- The method changes the size of the b array up to popSize, which corresponds to the number of search agents in the population.
- For each agent in the population (in a loop from 0 to popSize): resize the b [i].w array to coords, which corresponds to the number of coordinates (optimized parameters of the problem) for each individual.
- The b [i].w array is initialized to zeros using ArrayInitialize.
3. If all operations are successful, the method returns true, which indicates successful initialization.
The Init method is responsible for preparing the necessary data structures for the algorithm, ensuring correct initialization of parameters and population. This is an important step before executing the main algorithm that will use this data for optimization.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ABO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (b, popSize); for (int i = 0; i < popSize; i++) { ArrayResize(b [i].w, coords); ArrayInitialize (b [i].w, 0.0); } return true; } //——————————————————————————————————————————————————————————————————————————————
The Moving method of the C_AO_ABO class is responsible for the movement of buffaloes in the population across the search space during the optimization. Below is a detailed description of its operation:
1. The method first checks whether the revision if (!revision) has been performed. If the revision has not yet been performed, it initializes the population with random values:
- The outer loop goes through all individuals in the popSize population.
- The inner loop goes through all coords coordinates.
For each parameter:
- First, a random value is generated in the range from rangeMin [c] to rangeMax [c] using the u.RNDfromCI method.
- This value is then checked and adjusted using u.SeInDiSp, which limits the value to a given range, taking into account the rangeStep [c] step.
- After the initialization is complete, revision is set to true, and the method completes execution.
2. The basic logic of buffalo movement. If the revision has already been performed, the method proceeds to update the position of the buffaloes in space:
- The w, m, r1, r2, bg and bp variables are initialized for further calculations.
- The outer loop goes through all individuals in the popSize population.
- The inner loop goes through all coords coordinates:
- Two random values r1 and r2 are generated for use in updating the position of the buffaloes, introducing an element of randomness into their behavior.
- bg and bp get values from the corresponding arrays: cB [c] (global best herd coordinates) and a [i].cB [c] (best individual buffalo coordinates).
- m gets the value of the current position vector element a [i].c [c], while w gets the value of the current movement vector element b [i].w [c] of the buffalo at the corresponding coordinate.
- The value of the movement vector b [i].w [c] is updated according to the equation that takes into account both the global and local best position of the buffalo: b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m).
- Then the position by the corresponding m coordinate is updated using the lambda ratio.
- Finally, the new value of the search agent coordinate a [i].c [c] is calculated and adjusted using u.SeInDiSp.
The Moving method is responsible for initializing and updating the position and carries out the movement of population members during the optimization. It uses random values to initialize and update the buffalo positions using random numbers based on both global and local best known positions of the animals in the herd.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
The Revision method of the C_AO_ABO class is responsible for updating the best values of the function and parameters in the population. Method description:
1. The ind variable is initialized with the value of -1. It will be used to store an index of individuals with the best function.
2. Search for the global best individual:
- The for loop passes through all agents in the popSize population:
- For each agent, it is checked whether its fitness function value of a [i].f exceeds the current global best value of fB.
- If yes, fB is updated and the index of this agent is saved in the ind variable.
- After the loop is completed, if a better agent has been found (ind is not equal to -1), the ArrayCopy function is called. It copies the c parameters of the agent to the cB global best parameter array.
3. Updating local best values:
- The second for loop again passes through all agents in the population.
- For each agent, it is checked whether its fitness function value of a [i].f exceeds its local best value of a [i].fB.
- If yes, the local best value of a [i].fB is updated and the agent coordinates are copied to its cB local best coordinate array.
The Revision method performs two main tasks:
- It finds and updates the global best fitness function value and associated parameters.
- Besides, it updates local best fitness function values and parameters for each agent in the population.
This logic is typical for those optimization algorithms, for which it is important to track both global and local optima to improve the search for a solution.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
We have considered the entire implementation of the algorithm. It is quite simple. Now we can move on to the testing stage.
Let's check the performance of the original ABO version:
=============================
5 Hilly's; Func runs: 10000; result: 0.8495807203797128
25 Hilly's; Func runs: 10000; result: 0.5186057937632769
500 Hilly's; Func runs: 10000; result: 0.2642792490546295
=============================
5 Forest's; Func runs: 10000; result: 0.6554510234450559
25 Forest's; Func runs: 10000; result: 0.41662244493546935
500 Forest's; Func runs: 10000; result: 0.21044033116304034
=============================
5 Megacity's; Func runs: 10000; result: 0.6015384615384616
25 Megacity's; Func runs: 10000; result: 0.26430769230769224
500 Megacity's; Func runs: 10000; result: 0.11120000000000112
=============================
All score: 3.89203 (43.24%)
Not bad. However, I would not be myself if I did not try to improve the algorithm. In the original version, the new location of the buffaloes is calculated based on a preliminary calculation of the displacement vector (increment to the current position), based on information about the global best position in the herd, the best position of the buffalo in question, and its current location. This vector of movement acts as a kind of inertia in movement.
I came up with the idea of abandoning inertia and using information about the best positions of both myself and the herd directly, applying the calculation to the current situation. We will comment out the author's section of code and write a new, simpler one, while getting rid of one external parameter - lambda. The new code is highlighted in green.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { /* r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); */ r1 = u.RNDfromCI (-lp1, lp1); r2 = u.RNDfromCI (-lp2, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; m = m + r1 * (bg - m) + r2 * (bp - m); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Here are the results obtained after modifying the logic of buffalo movement:
=============================
5 Hilly's; Func runs: 10000; result: 0.833371781687727
25 Hilly's; Func runs: 10000; result: 0.6224659624836805
500 Hilly's; Func runs: 10000; result: 0.2996410968574058
=============================
5 Forest's; Func runs: 10000; result: 0.9217022975045926
25 Forest's; Func runs: 10000; result: 0.5861755787948962
500 Forest's; Func runs: 10000; result: 0.19722782275756043
=============================
5 Megacity's; Func runs: 10000; result: 0.6100000000000001
25 Megacity's; Func runs: 10000; result: 0.4315384615384614
500 Megacity's; Func runs: 10000; result: 0.13224615384615512
=============================
All score: 4.63437 (51.49%)
The results improved by almost 10%: 51.49% versus 43.24%. The improvements are particularly noticeable for functions with 50 and 1000 parameters, while for functions with 10 parameters the changes are almost imperceptible. This demonstrates the increased scalability of the algorithm for large-scale problems.
Now there is one more idea to test: What if the equation uses not the best position of the buffalo, but the best position of a randomly selected buffalo from the herd, while shifting the probability to the top of the list of individuals in the population? This is easy to test and only requires a few changes to the code. Shifting the probability to the beginning of the population list ensures that the random number [0.0;1.0] is raised to a power and the fractional part of the resulting number is discarded. In this case, the power "4" is used.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { /* r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); */ r1 = u.RNDfromCI (-lp1, lp1); r2 = u.RNDfromCI (-lp2, lp2); bg = cB [c]; //bp = a [i].cB [c]; double r = u.RNDprobab (); int ind = (int)pow (r - 1, 4); bp = a [ind].cB [c]; m = a [i].c [c]; m = m + r1 * (bg - m) + r2 * (bp - m); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
To apply probabilistic selection of individuals in a population with a bias towards the best buffaloes, we need to sort by the fitness level of individuals in the Revision method. Fortunately, the appropriate Sorting_fB method was already added in one of the previous articles.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Let's look at the results of applying the probabilistic selection of the best position of buffaloes in the herd for use in the equation for calculating the new position in the ABO algorithm:
ABO|African Buffalo Optimization|50.0|0.1|0.8|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.841272551476775
25 Hilly's; Func runs: 10000; result: 0.5701677694693293
500 Hilly's; Func runs: 10000; result: 0.28850644933225034
=============================
5 Forest's; Func runs: 10000; result: 0.9015705858486595
25 Forest's; Func runs: 10000; result: 0.49493378365495344
500 Forest's; Func runs: 10000; result: 0.1919604395333699
=============================
5 Megacity's; Func runs: 10000; result: 0.5692307692307692
25 Megacity's; Func runs: 10000; result: 0.35261538461538455
500 Megacity's; Func runs: 10000; result: 0.12010769230769343
=============================
All score: 4.33037 (48.12%)
The overall performance of the algorithm has deteriorated, but is still higher than that of the "pure" original version. In this regard, we will record the results of the first experiment on modifying the algorithm and enter them into the rating table. I would like to note that for each version of the algorithm, external parameters were selected in order to ensure maximum performance for all tests, since changing the logic of the algorithm leads to a change in its behavior in the search space.
Test results
In the visualization of the ABO algorithm, we can see the good elaboration of significant sections of hyperspace, which indicates a high ability to study the surface of the optimized function. Unfortunately, the small modification, while improving the scalability of the algorithm, increases the probability of getting stuck on small-dimensional problems, which can be seen from the scatter of results (green lines of the convergence graph in the visualization).
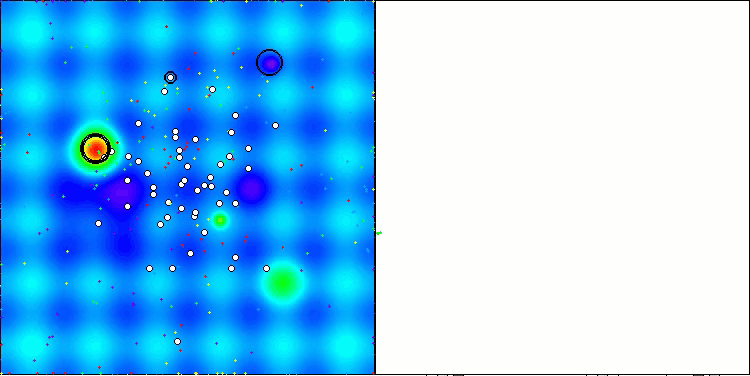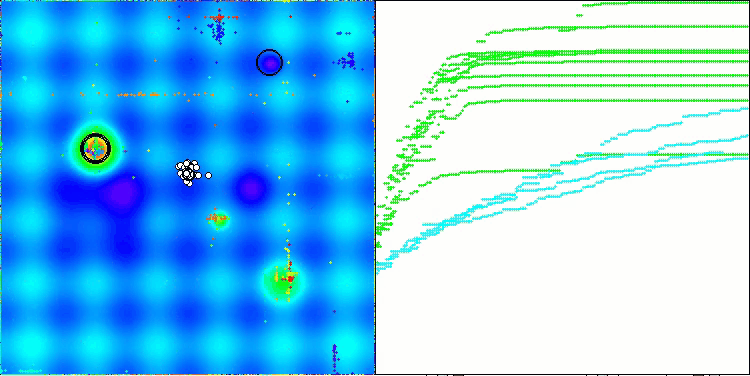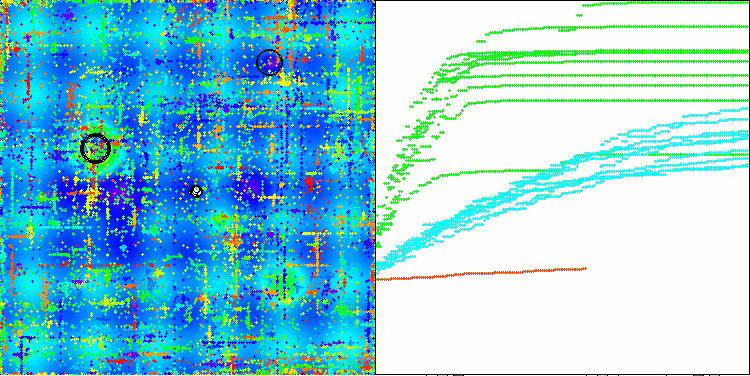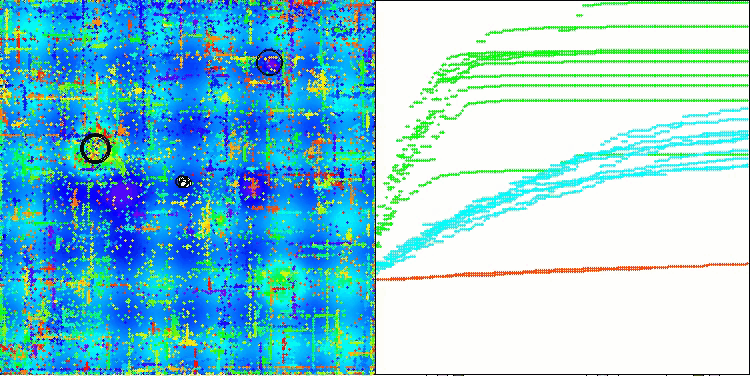
ABO on the Hilly test function
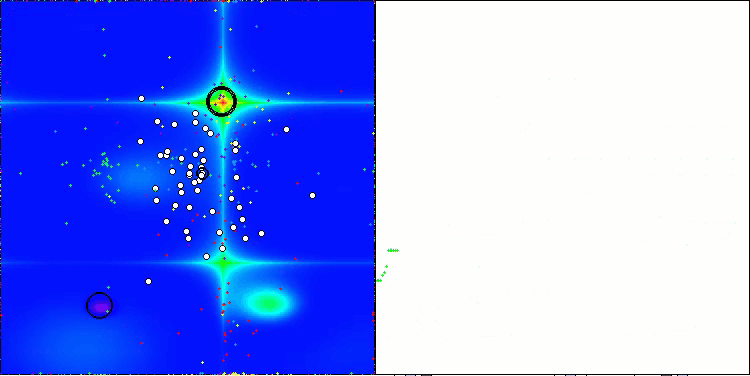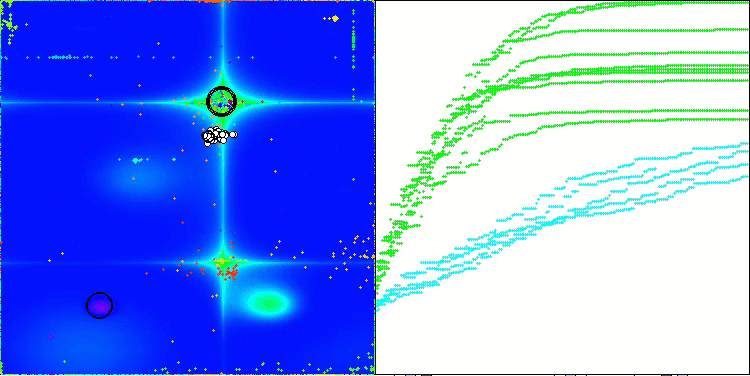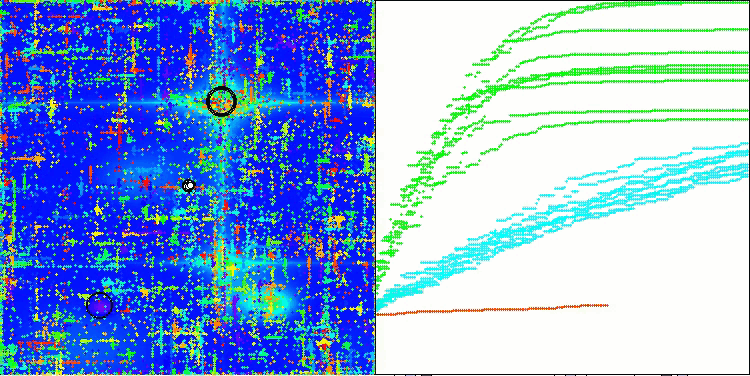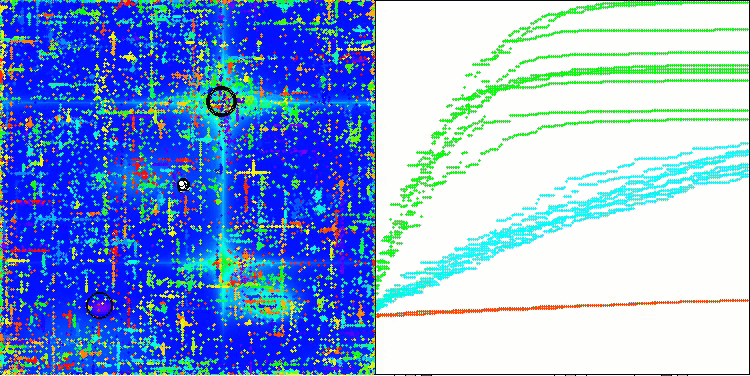
ABO on the Forest test function
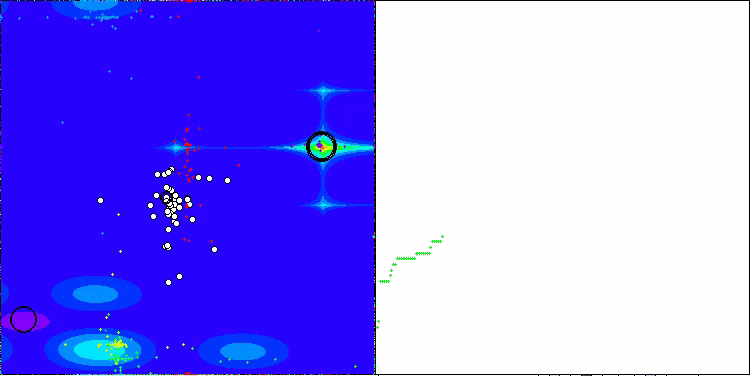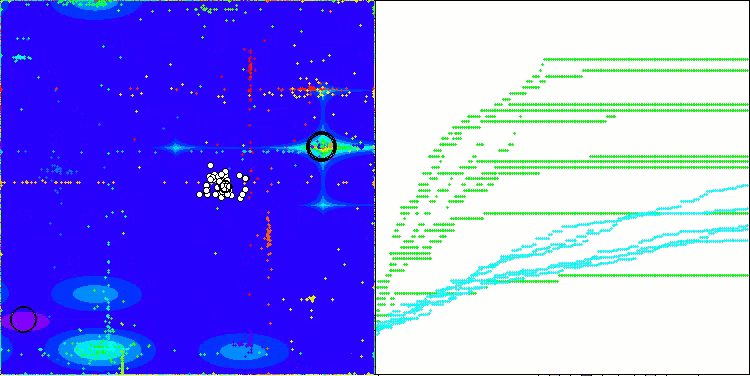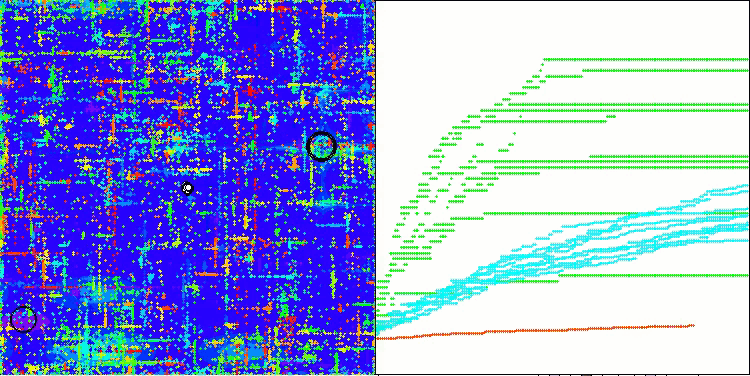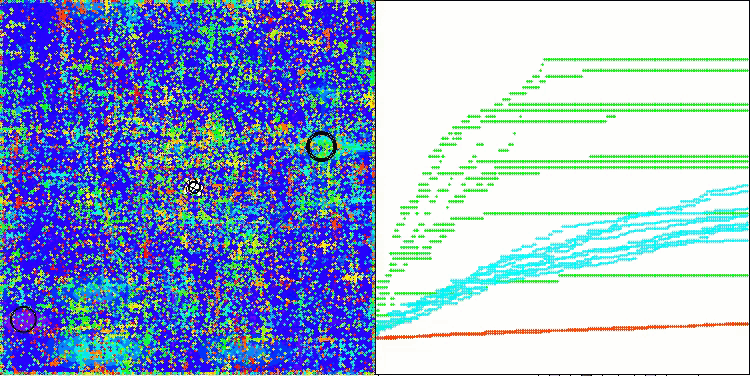
ABO on the Megacity test function
Based on the test results, the algorithm took a stable 19 th place in the overall ranking of the optimization algorithms.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration ptimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | evolution of social groups | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | simulated isotropic annealing | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 12 | TSEA | turtle shell evolution algorithm | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 13 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 14 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 15 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 16 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 17 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 18 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 19 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 20 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 21 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 22 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 23 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 24 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 25 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 26 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 27 | ABHA | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 28 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 29 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 30 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 31 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 32 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 33 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 34 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 35 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 36 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 37 | FAm | firefly algorithm M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 38 | GSA | gravitational search algorithm | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 39 | BFO | bacterial foraging optimization | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 40 | ABC | artificial bee colony | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 41 | BA | bat algorithm | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 42 | AAA | algae adaptive algorithm | 0.50007 | 0.32040 | 0.25525 | 1.07572 | 0.37021 | 0.22284 | 0.16785 | 0.76089 | 0.27846 | 0.14800 | 0.09755 | 0.52402 | 2.361 | 26.23 |
| 43 | SA | simulated annealing | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 44 | IWDm | intelligent water drops M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 45 | PSO | particle swarm optimisation | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
Summary
I have presented the versions of the ABO algorithm - the original one and the one with minor modifications. Changes in the algorithm logic led to simplification of calculations at each optimization step and a reduction in external parameters from three to two (not counting the parameter responsible for the population size), which had a positive effect on the overall results. The new algorithm also balances differently between exploring a new solution space and exploiting good solutions that have already been found.
Despite the algorithm's tendency to get stuck on low-dimensional problems, it demonstrates high efficiency in practical applications. Visualization of the algorithm operation showed its ability to deeply explore significant areas of hyperspace, which also indicates its improved research capabilities. As a result, the new version of the algorithm turned out to be more powerful and efficient compared to the original, demonstrating good scalability on all types of test functions, including discrete ones.
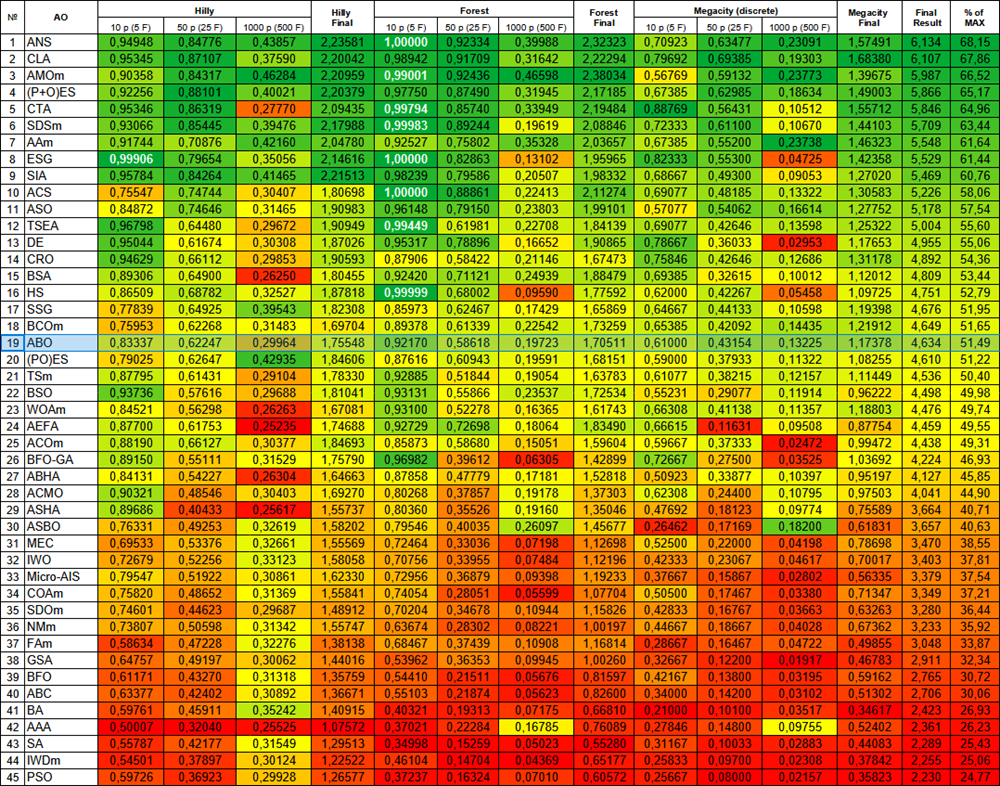
Figure 1. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white
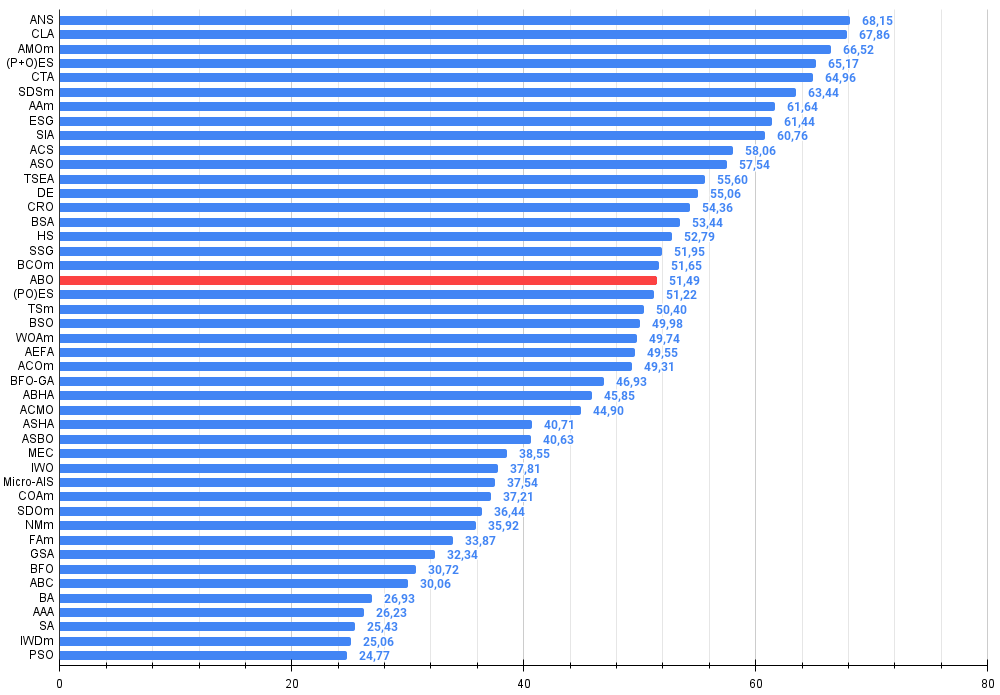
Figure 2. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,
where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)
ABO pros and cons:
Pros:
- Fast.
- Very simple implementation.
- Good scalability.
- Small number of external parameters.
Cons:
- High scatter of results on low-dimensional functions.
- Lack of mechanisms against getting stuck.
The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/16024
Price Action Analysis Toolkit Development (Part 22): Correlation Dashboard
From Basic to Intermediate: Arrays and Strings (II)
Neural Networks in Trading: Mask-Attention-Free Approach to Price Movement Forecasting
Raw Code Optimization and Tweaking for Improving Back-Test Results
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
The author is very good! As an absolute "dummy" in this topic, I am just amazed at how many different methods of optimisation there are. Probably with pearl buttons too? ))
Andrei, can you tell me please, in what software was the visualisation (for example ABO on the Forest test function) performed? Maybe it was mentioned somewhere, but I missed it....
Next article about Indian elephants or Mexican tushkans? ))
Very interesting article.
Thank you, Nikolay, for your kind words.
I haven't heard anything about the Jumping Grasshoppers algorithm, but there seem to be some on the topic of cats: Panther Optimisation Algorithm (POA) and Mountain Lion Algorithm (MLA). Might be considered by me if I can find a description sufficient to reproduce the logic of these search strategies.
The author is very good! As an absolute "dummy" in this topic, I am just amazed at how many different methods of optimisation there are. Probably with pearl buttons too? ))
Andrei, can you tell me please, in what software was the visualisation (for example ABO on the Forest test function) performed? Maybe it was mentioned somewhere, but I missed it....
Next article about Indian elephants or Mexican tushkans? ))
Thanks, Denis.
I use only MQL5 language in my articles on mql5.com, the visualisation is built in MT5 using standard tools. All source codes are available in the attachment to the article and you can reproduce my results.