MetaTrader 5 / エキスパートアドバイザー
English Русский 中文 Español Deutsch Português
preview
従来の機械学習手法を使用した為替レートの予測：ロジットモデルとプロビットモデル

従来の機械学習手法を使用した為替レートの予測：ロジットモデルとプロビットモデル

MetaTrader 5 — エキスパートアドバイザー |
146 9
Evgeniy Chernish
Evgeniy Chernish

はじめに

金融市場の研究者は常に、取引商品の将来の動向を予測するために、どの数学モデルを選択すべきかという難題に直面しています。今日までに非常に多くの予測モデルが開発されており、特に機械学習による予測を始めたばかりの人にとっては、どこから手を付けるべきか、またどのモデルに注目すべきか迷うところです。予測の課題を「明日の終値は今日の終値より高くなるか」という単純な問いに還元するならば、最も妥当な選択肢はバイナリ分類モデルとなります。中でも、ロジット回帰やプロビット回帰は最も基本的で広く利用されている手法です。これらは、機械学習の中でも最も一般的な手法である「教師あり学習」に分類されます。

教師あり学習の目的は、入力データ{x}（予測変数・特徴量）を、出力データ{y}（目的変数・ラベル）へとマッピングできるようモデルを学習させることです。本記事では、通貨ペアの価格が上昇するか下降するかという2つの市場状態のみを予測対象とするため、ラベルはy∊ {1, 0}の2クラスになります。予測変数には、一定のラグを持つ標準化された価格の増分（価格パターン）を用います。このデータから、モデルのパラメータ推定に用いる学習用データセット{x, y}を構築します。学習済みの分類器に基づく予測モデルは、「LogitExpert EA」として実装されます。


バイナリロジット回帰とプロビット回帰

理論的な部分を簡単に説明しましょう。バイナリ選択モデルの中で最も基本的なものは線形確率モデルであり、成功事象P(yn=1|xn)の確率を説明変数の線形関数として表現します。

P(yn=1|xn) = w0*1 + w1x1 + w2x2 + … + wkxk

しかし、このモデルには重大な欠点があります。予測される確率が0未満になったり1を超えたりすることがあり、それでは確率として解釈できません。この問題を解決するために、線形関数の出力を既知の確率分布関数に通すという手法が提案されました。

プロビットモデルは標準正規分布則N(0,1)に基づいています。

P(yn=1| x n ) = F( x n w )=μ n

  • n：観測（例）番号を示す下位のインデックス

  • yn：クラスラベル

  • F( )：正規分布関数（活性化関数）

  • xn：特徴量ベクトル

  • w：モデルパラメータのベクトル

  • xnw：ロジットまたは事前活性化（特徴量ベクトルとパラメータベクトルのスカラー積を表す）

xnw = w0*1 + w1x1 + w2x2 + … + wkxk

一方、ロジットモデルは確率分布のロジスティック法則に基づいています。

                                                            P(yn=1|xn) = L(xnw) = exp(xnw)/(1 + exp(xnw)) = μn

ロジスティック分布と正規分布の分布関数は非常に近く、[-1.2;1.2]の区間ではほぼ同じです。そのため、確率が0または1に極端に近くない限り、ロジットモデルとプロビットモデルはほぼ同じような結果を出すことが多いです。これらのモデルに特徴量ベクトルを入力すれば、各クラスラベルが選ばれる確率、すなわち将来の価格変動方向の確率を算出することができます。


データ準備

モデルのパラメータを推定する前に、まず特徴量を定義し、それらを標準化した上で、損失関数を最小化する目的でパラメータ最適化をおこなう関数に適した形式でデータを整形する必要があります。この処理を担う関数がGetDatasetです。

  • InpCount_：学習用データとして使用するサンプル数の設定

  • lag_：分析対象の特徴量の数（ラグによる価格増加）

  • 文字列X：特徴量を計算する対象の通貨ペア

  • 文字列y：ラベルを計算する対象の通貨ペア

  • int start：学習データの取得を開始するバー番号

説明のため、通貨ペアの価格ラグ増分を特徴量として使用する例を考えます。たとえば、関数の引数にlag_ = 4を指定した場合、特徴量はx={return-4, return-3, return-2, return-1}となります。このとき、学習に使用できるサンプル数は (InpCount_ - lag_) 個となります。

//+------------------------------------------------------------------+
//|Get data for analysis: features and corresponding labels          |
//+------------------------------------------------------------------+
bool GetDataset(int InpCount_,int lag_,int start,matrix &Input_X,vector & Target_y,string X,string y)
  {

   matrix rates;
   matrix target;
   target.CopyRates(y, PERIOD_CURRENT, COPY_RATES_OHLC, start+1, InpCount_);
   rates.CopyRates(X, PERIOD_CURRENT, COPY_RATES_OHLC, start+2, InpCount_-1);
   rates = rates.Transpose();
   target = target.Transpose();
   int Class_ [];
   ArrayResize(Class_,InpCount_);
   for(int i=0; i<InpCount_; i++)
     {
      if(target[i,3] >  target[i,0])
         Class_[i] = 1;
      else
         Class_[i] = 0;
     }

   vector label=vector::Zeros(InpCount_-lag_);
   for(int i=0; i<InpCount_-lag_; i++)
     {
      label[i] = Class_[i+lag_]; // class label
     }

   matrix returns=matrix::Zeros(InpCount_-lag_, lag_);
   for(int j=0; j<lag_; j++)
     {
      for(int i=0; i<InpCount_-lag_; i++)
        {
         returns[i,j] =rates[i+j,3] - rates[i+j,0]  ; // Input Data
        }
     }

   vector cols_mean=returns.Mean(0);
   vector cols_std=returns.Std(0);

   mean_ = cols_mean[lag_-1];
   std_ = cols_std[lag_-1];

   for(int j=0; j<lag_; j++)
     {
      for(int i=0; i<InpCount_-lag_; i++)
        {
         returns[i,j] = (returns[i,j] - cols_mean[lag_-1])/cols_std[lag_-1];
        }
     }
   Input_X = returns;
   Target_y = label;

   return true;
  }

出力として、特徴量行列Input_XとラベルベクトルTarget_yが得られます。学習データの作成が完了したら、次にモデルのパラメータ推定へと進みます。


モデルパラメータの推定

パラメータ推定には一般的に最大尤度法が用いられます。バイナリ分類の場合、ロジットモデルおよびプロビットモデルでは従属変数y がベルヌーイ分布に従うと仮定します。このとき、対数尤度関数は次のように表されます。

LLF

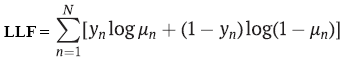
  • yn：クラスラベル

  • μn：ロジット回帰またはプロビット回帰を使用してクラスを予測する確率

  • N：学習例の数

パラメータを推定するためには、この関数の最大値を求める必要がありますが、機械学習では損失関数を最小化するのが一般的であり、ほとんどの最適化アルゴリズムも目的関数を最小化するよう設計されています。そのため、尤度関数にマイナス記号を付けて、負の対数尤度(NLL: Negative Log-Likelihood)とし、これを最小化します。この損失関数の最小化には、Alglibライブラリに実装されている二次準ニュートン法であるL-BFGS 法（記憶制限BFGS法）を用います。この数値最適化手法は、ロジットモデルやプロビットモデルのパラメータ推定によく使われます。また、もう一つの代表的な最適化手法として、反復最小二乗法(IRLS: Iteratively Reweighted Least Squares)もあります。

//+------------------------------------------------------------------+
//| Derived class from CNDimensional_Func                            |
//+------------------------------------------------------------------+
class CNDimensional_Logit : public CNDimensional_Func
  {
public:
                     CNDimensional_Logit(void) {}
                    ~CNDimensional_Logit(void) {}
   virtual void      Func(CRowDouble &w,double &func,CObject &obj);
  };

//+------------------------------------------------------------------+
//| Objective Function: Logit Negative loglikelihood                 |
//+------------------------------------------------------------------+
void CNDimensional_Logit::Func(CRowDouble &w,double &func,CObject &obj)
  {

   double LLF[],probit[],probitact[];
   vector logitact;
   ArrayResize(LLF,Rows_);
   ArrayResize(probit,Rows_);
   vector params=vector::Zeros(Cols_);

   for(int i = 0; i<Cols_; i++)
     {
      params[i] =  w[i]; // vector of parameters
     }

   vector logit=vector::Zeros(Rows_);
   logit = Input_X_gl.MatMul(params);

   for(int i=0; i <Rows_; i++)
     {
      probit[i] = logit[i];
     }

   if(probit_)
      MathCumulativeDistributionNormal(probit,0,1,probitact); // Probit activation
   else
      logit.Activation(logitact,AF_SIGMOID); // Logit activation

//--------------------to avoid NAN error when calculating logarithm ------------------------------------
   if(probit_)
     {
      for(int i = 0; i<Rows_; i++)
        {
         if(probitact[i]==1)
            probitact[i]= 0.999;
         if(probitact[i]==0)
            probitact[i]= 0.001;
        }
     }
   else
     {
      for(int i = 0; i<Rows_; i++)
        {
         if(logitact[i]==1)
            logitact[i]= 0.999;
         if(logitact[i]==0)
            logitact[i]= 0.001;
        }
     }
//-------------------------------------------------------------------------------------------------
   double L2_reg;
   if(L2_)
      L2_reg = 0.5 * params.Dot(params); //  L2_regularization
   else
      L2_reg =0;

//------------------ calculate loss function-------------------------------------------------------------
   if(probit_)
     {
      for(int i = 0; i<Rows_; i++)
        {

         LLF[i]=target_y_gl[i]*MathLog(probitact[i]) + (1-target_y_gl[i])*MathLog(1-probitact[i]) ;

         if(!MathIsValidNumber(LLF[i]))
           {
            break;
           }
        }
     }
   else
     {
      for(int i = 0; i<Rows_; i++)
        {

         LLF[i]=target_y_gl[i]*MathLog(logitact[i]) + (1-target_y_gl[i])*MathLog(1-logitact[i]);

         if(!MathIsValidNumber(LLF[i]))
           {
            break;
           }
        }
     }

   func = -MathSum(LLF) + L2_reg/(Rows_*C_); // Negative Loglikelihood + L2_regularization
//------------------------------------------------------------------------------------------------------
   func_ = func;
  }

ただし、パラメータ推定値を算出するだけでは不十分であり、特徴量がどの程度重要であるかを把握するために、これらの推定値の標準誤差も求める必要があります。

たとえば、人気の機械学習ライブラリであるscikit-learnは、なぜかロジットモデルに対してこの情報を計算しません。私はロジットモデルとプロビットモデルの両方について標準誤差の計算を実装しているため、特定の特徴量が統計的に有意に予測に影響を与えているかどうかを確認できます。これが、一般的な機械学習パッケージの既成モデルをONNXで変換して使うのではなく、MQLでロジットモデルのコードを自作する理由の一つです。もう一つの理由は、バーごと、あるいは任意の指定した頻度で分類器のパラメータを再最適化できる動的モデルが必要だからです。

さて、損失関数に話を戻しますが、これは若干の修正が必要です。重要なのは、私たちの分類器も高度なニューラルネットワークと同様に過剰適合しやすいという点です。これはパラメータ推定値が異常に大きくなる形で現れます。この負の現象を防ぐためには、推定値の大きさを抑制する方法が必要であり、それがL2正則化と呼ばれる手法です。

NLL_L2

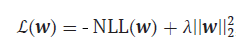
  • λ = 1/С、С = (0,1]

ここでは、パラメータベクトルのノルムの二乗にハイパーパラメータλを掛けたものを、既存の損失関数に単純に加えます。λの値が大きくなるほど、パラメータの大きな値に対するペナルティが強くなり、正則化の効果が高まります。

分類器のパラメータを評価する関数はFitLogitRegressionです。

  • bool L2 = false：デフォルトではL2正則化は無効になっています。
  • double C=1.0：正則化の強さを示すハイパーパラメータ。値が小さいほど、最適化されるパラメータの値がより強く制限されます。
  • bool probit = false：デフォルトはロジットモデルが有効です。
  • double alpha：LR統計量のカイ二乗分布に対する有意水準（αレベル）。

この関数は特徴量行列を引数に取り、すべての観測値で1となる「条件付き変数」または「ダミー変数」を追加します。これは、モデルのパラメータであるバイアス項w0を推定するために必要です。さらに、パラメータ推定値に加え、その共分散行列も計算し、標準誤差の算出に用います。

//+------------------------------------------------------------------+
//| Finding the optimal parameters for the Logit or Probit model     |
//+------------------------------------------------------------------+
vector FitLogitRegression(matrix &input_X, vector &target_y,bool L2 = false, double C=1.0,bool probit = false,double alpha = 0.05)
  {
   L2_=L2;
   probit_ = probit;
   C_ = C;
   double              w[],s[];
   CObject             obj;
   CNDimensional_Logit ffunc;
   CNDimensional_Rep   frep;
   ulong Rows = input_X.Rows();
   ulong Cols = input_X.Cols();
   matrix One=matrix::Ones(int(Rows),int(Cols+1));
   for(int i=0;i<int(Cols); i++)
     {
      One.Col(input_X.Col(i),i+1);  // design matrix
     }
   input_X = One;
   Cols = input_X.Cols();
   Rows_ = int(Rows);
   Cols_ = int(Cols);
   Input_X_gl = input_X;
   target_y_gl = target_y;
   ArrayResize(w,int(Cols));
   ArrayResize(s,int(Cols));
//--- initialization
   ArrayInitialize(w,0.0);
   ArrayInitialize(s,1.0);
//--- optimization stop conditions
   double epsg=0.000001;
   double epsf=0.000001;
   double epsx=0.000001;
   double diffstep=0.000001;
   int maxits=0;
//------------------------------
   CMinLBFGSStateShell state;
   CMinLBFGSReportShell rep;
   CAlglib::MinLBFGSCreateF(1,w,diffstep,state);
   CAlglib::MinLBFGSSetCond(state,epsg,epsf,epsx,maxits);
   CAlglib::MinLBFGSSetScale(state,s);
   CAlglib::MinLBFGSOptimize(state,ffunc,frep,0,obj);
   CAlglib::MinLBFGSResults(state,w,rep);
   Print("TerminationType ="," ",rep.GetTerminationType());
   Print("IterationsCount ="," ",rep.GetIterationsCount());

   vector parameters=vector::Zeros(Cols);
   for(int i = 0; i<int(Cols); i++)
     {
      parameters[i]= w[i];
     }
   Print("Parameters = "," ",parameters);

//-------Likelihood Ratio Test LR-----------------------------------------
   double S = target_y.Sum();   // number of "success"
   ulong All = target_y.Size(); // all data
   double L0 = S*MathLog(S/All) + (All-S)*MathLog((All-S)/All); // Log-likelihood for the trivial model
 //  Print("L0 = ",L0);
 //  Print("LLF = ",func_);
   double LR;
   LR = 2*(-func_ - L0); // Likelihood Ratio Test LR
   int err;
   double Chi2 = MathQuantileChiSquare(1-alpha,Cols-1,err); // If H0 true ---> Chi2Distribution(alpha,v)
   Print("LR ",LR," ","Chi2 = ",Chi2);
//--------------------------------------------------------------------------------
//-------------- calculate if model significant or not
   if(LR > Chi2)
      ModelSignificant = true;
   else
      ModelSignificant = false;
//----------------------------------------------------

//-------------Estimation of the covariance matrix of parameters for the Probit model------------
   vector logit = input_X.MatMul(parameters);  //
   vector activation;
   logit.Activation(activation,AF_SIGMOID); // Logit activation
   double probit_SE[],probitact[];
   ArrayResize(probit_SE,Rows_);

   for(int i=0; i <Rows_; i++)
     {
      probit_SE[i] = logit[i];
     }

   if(probit_)
     {
      ulong size_parameters = parameters.Size();
      matrix CovProbit=matrix::Zeros(int(size_parameters),int(size_parameters));
      int err;
      vector a_=vector::Zeros(Rows_);
      vector b=vector::Zeros(Rows_);
      vector c=vector::Zeros(Rows_);
      vector xt=vector::Zeros(int(size_parameters));

      for(int i = 0; i<Rows_; i++)
        {
         a_[i] = MathPow((MathProbabilityDensityNormal(probit_SE[i],0,1,err)),2);
         b[i] = MathCumulativeDistributionNormal(probit_SE[i],0,1,err);
         c[i] = a_[i]/(b[i]*(1-b[i]));
         xt = input_X.Row(i);
         CovProbit = CovProbit + c[i]*xt.Outer(xt);
        }
      CovProbit = CovProbit.Inv();
      vector SE;
      SE = CovProbit.Diag(0);
      SE = MathSqrt(SE);  // standard errors of parameters
      Print("Probit_SE = ", SE);
     }
   else
     {
      //-------------Estimation of the covariance matrix of parameters for the Logit model------------
      vector v = vector::Zeros(Rows_);

      for(int i = 0; i<Rows_; i++)
        {
         v[i] = activation[i]*(1-activation[i]);
        }

      matrix R,Hesse,X,a,CovLogit;
      R.Diag(v,0);
      X = input_X.Transpose();
      a = X.MatMul(R);
      Hesse = a.MatMul(input_X);
      CovLogit = Hesse.Inv();
      vector SE;
      SE = CovLogit.Diag(0);
      SE = MathSqrt(SE); // standard errors of parameters
      Print("Logit_SE = ", SE);
      //-----------------------------------------------
     }
   return parameters;
  }

パラメータが見つかり、共分散行列が計算されたら、予測に進むことができます。


予測

クラスラベルを予測し、それに応じて買いまたは売りのシグナルを生成する関数はTrade_PredictedTargetです。最適化されたパラメータを入力として受け取り、予測されたクラスラベルを出力します。その後、LogitExpert EAはポジションを開くためのルールを形成します。ルールは非常にシンプルです。買いシグナル(signal = 1)が出た場合、ロングポジションを新たにオープンします。既にロングポジションがある場合は、それを保持し続けます。売りシグナルが出た場合は、ロングポジションをクローズし、直ちにショートポジションをオープンします。

以下は、LogitExpert EAの実際のコードです。

//+------------------------------------------------------------------+
//|                                                  LogitExpert.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"

#include <\LogitReg.mqh>
#include <Trade\Trade.mqh>
#include <Trade\PositionInfo.mqh>
CTrade m_trade;
CPositionInfo m_position;

sinput string   symbol_X       = "EURUSD";    // Input symbol
sinput string   symbol_y       = "EURUSD";    // Target symbol
input bool     _probit_        = false;       // Probit model
input  int      InpCount       = 20;          // Depth of history
input  int     _lag_           = 4;           // Number of features
input bool     _L2_            = false;       // L2_regularization
input double   _C_             = 1;           // C(0,1) inverse of regularization strength
input double   alpha_          = 0.05;        // Significance level Alpha (0,1)
input int      reoptimize_step = 2;           // Reoptimize step

#define MAGIC_NUMBER 23092024

int prev_bars = 0;
MqlTick ticks;
double min_lot;
vector params_;
matrix _Input_X;
vector _Target_y;
static int count_ = 0;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   m_trade.SetExpertMagicNumber(MAGIC_NUMBER);
   m_trade.SetTypeFillingBySymbol(Symbol());
   m_trade.SetMarginMode();
   min_lot = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);

   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   Print(__FUNCTION__," Deinitialization reason code = ",reason);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
   if(!isnewBar(PERIOD_CURRENT))
      return;

   double step;
   step = count_ % reoptimize_step;
//------------------------------------Train Dataset-------------------------------------------------
   int start = 0;
   if(step == 0)
     {
      GetDataset(InpCount,_lag_,start,_Input_X,_Target_y,symbol_X,symbol_y);
      params_ = FitLogitRegression(_Input_X,_Target_y,_L2_,_C_,_probit_,alpha_);
     }
   count_ = count_+1;
//--------------------------------------------------------------------------------------------------

//--- Get trade signal
   int signal = Trade_PredictedTarget(params_,start,_lag_,InpCount,symbol_X);
   Comment("Trade signal: ",signal,"  ","ModelSignificant: ",ModelSignificant);  
//---------------------------------------------

//--- Open trades based on Signals
   SymbolInfoTick(Symbol(), ticks);
   if(signal==1)
     {
      if(!PosExists(POSITION_TYPE_BUY) && ModelSignificant)
        {
         m_trade.Buy(min_lot,Symbol(), ticks.ask);
         PosClose(POSITION_TYPE_SELL);
        }
      else
        {
         PosClose(POSITION_TYPE_SELL);
        }
     }
   else
     {
      if(!PosExists(POSITION_TYPE_SELL) && ModelSignificant)
        {
         m_trade.Sell(min_lot,Symbol(), ticks.bid);
         PosClose(POSITION_TYPE_BUY);
        }
      else
        {
         PosClose(POSITION_TYPE_BUY);
        }
     }
  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|   Function tracks the occurrence of a new bar event              |
//+------------------------------------------------------------------+
bool isnewBar(ENUM_TIMEFRAMES TF)
  {
   if(prev_bars == 0)
      prev_bars = Bars(Symbol(), TF);

   if(prev_bars != Bars(Symbol(), TF))
     {
      prev_bars = Bars(Symbol(), TF);
      return true;
     }

   return false;
  }

//+------------------------------------------------------------------+
//|Function determines whether there is an open buy or sell position |
//+------------------------------------------------------------------+
bool PosExists(ENUM_POSITION_TYPE type)
  {
   for(int i=PositionsTotal()-1; i>=0; i--)
      if(m_position.SelectByIndex(i))
         if(m_position.Symbol()==Symbol() && m_position.Magic() == MAGIC_NUMBER && m_position.PositionType()==type)
            return true;

   return false;
  }
//+------------------------------------------------------------------+
//|The function closes a long or short trade                         |
//+------------------------------------------------------------------+
void PosClose(ENUM_POSITION_TYPE type)
  {
   for(int i=PositionsTotal()-1; i>=0; i--)
      if(m_position.SelectByIndex(i))
         if(m_position.Symbol()==Symbol() && m_position.Magic() == MAGIC_NUMBER && m_position.PositionType()==type)
            if(!m_trade.PositionClose(m_position.Ticket()))
               printf("Failed to close position %d Err=%s",m_position.Ticket(),m_trade.ResultRetcodeDescription());
  }

このEAと他の多くのアプローチとを区別する点は何でしょうか。まず、reoptimize_stepバーごとに分類器パラメータの再最適化を可能にしていることです。次に、モデルのパラメータを単に推定するだけでなく、しばしば見落とされがちな推定値の標準誤差にも注目していることです。サンプルに対して「最適な」パラメータを見つけるだけでは不十分であり、これらのパラメータやモデル全体の有意性を確認することも必要です。パラメータが有意でない場合、そのような取引シグナルを無視する方が合理的でしょう。

そのため、このEAにはモデルの有意性を検定する手順も含まれています。この場合、帰無仮説H0は「すべてのモデルパラメータがゼロである」(H0:w1=0,w2=0,w3=0,..., wk=0)とし、対立仮説H1は「いくつかのパラメータがゼロではない」、つまりモデルが予測に役立つことを主張します。この仮説を検定するために、仮定モデルと自明モデルの差を評価する尤度比(LR: Likelihood Ratio)検定が用いられます。


LR = 2(LLF – LLF0)

  • LLF：尤度関数の対数値

  • LLF0：帰無仮説、すなわち自明なモデルにおける尤度対数

p0 = ∑(yn =1)/N：サンプル成功率

LLF0 = N(p0*Ln(p0) + (1- p0)*Ln(1 – p0))

差が大きいほど、単純なモデルに比べて完全なモデルの方が優れていることを示します。帰無仮説が成立する場合、LR統計量は自由度vのカイ二乗分布に従います（vは特徴量の数に等しい）。計算されたLR統計量の値が臨界領域、すなわちLR > X2crit (alpha; v=lag_)に入る場合、帰無仮説H0は棄却されます。したがって、取引シグナルは無視されず、取引ポジションがオープンされます。

以下は考えられるシナリオの一例である、GBPUSD、日足です。

GBPUSD日次バックテスト

ハイパーパラメータ

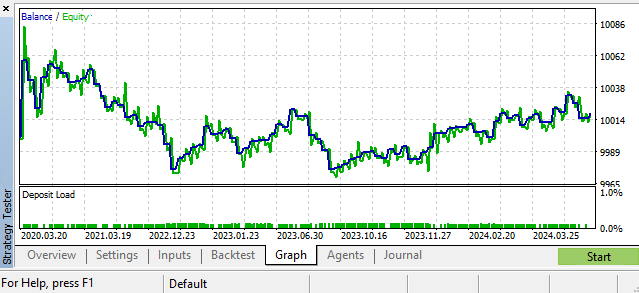
ハイパーパラメータ

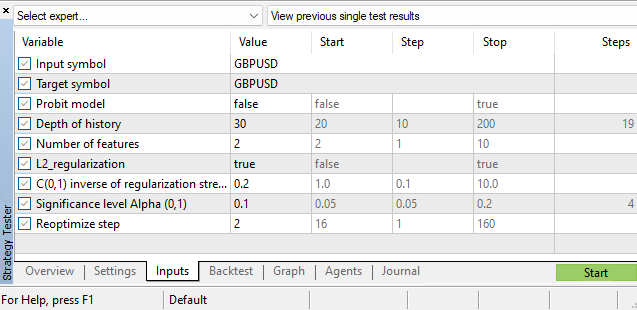
分類器モデル自体のパラメータ評価に加えて、多くのハイパーパラメータも存在します。

  • 履歴の深さ
  • 特徴量の数
  • アルファ有意水準
  • 再最適化ステップ

これらのハイパーパラメータはMetaTrader 5のストラテジーテスターで選択されます。EAのパフォーマンスを向上させるための一つの課題は、市場の現在の状態に応じて履歴の深さパラメータの依存関数を構築し、ロジットモデルやプロビットモデルのパラメータと同様に動的に調整することです。しかしそれはまた別の話です。ヒントとしては、無秩序指標の構築に関する問題を扱った私の記事「時系列の非定常性の指標としての2標本コルモゴロフ–スミルノフ検定」をご覧ください。


結論

本記事では、バイナリのパフォーマンス指標を用いた回帰モデルについて解説し、これらのモデルのパラメータ推定方法を学び、さらにこれらのモデルのテストおよび設定に用いるLogitExpert取引EAを実装しました。本EAの特徴は、最新かつ関連性の高いデータに基づき、分類器のパラメータをリアルタイムで再学習できる点にあります。

特に、ロジットモデルおよびプロビットモデルの共分散行列推定を伴うパラメータの標準誤差推定に重点を置きました。

また、モデル全体の有意性を検定するために尤度比基準を用いており、この統計量は統計的に信頼できない取引シグナルの選別に役立ちます。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16029

添付されたファイル |
ZIPをダウンロード
LogitReg.mqh (22.43 KB)
LogitExpert.mq5 (10.94 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

最後のコメント | ディスカッションに移動 (9)
Stanislav Korotky
Stanislav Korotky | 4 10月 2024 において 16:41
Evgeniy Chernish #:
すべての質問は外為市場と効率的市場仮説の陛下に。

タイトルは誤解を招く。

Evgeniy Chernish
Evgeniy Chernish | 4 10月 2024 において 17:12
Aleksey Nikolayev #:

ありがとう。

日帰り旅行でファンダメンタルズ・データを使うことはすでに可能だと思う。これは記事を批判するという意味ではなく、一つの考え方としてです。マクロ経済データを価格データとどのように適切に「混合」できるのか疑問です。例えば、その稀な変化が問題なのだ。例えば、名目為替レートから実質為替レートへの移行などである。

ありがとう、アレクセイ！正直なところ、私はファンダメンタルズに興味を持ったことがありません。ファンダメンタルズが付加的な情報を与えてくれないからというわけではなく、単に膨大な情報をカバーすることが不可能だからです。だから、まだこの方向には目を向けていないんだ。
Evgeniy Chernish
Evgeniy Chernish | 4 10月 2024 において 17:17
Stanislav Korotky #:

タイトルは誤解を招く。

なぜか？これは予測を行う分類予測モデルを使用している。それはモデルに投入されたものを正しくカウントする。では何が間違っているのか？モデルが素朴な予測に勝てないこと？そんな約束はしていない)
Stanislav Korotky
Stanislav Korotky | 4 10月 2024 において 17:48
Evgeniy Chernish #:
なぜか？予測を行う分類予測モデルを使用している。モデルに投入されたものは正しくカウントされる。では何が間違っているのか？モデルが素朴な予測に勝てないこと？そんな約束はしていない）

「古典的な方法で為替レートを予測することの不可能性..."

Evgeniy Chernish
Evgeniy Chernish | 4 10月 2024 において 18:20
Stanislav Korotky #:

「古典的手法による為替レートの予測の不可能性..."

不可能だとは思いもしなかった。私はただ予測し、パイソンライブラリでエラーをチェックしただけだ。もしかしたら誰かがフィルターや独自の機能を追加するかもしれないし、他の誰かがもっとうまくやるかもしれない。そして、あなたはすぐに不可能だと思った。
アフリカ水牛最適化(ABO) アフリカ水牛最適化(ABO)
この記事では、アフリカ水牛の特異な行動に着想を得て2015年に開発されたメタヒューリスティック手法、アフリカ水牛最適化(ABO)アルゴリズムを紹介します。アルゴリズムの実装プロセスと、複雑な問題の解決におけるその高い効率性について詳しく解説しており、最適化分野における有用なツールであることが示されています。
取引におけるニューラルネットワーク：一般化3次元指示表現セグメンテーション 取引におけるニューラルネットワーク：一般化3次元指示表現セグメンテーション
市場の状況を分析する際には、それを個別のセグメントに分割し、主要なトレンドを特定します。しかし、従来の分析手法は一つの側面に偏りがちで、全体像の適切な把握を妨げます。この記事では、複数のオブジェクトを選択できる手法を通じて、状況をより包括的かつ多層的に理解する方法を紹介します。
取引におけるニューラルネットワーク：制御されたセグメンテーション（最終部） 取引におけるニューラルネットワーク：制御されたセグメンテーション（最終部）
前回の記事で開始した、MQL5を使用したRefMask3Dフレームワークの構築作業を引き続き進めていきます。このフレームワークは、点群におけるマルチモーダルインタラクションと特徴量解析を包括的に研究し、自然言語で提供される説明に基づいてターゲットオブジェクトを特定・識別することを目的としています。
初級から中級まで：配列と文字列(III) 初級から中級まで：配列と文字列(III)
この記事では2つの側面について考察します。まず、標準ライブラリを使ってバイナリ値を8進数、10進数、16進数などの表現に変換する方法について説明します。次に、これまでに習得した知識を活用して、秘密のフレーズに基づいてパスワードの桁数をどのように決定できるかについて解説します。