MetaTrader 5 / 测试者
English Русский Español Deutsch 日本語 Português
preview
非洲水牛优化（ABO）

非洲水牛优化（ABO）

MetaTrader 5 — 测试者 |
218 5
Andrey Dik
Andrey Dik


内容

  1. 概述
  2. 算法实现
  3. 测试结果


概述

非洲水牛优化（ABO）算法是一种受这些动物在野外独特行为启发的元启发式方法。ABO算法是由科学家Julius Beneoluchi Odili和Mohd Nizam Kahar于2015年开发的，基于非洲水牛的社会互动和生存策略。

非洲水牛以其群体防御能力和寻找食物和水源的协调能力而闻名。这些动物生活在大型群体中，这为它们提供了抵御捕食者的保护，并帮助它们形成紧密的群体，由成年个体照顾幼崽和弱者。当受到捕食者攻击时，水牛展现出令人印象深刻的协调技能：它们可以围绕群体中的弱势成员形成一个圆圈，或者联合起来攻击敌人。

ABO算法的基本原则反映了水牛行为的关键方面。首先，是沟通：水牛使用声音信号来协调它们的行为，在算法中对应于智能体之间的信息交换。其次，是学习：水牛从自己的经验和群体中其他成员的经验中学习，这在算法中是通过根据收集到的信息更新智能体的位置来实现。

非洲水牛的独特行为使它们成为优化算法的有趣灵感来源。这些动物能够适应环境的变化，进行季节性迁徙以寻找食物和水源，并长途跋涉以寻找有利条件。在迁徙过程中，水牛采用搜索策略，使它们能够高效地定位资源并避免危险。

因此，非洲水牛高度协调、合作和适应性强的行为为开发ABO等优化算法提供了强大的动力。这些方面使该算法成为解决复杂问题的有效工具，其灵感来源于确保这些神奇动物在野外生存和繁衍的自然机制。


算法实现

ABO算法利用非洲水牛的行为本能，如合作和社会互动，来解决优化问题。其工作原理如下：

1. 算法首先初始化一群水牛，每只水牛代表解空间中的一个潜在解。水牛的位置在这个空间中随机初始化。

2. 使用适应度函数评估每个解（水牛位置）。如果当前水牛的适应度优于其最佳历史适应度bp_max，则保持其位置不变。同样，如果适应度优于整个群体的最优适应度bg_max，则该位置也保持不变。

3. 算法根据两个主要信号更新水牛的位置——“maaa”（停留并利用）和“waaa”（移动并探索）。这些信号帮助水牛优化它们寻找食物来源的过程。 

4.W.k + 1 = W.k + lp * r1 * (bgmaxt.k - m.k) + lp * r2 * (bpmax.k - m.k)：该方程更新水牛的移动。W.k表示探索的移动，而m.k标记水牛当前用于探索的位置。lp1和lp2是训练因子，而r1和r2是区间[0,1]内的随机数。bgmax是整个群体中的最优位置，而bpmax是特定水牛的最优位置。

在方程中，(bgmaxt.k - m.k)表示“maaa”信号，而(bpmax.k - m.k)表示“waaa”信号。

5. 接下来，使用以下方程根据第k只水牛的个人当前位置和前一个方程计算的移动，更新其位置：m.k + 1 = λ * (W.k + m.k)。该方程决定了水牛的新位置，其中λ是移动比率。

6. 如果未满足停止条件，我们返回到步骤2以再次更新适应度值。

7. 当达到停止条件时，算法终止并输出一个位置向量，表示为给定问题找到的最优解。

实现算法基础的S_Buffalo结构和C_AO_ABO类的描述。

  • S_Buffalo — 表示一只水牛的结构。它包含了w数组，描述算法中智能体的移动向量。
  • 在类构造函数中设置以下参数：popSize（群体大小）、lp1和lp2（学习因子），以及在算法中使用的λ。
  • SetParams方法允许根据存储在params数组中的值设置算法参数。
  • Init方法用于初始化算法。它接受最小和最大搜索范围、搜索步长和迭代次数。 
  • Moving和Revision方法实现了优化算法的主要步骤：移动（寻找新解）和修订（检查和更新解）。 
  • lp1、lp2和λ 类字段用于管理算法行为。 
  • b数组存储参与优化S_Buffalo类型的水牛实例。

//——————————————————————————————————————————————————————————————————————————————
struct S_Buffalo
{
    double w [];
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ABO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ABO () { }
  C_AO_ABO ()
  {
    ao_name = "ABO";
    ao_desc = "African Buffalo Optimization";
    ao_link = "https://www.mql5.com/en/articles/16024";

    popSize = 50;    // population size

    lp1     = 0.7;   // learning factor 1
    lp2     = 0.5;   // learning factor 2
    lambda  = 0.3;   // lambda for the movement equation

    ArrayResize (params, 4);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "lp1";     params [1].val = lp1;
    params [2].name = "lp2";     params [2].val = lp2;
    params [3].name = "lambda";  params [3].val = lambda;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    lp1     = params      [1].val;
    lp2     = params      [2].val;
    lambda  = params      [3].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double lp1;    // learning factor 1
  double lp2;    // learning factor 2
  double lambda; // lambda for the movement equation

  private: //-------------------------------------------------------------------
  S_Buffalo b [];
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_ABO类的Init方法负责初始化算法参数。方法参数：

  • rangeMinP []— 数组指定参数范围的最小值。
  • rangeMaxP [] — 数组指定参数范围的最大值。
  • rangeStepP [] — 数组指定参数值变化的步长。
  • epochsP — 迭代次数（迭代次数），默认值为0。此参数用于确定优化过程中迭代的次数。

 方法逻辑：

1. 标准初始化：该方法首先调用StandardInit，并传递数组rangeMinP、rangeMaxP和rangeStepP。如果初始化失败，返回false。

2. 种群初始化：

  • 该方法将b数组的大小调整为popSize，这对应于种群中搜索智能体的数量。
  • 对于种群中的每个智能体（在从0到popSize的循环中）：将b [i].w数组的大小调整为coords，这对应于每个个体的坐标数量（问题的优化参数）。
  • 使用ArrayInitialize将b [i].w数组初始化为0。

3. 如果所有操作成功，该方法返回true，表示初始化成功。

Init方法负责为算法准备必要的数据结构，确保参数和种群的正确初始化。这是执行将使用这些数据进行优化的主要算法之前的重要步骤。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ABO::Init (const double &rangeMinP [],
                     const double &rangeMaxP [],
                     const double &rangeStepP [],
                     const int epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (b, popSize);
  for (int i = 0; i < popSize; i++)
  {
    ArrayResize(b [i].w, coords);
    ArrayInitialize (b [i].w, 0.0);
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ABO类的Moving方法负责在优化过程中，种群中的水牛在搜索空间中的移动。以下是对其操作的详细描述：

1. 该方法首先检查是否已经执行了修订操作if (!revision)。如果尚未执行修订操作，则使用随机值初始化种群：

  • 外循环遍历popSize种群中的所有个体。
  • 内层循环遍历所有coords坐标。

     对于每个参数：

  • 首先，使用u.RNDfromCI方法在 rangeMin [c]到rangeMax [c]范围内生成一个随机值。
  • 然后，使用u.SeInDiSp检查并调整该值，该方法将值限制在给定范围内，并考虑rangeStep [c]步长。
  • 初始化完成后，将revision设置为true，方法执行结束。

2. 水牛移动的基本逻辑。如果已经执行了修订操作，方法将继续更新空间中水牛的位置：

  • 初始化w、m、r1、r2、bg和bp变量，以便进行后续计算。
  • 外循环遍历popSize种群中的所有个体。
  • 内循环遍历所有coords坐标。
  • 生成两个随机值r1和r2，用于更新水牛的位置，为其行为引入随机性。
  • bg和bp从对应的数组中获取值：cB [c]（全局最优群体坐标）和a [i].cB [c]（最优个体水牛坐标）。
  • m获取当前位置向量元素a [i].c [c]的值，而w获取对应坐标下水牛当前移动向量元素b [i].w [c]的值。
  • 根据考虑水牛全局和局部最佳位置的方程更新移动向量b [i].w [c]的值：b[i].w[c] = w + r1 * (bg - m) + r2 * (bp - m)。
  • 然后使用λ比率更新对应的m坐标位置。
  • 最后，使用u.SeInDiSp计算并调整搜索智能体坐标a [i].c [c]的新值。

Moving方法负责初始化和更新位置，并在优化过程中执行种群成员的移动。它使用随机值初始化，并根据群体中动物全局和局部已知的最优位置使用随机数更新水牛的位置。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double w  = 0.0;
  double m  = 0.0;
  double r1 = 0.0;
  double r2 = 0.0;
  double bg = 0.0;
  double bp = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      r1 = u.RNDfromCI (0, lp1);
      r2 = u.RNDfromCI (0, lp2);

      bg = cB [c];
      bp = a [i].cB [c];

      m = a [i].c [c];
      w = b [i].w [c];

      b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m);

      m = lambda * (m + b [i].w [c]);

      a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ABO类的Revision方法负责更新种群中函数和参数的最优值。方法描述：

1. 将ind变量初始化为-1。用于存储具有最优函数值的个体的索引。

2. 寻找全局最优个体：

  • for循环遍历 popSize种群中的所有智能体：
  • 对于每个智能体，检查其适应度函数值a [i].f是否超过了当前的全局最佳值fB。
  • 如果是，则更新fB，并将该智能体的索引保存在ind变量中。
  • 循环完成后，如果找到了更好的智能体（ind不等于-1），调用ArrayCopy函数。将智能体的c参数复制到全局最优参数数组cB中。

3. 更新局部最优值：

  • 第二个for循环再次遍历种群中的所有智能体。
  • 对于每个智能体，检查其适应度函数值a [i].f是否超过了其局部最优值a [i].fB。
  • 如果是，则更新智能体的局部最优值a [i].fB，并将智能体的坐标复制到其局部最佳坐标数组cB中。

Revision方法执行两个主要任务：

  • 找到并更新全局最优适应度函数值及其相关参数。
  • 此外，还更新种群中每个智能体的局部最优适应度函数值及其参数。

这种逻辑是那些需要同时跟踪全局最优和局部最优以改进解决方案搜索的优化算法的典型特征。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABO::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

我们已经考虑了整个算法的实现。非常简单。现在我们可以进入测试阶段。

让我们检查原始ABO版本的性能：

ABO|African Buffalo Optimization|50.0|0.2|0.9|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8495807203797128
25 Hilly's; Func runs: 10000; result: 0.5186057937632769
500 Hilly's; Func runs: 10000; result: 0.2642792490546295
=============================
5 Forest's; Func runs: 10000; result: 0.6554510234450559
25 Forest's; Func runs: 10000; result: 0.41662244493546935
500 Forest's; Func runs: 10000; result: 0.21044033116304034
=============================
5 Megacity's; Func runs: 10000; result: 0.6015384615384616
25 Megacity's; Func runs: 10000; result: 0.26430769230769224
500 Megacity's; Func runs: 10000; result: 0.11120000000000112
=============================
总分：3.89203 (43.24%)

整体还不错。然而，我还是会尝试改进该算法。在原始版本中，水牛的新位置是根据预先计算的位移向量（当前位置的增量）来计算的，这个向量基于群体中全局最优位置、该水牛的最优位置以及其当前位置的信息。这个移动向量发挥了惯性的作用。

我想出了一个放弃惯性并直接使用关于自身和群体最优位置的信息的想法，用来计算当前情况。我们将注释掉作者的代码部分，并写一个新的、更简单的代码，同时去掉一个外部参数——λ。新代码以绿色突出显示。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double w  = 0.0;
  double m  = 0.0;
  double r1 = 0.0;
  double r2 = 0.0;
  double bg = 0.0;
  double bp = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      /*
      r1 = u.RNDfromCI (0, lp1);
      r2 = u.RNDfromCI (0, lp2);

      bg = cB [c];
      bp = a [i].cB [c];

      m = a [i].c [c];
      w = b [i].w [c];

      b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m);

      m = lambda * (m + b [i].w [c]);

      a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]);
      */

      r1 = u.RNDfromCI (-lp1, lp1);
      r2 = u.RNDfromCI (-lp2, lp2);

      bg = cB [c];
      bp = a [i].cB [c];

      m = a [i].c [c];

      m = m + r1 * (bg - m) + r2 * (bp - m);

      a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]);

    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

以下是修改水牛移动逻辑后获得的结果：

ABO|African Buffalo Optimization|50.0|1.0|0.1|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.833371781687727
25 Hilly's; Func runs: 10000; result: 0.6224659624836805
500 Hilly's; Func runs: 10000; result: 0.2996410968574058
=============================
5 Forest's; Func runs: 10000; result: 0.9217022975045926
25 Forest's; Func runs: 10000; result: 0.5861755787948962
500 Forest's; Func runs: 10000; result: 0.19722782275756043
=============================
5 Megacity's; Func runs: 10000; result: 0.6100000000000001
25 Megacity's; Func runs: 10000; result: 0.4315384615384614
500 Megacity's; Func runs: 10000; result: 0.13224615384615512
=============================
总分：4.63437 (51.49%)

结果提高了近10%：51.49%对比43.24%。对于有50个和1000个参数的函数，改进尤为明显，而对于只有10个参数的函数，变化几乎难以察觉。这表明算法在大规模问题上的可扩展性有所提高。

现在还有一个理念需要测试：如果方程使用的是群体中随机选择的一只水牛的最优位置，而不是该水牛的最优位置，并且将概率向种群列表的顶部倾斜，结果会如何？这一点很容易测试，只需要对代码进行少许修改。将概率向种群列表的开头倾斜，确保随机数[0.0;1.0]被提升到一个幂次，并且丢弃结果数字的小数部分。在这种情况下，使用的是“4”次幂。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double w  = 0.0;
  double m  = 0.0;
  double r1 = 0.0;
  double r2 = 0.0;
  double bg = 0.0;
  double bp = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      /*
      r1 = u.RNDfromCI (0, lp1);
      r2 = u.RNDfromCI (0, lp2);

      bg = cB [c];
      bp = a [i].cB [c];

      m = a [i].c [c];
      w = b [i].w [c];

      b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m);

      m = lambda * (m + b [i].w [c]);

      a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]);
      */
      
      r1 = u.RNDfromCI (-lp1, lp1);
      r2 = u.RNDfromCI (-lp2, lp2);

      bg = cB [c];
      //bp = a [i].cB [c];
      
      
      double r = u.RNDprobab ();
      int ind = (int)pow (r - 1, 4);
      
      bp = a [ind].cB [c]; 

      m = a [i].c [c];

      m = m + r1 * (bg - m) + r2 * (bp - m);

      a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]);
      
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

为了在种群中应用偏向最优水牛的概率选择个体，我们需要在Revision方法中按个体的适应度水平进行排序。幸运的是，适用的Sorting_fB方法已经在之前的一篇文章中添加了。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABO::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  S_AO_Agent aT [];
  ArrayResize (aT, popSize);

  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

让我们看一下在ABO算法计算新位置的方程中，选择群体中水牛最优位置概率的结果：

ABO|African Buffalo Optimization|50.0|0.1|0.8|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.841272551476775
25 Hilly's; Func runs: 10000; result: 0.5701677694693293
500 Hilly's; Func runs: 10000; result: 0.28850644933225034
=============================
5 Forest's; Func runs: 10000; result: 0.9015705858486595
25 Forest's; Func runs: 10000; result: 0.49493378365495344
500 Forest's; Func runs: 10000; result: 0.1919604395333699
=============================
5 Megacity's; Func runs: 10000; result: 0.5692307692307692
25 Megacity's; Func runs: 10000; result: 0.35261538461538455
500 Megacity's; Func runs: 10000; result: 0.12010769230769343
=============================
总分：4.33037 (48.12%)

算法的整体性能有所下降，但仍高于“纯粹”的原始版本。因此，我们将记录对算法进行第一次修改的结果，并将其输入到排名表中。我想指出的是，对于每个版本的算法，外部参数的选择都是为了确保在所有测试中都能达到最优性能，因为改变算法的逻辑会导致其在搜索空间中的行为发生变化。


测试结果

在ABO算法的可视化中，我们可以看到对超空间重要部分的良好细化，这表明了对优化函数表面的高度学习能力。遗憾的是，小幅的修改虽然提高了算法的可扩展性，但增加了在小维问题上陷入局部最优的概率，这可以从结果的分散（可视化中收敛图的绿色线条）中看出。

Hilly值

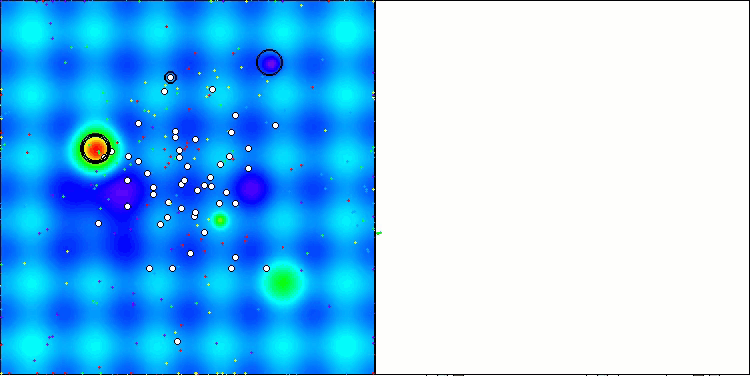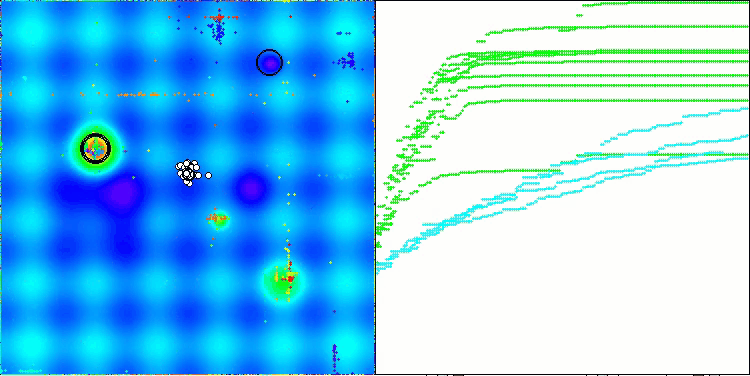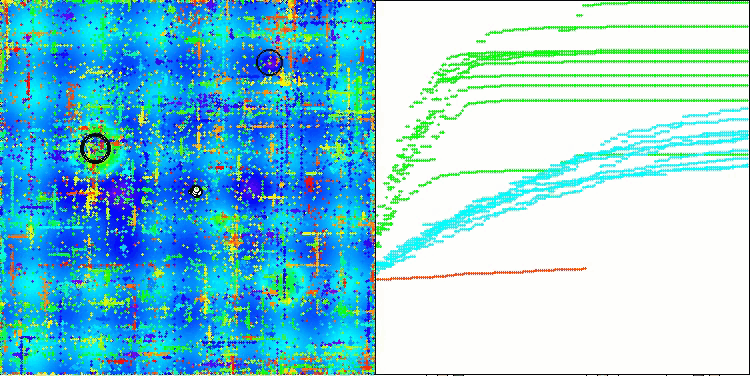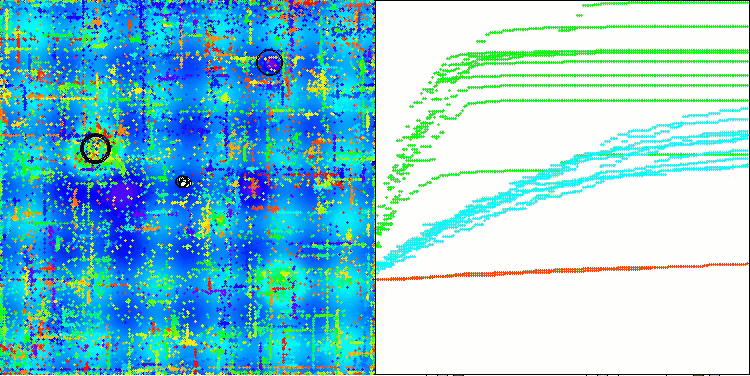
ABO在Hilly测试函数上

Forest值

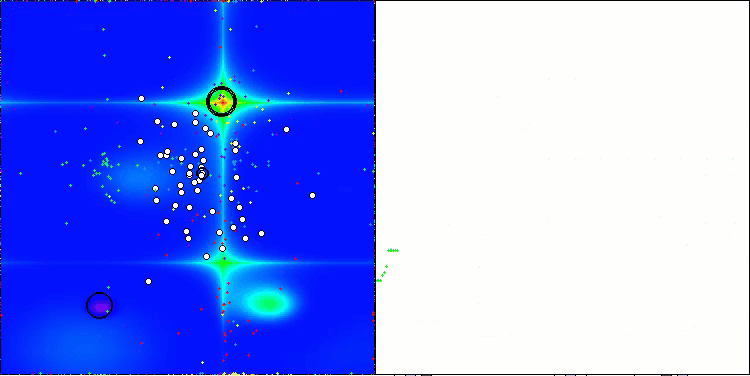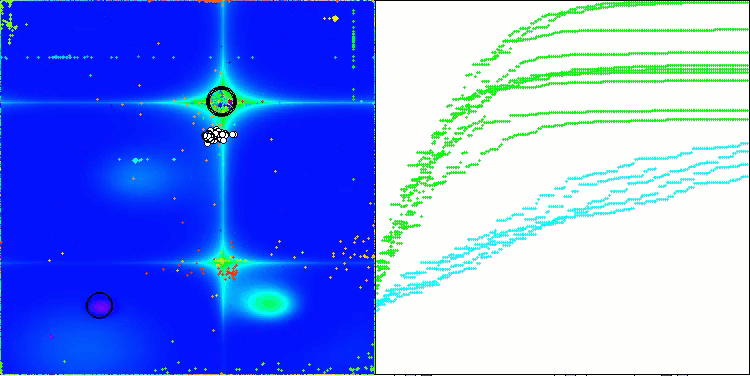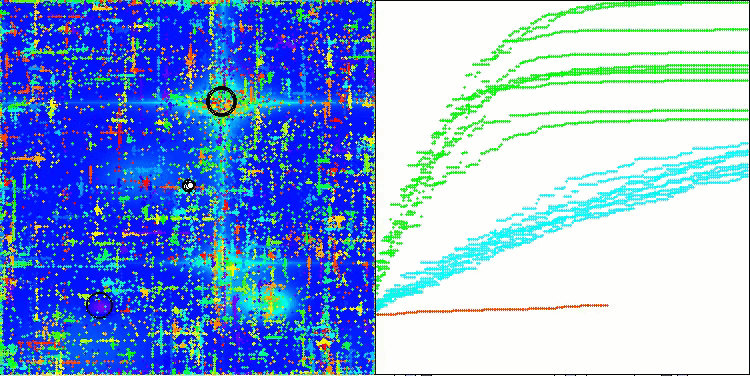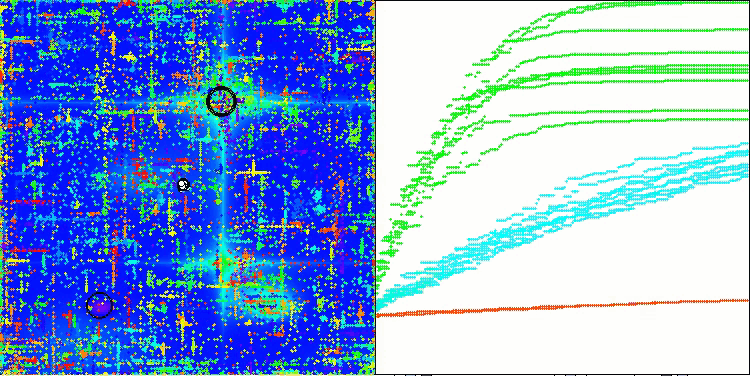
ABO在Forest测试函数上

Megacity

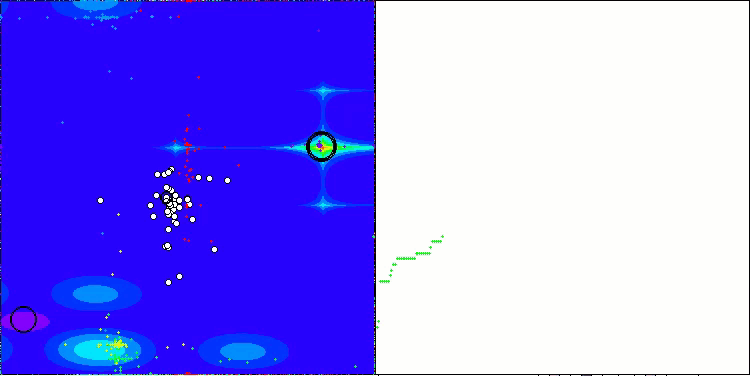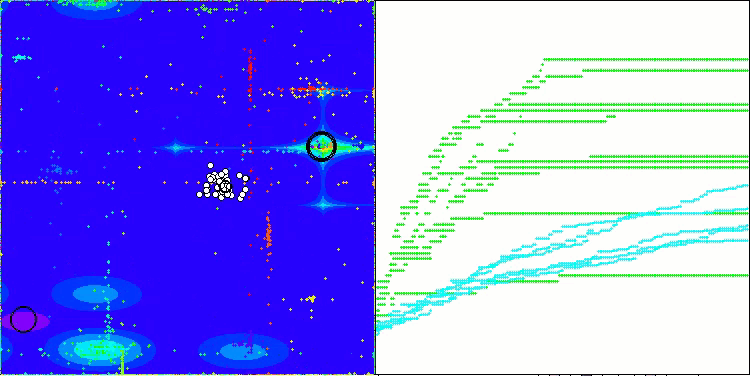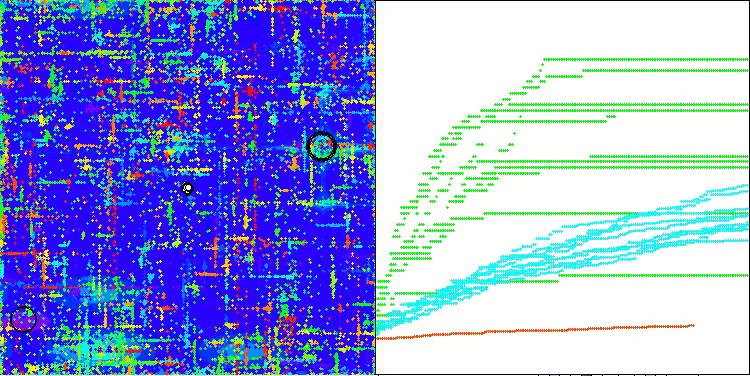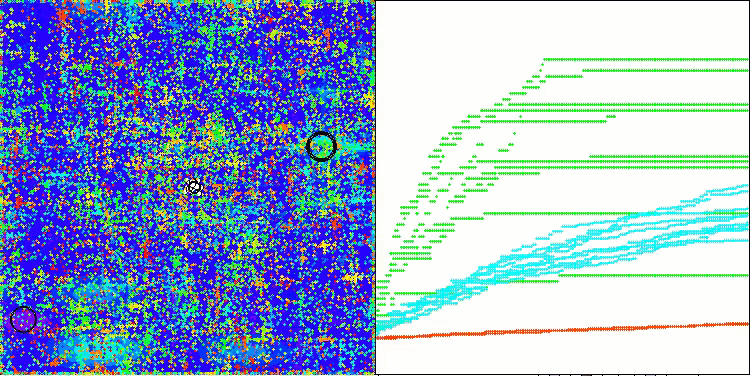
ABO在Megacity测试函数上

根据测试结果，该算法在优化算法的整体排名中稳列第19位。

# AO 说明 Hilly值 Hilly最终值 Forest值 Forest最终值 Megacity (离散) Megacity最终值 最终结果 最大百分比
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 ANS 跨邻域搜索 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
2 CLA 密码锁算法 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
3 AMOm 动物迁徙优化M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
4 (P+O)ES (P+O) 进化策略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA 彗星尾算法 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 AAm 射箭算法M 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
8 ESG 社会群体的进化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
9 SIA 模拟各向同性退火 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
10 ACS 人工协同搜索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
11 ASO 无序社会优化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
12 TSEA 龟壳演化算法 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
13 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
14 CRO 化学反应优化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
15 BSA 鸟群算法 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
16 HS 和声搜索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
17 SSG 树苗播种和生长 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
18 BCOm 细菌趋化性优化算法M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
19 ABO 非洲水牛优化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
20 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
21 TSm 禁忌搜索M 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
22 BSO 头脑风暴优化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
23 WOAm 鲸鱼优化算法M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
24 AEFA 人工电场算法 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
25 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
26 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
27 ABHA 人工蜂巢算法 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
28 ACMO 大气云模型优化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
29 ASHA 人工淋浴算法 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
30 ASBO 适应性社会行为优化 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
31 MEC 思维进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
32 IWO 入侵杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
33 Micro-AIS 微型人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
34 COAm 布谷鸟优化算法 M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
35 SDOm 螺旋动力学优化 M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
36 NMm Nelder-Mead方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
37 FAm 萤火虫算法 M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
38 GSA 引力搜索算法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
39 BFO 细菌觅食优化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
40 ABC 人工蜂群 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
41 BA 蝙蝠算法 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
42 AAA 人工藻类算法 0.50007 0.32040 0.25525 1.07572 0.37021 0.22284 0.16785 0.76089 0.27846 0.14800 0.09755 0.52402 2.361 26.23
43 SA 模拟退火 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
44 IWDm 智能水滴 M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
45 PSO 粒子群优化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77


总结

我展示了ABO算法的两个版本——原始版本和经过小幅修改的版本。对算法逻辑的修改使得每个优化步骤的计算简化，并且将外部参数从三个减少到两个（不包括负责种群大小的参数），这对整体结果产生了积极的作用。新算法在探索新的解空间和利用已经找到的良好解之间的差异也进行了平衡。

尽管该算法在低维问题上倾向于陷入局部最优，但在实际应用中它展示了很高的效率。算法运行的可视化显示了其深入探索超空间重要区域的能力，也表明了其改进的研究能力。最终，新版本的算法比原始版本更强大、更高效，在所有类型的测试函数（包括离散函数）上都展示了良好的可扩展性。

标签

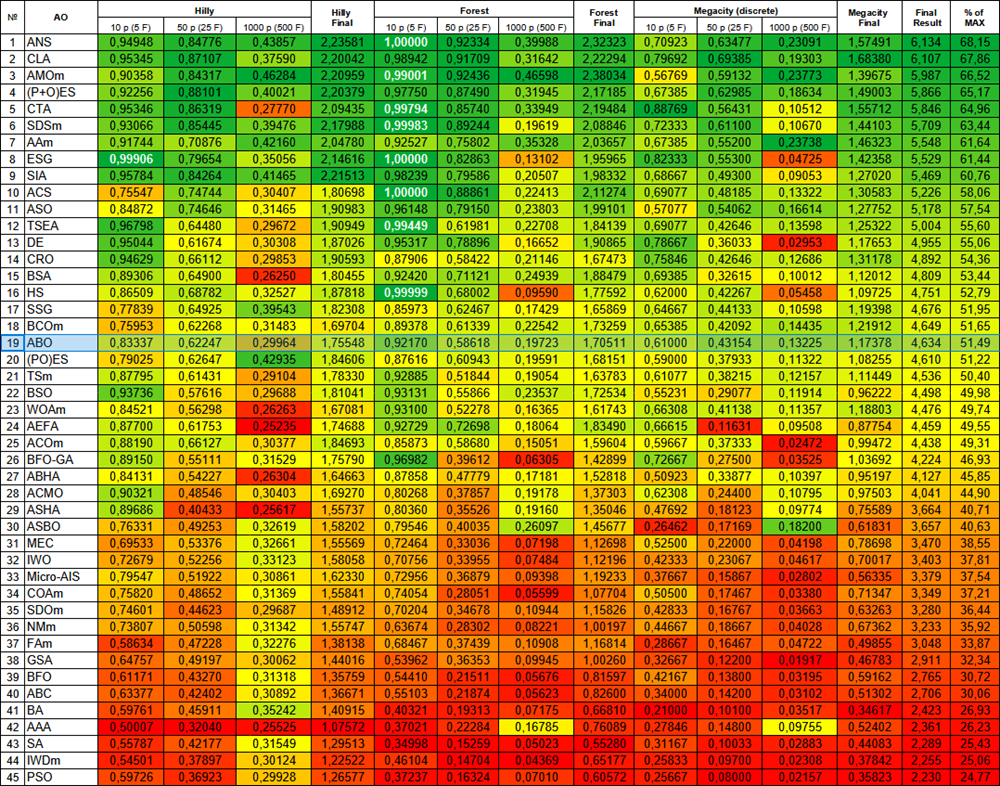
图1. 根据相关测试，将算法的颜色等级大于或等于0.99的结果以白色突出显示。

图表

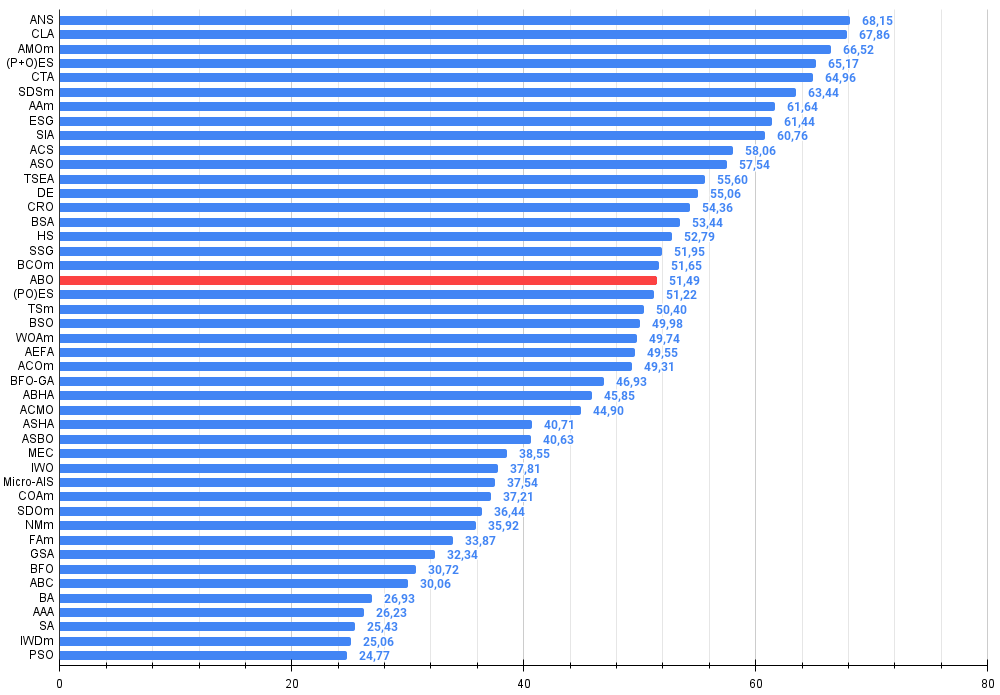
图例2. 算法测试结果的直方图（标尺从 0 到 100，数字越大结果越好，

其中 100 是理论上的最大可能结果，将计算评级表格的脚本存档）


ABO的优缺点：

优点：

  1. 快速。
  2. 实现简单。
  3. 良好的扩展性。
  4. 少量外部参数。

缺点：

  1. 在低维函数上表现出的高离散性结果。
  2. 缺乏防止陷入局部最优的机制。

文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/16024

附加的文件 |
下载ZIP
ABO.zip (35.98 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

该作者的其他文章

最近评论 | 前往讨论 (5)
BeeXXI Corporation
Nikolai Semko | 10 10月 2024 在 16:14
非常有趣的文章。
感谢安德鲁的辛勤工作和贡献。
期待您能在文章中介绍跳跃蚱蜢和攻击豹的优化方法。
Denis Kirichenko
Denis Kirichenko | 10 10月 2024 在 17:00

作者写得非常好！作为这个主题的绝对 "傻瓜"，我对有这么多不同的优化方法感到惊讶。也许还有珍珠按钮？))

安德烈，请告诉我，可视化是在什么软件中完成的（例如，森林测试函数的 ABO） ????。也许在什么地方提到过，但我错过了.....。

下一篇文章是关于印度大象还是墨西哥土司？))

Andrey Dik
Andrey Dik | 10 10月 2024 在 20:35
Nikolai Semko #:
非常有趣的文章。
感谢 Andrei 的劳动和贡献。
期待您能发表有关 "跳跃蚱蜢 "和 "攻击豹 "优化方法的文章。

谢谢你，尼古拉，谢谢你的美言。

我还没听说过有关 "跳跃蚱蜢 "算法的内容，但似乎有一些关于 "猫 "的内容：豹优化算法（POA）和山狮算法（MLA）。如果我能找到足以再现这些搜索策略逻辑的描述，我可能会考虑这些算法。

Andrey Dik
Andrey Dik | 10 10月 2024 在 20:39
Denis Kirichenko #:

作者写得非常好！作为这个主题的绝对 "傻瓜"，我对有这么多不同的优化方法感到惊讶。也许还有珍珠按钮？))

安德烈，请告诉我，可视化是在什么软件中完成的（例如，森林测试函数的 ABO） ????。也许在什么地方提到过，但我错过了....。

下一篇文章是关于印度象还是墨西哥大象？))

谢谢你，丹尼斯。

我在 mql5.com 上的文章只使用 MQL5 语言，可视化是使用标准工具在 MT5 中构建的。所有源代码都在文章附件中，您可以复制我的结果。

Andrey Dik
Andrey Dik | 11 10月 2024 在 00:01
我的一些文章中隐藏着 "复活节提示"，但迄今为止还没有被读者发现。
您应当知道的 MQL5 向导技术（第 37 部分）：配以线性和 Matérn 内核的高斯过程回归 您应当知道的 MQL5 向导技术（第 37 部分）：配以线性和 Matérn 内核的高斯过程回归
线性内核是机器学习中，针对线性回归和支持向量机所用的同类中最简单的矩阵。另一方面，Matérn 内核是我们在之前的文章中讲述的径向基函数的更普遍版本，它擅长映射不如 RBF 假设那样平滑的函数。我们构建了一个自定义信号类，即利用两个内核来预测做多和做空条件。
在MQL5中创建交易管理员面板（第三部分）：扩展内置类以进行主题管理（II） 在MQL5中创建交易管理员面板（第三部分）：扩展内置类以进行主题管理（II）
在本文的讨论中，我们将逐步扩展现有的对话框库，以纳入主题管理逻辑。此外，我们将把主题切换方法整合到管理员面板项目中使用的 CDialog、CEdit 和 CButton 类中。继续阅读，获取更多深入的了解。
开发基于订单簿的交易系统（第一部分）：指标 开发基于订单簿的交易系统（第一部分）：指标
市场深度无疑是执行快速交易的一个非常重要的因素，特别是在高频交易（HFT）算法中。在本系列文章中，我们将探讨这种类型的交易事件，这些事件可以通过经纪商在许多可交易的交易品种上获得。我们将从一个指标开始，您可以在其中自定义直接显示在图表上的直方图的调色板、位置和大小。我们还将研究如何生成 BookEvent 事件，以在特定条件下测试指标。未来文章的其他可能主题包括如何存储价格分布数据以及如何在策略测试器中使用它。
从基础到中级：Include 指令 从基础到中级：Include 指令
在今天的文章中，我们将讨论一个在 MQL5 中可以找到的各种代码中广泛使用的编译指令。虽然这里对这个指令的解释相当肤浅，但重要的是你要开始了解如何使用它，因为随着你进入更高层次的编程，它很快就会变得不可或缺。此处提供的内容仅用于教育目的。在任何情况下，除了学习和掌握所提出的概念外，都不应出于任何目的使用此应用程序。