Otimização com búfalos-africanos — African Buffalo Optimization (ABO)
111
0
Conteúdo
Introdução
O algoritmo de otimização com búfalos-africanos (African Buffalo Optimization, ABO) é uma abordagem meta-heurística inspirada no comportamento impressionante desses animais na natureza. Desenvolvido em 2015 pelos cientistas Julius Beneoluchi Odili e Mohd Nizam Kahar, o algoritmo ABO se baseia na interação social e nas estratégias de sobrevivência dos búfalos-africanos.
Os búfalos-africanos são conhecidos por sua capacidade de defesa coletiva e coordenação eficaz na busca por alimento e água. Esses animais vivem em grandes manadas, o que lhes proporciona proteção contra predadores e favorece a formação de grupos coesos, nos quais os adultos cuidam dos mais jovens e vulneráveis. Quando atacados por predadores, os búfalos demonstram uma impressionante capacidade de coordenação: podem formar um círculo ao redor dos membros mais frágeis da manada ou atacar o inimigo em conjunto.
Os princípios fundamentais do algoritmo ABO refletem aspectos-chave do comportamento desses animais. Primeiramente, a comunicação: os búfalos usam sinais sonoros para coordenar suas ações, o que no algoritmo corresponde à troca de informações entre os agentes. Segundo, o aprendizado: os búfalos aprendem com sua própria experiência e com a experiência de outros membros da manada, o que no algoritmo é implementado por meio da atualização das posições dos agentes com base nas informações reunidas.
O comportamento singular desses animais os torna uma fonte interessante de inspiração para algoritmos de otimização. Esses animais se adaptam às mudanças no ambiente, realizando migrações sazonais em busca de alimento e água e percorrendo grandes distâncias em busca de condições favoráveis. Durante essas migrações, os búfalos aplicam estratégias de busca que lhes permitem encontrar recursos de maneira eficiente e evitar perigos.
Assim, o comportamento dos búfalos-africanos, caracterizado por alto grau de coordenação, defesa coletiva e adaptação, serve como um poderoso estímulo para o desenvolvimento de algoritmos de otimização, como o ABO. Esses aspectos tornam o algoritmo uma ferramenta eficaz para resolver problemas complexos, inspirando-se em mecanismos naturais que garantem a sobrevivência e a prosperidade desses animais incríveis em seu habitat natural.
Implementação do algoritmo
O algoritmo African Buffalo Optimization (ABO) utiliza os instintos comportamentais dos búfalos-africanos, como cooperação e interação social, para resolver problemas de otimização. Os princípios de funcionamento são os seguintes:
1. O algoritmo começa com a inicialização da população de búfalos, onde cada búfalo representa uma solução potencial no espaço de soluções. As posições dos búfalos são inicializadas aleatoriamente dentro desse espaço.
2. Cada solução (posição do búfalo) é avaliada por meio de uma função de fitness. Se o fitness do búfalo atual for melhor do que seu melhor fitness anterior "bp_max", então sua posição é armazenada. Da mesma forma, se o fitness for melhor do que o melhor fitness de toda a manada "bg_max", então essa posição também é armazenada.
3. O algoritmo atualiza as posições dos búfalos com base em dois sinais principais: "maaa" (ficar e explorar) e "waaa" (mover-se e explorar). Esses sinais ajudam os búfalos a otimizar a busca por fontes de alimento.
4.W.k + 1 = W.k + lp * r1 * (bgmaxt.k - m.k) + lp * r2 * (bpmax.k - m.k): Esta equação atualiza o deslocamento do búfalo. W.k representa o deslocamento para exploração, e m.k, a posição atual do búfalo para exploração. lp1 e lp2 são os fatores de aprendizado, e r1 e r2 são números aleatórios no intervalo [0,1]. bgmax é a melhor posição da manada inteira, e bpmax, a melhor posição do búfalo específico.
Nesta equação, (bgmaxt.k - m.k) representa o sinal "maaa", e (bpmax.k - m.k), o sinal "waaa".
5. Em seguida, é atualizada a posição do búfalo k com base em sua posição pessoal atual e no deslocamento calculado na fórmula anterior, usando a seguinte equação: m.k + 1 = λ * (W.k + m.k). Esta equação determina a nova posição do búfalo, onde λ é o coeficiente de movimento.
6. Se os critérios de parada não forem atendidos, retorna-se ao passo 2 para reavaliar os valores de fitness.
7. Quando o critério de parada é alcançado, o algoritmo finaliza sua execução e retorna o vetor de posição que representa a melhor solução encontrada para o problema dado.
Vamos descrever a estrutura "S_Buffalo" e a classe "C_AO_ABO", que implementam a base do algoritmo.
- S_Buffalo — estrutura que representa um búfalo. Ela contém o array "w", que descreve o vetor de deslocamento do agente no algoritmo.
- No construtor da classe, são definidos os parâmetros como o tamanho da população "popSize", os fatores de aprendizado "lp1", "lp2" e o valor de "lambda", que são utilizados no algoritmo.
- O método "SetParams" permite configurar os parâmetros do algoritmo com base nos valores armazenados no array "params".
- O método "Init" serve para a inicialização do algoritmo. Ele recebe os limites mínimos e máximos de busca, o passo de busca e o número de épocas.
- Os métodos "Moving" e "Revision" implementam as etapas principais do algoritmo de otimização: movimentação (busca de uma nova solução) e revisão (verificação e atualização das soluções).
- Os campos da classe "lp1", "lp2" e "lambda" são usados para controlar o comportamento do algoritmo.
- O array "b" do tipo "S_Buffalo" armazena as instâncias dos búfalos que participam do processo de otimização.
//—————————————————————————————————————————————————————————————————————————————— struct S_Buffalo { double w []; }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— class C_AO_ABO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ABO () { } C_AO_ABO () { ao_name = "ABO"; ao_desc = "African Buffalo Optimization"; ao_link = "https://www.mql5.com/pt/articles/16024"; popSize = 50; // population size lp1 = 0.7; // learning factor 1 lp2 = 0.5; // learning factor 2 lambda = 0.3; // lambda for the movement equation ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "lp1"; params [1].val = lp1; params [2].name = "lp2"; params [2].val = lp2; params [3].name = "lambda"; params [3].val = lambda; } void SetParams () { popSize = (int)params [0].val; lp1 = params [1].val; lp2 = params [2].val; lambda = params [3].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double lp1; // learning factor 1 double lp2; // learning factor 2 double lambda; // lambda for the movement equation private: //------------------------------------------------------------------- S_Buffalo b []; }; //——————————————————————————————————————————————————————————————————————————————
O método "Init" da classe "C_AO_ABO" é responsável por inicializar os parâmetros do algoritmo. Parâmetros do método:
- rangeMinP [] — array que define os valores mínimos para os intervalos dos parâmetros.
- rangeMaxP [] — array que define os valores máximos para os intervalos dos parâmetros.
- rangeStepP [] — array que define os passos de variação para os valores dos parâmetros.
- epochsP — número de épocas (iterações), por padrão igual a 0. Esse parâmetro é usado para determinar a quantidade de iterações no processo de otimização.
Lógica de funcionamento do método:
1. Inicialização padrão: o método primeiro chama "StandardInit" com os arrays passados "rangeMinP", "rangeMaxP" e "rangeStepP". Se essa inicialização falhar, retorna "false".
2. Inicialização da população:
- O método ajusta o tamanho do array "b" para o valor de "popSize", o que corresponde à quantidade de agentes de busca na população.
- Para cada agente na população (em um laço de 0 até "popSize"): o tamanho do array "b [i].w" é ajustado para o valor de "coords", que corresponde à quantidade de coordenadas (parâmetros a serem otimizados) para cada indivíduo.
- O array "b [i].w" é inicializado com zeros usando "ArrayInitialize".
3. Se todas as operações forem bem-sucedidas, o método retorna "true", sinalizando que a inicialização foi concluída com sucesso.
O método "Init" é responsável por preparar as estruturas de dados necessárias para o algoritmo, garantindo a inicialização correta dos parâmetros e da população. Esse é um passo essencial antes da execução do algoritmo principal, que utilizará esses dados para realizar a otimização.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ABO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (b, popSize); for (int i = 0; i < popSize; i++) { ArrayResize(b [i].w, coords); ArrayInitialize (b [i].w, 0.0); } return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" da classe "C_AO_ABO" é responsável pela movimentação dos búfalos da população no espaço de busca durante o processo de otimização. Abaixo está uma descrição detalhada de seu funcionamento:
1. O método verifica primeiro se a revisão foi realizada "if (!revision)"; se ainda não tiver sido feita, ele inicializa a população com valores aleatórios:
- O laço externo percorre todos os indivíduos na população "popSize".
- O laço interno percorre todas as coordenadas "coords".
Para cada parâmetro:
- Primeiro, é gerado um valor aleatório no intervalo de "rangeMin [c]" até "rangeMax [c]" utilizando o método "u.RNDfromCI".
- Em seguida, esse valor passa por verificação e ajuste com o método "u.SeInDiSp", que limita o valor dentro do intervalo especificado considerando o passo "rangeStep [c]".
- Após a finalização da inicialização, "revision" é definido como "true", e o método é encerrado.
2. A lógica principal da movimentação dos búfalos. Se a revisão já tiver sido realizada, o método passa à atualização da posição dos búfalos no espaço:
- São inicializadas as variáveis "w", "m", "r1", "r2", "bg" e "bp" para os cálculos seguintes.
- O laço externo percorre todos os indivíduos na população "popSize".
- O laço interno percorre todas as coordenadas "coords":
- Dois valores aleatórios "r1" e "r2" são gerados para serem usados na atualização da posição dos búfalos, adicionando um elemento de aleatoriedade ao seu comportamento.
- "bg" e "bp" recebem valores dos arrays correspondentes: "cB [c]" (melhores coordenadas globais da manada) e "a [i].cB [c]" (melhores coordenadas individuais do búfalo).
- "m" recebe o valor do elemento do vetor de posição atual "a [i].c [c]", enquanto "w" — o valor do vetor de deslocamento atual "b [i].w [c]" do búfalo na coordenada correspondente.
- O valor do vetor de deslocamento "b [i].w [c]" é atualizado com a fórmula que leva em conta tanto a melhor posição global quanto a local do búfalo: b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m).
- Depois, a posição na coordenada correspondente "m" é atualizada levando em conta o coeficiente "lambda".
- Por fim, o novo valor da coordenada do agente de busca "a [i].c [c]" é calculado e ajustado com o auxílio de "u.SeInDiSp".
O método "Moving" é responsável pela inicialização e atualização das posições e realiza o deslocamento dos membros da população durante o processo de otimização. Ele utiliza valores aleatórios para a inicialização e também aplica números aleatórios para a atualização das posições dos búfalos, com base tanto nas melhores posições conhecidas globais quanto nas locais dentro da manada.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" da classe "C_AO_ABO" é responsável por atualizar os melhores valores da função e os parâmetros da população. Descrição do método:
1. A variável "ind" é inicializada com o valor "-1". Ela será usada para armazenar o índice do indivíduo com a melhor função.
2. Busca do melhor indivíduo global:
- O laço "for" percorre todos os agentes da população "popSize":
- Para cada agente, verifica-se se o valor de sua função de adaptabilidade "a [i].f" excede o valor global atual "fB".
- Se isso ocorrer, "fB" é atualizado e o índice desse agente é armazenado na variável "ind".
- Após a conclusão do laço, se um melhor agente foi encontrado (ou seja, "ind" é diferente de "-1"), a função "ArrayCopy" é chamada, copiando os parâmetros "c" desse agente para o array global de melhores parâmetros "cB".
3. Atualização dos melhores valores locais:
- Um segundo laço "for" percorre novamente todos os agentes da população.
- Para cada agente, verifica-se se seu valor de função de adaptabilidade "a [i].f" supera seu valor local anterior "a [i].fB".
- Se sim, o valor local "a [i].fB" é atualizado, e as coordenadas desse agente são copiadas para seu array local de melhores coordenadas "cB".
O método "Revision" executa duas funções principais:
- Encontra e atualiza o melhor valor global da função de adaptabilidade e os parâmetros correspondentes.
- Atualiza os melhores valores locais da função de adaptabilidade e os parâmetros de cada agente da população.
Essa lógica é característica de algoritmos de otimização nos quais é importante acompanhar tanto os ótimos globais quanto os locais para melhorar a busca por soluções.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Com isso, abordamos toda a implementação do algoritmo, que é bastante simples, e agora podemos passar para a etapa de testes.
Vamos ver como funciona a versão original dos autores do algoritmo ABO:
=============================
5 Hilly's; Func runs: 10000; result: 0.8495807203797128
25 Hilly's; Func runs: 10000; result: 0.5186057937632769
500 Hilly's; Func runs: 10000; result: 0.2642792490546295
=============================
5 Forest's; Func runs: 10000; result: 0.6554510234450559
25 Forest's; Func runs: 10000; result: 0.41662244493546935
500 Forest's; Func runs: 10000; result: 0.21044033116304034
=============================
5 Megacity's; Func runs: 10000; result: 0.6015384615384616
25 Megacity's; Func runs: 10000; result: 0.26430769230769224
500 Megacity's; Func runs: 10000; result: 0.11120000000000112
=============================
All score: 3.89203 (43.24%)
Digamos que o resultado não é ruim. Porém, eu não seria eu mesmo se não tentasse melhorar o algoritmo. Na versão original dos autores, a nova posição dos búfalos é calculada com base no vetor de deslocamento previamente computado (incremento da posição atual), com base nas informações sobre a melhor posição global da manada, a melhor posição do búfalo em questão e sua posição atual. Esse vetor de deslocamento atua como uma espécie de inércia no movimento.
Tive a ideia de eliminar a inércia e usar diretamente as informações das melhores posições, tanto do indivíduo quanto da manada, aplicando o cálculo diretamente à posição atual. Comentaremos o trecho original do código dos autores e escreveremos um novo, mais simples, eliminando ao mesmo tempo um dos parâmetros externos — o lambda. Novo código está destacado em verde.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { /* r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); */ r1 = u.RNDfromCI (-lp1, lp1); r2 = u.RNDfromCI (-lp2, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; m = m + r1 * (bg - m) + r2 * (bp - m); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Aqui estão os resultados obtidos após a modificação da lógica de movimentação dos búfalos:
=============================
5 Hilly's; Func runs: 10000; result: 0.833371781687727
25 Hilly's; Func runs: 10000; result: 0.6224659624836805
500 Hilly's; Func runs: 10000; result: 0.2996410968574058
=============================
5 Forest's; Func runs: 10000; result: 0.9217022975045926
25 Forest's; Func runs: 10000; result: 0.5861755787948962
500 Forest's; Func runs: 10000; result: 0.19722782275756043
=============================
5 Megacity's; Func runs: 10000; result: 0.6100000000000001
25 Megacity's; Func runs: 10000; result: 0.4315384615384614
500 Megacity's; Func runs: 10000; result: 0.13224615384615512
=============================
All score: 4.63437 (51.49%)
Os resultados melhoraram quase 10%: 51,49% contra 43,24%. As melhorias são especialmente perceptíveis nas funções com 50 e 1000 parâmetros, enquanto nas funções com 10 parâmetros as mudanças são quase imperceptíveis. Isso indica um aumento na capacidade do algoritmo de escalar para problemas de alta dimensionalidade.
Agora resta testar mais uma ideia: e se, na fórmula, em vez da melhor posição do búfalo, usarmos a melhor posição de um búfalo escolhido aleatoriamente da manada, com uma probabilidade enviesada para o início da lista de indivíduos da população? Isso é fácil de verificar e exige apenas algumas alterações no código. O viés de probabilidade para o início da lista da população é obtido elevando um número aleatório no intervalo [0.0;1.0] a uma potência e descartando a parte fracionária do resultado. Neste caso, é usada a potência "4".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { /* r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); */ r1 = u.RNDfromCI (-lp1, lp1); r2 = u.RNDfromCI (-lp2, lp2); bg = cB [c]; //bp = a [i].cB [c]; double r = u.RNDprobab (); int ind = (int)pow (r - 1, 4); bp = a [ind].cB [c]; m = a [i].c [c]; m = m + r1 * (bg - m) + r2 * (bp - m); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Para aplicar a escolha probabilística dos indivíduos da população com viés em direção aos melhores búfalos, será necessário realizar uma ordenação com base no nível de adaptabilidade dos indivíduos, dentro do método "Revision". Felizmente, o método correspondente "Sorting_fB" já havia sido incluído em um dos artigos anteriores.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Vamos observar os resultados da aplicação da escolha probabilística da melhor posição dos búfalos da manada na fórmula de cálculo da nova posição no algoritmo ABO:
ABO|African Buffalo Optimization|50.0|0.1|0.8|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.841272551476775
25 Hilly's; Func runs: 10000; result: 0.5701677694693293
500 Hilly's; Func runs: 10000; result: 0.28850644933225034
=============================
5 Forest's; Func runs: 10000; result: 0.9015705858486595
25 Forest's; Func runs: 10000; result: 0.49493378365495344
500 Forest's; Func runs: 10000; result: 0.1919604395333699
=============================
5 Megacity's; Func runs: 10000; result: 0.5692307692307692
25 Megacity's; Func runs: 10000; result: 0.35261538461538455
500 Megacity's; Func runs: 10000; result: 0.12010769230769343
=============================
All score: 4.33037 (48.12%)
A performance geral do algoritmo piorou, mas ainda assim permanece superior à da versão "pura" dos autores. Com isso, registramos os resultados do primeiro experimento de modificação do algoritmo e os adicionamos à tabela de classificação. Vale destacar que, para cada versão do algoritmo, os parâmetros externos foram ajustados com o objetivo de obter o melhor desempenho possível em todos os testes, uma vez que a mudança na lógica do algoritmo altera seu comportamento no espaço de busca.
Resultados dos testes
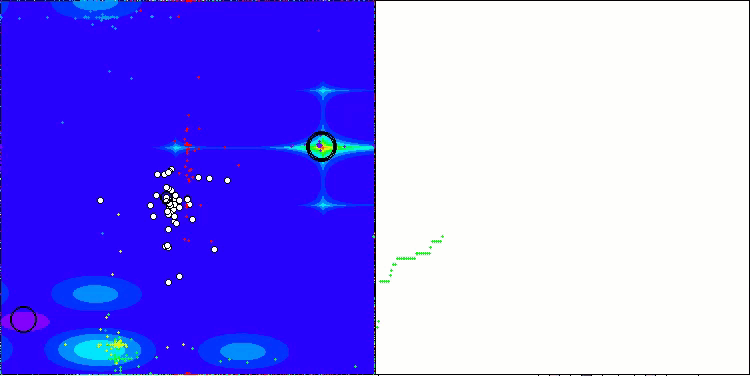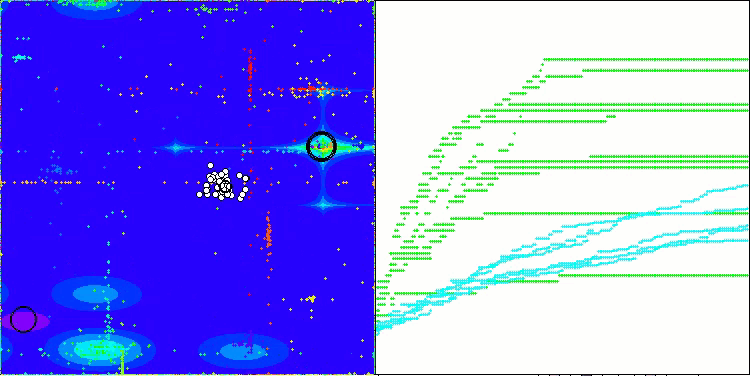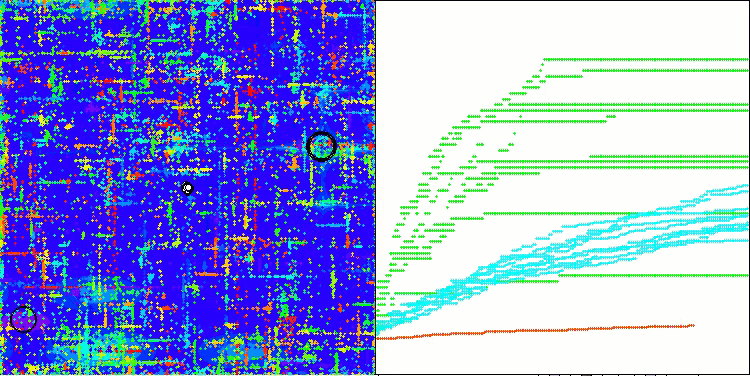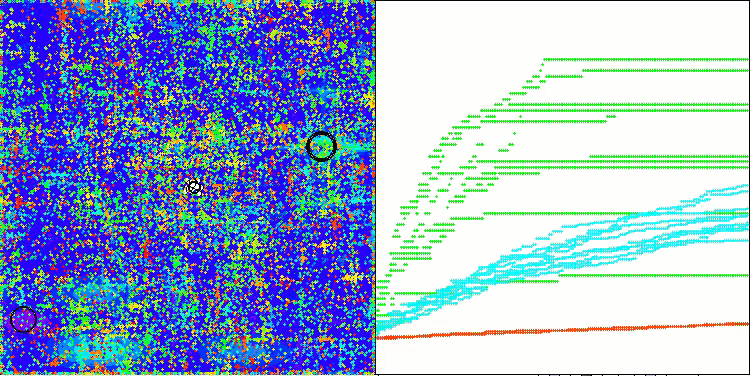
Na visualização do funcionamento do algoritmo ABO, observa-se uma boa exploração das regiões relevantes do hiperespaço, o que demonstra uma alta capacidade de investigar a superfície da função a ser otimizada. Infelizmente, a pequena modificação que melhora a escalabilidade do algoritmo também aumenta a probabilidade de ele ficar preso em problemas de baixa dimensionalidade, como pode ser visto pela dispersão dos resultados (linhas verdes no gráfico de convergência na visualização).
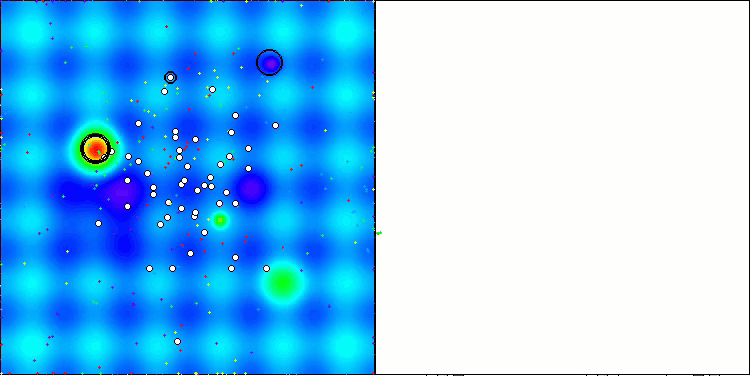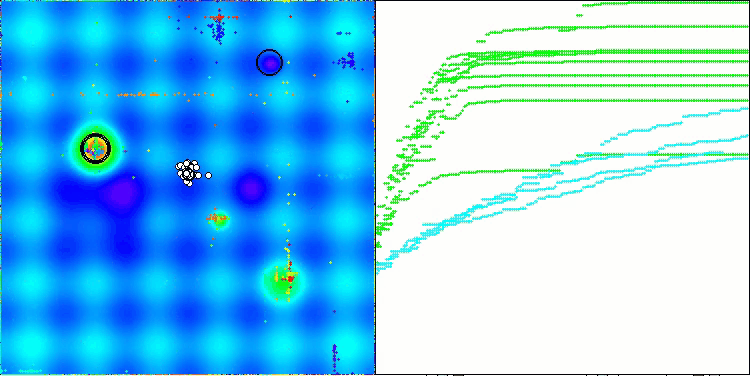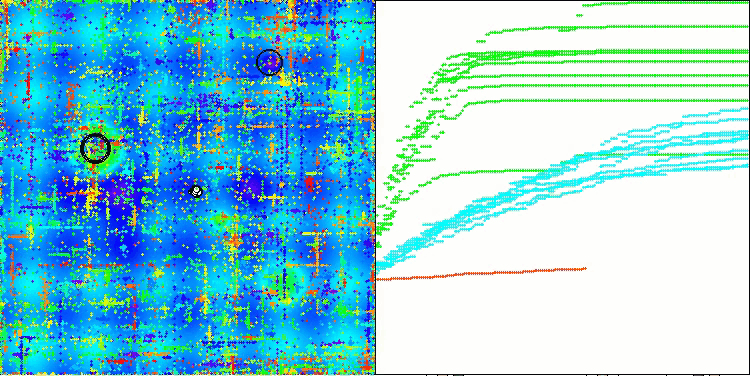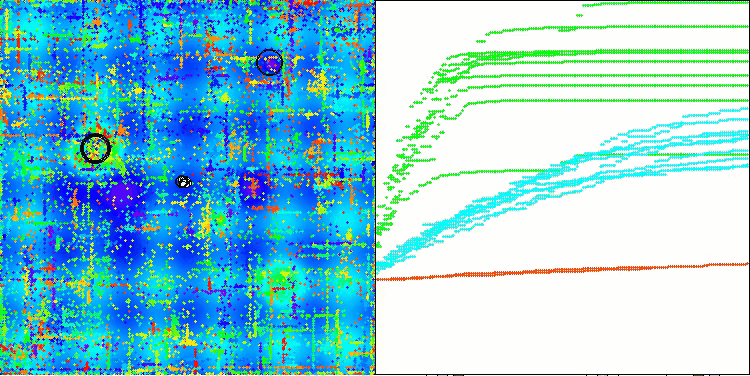
ABO na função de teste Hilly
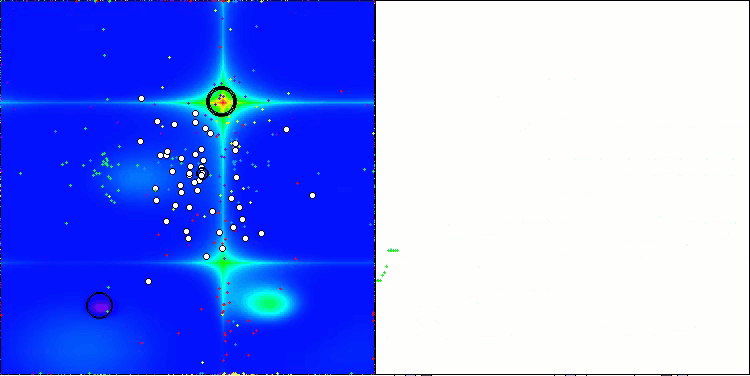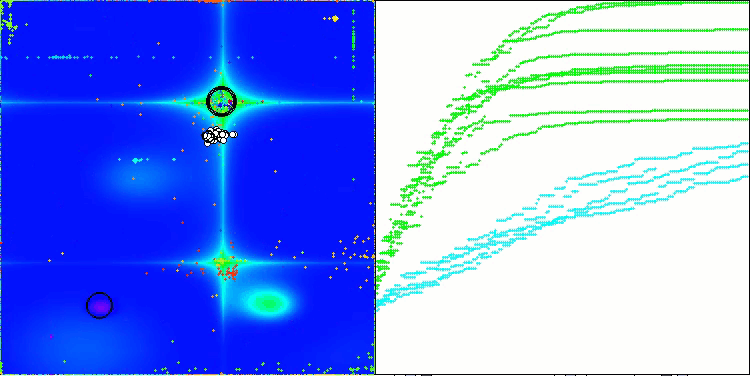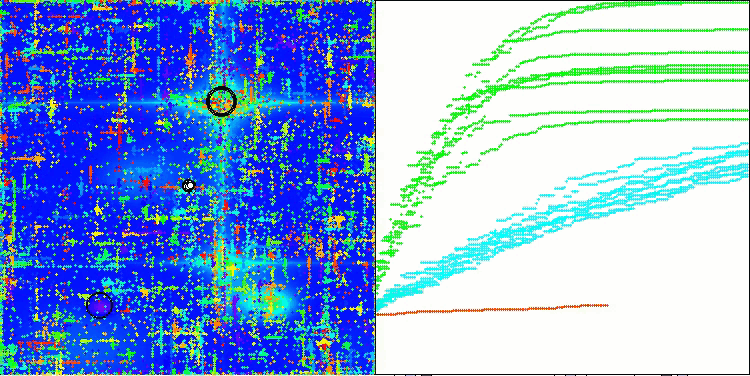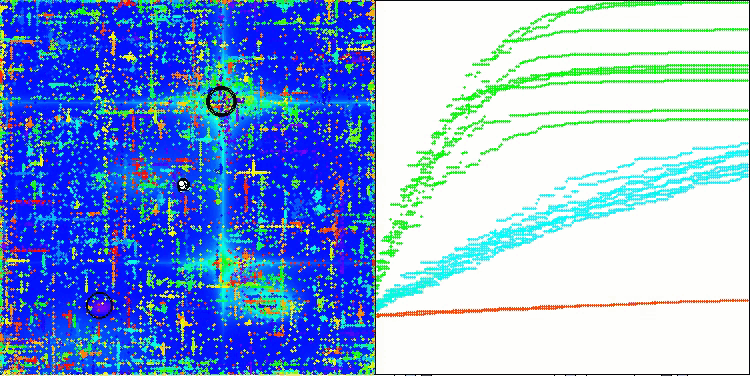
ABO na função de teste Forest
ABO na função de teste Megacity
O algoritmo, ao final dos testes, conquistou uma posição estável de 19º lugar no ranking geral dos algoritmos de otimização.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 12 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 13 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 14 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 15 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 16 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 17 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 18 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 19 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 20 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 21 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 22 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 23 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 24 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 25 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 26 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 27 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 28 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 29 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 30 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 31 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 32 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 33 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 34 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 35 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 36 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 37 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 38 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 39 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 40 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 41 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 42 | AAA | algae adaptive algorithm | 0,50007 | 0,32040 | 0,25525 | 1,07572 | 0,37021 | 0,22284 | 0,16785 | 0,76089 | 0,27846 | 0,14800 | 0,09755 | 0,52402 | 2,361 | 26,23 |
| 43 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 44 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 45 | PSO | particle swarm optimisation | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
Considerações finais
Foram apresentadas a você as versões do algoritmo ABO: a original e uma com pequenas modificações. As alterações na lógica do algoritmo resultaram na simplificação dos cálculos em cada etapa da otimização e na redução do número de parâmetros externos de três para dois (sem contar o parâmetro que define o tamanho da população), o que impactou positivamente nos resultados gerais. O novo algoritmo também equilibra de forma diferente a exploração de novos espaços de solução e a exploração de boas soluções já encontradas.
Apesar da tendência do algoritmo a ficar preso em problemas de baixa dimensionalidade, ele demonstra alta eficiência em aplicações práticas. A visualização do funcionamento do algoritmo mostrou sua capacidade de investigar profundamente regiões relevantes do hiperespaço, o que também evidencia suas habilidades de exploração aprimoradas. Como resultado, a nova versão do algoritmo se mostrou mais poderosa e eficiente em comparação com a original, apresentando boa escalabilidade em todos os tipos de funções de teste, incluindo as discretas.
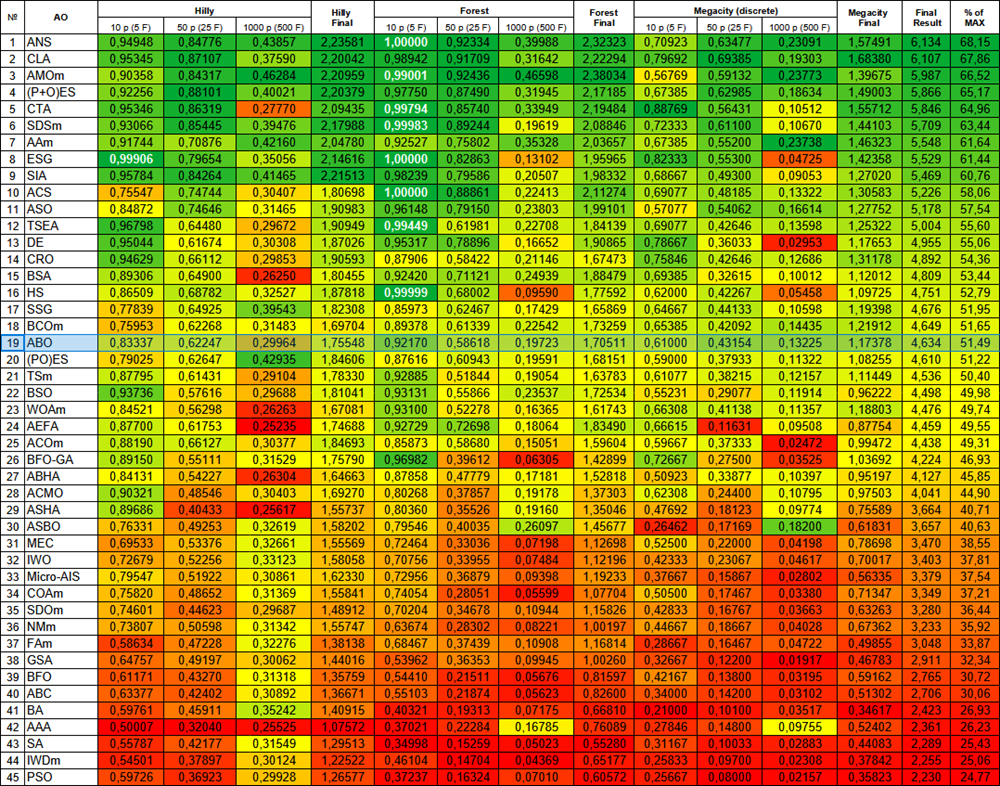
Figura 1. Graduação de cores dos algoritmos conforme os testes correspondentes. Branco destaca resultados maiores ou iguais a 0.99
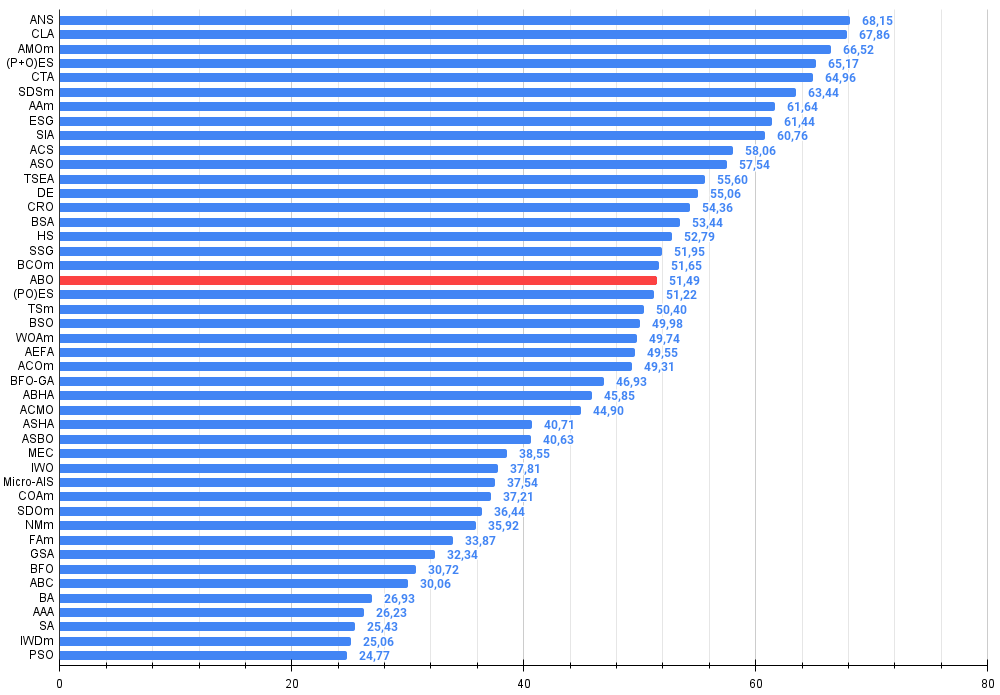
Figura 2. Histograma dos resultados de teste dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor,
onde 100 é o resultado teórico máximo possível, no arquivo há um script para cálculo da tabela de classificação)
Vantagens e desvantagens do algoritmo ABO:
Vantagens:
- Rápido.
- Implementação muito simples.
- Boa escalabilidade.
- Poucos parâmetros externos.
Desvantagens:
- Alta variabilidade nos resultados em funções de baixa dimensionalidade.
- Ausência de mecanismos para evitar o travamento.
O artigo é acompanhado por um arquivo compactado com as versões atuais dos códigos dos algoritmos. Autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar suas capacidades de busca. As conclusões e observações apresentadas nos artigos são baseadas nos resultados dos experimentos realizados.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16024
De Novato a Especialista: A Jornada Essencial no Comércio MQL5
Análise de Sentimento no Twitter com Sockets
Redes neurais em trading: Segmentação guiada (Conclusão)
Redes neurais em trading: Segmentação guiada
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso