Algorithmus für künstliche elektrische Felder (AEFA)
103
0
Einführung
Der Algorithmus für künstliche elektrische Felder ist eine erstaunliche Schöpfung, die die Harmonie von Technik und Natur verkörpert. Inspiriert vom Coulombschen Gesetz der elektrostatischen Kraft, zieht dieser Algorithmus die Aufmerksamkeit auf sich, weil er auf einzigartige Weise elektrische Phänomene modellieren kann, um komplexe Optimierungsprobleme zu lösen. Im Kontext der bereits bekannten und in früheren Artikeln beschriebenen Algorithmen, die sich auf die Naturgesetze beziehen, wie z. B. Charged System Search (CSS), ElectroMagnetism-like Algorithm (ЕМ), Gravitational Search Algorithm (GSA) und andere, ist das künstliche elektrische Feld eine aufregende Innovation, die keinen Forscher gleichgültig lassen wird.
Der Algorithmus für das künstliche elektrische Feld basiert auf dem Coulombschen Gesetz, das besagt, dass die elektrostatische Kraft (Anziehung oder Abstoßung) zwischen zwei geladenen Teilchen direkt proportional zum Produkt ihrer Ladungen und umgekehrt proportional zum Quadrat des Abstands zwischen ihnen ist. In dem vorgeschlagenen Algorithmus werden die Agenten als geladene Teilchen betrachtet, und ihre Stärke wird anhand ihrer Ladungen gemessen. Alle diese Teilchen können sich durch elektrostatische Kraft anziehen oder abstoßen, und aufgrund dieser Kraft bewegen sich die Objekte im Suchraum. Daher werden Ladungen als eine direkte Form der Kommunikation durch elektrostatische Kraft verwendet, und die Position der Ladung entspricht der Lösung des Problems. Die Ladungen werden als Funktion der Fitness der Kandidatenlösung und der Fitness der Population definiert. In dem vorgeschlagenen Algorithmus berücksichtigen wir nur die Anziehungskraft der elektrostatischen Kraft, sodass das geladene Teilchen mit der höchsten Ladung (das „beste“ Individuum) alle anderen Teilchen mit einer niedrigeren Ladung anzieht und sich langsam im Suchraum bewegt.
Somit kann die AEFA als isoliertes Ladungssystem betrachtet werden, das dem ersten Coulombschen Gesetz der Elektrostatik der elektrostatischen Kraft und dem Bewegungsgesetz (gleich geladene Teilchen stoßen sich gegenseitig ab und entgegengesetzt geladene Teilchen ziehen sich an) und dem zweiten Coulombschen Gesetz der Elektrostatik (die Anziehungskraft zwischen entgegengesetzt geladenen Teilchen bzw. die Abstoßungskraft zwischen gleich geladenen Teilchen ist direkt proportional zum Produkt ihrer Ladungen und umgekehrt proportional zum Quadrat der Entfernung zwischen den Ladungsschwerpunkten) sowie dem Bewegungsgesetz (die aktuelle Geschwindigkeit einer Ladung ist gleich der Summe der Anteile ihrer vorherigen Geschwindigkeit und der Geschwindigkeitsänderungen) entspricht. Die Änderung der Geschwindigkeit oder Beschleunigung einer beliebigen Ladung ist gleich der auf das System wirkenden Kraft geteilt durch die Masse des Teilchens.
AEFA (Artificial Electric Field Algorithm) wurde entwickelt von:
1. Anita - Fachbereich Wissenschaften und Geisteswissenschaften, Uttarakhand National Institute of Technology, Srinagar, Indien.
2. Anupam Yadav - Dr. B.R., Abteilung für Mathematik, Nationales Technologieinstitut, Ambedkara, Dschalandchar, Indien.
AEFA wurde im Jahr 2019 vorgeschlagen und in der Zeitschrift „warm and Evolutionary Computation“ veröffentlicht. Die Autoren des Artikels stellen fest, dass das Konzept eines elektrischen Feldes und geladener Teilchen uns eine solide Theorie dafür liefert, wie die anziehende oder abstoßende Kraft zwischen zwei geladenen Teilchen funktioniert. AEFA nutzt also die Prinzipien der elektrostatischen Kraft, um einen Algorithmus zur Populationsoptimierung zu entwickeln.
Implementierung des Algorithmus
AEFA ist reich an verschiedenen Gleichungen, und bevor wir darauf eingehen, wollen wir die wichtigsten Punkte festhalten:
- Die Agenten des Algorithmus (Entscheidung) werden als geladene Teilchen dargestellt, die sich unter der Einwirkung einer elektrostatischen Kraft bewegen.
- Die Ladung eines Partikels hängt von seinem persönlichen besten Ergebnis und den aktuellen besten und schlechtesten Ergebnissen in der Population ab (nicht von den besten Ergebnissen, die während der Optimierung erzielt wurden, sondern von den aktuellen Ergebnissen in der Population).
- Die Kraft, die auf ein Teilchen wirkt, hängt von den Ladungen der Teilchen und dem Abstand zwischen ihnen ab.
- Die Coulomb-Konstante K(t) nimmt mit zunehmender Iteration ab und steuert das Gleichgewicht zwischen globaler Suche und lokaler Optimierung.
Gehen wir nun zur Formalisierung des Algorithmus über und betrachten wir die darin verwendeten Gleichungen genauer.
Die Position des i-ten Partikels im d-dimensionalen Suchraum wird bezeichnet als X_i = (x_1, x_2, ..., x_d), wobei i = 1, 2, ..., N, und N eine Pipulationsgröße ist.
Die beste Position, die mit dem i-ten Partikel gefunden wurde, wird als P_i bezeichnet, während die global beste Position als P_best bezeichnet wird.
1. Coulombsche Gleichung für die elektrostatische Kraft: F_ij = K * Q_i * Q_j / R^2, wobei:
- F_ij - die Größe der elektrostatischen Kraft zwischen zwei geladenen Objekten i-ter und j-ter
- K - die Coulomb-Konstante
- Q_i und Q_j - die Ladungen des i-ten bzw. j-ten Objekts
- R - der Abstand zwischen zwei Ladungen Q_i und Q_j
2. Gleichung für das elektrische Feld um die Ladung Q_i: E_i = F_ij / Q_i, wobei:
- E_i - das elektrisches Feld um die Ladung Q_i
- F_ij - die Kraft, die auf die Ladung Q_i wirkt
3. Gleichung für die Teilchenbeschleunigung nach dem zweiten Newtonschen Gesetz: a_i = F_ij / M, wobei:
- a_i - die Beschleunigung des i-ten Teilchens
- F_ij - die Kraft, die auf ein Teilchen wirkt
- M - die Teilchenmasse
4. Gleichung für die Teilchenbeschleunigung durch das elektrische Feld: a_i = E_i * Q_i / M, wobei:
- a_i - die Beschleunigung des i-ten Teilchens
- E_i - das elektrisches Feld um das Teilchen
- Q_i - die Teilchenladung
- M - die Teilchenmasse
5. Die Gleichung zur Aktualisierung der besten Partikelposition: p_di (t+1) = {p_di (t) und X_i (t+1) = X_i (t)}, wenn f (X_i (t+1)) > f (X_i (t)), wobei:
- p_di (t) - die Fitness des i-ten Teilchens zu einem bestimmten Zeitpunkt t
- p_di (t+1) - die Fitness des i-ten Teilchens zu einem bestimmten Zeitpunkt (t+1)
- X_i (t) - die Position des i-ten Teilchens zu einem bestimmten Zeitpunkt t
- X_i (t+1) - die neue Position des i-ten Teilchens zu einem bestimmten Zeitpunkt (t+1)
- f(X_i (t)) - die Zielfunktion für die vorherige Position des i-ten Teilchens zu einem bestimmten Zeitpunkt t
- f(X_i (t+1)) - die Zielfunktion für die neue Position des i-ten Teilchens zu einem bestimmten Zeitpunkt (t+1)
6. Gleichung für die Kraft, die vom j-ten Teilchen auf das i-te Teilchen wirkt: F_dij (t) = K (t) * (Q_i (t) * Q_j (t) * (p_dj (t) - X_di (t))) / (R_ij (t)^2 + ε), wobei:
- F_dij (t) - die Kraft, die auf das i-te Teilchen vom j-ten Teilchen zu einem bestimmten Zeitpunkt t wirkt
- K (t) - die Coulomb-Konstante zum Zeitpunkt t
- Q_i (t) und Q_j (t) - die Ladungen der i-ten und j-ten Teilchen zu einem bestimmten Zeitpunkt t
- p_dj (t) - die beste Position des j-ten Teilchens zum Zeitpunkt t
- X_di (t) - die Position des i-ten Teilchens zu einem bestimmten Zeitpunkt in t
- R_ij (t) - der Euklidischer Abstand zwischen dem i-ten und dem j-ten Teilchen zu einem bestimmten Zeitpunkt von t
- ε - die kleine positive Konstante, um die Division durch 0 zu verhindern.
7. Gleichung für den euklidischen Abstand zwischen dem i-ten und j-ten Teilchen: R_ij (t) = (X_i (t) - X_j (t))^2
8. Gleichung für die Coulomb-Konstante: K (t) = K_0 * exp (-α * t / maxiter), wobei:
- K_0 - Anfangswert der Coulomb-Konstante
- α - externer Parameter
- t - aktueller Moment in der Zeit (Epoche)
- maxiter - maximale Anzahl von Iterationen
9. Gleichung für die Gesamtkraft, die auf das i-te Teilchen wirkt: F_di (t) = Σ(rand () * F_dij (t)), j=(von 1 bis N), j≠i, wobei:
- F_di (t) - die Gesamtkraft, die auf das i-te Teilchen zum Zeitpunkt t wirkt
- rand () - die Zufallszahl im Intervall [0, 1]
- N - Anzahl der Teilchen im Suchraum
10. Gleichung für das elektrische Feld, das auf das i-te Teilchen wirkt: E_di (t) = F_di (t) / Q_i (t), wobei:
- E_di (t) - die elektrisches Feld, das auf das i-te Teilchen zum Zeitpunkt t wirkt
- F_di (t) - die Gesamtkraft, die auf das i-te Teilchen wirkt
- Q_i (t) - die Ladung des i-ten Teilchens zum Zeitpunkt t
11. Die Gleichung aktualisiert die Teilchengeschwindigkeit i zum Zeitpunkt t+1: V_i (t+1) = rand () * V_i (t) + a_i (t), wobei:
- V_i(t) - die vorherige Geschwindigkeit
- a_i(t) - die Beschleunigung, die auf ein Teilchen einwirkt
- rand () - die Zufallszahl im Intervall [0, 1]
12. Die Gleichung aktualisiert die Position des Teilchens i zum Zeitpunkt t+1: X_i (t+1) = X_i (t) + V_i (t+1), wobei:
- V_i (t+1) - die neue Geschwindigkeit
13. Die Gleichung besagt, dass die Ladung aller Teilchen in der Population gleich ist und gleich Q_i (t) = Q_j (t) für alle i, j = 1, 2, ..., N
14. Die Gleichung berechnet die relative Ladung q_i (t) eines jeden Teilchens i zum Zeitpunkt t: q_i (t) = exp ((fit_p_i (t) - worst(t)) / (best(t) - worst(t))), wobei:
- fit_p_i (t) - der Fitnesswert der persönlich besten Position des Partikels
- fit_best (t) - der Fitnesswert der global besten Position
- fit_worst(t) - der Fitnesswert des schlechtesten Partikels in der Population
15. Gleichung: Q_i (t) = q_i (t) / Σ_j=1...N q_j (t).
Die Gleichung normalisiert die relativen Ladungen q_i (t) aller Teilchen so, dass ihre Summe gleich 1 ist. Auf diese Weise erhält man die normierten Ladungen Q_i (t) für jedes Teilchen.
16. Gleichung: best (t) = max (fit_j (t)) für j = 1, 2,..., N
Diese Gleichung berechnet den aktuell besten Fitnesswert - den Wert best (t) in der Population zum Zeitpunkt t als das Maximum der Fitnesswerte aller Partikel.
17. Gleichung: worst(t) = min (fit_j (t)) für j = 1, 2,..., N
Die Gleichung berechnet den aktuell schlechtesten Fitnesswert worst (t) in der Population zum Zeitpunkt t als das Minimum der Fitnesswerte aller Partikel.
Da wir nun die Gleichungen für die Gesetze der Partikelbewegung im Algorithmus kennen, können wir einen Pseudocode erstellen, mit dessen Hilfe wir in Zukunft den Code des AEFA-Algorithmus in MQL5 schreiben können.
AEFA-Pseudocode:
Schritt 1: Initialisierung
- Initialisiere die Partikelpositionen nach dem Zufallsprinzip.
- Berechne die Werte der Zielfunktion für jedes Partikel.
- Setze die aktuelle Iteration t = 0.
Schritt 2: Aktualisiere die Partikelpositionen, bis die Stoppbedingung erfüllt ist:
1. Berechne die Coulomb-Konstante K(t) nach der Gleichung (8)
2. Berechne den besten fit_best (t) und den schlechtesten fit_worst(t) Wert der Zielfunktion in der aktuellen Iteration.
3. Für jedes Teilchen i = 1, 2, ..., N:
a. Berechne die Teilchenladung Q_i (t) nach der Gleichung (14)
b. Berechne die Kraft, die vom Teilchen j auf das Teilchen i wirkt, nach der Gleichung (6)
c. Berechne die Gesamtkraft, die auf das Teilchen i wirkt, anhand der Gleichung (9)
d. Berechne die Beschleunigung des Teilchens i anhand der Gleichung (4)
B. Aktualisiere die Geschwindigkeit mit Hilfe der Gleichung (11) und die Partikelposition mit Hilfe der Gleichung (12)
4. Erhöhe den Iterationszähler t = t + 1
Schritt 3: Bedingung für das Anhalten. Überprüfe die Stopp-Bedingung (z.B. Erreichen der maximalen Anzahl von Iterationen). Wenn die Bedingung nicht erfüllt ist, fahre mit Schritt 2 fort.
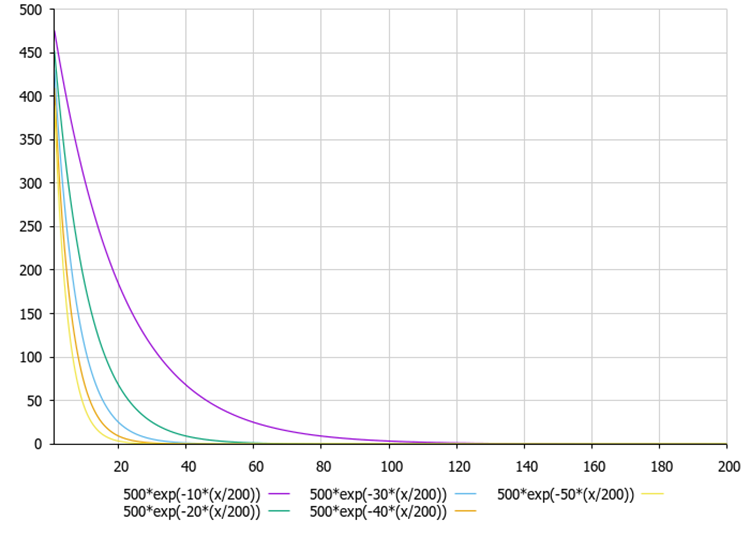
Abbildung 1. Abhängigkeit der elektrostatischen Kraft nach der Coulomb-Formel von dem Verhältnis α (externer Parameter).
Nun, endlich haben wir die Beschreibung, die Gleichungen und den Pseudocode des Algorithmus herausgefunden. Nun müssen wir mit der Generierung des Codes fortfahren.
Implementieren wir die Struktur S_AEFA_Agent, die zur Beschreibung der Agenten im Algorithmus dient. Die Struktur enthält folgende Felder:
- best_fitness - die Variable stellt die beste Fitness des Agenten dar.
- best_position[] - das Array mit den Koordinaten der besten Position des Agenten im Suchraum.
- velocity[] - das Array, das den Geschwindigkeitsvektor des Partikels darstellt.
- charge - die Ladung des Agenten.
- relative_charge - die relative Ladung des Teilchens.
Die Struktur definiert auch die Funktion Init, die das Partikel (den Agenten) initialisiert. Sie nimmt den Parameter coords, der die Anzahl der Agenten-Koordinaten angibt, und ändert die Größe der Arrays best_position und velocity entsprechend. Danach setzen Sie best_fitness auf den kleinstmöglichen Wert für den Typ „double“,-DBL_MAX, während charge und relative_charge auf 0 gesetzt werden.
Der Code bietet eine Grundlage für die Beschreibung von Agenten im Algorithmus für künstliche elektrische Felder und bereitet sie auf weitere Arbeiten in diesem Zusammenhang vor.
//—————————————————————————————————————————————————————————————————————————————— struct S_AEFA_Agent { double best_fitness; double best_position []; double velocity []; double charge; double relative_charge; void Init (int coords) { ArrayResize (best_position, coords); ArrayResize (velocity, coords); best_fitness = -DBL_MAX; charge = 0; relative_charge = 0; } }; //——————————————————————————————————————————————————————————————————————————————
Beschreiben wir die Klasse C_AO_AEFA, die von der Klasse C_AO abgeleitet wurde. Die folgenden Methoden und Variablen sind innerhalb der Klasse definiert:
- C_AO_AEFA - der Konstruktor, in dem die Werte der Variablen und Parameter festgelegt werden.
- SetParams - die Methode setzt die Parameter basierend auf den im Array params gespeicherten Werten.
- Init - die Methode nimmt einen Satz von Werten und führt eine Initialisierung durch.
- Moving und Revision - die Methoden führen die Hauptlogik des Algorithmus aus.
- Mehrere Variablen vom Typ double, wie K0, alpha, particleMass, epsilon, sowie das Array agent und andere private Variablen.
- Die privaten Methoden CalculateK, UpdateCharges, CalculateForces, CalculateDistance und UpdateVelocityAndPosition führen Operationen zur Bewegung von Partikeln im Suchraum durch.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_AEFA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_AEFA () { } C_AO_AEFA () { ao_name = "AEFA"; ao_desc = "Artificial Electric Field Algorithm"; ao_link = ""; //"https://www.mql5.com/en/articles/15162"; popSize = 50; K0 = 500.0; alpha = 20.0; particleMass = 1.0; ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "K0"; params [1].val = K0; params [2].name = "alpha"; params [2].val = alpha; params [3].name = "particleMass"; params [3].val = particleMass; } void SetParams () { popSize = (int)params [0].val; K0 = params [1].val; alpha = params [2].val; particleMass = params [3].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //---------------------------------------------------------------------------- double K0; double alpha; double particleMass; double epsilon; S_AEFA_Agent agent []; private: //------------------------------------------------------------------- int epochs; int epochNow; double K; double CalculateK (int t); void UpdateCharges (double best, double worst); void CalculateForces (); double CalculateDistance (const double &x1 [], const double &x2 []); void UpdateVelocityAndPosition (int i); }; //——————————————————————————————————————————————————————————————————————————————
Als Nächstes implementieren wir die Methode Init der Klasse C_AO_AEFA. Die Methode initialisiert den AEFA-Algorithmus mit den angegebenen Parametern.
Die Eingaben von Init:
- rangeMinP - das Array von Werten der minimalen Bereichsgrenzen.
- rangeMaxP - das Array von Werten für die maximalen Bereichsgrenzen.
- rangeStepP - das Array von Bereichsschrittwerten.
- epochsP - die Anzahl der Epochen (Standard ist 0).
Aktionen, die in Init durchgeführt werden:
1. Es wird die Methode StandardInit aufgerufen. Sie empfängt die Arrays rangeMinP, rangeMaxP und rangeStepP. Wenn StandardInit false zurückgibt, gibt auch Init false zurück.
2. Die Variablen epochs und epochNow werden auf epochsP bzw. 0 gesetzt.
3. Die Größe des Agenten-Arrays wird auf popSize geändert.
4. In der Schleife wird jedes Element des Agenten-Arrays durch den Aufruf von Init initialisiert, indem ihr das Array coords übergeben wird.
5. Die Variable epsilon wird auf 1e-10 gesetzt.
6. Die Methode gibt true zurück.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_AEFA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; ArrayResize (agent, popSize); for (int i = 0; i < popSize; i++) agent [i].Init (coords); epsilon = 1e-10; return true; } //——————————————————————————————————————————————————————————————————————————————
Kommen wir nun zur Methode Moving() der Klasse C_AO_AEFA. Bei dieser Methode werden die Partikelpositionen im Optimierungsalgorithmus aktualisiert. Hier ein kurzer Überblick über den Stand der Dinge:
1. Der Wert der Variable epochNow wird erhöht.
2. Wenn die Revisionsvariable gleich false ist, werden die Anfangspositionen der Partikel initialisiert. Jede Partikelkoordinate wird auf einen zufälligen Wert in einem bestimmten Bereich gesetzt, dann wird dieser Wert in einem bestimmten Schritt transformiert.
3. Wenn Revision gleich true ist, wird der K-Wert zusammen mit den besten und schlechtesten Funktionsschätzungen für jedes Partikel berechnet. Die Kräfte werden berechnet, und die Geschwindigkeit und Position jedes Teilchens werden zusammen mit den Ladungen aktualisiert.
Die allgemeine Idee dieser Methode besteht darin, die Positionen der Teilchen im Optimierungsalgorithmus mit Hilfe spezieller Methoden zur Berechnung der Gleichungen der Teilchenbewegungsgesetze zu aktualisieren.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::Moving () { epochNow++; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- K = CalculateK (epochNow); double best = -DBL_MAX; double worst = DBL_MAX; for (int i = 0; i < popSize; i++) { if (a [i].f > best) best = a [i].f; if (a [i].f < worst) worst = a [i].f; } UpdateCharges (best, worst); CalculateForces (); for (int i = 0; i < popSize; i++) { UpdateVelocityAndPosition (i); } } //——————————————————————————————————————————————————————————————————————————————
In der Methode CalculateK() der Klasse C_AO_AEFA wird der Parameter K auf der Grundlage von t (aktueller Epochenindex) und anderen Parametern K0, alpha und epochs berechnet. Bei dieser Methode geschieht Folgendes:
1. Die Methode nimmt den Parameter t als Eingabe, der den Index der aktuellen Epoche im Algorithmus darstellt.
2. Dann wird der Wert von K berechnet.
3. Das Ergebnis der Berechnung auf der Grundlage der Gleichung wird als Wert der Methode zurückgegeben.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_AEFA::CalculateK (int t) { return K0 * MathExp (-alpha * t / epochs); } //——————————————————————————————————————————————————————————————————————————————
In der Methode UpdateCharges() der Klasse C_AO_AEFA aktualisieren wir die Partikelveränderungen auf der Grundlage der besten und schlechtesten Fitnesswerte. Kurze Beschreibung der Aktionen in der Methode:
1. Die Variable sum_q wird erstellt und auf 0 gesetzt.
2. Dann wird ein Zyklus durch alle Partikel innerhalb des Bereichs von 0 bis popSize durchgeführt.
3. Innerhalb der Schleife wird die relative Ladung für jedes Teilchen anhand der Gleichung berechnet.
4. Der relative Ladungswert wird zu der Variablen sum_q addiert.
5. Dann erfolgt eine zweite Schleife über alle Teilchen, in der jedem Teilchen ein Ladungswert zugewiesen wird, der der relativen Ladung geteilt durch sum_q entspricht.
Diese Methode aktualisiert also die Partikelladungen auf der Grundlage ihrer Fitness, sodass sie ihre relative Qualität im Vergleich zu den besten und schlechtesten Fitnesswerten widerspiegeln.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::UpdateCharges (double best, double worst) { double sum_q = 0; for (int i = 0; i < popSize; i++) { agent [i].relative_charge = MathExp ((a [i].f - worst) / (best - worst)); sum_q += agent [i].relative_charge; } for (int i = 0; i < popSize; i++) { agent [i].charge = agent [i].relative_charge / sum_q; } } //——————————————————————————————————————————————————————————————————————————————
Lassen Sie uns die Methoden CalculateForces() undCalculateDistance() der Klasse C_AO_AEFA bereitstellen.
Die Methode CalculateDistance() akzeptiert zwei Arrays x1[] und x2[], die die Koordinaten von zwei Partikeln darstellen, und berechnet den räumlichen Abstand zwischen ihnen. Dazu werden alle Koordinaten der Felder durchlaufen, und für jede Koordinate wird das Quadrat der Differenz der entsprechenden Elemente der Felder berechnet, woraufhin diese Quadrate addiert werden. Anschließend wird die Quadratwurzel der sich ergebenden Summe extrahiert, und dieser Wert wird als Abstand zwischen zwei Punkten im Raum (euklidischer Abstand) zurückgegeben.
Die Methode CalculateForces() berechnet die auf jedes Teilchen wirkenden Kräfte. Für jedes Teilchen wird der Kraftvektor im Verhältnis zu allen anderen Teilchen berechnet. Für jedes Partikelpaar, außer für identische (i != j), wird der Abstand zwischen ihnen mit der Methode CalculateDistance() berechnet. Dann wird für jede Koordinate im Raum die Kraft, die auf das Teilchen wirkt, anhand einer Gleichung berechnet, die die Ladungen der Teilchen, ihre Positionen und den Abstand zwischen ihnen enthält. Die Ergebnisse werden für jede Koordinate summiert, und die resultierenden Kräfte werden dann durch die Partikelladung geteilt, um ihre Auswirkungen auf die Partikelgeschwindigkeit zu berücksichtigen.
Die Methoden berechnen also die Kräfte, die zwischen den Teilchen im Algorithmus wirken, bzw. die Abstände zwischen ihnen im Raum.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::CalculateForces () { double force []; ArrayResize (force, coords); for (int i = 0; i < popSize; i++) { ArrayInitialize (force, 0); for (int j = 0; j < popSize; j++) { if (i != j) { double R = CalculateDistance (a [i].c, a [j].c); for (int d = 0; d < coords; d++) { force [d] += u.RNDprobab () * K * (agent [i].charge * agent [j].charge * (agent [j].best_position [d] - a [i].c [d])) / (R * R + epsilon); } } } for (int d = 0; d < coords; d++) { agent [i].velocity [d] = force [d] / agent [i].charge; } } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— double C_AO_AEFA::CalculateDistance (const double &x1 [], const double &x2 []) { double sum = 0; for (int d = 0; d < coords; d++) { sum += (x1 [d] - x2 [d]) * (x1 [d] - x2 [d]); } return MathSqrt (sum); } //——————————————————————————————————————————————————————————————————————————————
Als Nächstes kommt die Methode UpdateVelocityAndPosition() der Klasse C_AO_AEFA. Diese Methode aktualisiert die Geschwindigkeit und die Position des Partikels mit dem Index i. Für jede Koordinate eines Teilchens im Raum geschieht Folgendes:
1. Es wird die Beschleunigung berechnet, die von der Ladung des Teilchens, seiner aktuellen Geschwindigkeit und der Masse des Teilchens abhängt.
2. Die Partikelgeschwindigkeit wird durch Addition einer Zufallskomponente, multipliziert mit der aktuellen Geschwindigkeit und Beschleunigung, aktualisiert.
3. Die Partikelposition wird aktualisiert, indem die neue Geschwindigkeit zur aktuellen Position addiert wird. Die neue Position wird dann mit Hilfe von u.SeInDiSp() innerhalb der angegebenen Minimal- und Maximalwerte für jede Koordinate eingegrenzt.
So aktualisiert die Methode UpdateVelocityAndPosition() die Partikelgeschwindigkeit und -position im Optimierungsalgorithmus unter Berücksichtigung von Beschleunigung, Zufallsfaktoren und Beschränkungen der Partikelposition im Raum.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::UpdateVelocityAndPosition (int i) { for (int d = 0; d < coords; d++) { double acceleration = (agent [i].charge * agent [i].velocity [d]) / particleMass; agent [i].velocity [d] = (u.RNDfromCI (0, 1)) * agent [i].velocity [d] + acceleration; a [i].c [d] += agent [i].velocity [d]; a [i].c [d] = u.SeInDiSp (a [i].c [d], rangeMin [d], rangeMax [d], rangeStep [d]); } } //——————————————————————————————————————————————————————————————————————————————
Schließlich haben wir noch die Methode Revision() der Klasse C_AO_AEFA. Bei dieser Methode werden die Informationen über die besten Positionen der Partikel und ihre besten Fitnesswerte sowie die beste globale Lösung fB aktualisiert. Die Methode geht folgendermaßen vor:
1. Die Variable ind wird als Flag und als Index der Position im Array der besten Lösung erstellt und auf -1 gesetzt.
2. Dann wird ein Zyklus durch alle Partikel innerhalb des Bereichs von 0 bis popSize durchgeführt.
3. Innerhalb der Schleife wird geprüft, ob der Wert der Partikelfitnessfunktion den Wert von fB überschreitet. Wenn ja, wird fB aktualisiert und die Variable ind wird auf i gesetzt.
4. Dann wird geprüft, ob die Fitness des Partikels größer ist als die beste Fitness dieses Partikels über alle Epochen (gespeichert in agent[i].best_fitness). Wenn ja, werden die beste Punktzahl und die Position aktualisiert.
5. Ist ind schließlich ungleich -1, wird die Position cB durch Kopieren der Position des Teilchens mit dem Index ind aktualisiert.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } if (a [i].f > agent [i].best_fitness) { agent [i].best_fitness = a [i].f; ArrayCopy (agent [i].best_position, a [i].c, 0, 0, WHOLE_ARRAY); } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
3. Testergebnisse
AEFA-Prüfstandsergebnisse:
AEFA|Algorithmus für künstliche elektrische Felder|20.0|1000.0|10.0|100.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8769988087850553
25 Hilly's; Func runs: 10000; result: 0.617530930198765
500 Hilly's; Func runs: 10000; result: 0.2523539056281608
=============================
5 Forest's; Func runs: 10000; result: 0.927287032866128
25 Forest's; Func runs: 10000; result: 0.7269761843712702
500 Forest's; Func runs: 10000; result: 0.18063577020760296
=============================
5 Megacity's; Func runs: 10000; result: 0.6661538461538462
25 Megacity's; Func runs: 10000; result: 0.11630769230769236
500 Megacity's; Func runs: 10000; result: 0.0950769230769239
=============================
All score: 4.45932 (49.55%)
Wir können eine erhebliche Streuung der Ergebnisse von Test zu Test feststellen. Darüber hinaus zeigt der Algorithmus sehr schwache Suchfähigkeiten bei der Arbeit mit hochdimensionalen Funktionen, was auch durch seine Ergebnisse bestätigt wird. Besondere Probleme sind bei der Arbeit mit diskreten Funktionen aufgetreten.
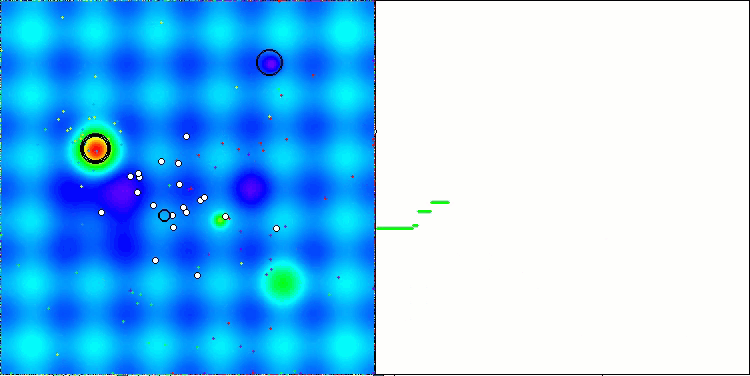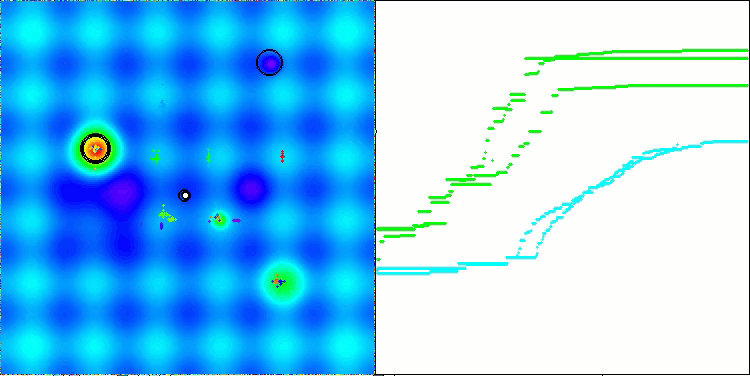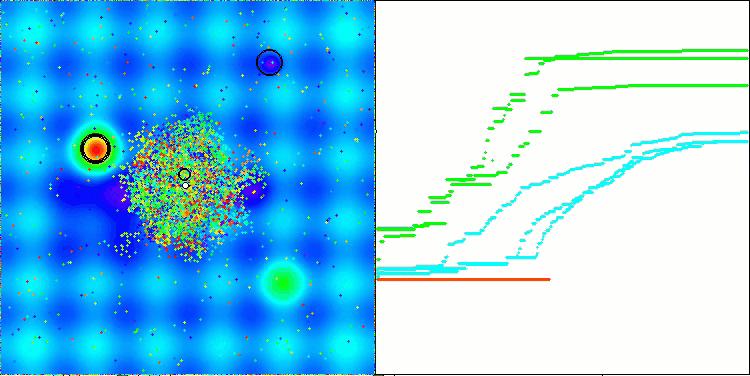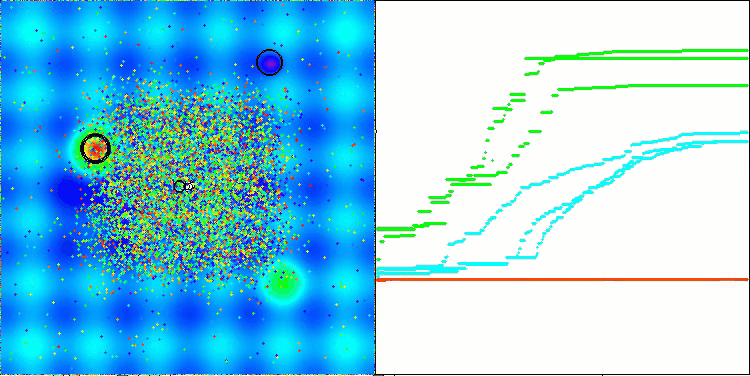
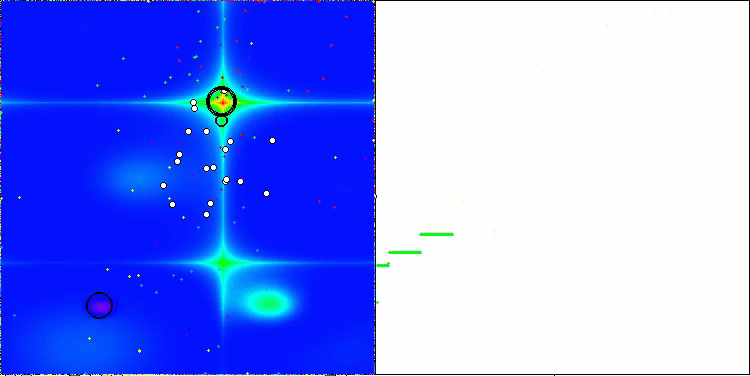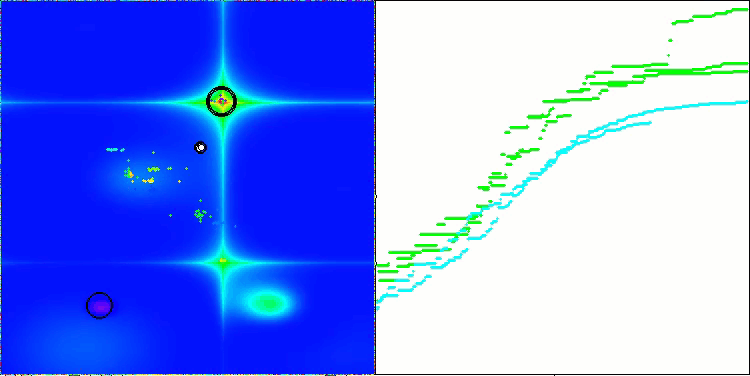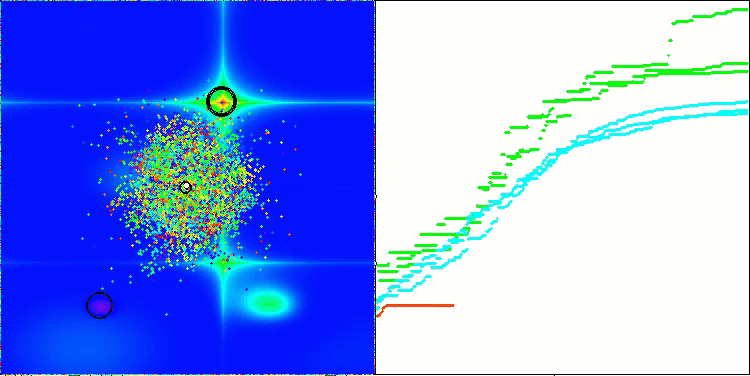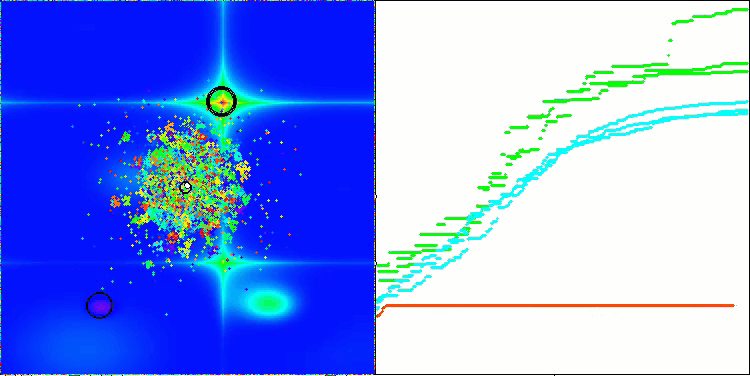
AEFA mit der Testfunktion Hilly
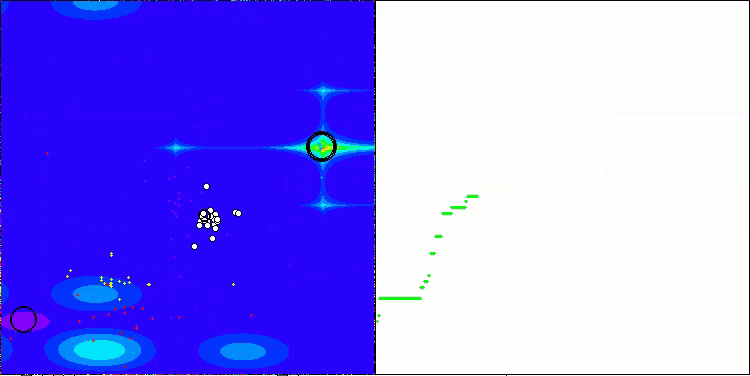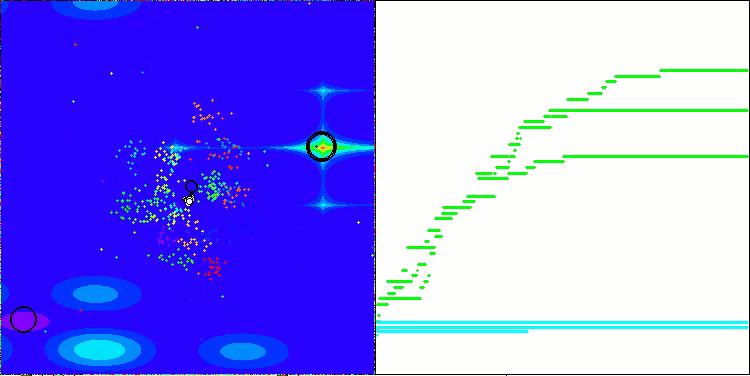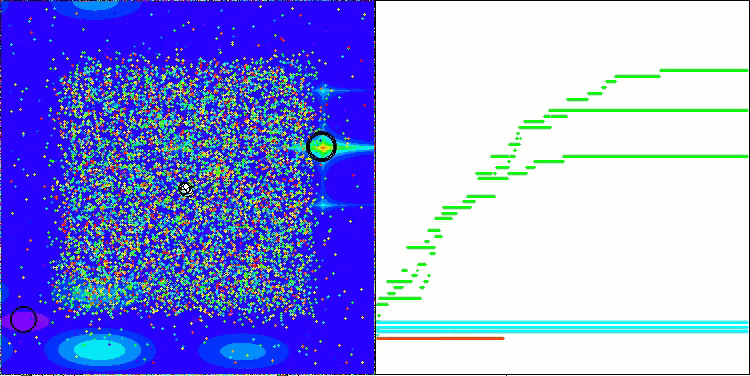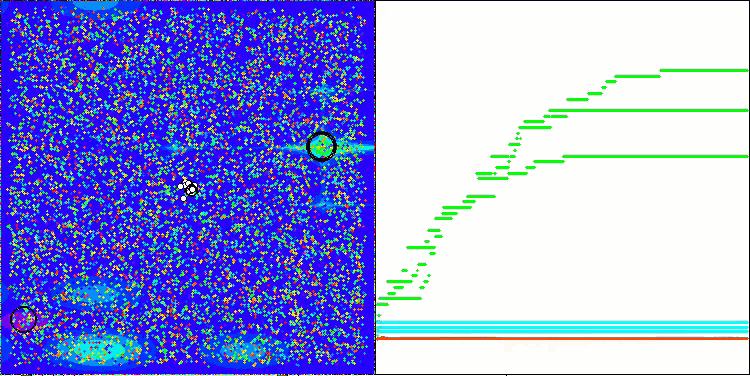
AEFA mit der Testfunktion Forest
AEFA mit der Testfunktion Megacity
Ich möchte einen wichtigen Aspekt des AEFA-Algorithmus hervorheben. Nachdem ich Standardtests mit 10 000 Starts der Fitnessfunktion durchgeführt hatte, beschloss ich, ein zusätzliches Experiment mit einer Erhöhung der Anzahl der Starts auf 100 000 durchzuführen, und das Ergebnis übertraf meine Erwartungen. Bei vielen Funktionen mit einer geringen Anzahl von Parametern erreichte der Algorithmus eine 100-prozentige Konvergenz, wenn die Anzahl der Durchläufe der Fitnessfunktion erhöht wurde. Es ist wichtig zu beachten, dass nicht alle Algorithmen in der Rangliste, auch nicht die auf den vorderen Plätzen, bei einer Erhöhung der Anzahl der Durchläufe eine 100%ige Konvergenz erreichen können, da sie in lokalen Extremen stecken bleiben. In diesem Fall zeigt der Algorithmus, dass er sich nicht festfahren kann. Bei der Suche in mehrdimensionalen Räumen, insbesondere bei diskreten Funktionen, stößt der Algorithmus jedoch auf die gleichen Schwierigkeiten.
AEFA-Testergebnisse mit 100 000 laufenden Testfunktionen:
SDSm|Stochastische Diffusionssuche M|100.0|100.0|0.05|
=============================
5 Hilly's; Func runs: 100000; result: 0.9874670077970368
25 Hilly's; Func runs: 100000; result: 0.9355482229513405
500 Hilly's; Func runs: 100000; result: 0.5943074120378588
=============================
5 Forest's; Func runs: 100000; result: 0.994126703499673
25 Forest's; Func runs: 100000; result: 0.9627011069578397
500 Forest's; Func runs: 100000; result: 0.5628894538341265
=============================
5 Megacity's; Func runs: 100000; result: 0.9015384615384615
25 Megacity's; Func runs: 100000; result: 0.7264615384615385
500 Megacity's; Func runs: 100000; result: 0.37464615384615396
=============================
All score: 7.03969 (78.22%)
Dieses Merkmal der Konvergenz des Algorithmus können Sie in den folgenden Bildern sehen.
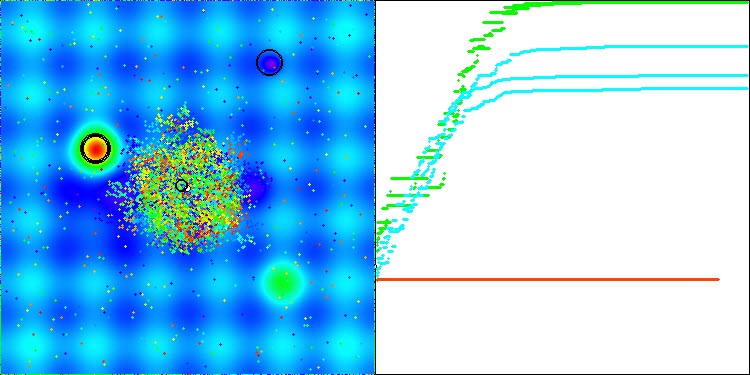
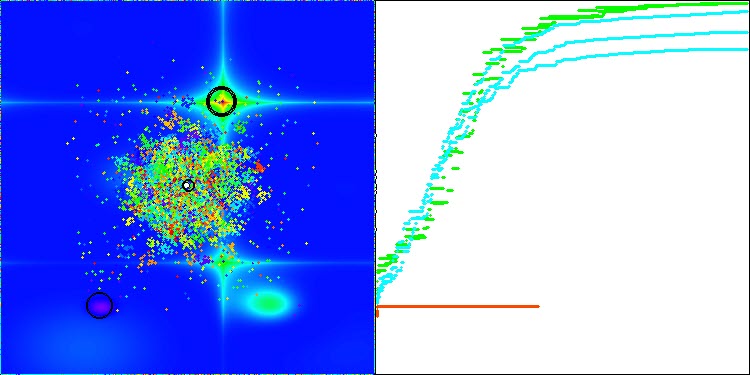
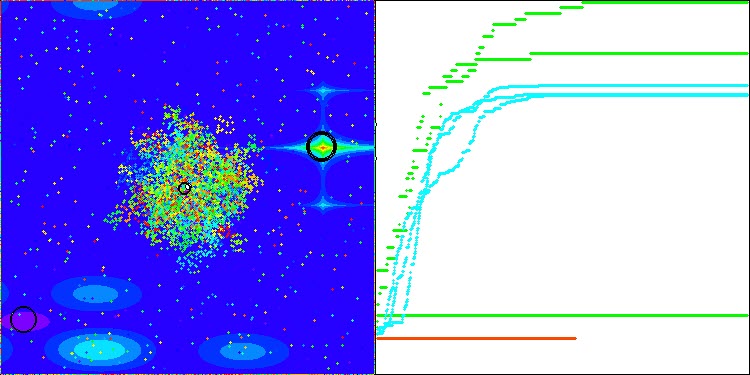
Bewertungstabelle der Algorithmen zur Populationsoptimierung:
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | binärer genetischer Algorithmus | 0.99989 | 0.99518 | 0.42835 | 2.42341 | 0.96153 | 0.96181 | 0.32027 | 2.24360 | 0.91385 | 0.95908 | 0.24220 | 2.11512 | 6.782 | 75.36 |
| 2 | ANS | Nachbarschaftsübergreifende Suche | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 3 | CLA | Zahlenschloss-Algorithmus | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | ESG | Entwicklung der sozialen Gruppen | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 8 | SIA | Simuliertes isotropes Abkühlen | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 9 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 10 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 11 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 12 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 13 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 14 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 15 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 16 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 17 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 18 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 19 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 20 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 21 | BFO-GA | Optimierung der bakteriellen Futtersuche - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 22 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 23 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 24 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 25 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 26 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 27 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 28 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 29 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 30 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 31 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 32 | BA | Fledermaus-Algorithmus | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 33 | SA | simuliertes Abkühlen | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 34 | IWDm | intelligente Wassertropfen M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 35 | PSO | Partikelschwarmoptimierung | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 36 | Gebote | Boids-Algorithmus | 0.43340 | 0.30581 | 0.25425 | 0.99346 | 0.35718 | 0.20160 | 0.15708 | 0.71586 | 0.27846 | 0.14277 | 0.09834 | 0.51957 | 2.229 | 24.77 |
| 37 | MA | Affen-Algorithmus | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 38 | SFL | schlurfender Froschsprung | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 39 | FSS | Fischschulsuche | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 40 | RND | zufällig | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
| 41 | GWO | Grauer-Wolf-Optimierung | 0.59169 | 0.36561 | 0.29595 | 1.25326 | 0.24499 | 0.09047 | 0.03612 | 0.37158 | 0.27667 | 0.08567 | 0.02170 | 0.38403 | 2.009 | 22.32 |
| 42 | CSS | Suche geladener Systeme | 0.44252 | 0.35454 | 0.35201 | 1.14907 | 0.24140 | 0.11345 | 0.06814 | 0.42299 | 0.18333 | 0.06300 | 0.02322 | 0.26955 | 1.842 | 20.46 |
| 43 | EM | elektromagnetismusähnlicher Algorithmus | 0.46250 | 0.34594 | 0.32285 | 1.13129 | 0.21245 | 0.09783 | 0.10057 | 0.41085 | 0.15667 | 0.06033 | 0.02712 | 0.24412 | 1.786 | 19.85 |
Zusammenfassung
Auf der Grundlage der Ergebnisse des AEFA-Algorithmus (Artificial Electric Field Algorithm) für Testfunktionen verschiedener Dimensionen können folgende Schlussfolgerungen gezogen werden:
1. AEFA zeigt zufriedenstellende Ergebnisse bei verschiedenen Testfunktionen, darunter Hilly, Forest und Megacity. Die Ergebnisse der diskreten Megacity-Funktion sind jedoch schlechter als die der anderen Funktionen.
2. Der Algorithmus zeigt eine gute Leistung bei einer großen Anzahl von Funktionsläufen (100 000), wodurch die Konvergenzgenauigkeit bei kleinen Dimensionen auf bis zu 100 % verbessert werden kann.
3. AEFA hat eine Gesamtnote von 4,45932 (49,55%) und liegt auf Platz 19 der Bewertungstabelle und damit im Mittelfeld.
Obwohl der AEFA-Algorithmus in unseren Standardtests nicht die besten Ergebnisse bei Testfunktionen unterschiedlicher Dimensionen zeigt, hat er einen zusätzlichen Vorteil: Mit zunehmender Anzahl von Durchläufen der Fitnessfunktion erreicht er ein beeindruckendes Gesamtergebnis von 7,03969 (78,22 %), was ihn bei Aufgaben mit kleinen Dimensionen, insbesondere bei solchen mit glatten Oberflächen, nützlich macht.
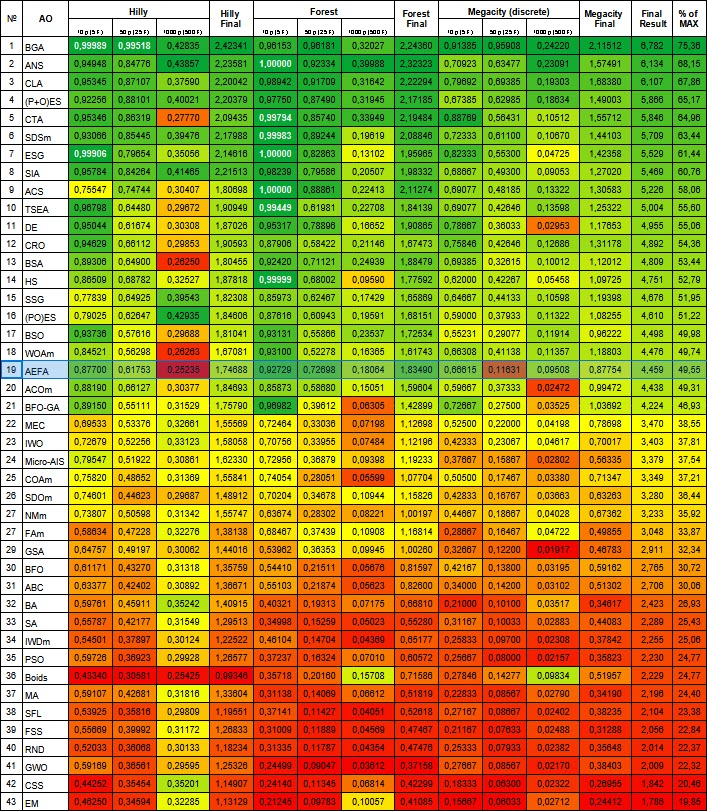
Abbildung 2. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben
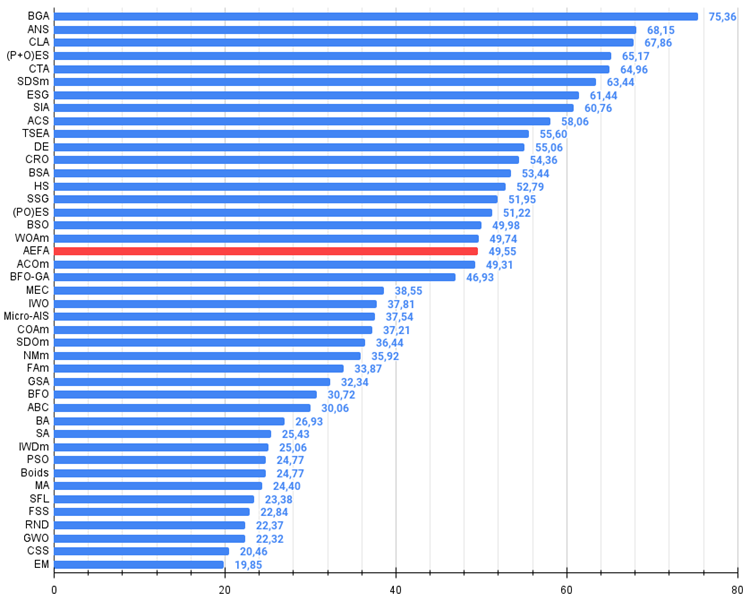
Abbildung 3. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; das Archiv enthält ein Skript zur Berechnung der Bewertungstabelle)
AEFA Pro und Kontra:
Vorteile:
- Hervorragende Konvergenz bei glatten Funktionen mit geringer Dimension und einer ausreichenden Anzahl von Durchläufen der Fitnessfunktion.
- Relativ geringe Anzahl von externen Parametern.
Nachteile
- Große Bandbreite der Ergebnisse bei den in unseren Standardtests verwendeten Funktionen.
- Schwache Ergebnisse bei diskreten Funktionen.
- Sehr geringe Skalierbarkeit.
- Komplexe Umsetzung.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Algorithmuscodes begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15162
Neuronale Netze im Handel: Stückweise, lineare Darstellung von Zeitreihen
Neuronale Netze leicht gemacht (Teil 97): Modelle mit MSFformer trainieren
Neuronale Netze im Handel: Das „Dual-Attention-Based Trend Prediction Model“
MQL5 beherrschen, vom Anfänger zum Profi (Teil III): Komplexe Datentypen und Include-Dateien
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.