
Algorithmen zur Optimierung mit Populationen: Vogelschwarm-Algorithmus (BSA)
Inhalt
1. Einführung
2. Beschreibung des Algorithmus
3. Testergebnisse
1. Einführung
Vögel sind erstaunliche Lebewesen, die einen wichtigen Platz in der Natur und im Ökosystem einnehmen. Man geht davon aus, dass sich die Vögel aus den Dinosauriern, ihren nächsten Verwandten, entwickelt haben. Eines der berühmtesten Beispiele ist der Archaeopteryx, der älteste bekannte Vogel, der vor etwa 150 Millionen Jahren lebte. Sie dienen oft als Indikatoren für die Gesundheit der Umwelt, da Veränderungen in ihrer Anzahl und ihrem Verhalten auf Probleme im Ökosystem hinweisen können, wie z. B. Verschmutzung, Lebensraumverlust und Klimawandel. Es gibt mehr als 10.000 bekannte Vogelarten auf der Erde, und jede von ihnen hat eine einzigartige Anpassung an ihre Lebensweise.
Einige Vögel sind in der Lage, große Entfernungen zu fliegen, andere können in die Tiefe tauchen, und wieder andere haben erstaunliche stimmliche Fähigkeiten. Vögel spielen eine wichtige Rolle im Ökosystem, sie verbreiten Pflanzensamen, kontrollieren die Population von Insekten und anderen Tieren und sind eine Nahrungsquelle für Raubtiere. Viele Vogelarten unternehmen lange Wanderungen, leben zusammen und interagieren mit anderen Mitgliedern ihrer Art in einem Schwarm und legen auf der Suche nach Nahrung oder einem Platz zum Brüten Tausende von Kilometern gemeinsam zurück. Dieses Phänomen unterstreicht die hervorragenden Navigationsfähigkeiten, die Ausdauer, die Interaktion und die Zusammenarbeit in einer Gruppe. Vögel sind ein unglaublich vielfältiger und wichtiger Teil unseres Planeten.
Der Bird Swarm Algorithm (BSA) ist ein aufregender bioinspirierter Evolutionsalgorithmus, der Schwarmintelligenz nutzt und auf sozialen Interaktionen und dem Verhalten von Vogelschwärmen basiert. BSA wurde 2015 von Meng und Kollegen entwickelt und ist ein einzigartiger Optimierungsansatz, der drei Schlüsselaspekte des Vogelverhaltens kombiniert: Flug, Futtersuche und Wachsamkeit. In den elektronischen Schwärmen, in denen jeder „Vogel“ individuelle Taktiken und Strategien verfolgt, entsteht ein einzigartiges System kollektiver Interaktion, das von algorithmischer Intelligenz und Kreativität geprägt ist. Wichtig ist dabei nicht nur der persönliche Einsatz, sondern auch die Fähigkeit zur Zusammenarbeit, zum Austausch und zur gegenseitigen Unterstützung bei der Verfolgung des gemeinsamen Ziels der Optimierung.
Verschiedene Personen in der BSA können unterschiedliche Suchstrategien haben. Vögel können willkürlich zwischen Flug-, Wachsamkeits- und Futtersuchverhalten wechseln. Der bionische Entwurfsalgorithmus umfasst die Nahrungssuche auf der Grundlage der globalen und individuellen Fitness. Die Vögel versuchen auch, sich in die Mitte der Population zu begeben (was zu Konkurrenz mit anderen Vögeln führen kann) oder sich von der Herde zu entfernen. Zum Verhalten der Vögel gehören regelmäßiger Flug und Zug sowie der Wechsel zwischen der Rolle des Produzenten (producer) und des Bettlers (beggar). In der Welt der BSA hat jedes Individuum in einer bestimmten Iteration seine eigene Suchstrategie, was den Algorithmus vielseitig macht und seine Macht ausspielen kann.
Wie viele Schwarmintelligenz-Algorithmen kann BSA jedoch unter vorzeitiger Konvergenz leiden und in lokalen Optima stecken bleiben. Um eine schnellere Konvergenz mit hoher Genauigkeit von schwarmbasierten Optimierungsalgorithmen zu erreichen, wurden verschiedene Methoden verwendet, um ein Gleichgewicht zwischen Ausbeutung und Erkundung herzustellen.
Der BSA-Algorithmus basiert auf dem Verhalten von Vögeln und ist inspiriert von den kollektiven Interaktionen von Vogelschwärmen in der Natur, deren Verhalten die Grundlage für diesen Algorithmus bildet:
- Rudelverhalten. Viele Vogelarten, wie z. B. Stare, Schwalben und Gänse, fliegen in Schwärmen, wenn sie gemeinsam fliegen. Dieses Verhalten hilft ihnen, den Luftwiderstand zu verringern und bei Wanderungen oder der Nahrungssuche Energie zu sparen.
- Kommunikation. Vögel nutzen verschiedene Arten der Kommunikation wie Laute, Gesten und Körperhaltungen, um miteinander zu kommunizieren. So können sie ihre Handlungen koordinieren, ihre Verwandten vor Gefahren warnen und die Nahrungssuche koordinieren.
- Anpassungsfähigkeit. Vögel haben ein hohes Maß an Anpassungsfähigkeit an sich verändernde Umweltbedingungen. Sie können schnell auf Gefahren, Veränderungen des Wetters und des Nahrungsangebots reagieren und ihr Verhalten und ihre Wanderrouten den jeweiligen Umständen anpassen.
- Führen und Folgen. In einem Vogelschwarm gibt es normalerweise einen Anführer, der die Flugrichtung bestimmt, und die anderen Vögel folgen ihm. Dies verdeutlicht das Prinzip des Führens und Folgens, das auch im BSA-Algorithmus berücksichtigt wird, um effektiv optimale Lösungen zu finden.
Der BSA-Algorithmus nutzt diese Prinzipien des Vogelverhaltens, um eine effiziente Optimierungstechnik zu entwickeln, die das kollektive Verhalten von Vogelschwärmen simuliert, um verschiedene Optimierungsprobleme zu lösen. BSA ist mehr als nur ein Algorithmus, es ist eine faszinierende Reise in die Welt der Optimierung, bei der die sozialen Interaktionen der Vögel zu einer Inspirationsquelle für die effiziente Lösung komplexer Probleme werden.
2. Der Algorithmus
Gehen wir nun näher auf die Logik des BSA-Algorithmus ein, die auf den ersten Blick komplex und verwirrend erscheinen mag. Bevor wir mit der Implementierung des Codes beginnen, wollen wir einen Pseudocode des Algorithmus entwickeln, der als Grundlage für die Implementierung dienen wird. Dadurch wird es viel einfacher zu verstehen, wie BSA funktioniert.
Pseudocode für den Bird Swarm Algorithm (BSA), eine Beschreibung des Algorithmus, der das Verhalten von Vogelschwärmen modelliert, auf hoher Ebene:
1. Initialisierung von N Lösungen und zugehörigen Parametern
2. Generierung neuer Lösungen:
3. Wenn der Vogel fliegt:
4. Wenn der Vogel ein Produzenten ist:
5. Auf der Suche nach einer neuen Nahrungsquelle
6. sonst:
7. Der Bettelvogel folgt dem Produzenten
8. sonst:
9. Wenn der Vogel Futter bekommt:
10. Der Vogel füttert
11. sonst:
12. Der Vogel bleibt wachsam
13. Evaluierung neuer Lösungen
14. Aktualisierung der Lösungen
15. Wenn das Stoppkriterium erreicht ist:
16. Vervollständigung des Algorithmus
17. sonst:
18. Zurück zu Schritt 2
Die Gleichung für Punkt 5, für den Vogel auf der Suche nach einer neuen Futterstelle:
xn = RNDg (min, max, producerPower)
wobei:
- xn - neuer Koordinatenwert
- RNDg - normalverteilte Zufallszahl mit dem Zentrum der Verteilung an der aktuellen Koordinate
- min und max - Verteilungsgrenzen
- producerPower - Standardabweichung für den Produzenten
Nach dieser Gleichung kann der Brutvogel im gesamten Suchraum in jede beliebige Richtung wandern, wobei die Wahrscheinlichkeit in der Nähe seiner aktuellen Position erhöht ist. So können die Vögel auf der Suche nach Nahrung neue Gebiete erkunden.
Die Gleichung für Punkt 7 für den Bettelvogel, der dem Produzenten folgt:
xn = x + (xK - x) * FL * RNDg (-1.0, 1.0, scroungerPower)
wobei:
- xn - neuer Koordinatenwert
- x - die beste Bettelkoordinate der Geschichte
- xK - die beste Koordinate des Produzenten in der Vergangenheit, wobei ein zufälliger Vogel mit der Position K in der Population als Produzenten ausgewählt wird
- RNDg - normalverteilte Zufallszahl mit dem Verteilungszentrum bei 0 und den Grenzen „-1,0“ und „1,0“
- scroungerPower - Standardabweichung für den Bettler
Die Gleichung zeigt, dass sich der Bettelvogel an seinen besten Koordinaten und an den besten Koordinaten des besten Individuums im Schwarm orientiert (der Produzenten orientiert sich nicht an seinen besten Koordinaten, sondern an den aktuellen). Dies entspricht dem Verhalten, dem Anführer in einem Rudel zu folgen.
Die Gleichung unter Punkt 10 gilt für Vögel während der Fütterungszeit außerhalb des Fluges:
xn = x + (p - x) * C * r1 + (g - x) * S * r2
wobei:
- xn - neuer Koordinatenwert
- x - aktuelle Koordinate
- p - die beste Koordinierung des Vogels bei der Nahrungsaufnahme in der Geschichte
- g - die besten Bevölkerungskoordinaten der Geschichte (die beste globale Lösung)
- r1 - zufällige einheitliche Zahl im Bereich [0.0 ... 1.0]
- r2 - zufällige einheitliche Zahl im Bereich [0.0 ... 1.0]
- C - kognitives Verhältnis, externer Parameter
- S - Sozialquote, externer Parameter
Die Gleichung beschreibt den Moment der Nahrungsaufnahme, in dem das Verhalten des Vogels auf seiner eigenen Erfahrung (aktuelle Position und beste Position in der Vergangenheit) und der Erfahrung der Herde basiert.
Die Gleichung für Punkt 12 für den aufmerksamen Vogel:
xn = x + A1 * (mean [c] - x) * r1 + A2 * (xK - x) * r2
wobei:
- xn - neuer Koordinatenwert
- x - der beste wachsame Vogelkoordinator der Geschichte
- r1 - zufällige einheitliche Zahl im Bereich [0.0 ... 1.0]
- r2 - zufällige gleichmäßige Zahl im Bereich [-1.0 ... 1.0]
- mean [c] - Durchschnittswert der c-ten Koordinate auf der Grundlage der besten Koordinaten aller Vögel des Schwarms
A1 - Korrekturverhältnis des Einflusses der durchschnittlichen Koordinaten des Herdenzentrums:
A1 = a1 * exp (-pFit * N / (sumFit + e))
wobei:
- a1 - Verhältnis, externer Parameter
- e = DBL_MIN, um eine Division durch 0 zu vermeiden
- pFit - beste Fitness für den wachsamen Vogel
- sumFit - Summe der besten Fitnesswerte der Vögel einer Herde
- N - Anzahl der Vögel in einer Herde
A2 - Korrekturverhältnis, das den Einfluss der Position des zur Beobachtung ausgewählten Vogels (der in das Sichtfeld des aufmerksamen Vogels geraten ist) auf das Verhalten des letzteren berücksichtigt. Gleichung für A2:
A2 = a2 * exp (((pFit - pFitK) / (|pFitK - pFit| + e)) * (N * pFitK / (sumFit + e)))
wobei:
- a2 - Verhältnis, externer Parameter
- e = DBL_MIN, um eine Division durch 0 zu vermeiden
- pFit - beste Fitness für den wachsamen Vogel
- pFitK - die beste Fitness eines zufällig ausgewählten K-ten Vogels in der Population (der Vogel, der in das Blickfeld des aufmerksamen Vogels gekommen ist)
- sumFit - Summe der besten Fitnesswerte der Vögel einer Herde
- N - Anzahl der Vögel in einer Herde
So überwacht der wachsame Vogel seine Umgebung und kann so seine Verwandten rechtzeitig vor Gefahren warnen. Dies ist das komplexeste Verhalten, das im Algorithmus beschrieben wird. Es berücksichtigt die Fitness aller Vögel in der Population sowie die Fitness des aufmerksamen Vogels selbst und des zur Beobachtung ausgewählten Vogels. Im Wesentlichen wird sich ein wachsamer Vogel in die Richtung bewegen, in der die Gesamtpopulation am besten gedeiht, wenn er die Position seines Artgenossen, der in sein Blickfeld kommt, kennt.
Der hervorgehobene Text im Pseudocode entspricht den in Abbildung 1 dargestellten BSA-Logikelementen.
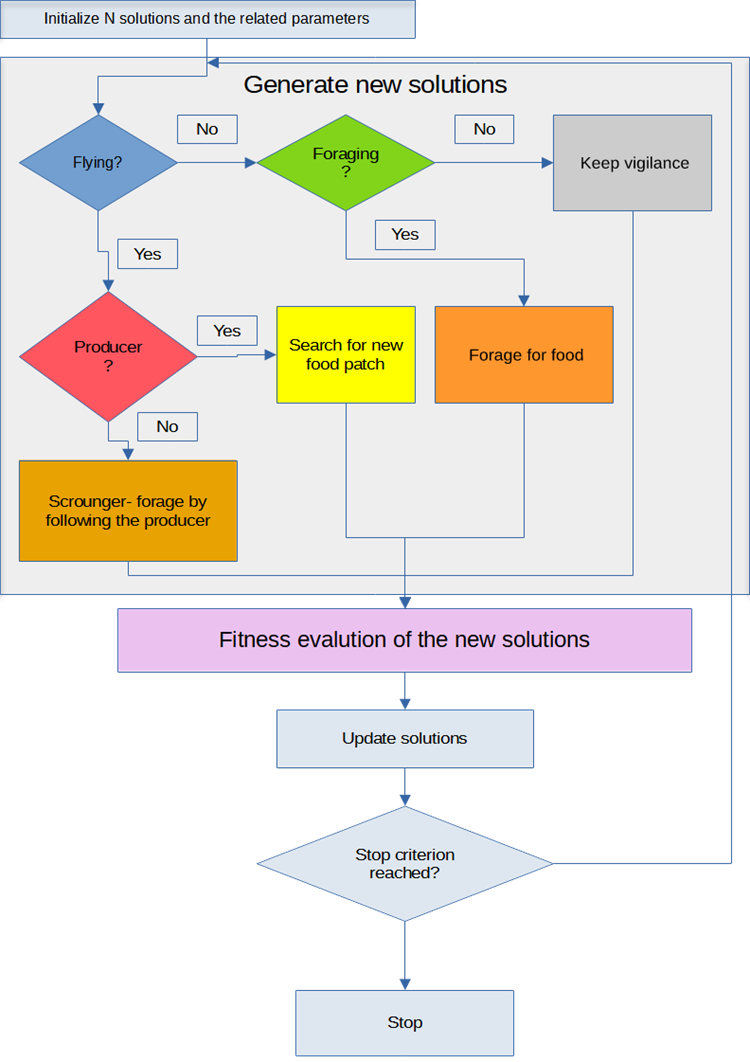
Abbildung 1. Logisches Diagramm des BSA-Algorithmus
Das Diagramm in Abbildung 1 ist eine Visualisierung des BSA-Algorithmus und modelliert das Verhalten eines Vogelschwarms. Hauptmerkmale des Algorithmus:
- Initialisierung von Lösungen. Der Algorithmus beginnt mit der Initialisierung einer Reihe von Lösungen und der zugehörigen Parameter. Dabei geht es um die anfängliche Verteilung der Vögel (oder Lösungen) im Suchraum.
- Flugverhalten. Während des Betriebs des Algorithmus kann jeder Vogel „fliegen“ oder „nicht fliegen“. Dieser Zustand beeinträchtigt die Fähigkeit des Vogels, neue Lösungen zu finden.
- Futtersuchverhalten. Wenn ein Vogel „fliegt“, kann er zum „Produzenten“ werden und sich auf die Suche nach einem neuen Gebiet mit Nahrung machen, oder er kann zum „Bettler“ werden und dem Produzenten folgen.
- Futtersuchverhalten. Wenn ein Vogel „nicht fliegt“, ist er entweder am Fressen oder er bleibt wachsam. Dies kann ein Zustand der Antizipation oder der Beobachtung der Umwelt sein.
- Bewertung und Aktualisierung der Lösungen. Nach der Generierung neuer Lösungen wird deren Eignung oder Qualität bewertet.
- Stopp-Kriterium. Der Algorithmus setzt den Zyklus der Erzeugung und Aktualisierung von Lösungen fort, bis ein bestimmtes Stoppkriterium erreicht ist. Dies kann eine bestimmte Anzahl von Iterationen, das Erreichen einer bestimmten Lösungsqualität oder ein anderes Kriterium sein.
Ich möchte betonen, dass BSA ein dynamischer Algorithmus ist, der sich bei der Suche nach der optimalen Lösung anpasst und weiterentwickelt.
Lassen Sie uns den Code für den BSA-Algorithmus implementieren. Für jeden Agenten definieren wir die Struktur S_BSA_Agent, die eine separate Lösung für das Optimierungsproblem und eine Beschreibung des Vogels in der Herde darstellt.
Die Struktur enthält folgende Felder:
- cBest[] - Array zum Speichern der besten Agentenkoordinaten.
- fBest - Variable zum Speichern der besten Fitnessbewertung des Agenten.
- Init - Methode der Struktur S_BSA_Agent, die die Felder der Struktur initialisiert. Sie nimmt das Integer-Argument „coords“, das zur Größenänderung des Arrays „cBest“ mit der Funktion ArrayResize verwendet wird.
Wir setzen den Anfangswert der Variablen „fBest“ auf den kleinstmöglichen doppelten Wert, d. h. die schlechteste Fitness.
//—————————————————————————————————————————————————————————————————————————————— struct S_BSA_Agent { double cBest []; //best coordinates double fBest; //best fitness void Init (int coords) { ArrayResize (cBest, coords); fBest = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Definieren wir die Klasse C_AO_BSA des BSA-Algorithmus, die ein Erbe der Basisklasse der C_AO-Populationsalgorithmen ist und die folgenden Felder und Methoden enthält:
1. Öffentliche Felder:
- ao_name - Name des Optimierungsalgorithmus.
- ao_desc - Beschreibung des Optimierungsalgorithmus.
- popSize - Größe der Bevölkerung.
- params - Array der Algorithmusparameter.
- flyingProb - Flugwahrscheinlichkeit.
- producerProb - Produzentenwahrscheinlichkeit.
- foragingProb - Wahrscheinlichkeit der Futtersuche.
- a1 - a1 Konstante [0...2].
- a2 - a2 Konstante [0...2].
- C - kognitives Verhältnis.
- S - Soziales Verhältnis.
- FL - FL-Konstante [0...2].
- producerPower - Standardabweichung im Produzentenverhalten.
- scroungerPower - Standardabweichung im Bettelverhalten.
2. Die verfügbaren Optionen sind:
- C_AO_BSA - Klassenkonstruktor, der die Klassenfelder initialisiert.
- SetParams - Methode zur Einstellung der Algorithmusparameter.
- Init - Methode zur Initialisierung des Algorithmus. Die Methode akzeptiert minimale und maximale Suchbereiche, Suchschritte und die Anzahl der Epochen.
- Umzug - Methode für den Umzug von Agenten.
- Revision - Methode zur Revision von Bearbeitern.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BSA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BSA () { } C_AO_BSA () { ao_name = "BSA"; ao_desc = "Bird Swarm Algorithm"; popSize = 20; //population size flyingProb = 0.8; //Flight probability producerProb = 0.25; //Producer probability foragingProb = 0.55; //Foraging probability a1 = 0.6; //a1 constant [0...2] a2 = 0.05; //a2 constant [0...2] C = 0.05; //Cognitive coefficient S = 1.1; //Social coefficient FL = 1.75; //FL constant [0...2] producerPower = 7.05; //Producer power scroungerPower = 2.60; //Scrounger power ArrayResize (params, 11); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "flyingProb"; params [1].val = flyingProb; params [2].name = "producerProb"; params [2].val = producerProb; params [3].name = "foragingProb"; params [3].val = foragingProb; params [4].name = "a1"; params [4].val = a1; params [5].name = "a2"; params [5].val = a2; params [6].name = "C"; params [6].val = C; params [7].name = "S"; params [7].val = S; params [8].name = "FL"; params [8].val = FL; params [9].name = "producerPower"; params [9].val = producerPower; params [10].name = "scroungerPower"; params [10].val = scroungerPower; } void SetParams () { popSize = (int)params [0].val; flyingProb = params [1].val; producerProb = params [2].val; foragingProb = params [3].val; a1 = params [4].val; a2 = params [5].val; C = params [6].val; S = params [7].val; FL = params [8].val; producerPower = params [9].val; scroungerPower = params [10].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); void Injection (const int popPos, const int coordPos, const double value); //---------------------------------------------------------------------------- double flyingProb; //Flight probability double producerProb; //Producer probability double foragingProb; //Foraging probability double a1; //a1 constant [0...2] double a2; //a2 constant [0...2] double C; //Cognitive coefficient double S; //Social coefficient double FL; //FL constant [0...2] double producerPower; //Producer power double scroungerPower; //Scrounger power S_BSA_Agent agent []; private: //------------------------------------------------------------------- double mean []; //represents the element of the average position of the whole bird’s swarm double N; double e; //epsilon void BirdProducer (int pos); void BirdScrounger (int pos); void BirdForaging (int pos); void BirdVigilance (int pos); }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Init der Klasse C_AO_BSA dient der Initialisierung von Klassenvariablen auf der Grundlage der übergebenen Parameter. Diese Methode führt eine Standardinitialisierung mit der Methode StandardInit durch, die den minimalen und maximalen Suchbereich sowie den Suchschritt übernimmt.
Wenn die Standardinitialisierung erfolgreich ist, fährt die Methode mit der Initialisierung der Variablen „N“ und „e“ fort. Der Wert von „N“ wird auf die Populationsgröße „popSize“ gesetzt, während „e“ ein Epsilon ist, das mit dem minimalen Doppelwert initialisiert wird.
Die Methode passt dann die Größe des Arrays „agent“ an die Größe von „popSize“ an. Die Methode Init wird mit dem Parameter „coords“ für jedes Element in „agent“ aufgerufen. Die Größe des Arrays „mean“ wird ebenfalls auf die Größe von „coords“ geändert. Das Array wird verwendet, um die durchschnittlichen Populationskoordinaten der Vögel zu speichern.
Die Methode gibt „true“ zurück, wenn die Initialisierung erfolgreich war, andernfalls „false“.
Diese Methode führt die anfängliche Einrichtung des BSA-Optimierungsalgorithmus mit gegebenen Parametern durch und bereitet ihn auf die Durchführung der Optimierung vor.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_BSA::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (agent, popSize); for (int i = 0; i < popSize; i++) agent [i].Init (coords); ArrayResize (mean, coords); N = popSize; e = DBL_MIN; return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving der Klasse C_AO_BSA wird verwendet, um Agenten während der Optimierung zu bewegen. Die Methode geht folgendermaßen vor:
- Wenn „Revision“ „false“ ist, werden die Koordinaten der Agenten „a[i].c[c]“ mit Zufallswerten in den angegebenen Bereichen initialisiert. Das Flag „revision“ wird dann auf „true“ gesetzt und die Methode wird beendet.
- Wenn „revision“ nicht „false“ ist, werden für jeden Agenten neue Koordinaten anhand von Gleichungen und Wahrscheinlichkeiten berechnet.
In der zweiten und den folgenden Epochen ruft die Methode Funktionen auf, die das Verhalten der einzelnen Vögel im Schwarm in Abhängigkeit von den erfüllten Wahrscheinlichkeiten bestimmen:
- Wenn die Wahrscheinlichkeit des Fliegens erfüllt ist - „flyingProb“, dann „fliegt“ der Agent. In diesem Fall gibt es zwei mögliche Verhaltensoptionen:
- Wenn die Wahrscheinlichkeit kleiner ist als „producerProb“, dann ist der Agent ein „Produzenten“ und sucht nach einem neuen Essensplatz.
- Andernfalls ist der Vertreter ein „Bettler“ und folgt dem Produzenten.
- Wenn er „nicht fliegt“, dann sind die folgenden zwei Verhaltensoptionen möglich:
- Wenn die Wahrscheinlichkeit kleiner ist als „foragingProb“, dann „sucht“ der Agent nach Nahrung.
- Andernfalls befindet sich der Agent im Zustand der „Wachsamkeit“.
Die Methode ist dafür zuständig, die Koordinaten der Agenten im BSA-Optimierungsalgorithmus entsprechend der aktuellen Epoche, den Zufallswerten und Wahrscheinlichkeiten zu aktualisieren.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BSA::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { //bird is flying------------------------------------------------------------ if (u.RNDprobab () < flyingProb) { //bird producer if (u.RNDprobab () < producerProb) BirdProducer (i); //bird is looking for a new place to eat //bird is not a producer else BirdScrounger (i); //scrounger follows the producer } //bird is not flying-------------------------------------------------------- else { //bird foraging if (u.RNDprobab () < foragingProb) BirdForaging (i); //bird feeds //bird is not foraging else BirdVigilance (i); //bird vigilance } } } //——————————————————————————————————————————————————————————————————————————————
Die BirdProducer-Methode der Klasse C_AO_BSA wird verwendet, um das „Produzenten“-Verhalten im BSA-Algorithmus zu simulieren. Die Methode geht folgendermaßen vor:
- Initialisiert die Variable „x“, die zum Speichern der aktuellen Position des Vogels verwendet wird.
- Dann werden die folgenden Aktionen für jede Agentenkoordinate durchgeführt:
- Der „x“-Wert wird auf die aktuelle Koordinate des Agenten gesetzt.
- Der „x“-Wert wird anhand einer Gauß-Verteilung aktualisiert, wobei der Mittelwert die aktuelle Koordinate ist und der Bereich und die Standardabweichung durch die Werte „rangeMin“, „rangeMax“ und „producerPower“ bestimmt werden.
- Der neue Wert der Agentenkoordinate wird mit der Methode SeInDiSp festgelegt, die den „x“-Wert entsprechend dem Suchbereich und dem Schritt anpasst.
Diese Methode modelliert das Verhalten eines „Produzenten“ im BSA-Algorithmus, der mit Hilfe einer Gauß-Verteilung den Suchraum nach neuen Nahrungsquellen (d. h. neuen potenziellen Lösungen) absucht.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BSA::BirdProducer (int pos) { double x = 0.0; //bird position for (int c = 0; c < coords; c++) { x = a [pos].c [c]; x = u.GaussDistribution (x, rangeMin [c], rangeMax [c], producerPower); a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Die Methode, die das „Bettler“-Verhalten modelliert, ist die Funktion BirdScrounger in der Klasse C_AO_BSA. Sie führt die folgenden Aktionen durch:
- 1. Initialisiert die Variablen „K“, „x“ und „xK“. „K“ ist die Position eines zufällig ausgewählten Vogels in der Herde, „x“ ist die beste Position des Vogels, und „xK“ ist die aktuell beste Position des zufällig ausgewählten Vogels in der Herde.
- 2. Führt eine Schleife durch alle Koordinaten durch.
- Wählt einen zufälligen Vogel aus, der nicht der aktuelle ist.
- Aktualisiert „x“ und „xK“ auf der Grundlage der besten Positionen des aktuellen Vogels und eines zufällig ausgewählten Vogels.
- Aktualisiert „x“ unter Verwendung der Gauß‘schen Verteilung.
- Schließlich wird die aktuelle Position des Vogels mit der Methode SeInDiSp aktualisiert, wobei der „x“-Wert entsprechend dem Suchbereich und dem Schritt angepasst wird.
Diese Methode modelliert das „Bettler“-Verhalten im BSA-Algorithmus mit Hilfe der Gauß-Verteilung, die dem „Produzenten“ folgt (d.h. ihre eigene Position relativ zur Position des Produzenten anpasst).
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BSA::BirdScrounger (int pos) { int K = 0; //position of a randomly selected bird in a swarm double x = 0.0; //best bird position double xK = 0.0; //current best position of a randomly selected bird in a swarm for (int c = 0; c < coords; c++) { do K = u.RNDminusOne (popSize); while (K == pos); x = agent [pos].cBest [c]; xK = agent [K].cBest [c]; x = x + (xK - x) * FL * u.GaussDistribution (0, -1.0, 1.0, scroungerPower); a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Die Methode BirdForaging in der Klasse C_AO_BSA ist für einen Vogel gedacht, der gerade nicht fliegt und mit dem Fressen beschäftigt ist. Die Methode führt innerhalb der Schleife für alle Koordinaten folgende Schritte aus:
- Aktualisiert „x“, „p“ und „g“ auf der Grundlage der aktuellen und besten Position des Vogels sowie der besten globalen Position.
- Erzeugt zwei Zufallszahlen „r1“ und „r2“.
- Aktualisiert „x“ mit diesen Zufallszahlen sowie den Konstanten „C“ und „S“.
- Passt die ermittelte Vogelposition mit der Funktion SeInDiSp an.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BSA::BirdForaging (int pos) { double x = 0.0; //current bird position double p = 0.0; //best bird position double g = 0.0; //best global position double r1 = 0.0; //uniform random number [0.0 ... 1.0] double r2 = 0.0; //uniform random number [0.0 ... 1.0] for (int c = 0; c < coords; c++) { x = a [pos].c [c]; p = agent [pos].cBest [c]; g = cB [c]; r1 = u.RNDprobab (); r2 = u.RNDprobab (); x = x + (p - x) * C * r1 + (g - x) * S * r2; a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Die neueste und komplexeste Methode, das Verhalten eines wachsamen Vogels zu simulieren, ist BirdVigilance. Sie führt die folgenden Aktionen durch:
- Berechnet die Summe der besten Fitnesswerte aller Vögel in der Herde.
- Berechnet den Durchschnittswert jeder Koordinate für alle Vögel der Herde.
- Wählt einen zufälligen Vogel aus, der nicht der aktuelle ist.
- Aktualisiert „pFit“ und „pFitK“ auf der Grundlage der besten Fitnesswerte des aktuellen Vogels und eines zufällig ausgewählten Vogels.
- Berechnet „A1“ und „A2“ anhand einer Exponentialfunktion, die von „pFit“, „pFitK“, „N“, „sumFit“ und „e“ abhängt.
- Führt eine Schleife durch alle Koordinaten durch:
- Erzeugt zwei Zufallszahlen „r1“ und „r2“.
- Aktualisiert „x“ und „xK“ auf der Grundlage der besten Positionen des aktuellen Vogels und eines zufällig ausgewählten Vogels.
- Aktualisiert „x“ mit „A1“, „A2“, „r1“ und „r2“.
- Passt die aktuelle Vogelposition mit der Funktion SeInDiSp an.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BSA::BirdVigilance (int pos) { int K = 0; //position of a randomly selected bird in a swarm double sumFit = 0.0; //best birds fitness sum double pFitK = 0.0; //best fitness of a randomly selected bird double pFit = 0.0; //best bird fitness double A1 = 0.0; double A2 = 0.0; double r1 = 0.0; //uniform random number [ 0.0 ... 1.0] double r2 = 0.0; //uniform random number [-1.0 ... 1.0] double x = 0.0; //best bird position double xK = 0.0; //best position of a randomly selected bird in a swarm ArrayInitialize (mean, 0.0); for (int i = 0; i < popSize; i++) sumFit += agent [i].fBest; for (int c = 0; c < coords; c++) { for (int i = 0; i < popSize; i++) mean [c] += a [i].c [c]; mean [c] /= popSize; } do K = u.RNDminusOne (popSize); while (K == pos); pFit = agent [pos].fBest; pFitK = agent [K].fBest; A1 = a1 * exp (-pFit * N / (sumFit + e)); A2 = a2 * exp (((pFit - pFitK) / (fabs (pFitK - pFit) + e)) * (N * pFitK / (sumFit + e))); for (int c = 0; c < coords; c++) { r1 = u.RNDprobab (); r2 = u.RNDfromCI (-1, 1); x = agent [pos].cBest [c]; xK = agent [K].cBest [c]; x = x + A1 * (mean [c] - x) * r1 + A2 * (xK - x) * r2; a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Die Revisionsmethode der Klasse C_AO_BSA wird verwendet, um die beste globale Lösung zu aktualisieren und die besten Positionen der Agenten zu aktualisieren. Die Methode geht folgendermaßen vor:
- Aktualisierung der globalen Lösung.
- Aktualisieren Sie die bisherigen Werte der besten Fitnessfunktion und die Koordinaten des Agenten.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BSA::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) ind = i; } if (ind != -1) { fB = a [ind].f; ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > agent [i].fBest) { agent [i].fBest = a [i].f; ArrayCopy (agent [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
3. Testergebnisse
Ich möchte auf die Ergebnisse des BSA-Algorithmus für verschiedene Funktionsmengen näher eingehen. Die BSA-Gesamtpunktzahl über alle Testfunktionen hinweg betrug 4,80947, was 53,44 % der maximal möglichen Punktzahl entspricht. Dieses Ergebnis zeigt die allgemeine Effizienz des Algorithmus. Der Vogelschwarm-Algorithmus hat das Potenzial, eine Vielzahl von Optimierungsproblemen mit unterschiedlichen Funktionen erfolgreich zu lösen.
BSA|Bird Swarm Algorithm|20.0|0.8|0.25|0.55|0.6|0.05|0.05|1.1|1.75|7.05|2.6|
=============================
5 Hilly's; Func runs: 10000; result: 0.8930600046782612
25 Hilly's; Func runs: 10000; result: 0.6489975525320968
500 Hilly's; Func runs: 10000; result: 0.262496551797822
=============================
5 Forest's; Func runs: 10000; result: 0.9241962617798402
25 Forest's; Func runs: 10000; result: 0.7112057472851052
500 Forest's; Func runs: 10000; result: 0.24938963509983267
=============================
5 Megacity's; Func runs: 10000; result: 0.6938461538461538
25 Megacity's; Func runs: 10000; result: 0.3261538461538461
500 Megacity's; Func runs: 10000; result: 0.1001230769230778
=============================
All score: 4.80947 (53.44%)
Die Visualisierung der Funktionsweise des Algorithmus zeigt eine erhebliche Streuung der Ergebnisse über verschiedene Testfunktionen. Trotz erfolgreicher Erkundung lokaler Oberflächenbereiche kann der Algorithmus in lokalen Fallen stecken bleiben. Dies schränkt seine Fähigkeit ein, ein globales Optimum zu erreichen und kann zu einem Mangel an Stabilität bei der Suche nach einer optimalen Lösung führen.
Die Visualisierung der Arbeit an der Hauttestfunktion ist nur ein Beispiel für die Funktionsweise des Algorithmus und nimmt nicht an der Zusammenstellung der Bewertungstabelle teil.
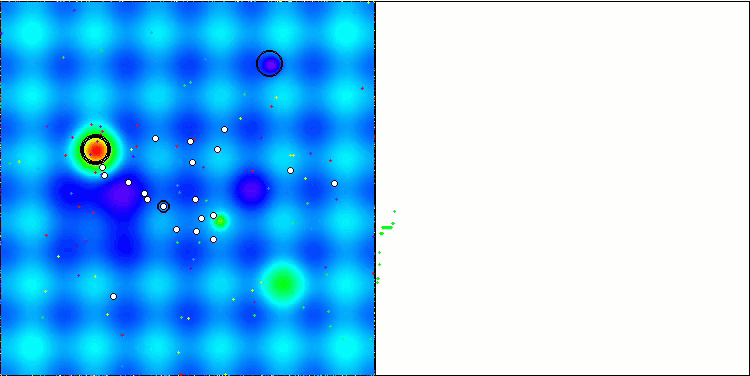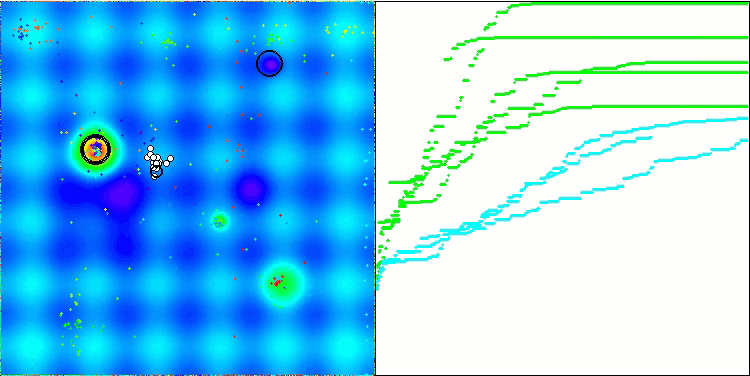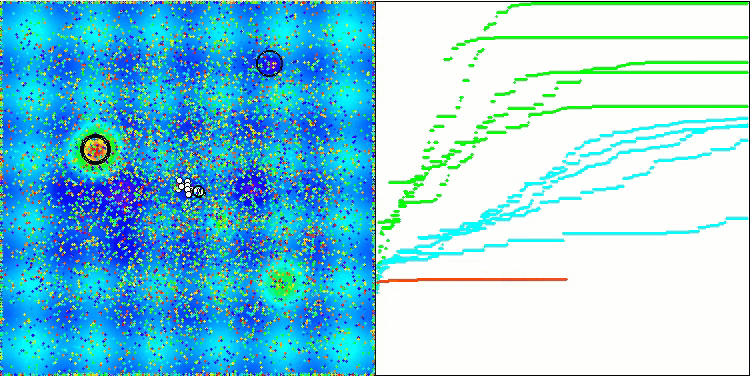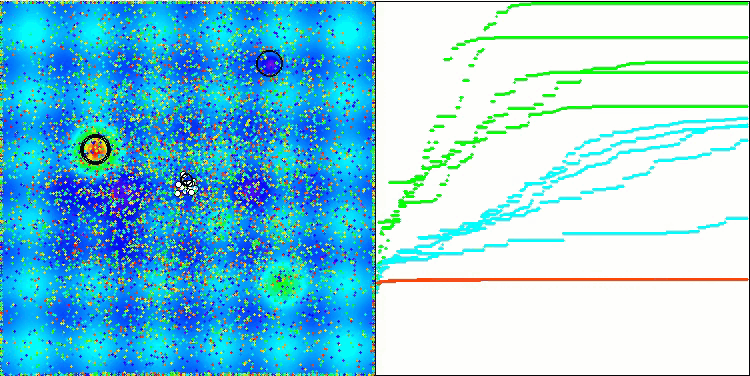
BSA mit der Testfunktion Hilly
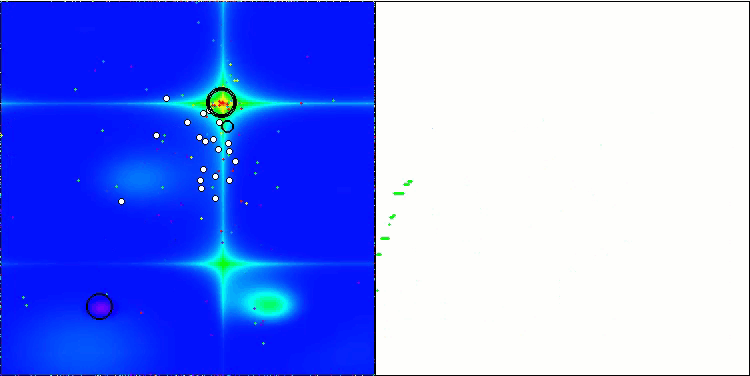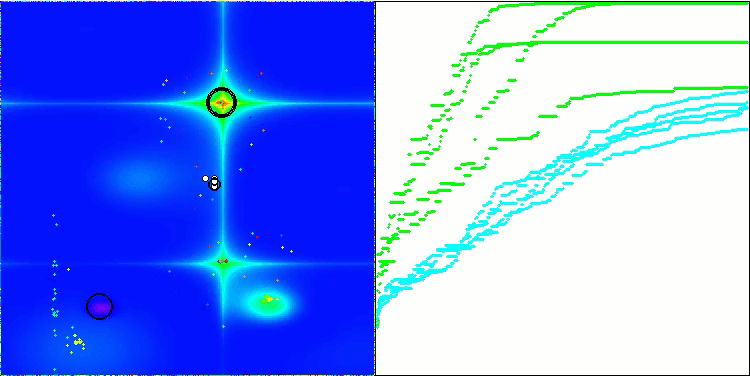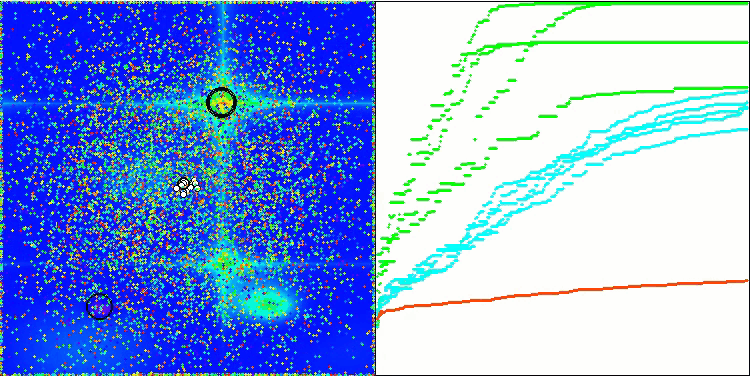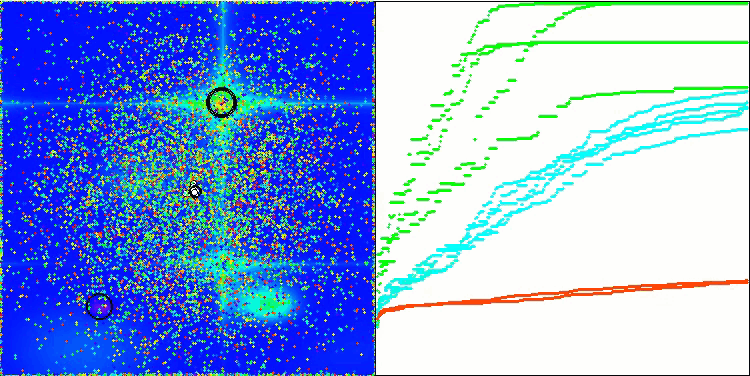
BSA mit der Testfunktion Forest
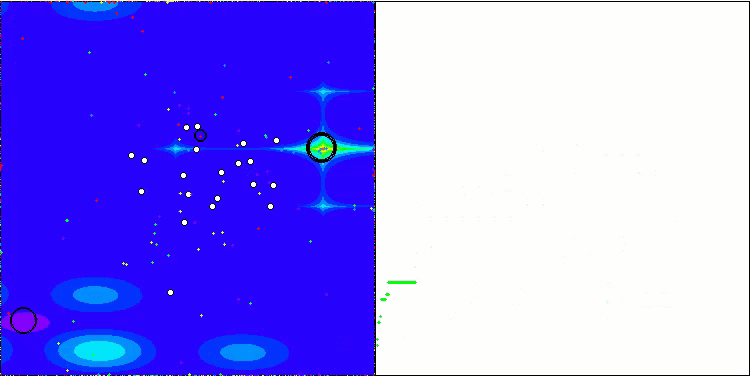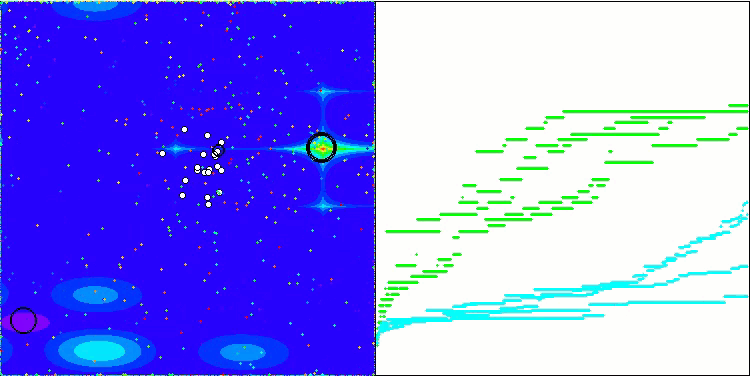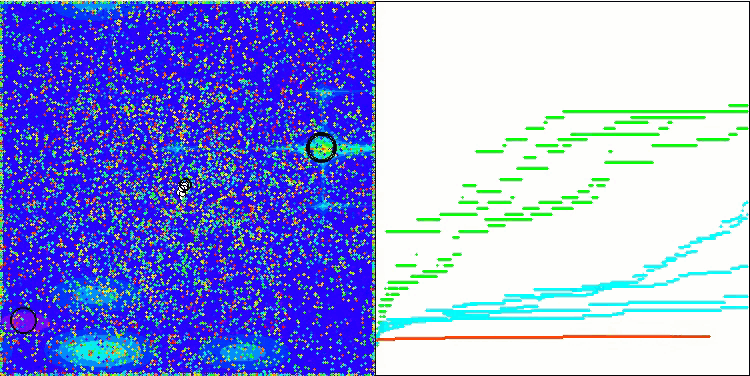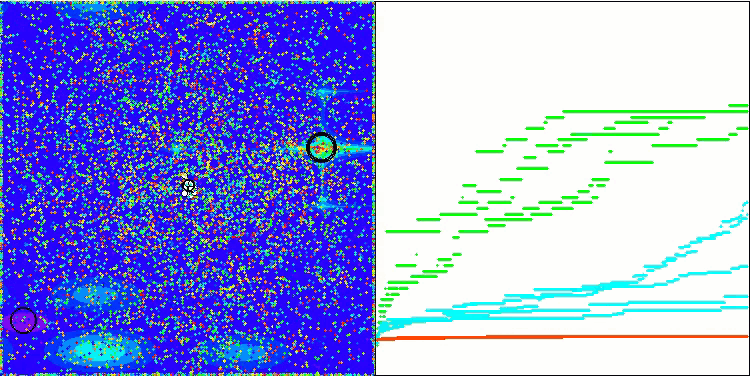
BSA mit der Testfunktion Megacity
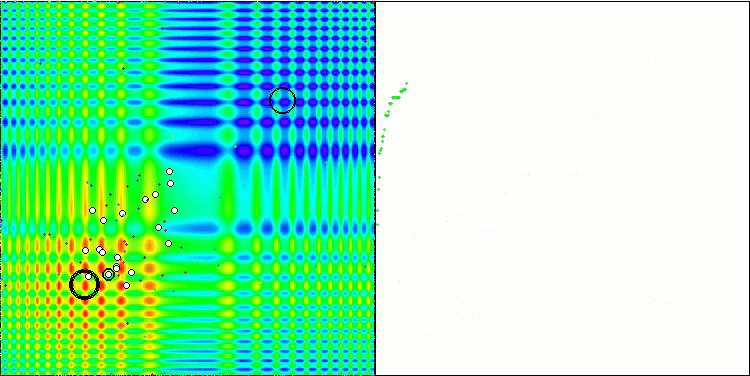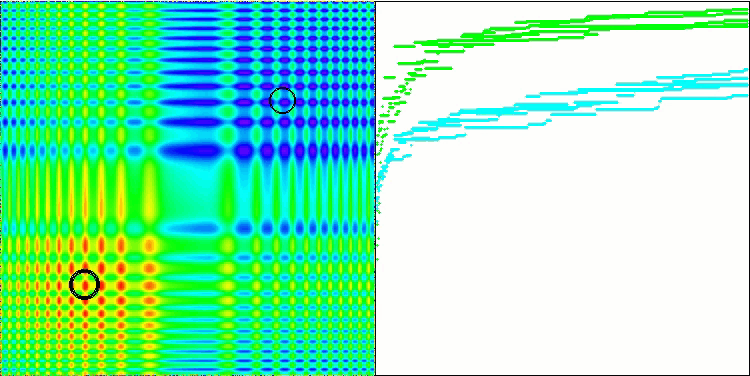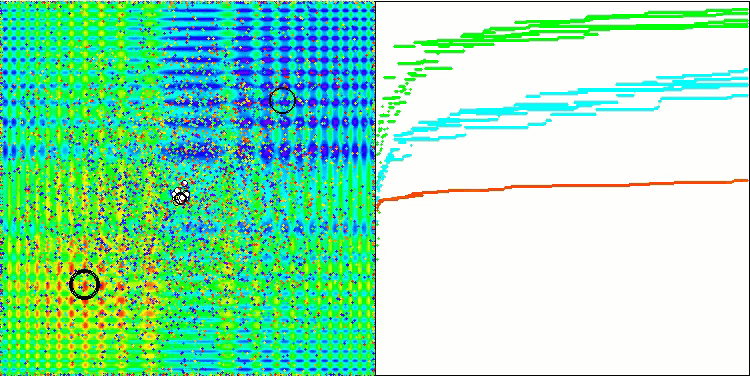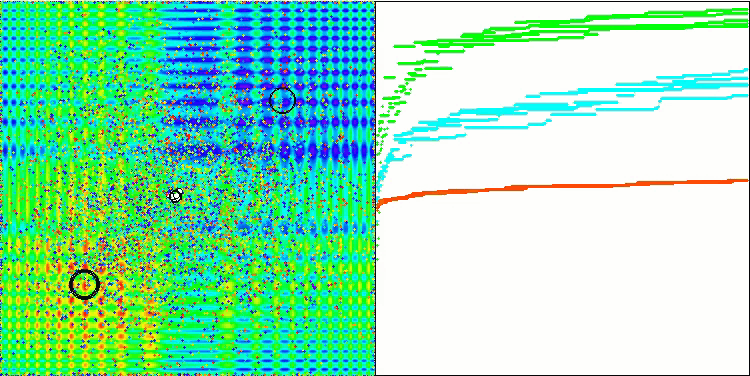
BSA mit der Testfunktion Skin
Es ist wichtig zu erwähnen, dass sich der Algorithmus bei der glatten Hilly-Testfunktion mit der hohen Anzahl von Variablen als äußerst ineffektiv erwies und das niedrigste Ergebnis in der Bewertungstabelle unter allen betrachteten Algorithmen aufwies. Obwohl BSA bei Forest- und diskreten Megacity-Funktionen hoher Dimensionen gute Ergebnisse im Vergleich zu anderen Algorithmen zeigt, auch zu denen, die weiter oben in der Tabelle stehen.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | binärer genetischer Algorithmus | 0.99992 | 0.99484 | 0.50483 | 2.49959 | 1.00000 | 0.99975 | 0.32054 | 2.32029 | 0.90667 | 0.96400 | 0.23035 | 2.10102 | 6.921 | 76.90 |
| 2 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.99934 | 0.91895 | 0.56297 | 2.48127 | 1.00000 | 0.93522 | 0.39179 | 2.32701 | 0.83167 | 0.64433 | 0.21155 | 1.68755 | 6.496 | 72.18 |
| 3 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 4 | ESG | Entwicklung der sozialen Gruppen | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 5 | SIA | Simuliertes isotropes Abkühlen | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 6 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 7 | BSA | Vogelschwarm-Algorithmus | 0.90857 | 0.73661 | 0.25767 | 1.90285 | 0.90437 | 0.81619 | 0.16401 | 1.88457 | 0.61692 | 0.54154 | 0.10951 | 1.26797 | 5.055 | 56.17 |
| 8 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 9 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 10 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 11 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 12 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 13 | BFO-GA | Optimierung der bakteriellen Futtersuche - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 14 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 15 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 16 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 17 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 18 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 19 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 20 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 21 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 22 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 23 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 24 | BA | Fledermaus-Algorithmus | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 25 | SA | simuliertes Abkühlen | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 26 | IWDm | intelligente Wassertropfen M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 27 | PSO | Partikelschwarmoptimierung | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 28 | MA | Affen-Algorithmus | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 29 | SFL | schlurfender Froschsprung | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 30 | FSS | Fischschulsuche | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 31 | RND | zufällig | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
| 32 | GWO | Grauer-Wolf-Optimierung | 0.59169 | 0.36561 | 0.29595 | 1.25326 | 0.24499 | 0.09047 | 0.03612 | 0.37158 | 0.27667 | 0.08567 | 0.02170 | 0.38403 | 2.009 | 22.32 |
| 33 | CSS | Suche geladener Systeme | 0.44252 | 0.35454 | 0.35201 | 1.14907 | 0.24140 | 0.11345 | 0.06814 | 0.42299 | 0.18333 | 0.06300 | 0.02322 | 0.26955 | 1.842 | 20.46 |
| 34 | EM | elektromagnetismusähnlicher Algorithmus | 0.46250 | 0.34594 | 0.32285 | 1.13129 | 0.21245 | 0.09783 | 0.10057 | 0.41085 | 0.15667 | 0.06033 | 0.02712 | 0.24412 | 1.786 | 19.85 |
Zusammenfassung
Der Vogelschwarm-Algorithmus (BSA) ist ein faszinierendes Forschungsinstrument, das mit seiner reichhaltigen Logik, die die verschiedenen Zustände und Strategien von Vogelschwärmen verkörpert, die Fantasie anregt. Die Arbeit an diesem Algorithmus war für mich interessant, weil er eine komplexe Dynamik aufweist, bei der Einzel- und Gruppenaktionen der Vögel unterschiedlichen Bedingungen und Kombinationen unterliegen.
Die Komplexität der BSA spiegelt sich auch in der großen Anzahl von Parametern wider, die sorgfältig abgestimmt werden müssen, um optimale Ergebnisse zu erzielen. Um die Parameter des Algorithmus zu optimieren, musste ich einen EA schreiben, der im mathematischen Berechnungsmodus des Standard-MetaTrader 5-Testers arbeitet, was mir ermöglichte, gute externe Parameter zu finden, die dem Algorithmus den 7. Platz in der Bewertung sicherten. Möglicherweise gibt es weiteres Verbesserungspotenzial, und ich möchte alle Interessierten ermutigen, mit diesem Algorithmus zu experimentieren. Ich glaube, dass es noch unerforschte Möglichkeiten gibt, um bessere Ergebnisse zu erzielen, da es viele Variationen in der Reihenfolge der Ausführung und der Kombination von Sequenzen der Verhaltensweisen von Vögeln gibt (in dem Artikel werden 4 Arten von Verhaltensweisen untersucht).
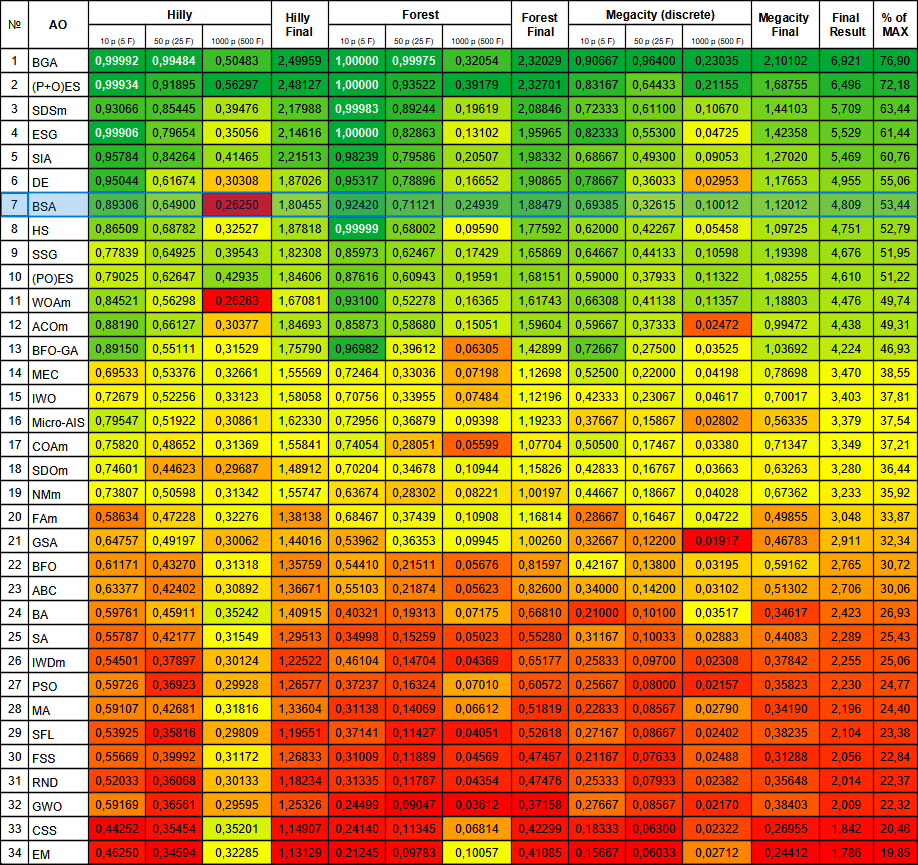
Bild 2. Farbliche Abstufung der Algorithmen nach relevanten Tests Ergebnisse größer oder gleich 0,99 sind weiß hervorgehoben
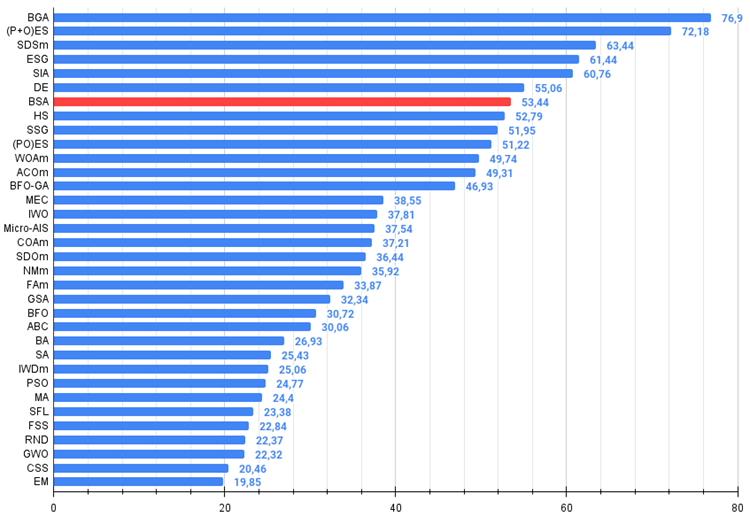
Abb. 3. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, größer ist besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; das Archiv enthält ein Skript zur Berechnung der Bewertungstabelle)
Vor- und Nachteile der BSA:
Vorteile:
- Gute Ergebnisse für die scharfe Forest-Funktion und die diskrete Megacity mit großer Dimension.
Nachteile
- Komplexe Umsetzung.
- Geringe Konvergenz.
- Geringe Skalierbarkeit bei glatten Funktionen wie Hilly (Probleme mit hochdimensionalen Aufgaben).
Der Artikel wird von einem Archiv mit den aktuellen Code-Versionen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/14491
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Entwicklung eines Expertenberaters für mehrere Währungen (Teil 7): Auswahl einer Gruppe auf der Grundlage der Vorwärtsperiode
Entwicklung eines Expertenberaters für mehrere Währungen (Teil 7): Auswahl einer Gruppe auf der Grundlage der Vorwärtsperiode
 Algorithmen zur Optimierung mit Populationen: Der Wal-Optimierungsalgorithmus (WOA)
Algorithmen zur Optimierung mit Populationen: Der Wal-Optimierungsalgorithmus (WOA)
 Erstellen eines täglichen Drawdown-Limits EA in MQL5
Erstellen eines täglichen Drawdown-Limits EA in MQL5
 Nicht-stationäre Prozesse und unechte Regression
Nicht-stationäre Prozesse und unechte Regression
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Welche AO konvergiert am schnellsten (Anzahl der FF-Berechnungen)? Es spielt keine Rolle, wohin sie konvergiert. Solange es ein Minimum an Schritten gibt.
Jede der Top 5, sehr schnell zu konvergieren.
Schade, dass es keinen numerischen Wert für schnell gibt.
Schade, dass es keinen numerischen Wert für Schnelligkeit gibt.
Sie könnten mehrere Testläufe durchführen, die FF-Werte für jede Epoche speichern und die durchschnittliche Verbesserung für jede entsprechende Epoche berechnen. Natürlich wird es für jede Anzahl von Variablen unterschiedliche Werte geben. Dies ist der Fall, wenn Sie mit numerischen Indikatoren für die "Konvergenzgeschwindigkeit" sehr pingelig werden.
In jedem ersten Test für alle drei Testfunktionen (10 Parameter) werden die Top 5 der Liste bereits um die 100. Epoche (bei einer Grundgesamtheit von 50) sehr nahe am theoretischen Maximum liegen.
Sie können natürlich mehrere Testläufe durchführen, die FF-Werte in jeder Epoche speichern und die durchschnittliche Verbesserung in jeder entsprechenden Epoche berechnen. Natürlich wird es für jede Anzahl von Variablen unterschiedliche Indikatoren geben. Dies ist, wenn Sie sehr pingelig mit numerischen Indikatoren der "Konvergenzgeschwindigkeit" sind.
In jedem ersten Test für alle drei Testfunktionen (10 Parameter) werden die Top 5 der Liste bereits um die 100. Epoche (bei einer Grundgesamtheit von 50) sehr nahe am theoretischen Maximum liegen.
~5000 FF?
~5000 FF?
Ja. Selbst bei der 50. Epoche sind bereits 70-80% des theoretischen Maximums erreicht.
Dies gilt natürlich für den Parameterschritt 0 (wie ich ihn beim Testen verwende). Wenn der Schritt von 0 verschieden ist, ist die Konvergenz noch höher.