
Algorithmus einer Anarchischen Gesellschaftsoptimierung (ASO)
Inhalt
1. Einführung
Das Thema der sozialen Beziehungen und die Möglichkeit, einen Algorithmus im Konzept der sozialen Verbindungen zu konstruieren, haben mich schon immer angezogen, da dies das interessanteste Phänomen in der Entwicklung der Gesellschaft ist und ein breites Betätigungsfeld für die Möglichkeit bietet, die Struktur des Beziehungssystems algorithmisch zu beschreiben und einen entsprechenden Optimierungsalgorithmus zu implementieren.
In den vorangegangenen Artikeln haben wir uns bereits mit Algorithmen für soziales Verhalten beschäftigt - Evolution sozialer Gruppen und künstliche kooperative Suche. In diesem Artikel werden wir versuchen, das Konzept einer anarchischen Gesellschaft zu verstehen - ein System sozialer Interaktion ohne zentralisierte Macht und hierarchische Strukturen, bei dem davon ausgegangen wird, dass die Menschen ihr Leben auf der Grundlage freiwilliger Vereinbarungen organisieren und interagieren können.
Die anarchistische Gesellschaft basiert auf den Grundsätzen der Autonomie und Freiheit, wo jeder Mensch unabhängig und selbständig Entscheidungen über sein Leben treffen kann, ohne Einmischung von außen, den Grundsätzen der freiwilligen Zusammenarbeit, bei der die Menschen auf der Grundlage der Zustimmung aller Beteiligten ohne Zwang zusammenarbeiten, der Gleichheit der Rechte und Möglichkeiten sowie den Grundsätzen der Solidarität, der gegenseitigen Hilfe und der Zusammenarbeit. Die Idee ist sehr interessant, was die Umsetzung im Algorithmus angeht. Es wurde der Versuch unternommen, eine solche soziale Konstruktion in den Optimierungsalgorithmus einer Anarchischen Gesellschaft (Anarchic Society Optimization, ASO) zu implementieren. Der Algorithmus wurde von Ahmadi-Javid vorgeschlagen und im Jahr 2011 veröffentlicht.
Die Hauptidee ist die Entwicklung einer Optimierungsmethode, die sich am Verhalten von Individuen in anarchischen Gesellschaften orientiert. Im Gegensatz zu den bestehenden Methoden der Schwarmintelligenz, die auf der Grundlage von Insekten- oder Tierschwärmen entwickelt wurden, wie PSO und ACO, kann die Entwicklung eines Algorithmus, der auf der Untersuchung des Aufbaus einer normalen menschlichen Gesellschaft basiert, nur begrenzten Erfolg haben, da eine gut organisierte Gesellschaft nicht in der Lage ist, ihre Wünsche durch individuelle Entscheidungen zu erreichen. Außerdem ist kein Mitglied der Gesellschaft wirklich unabhängig und autonom und kann seine Situation nicht innerhalb eines bestimmten Zeitraums radikal verbessern. Diese Erkenntnis brachte den Schöpfer des Algorithmus auf die Idee, das Grundkonzept für die Entwicklung von einer Gesellschaft zu übernehmen, die auf einer anomalen Struktur basiert.
Der Kern der ASO ist eine Gruppe von Personen, die wankelmütig und abenteuerlustig sind, keine Stabilität mögen und sich oft irrational verhalten, indem sie die schlechtesten Positionen einnehmen, die sie in der Erkundungsphase besucht haben. Der Grad des anarchischen Verhaltens unter den Mitgliedern steigt mit den Unterschieden in ihren Situationen. Mit Hilfe dieser Teilnehmer erkundet ASO den Lösungsraum und versucht zu vermeiden, in lokale Optimalitätsfallen zu tappen. Der Schöpfer von ASO versucht also, die Idee zu vermitteln, dass die Untersuchung und Anwendung von Prinzipien, die auf dem anomalen Verhalten von Gemeinschaften basieren, zur Entwicklung effizienter Algorithmen führen kann, die in der Lage sind, komplexe Optimierungsprobleme zu lösen. Wir werden einen einheitlichen Rahmen für ASO betrachten, der sowohl für kontinuierliche als auch für diskrete Probleme verwendet werden kann.
2. Implementierung des Algorithmus
Bevor wir den Code des Algorithmus schreiben, müssen wir verstehen, wie er aufgebaut ist und welche grundlegenden Mechanismen der Autor in ihn eingebaut hat. Der ASO-Algorithmus ist eine Optimierungsmethode, die die Vorteile des Partikelschwarm-Optimierungsalgorithmus (PSO) mit neuen, für anarchisches Sozialverhalten charakteristischen Mechanismen kombiniert. Das Hauptmerkmal des Algorithmus ist seine Anpassungsfähigkeit und die Fähigkeit, zwischen verschiedenen Bewegungsstrategien zu balancieren.
Beginnen wir mit einer detaillierten Beschreibung des ASO-Algorithmus:
1. Initialisierung:
- Eine Population (popSize) wird aus Mitgliedern der Gesellschaft gebildet.
- Jedes Mitglied wird auf eine zufällige Position im Suchraum initialisiert.
- Jedes Mitglied behält seine persönliche Bestleistung und seine bisherigen Platzierungen.
2. Grundlegende Optimierungsschleife:
Bei jeder Iteration führt der Algorithmus die folgenden Schritte für jedes Mitglied der Gesellschaft durch:
a) Berechnung der Indizes:
- Fickleness Index (FI) — der Index spiegelt die Instabilität eines Mitglieds der Gesellschaft wider und misst seine Unzufriedenheit im Vergleich zu anderen Personen.
- External Irregularity Index (EI) — der Index bewertet die Vielfalt der Positionen in der Gesellschaft und zeigt die Abweichung von der global besten Lösung.
- Internal Irregularity Index (II) — der Index bewertet die Veränderungen der individuellen Position während der Iteration und spiegelt die Abweichung von der persönlich besten Lösung wider.
b) Auswahl der Bewegungspolitik:
Auf der Grundlage eines Vergleichs der Indizes FI, EI und II wird eine Bewegungspolitik ausgewählt:
- Current Movement Policy (CurrentMP) verwendet die PSO-Gleichung mit Trägheits- und Beschleunigungsverhältnissen.
- Bei der Society Movement Policy (SocietyMP) wird ein Crossover mit einem zufällig ausgewählten Mitglied der Gesellschaft durchgeführt.
- Die Past-Movement-Policy (PastMP) verwendet Informationen über die frühere Position der Person.
c) Anarchisches Verhalten: Die Position des Individuums kann mit einer Wahrscheinlichkeit der Anarchie vollständig randomisiert werden.
d) Aktualisierung der Position: Die neue Position wird anhand der Suchraumbeschränkungen überprüft.
e) Aktualisierung der Spitzenpositionen:
- Die persönlich beste Position pBest wird aktualisiert, wenn die aktuelle Position besser ist.
- Die globale beste Position gBest wird aktualisiert, wenn eine neue bessere Lösung gefunden wird.
3. Anpassen der Parameter:
- Die Wahrscheinlichkeit anarchyProb für anarchistisches Verhalten nimmt allmählich ab.
- Der Parameter alpha für die Berechnung von FI steigt allmählich an.
- Das Trägheitsgewicht omega nimmt allmählich ab.
4. Parameter des Algorithmus:
- popSize — Größe der Population.
- omega, lambda1, lambda2 — Parameter zur Berechnung der Geschwindigkeit in CurrentMP (wie in PSO).
- anarchyProb — Wahrscheinlichkeit für anarchisches Verhalten.
- alpha, theta, delta — Parameter für die entsprechende Berechnung der Indizes FI, EI und II.
Der Algorithmus ist recht komplex. Ich werde versuchen, den Funktionsmechanismus in einer sehr klaren und strukturierten Weise zu beschreiben, um das Verständnis zu erleichtern. Der nächste Schritt ist die Analyse der im Algorithmus verwendeten Gleichungen.
Die Grundgleichung des ASO-Algorithmus wurde vom PSO-Algorithmus übernommen. Er führt die Berechnung der Geschwindigkeitsaktualisierung durch: V_i (k+1) = ω * V_i (k) + λ1 * r1 * (P_i (k) - X_i (k)) + λ2 * r2 * (G (k) - X_i (k)), wobei:
- V_i (k) — i Partikelgeschwindigkeit in k Iterationen.
- X_i (k) — i Partikelposition in k Iterationen.
- P_i (k) — beste Position, die das Partikel i vor k Iterationen gefunden hat.
- G (k) — global die beste Position, die von allen Partikeln vor k Iterationen gefunden wurde.
- ω — Trägheitsverhältnis.
- λ1, λ2 — Beschleunigungsverhältnisse.
- r1, r2 — Zufallszahlen aus dem Intervall (0, 1).
Der Autor weist darauf hin, dass die PSO-Gleichung ein Spezialfall der allgemeinen ASO-Struktur ist, wenn die entsprechenden Bewegungsstrategien und Kombinationsregeln definiert sind. In der ursprünglichen Fassung wurde die vorherige Geschwindigkeit des Agenten in die Berechnungen einbezogen. Ich änderte den Ansatz, indem ich nur den aktuellen Geschwindigkeitswert beließ, was zu einer spürbaren Verbesserung der Leistung des Algorithmus führte.
Die Gleichungen (1) und (2) definieren den Fickleness Index und FI für i Community-Mitglieder bei k Iterationen im ASO-Algorithmus. Diese Gleichungen helfen dabei, den Grad der Unzufriedenheit einer Person mit ihrer aktuellen Position im Vergleich zu anderen Positionen zu bewerten. Schauen wir sie uns im Detail an:
1. Gleichung (1) zur Berechnung des Fickleness Index: (kFI)i = α - α (f (Xi (k)) - f (Pi (k))) / (f (Xi (k*)) - f (Xi (k))).
Diese Gleichung zeigt, wie stark die aktuelle Position eines Individuums i von seiner besten persönlichen Position und seiner besten globalen Position, gewichtet mit dem Parameter α (alpha), abweicht.
2. Gleichung (2) zur Berechnung des Index der individuellen Unbeständigkeit von i bei k Iterationen: (kFI)i = α - α (f (Xi (k)) - f (Pi (k))) / (f (G (k)) - f (Xi (k))).
Diese Gleichung ähnelt der ersten, wird aber für andere Zwecke verwendet, wobei die aktuelle Position, die beste persönliche Position und die beste globale Position verglichen werden.
Beide Gleichungen dienen dazu, den Grad der Unzufriedenheit der Mitglieder der Gesellschaft zu bewerten, was es ihnen ermöglicht, fundiertere Entscheidungen darüber zu treffen, wie sie ihre Positionen auf der Suche nach einer optimalen Lösung ändern können.
Die Gleichungen (3) und (4) beschreiben den Index der externen Unregelmäßigkeit und den Index der internen Unregelmäßigkeit für die Mitglieder der Gesellschaft in dem Algorithmus.
3. Gleichung (3) — externer Unregelmäßigkeitsindex des Individuums i bei k Iterationen: (kEI)i = exp (-(θi) (f (G) - f (Xi (k)))).
4. Gleichung (4) — interner Unregelmäßigkeitsindex des Individuums i bei k Iterationen: (kEI)i = 1 - exp (-δi (kD)).
wo;
- (kFI)i — Fickleness Index des Individuums i bei k Iterationen.
- α — nichtnegatives „alpha“ im Intervall [0,1].
- f (Xi (k)) — Wert der Zielfunktion für i Individuum bei k Iterationen.
- f (Pi (k)) — Wert der Zielfunktion für die beste Position, die das Individuum i zuvor besucht hat.
- f (Xi (k)) — Wert der Zielfunktion für die Position des besten Individuums bei k Iterationen.
- f (G (k)) — Wert der Zielfunktion für die global beste Position, die von der Gesellschaft vor der Iteration k besucht wurde.
- (kEI)i — Index der externen Unregelmäßigkeit des Individuums i bei k Iterationen.
- θi — positive Theta-Zahl.
- kD — geeignetes Maß für die Vielfalt in der Gesellschaft, z. B. das Verhältnis der Variation der Zielfunktionswerte der Individuen.
- δi — positives delta.
Diese Gleichungen zeigen, dass, wenn die Vielfalt in einer Gesellschaft zunimmt (d. h. wenn die Individuen mehr unterschiedliche Werte der Zielfunktion haben), die Wahrscheinlichkeit steigt, dass sich die Individuen irregulär verhalten. Die Gleichungen werden verwendet, um die Variabilität des Verhaltens der Gesellschaftsmitglieder im ASO-Algorithmus zu bewerten, was es ihnen ermöglicht, bei der Suche nach der optimalen Lösung vielfältigere und anpassungsfähigere Entscheidungen zu treffen.
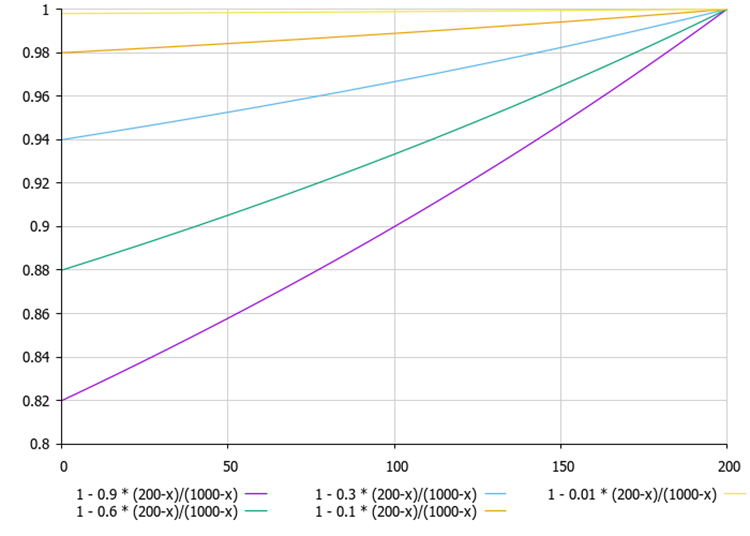
Abbildung 1. Wenn die aktuell beste Lösung des Agenten (200) viel kleiner ist als die beste Lösung für die Agentenpopulation (1000), dann ändert sich die Linie im Diagramm fast linear
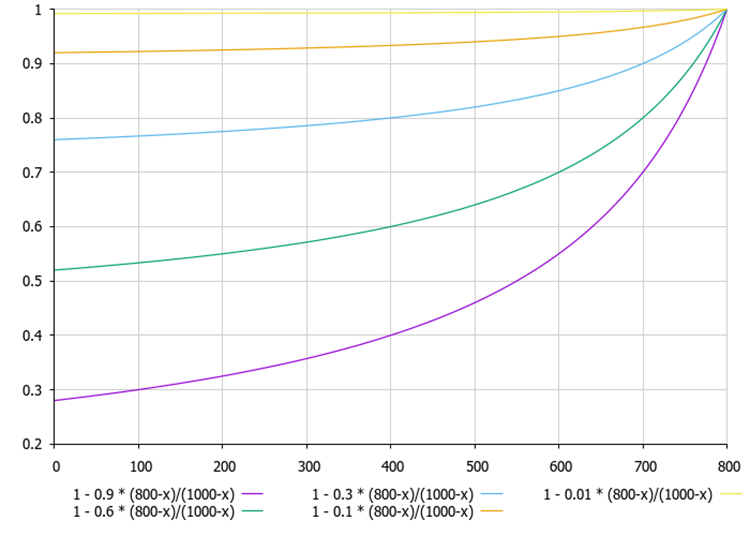
Abbildung 2. Je kleiner der Unterschied zwischen der aktuell besten Lösung des Agenten und der Population der Agenten (1000) ist, desto nicht-linearer ist die Linie im Diagramm
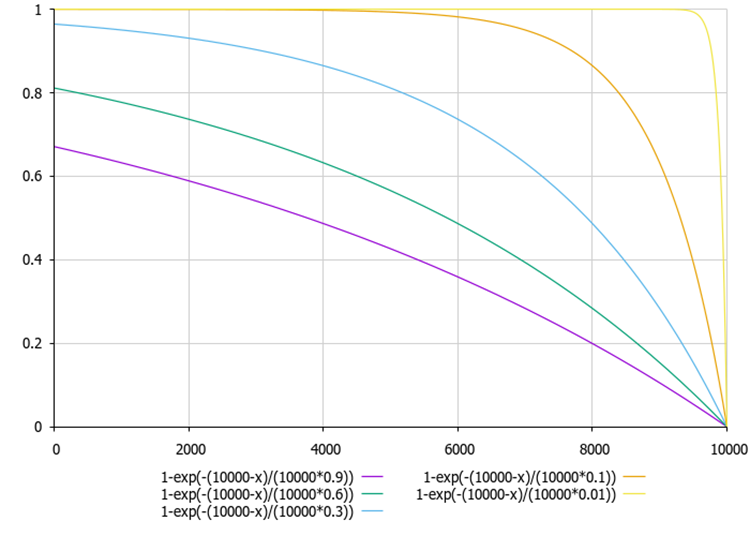
Abbildung 3. Das Diagramm der Abhängigkeit der externen Indizes und internen Unregelmäßigkeiten in Abhängigkeit von den Verhältnissen „theta“ und „delta“ (am Beispiel von Werten zwischen 0,01 und 0,9)
So können die Mitglieder einer Gesellschaft Informationen über andere Mitglieder nutzen, um Entscheidungen über ihre Bewegungen zu treffen, und auch darüber, wie ihr Verhalten je nach dem Grad der Vielfalt in der Gesellschaft variieren kann.
Jetzt wissen wir ein wenig mehr über den ASO-Algorithmus und können auf der Grundlage der gewonnenen Theorie zum praktischen Teil übergehen. Wir werden einen Pseudocode des Algorithmus für seine Implementierung in Code zusammenstellen. Pseudocode des ASO-Algorithmus:
Initialisierung:
1. Parameter einstellen: popSize, omega, lambda1, lambda2, anarchyProb, alpha, theta, delta, rangeMin [], rangeMax [], rangeStep []
2. Erstellen einer Population von popSize-Mitgliedern: für jedes i-Mitglied von 0 bis popSize-1: für jede c-Koordinate von 0 bis coords-1:
Position [i].[c] = Zufallszahl zwischen rangeMin [c] und rangeMax [c]
pBest [i].[c] = Position [i].[c]
prevPosition [i].[c] = Position [i].[c]
pBestFitness [i] = -Unendlichkeit
3. gBest = beste Position der Ausgangspopulation festlegen
4. Set gBestFitness = gBest Fitness
Hauptschleife:
5. Bis zum Erreichen des Abbruchkriteriums: für jedes i-Mitglied von 0 bis popSize-1:
5.1 Berechnung der Indizes
FI = BerechneFI (i)
EI = BerechneEI (i)
II = BerechneII (i)
5.2 Auswahl der Bewegungspolitik
Wenn FI > EI und FI > II: newPosition = CurrentMP (i)
Ansonsten, wenn EI > FI und EI > II: newPosition = SocietyMP (i)
Andernfalls: newPosition = PastMP (i)
5.3 Anarchisches Verhalten erzeugen
Wenn Zufallszahl < anarchyProb: für jede c-Koordinate von 0 bis coords-1:
newPosition [c] = Zufallszahl zwischen rangeMin [c] und rangeMax [c]
5.4 Aktualisierung der Position für jede c-Koordinate von 0 bis coords-1:
prevPosition [i].[c] = Position [i].[c]
position [i].[c] = limit (newPosition [c], rangeMin [c], rangeMax [c], rangeStep [c])
5.5 Neue „Fitness“ bewerten Position = rate_fitness (Position [i])
5.6 Persönliche „Bestleistung“ aktualisieren, wenn „Fitness“ > pBestFitness [i]:
pBestFitness [i] = Fitness
pBest [i] = Position [i]
5.7 Aktualisierung der globalen „besten“, wenn „Fitness“ > gBestFitness:
gBestFitness = Fitness
gBest = Position [i]
5.8 Den Parameter AdaptParameters() anpassen.
5.9 Funktion CalculateFI (i): return 1 - alpha * (fitness [i] - pBestFitness [i]) / (gBestFitness - fitness [i])
5.10 Funktion CalculateEI (i): return 1 - exp(-(gBestFitness - fitness [i]) / theta)
5.11 Funktion CalculateII (i): return 1 - exp(-(pBestFitness [i] - fitness [i]) / delta)
5.12 Funktion CurrentMP (i): für jede Koordinate c von 0 bis coords-1:
r1 = Zufallszahl zwischen 0 und 1
r2 = Zufallszahl zwischen 0 und 1
velocity = omega * (position [i].[c] - pBest [i].[c]) + lambda1 * r1 * (pBest [i].[c] - position [i].[c]) + lambda2 * r2 * (gBest [c] - position [i].[c])
newPosition [c] = position [i].[c] + velocity
return newPosition
5.13 Funktion SocietyMP (i): j = zufälliges Mitglied der Grundgesamtheit, nicht gleich i, für jede Koordinate c von 0 bis coords - 1:
Wenn die Zufallszahl < 0,5 ist:
neuePosition [c] = Position [i].[c]
Sonst: newPosition [c] = Position [j].[c]
return newPosition
5.14 Funktion PastMP (i): für jede Koordinate c von 0 bis coords - 1:
Wenn die Zufallszahl < 0,5 ist:
neuePosition [c] = Position [i].[c]
Sonst: newPosition [c] = prevPosition [i].[c]
return newPosition
Da wir nun den Pseudocode haben, können wir mit dem Schreiben des darauf basierenden Algorithmuscodes beginnen. Beschreiben wir nun die Struktur S_ASO_Member, die zur Darstellung eines Teilnehmers (Agenten) im Algorithmus verwendet wird.
1. Die Felder der Struktur:
- pPrev [] — das Array der vorherigen Positionen der Teilnehmer.
- pBest [] — das Array mit den besten bekannten Positionen der Teilnehmer (persönliche Bestwerte).
- pBestFitness — die Variable speichert den Fitnesswert (Qualität) der besten bekannten Position.
2. Die Methode Init initialisiert die Arrays pPrev und pBest und legt ihre Größe entsprechend der Anzahl der Koordinaten (oder der Dimensionalität des Suchraums) fest, die als Parameter coords übergeben wird. ArrayResize(pBest, coords) und ArrayResize(pPrev, coords) — diese Aufrufe passen die Größe von Arrays an den Wert von coords an. pBestFitness = -DBL_MAX — setzt den Anfangswert für die beste Positionsfitness, um sicherzustellen, dass jeder gefundene Wert besser ist als dieser.
Die Struktur S_ASO_Member dient dazu, Informationen über jeden Teilnehmer am Optimierungsalgorithmus zu speichern. Es ermöglicht uns, sowohl die aktuelle als auch die beste Position des Teilnehmers sowie seine Fitness zu verfolgen.
//—————————————————————————————————————————————————————————————————————————————— struct S_ASO_Member { double pPrev []; // Previous position double pBest []; // Personal best position double pBestFitness; // Personal best fitness void Init (int coords) { ArrayResize (pBest, coords); ArrayResize (pPrev, coords); pBestFitness = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Definition der Klasse C_AO_ASO, die von der Basisklasse C_AO abgeleitet wurde. Schauen wir uns das genauer an:
1. Die Parameter sind:
- popSize — Populationsgröße (Anzahl der Mitglieder der Gesellschaft).
- anarchyProb — Möglichkeit eines anarchischen Verhaltens, einige Teilnehmer können unabhängig von anderen handeln.
- omega, lambda1, lambda2 — Parameter für Trägheit und Beschleunigung, die zur Kontrolle des Verhaltens der Teilnehmer verwendet werden.
- alpha, theta, delta — Parameter, die zur Berechnung der Indikatoren (FI, EI, II) verwendet werden.
2. params — Array von Parametern, wobei jedes Element einen Namen und einen Wert enthält.
3. SetParams () — die Methode aktualisiert die Parameterwerte aus dem Array params, was die Änderung der Parameter des Algorithmus nach seiner Initialisierung ermöglicht.
4. Init () — die Methode initialisiert den Algorithmus mit den angegebenen Bereichen und Schritten. Sie akzeptiert die Arrays rangeMinP, rangeMaxP und rangeStepP sowie die Anzahl der Epochen epochsP.
5. Moving() und Revision () — Methoden implementieren die grundlegende Logik der Bewegung von Teilnehmern und ihrer Revision (Aktualisierung) in der Optimierung.
6. Felder der Klasse:
S_ASO_Member member [] — Array der Gesellschaftsmitglieder speichert Informationen über jeden Teilnehmer am Algorithmus.
7. Private Methoden:
- CalculateFI — die Methode zur Berechnung des FI-Wertes (Fitnessindikator) für einen bestimmten Teilnehmer.
- CalculateEI — die Methode zur Berechnung des EI (Explorationsindikators).
- CalculateII — die Methode zur Berechnung des Wertes von II (Trägheitsindikator).
- CurrentMP, SocietyMP, PastMP — die Methoden implementieren die Logik der Interaktion von Teilnehmern mit ihren aktuellen, sozialen und vergangenen Positionen.
Die Klasse C_AO_ASO ist eine Implementierung des Konzepts einer „anarchischen Gesellschaft“, in der die Teilnehmer sowohl gemeinsam als auch unabhängig voneinander handeln können. Sie enthält Parameter, die das Verhalten der Teilnehmer steuern, sowie Methoden für ihre Initialisierung und Aktualisierung.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ASO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ASO () { } C_AO_ASO () { ao_name = "ASO"; ao_desc = "Anarchy Society Optimization"; ao_link = "https://www.mql5.com/en/articles/15511"; popSize = 50; // Population size anarchyProb = 0.1; // Probability of anarchic behavior omega = 0.7; // Inertia weight lambda1 = 1.5; // Acceleration coefficient for P-best lambda2 = 1.5; // Acceleration coefficient for G-best alpha = 0.5; // Parameter for FI calculation theta = 1.0; // Parameter for EI calculation delta = 1.0; // Parameter for II calculation ArrayResize (params, 8); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "anarchyProb"; params [1].val = anarchyProb; params [2].name = "omega"; params [2].val = omega; params [3].name = "lambda1"; params [3].val = lambda1; params [4].name = "lambda2"; params [4].val = lambda2; params [5].name = "alpha"; params [5].val = alpha; params [6].name = "theta"; params [6].val = theta; params [7].name = "delta"; params [7].val = delta; } void SetParams () { popSize = (int)params [0].val; anarchyProb = params [1].val; omega = params [2].val; lambda1 = params [3].val; lambda2 = params [4].val; alpha = params [5].val; theta = params [6].val; delta = params [7].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //---------------------------------------------------------------------------- double anarchyProb; // Probability of anarchic behavior double omega; // Inertia weight double lambda1; // Acceleration coefficient for P-best double lambda2; // Acceleration coefficient for G-best double alpha; // Parameter for FI calculation double theta; // Parameter for EI calculation double delta; // Parameter for II calculation S_ASO_Member member []; // Vector of society members private: //------------------------------------------------------------------- double CalculateFI (int memberIndex); double CalculateEI (int memberIndex); double CalculateII (int memberIndex); void CurrentMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd); void SocietyMP (S_AO_Agent &agent, int coordInd); void PastMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd); }; //——————————————————————————————————————————————————————————————————————————————
Schauen wir uns die folgende Init-Methode der Klasse C_AO_ASO an. Die Logik der Methode:
- StandardInit — Methode wird aufgerufen, um eine Standardinitialisierung mit den übergebenen Bereichen durchzuführen. Wenn diese Methode false zurückgibt, ist ein Fehler aufgetreten.
- ArrayResize — die Methode ändert die Größe des Mitglieder-Arrays auf popSize, das die Anzahl der Teilnehmer (Mitglieder der Gesellschaft) im Algorithmus bestimmt.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ASO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (member, popSize); for (int i = 0; i < popSize; i++) member [i].Init (coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Schauen wir uns den Code der Methode Moving der Klasse C_AO_ASO an. Struktur und Logik der Methode:
1. Überprüfung des ersten Anrufs:
- Wenn revision false ist, initialisiert die Methode das Array a mit Zufallswerten innerhalb der angegebenen Bereiche rangeMin und rangeMax.
- Für jede c-Koordinate eines jeden Mitglieds der i-Population wird die Methode u.RNDfromCI aufgerufen. Es wird ein Zufallswert generiert, und dieser Wert wird dann mit u.SeInDiSp normalisiert.
- Die Werte werden in member [i].pPrev [c] zur weiteren Verwendung gespeichert.
- Danach wird revision auf true gesetzt, und die Methode wird ausgeführt.
2. Grundlegende Bewegungslogik:
- Für jedes Populationsmitglied i werden drei Indizes berechnet: fi, ei und ii. Dies sind Metriken, die den Zustand eines Populationsmitglieds charakterisieren.
- Für jede c-Koordinate wird Folgendes ausgeführt:
- Der aktuelle Wert wird in Mitglied [i].pPrev [c] gespeichert.
- Die Zfallszahl rnd wird mit u.RNDprobab () erzeugt.
- Wenn die Zufallszahl kleiner ist als anarchyProb (was bedeutet, dass die Wahrscheinlichkeit der Manifestation von Anarchie im Verhalten erfüllt ist), wird die c-Koordinate für das i-Mitglied zufällig aus dem Bereich initialisiert.
- Ansonsten werden je nach den Werten fi, ei und ii die Methoden CurrentMP, SocietyMP und PastMP aufgerufen.
- Nach allen Änderungen wird der Wert der einzelnen c-Koordinaten mit u.SeInDiSp angepasst.
Die Moving-Methode implementiert die Logik des Verschiebens von Mitgliedern der Population im Lösungsraum auf der Grundlage ihrer aktuellen Zustände und Metriken.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); member [i].pPrev [c] = a [i].c [c]; } } revision = true; return; } //---------------------------------------------------------------------------- double fi = 0.0; //fickleness index double ei = 0.0; //external irregularity index double ii = 0.0; //internal irregularity index double rnd = 0.0; for (int i = 0; i < popSize; i++) { fi = CalculateFI (i); ei = CalculateEI (i); ii = CalculateII (i); for (int c = 0; c < coords; c++) { member [i].pPrev [c] = a [i].c [c]; rnd = u.RNDprobab (); if (u.RNDprobab () < anarchyProb) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); else { if (rnd > fi) CurrentMP (a [i], member [i], c); else { if (rnd < ei) SocietyMP (a [i], c); else { if (rnd < ii) PastMP (a [i], member [i], c); } } } } for (int c = 0; c < coords; c++) { a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Gehen wir von der Methode Moving zur Revision über. Allgemeine Struktur und Logik:
1. Die Variable ind wird mit dem Wert -1 initialisiert. Er wird verwendet, um den Index des Populationsmitglieds zu speichern, das den besten Wert der Funktion f hat.
2. Die Methode durchläuft alle Mitglieder der Grundgesamtheit von 0 bis popSize - 1.
3. Ermittlung des besten Funktionswerts: Für jedes Mitglied der Grundgesamtheit wird a [i] daraufhin überprüft, ob sein f-Funktionswert durch den aktuell besten Wert von fB überschritten wird. Ist dies der Fall, wird fB durch ein [i].f aktualisiert, wobei der Index ind auf i gesetzt wird.
4. Aktualisierung des persönlichen Bestwertes: Die Methode prüft auch, ob der Wert der Funktion a [i].f den aktuellen Bestwert für dieses Bevölkerungsmitglied Mitglieds [i].pBestFitness überschreitet. Wenn ja, wird der Wert aktualisiert und die aktuellen Koordinaten a[i].c werden mit der Funktion ArrayCopy in member[i].pBest kopiert.
5. Kopieren der besten Lösung: Wenn nach Beendigung der Schleife der Index ind (d.h. mindestens ein Mitglied der Grundgesamtheit hatte einen Funktionswert größer als fB) gefunden wird, werden die Koordinaten dieses Mitglieds der Grundgesamtheit mit ArrayCopy nach cB kopiert.
Die Revisionsmethode ist für die Aktualisierung der besten in der Grundgesamtheit gefundenen Lösung sowie für die Aktualisierung der persönlichen Bestwerte für jedes Mitglied der Grundgesamtheit zuständig. Mit Hilfe einfacher Logik vergleicht es Funktionswerte, um zu ermitteln, welche Lösungen die besten sind, und speichert sie zur späteren Verwendung.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } if (a [i].f > member [i].pBestFitness) { member [i].pBestFitness = a [i].f; ArrayCopy (member [i].pBest, a [i].c, 0, 0, WHOLE_ARRAY); } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Als Nächstes die Methode CalculateFI der Klasse C_AO_ASO. Beschreibung der Methode:
1. Die Methode nimmt den Index des Populationsmitglieds memberIndex, für das die Fitness berechnet werden soll.
2. Fitnesswerte erhalten:
- currentFitness — holt den aktuellen Fitnesswert eines Populationsmitglieds aus dem Array a mit dem Index memberIndex.
- personalBestFitness — holt den persönlichen besten Fitnesswert dieses Mitglieds aus dem Mitglieder-Array.
- globalBestFitness — liefert den besten globalen Fitnesswert, der in der Variablen fB gespeichert ist.
3. Berechnung des Fitnessindex (FI) — die Methode gibt den anhand der Gleichung berechneten Wert zurück.
Die Gleichung normalisiert die Differenz zwischen persönlicher und aktueller Fitness, indem sie durch die Differenz zwischen globaler und aktueller Fitness dividiert wird. Die CalculateFI-Methode berechnet einen Fitnessindex für ein Mitglied der Population, der zur Bewertung seiner Qualität im Vergleich zu seinen persönlichen und globalen Bestwerten herangezogen wird.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateFI (int memberIndex) { double currentFitness = a [memberIndex].f; double personalBestFitness = member [memberIndex].pBestFitness; double globalBestFitness = fB; //1 - 0.9 * (800-x)/(1000-x) return 1 - alpha * (personalBestFitness - currentFitness) / (globalBestFitness - currentFitness); } //——————————————————————————————————————————————————————————————————————————————
Es folgt die Methode CalculateEI der Klasse C_AO_ASO. Die Methode macht fast dasselbe wie die vorherige, verwendet aber die beste globale und persönliche aktuelle Fitness, um sie zu berechnen.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateEI (int memberIndex) { double currentFitness = a [memberIndex].f; double globalBestFitness = fB; //1-exp(-(10000-x)/(10000*0.9)) return 1 - MathExp (-(globalBestFitness - currentFitness) / (globalBestFitness * theta)); } //——————————————————————————————————————————————————————————————————————————————
Die CalculateII-Methode der Klasse C_AO_ASO ist der vorherigen völlig ähnlich, verwendet aber die beste und die aktuelle eigene Fitness.
Die Exponentialfunktion hilft dabei, Veränderungen zu glätten und sorgt für einen sanften Übergang zwischen den Werten. Die Methode CalculateII berechnet einen Verbesserungsindex für ein Mitglied der Population, der berücksichtigt, wie gut der aktuelle Fitnesszustand im Vergleich zu den persönlichen Leistungen ist.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateII (int memberIndex) { double currentFitness = a [memberIndex].f; double personalBestFitness = member [memberIndex].pBestFitness; //1-exp(-(10000-x)/(10000*0.9)) return 1 - MathExp (-(personalBestFitness - currentFitness) / (personalBestFitness * delta)); } //——————————————————————————————————————————————————————————————————————————————
Kommen wir nun zur Methode CurrentMP der Klasse C_AO_ASO. Beschreibung:
1. Generierung von Zufallszahlen:
- r1 = u.RNDprobab () — erzeugt eine Zufallszahl r1 im Bereich [0, 1].
- r2 = u.RNDprobab () — erzeugt eine Zufallszahl r2 im Bereich [0, 1].
2. Berechnung der velocity — die Gleichung der Geschwindigkeit enthält drei Komponenten:
- omega * (agent.c [coordInd] - memb.pBest [coordInd]) — Trägheitskomponente, die Bewegung des Agenten unter Berücksichtigung seiner vorherigen Position.
- lambda1 * r1 * (memb.pBest[coordInd] - agent.c[coordInd]) — lenkt den Agenten unter Berücksichtigung seiner persönlichen besten Position
- lambda2 * r2 * (cB[coordInd] - agent.c[coordInd]) — lenkt den Agenten unter Berücksichtigung der besten Position der Population.
3. Aktualisierung der Position des Agenten durch Addition der Geschwindigkeit zum aktuellen Koordinatenwert.
Mit der CurrentMP-Methode wird die Position des Agenten im Raum auf der Grundlage seiner aktuellen Position, seiner persönlichen besten Position und der besten Position der Population aktualisiert.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::CurrentMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd) { double r1 = u.RNDprobab (); double r2 = u.RNDprobab (); double velocity = omega * (agent.c [coordInd] - memb.pBest [coordInd]) + lambda1 * r1 * (memb.pBest [coordInd] - agent.c [coordInd]) + lambda2 * r2 * (cB [coordInd] - agent.c [coordInd]); agent.c [coordInd] += velocity; } //——————————————————————————————————————————————————————————————————————————————
Die Methode SocietyMP der Klasse C_AO_ASO aktualisiert die Koordinaten des Agenten auf der Grundlage einer zufälligen Auswahl zwischen Gruppen- und persönlichen Informationen. Dies ermöglicht es dem Agenten, sich sowohl an den Zustand der gesamten Population als auch an den eines einzelnen Agenten anzupassen.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::SocietyMP (S_AO_Agent &agent, int coordInd) { int otherMember = u.RNDminusOne (popSize); agent.c [coordInd] = u.RNDprobab () < 0.5 ? cB [coordInd] : member [otherMember].pBest [coordInd]; } //——————————————————————————————————————————————————————————————————————————————
Die Methode PastMP der Klasse C_AO_ASO aktualisiert die Koordinaten des Agenten auf der Grundlage einer zufälligen Auswahl zwischen dem aktuell besten Zustand des Populationsmitglieds und seinem vorherigen Zustand. Dies ermöglicht es dem Agenten, sowohl die aktuellen Leistungen eines Populationsmitglieds als auch seine früheren Ergebnisse zu berücksichtigen. Dieser Ansatz verbessert die kombinatorischen Eigenschaften des Algorithmus.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::PastMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd) { agent.c [coordInd] = u.RNDprobab () < 0.5 ? memb.pBest [coordInd] : memb.pPrev [coordInd]; } //——————————————————————————————————————————————————————————————————————————————
3. Testergebnisse
Ergebnisse des ASO-Prüfstands:
ASO|Anarchy Society Optimization|50.0|0.01|0.7|1.5|1.5|0.5|0.1|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.8487202680440514
25 Hilly's; Func runs: 10000; result: 0.746458607174428
500 Hilly's; Func runs: 10000; result: 0.31465494017509904
=============================
5 Forest's; Func runs: 10000; result: 0.9614752193694915
25 Forest's; Func runs: 10000; result: 0.7915027321897546
500 Forest's; Func runs: 10000; result: 0.23802894131144553
=============================
5 Megacity's; Func runs: 10000; result: 0.5707692307692309
25 Megacity's; Func runs: 10000; result: 0.5406153846153848
500 Megacity's; Func runs: 10000; result: 0.16613846153846298
=============================
All score: 5.17836 (57.54%)
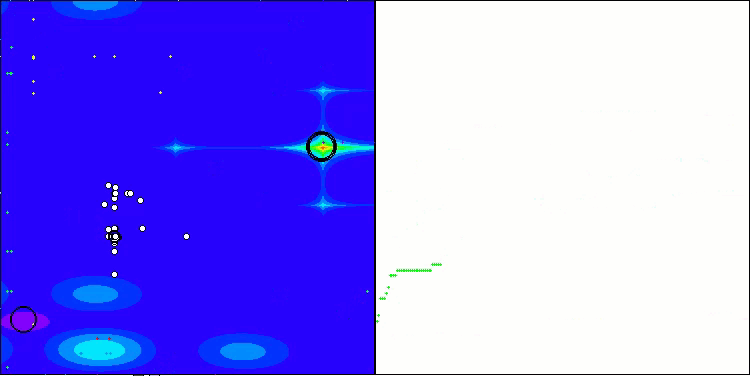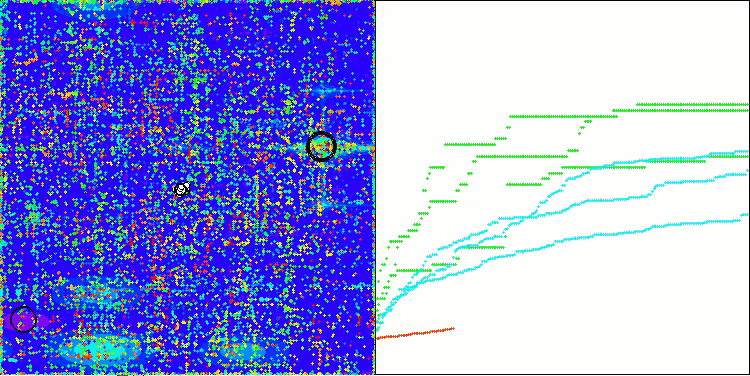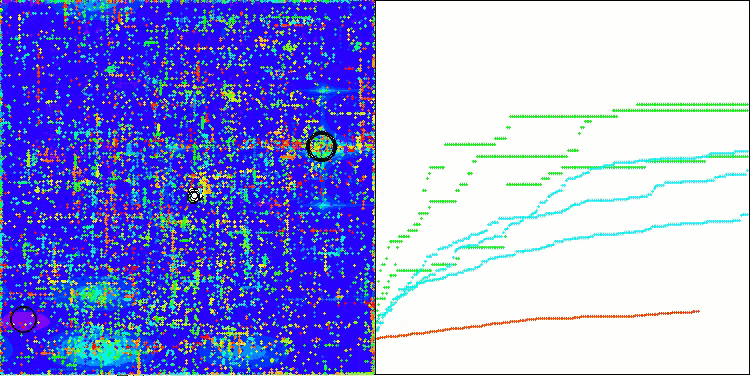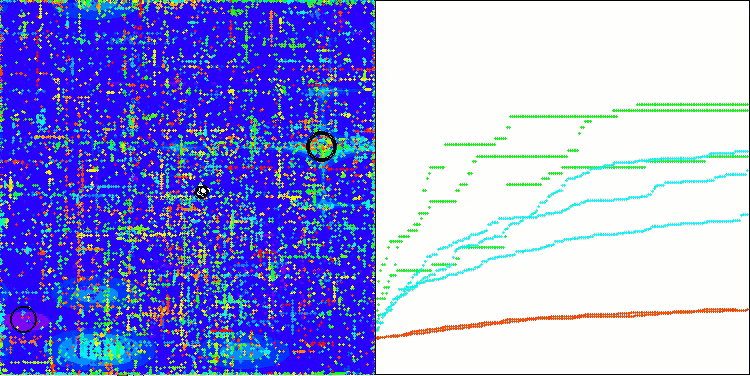
Wenn wir uns die Visualisierung der Algorithmusoperation ansehen, können wir einige Schlussfolgerungen ziehen: Es gibt eine Streuung der Ergebnisse. Der Algorithmus beweist jedoch gute Suchfähigkeiten bei der Arbeit mit großdimensionalen Funktionen, was auch durch seine Ergebnisse bestätigt wird.
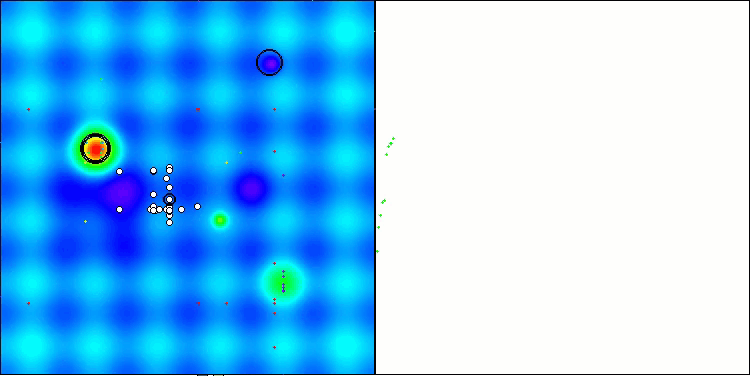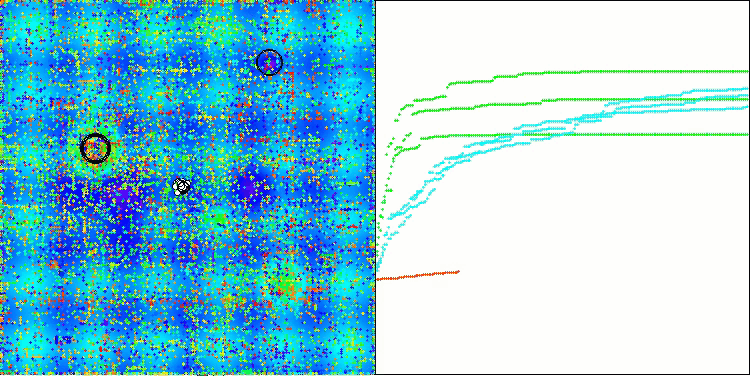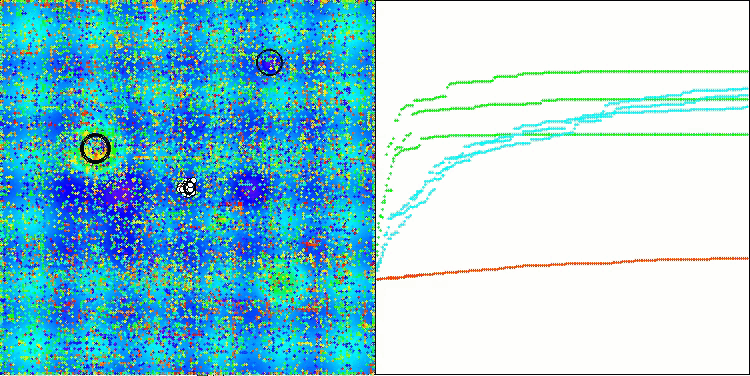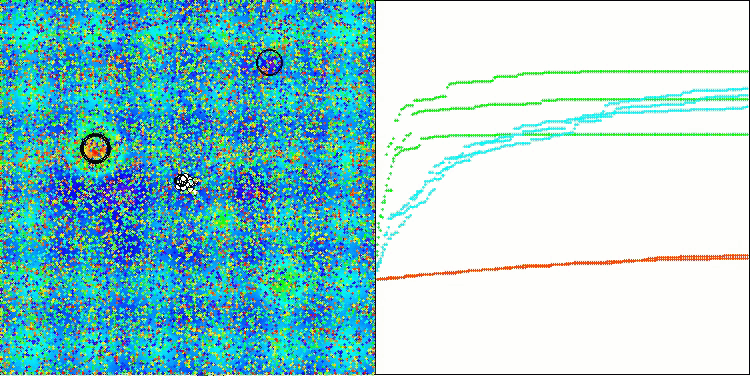
ASO mit der Testfunktion Hilly
ASO mit der Testfunktion Forest
ASO mit der Testfunktion Megacity
Bewertungstabelle der Algorithmen zur Populationsoptimierung: Der ASO-Algorithmus kam nach dem Test in die Top Ten und belegte in der Bewertungstabelle den 9.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Сode Lock Algorithmus | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 4 | CTA | Kometenschweif-Algorithmus | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 5 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 6 | ESG | Entwicklung der sozialen Gruppen | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 7 | SIA | Simuliertes isotropes Abkühlen | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 8 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 9 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 10 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 11 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 12 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 13 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 14 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 15 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 16 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 17 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 18 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 19 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 20 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 21 | BFO-GA | Optimierung der bakteriellen Futtersuche - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 22 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 23 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 24 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 25 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 26 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 27 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 28 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 29 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 30 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 31 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 32 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 33 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 34 | BA | Fledermaus-Algorithmus | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 35 | SA | simuliertes Abkühlen | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 36 | IWDm | intelligente Wassertropfen M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 37 | PSO | Partikelschwarmoptimierung | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 38 | Gebote | Boids-Algorithmus | 0.43340 | 0.30581 | 0.25425 | 0.99346 | 0.35718 | 0.20160 | 0.15708 | 0.71586 | 0.27846 | 0.14277 | 0.09834 | 0.51957 | 2.229 | 24.77 |
| 39 | MA | Affen-Algorithmus | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 40 | SFL | schlurfender Froschsprung | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 41 | FSS | Fischschulsuche | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 42 | RND | zufällig | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
| 43 | GWO | Grauer-Wolf-Optimierung | 0.59169 | 0.36561 | 0.29595 | 1.25326 | 0.24499 | 0.09047 | 0.03612 | 0.37158 | 0.27667 | 0.08567 | 0.02170 | 0.38403 | 2.009 | 22.32 |
| 44 | CSS | Suche geladener Systeme | 0.44252 | 0.35454 | 0.35201 | 1.14907 | 0.24140 | 0.11345 | 0.06814 | 0.42299 | 0.18333 | 0.06300 | 0.02322 | 0.26955 | 1.842 | 20.46 |
| 45 | EM | elektromagnetismusähnlicher Algorithmus | 0.46250 | 0.34594 | 0.32285 | 1.13129 | 0.21245 | 0.09783 | 0.10057 | 0.41085 | 0.15667 | 0.06033 | 0.02712 | 0.24412 | 1.786 | 19.85 |
Zusammenfassung
Auf der Grundlage der Ergebnisse des Algorithmus für die Testfunktionen verschiedener Dimensionen können die folgenden Schlussfolgerungen gezogen werden: ASO zeigt im Vergleich zu seinen nächsten Nachbarn in der Tabelle durchschnittliche Ergebnisse bei der glatten Funktion „Hilly“, aber sehr gute Ergebnisse beim ‚spitzen‘ „Forest“ und insbesondere bei der diskreten Funktion „Megacity“. Die Gesamtpunktzahl beträgt 5,17836 (57,54 %). Der Algorithmus beweist gute Suchfähigkeiten, insbesondere bei der Arbeit mit großdimensionalen Funktionen. Mit anderen Worten: Sie ist gut skalierbar. Der Algorithmus kann für die Lösung diskreter Optimierungsprobleme empfohlen werden, was für Händler eine Priorität ist.
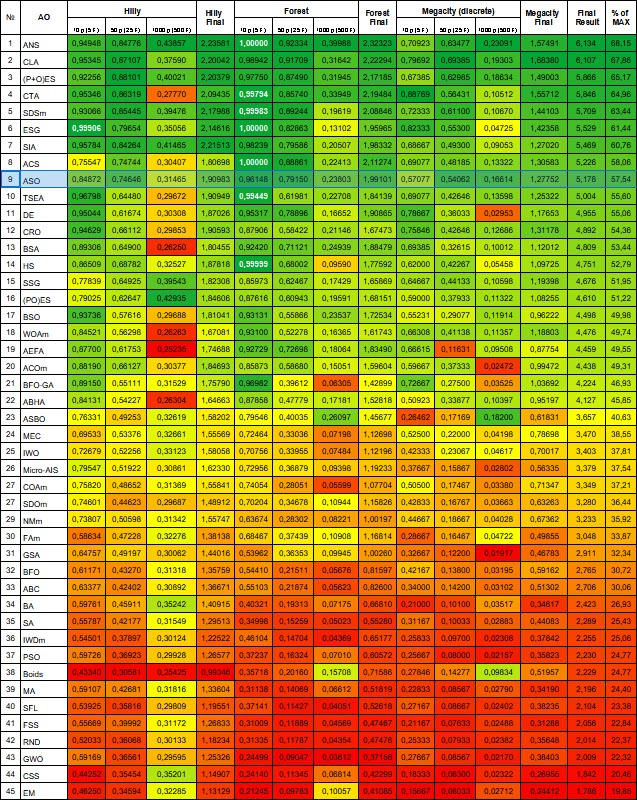
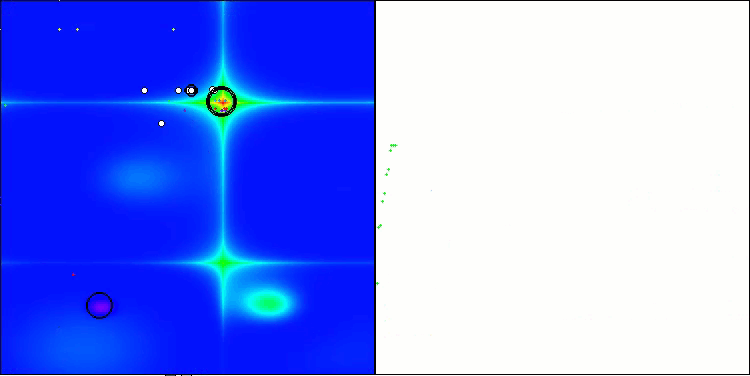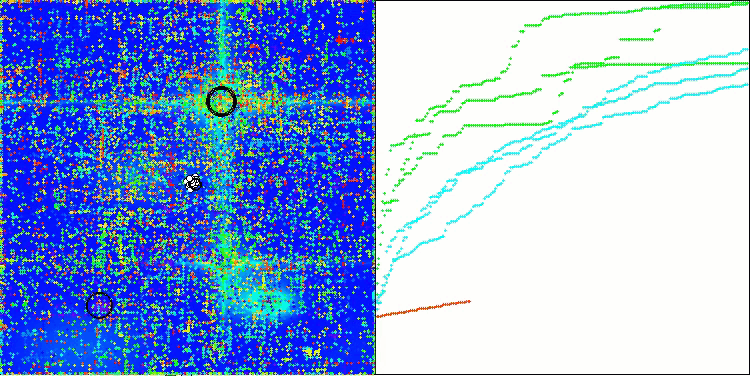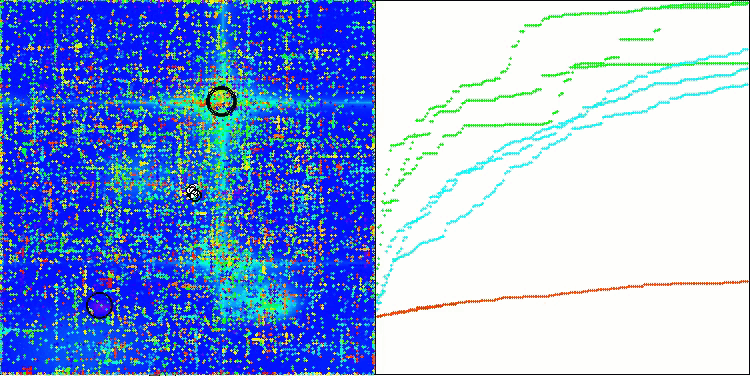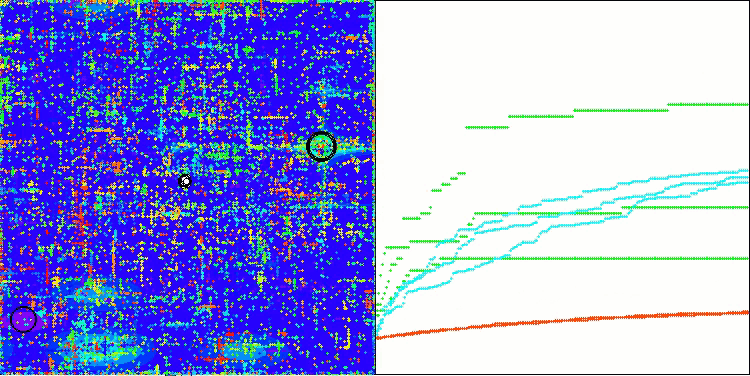
Abbildung 4. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben
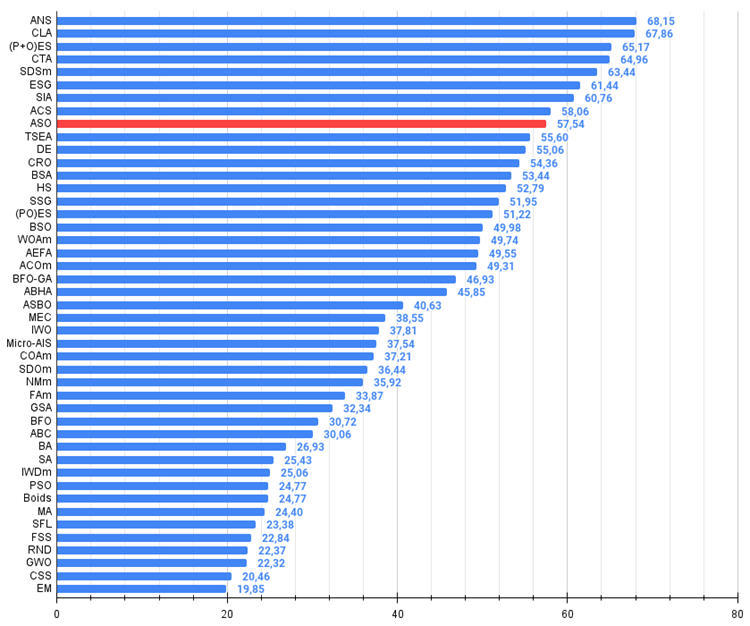
Abbildung 5. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Wertungstabelle)
Vor- und Nachteile des ASO-Algorithmus:
Vorteile:
- Gute Konvergenz bei verschiedenen Funktionen.
- Ausgezeichnete Ergebnisse bei diskreten Funktionen.
Nachteile
- Große Anzahl von Parametern (sehr schwierig zu konfigurieren).
- Streuung der Ergebnisse bei niedrigdimensionalen Funktionen.
- Komplexe Umsetzung.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Algorithmuscodes begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15511
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 William-Gann-Methoden (Teil II): Gann Square Indikator erstellen
William-Gann-Methoden (Teil II): Gann Square Indikator erstellen
 Methoden von William Gann (Teil I): Erstellen des Gann Angles-Indikators
Methoden von William Gann (Teil I): Erstellen des Gann Angles-Indikators
 Von der Grundstufe bis zur Mittelstufe: Operatoren
Von der Grundstufe bis zur Mittelstufe: Operatoren
 Neuronale Netze im Handel: Einspeisung globaler Informationen in unabhängige Kanäle (InjectTST)
Neuronale Netze im Handel: Einspeisung globaler Informationen in unabhängige Kanäle (InjectTST)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.