Algorithmen zur Optimierung mit Populationen: Der Wal-Optimierungsalgorithmus (WOA)
271
0
Inhalt
1. Einführung
2. Der Algorithmus
3. Testergebnisse
1. Einführung
Buckelwale sind majestätische Meeresriesen und Meister der Meere. Wenn Buckelwale ihren Jagdtanz beginnen, scheint die Zeit stillzustehen, und jede Bewegung ist von Anmut und Präzision geprägt. Die Meister des Blasennetzes erzeugen einen wässrigen Vorhang aus Luftblasen, um ihre Beute in der Mitte des Rings einzusperren und zu fangen. Diese einzigartige Fressmethode unterstreicht ihre Intelligenz und ihr strategisches Denken im Jagdprozess.
Die Synchronisierung ihrer Handlungen mit anderen Individuen, selbst mit unbekannten, zeugt von tiefem gegenseitigem Verständnis und Einigkeit und zeigt die Fähigkeit zu kollektiver Arbeit und Koordination, unabhängig von den Umständen.
Ihre Fähigkeit, bis zu 1,4 Tonnen Nahrung pro Tag zu verzehren, unterstreicht ihre Rolle im marinen Ökosystem als einer der stärksten Konsumenten des Ozeans. Ihr Lebensrhythmus, der von Zeiten reicher Jagd bis zu Zeiten der Ruhe und des Fastens reicht, erzählt uns von der Größe und Unberechenbarkeit des Ozeans, in dem sie herrschen. Die Winterzeit, in der Buckelwale kaum fressen, ist ein Beweis für ihre erstaunliche Überlebensfähigkeit. Sie sind auf die Fettreserven angewiesen, die sie sich bei reichen Fängen angeeignet haben, um Zeiten zu überleben, in denen die Nahrung knapp wird. Dies erinnert uns daran, wie die Natur die Tiere lehrt, sparsam und klug mit den Ressourcen umzugehen.
Buckelwale sind lebende Chroniken des Überlebens und der Anpassungsfähigkeit, Symbole der Weisheit, die Verkörperung der Kraft und Schönheit des Ozeans und eine unerschöpfliche Quelle der Inspiration für uns.
Der Wal-Optimierungsalgorithmus ist ein metaheuristischer Optimierungsalgorithmus, der 2016 von Mirjalili und Lewis vorgeschlagen wurde. Sie wurden durch das Jagdverhalten der Wale inspiriert.
Wale verwenden eine Vielzahl von Jagdstrategien, darunter „Blasennetz“ und „spiralförmiges Eindringen“. Bei einem „Blasennetz“ umzingeln Wale ihre Beute, indem sie ein „Netz“ aus Luftblasen erzeugen, um die Beute zu verwirren und zu erschrecken. Beim „spiralförmigen Eindringen“ steigen die Wale in einer spiralförmigen Bewegung aus den Tiefen des Ozeans auf, um Beute zu machen.
Diese Jagdstrategien wurden im Algorithmus WOA abstrakt modelliert. Beim Algorithmus WOA stehen die „Wale“ für die Lösungen eines Optimierungsproblems, während die „Jagd“ die Suche nach der optimalen Lösung darstellt.
2. Der Algorithmus
Der WOA-Algorithmus beginnt mit der Initialisierung einer Population von Walen mit zufälligen Positionen. Dann wird ein Anführer ausgewählt - der Wal mit dem besten Wert der Zielfunktion (d. h. der besten globalen Lösung). Die Positionen der übrigen Wale werden unter Berücksichtigung der Position des Anführers aktualisiert. Dies geschieht auf zwei Arten: im Forschungsmodus und im Verwertungsmodus. Im Erkundungsmodus aktualisieren die Wale ihre Positionen durch eine zufällige Suche um die derzeit beste globale Lösung herum. Im Ausbeutungsmodus aktualisieren die Wale ihre Positionen und nähern sich ihrer aktuell besten Lösung.
Der WOA-Algorithmus wurde erfolgreich zur Lösung vieler Optimierungsprobleme eingesetzt und hat gute Ergebnisse gezeigt. Doch wie jeder Optimierungsalgorithmus hat auch dieser seine Vor- und Nachteile. Zum Beispiel kann er dazu neigen, auf lokale Optima zu stoßen und eine relativ langsame Konvergenzrate zu zeigen.
Hier erfahren Sie, wie Sie interessante Fakten über Buckelwale mit den Prinzipien des WOA-Algorithmus in Verbindung bringen können:
- Zusammenarbeit und Koordination. Buckelwale jagen oft in Gruppen und kooperieren miteinander, um gemeinsam erfolgreich zu sein. Dies erinnert an die Prinzipien des WOA-Algorithmus, bei dem einzelne Agenten (wie Wale) zusammenarbeiten, Informationen austauschen und ihre Aktionen koordinieren, um eine optimale Lösung zu erreichen.
- Intelligente Strategien. Buckelwale nutzen eine Vielzahl intelligenter Jagdstrategien, wie die Bildung von Blasennetzen und die Gruppenkoordination. Der WOA-Algorithmus basiert ebenfalls auf intelligenten Optimierungsstrategien, einschließlich der Suche nach optimalen Lösungen und der Anpassung an sich ändernde Bedingungen.
- Anpassungsfähigkeit und Effizienz. Buckelwale beweisen Anpassungsfähigkeit und Effizienz bei der Jagd, indem sie ihre Methoden je nach Situation ändern. Der WOA-Algorithmus strebt auch nach Anpassungsfähigkeit und Effizienz, indem er verschiedene Optimierungsstrategien anwendet und sein Verhalten ändert, um bessere Ergebnisse zu erzielen.
Der WOA-Algorithmus lässt sich also von den einzigartigen Jagdstrategien und Verhaltensweisen der Buckelwale inspirieren, was ihm hilft, Optimierungsprobleme in verschiedenen Bereichen effizient und intelligent zu lösen.
Der modifizierte Optimierungsalgorithmus WOAm umfasst mehrere Hauptstufen:
1. Bewegung auf dem Weg zu einer globalen Lösung:
- In der Anfangsphase des Algorithmus bewegt sich jeder „Wal“ (Lösung) in Richtung der globalen optimalen Lösung. Dies hilft, den Lösungsraum zu erkunden und die allgemeine Richtung des Optimums zu finden.
2. Verbesserung der eigenen Position:
- Jeder Wal versucht, seine aktuelle Position zu verbessern und sich einer besseren Lösung zu nähern. Der Einzelne kann seine Parameter oder Strategien ändern, um bessere Leistungen zu erzielen.
3. Spiralförmige Bewegung:
- Diese Phase ist ein wichtiger Mechanismus des WOA-Algorithmus. Wale können sich spiralförmig um die beste Lösung herum bewegen, was ihnen hilft, den Suchraum effizienter zu erkunden und der optimalen Lösung näher zu kommen.
4. Migration:
- In diesem Schritt werden die Positionen der Individuen nach dem Zufallsprinzip verändert, um für Vielfalt zu sorgen und zu verhindern, dass sie in lokalen Optima stecken bleiben. Die Migration hilft dem Algorithmus zu vermeiden, dass er vorzeitig zu einer Lösung konvergiert, die nicht gut genug ist.
Diese Schritte zusammen ermöglichen eine effiziente Suche nach der optimalen Lösung im Raum des Optimierungsproblems. Ich habe Änderungen vorgenommen, indem ich die vierte Stufe hinzugefügt habe, um die Resistenz des Algorithmus gegen das Hängenbleiben zu verbessern. Die Modellierung der Migration von Walen in freier Wildbahn zu neuen Gebieten auf der Suche nach Nahrung ist notwendig, wenn die bisherigen Quellen erschöpft sind. Dieser Zusatz verleiht dem Algorithmus zusätzliche Flexibilität und hilft ihm, den Lösungsraum effizienter zu erkunden, was die Überlebens- und Anpassungsstrategien in der Natur widerspiegelt.
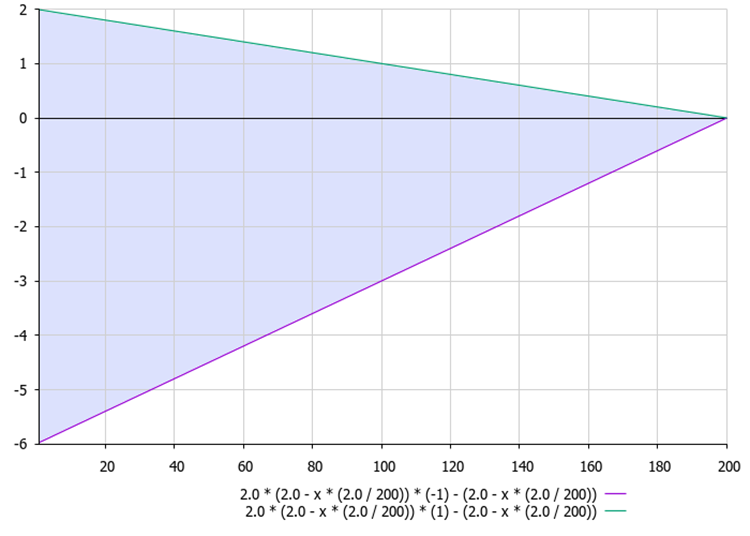
Abbildung 1. Der Bereich der A-Verhältniswerte in der Gleichung A = 2.0 * aKo * r - aKo in Abhängigkeit von der aktuellen Epoche
Pseudocode für den Algorithmus zur Optimierung der Walsuche (WOAm):
1. Initialisiere die Population mit einer zufälligen Position.2. Berechne die Fitness.
3. Berechne das Verhältnisses aKo: aKo = 2.0 - epochNow * (2.0 / epochs).
4. Erzeuge die Zufallszahl „r“ aus einer Gleichverteilung im Bereich von -1 bis 1.
5. Berechne die Variablen A und C:
- A = 2,0 * aKo * r - aKo (Abbildung 1)
- C = 2,0 * r
6. Legen Sie die Werte für „spiralCoeff“, die Zufallszahl „l“ aus der Gleichverteilung und die Zufallswahrscheinlichkeit „p“ fest.
7. Wenn „p“ kleiner ist als „refProb“:
- Wenn der absolute Wert von A größer als 1,0 ist: X = Xbest - A * |Xbest - Xprev|
- Ansonsten wähle den Zufallsindex „leaderInd“ von 0 bis „popSize“ und: X = Xbleed - A * |Xlead - Xprev|
8. Andernfalls, wenn die Zufallswahrscheinlichkeit kleiner ist als spiralProb: X = Xprev + | Xprev - X| * exp (b * l) * cos (2 * M_PI * l)
9. sonst: X = PowerDistribution (cB [c], rangeMin [c], rangeMin [c], 30)
10. Berechne die Fitness.
11. Aktualisiere die globale Lösung.
12. Wiederhole den Vorgang ab Schritt 3, bis das Stoppkriterium erfüllt ist.
Bild 2. Die „Blasen“-Waljagd, die den WOA-Optimierungsalgorithmus inspirierte
Fahren wir nun mit dem Schreiben des Codes für den WOAm-Algorithmus fort.
Wir definieren die Struktur „S_WOA_Agent“ zur Beschreibung jedes Wals. Schauen wir uns an, was hier vor sich geht:
1. Die Struktur enthält folgende Felder:
- cPrev[] - Array zum Speichern der vorherigen Koordinaten des Agenten.
- fPrev - Variable zum Speichern der vorherigen Bewertung (Fitness) des Agenten.
2. Init - Methode der Struktur „S_WOA_Agent“, die die Felder der Struktur initialisiert. Sie nimmt das Integer-Argument „coords“, das zur Größenänderung des Arrays „cPrev“ mit der Funktion ArrayResize verwendet wird.
3. fPrev = -DBL_MAX - setzt den Anfangswert der Variablen „fPrev“ auf den kleinstmöglichen Wert für „double“.
Dieser Code stellt die grundlegende Datenstruktur für Agenten im WOAm-Optimierungsalgorithmus dar und initialisiert deren Felder, wenn ein neuer Agent erstellt wird.
//—————————————————————————————————————————————————————————————————————————————— struct S_WOA_Agent { double cPrev []; //previous coordinates double fPrev; //previous fitness void Init (int coords) { ArrayResize (cPrev, coords); fPrev = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Definieren wir die Klasse „C_AO_WOAm“ des WOAm-Algorithmus, die ein Erbe der Basisklasse der „C_AO“-Populationsalgorithmen ist und die folgenden Felder und Methoden enthält:
1. Öffentliche Felder:
- ao_name - Name des Optimierungsalgorithmus.
- ao_desc - Beschreibung des Optimierungsalgorithmus.
- popSize - Größe der Population.
- params - Array der Algorithmusparameter.
- refProb - Verfeinerungswahrscheinlichkeit.
- spiralCoeff - Verhältnis der Spiralen.
- spiralProb - Spiralwahrscheinlichkeit.
- agent - Vektor der Agenten.
2. Die verfügbaren Optionen sind:
- C_AO_WOAm - Klassenkonstruktor, der die Klassenfelder initialisiert.
- SetParams - Methode zur Einstellung der Algorithmusparameter.
- Init - Methode zur Initialisierung des Algorithmus. Die Methode akzeptiert minimale und maximale Suchbereiche, Suchschritte und die Anzahl der Epochen.
- Moving - Methode für die Bewegung der Agenten.
- Revision - Methode zur Revision von Agenten.
3. Private Felder:
- epochs - Anzahl der Epochen.
- epochNow - aktuelle Epoche.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_WOAm : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_WOAm () { } C_AO_WOAm () { ao_name = "WOAm"; ao_desc = "Whale Optimization Algorithm M"; popSize = 100; //population size ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "refProb"; params [1].val = refProb; params [2].name = "spiralCoeff"; params [2].val = spiralCoeff; params [3].name = "spiralProb"; params [3].val = spiralProb; } void SetParams () { popSize = (int)params [0].val; refProb = params [1].val; spiralCoeff = params [2].val; spiralProb = params [3].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double refProb; //refinement probability double spiralCoeff; //spiral coefficient double spiralProb; //spiral probability S_WOA_Agent agent []; //vector private: //------------------------------------------------------------------- int epochs; int epochNow; }; //——————————————————————————————————————————————————————————————————————————————
Die Init-Methode der Klasse „C_AO_WOAm“ dient der Initialisierung von Klassenvariablen anhand der übergebenen Parameter. Diese Methode führt eine Standardinitialisierung mit der Methode StandardInit durch, die den minimalen und maximalen Suchbereich sowie den Suchschritt übernimmt.
Wenn die Standardinitialisierung erfolgreich ist, fährt die Methode mit der Initialisierung der Variablen „epochs“ und „epochNow“ fort. Der Wert von „epochs“ wird auf den übergebenen Parameter „epochsP“ gesetzt, und „epochNow“ wird auf 0 initialisiert.
Die Methode passt dann die Größe des Arrays „agent“ an die Größe von „popSize“ an. Die Methode Init wird mit dem Parameter „coords“ für jedes Element in „agent“ aufgerufen.
Die Methode gibt „true“ zurück, wenn die Initialisierung erfolgreich war, andernfalls „false“.
Diese Methode führt die Ersteinrichtung des WOAm-Optimierungsalgorithmus mit gegebenen Parametern durch und bereitet ihn darauf vor, die Optimierung für eine bestimmte Anzahl von Epochen durchzuführen.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_WOAm::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; ArrayResize (agent, popSize); for (int i = 0; i < popSize; i++) agent [i].Init (coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode „Moving“ der Klasse „C_AO_WOAm“ wird verwendet, um Agenten während der Optimierung zu bewegen. Die Methode geht folgendermaßen vor:
„epochNow++;“ - der aktuelle Epochenwert steigt.
„if (!revision)“ - Überprüfung, ob „revision“ „false“ ist.
Wenn „revision“ „falsch“ ist, dann:
- Die Koordinaten der Agenten „a[i].c[c]“ werden mit Zufallswerten in den angegebenen Bereichen initialisiert.
- Das Flag „revision“ wird auf „true“ gesetzt.
- Die Methode hat ihre Arbeit beendet.
Wenn „revision“ ungleich „false“ ist, dann:
- Für jeden Agenten werden anhand bestimmter Gleichungen und Wahrscheinlichkeiten neue Koordinaten berechnet.
- Verschiedene mathematische Berechnungen, Zufallszahlen und Wahrscheinlichkeiten werden verwendet, um die neuen Koordinaten der Agenten zu bestimmen.
- Neue „x“-Koordinaten werden entsprechend den Bedingungen und Wahrscheinlichkeiten berechnet.
- Die neuen Koordinaten „a[i].c[c]“ werden mit der Methode SeInDiSp gesetzt, um die Werte entsprechend den Suchbereichen und -schritten anzupassen.
Die Methode ist für die Aktualisierung der Koordinaten der Agenten im WOAm-Optimierungsalgorithmus in Abhängigkeit von der aktuellen Epoche, den Zufallswerten und Wahrscheinlichkeiten zuständig. Markieren wir die entsprechenden Codeabschnitte, die verschiedene Verhaltensweisen der Wale beschreiben, farbig:
Verbesserung der globalen Lösung: Mit jeder neuen Epoche erkunden die Wale vorsichtiger die Umgebung der gefundenen globalen Lösung gemäß dem linearen Gesetz und dem berechneten A-Verhältnis und versuchen, sich dem globalen Optimum zu nähern.
Erkundung der Umgebung des „Anführers“ der Population: Unter Berücksichtigung des A-Verhältnisses erkunden die Wale die Umgebung des „Anführers“ der Population, der nach dem Zufallsprinzip gemäß dem Gesetz der Gleichverteilung ausgewählt wird. Daher wird die Forschung in allen Gebieten fortgesetzt, in denen Wale in der Population vorkommen.
Spiralförmige Bewegung und „Blasennetz“: : Die Wale bewegen sich in einem spiralförmigen Muster, wobei sie ihre beste individuelle Position und ihren aktuellen Standort berücksichtigen, wodurch sichergestellt wird, dass die Fische in einer dichten Wolke gesammelt werden und die Nahrung an einem Ort konzentriert ist.
Die Migration der Wale: Die Migration der Wale wird simuliert, indem man sich abrupt von der besten globalen Potenzgesetzlösung entfernt. Dieser Prozess führt zu einer hohen Wahrscheinlichkeit, sich in der Nähe der globalen Lösung zu befinden, und zu einer geringen, aber von Null abweichenden Wahrscheinlichkeit, sehr weit davon entfernt zu sein.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_WOAm::Moving () { epochNow++; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double aKo = 2.0 - epochNow * (2.0 / epochs); double r = u.RNDfromCI (-1, 1); double A = 2.0 * aKo * r - aKo; double C = 2.0 * r; double b = spiralCoeff; double l = u.RNDfromCI (-1, 1); double p = u.RNDprobab (); double x; if (p < refProb) { if (MathAbs (A) > 1.0) { x = cB [c] - A * MathAbs (cB [c] - agent [i].cPrev [c]); //Xbest - A * |Xbest - X| } else { int leaderInd = u.RNDminusOne (popSize); x = agent [leaderInd].cPrev [c] - A * MathAbs (agent [leaderInd].cPrev [c] - agent [i].cPrev [c]); //Xlid - A * |Xlid - X|; } } else { if (u.RNDprobab () < spiralProb) { x = agent [i].cPrev [c] + MathAbs (agent [i].cPrev [c] - a [i].c [c]) * MathExp (b * l) * cos (2 * M_PI * l); //XbestPrev + |XbestPrev - X| * MathExp (b * l) * cos (2 * M_PI * l) } else { x = u.PowerDistribution (cB [c], rangeMin [c], rangeMin [c], 30); } } a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Die Revisionsmethode der Klasse „C_AO_WOAm“ wird zur Aktualisierung der besten globalen Lösung und der besten Positionen der Wale selbst verwendet. Die Methode geht folgendermaßen vor:
1. Aktualisiere die globale Lösung. In der „for“-Schleife durchläuft die Methode alle Individuen. Wenn der Wert der Fitnessfunktion des aktuellen Individuums den aktuell besten Wert der Fitnessfunktion übersteigt, wird der beste Wert aktualisiert und das Koordinatenfeld des aktuellen Individuums wird in das Koordinatenfeld der besten Lösung kopiert.
2. Aktualisiere die vorherigen Werte der Fitnessfunktion und die Koordinaten des Agenten. In der „for“-Schleife durchläuft die Methode alle Individuen. Wenn die Fitnessfunktion des aktuellen Individuums den vorherigen Wert der Fitnessfunktion des Agenten übersteigt, wird der vorherige Wert der Fitnessfunktion aktualisiert und das Koordinatenfeld des aktuellen Individuums in das Feld der vorherigen Koordinaten des Agenten kopiert.
Die Revisionsmethode ist verantwortlich für die Aktualisierung der besten Agenten auf der Grundlage ihrer Merkmalswerte sowie für die Aktualisierung früherer Merkmalswerte und Agentenkoordinaten als Teil des WOAm-Optimierungsalgorithmus.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_WOAm::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) ind = i; } if (ind != -1) { fB = a [ind].f; ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } for (int i = 0; i < popSize; i++) { if (a [i].f > agent [i].fPrev) { agent [i].fPrev = a [i].f; ArrayCopy (agent [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
3. Testergebnisse
Die von den Autoren vorgeschlagene Basisversion des Algorithmus lässt leider viel zu wünschen übrig und zeigt relativ schwache Ergebnisse (siehe unten).
WOA|Whale Optimization Algorithm|100.0|0.1|0.5|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.45323929163422483
25 Hilly's; Func runs: 10000; result: 0.3158990997230676
500 Hilly's; Func runs: 10000; result: 0.25544320870775555
=============================
5 Forest's; Func runs: 10000; result: 0.43485195446891795
25 Forest's; Func runs: 10000; result: 0.2454326019188397
500 Forest's; Func runs: 10000; result: 0.1557433572339264
=============================
5 Megacity's; Func runs: 10000; result: 0.3400000000000001
25 Megacity's; Func runs: 10000; result: 0.18800000000000003
500 Megacity's; Func runs: 10000; result: 0.10146153846153938
=============================
All score: 2.49007 (27.67%)
Mit viel Mühe und Kreativität wurden jedoch erhebliche Verbesserungen erzielt, darunter Elemente wie Migration und Potenzgesetz-Verteilung. Außerdem wird jetzt nicht mehr die aktuelle Position der Wale als Ausgangspunkt für die Berechnung der nächsten Position verwendet, sondern die besten vorherigen Positionen der Wale. Durch diese Änderungen wurde der Algorithmus umgestaltet, was ihm eine neue Qualität verlieh und die Ergebnisse der modifizierten Version erheblich verbesserte. Dadurch ist der Algorithmus effizienter geworden und in der Lage, größere Erfolge bei der Lösung der gestellten Aufgaben zu erzielen.
Nachfolgend sind die Ergebnisse einer modifizierten Version von WOAm aufgeführt, bei der eine Verbesserung von mehr als 22 % zu verzeichnen ist (wobei 0 % das schlechteste mögliche Ergebnis und 100 % das beste theoretisch erreichbare Ergebnis ist).
WOAm|Whale Optimization Algorithm|100.0|0.1|0.5|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.8452089588169466
25 Hilly's; Func runs: 10000; result: 0.562977678943021
500 Hilly's; Func runs: 10000; result: 0.262626056156147
=============================
5 Forest's; Func runs: 10000; result: 0.9310009723200832
25 Forest's; Func runs: 10000; result: 0.5227806126625986
500 Forest's; Func runs: 10000; result: 0.1636489301696601
=============================
5 Megacity's; Func runs: 10000; result: 0.6630769230769229
25 Megacity's; Func runs: 10000; result: 0.41138461538461535
500 Megacity's; Func runs: 10000; result: 0.11356923076923182
=============================
All score: 4.47627 (49.74%)
In der Visualisierung der modifizierten Version der Operation ist eine erhebliche Streuung der Ergebnisse für die Funktion Hilly und eine geringe Streuung für die diskrete Megacity zu erkennen. Interessanterweise ist die Megacity-Funktion bei den meisten Algorithmen komplexer und weist eine größere Streuung der Ergebnisse auf, und es ist umso überraschender, dass WOAm bei dieser Funktion sehr stabile und gute Ergebnisse zeigt.
Der Algorithmus erkundet erfolgreich lokale Oberflächenbereiche in verschiedenen Bereichen des Suchraums und zeigt vielversprechende Richtungen auf. Erleichtert wird dies durch die Unterteilung des allgemeinen Herdenverhaltens der Population in einzelne Verhaltensphasen, die darauf abzielen, die Situation der einzelnen Wale zu verbessern.
Dieser Ansatz ermöglicht es dem Algorithmus, den Suchraum für die optimale Lösung effektiv zu erkunden und sich dabei auf die Verbesserung der Positionen der einzelnen Agenten im Rudel zu konzentrieren. Dies ermöglicht eine genauere und gründlichere Erkundung potenziell vielversprechender Bereiche, was wiederum die Gesamtleistung des Algorithmus verbessert.
Die Basisversion ist in dieser Visualisierung nicht dargestellt. Zusätzlich wird eine Visualisierung der Funktionsweise des Algorithmus auf der Ackley-Testfunktion bereitgestellt. Diese Funktion ist nicht an der Berechnung der Bewertungstabelle beteiligt.
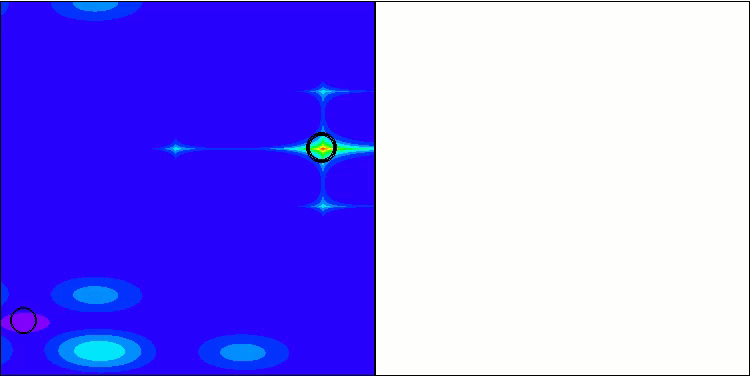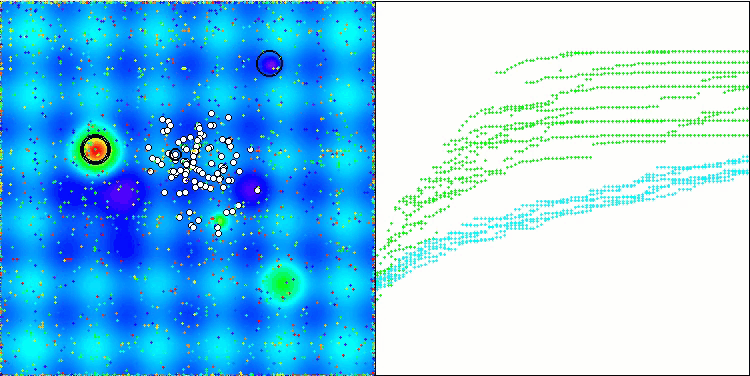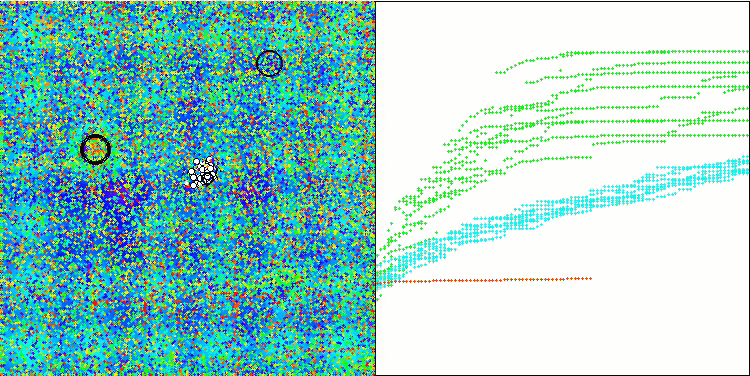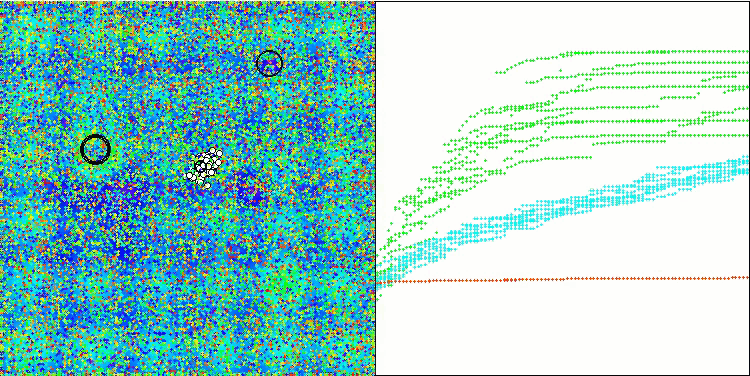
WOAm mit der Testfunktion Hilly
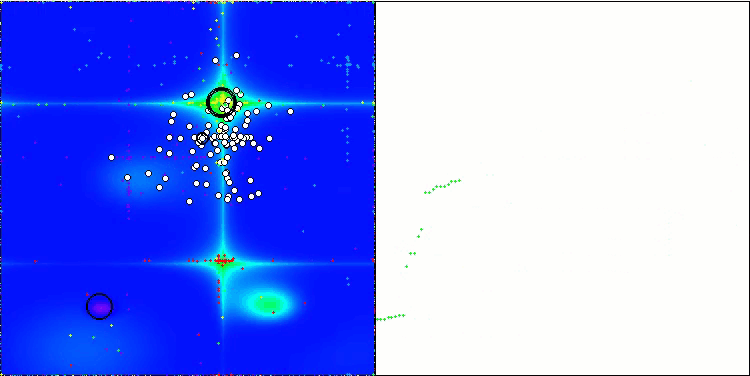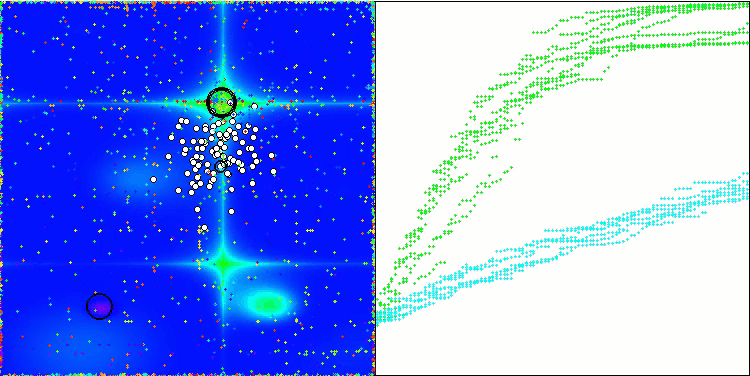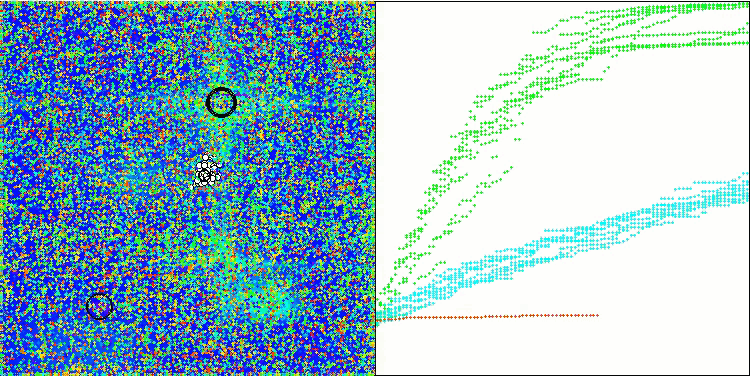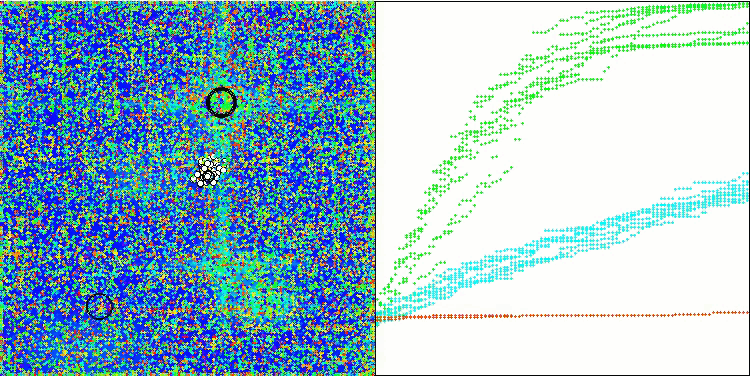
WOAm mit der Testfunktion Forest
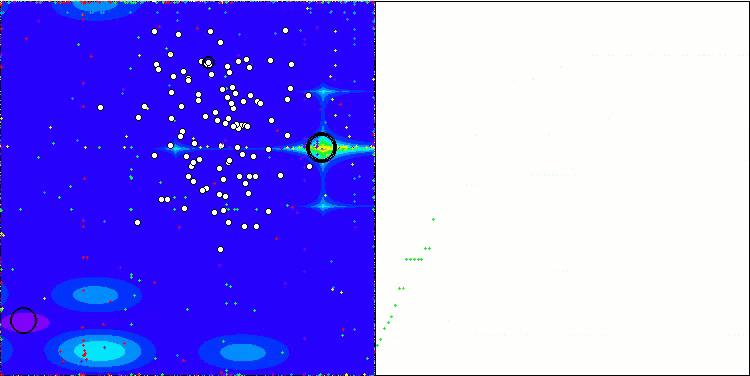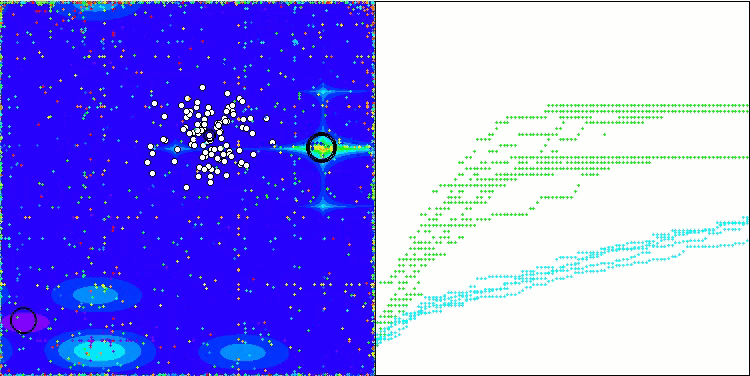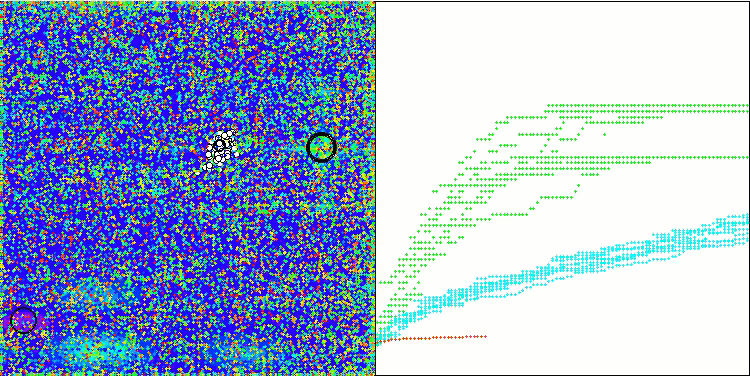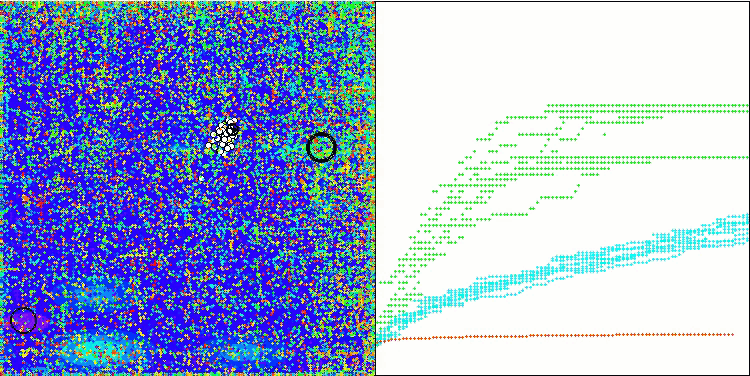
WOAm mit der Testfunktion Megacity
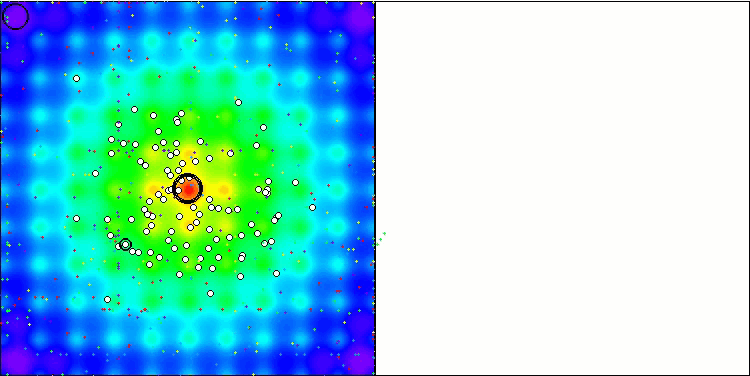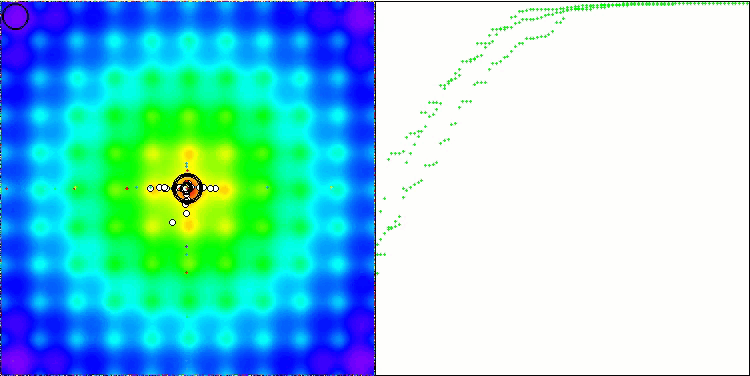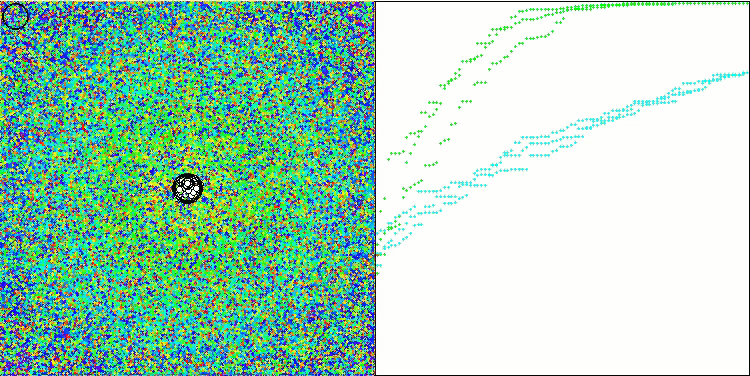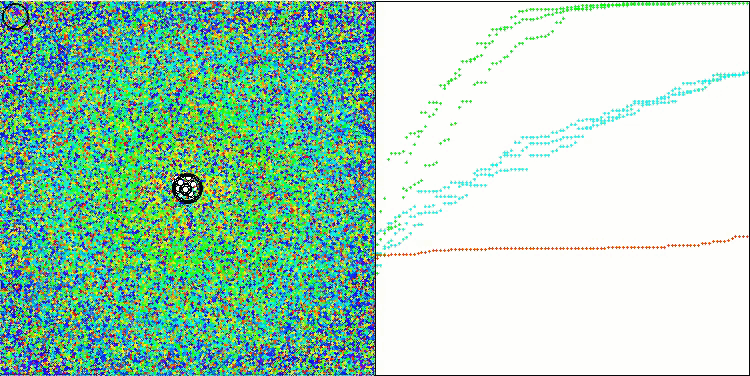
WOAm mit der Testfunktion Ackley
Der modifizierte WOAm-Algorithmus belegte einen ehrenvollen zehnten Platz im oberen Teil der Tabelle und zeigte gute und stabile Gesamtergebnisse.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | binärer genetischer Algorithmus | 0.99992 | 0.99484 | 0.50483 | 2.49959 | 1.00000 | 0.99975 | 0.32054 | 2.32029 | 0.90667 | 0.96400 | 0.23035 | 2.10102 | 6.921 | 76.90 |
| 2 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.99934 | 0.91895 | 0.56297 | 2.48127 | 1.00000 | 0.93522 | 0.39179 | 2.32701 | 0.83167 | 0.64433 | 0.21155 | 1.68755 | 6.496 | 72.18 |
| 3 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 4 | ESG | Entwicklung der sozialen Gruppen | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 5 | SIA | Simuliertes isotropes Abkühlen | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 6 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 7 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 8 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 9 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 10 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 11 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 12 | BFO-GA | Optimierung der bakteriellen Futtersuche - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 13 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 14 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 15 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 16 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 17 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 18 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 19 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 20 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 21 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 22 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 23 | BA | Fledermaus-Algorithmus | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 24 | SA | simuliertes Abkühlen | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 25 | IWDm | intelligente Wassertropfen M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 26 | PSO | Partikelschwarmoptimierung | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 27 | MA | Affen-Algorithmus | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 28 | SFL | schlurfender Froschsprung | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 29 | FSS | Fischschulsuche | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 30 | RND | zufällig | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
| 31 | GWO | Grauer-Wolf-Optimierung | 0.59169 | 0.36561 | 0.29595 | 1.25326 | 0.24499 | 0.09047 | 0.03612 | 0.37158 | 0.27667 | 0.08567 | 0.02170 | 0.38403 | 2.009 | 22.32 |
| 32 | CSS | Suche geladener Systeme | 0.44252 | 0.35454 | 0.35201 | 1.14907 | 0.24140 | 0.11345 | 0.06814 | 0.42299 | 0.18333 | 0.06300 | 0.02322 | 0.26955 | 1.842 | 20.46 |
| 33 | EM | elektromagnetismusähnlicher Algorithmus | 0.46250 | 0.34594 | 0.32285 | 1.13129 | 0.21245 | 0.09783 | 0.10057 | 0.41085 | 0.15667 | 0.06033 | 0.02712 | 0.24412 | 1.786 | 19.85 |
Zusammenfassung
Insgesamt bin ich mit den in diesem Artikel beschriebenen Verbesserungen des Algorithmus zufrieden. Es gibt jedoch tiefer gehende Forschungen zur Modifizierung dieser Version, die für diejenigen, die sich für dieses Thema begeistern und experimentierfreudig sind, eine Überlegung wert sind. Das Eintauchen in diese Techniken kann neue Horizonte eröffnen und zu noch besseren Lösungen für einen bestimmten Algorithmus inspirieren.
Hier sind einige Strategien, die helfen können, den Algorithmus zur Optimierung der Walsuche (WOA) zu verbessern und die Wahrscheinlichkeit zu verringern, an lokalen Extremen hängen zu bleiben:
1. Diversifizierung der Population. Die Vielfalt der Population kann dazu beitragen, dass man nicht in lokalen Optima stecken bleibt. Erwägen Sie Methoden zur Aufrechterhaltung der Populationsvielfalt, wie z. B. Mutationsmechanismen, Crossover oder die Untersuchung von Lösungsnachbarschaften.
2. Elite-Strategie. Bei dieser Strategie wird eine Reihe verschiedener bester Lösungen (Eliten) von Generation zu Generation beibehalten, wodurch eine Abnahme der Populationsvielfalt vermieden wird.
3. Multi-Strategie-Mechanismus. Bei diesem Ansatz werden mehrere Suchstrategien gleichzeitig eingesetzt, was dem Algorithmus helfen kann, den Lösungsraum besser zu erkunden und lokale Fallstricke zu vermeiden.
4. Hybridisierung mit anderen Algorithmen. Die Hybridisierung von WOA mit anderen Optimierungsalgorithmen kann seine Leistung ebenfalls verbessern. So können wir beispielsweise die differentielle Evolution oder Partikelschwärme einsetzen, um die Explorationsphase des Algorithmus zu verbessern.
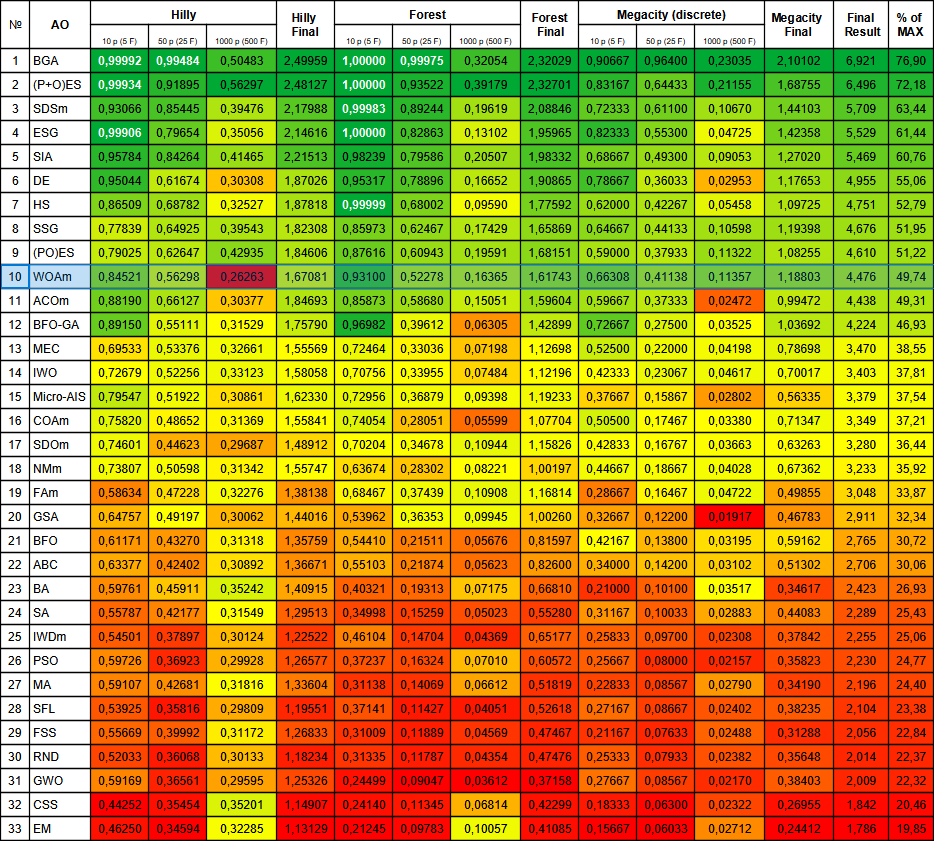
Abb. 3. Die farblichen Abstufungen der Algorithmen nach relevanten Tests Ergebnisse größer oder gleich 0,99 sind weiß hervorgehoben
Bemerkenswert ist die Farbe der Wertezelle bei der glatten Hilly-Funktion mit 1000 Variablen, die anzeigt, dass das Ergebnis das schlechteste unter allen in der Tabelle aufgeführten Algorithmen ist. Hervorzuheben ist auch der hohe Leistungsindikator für die Funktion Forest mit fünf Variablen und die allgemein gute Leistung für die Funktionen Forest und Megacity.
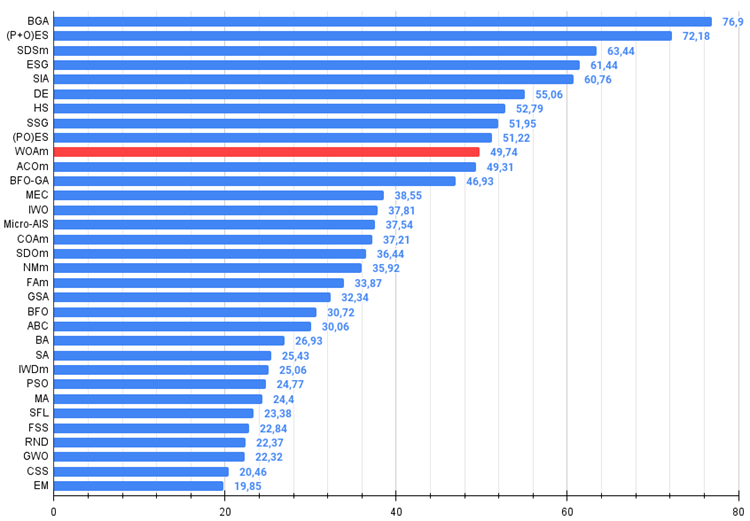
Abb. 4. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, größer ist besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; das Archiv enthält ein Skript zur Berechnung der Bewertungstabelle)
WOAm Pro und Kontra:
Vorteile:
- Einfache Architektur und Implementierung.
- Stabile und gute Ergebnisse für die scharfe Forest-Funktion und der diskreten Megacity.
- Keine hohen Anforderungen an die Computerressourcen.
Nachteile
- Geringe Konvergenz (keine Ergebnisse nahe an 100%).
- Geringe Skalierbarkeit bei glatten Funktionen wie Hilly (Probleme mit hochdimensionalen Aufgaben).
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Algorithmuscodes begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/14414
Algorithmen zur Optimierung mit Populationen: Vogelschwarm-Algorithmus (BSA)
Nicht-stationäre Prozesse und unechte Regression
Entwicklung eines Expertenberaters für mehrere Währungen (Teil 7): Auswahl einer Gruppe auf der Grundlage der Vorwärtsperiode
Verwendung des JSON Data APIs in Ihren MQL-Projekten
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.