Algorithmen zur Optimierung mit Populationen Cuckoo-Optimierungsalgorithmus (COA)

MetaTrader 5 — Beispiele | 1 Februar 2023, 09:29

444

Andrey Dik

Inhalt

1. Einführung
2. Algorithmusbeschreibung, Entscheidungsbaum und Levy-Flug
3. COA-Code
4. Testergebnisse

1. Einführung

Der Kuckuck (cuckoo) ist ein faszinierender Vogel, nicht nur wegen seines Gesangs, sondern auch wegen seiner aggressiven Brutstrategie, die darin besteht, Eier in Nester anderer Vögel zu legen. Damit verlagert der Vogel seine elterliche Verantwortung vollständig auf andere Arten. Jede Kuckucksart legt Eier in einer bestimmten Farbe und Größe, damit sie am besten zu den Eiern der verschiedenen Pflegeeltern passt. Kuckucksküken, die in die Nester anderer Vögel geworfen werden, sind in der Regel größer und kräftiger als die eigenen Küken der Nestbesitzer, sodass die Kuckucke mehr Futter benötigen. Während ihrer Entwicklung entwickeln Hodgson-Kuckucksküken ein spezielles Muster auf ihren Flügeln in Form eines offenen Schnabels, der es ihnen ermöglicht, mehr Nahrung von den Pflegeeltern aufzunehmen. Der Kuckuck ist nicht der einzige Vogel, der eine solche Eigenschaft aufweist. Nistparasitismus wurde bei mindestens 80 Vogelarten festgestellt. Dieses Phänomen ist auch bei einigen Arten sozialer Insekten weit verbreitet - Hummeln, Bienen und Ameisen, deren Weibchen in eine andere Kolonie eindringen, die Königin töten und ihre Eier ablegen. Nistparasitismus gibt es auch bei einigen Fischen, wie z. B. den Welsen aus dem Tanganjikasee in Afrika, die ihre Eier anderen Fischen zuwerfen, die die Eier in ihrem Maul ausbrüten.

Die Kuckuckssuche ist einer der neuesten von der Natur inspirierten heuristischen Algorithmen, der 2009 von Yang und Deb entwickelt wurde. Sie beruht auf dem Parasitismus einiger Kuckucksarten. Dieser Algorithmus wurde durch so genannte Levy-Flüge anstelle einfacher isotroper Random-Walk-Methoden weiter verbessert.

2. Beschreibung des Algorithmus

Der Cuckoo-Optimierungsalgorithmus (COA) wird für die kontinuierliche nichtlineare Optimierung verwendet. COA ist von der Lebensweise dieses Vogels inspiriert. Der Optimierungsalgorithmus basiert auf den Merkmalen der Eiablage und der Fortpflanzung der Arten. Wie andere evolutionäre Ansätze beginnt auch COA mit einer Ausgangspopulation. Die Grundlage des Algorithmus ist der Versuch, zu überleben. Während des Überlebenskampfes sterben einige der Vögel. Die überlebenden Kuckucke ziehen an bessere Orte und beginnen zu brüten und Eier zu legen. Schließlich konvergieren die überlebenden Kuckucke so, dass sich eine Kuckucksgesellschaft mit ähnlichen Fitnesswerten ergibt.
Der Hauptvorteil dieser Methode ist ihre Einfachheit: Die Kuckuckssuche erfordert nur vier verständliche Parameter, sodass die Abstimmung ein Kinderspiel ist.

Beim Kuckuckssuchalgorithmus werden die Eier im Nest als mögliche Lösungen für das Optimierungsproblem interpretiert, und das Kuckucksei stellt die neue Lösung dar. Ziel der Methode ist es, diese neuen (und potenziell besseren) Lösungen für parasitäre Kuckuckseier zu nutzen, um die derzeitige Lösung für Nesteier zu ersetzen. Diese Ersetzung, die iterativ durchgeführt wird, führt schließlich zu einer Lösung.

Die Professoren Yang und Deb schlugen die folgenden drei Gruppen von Idealzuständen für den Algorithmus vor:
1. Jeder Kuckuck legt ein Ei und legt es in ein zufällig ausgewähltes Nest.
2. Die besten Nester mit qualitativ hochwertigen Eiern werden an die nächsten Generationen weitergegeben.
3. Die Anzahl der verfügbaren Nester ist festgelegt, und das Nest kann ein fremdes Ei mit der Wahrscheinlichkeit „pa“ entdecken. In diesem Fall kann der Wirtsvogel das Ei entweder wegwerfen oder das Nest verlassen und das Ei stirbt.

Der Einfachheit halber kann die dritte Annahme durch den pa-Anteil der Nester approximiert werden. Bei einem Maximierungsproblem kann die Qualität oder Angemessenheit der Lösung einfach proportional zur Zielfunktion sein. Es können jedoch auch andere (komplexere) Ausdrücke für die Fitnessfunktion definiert werden.

Für jede Iteration g wird ein Kuckucksei i nach dem Zufallsprinzip ausgewählt, und neue Lösungen xi (g + 1) werden mit Hilfe des Levy-Fluges erzeugt, einer Art zufälliger Wanderung, bei der die Schritte innerhalb von Grenzen der Schrittlängen bestimmt werden, die eine bestimmte Wahrscheinlichkeitsverteilung haben, und die Richtungen der Schritte isotrop und zufällig sind. Nach Ansicht der Erfinder der Methode ist die Strategie der Levy-Flüge anderen einfachen Random Walks vorzuziehen, da sie zu einer besseren Gesamtleistung führt. Die allgemeine Levy-Fluggleichung sieht wie folgt aus

xi(g + 1) = xi(g) + α ⊕ levy(λ),

wobei g die Nummer der aktuellen Generation angibt, während α > 0 die Schrittweite angibt, die mit der Skala des untersuchten Problems in Beziehung stehen sollte. Das Symbol ⊕ wird zur Bezeichnung der elementweisen Multiplikation verwendet. Man beachte, dass es sich im Wesentlichen um eine Markov-Kette handelt, da der nächste Ort in der Generation g + 1 nur von dem aktuellen Ort in der Generation g und der Übergangswahrscheinlichkeit abhängt, die durch den ersten bzw. zweiten Term gegeben ist. Diese Übergangswahrscheinlichkeit wird durch die Levy-Verteilung wie folgt moduliert:

levy(λ) ∼ g−λ, (1 < λ ≤ 3),

die eine unendliche Varianz mit einem unendlichen Mittelwert hat. Die Praxis hat gezeigt, dass die besten Ergebnisse mit einem festen Grad von 2,0 erzielt werden. Hier bilden die Schritte im Wesentlichen einen Random-Walk-Prozess mit einer Power-Law-Verteilung der Schrittlänge mit starkem Schwanz. Aus rechnerischer Sicht besteht die Erzeugung von Zufallszahlen mit Hilfe von Levy-Flügen aus zwei Schritten: Zunächst wird eine Zufallsrichtung gemäß einer Gleichverteilung gewählt, dann werden Schritte gemäß der gewählten Levy-Verteilung erzeugt. Der Algorithmus bewertet dann die Eignung der neuen Lösung und vergleicht sie mit der aktuellen Lösung. Wenn die neue Lösung besser geeignet ist, ersetzt sie die bisherige. Andererseits werden einige Nester aufgegeben (der Besitzer des Nests hat das Kuckucksei weggeworfen oder das Nest verlassen und das Ei ist gestorben), um den Suchraum auf der Suche nach vielversprechenderen Lösungen weiter zu erkunden. Die Ersetzungsrate wird durch die Wahrscheinlichkeit pa bestimmt, ein Modellparameter, der zur Verbesserung der Leistung angepasst werden muss. Der Algorithmus wird iterativ angewandt, bis das Abbruchkriterium erfüllt ist. Übliche Abbruchkriterien sind, dass eine Lösung gefunden wurde, die einen unteren Schwellenwert erfüllt, dass eine feste Anzahl von Generationen erreicht wurde oder dass aufeinanderfolgende Iterationen keine besseren Ergebnisse mehr liefern.

Gehen wir näher auf den Prozess der Eiablage durch den Kuckuck ein. Aus allen Nestern wird nach dem Zufallsprinzip ein Nest ausgewählt, in das das Ei gelegt werden soll. Da das Ei eine Lösung ist, kann es durch die Qualität des Eies dargestellt werden. Wenn das Kuckucksei von besserer Qualität ist als das Eltern-Ei, wird es ersetzt. Andernfalls verbleibt das Eltern-Ei im Nest. Das überlebende Küken wird die Evolution fortsetzen. Das bedeutet, dass die Evolution von der gleichen Stelle aus weitergeht, wenn das Küken des Eltern-Eis überlebt hat. Eine Weiterentwicklung ist nur möglich, wenn sich das Kuckucksei als lebensfähiger erweist und die Suche nach der Lösung des Problems von einem neuen Ort aus fortgesetzt wird. Der Entscheidungsbaum ist in Abbildung 1 schematisch dargestellt.

Entscheidungsbaum

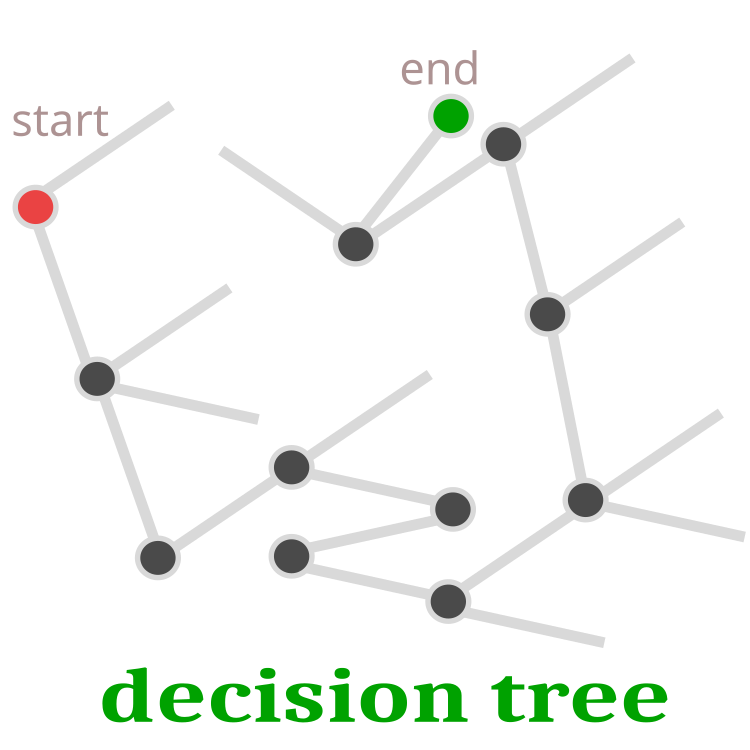
Abb. 1. Entscheidungsbäume Der rote Punkt ist der Anfang, der grüne Punkt ist die endgültige Entscheidung

Die zweite Komponente der Basis des Algorithmus nach dem Entscheidungsbaum ist Levy.Flug. Der Levy-Flug ist ein Random Walk (ein statistischer Markov-Prozess), bei dem sich die Länge der Sprünge schrittweise ändert, die Richtung der Sprünge sich zufällig ändert und die Wahrscheinlichkeitsverteilung ein Spezialfall der Pareto-Verteilung ist und sich durch starke Schwänze auszeichnet. Er ist als Sprung im Raum definiert, und der Sprung ist isotrop in beliebige Richtungen. Der Levy-Flug ist ein Instrument zur Beschreibung anomaler stochastischer Prozesse. Die Streuung ist unendlich (Sprünge von großer Länge sind möglich), die Längen der Sprünge sind auf allen Ebenen selbstähnlich (kurze Sprünge sind mit langen Flügen durchsetzt). Der Begriff „Levy Flight“ wird manchmal auch auf einen „Random Walk“ ausgedehnt, der nicht in einem kontinuierlichen Raum, sondern auf einem diskreten Gitter stattfindet.

Eine klare Anwendung des Levy-Fluges im Kuckuck-Algorithmus kann man sich vorstellen, wenn man ein Optimierungsproblem mit einem Parameter betrachtet. Nehmen wir eine hypothetische Funktion (die schwarze Linie in Abbildung 2), die sich über den größten Teil ihres Definitionsbereichs nicht ändert, d. h. eine horizontale Linie (y=x). Nur in einem kleinen Bereich ändert sich die Funktion und hat ein Maximum. Wenn wir die Suche nach dem Maximum beim orangefarbenen Punkt in Abbildung 2 beginnen und dann einen Zufallswert x mit der Levy-Verteilung erhalten, entfernen wir uns vom Ausgangspunkt, ohne eine Veränderung der Funktion zu erhalten. Mit einem starken Sprung im Schwanz der Verteilung erhalten wir jedoch einen grünen Punkt, der eine bessere Lösung als die ursprüngliche orangefarbene ist, und nur mit dem grünen Punkt können wir das Ergebnis verbessern, während wir uns dem Maximum der Funktion nähern. In diesem Beispiel verbessert der Levy-Flug die Suchfähigkeit des Algorithmus drastisch.

Levy-Flug

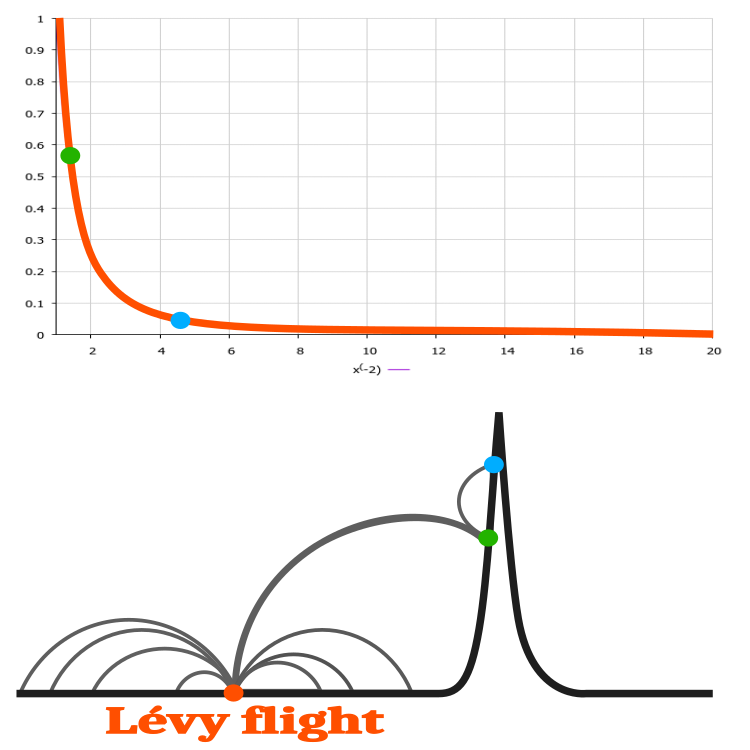
Abb. 2. Ein Beispiel für die Lösung einer hypothetischen eindimensionalen Funktion mit Hilfe des Levy-Flugs

Das Konzept der Levy-Flüge wird in der Chaostheorie verwendet, um zufällige oder pseudozufällige Naturphänomene zu modellieren (z. B. der Flug eines Albatros, der lange und kurze Flugbahnen kombiniert). Beispiele sind die Analyse von Erdbebendaten, Finanzmathematik, Kryptographie, Signalanalyse, turbulente Bewegungen sowie zahlreiche Anwendungen in Astronomie, Biologie und Physik.

Pseudocode des COA-Algorithmus (Abbildung 3):

1. Kuckuck-Initialisierung mit Zufallswerten.
2. Ermitteln der Fitness.
3. Eiablage in zufälligen Nestern.
4. Leeren der Nester mit einer bestimmten Wahrscheinlichkeit.
5. Kuckucke von der aktuellen Position in eine zufällige Richtung innerhalb der Levi-Flugdistanz senden
6. Ermitteln der Fitness.
7. Eiablage in zufälligen Nestern.
8. Leeren der Nester mit einer bestimmten Wahrscheinlichkeit.
9. Wiederholung ab Schritt 5, bis das Stoppkriterium erfüllt ist.

Schema

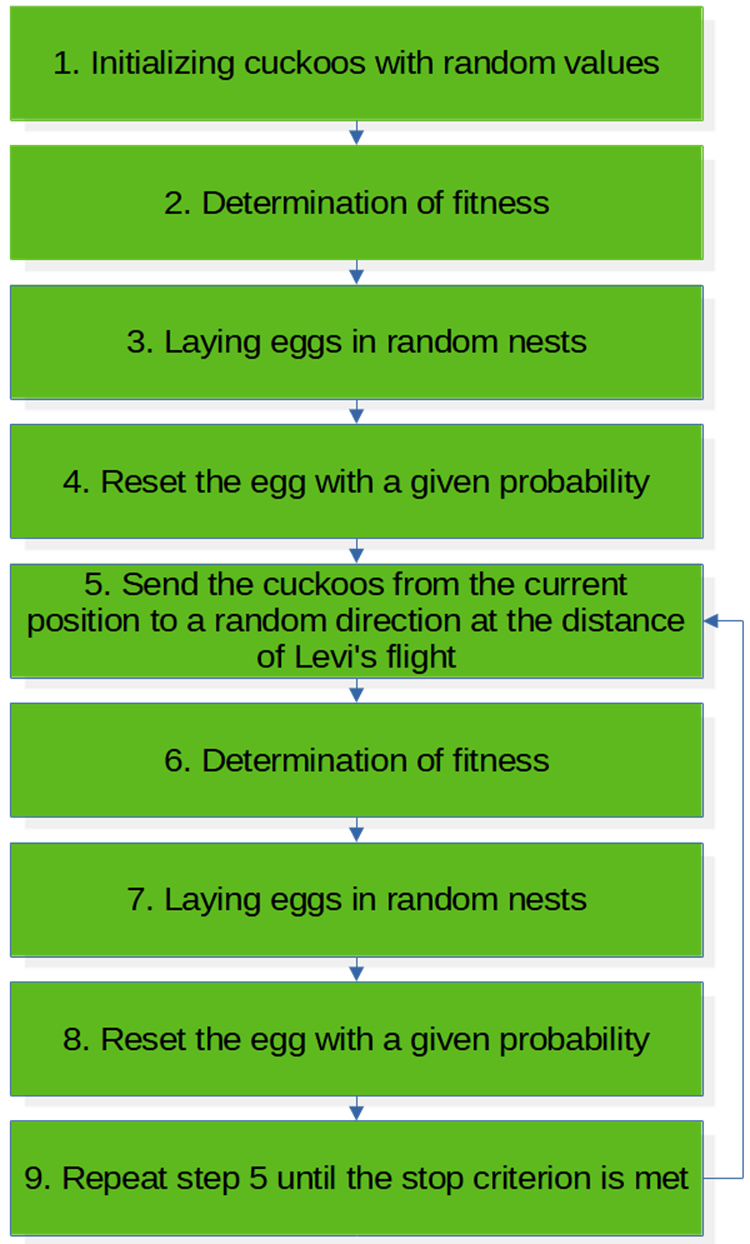
Abb. 3. Blockschaltbild des Algorithmus

3. COA-Code

Betrachten wir zunächst den Code des Algorithmus. Die Lösung des Problems ist der Kuckuck, der auch das Ei ist. Dies ist eine einfache Struktur, die die Koordinaten im Suchraum und den Wert der Fitnessfunktion (Eiqualität) enthält.

//——————————————————————————————————————————————————————————————————————————————
struct S_Cuckoo
{
  double c []; //coordinates (egg parameters)
  double e;    //egg quality 
};
//——————————————————————————————————————————————————————————————————————————————

Beschreiben wir das Nest in Form einer Struktur. Hier gibt es, genau wie bei der Struktur eines Eies, Koordinaten im Raum und den Wert der Fitnessfunktion. „Das Ei ins Nest zu legen“ bedeutet im Wesentlichen, die Struktur des Eies in die Struktur des Nestes zu kopieren. Bei Verwendung des Wahrscheinlichkeitsparameters pa wird das Ei aus dem Nest geworfen, wenn eine Zufallszahl von 0,0 bis pa in den Bereich [0,0;1,0] fällt und der Wert von e gleich -DBL_MAX gesetzt wird.

//——————————————————————————————————————————————————————————————————————————————
struct S_Nest
{
  void Init (int coordinates)
  {
    ArrayResize (c, coordinates);
    e = -DBL_MAX;
  }
  double c []; //coordinates (egg parameters)
  double e;    //egg quality
};
//——————————————————————————————————————————————————————————————————————————————

Algorithmus-Klasse. Hier werden die öffentlichen Initialisierungsmethoden, die beiden Hauptaufrufmethoden im Nutzerprogramm, die Wertebereiche der Argumente des Optimierungsproblems und zusätzliche private Methoden, die Servicefunktionen ausführen, deklariert.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_COA
{
  //============================================================================
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Cuckoo cuckoos []; //all the cuckoos
  public: double cB        []; //best coordinates (egg parameters)
  public: double eB;           //best eggs quality

  public: void Init (const int    coordinatesP, //number of opt. parameters
                     const int    cuckoosP,     //number of cuckoos
                     const int    nestsP,       //number of cuckoo nests
                     const double koef_paP,     //probability of detection of cuckoo eggs
                     const double koef_alphaP); //step control value

  public: void CuckooFlight ();
  public: void LayEggs      ();


  //============================================================================
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: S_Nest nests [];      //nests
  private: int    cuckoosNumber; //number of cuckoos
  private: int    nestsNumber;   //number of cuckoo nests
  private: double koef_pa;       //probability of detection of cuckoo eggs
  private: double koef_alpha;    //step control value
  private: double v     [];
  private: int    coordinates;   //coordinates number
  private: bool   clutchEggs;    //clutch of eggs
};
//——————————————————————————————————————————————————————————————————————————————

Die öffentliche Methode Init(). Hier werden die Werte von Variablen zurückgesetzt und Speicher für Arrays zugewiesen.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_COA::Init (const int    coordinatesP,  //number of opt. parameters
                     const int    cuckoosP,     //number of cuckoos
                     const int    nestsP,       //number of cuckoo nests
                     const double koef_paP,     //probability of detection of cuckoo eggs
                     const double koef_alphaP)  //step control value
{
  MathSrand (GetTickCount ());
  clutchEggs = false;
  eB         = -DBL_MAX;

  coordinates   = coordinatesP;
  cuckoosNumber = cuckoosP;
  nestsNumber   = nestsP;
  koef_pa       = koef_paP;
  koef_alpha    = koef_alphaP;

  ArrayResize (nests, nestsNumber);
  for (int i = 0; i < nestsNumber; i++)
  {
    nests  [i].Init (coordinates);
  }

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (cB,        coordinates);

  ArrayResize (v, coordinates);

  ArrayResize (cuckoos, cuckoosNumber);
  for (int i = 0; i < cuckoosNumber; i++)
  {
    ArrayResize (cuckoos [i].c, coordinates);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die erste öffentliche Methode, die bei jeder Iteration des „Kuckucksfluges“ aufgerufen wird. Wenn das Flag ClutchEggs ausgeschaltet ist, senden wir die Kuckucke in eine zufällige Richtung und erzeugen Zufallszahlen im Bereich der entsprechenden Koordinate. Ist das Flag aktiviert, so wird der tatsächliche Flug des Kuckucks entsprechend der Verteilung des Levy-Fluges im Bereich des V-Vektors durchgeführt. Der Vektor v wird in Init() für jede Koordinate einzeln vorberechnet, da jede Koordinate einen anderen Wertebereich haben kann.

Der Ausdruck cuckoos [i].c [c] = cuckoos [i].c [c] + r1 * v [c] * pow (r2, -2.0); bedeutet, dass wir den Offset r1 * v [c] * pow (r2, -2.0) addieren, wobei r1 gleich -1 oder 1 ist, was die Richtung des Offsets von der ursprünglichen Position bestimmt, v ist ein Verschiebungsvektor, r2 ist eine Zufallszahl im Bereich von 0.0 bis 20.0 hoch -2.0. Das Potenzieren einer Zufallszahl ist die Levy-Flugfunktion. Die Grafik ist in Abbildung 2 zu sehen.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_COA::CuckooFlight ()
{
  //----------------------------------------------------------------------------
  if (!clutchEggs)
  {
    for (int i = 0; i < coordinates; i++) v [i] = (rangeMax [i] - rangeMin [i]) * koef_alpha;

    for (int i = 0; i < cuckoosNumber; i++)
    {
      for (int c = 0; c < coordinates; c++)
      {
        cuckoos [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        cuckoos [i].c [c] = SeInDiSp (cuckoos [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    clutchEggs = true;
  }
  else
  {
    double r1 = 0.0;
    double r2 = 0.0;

    for (int i = 0; i < cuckoosNumber; i++)
    {
      for (int c = 0; c < coordinates; c++)
      {
        r1 = RNDfromCI (0.0, 1.0);
        r1 = r1 > 0.5 ? 1.0 : -1.0;
        r2 = RNDfromCI (1.0, 20.0);

        cuckoos [i].c [c] = cuckoos [i].c [c] + r1 * v [c] * pow (r2, -2.0);
        cuckoos [i].c [c] = SeInDiSp (cuckoos [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die zweite öffentliche Methode, die bei jeder Iteration aufgerufen wird, ist das „Eierlegen“. Bei dieser Methode wird die Simulation des Legens eines Kuckuckseis in einem Nest algorithmisch nachgebildet. Dies geschieht durch die Auswahl eines zufälligen Nests aus allen vorhandenen Nestern. Danach wird die Qualität des Kuckuckseis mit der des bereits im Nest befindlichen Eies verglichen. Wenn das Kuckucksei besser ist, dann findet ein Austausch statt. Ein interessantes Merkmal des Algorithmus bei dieser Methode ist, dass die Wahrscheinlichkeit, ob das Ei stirbt, nach dem Legen ermittelt wird, auch wenn das Kuckucksei besser geeignet war. Das bedeutet, es gibt eine Wahrscheinlichkeit koef_pa, dass irgendein Ei stirbt, egal, was darin liegt, genau wie in der Natur. Wenn das Ei gestorben ist oder aus dem Nest geworfen wurde, was faktisch dasselbe ist, ist das Nest frei für eine neue Eiablage mit beliebiger, auch geringerer Fitness, was algorithmisch bedeutet, dass an einem neuen Ort geforscht wird.

Auf diese Weise kann eine der Methoden der natürlichen Evolution, wie z. B. der Nestparasitismus, in nur wenigen Zeilen Code beschrieben werden. Viele Autoren empfehlen in ihren Veröffentlichungen, das Nest nach dem Entfernen des Eies mit neuen Zufallswerten zu initialisieren, d.h. die Suche von Anfang an zu beginnen. In den meisten Fällen führt dies nicht zu dem gewünschten Ergebnis in Bezug auf die Verbesserung der Erkundungsfähigkeit des Algorithmus. Meine eigenen Untersuchungen haben gezeigt, dass es sinnvoller ist, das Nest einfach leer zu lassen, damit einer der Kuckucke ein Ei hineinlegen kann, unabhängig von der Qualität des Eies. Dies ist besser als nur zufällige Werte. Die Variabilität in der Studie wird durch zufällige Sprünge in zufällige Richtungen von den aktuellen Koordinaten aus gewährleistet. Infolgedessen sind weniger Iterationen bei der Suche nach der besten Lösung erforderlich, wodurch sich die Konvergenzrate des Algorithmus insgesamt erhöht.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_COA::LayEggs ()
{
  int ind = 0;

  //^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
  for (int i = 0; i < cuckoosNumber; i++)
  {
    ind = (int)round (RNDfromCI (0.0, nestsNumber - 1));

    if (cuckoos [i].e > nests [ind].e)
    {
      nests [ind].e = cuckoos [i].e;
      ArrayCopy (nests [ind].c, cuckoos [i].c, 0, 0, WHOLE_ARRAY);

      if (cuckoos [i].e > eB)
      {
        eB = cuckoos [i].e;
        ArrayCopy (cB, cuckoos [i].c, 0, 0, WHOLE_ARRAY);
      }
    }
    else
    {
      ArrayCopy (cuckoos [i].c, nests [ind].c, 0, 0, WHOLE_ARRAY);
    }
  }
  //vvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv

  for (int n = 0; n < nestsNumber; n++)
  {
    if (RNDfromCI (0.0, 1.0) < koef_pa)
    {
      nests [ind].e = -DBL_MAX;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

4. Testergebnisse

Hier sind die Testergebnisse:

2022.11.30 11:31:54.490    Test_AO_COA_fast (EURUSD,M1)    =============================
2022.11.30 11:31:54.507    Test_AO_COA_fast (EURUSD,M1)    1 Skin; Funktionsdurchläufe 10000 Ergebnis: 4.918379100238852
2022.11.30 11:31:54.507    Test_AO_COA_fast (EURUSD,M1)    Ergebnis: 1.00000
2022.11.30 11:31:54.854    Test_AO_COA_fast (EURUSD,M1)    20 Skins; Funktionsdurchläufe 10000 Ergebnis: 4.257477577760983
2022.11.30 11:31:54.854    Test_AO_COA_fast (EURUSD,M1)    Ergebnis: 0.84220
2022.11.30 11:32:02.346    Test_AO_COA_fast (EURUSD,M1)    500 Skins; Funktionsdurchläufe 10000 Ergebnis: 1.3521208312080903
2022.11.30 11:32:02.346    Test_AO_COA_fast (EURUSD,M1)    Ergebnis: 0.14849
2022.11.30 11:32:02.346    Test_AO_COA_fast (EURUSD,M1)    =============================
2022.11.30 11:32:02.368    Test_AO_COA_fast (EURUSD,M1)    1 Forest; Funktionsdurchläufe 10000 Ergebnis: 1.7600394018343262
2022.11.30 11:32:02.368    Test_AO_COA_fast (EURUSD,M1)    Ergebnis: 0.99557
2022.11.30 11:32:02.775    Test_AO_COA_fast (EURUSD,M1)    20 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.4968964923017033
2022.11.30 11:32:02.775    Test_AO_COA_fast (EURUSD,M1)    Ergebnis: 0.28107
2022.11.30 11:32:13.125    Test_AO_COA_fast (EURUSD,M1)    500 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.07638950254648778
2022.11.30 11:32:13.125    Test_AO_COA_fast (EURUSD,M1)    Ergebnis: 0.04321
2022.11.30 11:32:13.125    Test_AO_COA_fast (EURUSD,M1)    =============================
2022.11.30 11:32:13.148    Test_AO_COA_fast (EURUSD,M1)    1 Megacity; Funktionsdurchläufe 10000 Ergebnis: 12.0
2022.11.30 11:32:13.148    Test_AO_COA_fast (EURUSD,M1)    Ergebnis: 1.00000
2022.11.30 11:32:13.584    Test_AO_COA_fast (EURUSD,M1)    20 Megacities; Funktionsdurchläufe 10000 Ergebnis: 2.69
2022.11.30 11:32:13.584    Test_AO_COA_fast (EURUSD,M1)    Ergebnis: 0.22417
2022.11.30 11:32:24.379    Test_AO_COA_fast (EURUSD,M1)    500 Megacities; Funktionsdurchläufe 10000 Ergebnis: 0.40800000000000003
2022.11.30 11:32:24.379    Test_AO_COA_fast (EURUSD,M1)    Ergebnis: 0.03400
2022.11.30 11:32:24.379    Test_AO_COA_fast (EURUSD,M1)    =============================
2022.11.30 11:32:24.379    Test_AO_COA_fast (EURUSD,M1)    Alle Ergebnisse für C_AO_COA: 0.507633670637353

Der Suchalgorithmus von Levy Flight Cuckoo zeigte beeindruckende Ergebnisse. In den meisten Tests schnitt er besser ab als andere Optimierungsalgorithmen. Insbesondere zeigte der Algorithmus 100% Konvergenz für die glatte Skin-Funktion mit zwei Variablen und für die diskrete Megacity-Funktion mit zwei Variablen. Was noch überraschender ist, ist die hervorragende Skalierbarkeit bei einer diskreten Funktion. In anderen Tests ist er dem Ameisenkolonie-Algorithmus nur geringfügig unterlegen. Zurzeit haben wir einen unbestrittenen Spitzenreiter in der Bewertungstabelle.

Ich möchte klarstellen, dass alle Algorithmen Abstimmungsparameter haben, die das Endergebnis in gewissem Maße beeinflussen. Es ist also durchaus möglich, dass einige dieser Algorithmen noch optimalere Parameter haben und die Bewertungstabelle anders aussehen kann. Ich habe nur die Ergebnisse der Tests mit den Parametern gezeigt, die ich finden konnte, um das beste Ergebnis zu gewährleisten. Wenn es Ihnen gelingt, optimalere Parameter zu finden und bessere Ergebnisse zu erzielen, kann ich die Bewertungstabelle anhand dieser Parameter korrigieren. Es wird davon ausgegangen, dass der Ameisenalgorithmus erfolgreich mit dem derzeit führenden Algorithmus konkurrieren kann, da er bei einigen Indikatoren vor dem Kuckuckssuchalgorithmus liegt und bei den Endindikatoren nur minimal hinter ihm zurückbleibt. GWO ist immer noch führend bei der Skin-Funktion mit 1000 Variablen. In jedem Fall können diejenigen, die in ihren Projekten Algorithmen zur Lösung ihrer Optimierungsprobleme verwenden werden, in der Tabelle navigieren und einen Algorithmus für ihre spezifischen Bedürfnisse auswählen.

Skin

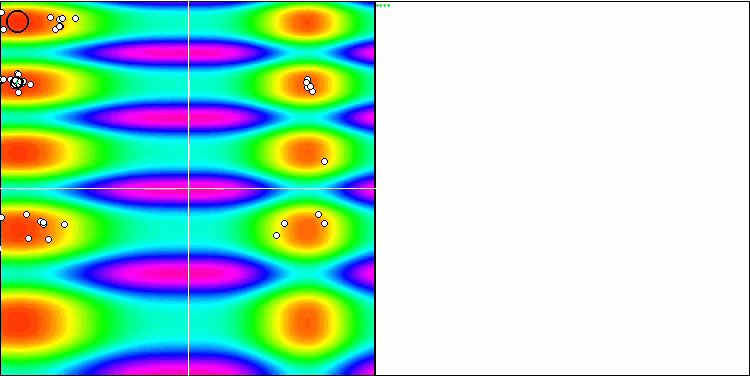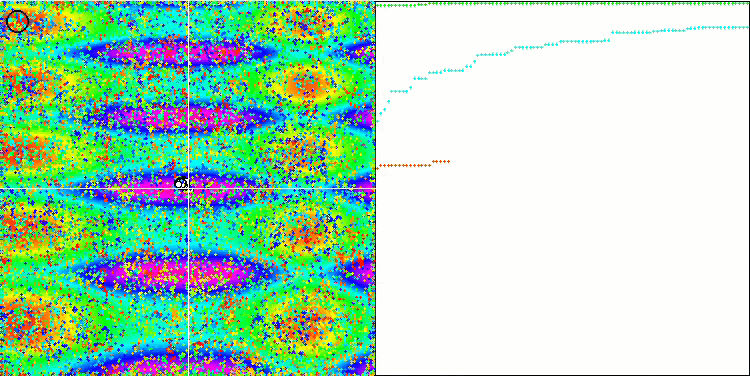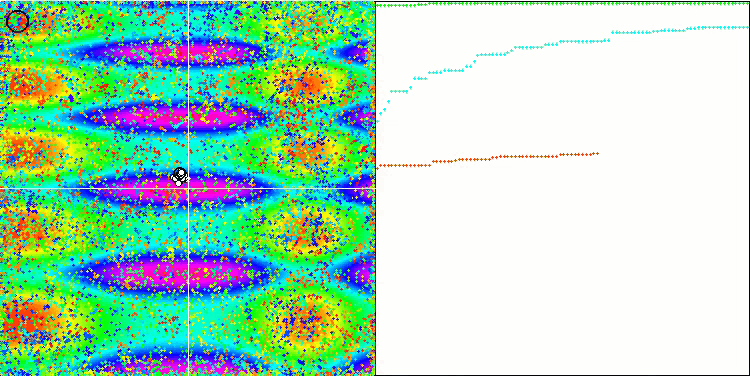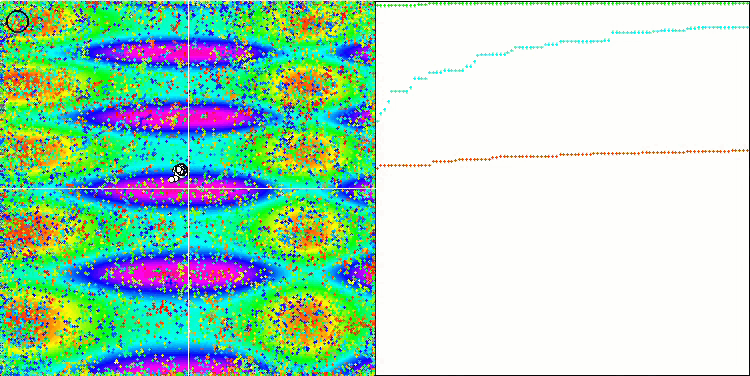
ACO mit der Testfunktion Skin

Forest

ACO mit der Testfunktion Forest

Megacity

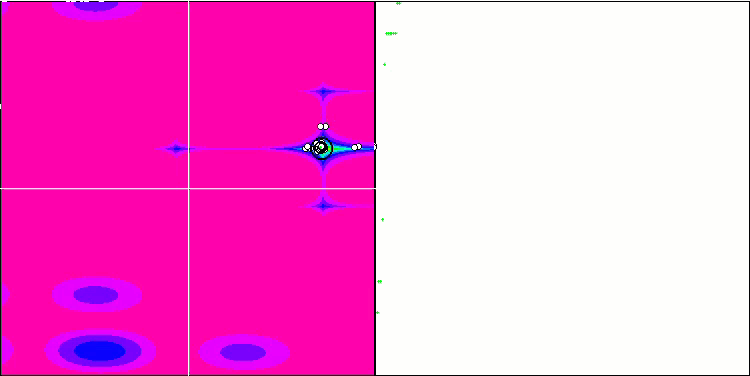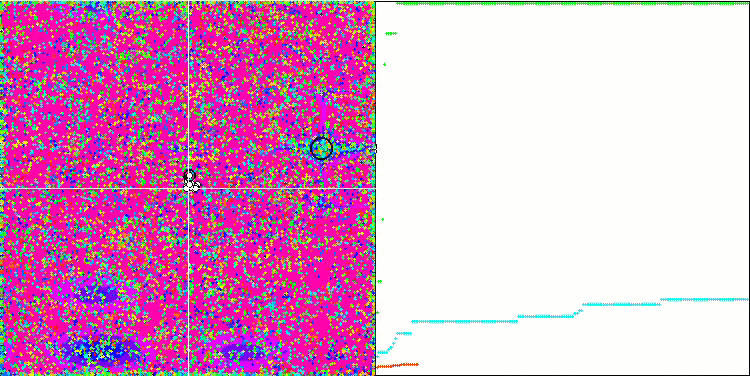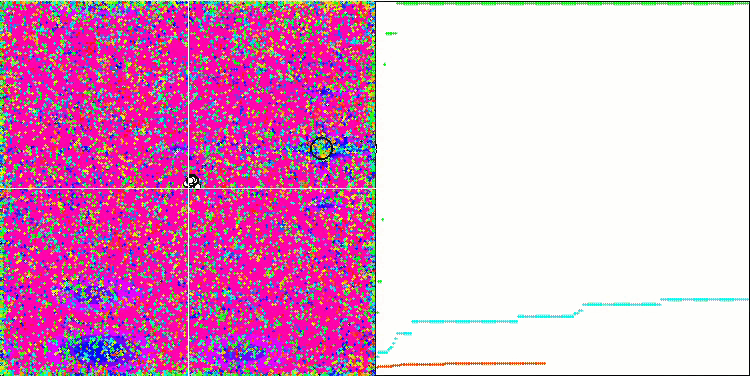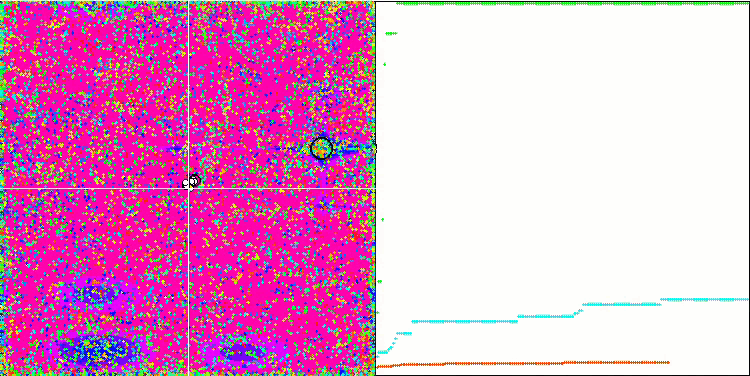
ACO mit der Testfunktion Megacity

Bei der Visualisierung der Testentwicklung unterscheidet sich das Verhalten des Algorithmus von den zuvor betrachteten Algorithmen, jedoch gibt es einige Merkmale, die für Algorithmen charakteristisch sind, die die Aufgabe in Untersuchungsbereiche aufteilen, wie z. B. der Bienenvolk-Algorithmus. Dies kennzeichnet die Fähigkeit des Algorithmus, sich nicht auf ein einziges Extremum zu konzentrieren, sondern mehrere potenziell vielversprechende Bereiche zu erkunden, was den Algorithmus davor bewahrt, in lokalen Extremen stecken zu bleiben. In dieser Hinsicht könnte der Algorithmus verbessert werden, indem die Nester sortiert und vom Kuckuck entsprechend ihrer Qualität ausgewählt werden. Dies würde bedeuten, dass der Kuckuck Nester auswählt, anstatt ein Ei in ein zufällig ausgewähltes Nest zu legen, wie in der kanonischen Version des Algorithmus. Dies führte jedoch nicht zu einer Verbesserung der Ergebnisse, was die Zweckmäßigkeit der zufälligen Auswahl der Nester belegt. Vielleicht ist dies ein Abbild dessen, was in der Natur geschieht. Das Ersetzen eines Eies im Falle intelligenterer Wirte ist schwieriger, sodass es zufällig und statistisch nicht gerechtfertigt ist.

Ein weiteres Merkmal des Algorithmus ist, dass er sich wie ein Random Walk auf Funktionen mit vielen Variablen verhält. Optisch sieht es aus wie weißes Rauschen oder ein alter Fernsehbildschirm. Eine gewisse Konzentration der Koordinaten an den Orten der lokalen Extrema ist erst am Ende der Iterationen zu erkennen. Ich möchte eine klarere „Kristallisierung“ der Parameter erreichen, wie es beim Ameisenkolonie-Algorithmus der Fall ist. Damit sind wir bei dem allgemeinen Problem aller Optimierungsalgorithmen angelangt, für das es keine allgemeine Lösung gibt. Viele Autoren klassischer und relativ neuer Algorithmen haben versucht, dieses Problem zu lösen.

Das Problem besteht im Wesentlichen darin, dass nicht sicher bekannt ist, welcher der optimierten Parameter der zu untersuchenden Funktion Vorrang oder Stärke hat, und dass nicht bekannt ist, in welchem Umfang und wie jeder der Parameter das Ergebnis beeinflusst. Es gibt zum Beispiel mehrere Parameter und der Algorithmus hat bereits den richtigen gefunden, aber welcher genau, ist unbekannt. Der Algorithmus wird immer wieder versuchen, sie alle zu ändern, obwohl es ausreicht, nur einige wenige zu ändern, um das globale Extrem zu erreichen. Das Problem verschärft sich noch, wenn es sich um eine Funktion mit vielen zehntausenden Variablen handelt. Je mehr Variablen, desto akuter das Problem. Optisch sieht dies wie weißes Rauschen auf dem Bildschirm aus.

Ich habe einen Versuch unternommen, dieses Problem zumindest teilweise zu lösen. Wenn nicht von vornherein bekannt ist, welche Parameter der zu untersuchenden Funktion geändert werden sollen und welche gleich bleiben sollen, kann man versuchen, dies auf probabilistische Weise zu lösen. Wir gehen davon aus, dass nur ein Teil aller Parameter geändert werden muss, und zwar nicht alle gleichzeitig. Der PSO-Algorithmus verhält sich auf eine charakteristische Weise. Wenn die Anzahl der Parameter (Argumente) der optimierten Funktion zunimmt, verhält sie sich wie eine Wolke, die sich nicht konzentrieren kann. Zu diesem Zweck habe ich einen neuen Parameter für den Algorithmus eingeführt, der die Wahrscheinlichkeit festlegt, dass die Koordinate geändert wird, andernfalls wird sie unverändert gelassen.

Und das Ergebnis ist... Positiv!!! Die Testergebnisse haben sich verbessert. Die „Kristallisierung“, die ich erreichen wollte, ist bei Funktionen mit vielen Variablen aufgetreten.

Die Ergebnisse des Prüfstands sehen wie folgt aus:

2022.12.03 16:01:26.256    Test_AO_COAm (EURUSD,M1)    =============================
2022.12.03 16:01:27.511    Test_AO_COAm (EURUSD,M1)    1 Skin; Funktionsdurchläufe 10000 Ergebnis: 4.918367945334852
2022.12.03 16:01:27.511    Test_AO_COAm (EURUSD,M1)    Ergebnis: 1.00000
2022.12.03 16:01:30.291    Test_AO_COAm (EURUSD,M1)    20 Skins; Funktionsdurchläufe 10000 Ergebnis: 4.328327964103814
2022.12.03 16:01:30.291    Test_AO_COAm (EURUSD,M1)    Ergebnis: 0.85911
2022.12.03 16:01:59.306    Test_AO_ABCm (EURUSD,M1)    500 Skins; Funktionsdurchläufe 10000 Ergebnis: 1.3297901702583084
2022.12.03 16:01:59.306    Test_AO_COAm (EURUSD,M1)    Ergebnis: 0.14316
2022.12.03 16:01:59.306    Test_AO_COAm (EURUSD,M1)   =============================
2022.12.03 16:02:00.511    Test_AO_ABCm (EURUSD,M1)    1 Forest; Funktionsdurchläufe 10000 Ergebnis: 1.755200932219688
2022.12.03 16:02:00.511    Test_AO_COAm (EURUSD,M1)    Ergebnis: 0.99283
2022.12.03 16:02:03.566    Test_AO_ABCm (EURUSD,M1)    20 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.5089243656052672
2022.12.03 16:02:03.566    Test_AO_COAm (EURUSD,M1)    Ergebnis: 0.28787
2022.12.03 16:02:35.468    Test_AO_ABCm (EURUSD,M1)    500 Forests; Funktionsdurchläufe 10000 Ergebnis: 0.08044934398920801
2022.12.03 16:02:35.468    Test_AO_COAm (EURUSD,M1)    Ergebnis: 0.04551
2022.12.03 16:02:35.468    Test_AO_COAm (EURUSD,M1)   =============================
2022.12.03 16:02:36.628    Test_AO_ABCm (EURUSD,M1)    1 Megacities; Funktionsdurchläufe 10000 Ergebnis: 12.0
2022.12.03 16:02:36.628    Test_AO_COAm (EURUSD,M1)    Ergebnis: 1.00000
2022.12.03 16:02:39.628    Test_AO_ABCm (EURUSD,M1)    20 Megacities; Funktionsdurchläufe 10000 Ergebnis: 2.9899999999999998
2022.12.03 16:02:39.628    Test_AO_COAm (EURUSD,M1)    Ergebnis: 0.24917
2022.12.03 16:03:11.892    Test_AO_ABCm (EURUSD,M1)    500 Megacities; Funktionsdurchläufe 10000 Ergebnis: 0.4244
2022.12.03 16:03:11.892    Test_AO_COAm (EURUSD,M1)   Ergebnis: 0.03537
2022.12.03 16:03:11.892    Test_AO_COAm (EURUSD,M1)   =============================
2022.12.03 16:03:11.892    Test_AO_COAm (EURUSD,M1)   Alle Ergebnisse für C_AO_COAm: 0.5125572342985216

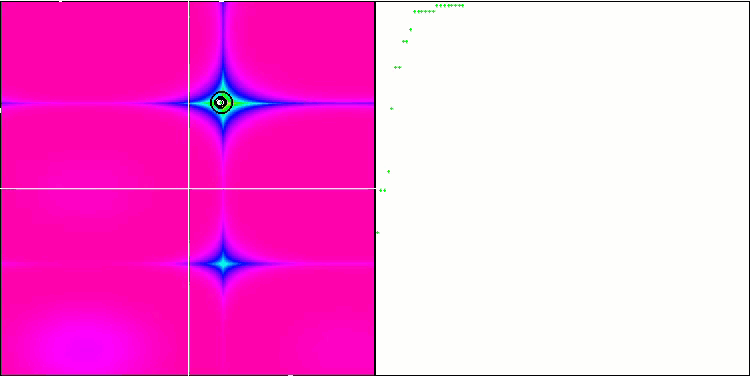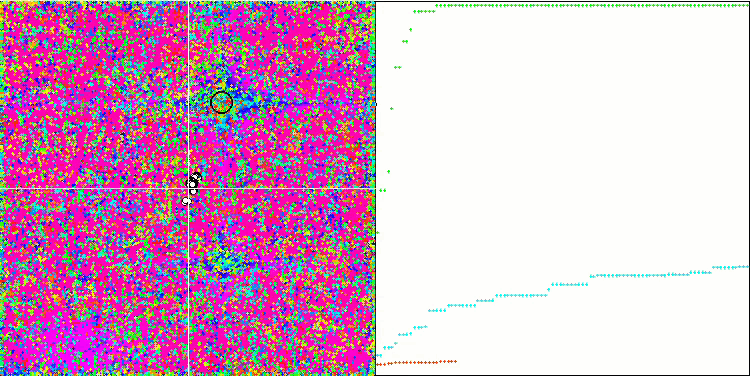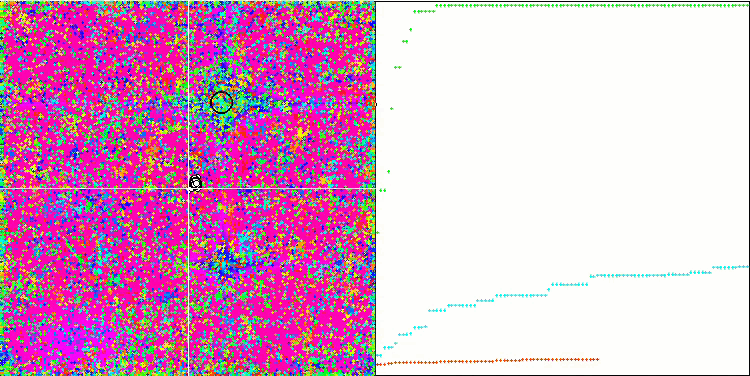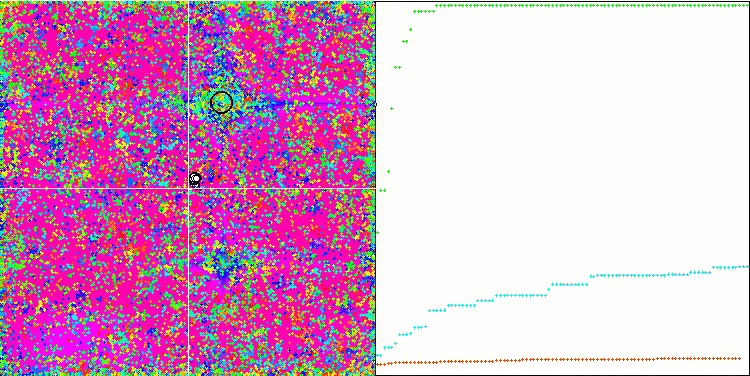
In der Visualisierung ist die „Kristallisation“ deutlich zu erkennen. Der Bildschirm, der zunächst wie ein weißes Rauschen aussieht, wird gelöscht, die Koordinaten beginnen sich zu konzentrieren, die Konzentrationszentren werden mobil:

cristal

ACO mit der Testfunktion Megacity Der Effekt der „Kristallisation“ ist deutlicher sichtbar.

Auf der einen Seite steht die Variabilität, d. h. die Fähigkeit, dynamisch nach neuen Bereichen zu suchen, auf der anderen Seite die Fähigkeit, die Koordinaten bereits erreichter Extreme zu klären. Unten sehen Sie die Animation des Ameisenkolonie-Algorithmus mit einer ausgeprägten „Kristallisation“ zum Vergleich:

cristACO

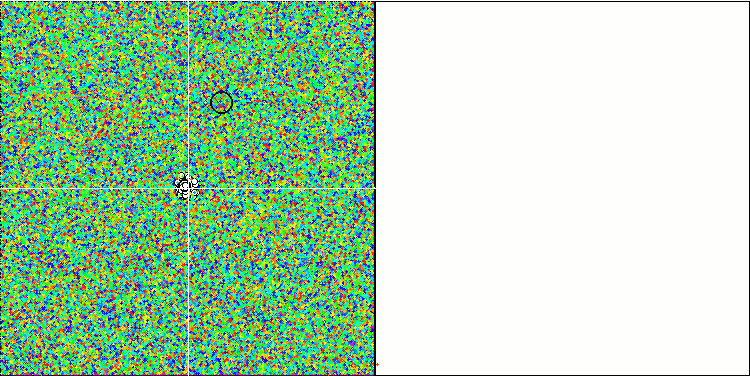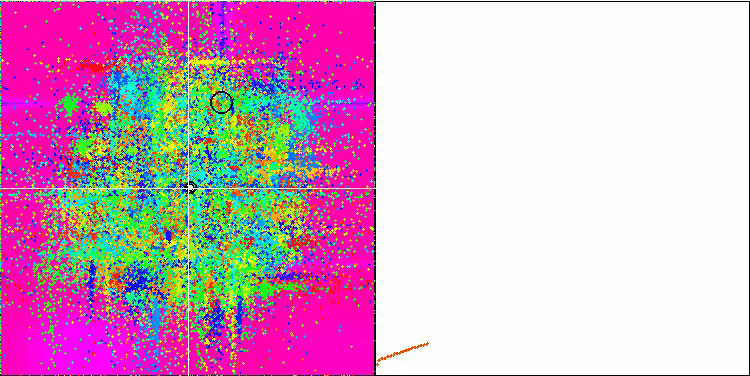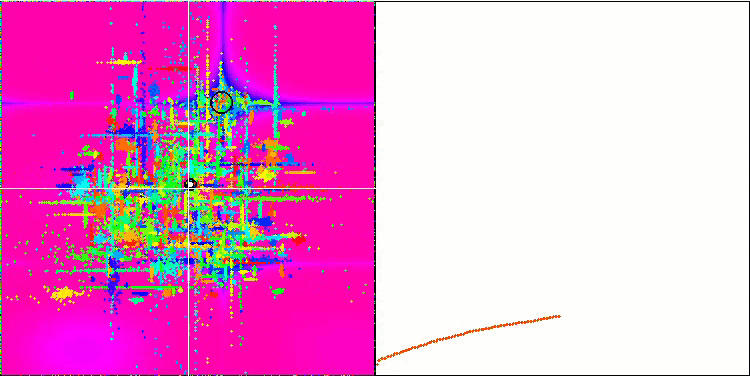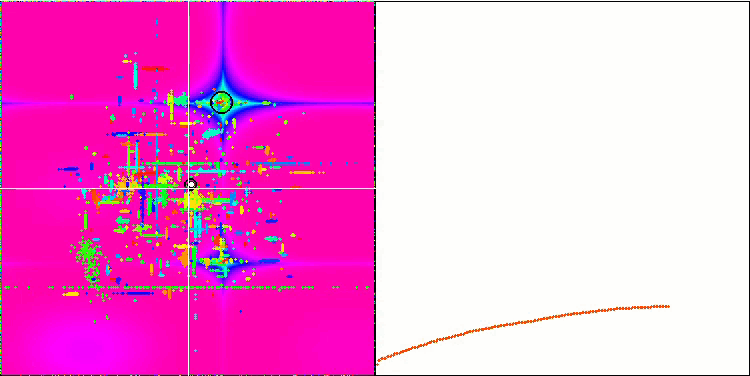
ACO mit der Testfunktion Forest

Testergebnisse

AO	Beschreibung	Skin			Forest			Megacity (diskret)			Endergebnis
AO	Beschreibung	2 Parameter (1 F)	40 Parameter (20 F)	1000 Parameter (500 F)	2 Parameter (1 F)	40 Parameter (20 F)	1000 Parameter (500 F)	2 Parameter (1 F)	40 Parameter (20 F)	1000 Parameter (500 F)	Endergebnis
COAm	Kuckuck-Optimierungsalgorithmus	1.00000	0.85911	0.14316	0.99283	0.28787	0.04551	1.00000	0.24917	0.03537	0.51255778
ACOm	Ameisenkolonie-Optimierung (ACO)	0.98229	0.79108	0.12602	1.00000	0.62077	0.11521	0.38333	0.44000	0.02377	0.49805222
ABCm	Künstliches Bienenvolk M (Artificial Bee Colony, ABC)	1.00000	0.63922	0.08076	0.99908	0.20112	0.03785	1.00000	0.16333	0.02823	0.46106556
ABC	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	0.99339	0.73381	0.11118	0.99934	0.21437	0.04215	0.85000	0.16833	0.03130	0.46043000
GWO	Grauer-Wolf-Optimierung	0.99900	0.48033	0.18924	0.83844	0.08755	0.02555	1.00000	0.10000	0.02187	0.41577556
PSO	Partikelschwarmoptimierung	0.99627	0.38080	0.05089	0.93772	0.14540	0.04856	1.00000	0.09333	0.02233	0.40836667
RND	zufällig	0.99932	0.44276	0.06827	0.83126	0.11524	0.03048	0.83333	0.09000	0.02403	0.38163222

Ein Vorteil des Kuckuckssuchalgorithmus ist, dass bei der globalen Suche Flüge oder ein Levy-Prozess anstelle von Standard-Zufallswegen verwendet werden. Da Levy-Flüge einen unendlichen Mittelwert und eine unendliche Varianz haben, kann COA den Suchraum effizienter erkunden als Standard-Gauß-Prozess-Algorithmen. Levy-Flug: Ein Random-Walk-Prozess, der durch eine Reihe von augenblicklichen Sprüngen gekennzeichnet ist, die aus einer Wahrscheinlichkeitsdichtefunktion ausgewählt werden, die einen Potenzgesetz-Schwanz hat.

Derzeit führt der Algorithmus die Tabelle an, wobei er andere Algorithmen in einzelnen Tests deutlich übertrifft und auch in anderen „Disziplinen“ nicht weit zurückbleibt. Es gibt hervorragende Ergebnisse für die diskrete Funktion Megacity mit 1000 Argumenten, was die Kuckuckssuche zu einem großartigen Werkzeug für die Aufgaben von Händlern macht (die in den meisten Fällen diskret sind). Hervorragende (aber nicht die besten) Ergebnisse für die Skin-Funktion mit 1000 Argumenten lassen darauf schließen, dass der Algorithmus für das Training neuronaler Netze im Besonderen und für maschinelles Lernen im Allgemeinen geeignet ist.

Vorteile:
1. Hohe Geschwindigkeit.
2. Vielseitigkeit. Der Algorithmus kann für eine Vielzahl von Optimierungsproblemen verwendet werden.
3. Die Fähigkeit, sich nicht nur auf lokale Extrema zu konzentrieren.
4. Ziemlich gute Konvergenz sowohl für kontinuierliche als auch für diskrete Funktionen.
5. Skalierbar.

Nachteile
1. Viele Einstellungen.

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/11786

Beigefügte Dateien |

ZIP herunterladen

26_The_world_of_AO_8COAn.zip (57.59 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum

DoEasy. Steuerung (Teil 29): Das Hilfssteuerelement der ScrollBar

In diesem Artikel werde ich mit der Entwicklung des ScrollBar-Hilfssteuerelements und seiner abgeleiteten Objekte beginnen — vertikale und horizontale Bildlaufleisten. Eine Bildlaufleiste wird verwendet, um den Inhalt des Formulars zu verschieben, wenn er über den Container hinausgeht. Die Bildlaufleisten befinden sich in der Regel am unteren und rechten Rand des Formulars. Die horizontale am unteren Rand blättert den Inhalt nach links und rechts, während die vertikale nach oben und unten blättert.

DoEasy. Steuerung (Teil 28): Balkenstile im ProgressBar-Steuerelement

In diesem Artikel werde ich Anzeigestile und Beschreibungstext für die Fortschrittsleiste des Steuerelements der ProgressBar entwickeln.

DoEasy. Steuerung (Teil 30): Animieren des ScrollBar-Steuerelements

In diesem Artikel werde ich die Entwicklung des ScrollBar-Steuerelements fortsetzen und mit der Implementierung der Interaktionsfunktionen der Maus beginnen. Außerdem werde ich die Listen der Status-Flags der Maus und der Ereignisse erweitern.

MQL5 Kochbuch — Dienste

Der Artikel beschreibt die vielseitigen Möglichkeiten der Dienste — MQL5-Programme, die nicht an Charts gebunden sind. Ich werde auch die Unterschiede von Diensten zu anderen MQL5-Programmen hervorheben und die Feinheiten der Arbeit des Entwicklers mit Diensten betonen. Als Beispiele werden dem Leser verschiedene Aufgaben angeboten, die ein breites Spektrum an Funktionen abdecken, die als Dienst implementiert werden können.