
Algorithmen zur Optimierung mit Populationen: Saplings Sowing and Growing up (SSG)
Inhalt:
1. Einführung
2. Algorithmus
3. Testergebnisse
1. Einführung
Alle lebenden Organismen in der Natur unterliegen bestimmten Gesetzen. Dies hilft ihnen, unter wechselnden Umweltbedingungen zu überleben. Für die Anpassungsfähigkeit von Pflanzen an die Umwelt gibt es verschiedene Möglichkeiten. Einige von ihnen sind in der Lage, jahreszeitliche Veränderungen zu tolerieren, andere können sich an Feuchtigkeitsmangel, hohe oder niedrige Temperaturen und das Fehlen von Bestäubern anpassen. Einer der stabilsten Organismen unter den Pflanzen sind die Bäume, von denen einige mehr als 50.000 Jahre lang leben und Kolonien bilden können.
Die Natur ist ein unerschöpfliches Inspirationsfeld für viele wirksame Ideen bei der Entwicklung und Erfindung von Berechnungsmethoden. In der Tat ist das evolutionäre Rechnen eine Projektion der Evolution in Computersimulationen. Es gibt viele Optimierungsmethoden, die von in der Natur vorkommenden Prozessen inspiriert sind, z. B. evolutionäre Berechnungen, künstliche Immunologie, Populationsmethoden und andere. SSG wird grundsätzlich als iterativer Generierungs- und Kombinationsprozess definiert, der mit einem Garten potenzieller Lösungen arbeitet, die als Keimlinge bezeichnet werden. Der SSG-Algorithmus (Saplings Sowing and Growing, Setzen, Säen und Wachsen) wurde von A. Karci und seinen Mitautoren im Jahr 2002 vorgeschlagen. Der Algorithmus ist von der Evolution wachsender Bäume inspiriert und modelliert das Wachstum und die Zweigbildung von Bäumen.
2. Algorithmus
Der Algorithmus ist einer der wenigen, die von den Autoren nicht klar beschrieben werden (es werden nur allgemeine Bestimmungen und Ideen geliefert). Auch die von den Autoren vorgestellten Algorithmus-Operatoren sind keine vorgefertigten Anweisungen für die algorithmische Implementierung des Programms. Es gibt keine klaren Anweisungen für Kinder- und Elternbäume und deren Interaktion. Es gibt keine Vorgaben für die Reihenfolge, in der die Operatoren ausgeführt werden, und jeder Nutzer kann seine Reihenfolge ändern, um einen besseren Setzling zu erhalten.
Im weitesten Sinne ist SSG kein Optimierungsalgorithmus, sondern ein allgemeiner Satz von Regeln, der andere Algorithmen ergänzen soll, um die Qualität der Optimierung zu verbessern. Mit anderen Worten: SSG ist ein Add-on für jeden evolutionären Populationsalgorithmus, sodass ich Raum für Phantasie und die Möglichkeit habe, mit einer spezifischen Implementierung des Optimierungsalgorithmus zu experimentieren. Ich habe einige meiner eigenen Gedanken und Erfahrungen beim Schreiben früherer Algorithmen angewandt und sie bei der Arbeit mit SSG eingesetzt. Die Ergebnisse der Versuche werden im Folgenden zur Beurteilung durch den Leser dargestellt.
Um den Algorithmus zu verstehen, müssen wir uns einen Baum als einen Optimierungsagenten vorstellen. Ein Baum ist eine Lösung für ein Optimierungsproblem, wobei jeder Zweig ein optimierter Parameter des Problems ist. Eine abstrakte und künstlerische Darstellung von Kind- und Elternbäumen ist in Abbildung 1 zu sehen. Der Baumstamm ist eine Reihe von zu optimierenden Parametern. Jeder Zweig ist ein separater optimierter Parameter, wobei die Länge des Zweigs durch den zulässigen Wertebereich des entsprechenden Parameters begrenzt ist. Die Richtung der Zweige spielt keine Rolle und wird in der Abbildung nur gezeigt, um ihren Unterschied zu verdeutlichen.
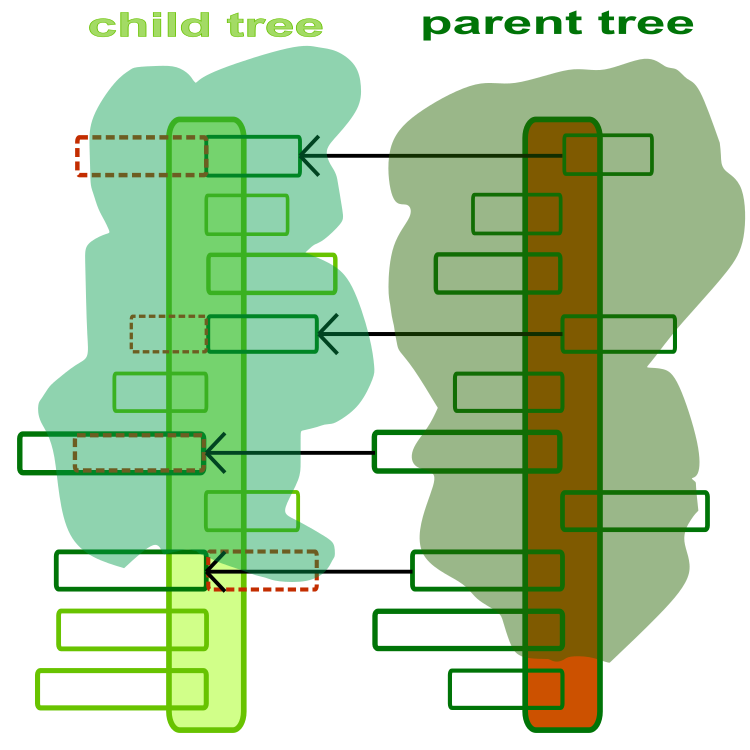
Bild 1. Kind- und Elternbaum. Die gestrichelte Linie zeigt an, dass die untergeordneten Zweige durch die übergeordneten Zweige ersetzt wurden.
Die Zweige der Bäume sind also die Koordinaten der Bäume im Suchraum.
Der SSG-Algorithmus besteht aus Variationsoperatoren, die neue Lösungen - Kandidaten für den gemeinsamen Lösungspool - erzeugen. Die wichtigsten Variationsoperatoren sind Kreuzung, Zweigbildung und Impfung. Die Setzlinge sollten in gleichem Abstand zueinander gepflanzt werden (Westen, Osten, Norden, Süden), und dies ist die erste Phase der Methode. Wenn die Koordinaten (optimierte Parameter) viel mehr als drei sind, dann ist die „gleichmäßige“ Bepflanzung eine einfache Zufallsverteilung von Setzlingen über den Suchraum. Dann wachsen die Sämlinge heran, kreuzen sich, bilden Zweige und der Impfprozess findet statt.
Betrachten wir nun die Schritte und Operatoren des SSG-Algorithmus:
1) Anpflanzen von Setzlingen.
Man kann sich den Suchraum als einen Garten von Setzlingen vorstellen, und daher müssen alle Setzlinge gleichmäßig im Garten verteilt werden. Bei der Aussaat sät der Landwirt die Setzlinge einfach in gleichem Abstand zueinander aus, damit die Setzlinge schneller wachsen, ohne sich gegenseitig zu behindern. Um das Problem durch Simulation des Anbaus von Setzlingen zu lösen, müssen die anfangs zu generierenden willkürlichen Lösungen gleichmäßig im gültigen Suchraum verteilt werden.
Wenn es zwei oder drei Koordinaten gibt, ist es kein Problem, die Setzlinge gleichmäßig zu verteilen, aber wenn es viel mehr als drei Koordinaten gibt, ist es einfacher, eine Zufallsverteilung zu verwenden. In der Praxis ist es bei einer geringen Anzahl von Koordinaten nicht notwendig, sich um die gleichmäßige Verteilung der Setzlinge zu kümmern, da diese Aufgabe kein großes Problem darstellt und die Lösung mit hoher Genauigkeit erzielt wird. Unabhängig von der Anzahl der Koordinaten im Algorithmus werden wir daher eine zufällige Verteilung der Setzlinge im Garten verwenden.
2) Anzucht von Setzlingen (Bäumen), drei nacheinander ausgeführte Operatoren.
2.1) Kreuzung.
Der Zweck des Operators „Kreuzung“ besteht darin, einen neuen Sämling aus bereits vorhandenen Sämlingen zu erzeugen, indem Informationen zwischen ihnen ausgetauscht werden. Eine Kreuzung ist im Wesentlichen die Verpflanzung einer Kopie von einem Zweig des Elternbaum auf den Kindbaum (Abbildung 1). Für jedes Sämlingspaar wird ein anderer Kreuzungskoeffizient verwendet, der die Wahrscheinlichkeit der Kreuzung angibt. Die Wahrscheinlichkeit einer Kreuzung hängt vom Abstand zwischen den Sämlingen eines Paares ab, je größer der Abstand, desto geringer die Wahrscheinlichkeit einer Kreuzung. Der Kreuzungsoperator ist eine sehr wichtige Methode des Algorithmus, die kombinatorische Mechanismen bereitstellt. Die Kombination von Informationen zwischen Agenten kann die Gesamtqualität des Optimierungsalgorithmus erheblich verbessern.
2.2) Zweigbildung.
Der Operator modelliert das Wachstum von Zweigen. Das Wachstum kann entweder positiv (strecken) oder negativ (austrocknen) sein. „Um einen Zweig an irgendeiner Stelle des Keimlings wachsen zu lassen, darf es in der Nähe keinen Zweig geben, der dort schon einmal gekeimt ist“. Dies ist eine ungefähre Beschreibung des Operators durch die Autoren des Algorithmus. Dieser Prozess ist einfacher und klarer, als es auf den ersten Blick scheinen mag, und besteht in einer Änderung der bestehenden Zweige des untergeordneten Baums (die spezifische Methode der Änderung ist nicht angegeben).
Die Änderung jedes einzelnen Zweiges ist umso wahrscheinlicher, je mehr Iterationen zwischen der aktuellen Iteration und derjenigen, bei der die letzte Änderung des Zweiges vorgenommen wurde, vergangen sind. Meine Experimente haben gezeigt, dass dieser Operator ineffizient ist. Außerdem gibt es keine direkten Hinweise auf die Anwendung der Änderungsmethode, und ich habe in dieser Angelegenheit die Initiative ergriffen und die Änderung der Länge des Zweigs nach dem Levy-Flugverteilungsgesetz angewendet. Die Änderung wird mit der Wahrscheinlichkeit und der Intensität durchgeführt, die als externe Parameter des Algorithmus angegeben werden.
2.3) Impfung.
Die Impfung findet zwischen zwei verschiedenen Sämlingen statt, wenn die Sämlinge ähnlich sind. Die Ähnlichkeit der Sämlinge wirkt sich auf den Erfolg der Impfung aus und ist proportional zum arithmetischen Mittel des gewichteten Abstands. Der Operator ähnelt dem Kreuzungsoperator und besteht aus dem Austausch von Zweigen, was dem Algorithmus eine zusätzliche Möglichkeit bietet, Informationen zwischen Agenten zu kombinieren. Der Operator wird in dem Artikel hervorgehoben, aber dieser Operator ist in den Quellcodes auskommentiert und die Testergebnisse werden ohne seine Beteiligung dargestellt, da die Impfung die Ergebnisse verschlechtert.
3) Berechnung der Fitness von Bäumen.
4) Anpflanzen neuer Setzlinge im Garten.
Bei den durch Kreuzung, Zweigbildung und Impfung gewonnenen Sämlingen handelt es sich um vorübergehende Lösungen (Tochtergarten). In diesem Stadium müssen die n besten Setzlinge (ein externer Parameter des Algorithmus) ausgewählt und in den Garten gesetzt werden, um die n schlechtesten Bäume im Garten zu ersetzen. Es sei darauf hingewiesen, dass der Ersatz durch Setzlinge in jedem Fall erfolgen wird, auch wenn sie schlechter sind als die schlechtesten Bäume im Garten.
Dies ist ein guter Zeitpunkt, um einen Blick auf den Code des wachsenden Baumalgorithmus zu werfen, was uns dem spannenden Höhepunkt dieser Studie - der Überprüfung der Testergebnisse - immer näher bringt.
Daher ist es sinnvoll, jeden Baum als Gartenstruktur darzustellen, die als Grundlage für die Anlage eines blühenden Gartens dienen soll. In diesem Algorithmus gibt es nichts Einfacheres als die Entität „Baum“, die nur zwei Komponenten benötigt: die Koordinaten mit [] und den Fitnesswert f.
//—————————————————————————————————————————————————————————————————————————————— struct S_Garden { double c []; //coordinates double f; //fitness }; //——————————————————————————————————————————————————————————————————————————————
Die Klasse C_AO_SSG des SG-Algorithmus ist nichts Besonderes. Alles hier ist uns von den zuvor betrachteten Algorithmen sehr vertraut. In der Klasse werden wir Mitglieder und Methoden deklarieren, um mit den Eltern- und Kindergärten zu arbeiten. Ein temporärer Garten ist für das Funktionieren der Sortiermethode erforderlich, da wir sowohl den untergeordneten als auch den übergeordneten Garten sortieren müssen. Wir deklarieren ein Array mit den besten Koordinaten der Gesamtlösung und dem besten Fitnesswert sowie konstante Variablen zur Speicherung der externen Parameter des Algorithmus.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_SSG { //============================================================================ public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: S_Garden pGarden []; //parent's garden public: S_Garden cGarden []; //child's garden public: S_Garden gardenT []; //temp garden public: double cB []; //best coordinates public: double fB; //fitness of the best coordinates public: void Init (const int coordinatesP, //Number of coordinates const int numberTreesP, //Number of trees const double seedlingsReplacementP, //Seedlings replacement const double probabMatingOperatorP, //Probability mating operator const double probabBranchOperatorP, //Probability branching operator const double powerBranchOperatorP); //Power branching operator public: void Sowing (int iter); public: void Germination (); //============================================================================ private: void Sorting (S_Garden &garden []); private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double Min, double Max); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers); private: double vec []; //Vector private: int ind []; private: double val []; private: double r; private: bool sowing; //Sowing private: int coordinates; //Coordinates number private: int numberTrees; //Number of trees private: int seedlingsReplacement; //Seedlings replacement private: double probabMatingOperator; //Probability mating operator private: double probabBranchOperator; //Probability branching operator private: double powerBranchOperator; //Power branching operator }; //——————————————————————————————————————————————————————————————————————————————
In der Initialisierungsmethode Init() weisen wir Speicher für Arrays und die Werte der konstanten Parameter zu. Da der Parameter seedlingsReplacementP in Bruchteilen der Gartengröße (von 0,0 bis 1,0) angegeben wird, die für die Anzahl der im Elterngarten zu pflanzenden Setzlinge verantwortlich ist, sollte er in eine ganzzahlige Darstellung der Gartengröße umgewandelt werden. Setzen wir das ursprüngliche Garten-Setzling-Flag zurück und initialisieren die globale Entscheidungsvariable mit dem kleinstmöglichen ‚double‘-Wert.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_SSG::Init (const int coordinatesP, //Number of coordinates const int numberTreesP, //Number of trees const double seedlingsReplacementP, //Seedlings replacement const double probabMatingOperatorP, //Probability mating operator const double probabBranchOperatorP, //Probability branching operator const double powerBranchOperatorP) //Power branching operator { MathSrand (GetTickCount ()); sowing = false; fB = -DBL_MAX; coordinates = coordinatesP; numberTrees = numberTreesP; if (seedlingsReplacementP >= 1.0) { seedlingsReplacement = numberTreesP; } else { if (seedlingsReplacementP <= 0.0) { seedlingsReplacement = 1; } else seedlingsReplacement = int(numberTreesP * seedlingsReplacementP); } probabMatingOperator = probabMatingOperatorP; probabBranchOperator = probabBranchOperatorP; powerBranchOperator = powerBranchOperatorP; ArrayResize (rangeMax, coordinates); ArrayResize (rangeMin, coordinates); ArrayResize (rangeStep, coordinates); ArrayResize (vec, coordinates); ArrayResize (cB, coordinates); ArrayResize (pGarden, numberTrees); ArrayResize (cGarden, numberTrees); ArrayResize (gardenT, numberTrees); ArrayResize (ind, numberTrees); ArrayResize (val, numberTrees); for (int i = 0; i < numberTrees; i++) { ArrayResize (pGarden [i].c, coordinates); ArrayResize (cGarden [i].c, coordinates); ArrayResize (gardenT [i].c, coordinates); cGarden [i].f = -DBL_MAX; } } //——————————————————————————————————————————————————————————————————————————————
Die erste öffentliche Methode, die bei jeder Iteration aufgerufen wird, Sowing(), ist die Aussaat. Bei der ersten Iteration, wenn der Algorithmus gerade läuft, werden wir die Setzlinge nach dem Zufallsprinzip mit einer gleichmäßigen Verteilung im Garten (Suchraum) verteilen. Hier sehen wir, dass die Koordinaten zufällig im zulässigen Bereich zwischen dem Minimum und dem Maximum der optimierten Parameter generiert werden, wir prüfen, ob der zulässige Bereich verlassen wird, und bringen dann die Koordinatenwerte in Übereinstimmung mit dem Optimierungsschritt.
In diesem Stadium ist die Anpassungsfähigkeit der Sämlinge minimal. Wir setzen den Vektor vec[]. Wir benötigen ihn, um die Inkremente der Zweige im Operator der Zweigbildung zu skalieren und um den maximal möglichen euklidischen Abstand r im Suchraum zu berechnen. Im Kreuzungsoperator wird es nützlich sein, die Wahrscheinlichkeit in Abhängigkeit vom Abstand zwischen den Baumpaaren zu bestimmen.
//the first planting of trees------------------------------------------------- if (!sowing) { fB = -DBL_MAX; r = 0.0; for (int t = 0; t < numberTrees; t++) { for (int c = 0; c < coordinates; c++) { cGarden [t].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); cGarden [t].c [c] = SeInDiSp (cGarden [t].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } cGarden [t].f = -DBL_MAX; } for (int c = 0; c < coordinates; c++) { vec [c] = rangeMax [c] - rangeMin [c]; r += vec [c] * vec [c]; } r = sqrt (r); return; }
Anschließend werden in der Methode Aussaat() die Operatoren Kreuzung, Zweigbildung und Impfung bei der zweiten und den folgenden Iterationen ausgeführt. Die Operatoren werden nacheinander in der Hauptschleife ausgeführt:
//tree growth----------------------------------------------------------------- int child, parent; double rnd; double ed; //euclidean distance double eM; double u; double temp; for (int t = 0; t < numberTrees; t++)
Bei der Ausführung von Operatoren sind die Begriffe „Kind“ und „Eltern“ sehr willkürlich. Tatsächlich sind sie nur Quellen für grundlegende Informationen zur Schaffung eines neuen Setzlings. Der neue Sämling kopiert alle Zweige (wie Sie sich vielleicht erinnern, sind Zweige die zu optimierenden Parameter) aus dem Kindbaum und erhält neue Zweige aus dem Elternbaum.
Für jeden neuen Setzling werden zwei Bäume einzeln aus dem Garten ausgewählt, ein Kind und ein Elternteil nach dem Zufallsprinzip, wobei die Wahrscheinlichkeit für alle Bäume im Garten gleich ist. Mit anderen Worten: Alle Bäume können mit gleicher Wahrscheinlichkeit und unabhängig von ihrer Fitness an der Entstehung eines neuen Setzlings beteiligt sein. Kind“ und „Elternteil“ sind also einfach die Indizes der beiden ursprünglichen Bäume im Array des Elterngartens.
ed = 0.0; rnd = RNDfromCI (0.0, numberTrees - 1); child = (int)MathRound (rnd); if (child < 0) child = 0; if (child > numberTrees - 1) child = numberTrees - 1; rnd = RNDfromCI (0.0, numberTrees - 1); parent = (int)MathRound (rnd); if (parent < 0) parent = 0; if (parent > numberTrees - 1) parent = numberTrees - 1; if (child == parent) parent++; if (parent > numberTrees - 1) parent = 0; ArrayCopy (cGarden [t].c, pGarden [child].c, 0, 0, WHOLE_ARRAY);
Der erste Operator ist die Kreuzung bzw. Konjugation (Paarung). Um den Operator für das Kreuzen an einem Sämling mit dem Index t auszuführen, muss der euklidische Raum zwischen dem Kind- und dem Elternbaum mit den Indizes „Kind“ und „Eltern“ berechnet werden:
//mating operator----------------------------------------------------------- for (int c = 0; c < coordinates; c++) { temp = pGarden [child].c [c] - pGarden [parent].c [c]; ed += temp * temp; } ed = sqrt (ed);
Der euklidische Abstand geht in die Gleichung zur Berechnung der Kreuzungswahrscheinlichkeit durch Normierung auf den maximal möglichen euklidischen Abstand r im Suchraum ein:
eM = 1.0 - (ed / r); Erzeugen Sie eine Zufallszahl im Bereich [0.0;1.0]. Wenn die sich ergebende Zahl innerhalb der berechneten Wahrscheinlichkeit eM liegt, führen wir eine Kreuzung durch, indem wir Zweige aus dem übergeordneten Baum mit der probabMatingOperator-Wahrscheinlichkeit für jeden Zweig kopieren. Wenn die eM-Wahrscheinlichkeit nicht erfüllt ist, fährt der Sämling mit der Ausführung der nächsten Anweisung mit allen ursprünglichen Zweigen des Kindbaums fort.
rnd = RNDfromCI (0.0, 1.0); if (rnd <= eM) { for (int c = 0; c < coordinates; c++) { rnd = RNDfromCI (0.0, 1.0); if (rnd <= probabMatingOperator) cGarden [t].c [c] = pGarden [parent].c [c]; } }
Anschließend wird der Operator der Zweigbildung ausgeführt. Die Zweigbildung bietet eine Variation von Zweigen - Verlängern und Verkürzen. Dies ist der Hauptoperator, der Zweige mit einer neuen Länge erzeugt. Die übrigen Operatoren haben lediglich eine kombinatorische Funktion und schaffen keine neuen, einzigartigen Zweige. Für jeden Zweig generieren wir eine Zufallszahl aus dem Bereich [0.0;1.0], und wenn die Wahrscheinlichkeit von probabBranchOperator erfüllt ist, dann führen wir eine Zweigbildung durch, indem wir die Länge des Zweigs gemäß der hier vorgestellten Verteilung nach dem Levy-Flug verändern.
Wie Sie sehen können, werden nicht alle Zweige des Setzlings verändert. Sie werden unabhängig davon geändert, ob der Zweig in der vorherigen Anweisung aus dem übergeordneten Baum kopiert wurde oder ob es sich um den ursprünglichen untergeordneten Zweig handelt. Nach der Änderung der Zweige prüfen wir, ob die Werte außerhalb des Bereichs liegen, und bringen sie mit dem Optimierungsschritt in Einklang.
//branching operator-------------------------------------------------------- for (int c = 0; c < coordinates; c++) { rnd = RNDfromCI (0.0, 1.0); if (rnd < probabBranchOperator) { double r1 = RNDfromCI (0.0, 1.0); r1 = r1 > 0.5 ? 1.0 : -1.0; double r2 = RNDfromCI (1.0, 20.0); cGarden [t].c [c] = cGarden [t].c [c] + r1 * vec [c] * powerBranchOperator * pow (r2, -2.0); cGarden [t].c [c] = SeInDiSp (cGarden [t].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } }
Der dritte Operator ist die Impfung. Der Impfoperator wurde von den Autoren offenbar als kombinatorischer Operator konzipiert und sollte durchgeführt werden, um Zweige aus dem Elternbaum zu kopieren, wenn sich die Zweige des Kind- und des Elternbaums um mehr als die durchschnittliche Differenz über alle Zweige des Paares unterscheiden. Das hört sich sehr kompliziert an, aber es gibt nur wenig Verwendung für diesen Operator, und deshalb ist er in den Quelldateien auskommentiert. In diesem Fall kann ich nicht als Experte auftreten und gebe daher zu, dass ich diesen Operator möglicherweise nicht richtig verstehe.
//vaccinating operator------------------------------------------------------ u = 0.0; for (int c = 0; c < coordinates; c++) { u += fabs (cGarden [t].c [c] - pGarden [parent].c [c]) / vec [c]; } u /= coordinates; for (int c = 0; c < coordinates; c++) { if (fabs (cGarden [t].c [c] - pGarden [parent].c [c]) / vec [c] >= u) { cGarden [t].c [c] = pGarden [parent].c [c]; } }
Es ist Zeit für die letzte, aber nicht weniger wichtige Operation des Algorithmus - das Keimen. Wir führen die zweite öffentliche Methode „Germination()“ (Keimung) aus, die bei jeder Iteration ausgeführt werden muss.
Wenn sich die erste Iteration dem Ende zuneigt (das erkennen wir am Flag „Aussaat“), bedeutet dies, dass der Elterngarten leer ist. Wir pflanzen alle Setzlinge aus dem Kindgarten in den Elterngarten, indem wir einfach alle jungen Bäume nacheinander kopieren. Danach sortieren wir den übergeordneten Garten mit der Methode Sorting() nach dem Fitnesswert. Wenn die Bäume sortiert sind, hat der Baum mit dem Index 0 die beste Fitness, und wir können die beste globale Lösung aktualisieren, wenn sie nicht bereits die beste ist.
if (!sowing) { for (int t = 0; t < numberTrees; t++) pGarden [t] = cGarden [t]; Sorting (pGarden); if (pGarden [0].f > fB) { fB = pGarden [0].f; ArrayCopy (cB, pGarden [0].c, 0, 0, WHOLE_ARRAY); } sowing = true; return; }
Im weiteren Verlauf des Codes kommen wir nur noch zur zweiten und den folgenden Iterationen des Algorithmus, da das Flag „Aussaat“ vorsichtshalber auf „wahr“ gesetzt wurde. Bei der zweiten und den folgenden Iterationen muss der Kindgarten sortiert werden, bevor die Setzlinge in den Elterngarten übertragen und die schlechtesten Bäume ersetzt werden. Überprüfen wir, ob sich die Gesamtlösung verbessert hat, und kopieren wir die besten n Setzlinge an das Ende des Elterngartens.
Zum Schluss bleibt nur noch, den Elterngarten zu sortieren. Die neuen Mitglieder der Gartengesellschaft werden in der Lage sein, die Bäume der älteren Generationen zu ersetzen, um uns mit Blumen bzw. den Ergebnissen der Lösung von Optimierungsproblemen zu erfreuen.
//planting some part from all child trees------------------------------------- Sorting (cGarden); if (cGarden [0].f > fB) { fB = cGarden [0].f; ArrayCopy (cB, cGarden [0].c, 0, 0, WHOLE_ARRAY); } for (int t = 0; t < seedlingsReplacement; t++) pGarden [numberTrees - seedlingsReplacement + t] = cGarden [t]; Sorting (pGarden);
3. Testergebnisse
Ergebnisse des SSG-Prüfstands:
2023.03.09 12:50:37.207 Test_AO_SSG (GBPUSD,M1) C_AO_SSG:50;0.3;0.5;0.4;0.1
2023.03.09 12:50:37.207 Test_AO_SSG (GBPUSD,M1) =============================
2023.03.09 12:50:45.954 Test_AO_SSG (GBPUSD,M1) 5 Rastrigin; Funktionsdurchläufe10000 Ergebnis: 80.7052793572295
2023.03.09 12:50:45.954 Test_AO_SSG (GBPUSD,M1) Score: 0.99998
2023.03.09 12:50:59.290 Test_AO_SSG (GBPUSD,M1) 25 Rastrigin; Funktionsdurchläufe10000 Ergebnis: 77.3972262608643
2023.03.09 12:50:59.290 Test_AO_SSG (GBPUSD,M1) Score: 0.95900
2023.03.09 12:52:25.368 Test_AO_SSG (GBPUSD,M1) 500 Rastrigin; Funktionsdurchläufe10000 Ergebnis: 52.24518909141432
2023.03.09 12:52:25.368 Test_AO_SSG (GBPUSD,M1) Score: 0.64735
2023.03.09 12:52:25.368 Test_AO_SSG (GBPUSD,M1) =============================
2023.03.09 12:52:31.419 Test_AO_SSG (GBPUSD,M1) 5 Forest; Funktionsdurchläufe10000 Ergebnis: 1.331178589711503
2023.03.09 12:52:31.419 Test_AO_SSG (GBPUSD,M1) Score: 0.75298
2023.03.09 12:52:42.575 Test_AO_SSG (GBPUSD,M1) 25 Forest; Funktionsdurchläufe10000 Ergebnis: 1.019329018074209
2023.03.09 12:52:42.575 Test_AO_SSG (GBPUSD,M1) Score: 0.57658
2023.03.09 12:53:48.922 Test_AO_SSG (GBPUSD,M1) 500 Forest; Funktionsdurchläufe10000 Ergebnis: 0.25410121872226443
2023.03.09 12:53:48.922 Test_AO_SSG (GBPUSD,M1) Score: 0.14373
2023.03.09 12:53:48.922 Test_AO_SSG (GBPUSD,M1) =============================
2023.03.09 12:53:57.201 Test_AO_SSG (GBPUSD,M1) 5 Megacity; Funktionsdurchläufe10000 Ergebnis: 6.4
2023.03.09 12:53:57.201 Test_AO_SSG (GBPUSD,M1) Score: 0.53333
2023.03.09 12:54:08.004 Test_AO_SSG (GBPUSD,M1) 25 Megacity; Funktionsdurchläufe10000 Ergebnis: 4.504
2023.03.09 12:54:08.004 Test_AO_SSG (GBPUSD,M1) Score: 0.37533
2023.03.09 12:56:07.061 Test_AO_SSG (GBPUSD,M1) 500 Megacity; Funktionsdurchläufe10000 Ergebnis: 1.2336
2023.03.09 12:56:07.061 Test_AO_SSG (GBPUSD,M1) Score: 0.10280
2023.03.09 12:56:07.061 Test_AO_SSG (GBPUSD,M1) =============================
2023.03.09 12:56:07.061 Test_AO_SSG (GBPUSD,M1) All score: 5.09109
Die SSG hat nicht zu viele Parameter, obwohl dies eine Folge der Optimierung des Algorithmus ist (die ursprüngliche SSG hat noch weniger Parameter). Alle Parameter verdienen jedoch eine besondere Aufmerksamkeit. Bei den Tests wurden die folgenden Parameter verwendet. Wie Sie sich vielleicht erinnern, gebe ich in jedem Artikel die besten Algorithmusparameter an, die bei den Tests das bestmögliche Ergebnis erzielen.
C_AO_SSG:50;0.3;0.5;0.4;0.1
input int NumberTrees_P = 50; - Anzahl der Bäume im Garten. Ich habe mit diesem Parameter nicht experimentiert, sondern den Standardwert belassen (der Standardwert in meinen Experimenten). Bei einem Wert von 100 liefert der Algorithmus noch bessere Gesamtergebnisse, aber die Skalierbarkeit nimmt ab, da die Anzahl der zulässigen Iterationen pro Garten mit der Größe des Gartens abnimmt. Ein Garten mit einer großen Anzahl von Zweigen hat keine Zeit, sich zu entwickeln.
input double SeedlingsReplacement_P = 0.3; - Anteil der Setzlinge aus dem Tochtergarten, die in den Muttergarten übertragen werden.
input double ProbabMatingOperator_P = 0.5; - Wahrscheinlichkeit der Kreuzung (Kopieren von Zweigen aus dem Elternbaum), wenn die Wahrscheinlichkeit unter Berücksichtigung des Abstands zwischen einem Baumpaar erfüllt ist.
input double ProbabBranchOperator_P = 0.4; - Wahrscheinlichkeit der Zweigbildung (Wachstum/Schrumpfung der Zweige). Dies ist ein wichtiger Parameter, der die Leistung des Algorithmus erheblich beeinflusst (im Allgemeinen sind alle Parameter wichtig).
input double PowerBranchOperator_P = 0.1; - Stärke der Zweigbildung. Dies ist ein Skalierungsfaktor in der Dimension der zu optimierenden Parameter, 1,0 oder mehr bedeutet das Wachstum von Zweigen bis zu den Grenzen des Gartens, 0,0 - kein Wachstum von Zweigen, d.h. neue Zweiggrößen entstehen nicht und der Algorithmus degeneriert zu einem einfachen Kombinatorik-Tool (was wahrscheinlich eine großartige Idee für die Verwendung von SSG ist, allerdings wäre hier mehr Forschung erforderlich).
Wenn Sie sich die Animation des SSE-Algorithmus zu den Testfunktionen ansehen, werden Sie feststellen, dass es keine Bewegungsmuster der Bäume im Garten gibt, sondern nur eine gewisse „Verklumpung“ in den lokalen Extrema zu erkennen ist. Im Vergleich zu den bisher betrachteten Algorithmen fällt jedoch sofort die hohe Qualität der Konvergenz auf. Bemerkenswert ist auch die stabile Reproduzierbarkeit der Ergebnisse.
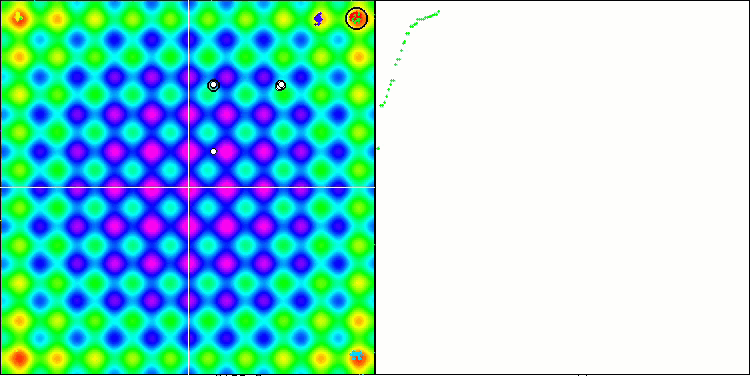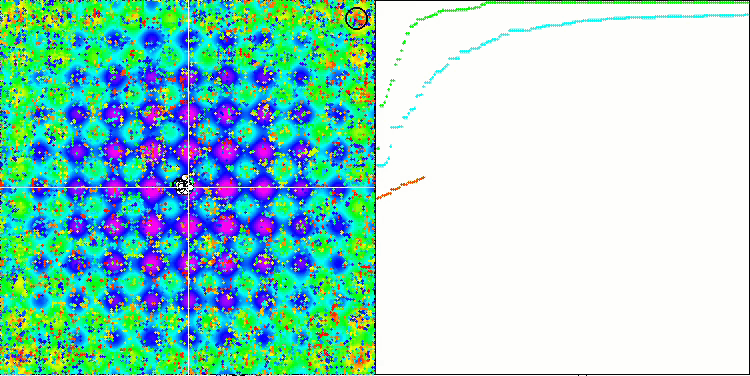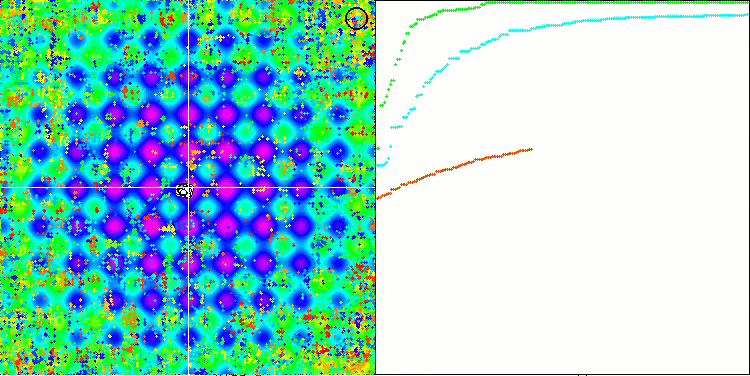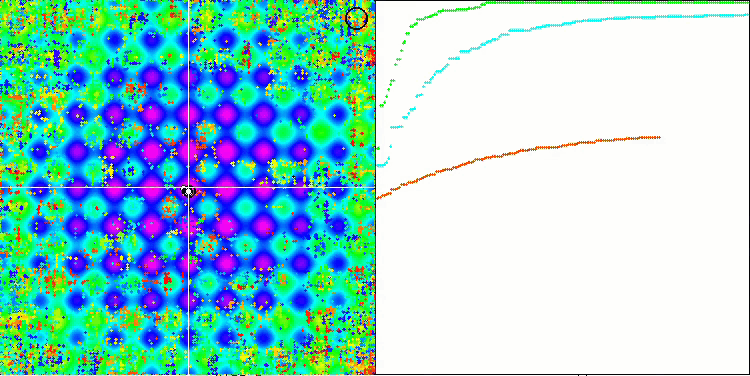
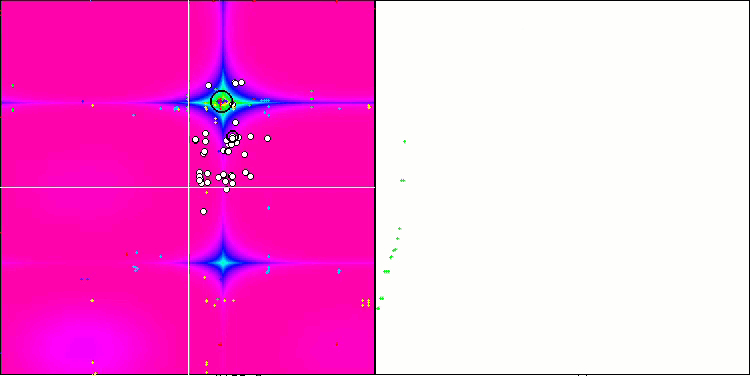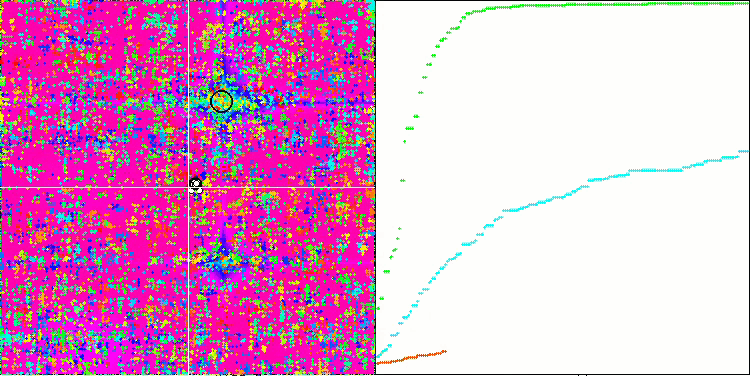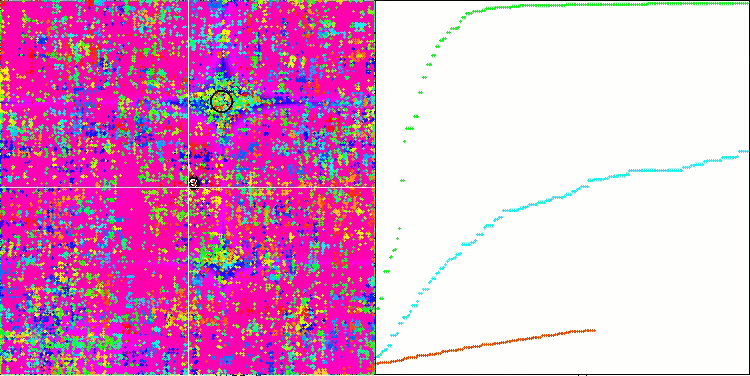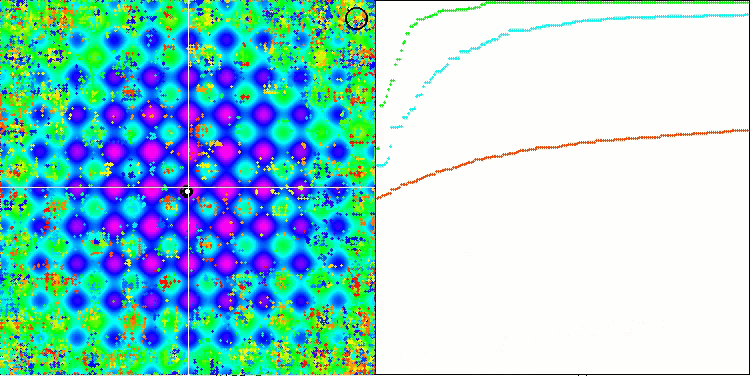
SSG mit der Rastrigin-Testfunktion.
SSG mit der Forest-Testfunktion.
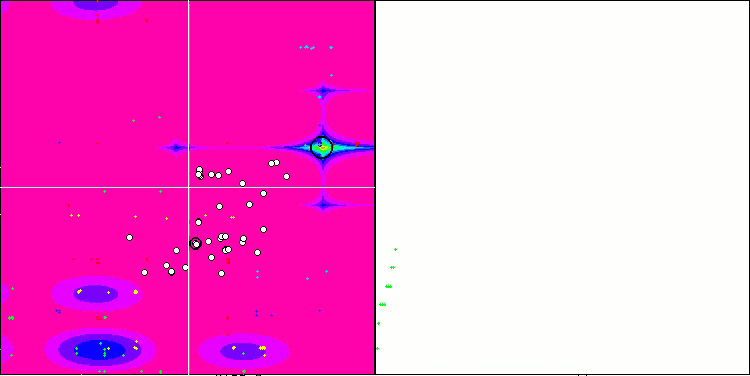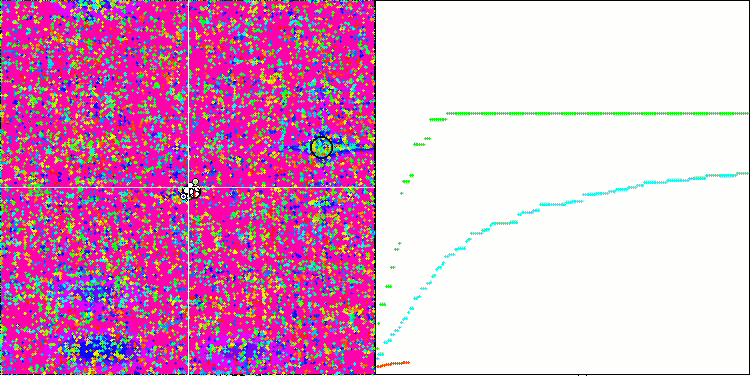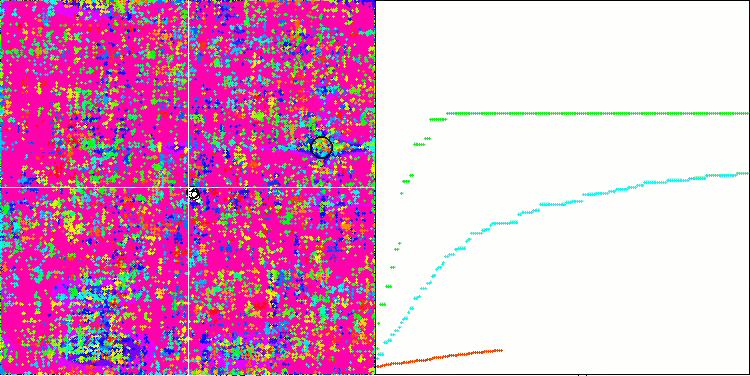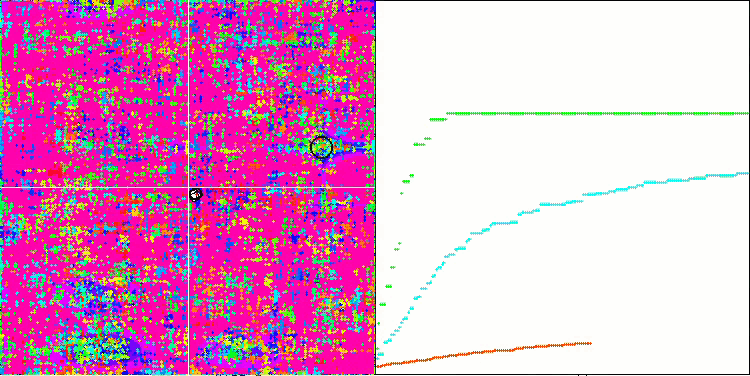
SSG mit der Megacity-Testfunktion.
Kommen wir nun zu den Ergebnissen des SSG-Algorithmus. Es gibt auf jeden Fall etwas zu besprechen. Der Algorithmus ist triumphierend auf den ersten Platz der Bewertung gestürmt und hat die Konkurrenten hinter sich gelassen! Der Algorithmus nutzt das Wissen über die Fitness nicht direkt, um Entscheidungsbäume zu verändern. Die Fitness wird nur benötigt, um den Kindgarten und den Elterngarten zu sortieren. Umso überraschender ist es, dass der Algorithmus in den Tests so bemerkenswerte Ergebnisse erzielen konnte.
Das ist dasselbe, wie wenn die Mannschaft der Blinden die Mannschaft der Sehenden beim Orientierungslauf besiegt. In vier von sechs Tests lag der Algorithmus vor den Teilnehmern in der Tabelle, während er in den Tests, in denen er nicht führend war, nicht weit zurücklag. Den beeindruckendsten Vorsprung vor den Konkurrenten zeigte die SSG bei der diskreten Funktion Megacity, bei der sie den härtesten Konkurrenten HS um fast 60 % übertraf! Dies beweist die hervorragende Skalierbarkeit des Algorithmus. Das beste Skalierbarkeitsergebnis wurde auch bei der "scharfen" Forest-Testfunktion beobachtet. Die SSG übertraf den besten Wettbewerber in diesem Test (ACOm) um fast 30 %.
| AO | Beschreibung | Rastrigin | Rastrigin final | Forest | Forest final | Megacity (diskret) | Megacity final | Endergebnis | ||||||
| 10 Parameter (5 F) | 50 Parameter (25 F) | 1000 Parameter (500 F) | 10 Parameter (5 F) | 50 Parameter (25 F) | 1000 Parameter (500 F) | 10 Parameter (5 F) | 50 Parameter (25 F) | 1000 Parameter (500 F) | ||||||
| SSG | Setzen, Säen und Wachsen | 1.00000 | 1.00000 | 0.65914 | 2.65914 | 0.70823 | 0.94522 | 1.00000 | 2.65345 | 0.71532 | 0.85412 | 1.00000 | 2.56944 | 100.000 |
| HS | Harmoniesuche | 0.99676 | 0.95282 | 0.57048 | 2.52006 | 1.00000 | 0.98931 | 0.44806 | 2.43736 | 1.00000 | 1.00000 | 0.41537 | 2.41537 | 93.370 |
| ACOm | Ameisen-Kolonie-Optimierung M | 0.34611 | 0.17985 | 0.20182 | 0.72778 | 0.85966 | 1.00000 | 0.77362 | 2.63327 | 1.00000 | 0.88484 | 0.05606 | 1.94090 | 66.407 |
| IWO | Optimierung mit invasiven Unkräutern | 0.95828 | 0.67083 | 0.35295 | 1.98207 | 0.68718 | 0.46349 | 0.31773 | 1.46840 | 0.75912 | 0.39732 | 0.33289 | 1.48933 | 61.691 |
| COAm | Kuckuck-Optimierungsalgorithmus M | 0.92400 | 0.46794 | 0.30792 | 1.69987 | 0.55451 | 0.34034 | 0.16526 | 1.06012 | 0.67153 | 0.30326 | 0.17083 | 1.14561 | 48.226 |
| FAm | Firefly-Algorithmus M | 0.59825 | 0.33980 | 0.20290 | 1.14095 | 0.47632 | 0.42299 | 0.49790 | 1.39721 | 0.21167 | 0.25143 | 0.35258 | 0.81568 | 41.042 |
| ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.78170 | 0.32715 | 0.24656 | 1.35541 | 0.50591 | 0.21455 | 0.13344 | 0.85390 | 0.47444 | 0.23609 | 0.13926 | 0.84979 | 37.204 |
| BA | Fledermaus-Algorithmus | 0.40526 | 0.63761 | 1.00000 | 2.04287 | 0.15275 | 0.17477 | 0.25989 | 0.58741 | 0.15329 | 0.06334 | 0.17371 | 0.39034 | 36.703 |
| GSA | Algorithmus für die Schwerkraftsuche | 0.70167 | 0.45217 | 0.00000 | 1.15384 | 0.26854 | 0.36416 | 0.33204 | 0.96475 | 0.51095 | 0.32436 | 0.00000 | 0.83531 | 35.834 |
| BFO | Optimierung der bakteriellen Futtersuche | 0.67203 | 0.30963 | 0.13988 | 1.12154 | 0.35462 | 0.26623 | 0.20652 | 0.82736 | 0.42336 | 0.30519 | 0.18932 | 0.91786 | 34.700 |
| MA | Affen-Algorithmus | 0.33192 | 0.33451 | 0.17340 | 0.83983 | 0.03684 | 0.07891 | 0.08932 | 0.20508 | 0.05838 | 0.00383 | 0.10720 | 0.16941 | 13.185 |
| FSS | Fischschulsuche | 0.46812 | 0.25337 | 0.13383 | 0.85532 | 0.06711 | 0.05013 | 0.06516 | 0.18240 | 0.00000 | 0.00959 | 0.08283 | 0.09242 | 12.089 |
| PSO | Partikelschwarmoptimierung | 0.20449 | 0.08200 | 0.08478 | 0.37127 | 0.13192 | 0.10486 | 0.21738 | 0.45415 | 0.08028 | 0.02110 | 0.01957 | 0.12095 | 9.696 |
| RND | zufällig | 0.16826 | 0.09743 | 0.09495 | 0.36065 | 0.07413 | 0.04810 | 0.04715 | 0.16938 | 0.00000 | 0.00000 | 0.04922 | 0.04922 | 4.916 |
| GWO | Grauer-Wolf-Optimierung | 0.00000 | 0.00000 | 0.02672 | 0.02672 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.18977 | 0.03645 | 0.02557 | 0.25179 | 1.000 |
Zusammenfassung
SSG-Merkmale: keine Anforderungen an die Differenzierbarkeit und Stetigkeit der optimierten Funktion, keine Einschränkungen hinsichtlich der Art der angewandten Darstellung und Kodierungen. Der Algorithmus verwendet keine Fitness-Informationen der einzelnen Agenten und die beste Lösung als Ganzes. Dank dieser Eigenschaften kann die SSG leicht auf verschiedene, auch sehr komplexe Optimierungsprobleme angewendet werden. SSG kann definitiv für den Einsatz bei Problemen von Händlern und maschinellem Lernen empfohlen werden. Zum Zeitpunkt der Erstellung dieses Dokuments ist der Saplings-Aussaat- und Aufwuchs-Algorithmus unangefochtener Spitzenreiter, was die Qualität der Konvergenz, die Stabilität der Ergebnisse und die Skalierbarkeit betrifft.
Abb. 2 zeigt die Testergebnisse des Algorithmus
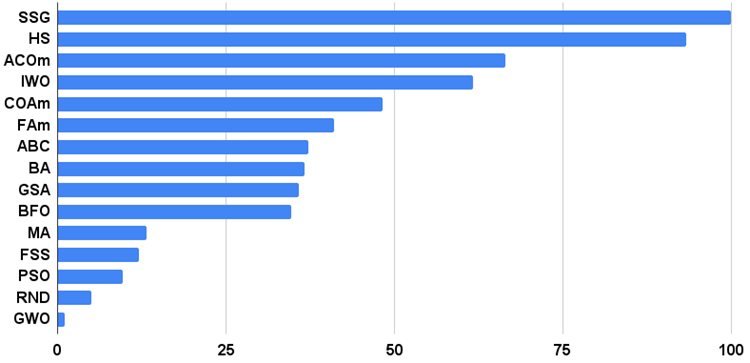
Bild 2. Histogramm der Testergebnisse der Algorithmen
Vor- und Nachteile der SSG-Algorithmen:
Vorteile:
1. Einfache Implementierung.
2. Hervorragende Konvergenz bei allen Arten von Funktionen, ohne Ausnahme.
3. Beeindruckende Skalierbarkeit.
Nachteile
1. Viele Anpassungsmöglichkeiten, die jedoch intuitiv verständlich sind.
Jeder Artikel verfügt über ein Archiv, das aktualisierte aktuelle Versionen der Algorithmuscodes für alle früheren Artikel enthält. Der Artikel basiert auf den gesammelten Erfahrungen des Autors und stellt seine persönliche Meinung dar. Die Schlussfolgerungen und Urteile beruhen auf den Experimenten.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/12268
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Die Berechnung für multivariate Varianten ist eher pessimistisch.
Im Allgemeinen, ja. Deshalb wird in der Regel in mehrdimensionalen Fällen die Aufgabe einer vollständigen Untersuchung des Oberflächengeräts der Verlustfunktion nicht gestellt. Ebenso wenig wie die Suche nach dem globalen Extremum. In der Tat ist man darauf beschränkt, einfach nur genügend gute Punkte zu finden. Nun, vielleicht mit Ausnahme der Fälle, in denen es möglich ist, eine Verlustfunktion mit guten Eigenschaften zu konstruieren, wie z.B. in MO.
Ich habe ein Problem mit MT5, die nicht zulässt, dass ich auf den Ordner zugreifen: öffnen Data Folder, zusätzlich zu, dass ich nicht über die volle Elemente auf der Plattform MT 5 anpassbar, ich meine damit, dass ich nicht über die volle Werkzeuge wie Rechteck, Quadrat oder und Dreieck, etc. Also bitte, wenn jemand etwas über die Lösung dieser Probleme weiß, bitte geben Sie mir einen Schrei.
Sie werden keine Hilfe bekommen, wenn Sie in einem Thread posten, der nichts mit Ihrem Beitrag zu tun hat. Erstellen Sie Ihr eigenes Thema. Und da es sich hier um ein technisches Forum handelt, müssen Sie mehr Informationen als die, die Sie angegeben haben, zur Verfügung stellen, einschließlich der ersten 3 Zeilen des Journals, wenn Sie mt5 öffnen, das Ihre Systemdetails enthält.
Versuchen Sie, mt5 zu deinstallieren, und löschen Sie alle verbleibenden Ordner, einschließlich der Ordner wie "config", die oft nicht korrekt deinstalliert werden. Versuchen Sie dann, es erneut zu installieren.