Algorithmen zur Optimierung mit Populationen: Harmonie-Suche (HS)

Inhalt:

1. Einführung
2. Algorithmus
3. Testergebnisse

1. Einführung

Die musikalische Komposition besteht aus mehreren Komponenten - Rhythmus, Melodie und Harmonie. Während Rhythmus und Melodie ein einheitliches Ganzes eines musikalischen Werkes bilden, ist die Harmonie das, was es auszeichnet. Ein Theaterstück oder ein Lied ohne Harmonie ist wie ein ungefärbtes Bild in einem Kinderbuch - es ist zwar gezeichnet, aber es hat keine Farbe, keinen Glanz, keine Ausdruckskraft. Eine richtig gewählte Harmonie umschmeichelt die Ohren, veredelt den Klang und ermöglicht es uns, die wunderbaren Klänge des Klaviers, der Gitarre oder eines anderen Musikinstruments voll zu genießen. Eine Melodie kann gesungen werden, während eine Harmonie nur gespielt werden kann. Musikalische Harmonie ist eine Reihe von Akkorden, ohne die kein einziges Lied oder Musikstück vollwertig und klangvoll sein kann.

Harmonie entsteht genau in dem Moment, in dem wir zwei Klänge miteinander verbinden - nacheinander oder im gleichzeitigen Fluss. Ein umfassenderes Synonym wäre „Kombination“. Nachdem ein Klang mit einem anderen verbunden wurde, entsteht eine Kombination, bei der die Hierarchie bereits versucht, sich auf ihre eigene Weise aufzustellen. In Musikschulen, Hochschulen und Konservatorien gibt es ein spezielles Fach - die Harmonielehre, in der die Schüler alle in der Musiktheorie vorkommenden Akkorde studieren, lernen, sie in der Praxis anzuwenden und sogar Probleme in der Harmonielehre zu lösen.

Während einer musikalischen Improvisation versuchen die Musiker, die Tonhöhe ihrer Instrumente so zu stimmen, dass eine angenehme Harmonie entsteht (bester Zustand). In der Natur wird die Harmonie durch eine besondere Beziehung zwischen mehreren Schallwellen mit unterschiedlichen Frequenzen bestimmt. Die Qualität der improvisierten Harmonie wird durch die ästhetische Bewertung bestimmt. Um das ästhetische Empfinden zu verbessern und die beste Harmonie zu finden, üben Musiker immer wieder. Zwischen Improvisation und Optimierung gibt es eine Ähnlichkeit.

Die Methode der Harmonie-Suche (Harmony Search, HS) ist ein aufstrebender metaheuristischer Optimierungsalgorithmus, der in den letzten zehn Jahren zur Lösung zahlreicher komplexer Probleme eingesetzt wurde. Der Algorithmus der Harmonie-Suche (HS) wurde erstmals im Jahr 2001 von Z. W. Geem vorgeschlagen. Die HS-Methode ist inspiriert von den Grundprinzipien der musikalischen Improvisation und der Suche nach musikalischer Harmonie. Die Kombinationen der perfekten Harmonie der Klänge werden mit dem globalen Extremum in dem mehrdimensionalen Optimierungsproblem abgestimmt, während der musikalische Improvisationsprozess mit der Suche nach dem Extremum abgestimmt wird.

Bei der Improvisation gibt jeder Musiker in jedem Takt eines Musikstücks (im Rahmen der Möglichkeiten seines Musikinstruments) einen Ton wieder, sodass die Töne aller Musiker des Orchesters in diesem Takt einen Vektor der Harmonie bilden. Kombinationen von Klängen, die „gute“ Harmonien bilden, werden von jedem der Musiker gespeichert und können von ihnen verwendet werden, um in den nachfolgenden Takten des Musikstücks noch bessere Harmonien zu bilden.

In der Regel erfüllt ein Musiker während der Improvisation eine der folgenden drei Anforderungen: Er bildet einen absolut zufälligen Klang aus der Palette der verfügbaren Klänge; er spielt einen beliebigen Klang aus dem Harmoniespeicher; er spielt einen benachbarten Harmonievektor aus demselben Speicher. Die wichtigsten Merkmale des HS-Algorithmus sind die Möglichkeit, ihn sowohl zur Lösung kontinuierlicher als auch diskreter Optimierungsprobleme einzusetzen.

Die besonderen Merkmale von HS sind die Einfachheit des Algorithmus und die Effizienz der Suche. Aus diesem Grund zieht der Algorithmus die Aufmerksamkeit der Forscher auf sich und entwickelt sich sowohl in theoretischer als auch in praktischer Hinsicht rasch weiter. HS ist eine metaheuristische Technik, die eine hohe Stabilität zwischen Explorations- und Exploitationsphasen im Suchprozess bietet. HS ist von der menschlichen Kreativität inspiriert, und die Methode, die perfekte Lösung für ein bestimmtes Problem zu finden, ähnelt der eines Musikers, der versucht, eine angenehme Harmonie zu finden. Die Methode zur Ermittlung des Werts der Fitnessfunktion ähnelt der Methode zur Ermittlung einer Referenz anhand der Tonhöhe eines jeden Musikinstruments.

2. Algorithmus

Die Arbeit der HS-Logik ist vergleichbar mit der Arbeit eines Musikers, der eine perfekte Harmonie schafft. Der Musiker versucht, die verschiedenen Töne zu verändern, bis die perfekte Harmonie gefunden ist. Danach wird die Sammlung der gefundenen Harmonien im Speicher abgelegt. In einem Optimierungsproblem werden die Harmonien verschiedenen Veränderungen unterzogen; wenn die Ergebnisse der Variationen günstig sind, wird der Speicher erneuert, indem die Harmonie dem Speicher hinzugefügt und die unerwünschten Elemente entfernt werden... All dies mag ziemlich verwirrend klingen. Was also ist Harmonie? Was sind Töne? Versuchen wir, den Algorithmus mit unseren eigenen Begriffen zu verstehen.

Was ist ein Musikstück? Natürlich bin ich kein Musiker (was schade ist), sondern ein Programmierer. Für das Erkennen des Algorithmus reicht es jedoch aus, das Konzept der „Note“ anzuwenden. Ein Musikstück besteht aus Noten (Akkorden). Abbildung 1 zeigt schematisch den „Mechanismus“ für den Aufbau eines Musikstücks. Die Auswahl der Noten entspricht einem Musikstück, das auch ohne musikalisches Gehör oder musikalische Ausbildung leicht zu erkennen ist. Wer mitraten möchte, kann unten einen Kommentar hinterlassen.

Die Optimierung des HS-Algorithmus besteht darin, die grünen Balken mit Noten über den blauen Balken des Stücks selbst zu verschieben. Der Bereich des grünen Balkens ist eine Oktave, die sich aus einzelnen Noten zusammensetzt. Das Produkt (blauer Balken) entspricht einer der Optimierungslösungen. Die Hinweise auf dem grünen Balken sind die entsprechenden Optimierungsparameter des Problems. Im Gedächtnis des Musikers sind mehrere Versionen des Stücks gespeichert (mehrere Varianten der blauen Balken), das ist die Algorithmuspopulation.

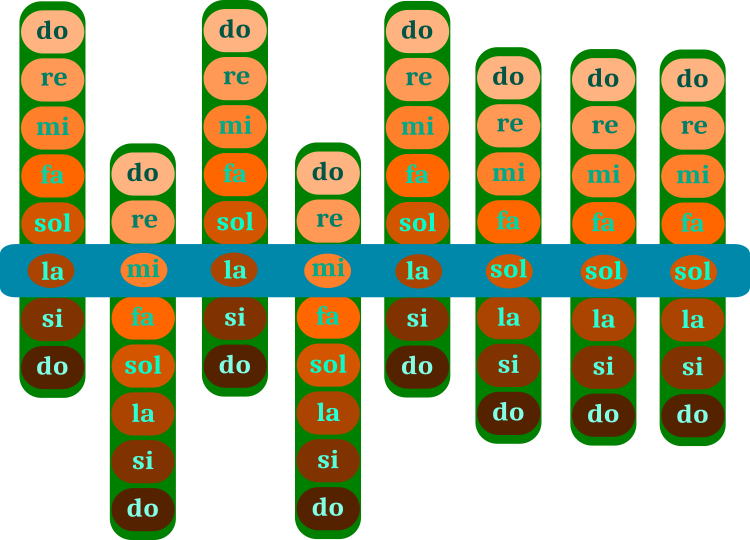
Bild 1. Auswahl von Noten in einem Musikstück (Suche nach Harmonie). Der blaue Balken ist ein Stück. Die grünen Balken sind ein Satz von Noten

Das Beispiel in Abbildung 1 entspricht der Lösung eines diskreten Problems, bei dem es acht Schritte in den Parametern gibt. Das Beispiel dient dem besseren Verständnis der Funktionsweise des Algorithmus. In einer beliebigen Aufgabe kann es jedoch jede Stufe der optimierten Parameter geben, und es gibt auch Zwischentöne - Halbtöne. Die richtigen Parameter zur Lösung der Aufgabe entsprechen den richtigen Noten im Stück.

Der Entstehungsprozess eines Musikstücks beginnt also mit einer zufälligen Auswahl von Klängen eines Musikinstruments, die im Bereich der reproduzierbaren Frequenzen des Instruments liegen. Es ist notwendig, mehrere Varianten eines Stückes zu erstellen, um einzelne Abschnitte der Variantennoten kombinieren zu können. Der nächste Schritt ist die Veränderung der Noten in diesen Variationen. Hierfür gibt es drei Möglichkeiten:

1. Ändern Sie zufällig eine der Noten des Stücks, die im Tonumfang des Musikinstruments liegt.
2. Wir können eine Note mit der entsprechenden Seriennummer von anderen Versionen des Stücks nehmen.
3. Wir können eine Note aus einer anderen Version des Stücks nehmen und sie leicht verändern, sodass sie in der Tonart höher oder tiefer liegt.

Nachdem wir auf diese Weise einen neuen Satz von Varianten eines Musikstücks erhalten haben, bewerten wir jede der Varianten im Hinblick auf die Klangharmonie und speichern die Varianten an ihrer ursprünglichen Position im Speicher, sofern die neue Version besser ist als die vorherige Version. Das Besondere an dem Algorithmus ist, dass die Grundgesamtheit, in unserem Fall die Menge der Produkte, nicht sortiert werden muss. Jede neue beste Option ersetzt die alte schlechteste Option an derselben Stelle. Dieser Prozess ähnelt ein wenig der Arbeit genetischer Algorithmen, die die Evolution nachahmen, wenn die fittesten Individuen überleben. Auch bei der Kombination von Genen im Chromosom sind Ähnlichkeiten festzustellen.

Auf der Grundlage der obigen Ausführungen können wir den Pseudocode des HS-Algorithmus vorläufig zusammenstellen:

1. Erzeugen von Zufallsharmonien.
2. Messen der Qualität der Harmonien (Berechnung der Fitnessfunktion).
3. Verwenden der Akkordauswahl einer zufällig ausgewählten Harmonie mit der Wahrscheinlichkeit von Eh.
  3.1 Ändern des Akkords gemäß der Gleichung, wenn der Akkord aus einer Harmonie mit der Wahrscheinlichkeit Ep ausgewählt wird.
    3.1.1 Belassen des ausgewählten Akkords ohne Änderung.
  3.2 Neue Akkord gemäß der Gleichung.
4. Messen der Qualität der Harmonien (Berechnung der Fitnessfunktion).
5. Wiederholen des Vorgang ab S.3, bis das Stoppkriterium erfüllt ist.

Gehen wir also zur Beschreibung der Eingabeparameter des Algorithmus über, die wenig und intuitiv sind.

input int Population_P = 50; // Populationsgröße
input double Eh_P       = 0.9; // zufällige Auswahlhäufigkeit
input double Ep_P       = 0.1; // Häufigkeit der schrittweisen Anpassung
input double Range_P = 0.2; // Bereich

• Population_P - die Anzahl der Varianten eines Stücks im Speicher des Musikers (Populationsgröße);
• Eh_P - wie oft eine Variante eines Stücks aus dem Speicher ausgewählt wird, wirkt sich darauf aus, wie oft wir auf eine andere Variante zurückgreifen, um eine Note zu entleihen. Ein höherer Wert bedeutet bessere kombinatorische Eigenschaften des Algorithmus;
• Ep_P - wie oft müssen Sie die Note leicht verändern, höher oder tiefer, wenn die Note aus einer anderen Version des Stücks ausgewählt wurde;
• Bereich_P - der Bereich der Note in der bearbeiteten Version des Stücks, wenn sie nicht aus einer anderen Version übernommen wurde. 0,2 würde beispielsweise 20% des Notenbereichs eines Musikinstruments bedeuten.
• 
  

Der HS-Algorithmus arbeitet mit Harmonien (musikalischen Kompositionen), die durch die Struktur S_Harmony beschrieben werden können. Die Harmonie besteht aus Noten (Akkorden); dies ist ein Array, das die zu optimierenden c[]-Parameter darstellt. Die besten Akkorde des Stücks werden in dem Array cB[] gespeichert. In dieses Array wird die erfolgreiche Komposition gesendet, und mit diesen Kompositionen (Harmonien) werden wir kombinatorische Permutationen durchführen, bei denen wir uns Noten aus ihnen ausleihen. Die Qualität der Harmonie wird in der Variablen h gespeichert, und die beste Harmonie wird in der Variablen hB gespeichert.

//——————————————————————————————————————————————————————————————————————————————
struct S_Harmony //musical composition
{
  double c  []; //chords
  double cB []; //best chords
  double h;     //harmony quality
  double hB;    //best harmony quality
};
//——————————————————————————————————————————————————————————————————————————————

Das Array der Harmoniestrukturen wird in der Klasse C_AO_HS verwendet. Die Deklarationen in der Methode und in der Mitgliedsklasse sind kompakt, da der Algorithmus äußerst prägnant ist und wenig Rechenaufwand erfordert. In vielen anderen Optimierungsalgorithmen wird die Sortierung nicht verwendet. Wir benötigen Arrays, um das Maximum, das Minimum und den Schritt der zu optimierenden Parameter festzulegen (sie spielen die Rolle des Bereichs und des Schritts der Akkorde) und konstante Variablen, um ihnen die externen Parameter des Algorithmus zu übertragen. Kommen wir nun zur Beschreibung der Methoden, die die Hauptlogik von HS enthalten.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_HS
{
  //----------------------------------------------------------------------------
  public: S_Harmony h      []; //harmonies matrix
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best chords
  public: double hB;           //best harmony quality

  public: void Init (const int    chordsNumberP,      //chords number
                     const int    harmoniesNumberP,   //harmonies number
                     const double EhP,                //random selection frequency
                     const double EpP,                //frequency of step-by-step adjustment
                     const double rangeP,             //range
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    chordsNumber;      //chords number
  private: int    harmoniesNumber;   //harmonies number
  private: double Eh;                //random selection frequency
  private: double Ep;                //frequency of step-by-step adjustment
  private: double range;             //range
  private: int    maxIterations;
  private: double frequency [];      //frequency range
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Die öffentliche Methode Init() initialisiert den Algorithmus. Hier legen wir die Größe der Arrays fest. Wir initialisieren den Qualitätsindikator der besten gefundenen Harmonie mit dem Minimum der double Zahl. Wir werden das Gleiche mit den entsprechenden Variablen des Arrays der Harmoniestrukturen tun.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_HS::Init (const int    chordsNumberP,      //chords number
                    const int    harmoniesNumberP,   //harmonies number
                    const double EhP,                //random selection frequency
                    const double EpP,                //frequency of step-by-step adjustment
                    const double rangeP,             //range
                    const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  hB       = -DBL_MAX;
  revision = false;

  chordsNumber    = chordsNumberP;
  harmoniesNumber = harmoniesNumberP;
  Eh              = EhP;
  Ep              = EpP;
  range           = rangeP;
  maxIterations   = maxIterationsP;

  ArrayResize (rangeMax,  chordsNumber);
  ArrayResize (rangeMin,  chordsNumber);
  ArrayResize (rangeStep, chordsNumber);
  ArrayResize (frequency, chordsNumber);

  ArrayResize (h, harmoniesNumberP);

  for (int i = 0; i < harmoniesNumberP; i++)
  {
    ArrayResize (h [i].c,  chordsNumber);
    ArrayResize (h [i].cB, chordsNumber);
    h [i].h  = -DBL_MAX;
    h [i].hB = -DBL_MAX;
  }

  ArrayResize (cB, chordsNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Die erste öffentliche Methode Moving(), die bei jeder Iteration ausgeführt werden muss, hat die Eingabe ‚iter‘ - die aktuelle Iteration. Bei der ersten Iteration, wenn die „Revision“-Flagge „false“ ist, müssen die Harmonien mit Zufallswerten aus dem Bereich der Musikinstrumente initialisiert werden, was dem zufälligen Spielen von Akkorden durch einen Musiker entspricht. Um sich wiederholende Operationen zu reduzieren, speichern wir den Tonfrequenzbereich der entsprechenden Akkorde (optimierte Parameter) im Array frequency[].

//----------------------------------------------------------------------------
if (!revision)
{
  hB = -DBL_MAX;

  for (int har = 0; har < harmoniesNumber; har++)
  {
    for (int c = 0; c < chordsNumber; c++)
    {
      h [har].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      h [har].c [c] = SeInDiSp  (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      h [har].h     = -DBL_MAX;
      h [har].hB    = -DBL_MAX;

      frequency [c] = rangeMax [c] - rangeMin [c];
    }
  }

  revision = true;
}

Bei der zweiten und den folgenden Iterationen wird improvisiert, d. h. die Akkorde und ihre Kombinationen werden nacheinander gewechselt. Es gibt mehrere Harmonien im Speicher, die wir verändern und kombinieren werden. Für jede neue Harmonie werden wir nacheinander die Akkorde durchgehen. Für jeden Akkord gibt es eine Wahrscheinlichkeit, dass er zufällig aus dem Speicher der Harmonie ausgewählt wird, d.h. die Harmonie wird zufällig ausgewählt (gleichmäßig für alle Harmonien). Wird der Akkord aus dem Harmoniespeicher entnommen, so wird die Wahrscheinlichkeit seiner Veränderung ebenfalls durch die Gleichung überprüft:

h [har].c [c] = h [har].c [c] + r * B * frequency[c];

wobei:

r - Zufallszahl zwischen -1 und 1
frequency - Frequenzbereich des Geräts
B - Koeffizient berechnet nach der Formel:

B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;

wobei:

maxIterations - maximale Anzahl von Iterationen
iter - aktuelle Iteration
maxB - Obergrenze des Koeffizienten
minB - Untergrenze des Koeffizienten

Abbildung 2 zeigt die Abhängigkeit des Koeffizienten B von den Einstellungsparametern des Algorithmus und der aktuellen Iteration.

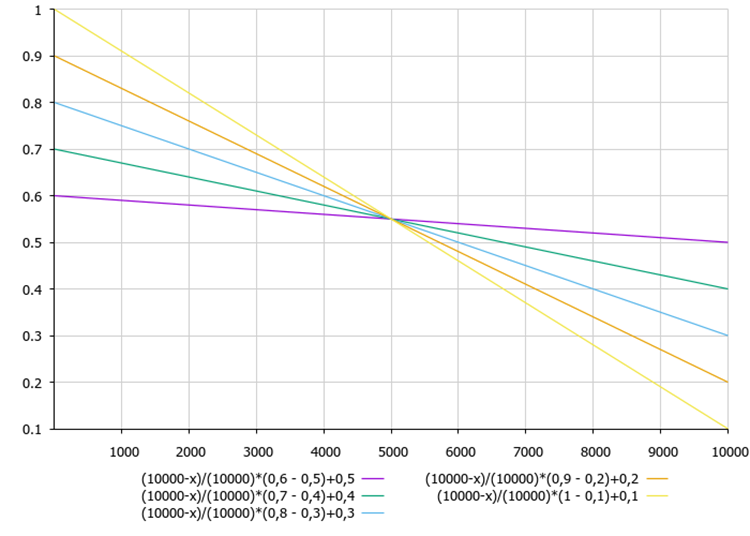
Bild 2. Die Abhängigkeit des Koeffizienten B von den Abstimmungsparametern des maxB, minB Algorithmus und der aktuellen Iteration

Die Gleichung zur Berechnung des B-Koeffizienten zeigt, dass der B-Koeffizient mit jeder Iteration abnimmt. So werden die gefundenen Extremwerte am Ende der Optimierung verfeinert.
Wenn kein Akkord aus dem Harmoniespeicher ausgewählt wurde, wird derjenige geändert, der zu diesem Zeitpunkt bereits existiert. Der Unterschied zwischen einem Akkordwechsel und dem vorangegangenen Wechsel ist der festgelegte Bereich der Schallwellenwerte.

Nachdem der Prozess der Akkordänderung abgeschlossen ist, überprüfen wir den resultierenden Akkord darauf, ob er die zulässigen Werte des Musikinstruments überschreitet.

//----------------------------------------------------------------------------
else
{
  double r         = 0.0;
  int    harAdress = 0;
  double minB      = 0.0;
  double maxB      = 0.3;
  double B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;

  for (int har = 0; har < harmoniesNumber; har++)
  {
    for (int c = 0; c < chordsNumber; c++)
    {
      r = RNDfromCI (0.0, 1.0);

      if (r <= Eh)
      {
        r = RNDfromCI (0.0, harmoniesNumber - 1);
        harAdress = (int)MathRound (r);
        if (harAdress < 0) harAdress = 0;
        if (harAdress > harmoniesNumber - 1) harAdress = harmoniesNumber - 1;

        h [har].c [c] = h [harAdress].cB [c];

        r = RNDfromCI (0.0, 1.0);

        if (r < Ep)
        {
          r = RNDfromCI (-1.0, 1.0);
          h [har].c [c] = h [har].c [c] + r * B * frequency [c];
        }
      }
      else
      {
        r = RNDfromCI (-1.0, 1.0);
        h [har].c [c] = h [har].cB [c] + r * range * frequency [c];
      }

      h [har].c [c] = SeInDiSp (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Revision() ist die zweite öffentliche Methode, die bei jeder Iteration aufgerufen wird, nachdem die Fitnessfunktion berechnet wurde. Sie dient dazu, die gefundene globale Lösung zu aktualisieren. Wenn die Harmonie besser ist als ihre beste Version h > hB, dann aktualisieren wir die beste Version dieser Harmonie.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_HS::Revision ()
{
  for (int har = 0; har < harmoniesNumber; har++)
  {
    if (h [har].h > hB)
    {
      hB = h [har].h;
      ArrayCopy (cB, h [har].c, 0, 0, WHOLE_ARRAY);
    }
    if (h [har].h > h [har].hB)
    {
      h [har].hB = h [har].h;
      ArrayCopy (h [har].cB, h [har].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Nachdem wir den Code sorgfältig studiert haben, stellen wir fest, dass der Algorithmus für die Harmoniesuche keine grundlegend neuen Ideen enthält. Der Harmony-Search-Algorithmus lehnt sich an früher verwendete Ideen evolutionärer Algorithmen an, einschließlich globaler einheitlicher Rekombination, einheitlicher Mutation, Gaußscher Mutation und Ersetzung des schlechtesten Individuums in jeder Generation. Einige Quellen weisen auf die Notwendigkeit hin, die schlechteste Harmonie im Speicher durch eine neue zu ersetzen. In unserem Algorithmus kann die Harmonie nur ihre beste Lösung ersetzen. Dies unterscheidet sich geringfügig von der klassischen Version, da meine Studien darauf hindeuten, dass diese Implementierung des Algorithmus produktiver sein wird.

Der Beitrag des Harmoniesuchalgorithmus liegt in zwei Bereichen: Die Kombination dieser Ideen in diesem Algorithmus ist neu; die musikalische Motivation des Harmoniesuchalgorithmus ist neu. Nur sehr wenige Veröffentlichungen zur Harmoniesuche behandeln musikalische Motive oder Erweiterungen des Algorithmus zur Harmoniesuche. Die meisten Veröffentlichungen befassen sich mit der Hybridisierung des Harmonie-Suchalgorithmus mit anderen evolutionären Algorithmen, der Anpassung der Harmonie-Suchparameter oder der Anwendung des Harmonie-Suchalgorithmus auf spezifische Probleme. Wenn auf den HS-Algorithmus mehr musikalisch bedingte Erweiterungen angewendet werden könnten, würde dies dazu beitragen, ihn als eigenständigen evolutionären Algorithmus zu kennzeichnen. Eine solche Forschung würde das Studium der Musiktheorie, das Studium des Prozesses der musikalischen Komposition und des Arrangements, das Studium der pädagogischen Theorien der Musik und die erfinderische Anwendung dieser Theorien im Algorithmus der Harmoniesuche erfordern.

3. Testergebnisse

Die Ergebnisse des HS-Prüfstands sehen wie folgt aus:

2023.02.08 17:30:05.710    Test_AO_HS (EURUSD,M1)    C_AO_HS:50;0.9;0.1;0.2
2023.02.08 17:30:05.711    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:30:07.919    Test_AO_HS (EURUSD,M1)    5 Rastrigin; Funktionsdurchläufe 10000 Ergebnis: 80.62868417575105
2023.02.08 17:30:07.919    Test_AO_HS (EURUSD,M1)    Score: 0.99903
2023.02.08 17:30:11.563    Test_AO_HS (EURUSD,M1)    25 Rastrigin; Funktionsdurchläufe 10000 Ergebnis: 75.85009280972398
2023.02.08 17:30:11.563    Test_AO_HS (EURUSD,M1)    Score: 0.93983
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    500 Rastrigin; Funktionsdurchläufe 10000 Ergebnis: 50.26867628386793
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    Score: 0.62286
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:30:47.878    Test_AO_HS (EURUSD,M1)    5 Forest; Funktionsdurchläufe 10000 Ergebnis: 1.7224980742302596
2023.02.08 17:30:47.878    Test_AO_HS (EURUSD,M1)    Score: 0.97433
2023.02.08 17:30:51.546    Test_AO_HS (EURUSD,M1)    25 Forest; Funktionsdurchläufe 10000 Ergebnis: 1.0610723369605124
2023.02.08 17:30:51.546    Test_AO_HS (EURUSD,M1)    Score: 0.60020
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    500 Forest; Funktionsdurchläufe 10000 Ergebnis: 0.13820341163584177
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    Score: 0.07817
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:31:34.315    Test_AO_HS (EURUSD,M1)    5 Megacity; Funktionsdurchläufe 10000 Ergebnis: 7.959999999999999
2023.02.08 17:31:34.315    Test_AO_HS (EURUSD,M1)    Score: 0.66333
2023.02.08 17:31:42.862    Test_AO_HS (EURUSD,M1)    25 Megacity; Funktionsdurchläufe 10000 Ergebnis: 5.112
2023.02.08 17:31:42.862    Test_AO_HS (EURUSD,M1)    Score: 0.42600
2023.02.08 17:32:25.172    Test_AO_HS (EURUSD,M1)    500 Megacity; Funktionsdurchläufe 10000 Ergebnis: 0.6492
2023.02.08 17:32:25.172    Test_AO_HS (EURUSD,M1)    Score: 0.05410

Auffallend sind die hohen Werte der Testfunktionen, die hoffen lassen, dass die Ergebnisse im Gesamttest hervorragend sein werden. Ein charakteristisches Merkmal der HS-Visualisierung ist, dass wir keine strukturellen Formationen in Form von Koordinatengruppen sehen, wie es bei einigen der vorherigen Algorithmen der Fall ist. Visuell gibt es keine Muster in der Bewegung der Agenten im Suchraum. Dies ähnelt dem Verhalten des RND-Optimierungsalgorithmus, obwohl sich die Konvergenzgraphen sehr sicher verhalten und sich schrittweise der Lösung des Optimierungsproblems nähern. Das Steckenbleiben in lokalen Extremen ist nicht typisch für diesen Algorithmus.

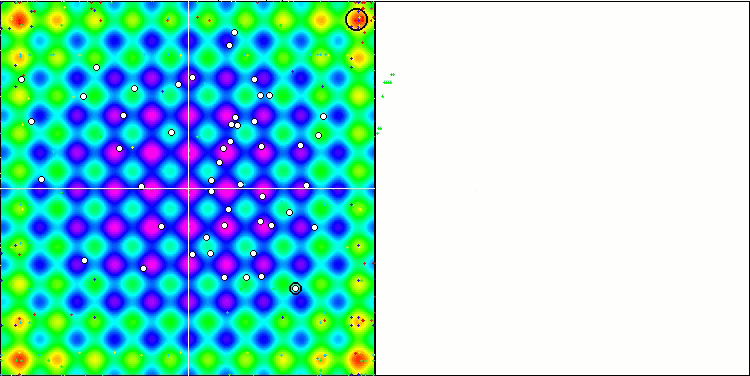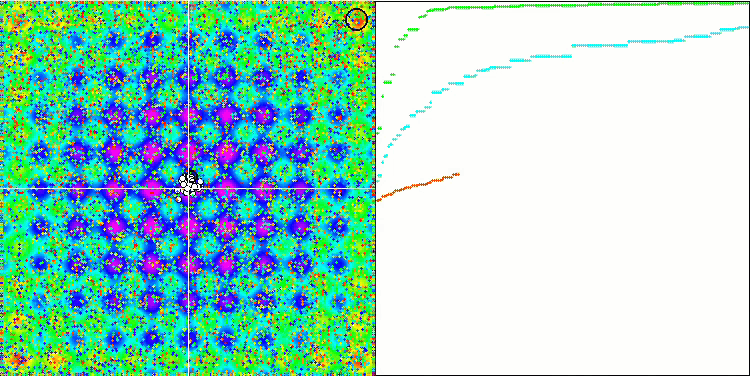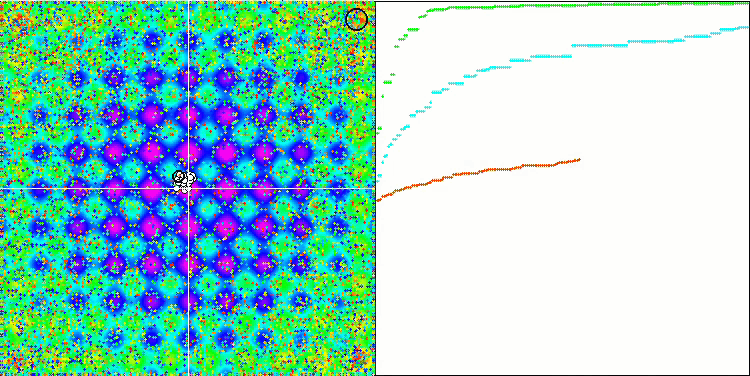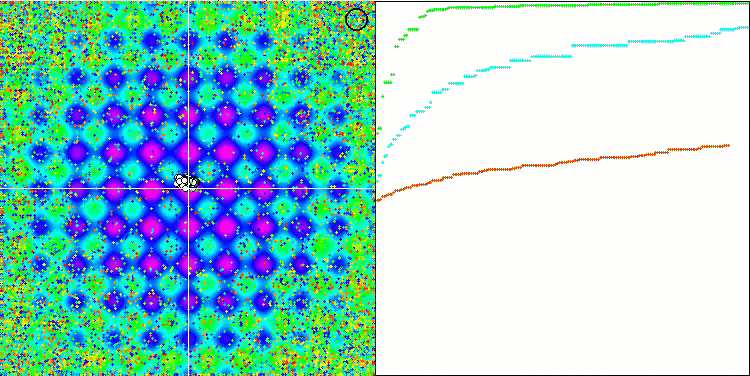
  HS über die Testfunktion Rastrigin

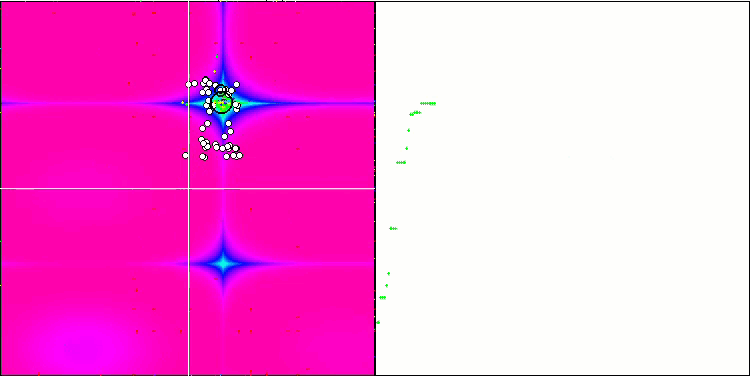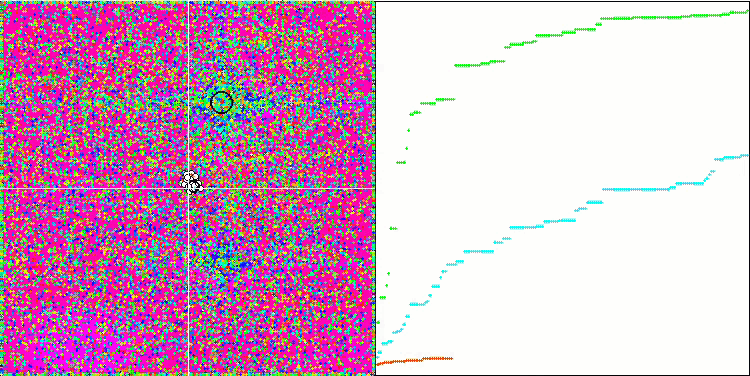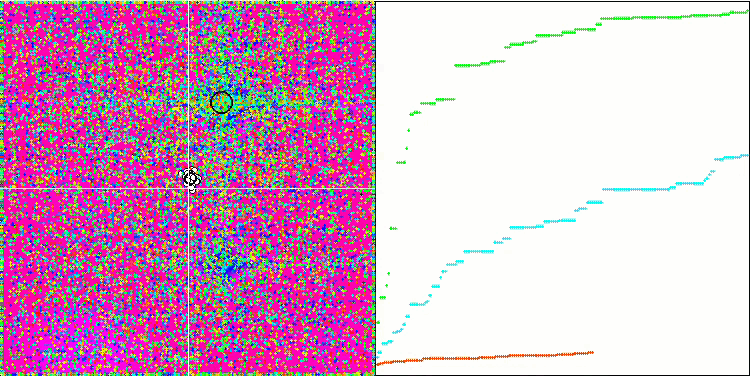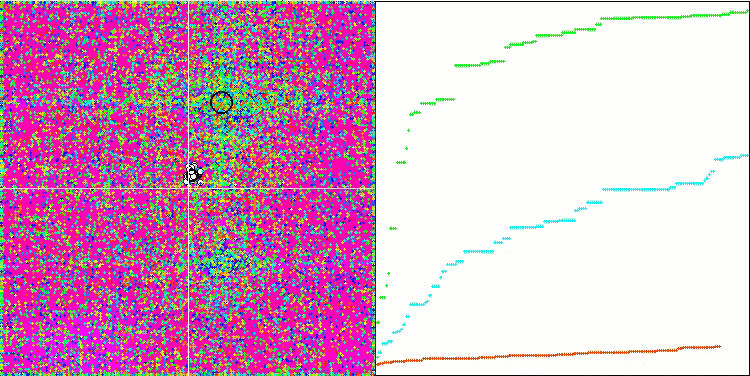
  HS über die Testfunktion Forest

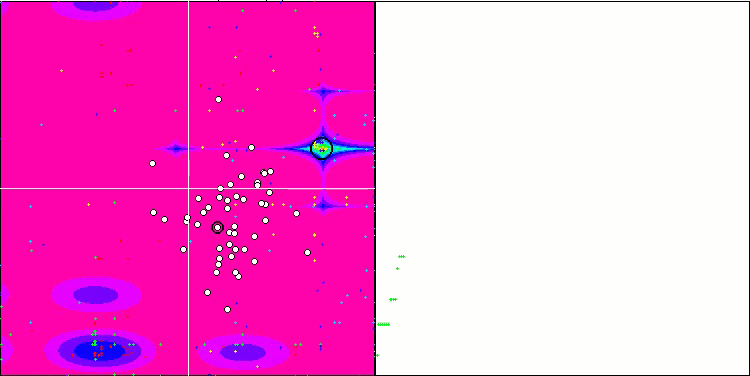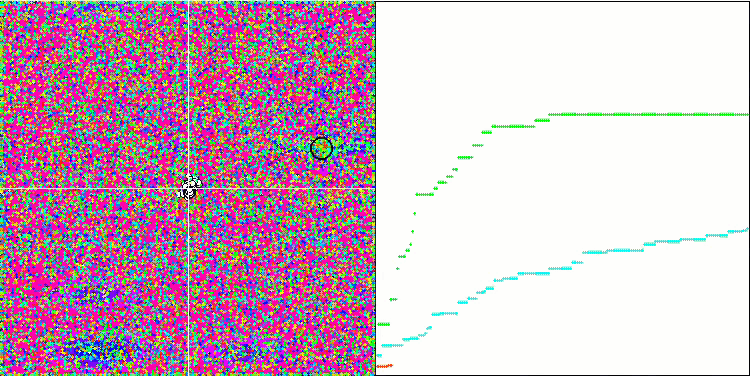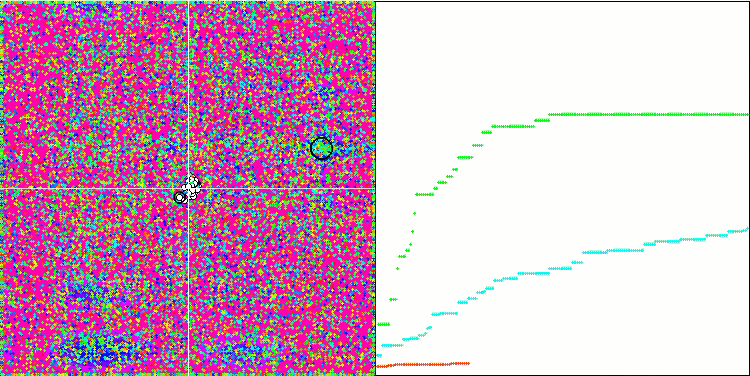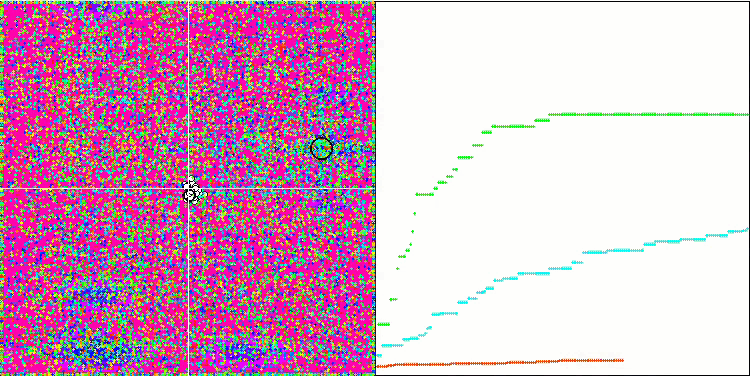
  HS über die Testfunktion Megacity

Nun ist es an der Zeit, die Ergebnisse in der Tabelle zu analysieren und die im Titel des Artikels gestellte Frage zu beantworten. In früheren Artikeln habe ich Zweifel geäußert, ob wir einen Algorithmus sehen können, der den Spitzenreiter in der Bewertungstabelle bei einer diskreten Funktion umgeht. Der Algorithmus, der optisch wie ein Zufallsalgorithmus aussieht, war in der Lage, nicht nur bei einer diskreten Funktion (bester in drei Tests), sondern auch bei anderen Testfunktionen führend zu werden und schließlich in 6 von 9 Tests der Beste zu werden.

AO	Beschreibung	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (diskret)			Megacity final	Endergebnis
		10 Parameter (5 F)	50 Parameter (25 F)	1000 Parameter (500 F)		10 Parameter (5 F)	50 Parameter (25 F)	1000 Parameter (500 F)		10 Parameter (5 F)	50 Parameter (25 F)	1000 Parameter (500 F)
HS	Harmoniesuche	1.00000	1.00000	0.57048	2.57048	1.00000	0.98931	0.57917	2.56848	1.00000	1.00000	1.00000	3.00000	100.00000
ACOm	Ameisen-Kolonie-Optimierung M	0.34724	0.18876	0.20182	0.73782	0.85966	1.00000	1.00000	2.85966	1.00000	0.88484	0.13497	2.01981	68.094
IWO	Optimierung mit invasiven Unkräutern	0.96140	0.70405	0.35295	2.01840	0.68718	0.46349	0.41071	1.56138	0.75912	0.39732	0.80145	1.95789	67.087
COAm	Kuckuck-Optimierungsalgorithmus M	0.92701	0.49111	0.30792	1.72604	0.55451	0.34034	0.21362	1.10847	0.67153	0.30326	0.41127	1.38606	50.422
FAm	Firefly-Algorithmus M	0.60020	0.35662	0.20290	1.15972	0.47632	0.42299	0.64360	1.54291	0.21167	0.25143	0.84884	1.31194	47.816
BA	Fledermaus-Algorithmus	0.40658	0.66918	1.00000	2.07576	0.15275	0.17477	0.33595	0.66347	0.15329	0.06334	0.41821	0.63484	39.711
ABC	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	0.78424	0.34335	0.24656	1.37415	0.50591	0.21455	0.17249	0.89295	0.47444	0.23609	0.33526	1.04579	38.937
BFO	Optimierung der bakteriellen Futtersuche	0.67422	0.32496	0.13988	1.13906	0.35462	0.26623	0.26695	0.88780	0.42336	0.30519	0.45578	1.18433	37.651
GSA	Algorithmus für die Schwerkraftsuche	0.70396	0.47456	0.00000	1.17852	0.26854	0.36416	0.42921	1.06191	0.51095	0.32436	0.00000	0.83531	35.937
FSS	Fischschulsuche	0.46965	0.26591	0.13383	0.86939	0.06711	0.05013	0.08423	0.20147	0.00000	0.00959	0.19942	0.20901	13.215
PSO	Partikelschwarmoptimierung	0.20515	0.08606	0.08448	0.37569	0.13192	0.10486	0.28099	0.51777	0.08028	0.21100	0.04711	0.33839	10.208
RND	zufällig	0.16881	0.10226	0.09495	0.36602	0.07413	0.04810	0.06094	0.18317	0.00000	0.00000	0.11850	0.11850	5.469
GWO	Grauer-Wolf-Optimierung	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.03645	0.06156	0.28778	1.000

Fassen wir zusammen. Zum Zeitpunkt der Erstellung dieses Berichts nimmt der HS-Algorithmus eine führende Position im Histogramm der Testergebnisse ein, mit einem großen Vorsprung gegenüber anderen Optimierungsalgorithmen, was auf die Stärke und Leistungsfähigkeit des Algorithmus und sein Potenzial im Bereich der Optimierung von Problemlösungsprozessen unterschiedlicher Komplexität hinweist.

Meiner Meinung nach ist ein sehr wichtiger Faktor, der es ermöglicht, beeindruckende Ergebnisse bei verschiedenen Arten von Testfunktionen, einschließlich sehr komplexer Funktionen, zu erzielen, die Vererbung einiger Methoden (Techniken), die in anderen Optimierungsalgorithmen vorhanden sind: HS verfügt nicht über eine Lösungspoolsortierung, jede Lösung aktualisiert nur ihre lokale Entscheidung - dies ist typisch für den Optimierungsalgorithmus der Kuckuckssuche, bei dem ein neuer Pfad für die Entwicklung eines Entscheidungszweigs nur dann entsteht, wenn das Ei besser ist als das im Nest. Außerdem ähneln die HS-Methoden den in genetischen Algorithmen verwendeten Methoden - Kombinatorik der Lösungselemente.

Der leistungsstarke HS-Optimierungsalgorithmus, der eine außergewöhnlich hohe Leistung aufweist, kann für die Lösung einer Vielzahl komplexer Probleme mit vielen Variablen empfohlen werden, sowohl für glatte Skalierungsfunktionen als auch für komplexe diskrete kombinatorische Probleme. Der HS-Algorithmus wurde bereits in vielen Bereichen des Maschinenbaus (Optimierung der Topologie von Strukturen und der optimalen Form von Teilen), der Elektronik und der Logistik erfolgreich eingesetzt.

Die einfache Implementierung des HS-Algorithmus bietet Raum für Forschung und ermöglicht es uns, verschiedene Optimierungsstrategien hinzuzufügen und zu kombinieren. Dies deutet darauf hin, dass die Möglichkeiten des Algorithmus noch lange nicht ausgeschöpft sind.

Das Histogramm der Testergebnisse des Algorithmus ist unten dargestellt.

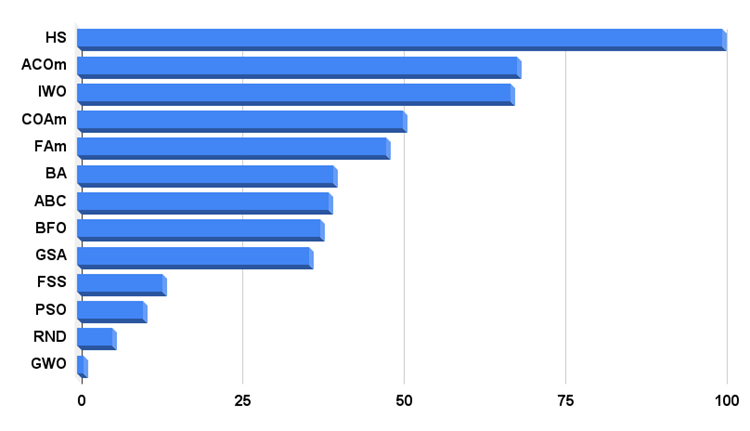
Abb. 3. Histogramm der Testergebnisse der Algorithmen

Vor- und Nachteile des harmonischen HS-Suchalgorithmus:

Vorteile:
1. Einfache Implementierung.
2. Hervorragende Konvergenz bei allen Arten von Funktionen, ohne Ausnahme.
3. Beeindruckende Skalierbarkeit.
4. Sehr schnell.
5. Geringe Anzahl von externen Parametern.

Nachteile
Nicht gefunden.

Jeder Artikel verfügt über ein Archiv, das aktualisierte aktuelle Versionen der Algorithmuscodes für alle früheren Artikel enthält. Der Artikel basiert auf den gesammelten Erfahrungen des Autors und stellt seine persönliche Meinung dar. Die Schlussfolgerungen und Urteile beruhen auf den Experimenten.