Algorithmus zur Optimierung der Migration der Tiere (AMO)
126
0
Einführung
Tierwanderung: Harmonie und Naturstrategie der Natur. Normalerweise wandern Tiere zwischen Überwinterungs- und Brutgebieten und folgen dabei festgelegten Routen, die sich im Laufe der Jahrhunderte der Evolution entwickelt haben. Bei diesen saisonalen Reisen handelt es sich nicht um zufällige Wanderungen, sondern um sorgfältig geplante Routen, die zu den Gebieten führen, die für ihr Überleben und ihre Fortpflanzung am günstigsten sind. Je nach Jahreszeit sind die Tiere auf der Suche nach Nahrung, Schutz und geeigneten Bedingungen für die Fortpflanzung unterwegs und werden dabei von den natürlichen Bedürfnissen ihres Rudels und ihren Instinkten geleitet. Jede dieser Reisen ist nicht nur ein Kampf ums Dasein, sondern auch ein Ausdruck der Harmonie mit der Natur, wobei jedes Individuum eine einzigartige Rolle im gesamten Ökosystem spielt.
Rentiere beispielsweise legen auf der Suche nach besseren Weideflächen weite Strecken zurück, und Vögel wie Kraniche und Gänse legen lange Flüge zwischen Überwinterungs- und Nistplätzen zurück. Dabei benutzen sie bestimmte Routen, die von Generation zu Generation weitergegeben werden. Diese Wanderungen sichern nicht nur das Überleben einzelner Arten, sondern unterstützen auch das Ökosystem als Ganzes, indem sie die Bestäubung der Pflanzen und die Verbreitung der Samen erleichtern.
Inspiration aus der Natur. Der AMO-Algorithmus (Animal Migration Optimization) wurde 2013 vom Forscher Xiantao Li vorgeschlagen. Die Hauptidee dieses Algorithmus besteht darin, den Prozess der saisonalen Migration von Tieren auf der Suche nach optimalen Bedingungen für Leben und Fortpflanzung in der Natur zu modellieren. Die Inspiration für den Algorithmus stammt aus der Beobachtung des Verhaltens wandernder Tiere wie Vögel, Fische und Säugetiere. Diese Tiere bewegen sich saisonal zwischen ihren Überwinterungs- und Brutgebieten und folgen dabei bestimmten Interaktionsregeln, die die Natur während der Migration entwickelt hat.
Der AMO-Algorithmus simuliert drei Hauptkomponenten der Tierbewegung über weite Distanzen: Vermeidung von Kollisionen mit benachbarten Individuen, Bewegung in die gleiche Richtung wie die Herde (Gruppe) und Wahrung eines ausreichenden Abstands zueinander. Diese Grundsätze tragen nicht nur zur Konfliktvermeidung bei, sondern sorgen auch für ein kollektives Verhalten, das für das Überleben in der Wildnis von entscheidender Bedeutung ist.
Optimierungsstufen im AMO-Algorithmus. Der Algorithmus umfasst zwei wichtige Optimierungsphasen in einer Iteration:
- Migration: Während dieser Phase wird die Position des Individuums unter Berücksichtigung seiner Nachbarn aktualisiert.
- Populationserneuerung: In dieser Phase werden Individuen teilweise durch neue ersetzt, wobei die Wahrscheinlichkeit von der Position des Individuums im Schwarm abhängt.
Die Modellierung des Kollektivverhaltens wandernder Tiere kann ein effektiver Ansatz zur Lösung komplexer Optimierungsprobleme sein. Der Algorithmus versucht, ein Gleichgewicht zwischen der Erkundung des Suchraums und der Nutzung der besten gefundenen Lösungen herzustellen und dabei natürliche Prozesse nachzuahmen.
2. Algorithmusimplementierungen
Das Grundkonzept dieses algorithmischen Modells der Tierwanderung besteht darin, um jedes Tier herum konzentrische „Zonen“ zu schaffen. In der Abstoßungszone neigt das Tier dazu, sich von seinen Nachbarn zu entfernen, um Kollisionen zu vermeiden. Der Algorithmus der Tiermigration gliedert sich laut Autor in zwei Hauptprozesse:
1. Tierwanderung. Ein topologischer Ring wird verwendet, um eine begrenzte Nachbarschaft von Individuen zu beschreiben. Der Einfachheit halber wird die Nachbarschaftslänge für jede Dimension auf fünf festgelegt. Die Nachbarschaftstopologie bleibt stationär und wird anhand der Indizes eines Individuums in der Population bestimmt. Wenn der Index des Tieres „j“ ist, dann haben seine Nachbarn die Indizes [j – 2, j – 1, j, j + 1 und j + 2]. Wenn der Index eines Tieres „1“ ist, haben seine Nachbarn die Indizes [N - 1, N, 1, 2, 3] und so weiter. Sobald die Nachbarschaftstopologie erstellt ist, wird ein Nachbar nach dem Zufallsprinzip ausgewählt und die Position des Einzelnen aktualisiert, um die Position dieses Nachbarn widerzuspiegeln. Diese Beschreibung stammt von den Autoren des ursprünglichen Algorithmus. In diesem Fall kann die Beschränkung der Anzahl der Nachbarn in die Parameter des Algorithmus übergeben werden, um durch Experimente die beste Anzahl von Nachbarn zu finden, um die höchstmögliche Effizienz des Algorithmus sicherzustellen.
2. Populationserneuerung. Während der Populationserneuerung modelliert der Algorithmus, wie einige Tiere die Gruppe verlassen und andere sich der Population anschließen. Individuen können mit einer Wahrscheinlichkeit von „p“, die auf der Qualität der Fitnessfunktion basiert, durch neue Tiere ersetzt werden. Wir sortieren die Population in absteigender Reihenfolge der Fitnessfunktionswerte, was bedeutet, dass die Wahrscheinlichkeit, ein Individuum mit der besten Fitness zu ändern, 1/N beträgt, während die Wahrscheinlichkeit, ein Individuum mit der schlechtesten Fitness zu ändern, 1 beträgt.
Die Tierwanderung und die Populationserneuerung können nach der Version des Autors algorithmisch beschrieben werden, wie unten gezeigt.
Tierwanderung:
1. Für jedes Tier: a. Bestimme die topologische Nachbarschaft eines Tieres (5 nächste Nachbarn).b. Wähle einen zufälligen Nachbarn aus der Nachbarliste.
c. Aktualisiere die Position des Tieres in Richtung des ausgewählten Nachbarn mithilfe der folgenden Gleichung:
x_j_new = x_j_old + r * (x_neighbor - x_j_old), wobei:
- x_j_new — neue Position des j-ten Tieres,
- x_j_old — aktuelle Position,
- x_neighbor — ausgewählte Nachbarposition,
- r — normalverteilte Zufallszahl.
d. Bewerte die neue Position des Tieres mithilfe der Zielfunktion.
Populationserneuerung:
1. Sortiere die Tiere nach dem Wert der Zielfunktion in absteigender Reihenfolge. 2. Für jedes Tier: a. Berechne dir Wahrscheinlichkeit, ein Tier durch ein neues zufällig ausgewähltes Tier zu ersetzen:p = 1.0 - (1.0 / (x + 1)), wobei x der Rang (Index) des i-ten Tieres in der sortierten Liste ist.
b. Wenn eine Zufallszahl kleiner als p ist, ersetze das Tier (änder die Koordinate auf den Durchschnittswert der Koordinaten zweier zufällig ausgewählter Tiere aus der Population). c. Ansonsten lasse das Tier unverändert.3. Schätzen einer neuen Population mithilfe einer Zielfunktion.
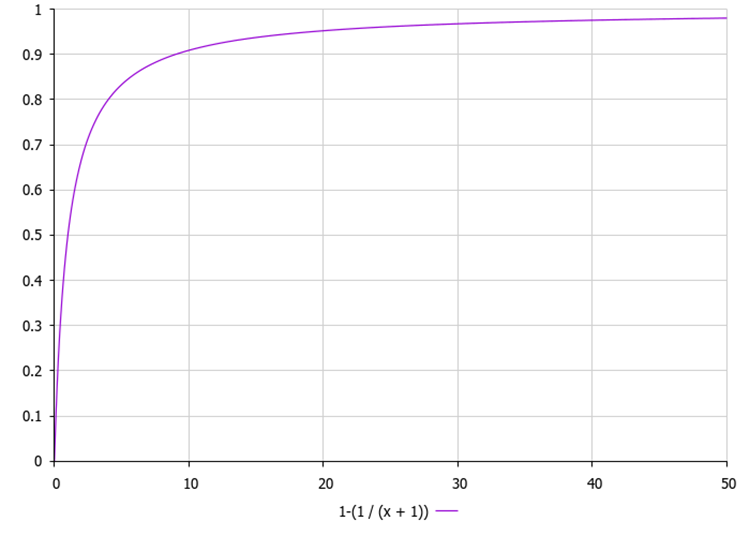
Abbildung 1. Die Veränderungswahrscheinlichkeit für ein Individuum in Abhängigkeit von seiner Position in der Population, wobei „x“ der Index des Individuums in der Population ist.
Schreiben wir einen Pseudocode für den AMO-Tiermigrationsalgorithmus.
1. Initialisierung der Tierpopulation mit zufälligen Positionen.
2. Hauptschleife:
a. Für jedes Tier:
Definiere eine topologischen Nachbarschaft.Wähle einen zufälligen Nachbarn.
Aktualisiere der Position des Tiers in Richtung seines Nachbarn.
Evaluiere eine neue Position.
b. Sortiere die Population nach den Werten der Zielfunktion.
c. Ersetze auf Basis von Wahrscheinlichkeiten minderwertiger Tiere durch neue.
d. Schätze die aktualisierte Population.
B. Aktualisiere die beste Lösung.
3. Wiederhole den Vorgang ab Schritt 2, bis das Stoppkriterium erfüllt ist.
Nachdem wir nun mit dem Algorithmus vertraut sind, können wir mit dem Schreiben des Codes fortfahren. Schauen wir uns den Code der Klasse C_AO_AMO genauer an:
1. Die Klasse C_AO_AMO wird von der Basisklasse C_AO abgeleitet, was es ermöglicht, ihre Funktionalität zu nutzen und zu erweitern.
2. Der Konstruktor gibt die grundlegenden Eigenschaften des Algorithmus an, etwa den Namen, die Beschreibung und den Link zum Artikel. Außerdem werden die Algorithmusparameter initialisiert, darunter Populationsgröße, Bias und Anzahl der Nachbarn.
3. popSize, deviation, neighborsNumberOnSide – diese Variablen bestimmen die Populationsgröße, die Standardabweichung und die Anzahl der Nachbarn auf einer Seite, die bei der Migration berücksichtigt werden.
4. SetParams – die Methode ist für die Aktualisierung der Algorithmusparameter basierend auf den im Array der Parameter gespeicherten Werten verantwortlich.
5. Init – Initialisierungsmethode, die Arrays für die minimalen und maximalen Bereichswerte, Schritte und Anzahl der Epochen akzeptiert.
6. Moving() – die Methode ist für das Verschieben von Agenten im Suchraum verantwortlich, Revision() – die Methode überprüft und aktualisiert den Status der Agenten in der Population.
7. S_AO_Agent population [] — das Array speichert die aktuelle Population von Agenten (Tieren), S_AO_Agent pTemp [] — temporäres Array, das beim Sortieren der Population verwendet wird.
8. GetNeighborsIndex – private Methode zum Abrufen von Nachbarindizes für einen bestimmten Agenten.
Die Klasse C_AO_AMO implementiert einen auf Tierwanderungen basierenden Optimierungsalgorithmus und stellt die erforderlichen Methoden und Parameter zum Einrichten und Ausführen des Algorithmus bereit. Sie erbt die Funktionsweise von der Basisklasse, wodurch wir sein Verhalten je nach Aufgabenanforderungen erweitern und ändern können.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_AMOm : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_AMOm () { } C_AO_AMOm () { ao_name = "AMOm"; ao_desc = "Animal Migration Optimization M"; ao_link = "https://www.mql5.com/en/articles/15543"; popSize = 50; // Population size deviation = 8; neighborsNumberOnSide = 10; ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "deviation"; params [1].val = deviation; params [2].name = "neighborsNumberOnSide"; params [2].val = neighborsNumberOnSide; } void SetParams () { popSize = (int)params [0].val; deviation = params [1].val; neighborsNumberOnSide = (int)params [2].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //---------------------------------------------------------------------------- double deviation; int neighborsNumberOnSide; S_AO_Agent population []; // Animal population S_AO_Agent pTemp []; // Temporary animal population private: //------------------------------------------------------------------- int GetNeighborsIndex (int i); }; //——————————————————————————————————————————————————————————————————————————————
Als nächstes betrachten wir den den Code der MethodeInit in der Klasse C_AO_AMO. Die Beschreibung der einzelnen Teile der Methode:
1. rangeMinP [], rangeMaxP [], rangeStepP [] — Arrays zur Bestimmung der minimalen und maximalen Bereiche der optimierten Parameter und ihrer Schritte.
2. Die Methode StandardInit führt eine Standardinitialisierung basierend auf den übergebenen Bereichen durch.
3. Größenanpassung der Arrays von population und pTemp Arrays auf popSize.
4. Die Initialisierung der Agenten wird für alle Elemente des Arrays population durchgeführt und initialisiert jeden Agenten mithilfe von Init, wobei ihm die Anzahl der Koordinaten übergeben wird.
5. Wenn alle Operationen erfolgreich waren, gibt die Methode true zurück.
Die Methode Init der Klasse C_AO_AMO ist für die Initialisierung der Agentenpopulation unter Berücksichtigung der angegebenen Bereiche und Parameter verantwortlich.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_AMO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (population, popSize); ArrayResize (pTemp, popSize); for (int i = 0; i < popSize; i++) population [i].Init (coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Als nächstes schauen wir uns die Methode Moving der Klasse C_AO_AMO an, die für die Bewegung von Agenten in der Population verantwortlich ist. Hauptteile des Codes:
1. Überprüfen des Revisionsstatus :
- Wenn revision gleich false ist, wird die Methode zum ersten Mal oder nach einem Reset aufgerufen. In diesem Fall wird die Population initialisiert.
- Für jedes Individuum in der Population (von 0 bis popSize) und für jede Koordinate (von 0 bis coords) werden Zufallswerte im angegebenen Bereich (rangeMin und rangeMax) generiert.
- Diese Werte werden dann von der Funktion SeInDiSp verarbeitet, die sie unter Berücksichtigung des angegebenen Schrittes (rangeStep) anpasst.
2. Setzen des Revisionsflags:
- Nach der Initialisierung wird revision auf true gesetzt und die Methode beendet.
3. Grundlegender Migrationszyklus:
- Wenn revision true ist, wechselt die Methode zur Hauptmigrationslogik.
- Für jedes Individuum erfolgt erneut eine Iteration über die Koordinaten.
- GetNeighborsIndex(i) wird verwendet, um den Index des Nachbarn zu erhalten, mit dem das aktuelle Individuum verglichen wird.
- Die Distanz zwischen den Koordinaten des Nachbarn und der aktuellen Person wird berechnet.
- Basierend auf dieser Distanz werden die minimalen und maximalen Grenzen (min und max), in denen sich die neue Koordinate befindet, bestimmt.
- Wenn die berechneten Grenzen außerhalb des akzeptablen Bereichs liegen, werden sie angepasst, um rangeMin und rangeMax zu berücksichtigen.
- Anschließend wird der neue Koordinatenwert mit Hilfe der Normalverteilung (Funktion GaussDistribution) berechnet, welche eine Berücksichtigung der Standardabweichung (deviation) ermöglicht.
- Wie im ersten Fall wird auch der neue Wert mit SeInDiSp behandelt.
Die Methode Moving ist für die Aktualisierung der Positionen von Agenten in Abhängigkeit von ihren Nachbarn und Zufallsfaktoren verantwortlich.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AMO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- int ind1 = 0; double dist = 0.0; double x = 0.0; double min = 0.0; double max = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { //------------------------------------------------------------------------ ind1 = GetNeighborsIndex (i); dist = fabs (population [ind1].c [c] - a [i].c [c]); x = a [i].c [c]; min = x - dist; max = x + dist; if (min < rangeMin [c]) min = rangeMin [c]; if (max > rangeMax [c]) max = rangeMax [c]; a [i].c [c] = u.GaussDistribution (x, min, max, deviation); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Der folgende Code zeigt die Methode Revision von C_AO_AMO. Schauen wir uns das Stück für Stück an:
1. Die beste Individuum finden:
- Die Variable ind wird verwendet, um den Index des Individuums mit der besten Funktion (f) zu speichern.
- Der Code durchläuft die gesamte Population (von 0 bis popSize) und aktualisiert den Wert fB, wenn das aktuelle Individuum den besten Funktionswert hat.
- Wenn das beste Individuum gefunden wurde, werden seine Eigenschaften (Koordinaten) in das Array cB kopiert.
- Für jedes Individuum in der Population (von 0 bis popSize) wird die Wahrscheinlichkeit berechnet, die vom Index i abhängt.
- Für jede Koordinate (von 0 bis Koordinaten) wird ein zufälliger Vergleich mit der Wahrscheinlichkeit prob durchgeführt.
- Wenn die Zufallszahl kleiner als prob ist, werden zwei zufällige Individuen ind1 und ind2 ausgewählt.
- Wenn beide Individuen übereinstimmen, wird ind2 erhöht, um zu vermeiden, dass dasselbe Individuum ausgewählt wird.
- Der neue Koordinatenwert der aktuellen Person wird als Durchschnitt der Koordinaten zweier zufällig ausgewählter Personen berechnet und anschließend mithilfe der Funktion SeInDiSp angepasst, die den Wert auf einen bestimmten Bereich begrenzt.
- Sobald die Änderungen abgeschlossen sind, wird die gesamte Population durch Kopieren der Werte aus dem Array aktualisiert.
- Als nächstes wird die Sortierfunktion aufgerufen. Es sortiert die Population nach der Funktion f.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AMO::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- int ind1 = 0; int ind2 = 0; double dist = 0.0; double x = 0.0; double min = 0.0; double max = 0.0; double prob = 0.0; for (int i = 0; i < popSize; i++) { prob = 1.0 - (1.0 / (i + 1)); for (int c = 0; c < coords; c++) { if (u.RNDprobab() < prob) { ind1 = u.RNDminusOne (popSize); ind2 = u.RNDminusOne (popSize); if (ind1 == ind2) { ind2++; if (ind2 > popSize - 1) ind2 = 0; } a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5; a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) population [i] = a [i]; u.Sorting (population, pTemp, popSize); } //——————————————————————————————————————————————————————————————————————————————
Betrachten wir abschließend den Code der Methode GetNeighborsIndex der Klasse C_AO_AMO, die für die Ermittlung des Index eines zufälligen Nachbarn für den angegebenen Index i unter Berücksichtigung der Array-Grenzen verantwortlich ist.
1. Initialisierung von Variablen:
- Ncount – Anzahl der Nachbarn, bestimmt durch die Variable neighborsNumberOnSide.
- N — Die Gesamtzahl der Nachbarn, einschließlich des Elements selbst, wird definiert als Ncount * 2 + 1.
2. Die Methode verwendet bedingte Anweisungen, um die Position des Index i relativ zu den Array-Grenzen zu überprüfen.
3. Behandlung der ersten Elemente Ncount (Ränder auf der linken Seite). Wenn der Index i kleiner als Ncount ist, bedeutet dies, dass er sich am Anfang des Arrays befindet. In diesem Fall generiert die Methode einen zufälligen Nachbarindex von 0 bis N-1.
4. Behandlung der letzten Elemente Ncount (Ränder auf der rechten Seite). Wenn der Index i größer oder gleich popSize - Ncount ist, bedeutet dies, dass er sich am Ende des Arrays befindet. Die Methode generiert einen Nachbarindex beginnend bei popSize - N, um die Grenzen zu berücksichtigen.
5. Behandlung aller anderen Elemente. Wenn der Index i irgendwo in der Mitte des Arrays liegt, generiert die Methode einen Nachbarindex, der um Ncount nach links versetzt ist, und fügt einen zufälligen Wert von 0 bis N-1 hinzu.
6. Am Ende gibt die Methode den generierten Nachbarindex zurück.
Mit der Methode GetNeighborsIndex kann der Index eines zufälligen Nachbarn für einen gegebenen Index von i unter Berücksichtigung der Array-Grenzen abgerufen werden.
//—————————————————————————————————————————————————————————————————————————————— int C_AO_AMO::GetNeighborsIndex (int i) { int Ncount = neighborsNumberOnSide; int N = Ncount * 2 + 1; int neighborIndex; // Select a random neighbor given the array boundaries if (i < Ncount) { // For the first Ncount elements neighborIndex = MathRand () % N; } else { if (i >= popSize - Ncount) { // For the last Ncount elements neighborIndex = (popSize - N) + MathRand () % N; } else { // For all other elements neighborIndex = i - Ncount + MathRand () % N; } } return neighborIndex; } //——————————————————————————————————————————————————————————————————————————————
Nachdem wir nun mit dem Schreiben des Algorithmus fertig sind, überprüfen wir, wie er funktioniert. Ergebnisse der ursprünglichen Version des Algorithmus:
AMO|Animal Migration Optimization|50.0|1.0|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.43676335174918435
25 Hilly's; Func runs: 10000; result: 0.28370099295372453
500 Hilly's; Func runs: 10000; result: 0.25169663266864406
=============================
5 Forest's; Func runs: 10000; result: 0.312993148861033
25 Forest's; Func runs: 10000; result: 0.23960515885149344
500 Forest's; Func runs: 10000; result: 0.18938496103401775
=============================
5 Megacity's; Func runs: 10000; result: 0.18461538461538463
25 Megacity's; Func runs: 10000; result: 0.12246153846153851
500 Megacity's; Func runs: 10000; result: 0.10223076923076994
=============================
All score: 2.12345 (23.59%)
Leider weist die Originalversion schwache Sucheigenschaften auf. Solche Indikatoren werden nicht in die Bewertungstabelle aufgenommen. Bei der Analyse der Ergebnisse zeigte sich, dass zwischen dem Algorithmus und denen der anderen Teilnehmer eine erhebliche Lücke bestand, was mich dazu veranlasste, noch einmal gründlich darüber nachzudenken.
Bei näherer Betrachtung der Strategie wurde ein entscheidender Fehler entdeckt: Das Sortieren der Population trug nicht zur Ansammlung genetischen Materials der besten Individuen bei. Dadurch wurde lediglich ihre topologische Anordnung geändert, ohne ihr Wesen zu beeinträchtigen. Der Einfluss der Sortierung beschränkte sich darauf, nur die Wahrscheinlichkeit einer Änderung der Koordinaten von Personen im Suchraum anzupassen, und diese Wahrscheinlichkeit ist umgekehrt proportional zu ihrer Fitness.
Bemerkenswert ist, dass die neuen Koordinaten ausschließlich auf Basis der in der Population bereits vorhandenen Koordinaten gebildet wurden, und zwar durch Mittelung der Werte zweier zufällig ausgewählter Individuen. Das Erkennen dieser Nuancen führte zu der Idee, die Population zu erweitern, um die Nachkommen vor der Sortierung in die Elterngruppe zu integrieren. Durch diesen Ansatz bleiben nicht nur die besten genetischen Kombinationen erhalten, sondern es werden auch weniger angepasste Individuen auf natürliche Weise verdrängt. Zweifellos bleibt das Problem der Aktualisierung des Genpools der Population relevant, aber die vorgeschlagene Modifikation dürfte die Dynamik des Evolutionsprozesses deutlich erhöhen. Um diese Idee umzusetzen, ändern wir zunächst die Initialisierungsmethode, indem wir die Größe der übergeordneten Population verdoppeln.
Lassen Sie uns den vollständigen Initialisierungscode darstellen, in dem wir die Verdoppelung der übergeordneten Population sehen können.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_AMOm::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (population, popSize * 2); ArrayResize (pTemp, popSize * 2); for (int i = 0; i < popSize * 2; i++) population [i].Init (coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Dementsprechend ist eine Korrektur der Revisionsmethode erforderlich:
//---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) population [i + popSize] = a [i]; u.Sorting (population, pTemp, popSize * 2);
Nach den entsprechenden Anpassungen testen wir den Algorithmus erneut und vergleichen die Ergebnisse:
AMOm|Animal Migration Optimization M|50.0|1.0|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.4759595972704031
25 Hilly's; Func runs: 10000; result: 0.31711543296080447
500 Hilly's; Func runs: 10000; result: 0.2540492181444619
=============================
5 Forest's; Func runs: 10000; result: 0.40387880560608347
25 Forest's; Func runs: 10000; result: 0.27049305409901064
500 Forest's; Func runs: 10000; result: 0.19135802944407254
=============================
5 Megacity's; Func runs: 10000; result: 0.23692307692307696
25 Megacity's; Func runs: 10000; result: 0.14461538461538465
500 Megacity's; Func runs: 10000; result: 0.10109230769230851
=============================
All score: 2.39548 (26.62%)
In diesem Fall sehen wir eine Verbesserung des Gesamtergebnisses um 3 %, was die Erfolgsaussichten des gewählten Weges anzeigt.
Als nächstes versuchen wir, die probabilistische Änderung von Individuen je nach Rang an die Methode Moving zu übergeben. Dadurch können Änderungen an den Koordinaten einzelner Personen vorgenommen werden, unmittelbar nachdem diese neue Koordinaten von ihren nächsten Nachbarn erhalten haben.
//---------------------------------------------------------------------------- int ind1 = 0; int ind2 = 0; double dist = 0.0; double x = 0.0; double min = 0.0; double max = 0.0; double prob = 0.0; for (int i = 0; i < popSize; i++) { prob = 1.0 - (1.0 / (i + 1)); for (int c = 0; c < coords; c++) { //------------------------------------------------------------------------ ind1 = GetNeighborsIndex (i); dist = fabs (population [ind1].c [c] - a [i].c [c]); x = a [i].c [c]; min = x - dist; max = x + dist; if (min < rangeMin [c]) min = rangeMin [c]; if (max > rangeMax [c]) max = rangeMax [c]; a [i].c [c] = u.GaussDistribution (x, min, max, deviation); //---------------------------------------------------------------------------- if (u.RNDprobab() < prob) { ind1 = u.RNDminusOne (popSize); ind2 = u.RNDminusOne (popSize); if (ind1 == ind2) { ind2++; if (ind2 > popSize - 1) ind2 = 0; } a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5; } a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } }
Schauen wir uns die Ergebnisse noch einmal an:
AMO|Animal Migration Optimization|50.0|1.0|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.7204154413083147
25 Hilly's; Func runs: 10000; result: 0.4480389094268583
500 Hilly's; Func runs: 10000; result: 0.25286213277651365
=============================
5 Forest's; Func runs: 10000; result: 0.7097109421461968
25 Forest's; Func runs: 10000; result: 0.3299544372347476
500 Forest's; Func runs: 10000; result: 0.18667655927410348
=============================
5 Megacity's; Func runs: 10000; result: 0.41076923076923083
25 Megacity's; Func runs: 10000; result: 0.20400000000000001
500 Megacity's; Func runs: 10000; result: 0.09586153846153929
=============================
All score: 3.35829 (37.31%)
Das ist viel besser und eine Fortsetzung wert. Nach einigen Experimenten mit dem Code haben wir die endgültige Version der Methode Moving erhalten:
//---------------------------------------------------------------------------- int ind1 = 0; int ind2 = 0; double dist = 0.0; double x = 0.0; double min = 0.0; double max = 0.0; double prob = 0.0; for (int i = 0; i < popSize; i++) { prob = 1.0 - (1.0 / (i + 1)); for (int c = 0; c < coords; c++) { //------------------------------------------------------------------------ ind1 = GetNeighborsIndex (i); dist = fabs (population [ind1].c [c] - a [i].c [c]); x = population [ind1].c [c]; min = x - dist; max = x + dist; if (min < rangeMin [c]) min = rangeMin [c]; if (max > rangeMax [c]) max = rangeMax [c]; a [i].c [c] = u.GaussDistribution (x, min, max, deviation); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); //------------------------------------------------------------------------ if (u.RNDprobab() < prob) { if (u.RNDprobab() <= 0.01) { ind1 = u.RNDminusOne (popSize); ind2 = u.RNDminusOne (popSize); //if (ind1 == ind2) { //ind2++; //if (ind2 > popSize - 1) ind2 = 0; a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5; a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } //ind1 = u.RNDminusOne (popSize); //a [i].c [c] = population [ind1].c [c]; } } } } //——————————————————————————————————————————————————————————————————————————————
Kommen wir von der Methode Moving zur endgültigen Version der Methode Revision von C_AO_AMO, die für die Aktualisierung und Sortierung der Agentenpopulation verantwortlich ist.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AMO::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) population [popSize + i] = a [i]; u.Sorting (population, pTemp, popSize * 2); } //——————————————————————————————————————————————————————————————————————————————Sobald der Code endgültig erstellt ist, führen wir erneut den Test durch.
3. Testergebnisse
Ergebnisse des AMO-Prüfstands:
AMOm|Animal Migration Optimization|50.0|8.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9627642143272663
25 Hilly's; Func runs: 10000; result: 0.8703754433240446
500 Hilly's; Func runs: 10000; result: 0.467183248460726
=============================
5 Forest's; Func runs: 10000; result: 0.9681183408862706
25 Forest's; Func runs: 10000; result: 0.9109372988714968
500 Forest's; Func runs: 10000; result: 0.4719026790932256
=============================
5 Megacity's; Func runs: 10000; result: 0.6676923076923076
25 Megacity's; Func runs: 10000; result: 0.5886153846153845
500 Megacity's; Func runs: 10000; result: 0.23546153846153978
=============================
All score: 6.14305 (68.26%)
In der Wertungstabelle können wir hohe Ergebnisse sehen. Der Preis dafür ist allerdings eine große Streuung der Endwerte bei Funktionen mit kleiner Dimension. Führen wir 50 Tests statt der üblichen 10 durch.
AMOm|Animal Migration Optimization|50.0|8.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.903577388020872
25 Hilly's; Func runs: 10000; result: 0.8431723262743616
500 Hilly's; Func runs: 10000; result: 0.46284266807030283
=============================
5 Forest's; Func runs: 10000; result: 0.9900061169785055
25 Forest's; Func runs: 10000; result: 0.9243600311397848
500 Forest's; Func runs: 10000; result: 0.4659761237381695
=============================
5 Megacity's; Func runs: 10000; result: 0.5676923076923077
25 Megacity's; Func runs: 10000; result: 0.5913230769230771
500 Megacity's; Func runs: 10000; result: 0.23773230769230896
=============================
All score: 5.98668 (66.52%)
Nun sind die Ergebnisse realistischer, allerdings hat auch die Effizienz leicht abgenommen.
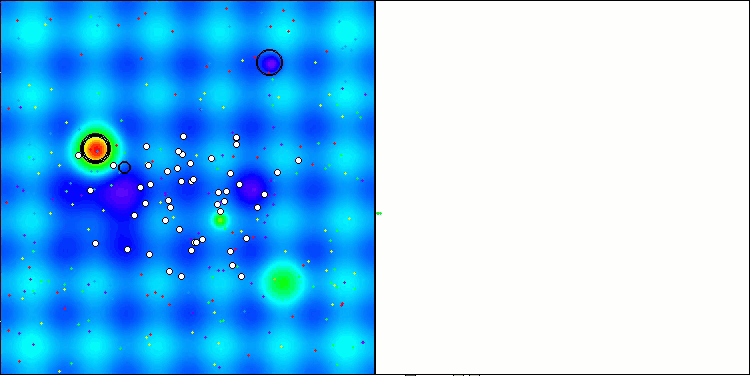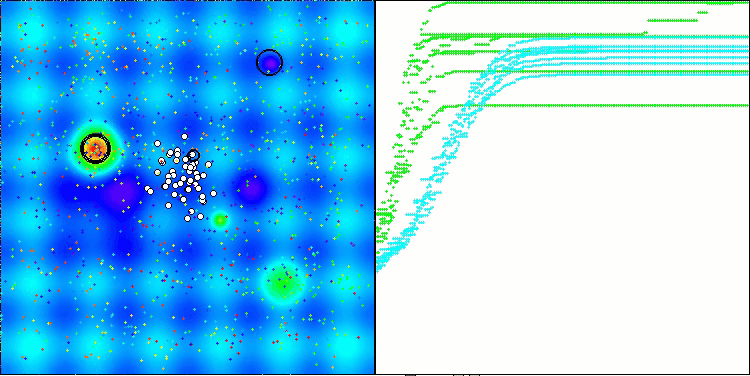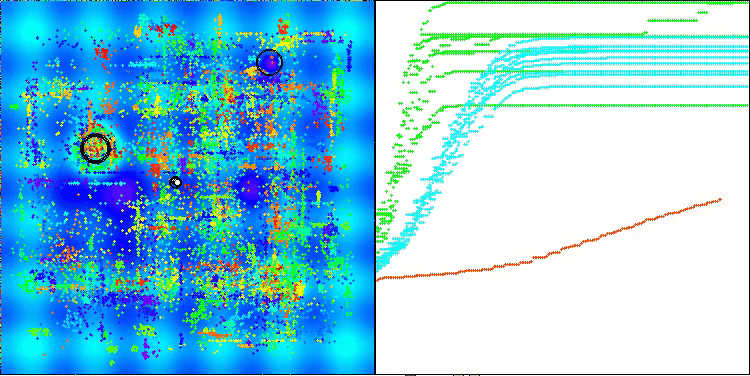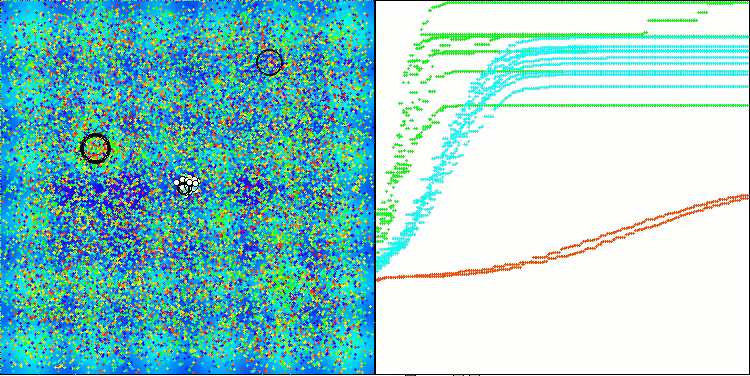
AMOm mit der Testfunktion Hilly
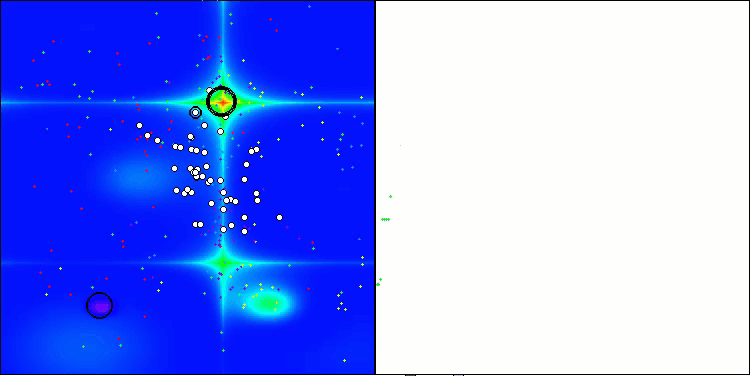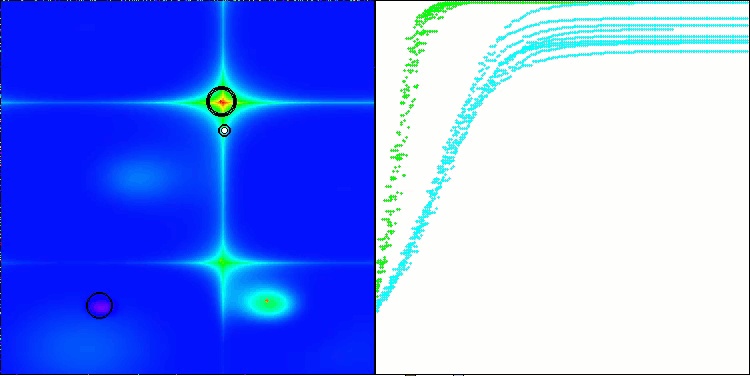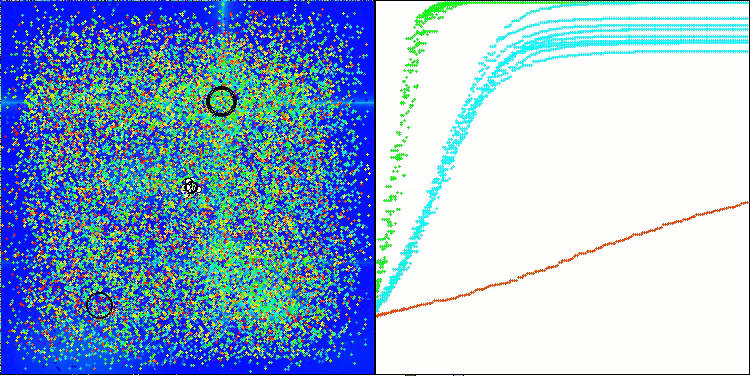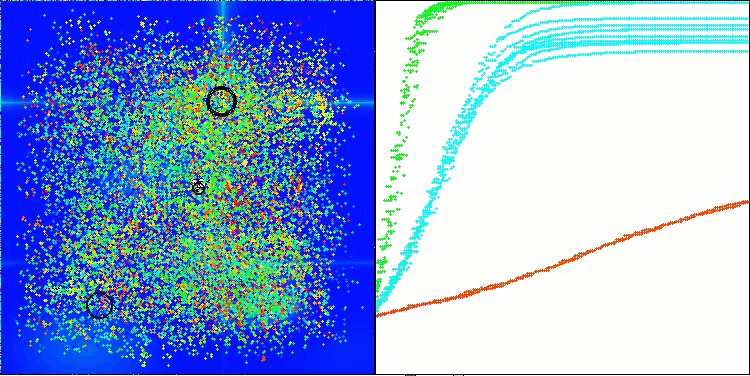
AMOm mit der Testfunktion Forest
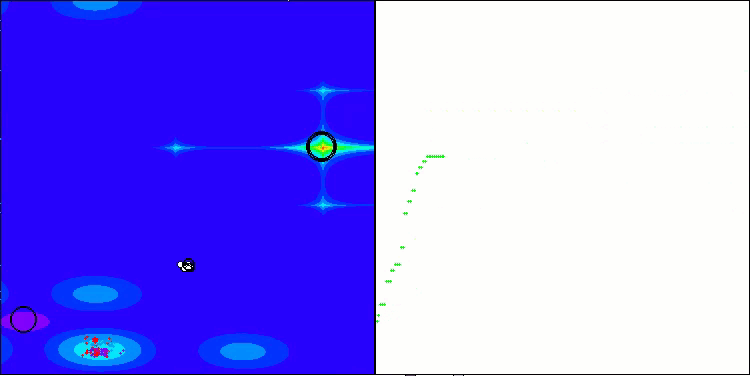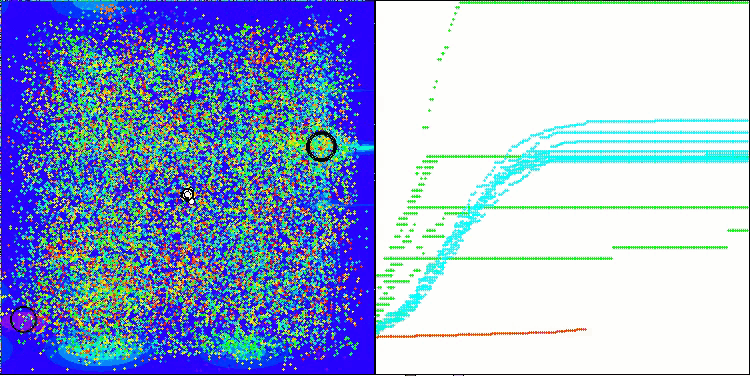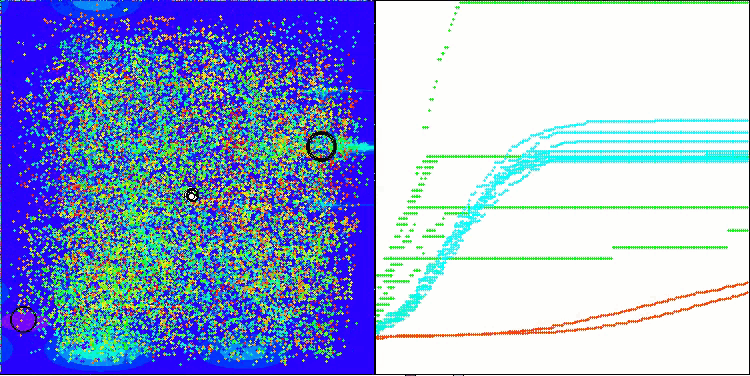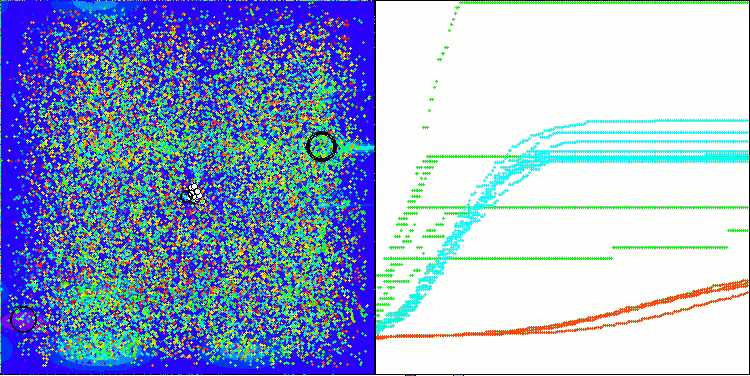
AMOm mit der Testfunktion Megacity
Nach einigen erstaunlichen Transformationen belegt der Algorithmus souverän den dritten Platz in der Bewertungstabelle.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Сode Lock Algorithmus | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | ESG | Entwicklung der sozialen Gruppen | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 8 | SIA | Simuliertes isotropes Abkühlen | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 9 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 10 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 11 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 12 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 13 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 14 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 15 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 16 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 17 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 18 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 19 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 20 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 21 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 22 | BFO-GA | Optimierung der bakteriellen Futtersuche - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 23 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 24 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 25 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 26 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 27 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 28 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 29 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 30 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 31 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 32 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 33 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 34 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 35 | BA | Fledermaus-Algorithmus | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 36 | SA | simuliertes Abkühlen | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 37 | IWDm | intelligente Wassertropfen M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 38 | PSO | Partikelschwarmoptimierung | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 39 | Gebote | Boids-Algorithmus | 0.43340 | 0.30581 | 0.25425 | 0.99346 | 0.35718 | 0.20160 | 0.15708 | 0.71586 | 0.27846 | 0.14277 | 0.09834 | 0.51957 | 2.229 | 24.77 |
| 40 | MA | Affen-Algorithmus | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 41 | SFL | schlurfender Froschsprung | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 42 | FSS | Fischschulsuche | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 43 | RND | zufällig | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
| 44 | GWO | Grauer-Wolf-Optimierung | 0.59169 | 0.36561 | 0.29595 | 1.25326 | 0.24499 | 0.09047 | 0.03612 | 0.37158 | 0.27667 | 0.08567 | 0.02170 | 0.38403 | 2.009 | 22.32 |
| 45 | CSS | Suche geladener Systeme | 0.44252 | 0.35454 | 0.35201 | 1.14907 | 0.24140 | 0.11345 | 0.06814 | 0.42299 | 0.18333 | 0.06300 | 0.02322 | 0.26955 | 1.842 | 20.46 |
Zusammenfassung
Basierend auf den Ergebnissen des AMOm-Algorithmus bei Testfunktionen können die folgenden Schlussfolgerungen gezogen werden: Trotz der Streuung der Werte bei Funktionen mit kleiner Dimension zeigt der Algorithmus eine hervorragende Skalierbarkeit bei Funktionen mit großer Dimension. Die umfassenden Änderungen an der Originalversion des Algorithmus haben dessen Leistung deutlich verbessert. In diesem Fall war es durch die Verdoppelung der Elternpopulation (für die gemeinsame Sortierung mit den Tochterindividuen) und die Änderung der Ausführungsreihenfolge der Algorithmusschritte möglich, eine größere Bandbreite unterschiedlicher Lösungen zu erhalten. Dieser Algorithmus wurde zu einem klaren Beispiel für die Möglichkeiten der Verwendung zusätzlicher Techniken zu seiner Modifikation, was zu erheblichen Verbesserungen führte. Dies wurde durch die Verbesserung der Algorithmuslogik selbst möglich, die im Verhältnis zu anderen Optimierungsalgorithmen nicht immer funktioniert.
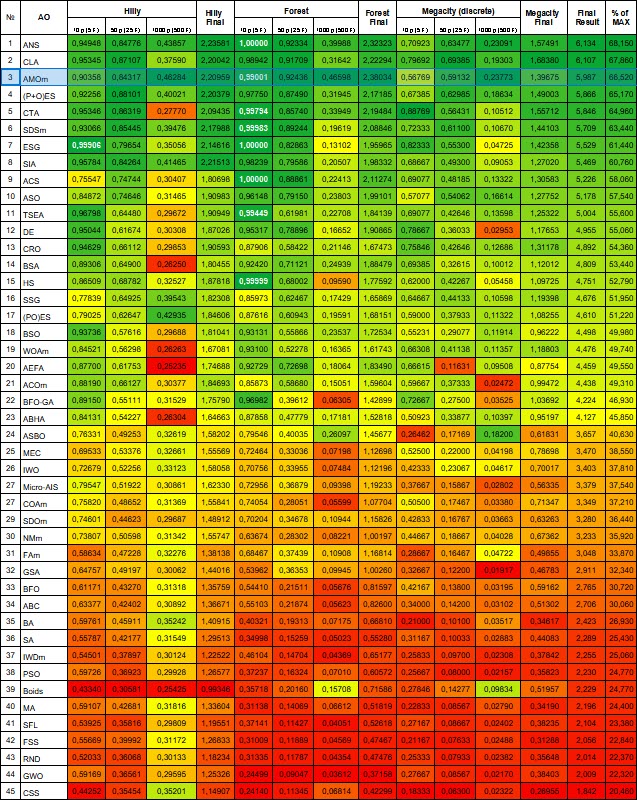
Abbildung 2. Farbabstufung der Algorithmen nach relevanten Tests Ergebnisse größer oder gleich 0,99 sind weiß hervorgehoben
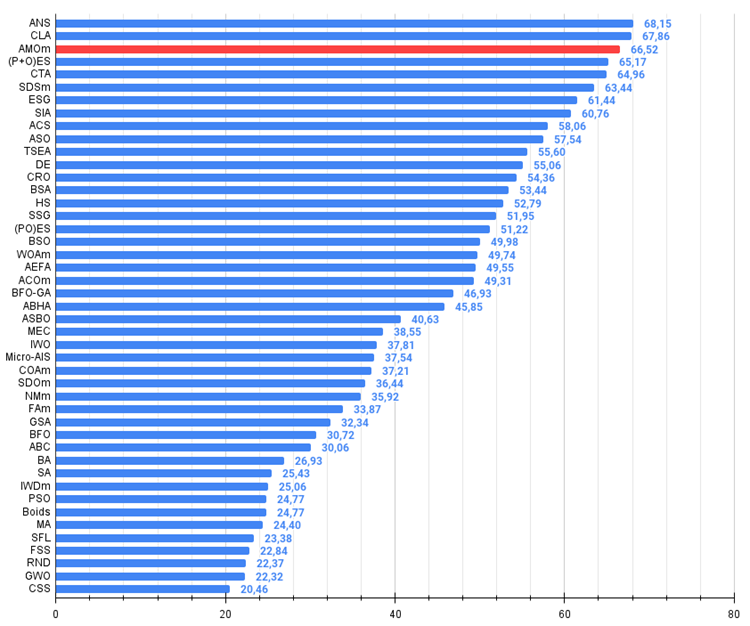
Abbildung 3. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,
wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Wertungstabelle)
AMOm Vor- und Nachteile:
Vorteile:
- Hervorragende Konvergenz.
- Hohe Skalierbarkeit.
- Wenige Parameter.
- Einfache Umsetzung.
Nachteile
- Streuung der Ergebnisse bei niedrigdimensionalen Funktionen.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Algorithmuscodes begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15543
Neuronale Netze im Handel: Praktische Ergebnisse der Methode TEMPO
Dekonstruktion von Beispielen für Handelsstrategien im Client-Terminal
Neuronale Netze im Handel: Einspeisung globaler Informationen in unabhängige Kanäle (InjectTST)
Meistern Sie MQL5 vom Anfänger bis zum Profi (Teil IV): Über Arrays, Funktionen und globale Terminalvariablen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.