Brain Storm Optimierungsalgorithmus (Teil I): Clustering
21
0
Inhalt
1. Einführung
2. Beschreibung des Algorithmus
3. K-Means
1. Einführung
Brain Storm Optimization (BSO) ist ein aufregender und innovativer Optimierungsalgorithmus für Populationen, der durch das natürliche Phänomen des Brainstormings inspiriert wurde. Diese Optimierungsmethode ist ein effektiver Ansatz zur Lösung komplexer Probleme, der die Prinzipien der kollektiven Intelligenz und des kollektiven Verhaltens nutzt. BSO simuliert den Prozess der Generierung neuer Ideen und Lösungen, ähnlich wie in Gruppendiskussionen, was es zu einem einzigartigen und vielversprechenden Werkzeug für die Suche nach optimalen Lösungen in verschiedenen Bereichen macht. In diesem Artikel werden die Grundprinzipien von BSO, ihre Vorteile und Anwendungsbereiche erläutert.Populationsbasierte Methoden sind ein wichtiges Instrument zur Lösung komplexer Optimierungsprobleme. Im Zusammenhang mit multimodalen Problemen, bei denen mehrere optimale Lösungen gefunden werden müssen, stoßen die bestehenden Ansätze jedoch an ihre Grenzen. In diesem Artikel wird eine neue Optimierungsmethode vorgestellt, die sogenannte Brainstorming-Optimierungsmethode.
Bestehende Ansätze, wie z. B. die Methoden von „Niching“ (Nischen) und „Clustering“ (Haufen), teilen die Population in der Regel in Teilpopulationen auf, um nach mehreren Lösungen zu suchen. Diese Methoden leiden jedoch darunter, dass die Anzahl der Teilpopulationen im Voraus festgelegt werden muss, was eine Herausforderung darstellen kann, insbesondere wenn die Anzahl der optimalen Lösungen nicht im Voraus bekannt ist. BSO gleicht diesen Mangel aus, indem es den Zielraum in einen Raum umwandelt, in dem die Individuen anhand ihrer Koordinaten geclustert und aktualisiert werden. Im Gegensatz zu bestehenden Methoden, die ein globales Optimum anstreben, lenkt die vorgeschlagene BSO-Methode den Suchprozess auf mehrere „sinnvolle“ Lösungen.
Schauen wir uns die BSO-Methode und ihre Anwendbarkeit auf multimodale Optimierungsprobleme näher an. Der Algorithmus für die Brainstorming-Optimierung (BSO) wurde 2015 von Shi et al. entwickelt. Es ist inspiriert von dem natürlichen Prozess des Brainstormings, bei dem Menschen zusammenkommen, um Ideen zur Lösung eines Problems zu entwickeln und auszutauschen.
Es gibt mehrere Varianten des Algorithmus, wie z. B. die Hypo-Varianz-Hirnsturm-Optimierung, bei der die Schätzung der Objektfunktion auf der Hypo- oder Subvarianz anstelle der Gaußschen Varianz beruht. Es gibt noch andere Varianten, wie z. B. Global-best Brain Storm Optimization, bei der Global best ein Reinitialisierungsschema beinhaltet, das durch den aktuellen Zustand der Population ausgelöst wird, kombiniert mit variablenbasierten Updates und fitnessbasierter Gruppierung.
Jedes Individuum im BSO-Algorithmus stellt nicht nur eine Lösung für das zu optimierende Problem dar, sondern auch einen Datenpunkt, der die Problemlandschaft offenbart. Durch die Kombination von kollektiver Intelligenz und Datenanalysetechniken lassen sich Vorteile erzielen, die über das hinausgehen, was eine der beiden Methoden allein erreichen könnte.
2. Der Algorithmus
Der BSO-Algorithmus funktioniert, indem er diesen Prozess modelliert, bei dem eine Population von Lösungskandidaten (genannt „Individuen“ oder „Ideen“) iterativ aktualisiert wird, um auf eine optimale Lösung zu konvergieren. Der Algorithmus besteht aus den folgenden Hauptphasen:
1. Initialisierung:
- Der Algorithmus beginnt mit der Erzeugung einer Anfangspopulation von Individuen, wobei jedes Individuum eine potenzielle Lösung für das Optimierungsproblem darstellt.
- Jedes Individuum wird durch eine Reihe von Lösungsvariablen dargestellt, die die Merkmale der Lösung definieren.
2. Brainstorming:
- In dieser Phase simuliert der Algorithmus ein Brainstorming, bei dem Einzelpersonen neue Ideen (d. h. neue Lösungskandidaten) generieren, indem sie ihre eigenen Ideen und die Ideen anderer Personen kombinieren und abändern.
- Das Brainstorming wird von einer Reihe von Regeln geleitet, die bestimmen, wie neue Ideen entstehen. Diese Regeln sind vom menschlichen Brainstorming inspiriert und beinhalten:
- Zufällige Generierung neuer Ideen
- Kombination von Ideen verschiedener Personen
- Modifizierung bestehender Ideen
3. Bewertung:
- Neu generierte Ideen (d.h. neue Lösungsvorschläge) werden anhand der Zielfunktion des Optimierungsproblems bewertet.
- Die Zielfunktion misst die Qualität oder Eignung der einzelnen Lösungskandidaten, und der Algorithmus versucht, eine Lösung zu finden, die diese Funktion minimiert (oder maximiert).
4. Auswahl:
- Nach dem Bewertungsschritt wählt der Algorithmus die besten Individuen aus der Population aus, die er für die nächste Iteration beibehält.
- Die Auswahl basiert auf den Fitnesswerten der Individuen, wobei fittere Individuen eine höhere Wahrscheinlichkeit haben, ausgewählt zu werden.
5. Fertigstellung:
- Der Algorithmus durchläuft die Phasen Brainstorming, Bewertung und Auswahl so lange, bis ein Abbruchkriterium erfüllt ist, z. B. die maximale Anzahl der Iterationen oder das Erreichen einer bestimmten Lösungsqualität.
Im Folgenden werden einige charakteristische BSO-Methoden und Algorithmusmerkmale aufgeführt, die sie von anderen Populationsoptimierungsmethoden unterscheiden:
1. Clustering. Die Individuen werden auf der Grundlage der Ähnlichkeit ihrer Lage im Suchraum zu Clustern zusammengefasst. Dies wird mit dem Clusteralgorithmus K-Means umgesetzt.
2. Konvergenz. In diesem Stadium werden die Individuen innerhalb jedes Clusters um den Clusterschwerpunkt gruppiert. Dies simuliert die Brainstorming-Phase, in der die Teilnehmer zusammenkommen, um Ideen zu diskutieren.
3. Divergenz. In dieser Phase werden neue Individuen erzeugt. Neue Individuen können auf der Grundlage von einem oder zwei Individuen in einem Cluster erzeugt werden. Dieser Prozess ähnelt der Brainstorming-Phase, in der die Teilnehmer beginnen, über den Tellerrand zu schauen und neue Ideen zu entwickeln.
4. Auswahl. Nachdem neue Individuen generiert wurden, werden sie in die übergeordnete Hauptgruppe eingeordnet, woraufhin die Gruppe sortiert wird. Dementsprechend wird es bei der nächsten Iteration darum gehen, aktualisierte und verbesserte Ideen zu behandeln.
5. Mutation. Nach der Kombination von Ideen und der Schaffung neuer Ideen werden alle neu entstandenen Ideen mutiert, um der Population zusätzliche Vielfalt zu verleihen und eine vorzeitige Konvergenz zu verhindern.
Wir wollen die Logik des BSO-Algorithmus als Pseudocode darstellen:
1. Initialisierung der Parameter und Generierung der Ausgangspopulation
2. Berechnung der Fitness jedes Individuums in einer Population
3. Bis die Abbruchkriterien erfüllt sind:
4. Berechnung der Fitness jedes Individuums in einer Population
5. Bestimmung des besten Individuums in einer Population
6. Aufteilung der Population in Cluster, wobei die beste Lösung im Cluster als Clusterzentrum festgelegt wird
7. Für jedes neue Individuum in der Population:
|7.1. Wenn die Wahrscheinlichkeit pReplace erfüllt:
| | ein neuer verschobener Mittelpunkt eines zufällig ausgewählten Clusters wird erzeugt (der Mittelpunkt des Clusters wird verschoben)
| | 7.2. Wenn die Wahrscheinlichkeit pOne erfüllt ist:
| | Auswahl eines zufälligen Clusters
| | Wenn die Wahrscheinlichkeit von pOne_center erfüllt ist:
| | | 7.2.a Auswahl des Clusterzentrums
| | Ansonsten:
| | 7.2.b ein zufälliges Individuum aus dem Cluster auswählen
| | 7.3 Ansonsten:
| | Auswahl von zwei Clustern
| | Wenn die pTwo_center-Wahrscheinlichkeit erfüllt ist:
| |7.3.a Ein neues Individuum wird durch Zusammenlegung zweier Clusterzentren gebildet
| | Ansonsten:
| | 7.3.b Erstellen eines neuen Individuums durch Zusammenführen der Positionen der beiden ausgewählten Individuen aus jedem ausgewählten Cluster (die Cluster sollten unterschiedlich sein )
| | 7.4 Mutation: Hinzufügen einer zufälligen Gaußschen Abweichung zur Position des neuen Individuums
| | 7.5 Wenn das neue Individuum außerhalb des Suchraums liegt, spiegeln Sie es zurück in den Suchraum
8. Aktualisierung der aktuellen Population mit neuen Personen
9. Zurück zu Schritt 4, bis das Stoppkriterium erfüllt ist
10. Rückgabe des besten Individuums der Population als Lösung
11. Ende des BSO-Betriebs
Schauen wir uns die Vorgänge in Schritt 7 des Pseudocodes an.
Die allererste Operation 7.1 schafft nämlich kein neues Individuum, sondern verschiebt das Zentrum des Clusters, von dem aus in weiteren Operationen des Algorithmus neue Individuen geschaffen werden können. Die Verschiebung erfolgt zufällig für jede Koordinate mit einer Normalverteilung in einem in den externen Parametern angegebenen Abstand von der ursprünglichen Position.
Operation 7.2 wählt entweder das Clusterzentrum oder ein Individuum im ausgewählten Cluster, das in Schritt 7.4 mutiert wird, um das neue Individuum zu erstellen.
Operation 7.3 dient dazu, ein neues Individuum zu erstellen, indem entweder die Zentren von zwei zufällig ausgewählten Clustern oder zwei Individuen aus diesen ausgewählten Clustern zusammengeführt werden. Die Cluster sollten unterschiedlich sein, aber wenn es nur einen nicht leeren Cluster gibt (die Cluster können leer sein), wird die Zusammenführungsoperation an den beiden ausgewählten Individuen in diesem einzigen nicht leeren Cluster durchgeführt. Diese Aktion ist als Ideenaustausch zwischen Ideenclustern gedacht.
Der Zusammenführungsvorgang läuft wie folgt ab:
wobei:
Xf - neues Individuum nach dem Zusammenschluss,
v - Zufallszahl von 0 bis 1,
X1 und X2 - zwei zufällige Individuen (oder zwei Clusterzentren), die kombiniert werden sollen.
Die Bedeutung der Verschmelzungsgleichung ist, dass eine Idee an einer zufälligen Stelle zwischen zwei anderen Ideen entsteht.
Der Mutationsvorgang kann durch die folgende Gleichung beschrieben werden:
wobei:
Xm - neues Individuum nach Mutation,
Xs - ausgewähltes Individuum, das mutiert werden soll,
n(µ, σ) - Gaußsche Zufallszahl mit Mittelwert µ und Varianz σ,
ξ - Mutationsverhältnis, ausgedrückt durch einen mathematischen Ausdruck.
Das Mutationsverhältnis wird anhand der folgenden Gleichung berechnet:
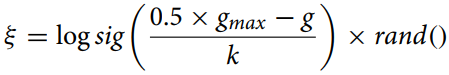
wobei:
gmax - maximale Anzahl von Iterationen,
g - aktuelle Iterationsnummer,
k - Korrekturverhältnis.
Diese Gleichung (Mutationsverhältnis) wird verwendet, um den schrumpfenden Abstand zwischen den Individuen im Optimierungsalgorithmus für die adaptive Änderung des Mutationsparameters zu berechnen. Die Funktion „logsig()“ sorgt für eine sanfte, nicht lineare Abnahme des Wertes und die Multiplikation mit „rand“ fügt ein stochastisches Element hinzu, das nützlich sein kann, um eine vorzeitige Konvergenz zu vermeiden und die Vielfalt der Population zu erhalten.
Das Korrekturverhältnis „k“ im BSO-Algorithmus (Brain Storm Optimization) spielt eine wichtige Rolle bei der Kontrolle der Änderungsrate des Verhältnisses “ξ“ im Laufe der Zeit. Der Wert von „k“ kann je nach spezifischem Problem und Daten variieren und wird empirisch oder mit Hilfe von Hyperparameter-Abstimmungsmethoden berechnet.
Im Allgemeinen sollte „k“ so gewählt werden, dass ein Gleichgewicht zwischen Erkundung und Ausbeutung im Algorithmus besteht. Wenn „k“ zu groß ist, ändert sich „ξ“ sehr langsam, was zu einer vorzeitigen Konvergenz des Algorithmus führen kann. Wenn „k“ zu klein ist, ändert sich „ξ“ sehr schnell, was zu einer übermäßigen Erkundung des Suchraums und einer langsamen Konvergenz führen kann.
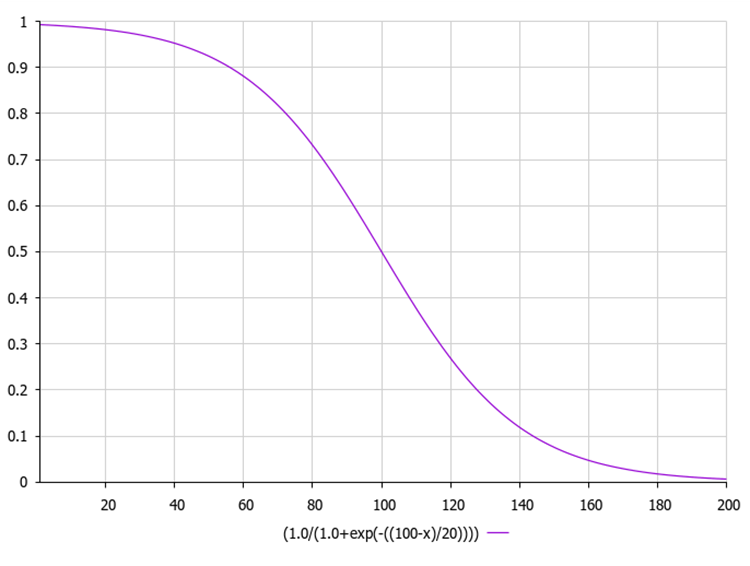
Die logarithmische Sigmoidfunktion, auch bekannt als logistische Funktion, wird üblicherweise als σ σ(x) or sig(x) bezeichnet. Sie wird anhand der folgenden Gleichung berechnet:
wobei:
exp(-x) - bezeichnet den Exponenten mit der Potenz -x.
1 / (1 + exp(-x)) liefert einen Ausgangswert im Bereich von 0 bis 1.
Die folgende Abbildung zeigt den Graphen der Sigmoidfunktion. Die ungleichmäßige Funktionsreduktion ermöglicht die Erkundung in frühen Iterationen und die Verfeinerung in späteren Iterationen.
Nachfolgend finden Sie einen Beispielcode für die Berechnung des Mutationsverhältnisses zusammen mit der Sigmoidfunktion, die mit Hilfe der Exponentialfunktion berechnet wird.
In diesem Code berechnet die Funktion „sigmoid“ den sigmoidalen Wert der eingegebenen Zahl „x“ und die Funktion „xi“ berechnet den Wert von „ξ“ gemäß der obigen Gleichung. Dabei steht „gmax“ für die maximale Anzahl von Iterationen, „g“ für die aktuelle Iterationszahl und „k“ für das Korrekturverhältnis. Die Funktion MathRand erzeugt eine Zufallszahl zwischen 0 und 32 767, die wir durch 32 767,0 dividieren, um eine Zufallszahl zwischen 0 und 1 zu erhalten. Dann berechnen wir den Sigmoid-Wert dieser Zufallszahl. Dieser Wert wird von der Funktion „xi“ zurückgegeben.
double sigmoid(double x) { return 1.0 / (1.0 + MathExp(-x)); } double xi(int gmax, int g, double k) { double randNum = MathRand() / 32767.0; // Generate a random number from 0 to 1 return sigmoid (0.5 * (gmax - g) / k) * randNum; }
3. Das Clustering-Verfahren K-Means
Der BSO-Algorithmus verwendet die Cluster-Analyse K-Means, um Ideen in verschiedene Gruppen einzuteilen. Die aktuelle Menge von „n“ Lösungen für die Eingabe in die Iteration wird in „m“ Kategorien unterteilt, um das Verhalten von Gruppendiskussionsteilnehmern zu simulieren und die Sucheffizienz zu verbessern.
Wir werden einen separaten Cluster mit Hilfe der S_Cluster-Struktur beschreiben, die den K-Means-Algorithmus implementiert und eine beliebte Clustermethode ist.
Werfen wir einen Blick auf die Struktur:
- centroid[] - Array, das den Schwerpunkt des Clusters darstellt.
- f - Schwerpunkt-Fitnesswert.
- count - Anzahl der Punkte des Clusters.
- ideasList[] - Liste der Ideen.
Die Funktion Init initialisiert die Struktur, indem sie die Größe der Arrays „centroid“ und „ideasList“ ändert und den Anfangswert von „f“ setzt.
//—————————————————————————————————————————————————————————————————————————————— struct S_Cluster { double centroid []; //cluster centroid double f; //centroid fitness int count; //number of points in the cluster int ideasList []; //list of ideas void Init (int coords) { ArrayResize (centroid, coords); f = -DBL_MAX; ArrayResize (ideasList, 0, 100); } }; //——————————————————————————————————————————————————————————————————————————————
Die Klasse C_BSO_KMeans ist eine Implementierung des Algorithmus K-Means für das Clustering von Agenten im BSO Optimierungsalgorithmus. Nachfolgend wird erläutert, was die einzelnen Methoden bewirken:
- KMeansInit - Methode initialisiert die Clusterschwerpunkte durch Auswahl zufälliger Agenten aus den Daten. Für jeden Cluster wird ein zufälliger Agent ausgewählt und seine Koordinaten werden in den Clusterschwerpunkt kopiert.
- VectorDistance - die Methode berechnet den euklidischen Abstand zwischen zwei Vektoren. Sie nimmt zwei Vektoren als Argumente und gibt deren euklidischen Abstand zurück.
- KMeans - die Methode implementiert die grundlegende Logik des Algorithmus K-Means- zur Datenclusterung. Sie nimmt die Daten- und Cluster-Arrays als Argumente entgegen.
- Zuweisung von Datenpunkten zum nächstgelegenen Schwerpunkt.
- Aktualisieren der Zentren auf der Grundlage des Mittelwerts der jedem Cluster zugewiesenen Punkte.
- Wiederholen dieser beiden Schritte, bis sich die Zentren nicht mehr ändern oder die maximale Anzahl der Iterationen erreicht ist.
Der Schwerpunkt bei der K-Mittelwert-Clustermethode ist ein zentraler Zeiger des Clusters. Im Zusammenhang mit der K-Means-Methode ist der Schwerpunkt das arithmetische Mittel aller Datenpunkte, die zu einem bestimmten Cluster gehören.
In jeder Iteration des K-Means-Algorithmus werden die Zentren neu berechnet, woraufhin die Datenpunkte erneut in Gruppen eingeteilt werden, je nachdem, welches der neuen Zentren nach der gewählten Metrik näher liegt.
Die Zentroide spielen also eine Schlüsselrolle bei der K-Means-Methode, da sie die Form und Position der Cluster bestimmen.
Diese Klasse stellt einen wichtigen Teil des BSO-Optimierungsalgorithmus dar, indem sie die Agenten gruppiert, um den Suchprozess zu verbessern. Der K-Means-Algorithmus ordnet die Punkte iterativ den Clustern zu und berechnet die Zentroide neu, bis keine Änderungen mehr auftreten oder die maximale Anzahl der Iterationen erreicht ist.
//—————————————————————————————————————————————————————————————————————————————— class C_BSO_KMeans { public: //-------------------------------------------------------------------- void KMeansInit (S_BSO_Agent &data [], int dataSizeClust, S_Clusters &clust []) { for (int i = 0; i < ArraySize (clust); i++) { int ind = MathRand () % dataSizeClust; ArrayCopy (clust [i].centroid, data [ind].c, 0, 0, WHOLE_ARRAY); } } double VectorDistance (double &v1 [], double &v2 []) { double distance = 0.0; for (int i = 0; i < ArraySize (v1); i++) { distance += (v1 [i] - v2 [i]) * (v1 [i] - v2 [i]); } return MathSqrt (distance); } void KMeans (S_BSO_Agent &data [], int dataSizeClust, S_Clusters &clust []) { bool changed = true; int nClusters = ArraySize (clust); int cnt = 0; while (changed && cnt < 100) { cnt++; changed = false; //Assigning data points to the nearest centroid for (int d = 0; d < dataSizeClust; d++) { int closest_centroid = -1; double closest_distance = DBL_MAX; if (data [d].f != -DBL_MAX) { for (int cl = 0; cl < nClusters; cl++) { double distance = VectorDistance (data [d].c, clust [cl].centroid); if (distance < closest_distance) { closest_distance = distance; closest_centroid = cl; } } if (data [d].label != closest_centroid) { data [d].label = closest_centroid; changed = true; } } else { data [d].label = -1; } } //Updating centroids double sum_c []; ArrayResize (sum_c, ArraySize (data [0].c)); for (int cl = 0; cl < nClusters; cl++) { ArrayInitialize (sum_c, 0.0); clust [cl].count = 0; ArrayResize (clust [cl].ideasList, 0); for (int d = 0; d < dataSizeClust; d++) { if (data [d].label == cl) { for (int k = 0; k < ArraySize (data [d].c); k++) { sum_c [k] += data [d].c [k]; } clust [cl].count++; ArrayResize (clust [cl].ideasList, clust [cl].count); clust [cl].ideasList [clust [cl].count - 1] = d; } } if (clust [cl].count > 0) { for (int k = 0; k < ArraySize (sum_c); k++) { clust [cl].centroid [k] = sum_c [k] / clust [cl].count; } } } } } }; //——————————————————————————————————————————————————————————————————————————————
Im Algorithmus Brain Storm Optimization (BSO) ist die Fitness eines Individuums definiert als die Qualität der Lösung, die es repräsentiert. Bei einem Optimierungsproblem kann die Fitness gleich dem Wert der zu optimierenden Funktion sein.
Die spezifische Clustermethode kann variieren. Ein gängiger Ansatz ist die k-means-Methode, bei der die Clusterschwerpunkte nach dem Zufallsprinzip initialisiert und dann iterativ aktualisiert werden, um die Summe der quadratischen Abstände zwischen jedem Punkt und seinem Clusterschwerpunkt zu minimieren.
Obwohl die Fitness eine Schlüsselrolle bei der Clusterbildung spielt, ist sie nicht der einzige Faktor, der die Clusterbildung beeinflusst. Andere Aspekte, wie der Abstand zwischen den Personen im Entscheidungsraum, können ebenfalls eine wichtige Rolle spielen. Dies hilft dem Algorithmus, die Vielfalt in der Population zu erhalten und eine vorzeitige Konvergenz zu ungeeigneten Lösungen zu verhindern.
Die Anzahl der Iterationen, die erforderlich sind, damit der K-Means-Algorithmus konvergiert, hängt in hohem Maße von verschiedenen Faktoren ab, wie z. B. dem Anfangszustand der Zentroide, der Verteilung der Daten und der Anzahl der Cluster. Im Allgemeinen konvergiert K-Means jedoch in einigen Dutzend bis einigen hundert Iterationen.
Es sollte auch bedacht werden, dass K-Means die Summe der quadratischen Abstände zwischen den Punkten und ihren nächstgelegenen Zentren minimiert, was je nach der spezifischen Aufgabe und der Form der Cluster in den Daten nicht immer optimal sein kann. In einigen Fällen können andere Clustering-Algorithmen besser geeignet sein.
K-Means++ ist eine verbesserte Version des K-Means-Algorithmus, der 2007 von David Arthur und Sergei Vassilvitskii vorgeschlagen wurde. Der Hauptunterschied zwischen K-Means++ und Standard-K-Means besteht in der Art und Weise, wie die Zentroide initialisiert werden. Anstatt die anfänglichen Zentren zufällig zu wählen, wählt K-Means++ sie so aus, dass der Abstand zwischen ihnen maximiert wird. Dies trägt dazu bei, die Qualität der Clusterbildung zu verbessern und die Konvergenz des Algorithmus zu beschleunigen.
Hier sind die wichtigsten Initialisierungsschritte in K-Means++:
- Wähle zufällig den ersten Schwerpunkt aus den Datenpunkten aus.
- Berechne für jeden Datenpunkt den Abstand zum nächstgelegenen, zuvor ausgewählten Schwerpunkt.
- Wähle den nächsten Schwerpunkt aus den Datenpunkten so aus, dass die Wahrscheinlichkeit, einen Punkt als Schwerpunkt auszuwählen, direkt proportional zu seinem Abstand zum nächsten, zuvor ausgewählten Schwerpunkt ist (d. h. der Punkt mit dem größten Abstand zum nächsten Schwerpunkt wird mit größter Wahrscheinlichkeit als nächster Schwerpunkt ausgewählt).
- Wiederhole die Schritte 2 und 3, bis k Zentren ausgewählt sind.
Nach der Initialisierung der Zentroide arbeitet K-Means++ genauso wie das Standardverfahren. Diese Initialisierungsmethode trägt dazu bei, die Qualität des Clustering zu verbessern und die Konvergenz des Algorithmus zu beschleunigen. Diese Methode ist jedoch sehr rechenintensiv.
Wenn Sie 1000 Koordinaten für jeden Punkt haben, bedeutet dies einen zusätzlichen Rechenaufwand für den K-Means++ Algorithmus, da er Abstände in einem hochdimensionalen Raum berechnen muss. K-Means++ könnte jedoch immer noch effektiv sein (zur Bestätigung dieser Annahme sind Experimente erforderlich), da es in der Regel zu einer schnelleren Konvergenz und einer besseren Clusterqualität führt.
Bei der Arbeit mit hochdimensionalen Daten (z. B. 1000 Koordinaten) können zusätzliche Probleme im Zusammenhang mit dem „Fluch der Dimensionen“ auftreten. Dies kann dazu führen, dass die Abstände zwischen den Punkten weniger aussagekräftig sind und das Clustering erschweren. In solchen Fällen kann es sinnvoll sein, vor der Anwendung von K-Means oder K-Means++ Methoden zur Dimensionenreduktion wie PCA (Principal Component Analysis) einzusetzen. Dies kann dazu beitragen, die Dimensionen der Daten zu verringern und das Clustering effizienter zu gestalten.
Die Reduzierung der Dimensionen von Daten ist ein wichtiger Schritt in der Datenverarbeitung, insbesondere bei der Arbeit mit einer großen Anzahl von Koordinaten oder Merkmalen. Dies trägt zur Vereinfachung der Daten, zur Verringerung der Rechenkosten und zur Verbesserung der Leistung von Clustering-Algorithmen bei. Hier sind einige Methoden zur Dimensionenreduzierung, die häufig beim Clustering verwendet werden:
- Hauptkomponentenanalyse (PCA). Diese Methode wandelt einen Datensatz mit einer großen Anzahl von Variablen in einen Datensatz mit weniger Variablen um, wobei ein Maximum an Informationen erhalten bleibt.
- Multidimensionale Skalierung (MDS). Die Methode versucht, eine niedrigdimensionale Struktur zu finden, bei der die Abstände zwischen den Punkten wie im ursprünglichen hochdimensionalen Raum erhalten bleiben.
- t-distributed Stochastic Neighbor Embedding (t-SNE). Es handelt sich um eine nichtlineare Dimensionenreduktionsmethode, die sich besonders gut für die Visualisierung hochdimensionaler Daten eignet.
- Auto-Kodierer. Dies sind neuronale Netze, die zur Reduzierung der Dimensionen von Daten verwendet werden. Sie funktionieren, indem sie lernen, Eingabedaten in eine kompakte Darstellung zu kodieren und diese Darstellung dann wieder in die Originaldaten zu dekodieren.
- Unabhängige Komponentenanalyse (ICA). Dabei handelt es sich um eine statistische Methode, die einen Datensatz in unabhängige Komponenten zerlegt, die möglicherweise informativer sind als die ursprünglichen Daten. Die Komponenten können die Struktur oder wichtige Aspekte der Daten besser widerspiegeln, z. B. können sie einige verborgene Faktoren sichtbar machen oder eine bessere Trennung der Klassen bei einem Klassifizierungsproblem ermöglichen.
- Lineare Diskriminanzanalyse (LDA). Die Methode wird verwendet, um lineare Kombinationen von Merkmalen zu finden, die zwei oder mehr Klassen gut trennen.
Obwohl K-Means++ in der Initialisierungsphase, insbesondere bei hochdimensionalen Daten, rechenintensiver ist, kann es sich in einigen Fällen lohnen. Es lohnt sich jedoch immer, zu experimentieren und verschiedene Ansätze zu vergleichen, um festzustellen, was für Ihr spezielles Problem und Ihren Datensatz am besten geeignet ist.
Falls Sie weiter mit der K-Means++ Methode experimentieren möchten, finden Sie hier die Initialisierungsmethode für diesen Algorithmus (der Rest des Codes unterscheidet sich nicht vom herkömmlichen K-Means Code).
Der folgende Code ist eine Implementierung der Initialisierung des K-Means++ Algorithmus. Die Funktion nimmt ein Array von Datenpunkten, dargestellt durch die Struktur S_BSO_Agent, eine Datengröße (dataSizeClust) und ein Array von Clustern, dargestellt durch die Struktur S_Cluster, entgegen. Die Methode initialisiert den ersten Schwerpunkt zufällig aus den Datenpunkten. Dann berechnet der Algorithmus für jeden nachfolgenden Schwerpunkt den Abstand zwischen jedem Datenpunkt und dem nächstgelegenen Schwerpunkt und wählt den nächsten Schwerpunkt mit einer Wahrscheinlichkeit, die proportional zum Abstand ist. Dazu wird eine Zufallszahl „r“ zwischen 0 und der Summe aller Entfernungen erzeugt und dann in einer Schleife alle Datenpunkte durchlaufen, wobei „r“ um die Entfernung eines jeden Punktes verringert wird, bis „r“ kleiner oder gleich der Entfernung des aktuellen Punktes ist. In diesem Fall wird der aktuelle Punkt als nächster Schwerpunkt gewählt. Dieser Vorgang wird so lange wiederholt, bis alle Zentroide initialisiert sind.
Insgesamt ist die Initialisierung von K-Means++ implementiert, die eine verbesserte Version der Initialisierung des Standard-K-Means-Algorithmus ist. Die Zentren werden so gewählt, dass die Summe der quadratischen Abstände zwischen den Zentren und den Datenpunkten minimiert wird, was zu einer effizienteren und stabileren Clusterbildung führt.
void KMeansPlusPlusInit (S_BSO_Agent &data [], int dataSizeClust, S_Cluster &clust []) { // Choose the first centroid randomly int ind = MathRand () % dataSizeClust; ArrayCopy (clust [0].centroid, data [ind].c, 0, 0, WHOLE_ARRAY); for (int i = 1; i < ArraySize (clust); i++) { double sum = 0; // Compute the distance from each data point to the nearest centroid for (int j = 0; j < dataSizeClust; j++) { double minDist = DBL_MAX; for (int k = 0; k < i; k++) { double dist = VectorDistance (data [j].c, clust [k].centroid); if (dist < minDist) { minDist = dist; } } data [j].minDist = minDist; sum += minDist; } // Choose the next centroid with a probability proportional to the distance double r = MathRand () * sum; for (int j = 0; j < dataSizeClust; j++) { if (r <= data [j].minDist) { ArrayCopy (clust [i].centroid, data [j].c, 0, 0, WHOLE_ARRAY); break; } r -= data [j].minDist; } } }
Fortsetzung folgt...
In diesem Artikel haben wir die logische Struktur des BSO-Algorithmus sowie Clustermethoden und Möglichkeiten zur Reduzierung der Dimensionen des Optimierungsproblems untersucht. Im nächsten Artikel werden wir unsere Untersuchung des BSO-Algorithmus abschließen und seine Leistung zusammenfassen.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/14707
Neuronale Netze leicht gemacht (Teil 84): Umkehrbare Normalisierung (RevIN)
Entwicklung eines Expertenberaters für mehrere Währungen (Teil 8): Belastungstest und Handhabung eines neuen Balkens
Der Optimierungsalgorithmus Brain Storm (Teil II): Multimodalität
Neuronale Netze leicht gemacht (Teil 83): Der „Conformer“-Algorithmus für räumlich-zeitliche kontinuierliche Aufmerksamkeitstransformation
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.