Algorithmen zur Optimierung mit Populationen: der Gravitationssuchalgorithmus (GSA)

Inhalt

1. Einführung
2. Algorithmus
3. Testergebnisse

1. Einführung

Der Gravitationssuchalgorithmus (GSA) wurde von E. Rashedi vorgeschlagen, um Optimierungsprobleme, insbesondere nicht-lineare Probleme, nach den Prinzipien des Newtonschen Gravitationsgesetzes zu lösen. In dem vorgeschlagenen Algorithmus werden die Partikel als Objekte betrachtet und ihre Leistung wird unter Berücksichtigung ihrer Masse geschätzt. Die Schwerkraft ist die Tendenz von Massen, sich gegenseitig zu beschleunigen. Sie ist eine der vier fundamentalen Kräfte in der Natur (die anderen sind die elektromagnetische Kraft, die schwache Kernkraft und die starke Kernkraft).

Jedes Teilchen im Universum zieht jedes andere Teilchen an. Die Schwerkraft existiert überall. Obwohl sie die schwächste Kraft ist, ist sie die sichtbarste. Aufgrund der Gravitationskraft können Menschen auf der Erde laufen und Planeten die Sonne umkreisen. Die Anziehungskraft eines beliebigen Objekts ist proportional zu seiner Masse. Daher haben Objekte mit mehr Masse eine höhere Schwerkraft. Die Unausweichlichkeit der Schwerkraft unterscheidet sie von allen anderen Naturkräften. Die Art und Weise, wie sich die Newtonsche Gravitationskraft verhält, wird als Fernwirkung bezeichnet. Es handelt sich um ein allgemeines physikalisches Gesetz, das aus empirischen Beobachtungen abgeleitet wurde, und zwar durch das, was Isaac Newton induktives Denken nannte. Sie ist Teil der klassischen Mechanik, die in Newtons Philosophiae Naturalis Principia Mathematica (Principia) formuliert und erstmals am 5. Juli 1687 veröffentlicht wurde.

Als Newton im April 1686 das erste unveröffentlichte Buch der Royal Society vorstellte, behauptete Robert Hooke, Newton habe das Gesetz des umgekehrten Quadrats von ihm erhalten. In heutiger Sprache besagt das Gesetz, dass jede Punktmasse jede andere Punktmasse durch eine Kraft anzieht, die entlang einer Linie wirkt, die zwei Punkte verbindet.

2. Algorithmus

Der Artikel stellt einen Optimierungsalgorithmus vor, der auf dem Newtonschen Gravitationsgesetz basiert: „Jedes Teilchen im Universum zieht jedes andere Teilchen mit einer Kraft an, die direkt proportional zum Produkt ihrer Massen und umgekehrt proportional zum Quadrat des Abstands zwischen ihnen ist“. In dem vorgeschlagenen Algorithmus sind die Suchagenten eine Gruppe von Massen, die auf der Grundlage der Newtonschen Gravitation und der Bewegungsgesetze miteinander interagieren. Gleichzeitig können alle Agenten untereinander Informationen austauschen, unabhängig davon, wo sie sich im Suchraum befinden, und zwar durch eine Anziehungskraft, die von der Masse (berechnet aus den Werten der Zielfunktion) und dem Abstand zwischen ihnen abhängt.

Agenten werden als Objekte behandelt, und ihre Fitness wird anhand ihrer Masse gemessen. Allgemein ausgedrückt (mit den Einstellungen des Algorithmus, die den realen physikalischen Gesetzen nahe kommen), werden alle diese Objekte durch die Schwerkraft zueinander hingezogen, und diese Kraft bewirkt eine globale Bewegung aller Objekte in Richtung von Objekten mit einer größeren Masse. Die Massen interagieren also über eine direkte Verbindung durch die Gravitationskraft.

Im klassischen GSA hat jedes Teilchen drei Arten von Massen:

a) aktive Masse
b) passive Masse
c) Trägheitsmasse

In den meisten Fällen ist es bequem und zweckmäßig, die Gleichheit dieser Konzepte zu nutzen, um Codes und Berechnungen zu vereinfachen und die Effizienz der Suchfunktionen des Algorithmus zu erhöhen. Daher gibt es im Algorithmus eine Masse und nicht drei. Die in dem GSA verwendeten physikalischen Gesetzesgleichungen sind in Abbildung 1 dargestellt.

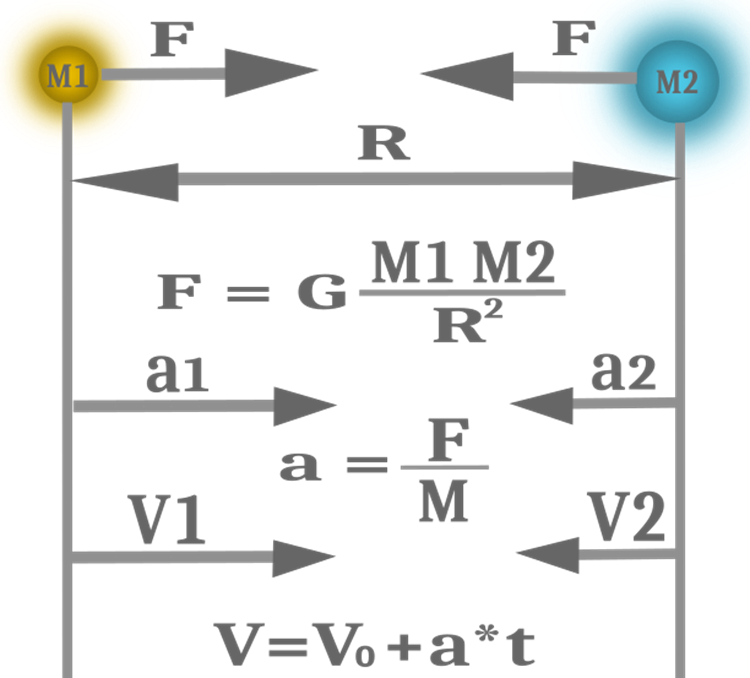
Bild 1. Schwerkraft, Beschleunigung und Geschwindigkeit

Die Position der Partikel liefert die Lösung des Problems, während die Fitnessfunktion zur Berechnung der Massen verwendet wird. Der Algorithmus besteht aus zwei Phasen: Erkunden und Verwerten. Dieser Algorithmus nutzt zu Beginn die Fähigkeiten der Intelligenz, um zu vermeiden, dass er im lokalen Optimum stecken bleibt, und danach nutzt er die Regionen der Extrema.

Der Algorithmus für die Gravitationssuche muss ein sich im Raum bewegendes Teilchen in ein Objekt mit einer bestimmten Masse verwandeln. Diese Objekte werden aufgrund der Gravitationswechselwirkung voneinander angezogen, und jedes Teilchen im Raum wird aufgrund der gegenseitigen Anziehung von Teilchen, die Beschleunigungen erzeugen, angezogen. Jedes Teilchen wird von anderen Teilchen angezogen und bewegt sich in Richtung der Kraft. Teilchen mit geringer Masse bewegen sich auf Teilchen mit größerer Masse zu, aber auch massive Objekte bewegen sich, allerdings mit einer geringeren Geschwindigkeit, die umgekehrt proportional zur Masse ist. Die optimale Lösung wird von „großen“ Objekten gefunden, die die Lösung verfeinern, indem sie sich mit geringerer Geschwindigkeit bewegen, als „kleinere“ Objekte, die sich schneller bewegen. GSA implementiert die Übertragung von Informationen durch die Interaktion zwischen Objekten.

GSA-Schritte:

1. Initialisierung des Agenten
2. Entwicklung der Fitness
3. Berechnung der Gravitationskonstante
4. Berechnung der Wirkstoffmassen

1. Initialisierung des Agenten.
Alle Agenten werden nach dem Zufallsprinzip initialisiert. Jeder Agent wird als ein Lösungskandidat betrachtet. Damit die Stabilitätsanalyse aussagekräftig und zuverlässig ist, ist es äußerst wichtig, die Anfangsbedingungen für das Gleichgewicht anzugeben. Denn wenn die ursprüngliche „Scheibe“ von Objekten nicht im Gleichgewicht ist, kann ihre Entspannung in den ersten Zeitschritten der Simulation Instabilitäten verursachen, die für unser Verständnis der Stabilität von „Scheibengalaxien“ von geringer Bedeutung sind. Leider ist keine analytische Lösung für die Dichte, das Geschwindigkeitsfeld und die Temperatur einer dreidimensionalen Gasscheibe im hydrostatischen Gleichgewicht im äußeren Potential des Halos der dunklen Materie und/oder der stellaren Scheibe bekannt.

2. Fitness-Evolution.
Die Zuverlässigkeit und Wirksamkeit des GSA hängt von der Ausgewogenheit zwischen Forschungs- und Nutzungsmöglichkeiten ab. In den ersten Iterationen der Lösungssuche wird dem Erkunden des Suchraums Vorrang eingeräumt. Dies kann erreicht werden, indem man den Agenten erlaubt, in den ersten Iterationen große Schrittweiten zu verwenden. In späteren Iterationen ist eine Verfeinerung des Suchraums erforderlich, um zu vermeiden, dass globale Optima fehlen. Daher sollten die Kandidatenlösungen kleine Schrittweiten haben, um in den nachfolgenden Iterationen verwendet werden zu können.

3. Berechnung der Gravitationskonstante.
Die Gravitationskonstante (auch bekannt als universelle Gravitationskonstante, Newtonsche Gravitationskonstante oder Cavendish-Gravitationskonstante), bezeichnet mit dem Buchstaben G, ist eine empirische physikalische Konstante, die in die Berechnung der Gravitationswirkungen in Isaac Newtons Gesetz der universellen Gravitation und in Albert Einsteins allgemeiner Relativitätstheorie einfließt. Im Newton'schen Gesetz ist es die Proportionalitätskonstante, die die Gravitationskraft zwischen zwei Körpern mit dem Produkt aus ihrer Masse und dem inversen Quadrat ihres Abstands verbindet. In den Einsteinschen Feldgleichungen quantifiziert er die Beziehung zwischen der Geometrie der Raumzeit und dem Energie-Impuls-Tensor.

4. Berechnung der Wirkstoffmassen.
Die Masse ist die Menge der im Raum vorhandenen Materie.

Pseudocode des Algorithmus:

1. Erzeugen eines Systems von Objekten nach dem Zufallsprinzip.
2. Bestimmung der Eignung der einzelnen Objekte.
3. Aktualisieren der Werte der Gravitationskonstante, Berechnen der Massen, des besten und des schlechtesten Objekts.
4. Berechnung der auf jede Koordinate wirkenden Kräfte.
5. Berechnung von Beschleunigungen und Geschwindigkeiten von Objekten.
6. Aktualisieren der Positionen von Objekten.
7. Bestimmen der Eignung der einzelnen Objekte.
8. Wiederholen des Vorgangs ab S. 3, bis das Abbruchkriterium erfüllt ist.

Schauen wir uns den GSA-Code an. Um ein Objekt im System der Gravitationswechselwirkung zu beschreiben, benötigen wir die Struktur S_Object, die alle notwendigen physikalischen Eigenschaften des Objekts beschreibt, die für die Durchführung einer Gravitationssuche ausreichen: c[] - Koordinaten im Suchraum, v[] - Geschwindigkeitsvektor für jede der Koordinaten (die Array-Dimension ist die Anzahl der Koordinaten), M ist die Masse des Objekts (im GSA ist die Masse ein relativer Wert, der in Abhängigkeit vom Wert der maximalen und minimalen Fitness über das gesamte System der Objekte berechnet wird), f ist der Wert der Fitness, R[] ist der euklidische Abstand zu anderen Objekten (die Dimension des Arrays ist die Anzahl der Objekte), F[] ist der Vektor der Kräfte für jede der Koordinaten (die Dimension des Arrays ist die Anzahl der Koordinaten).

//——————————————————————————————————————————————————————————————————————————————
struct S_Object
{
  double c  [];   //coordinates
  double v  [];   //velocity
  double M;       //mass
  double f;       //fitness
  double R  [];   //euclidean distance to other objects
  double F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

Deklarieren wir die Klasse des Gravitationssuchalgorithmus C_AO_GSA. Von den physikalischen Eigenschaften der Objekte, die als Agenten an dem Algorithmus teilnehmen, wird nur eine Sache benötigt: die Koordinaten, die die beste Lösung darstellen - der Wert von fB. Die Klasse deklariert gültige Bereiche von Suchraumkoordinaten und einen Schritt. Das System der gravitativ gebundenen Objekte wird als ein Array von S_Object-Strukturen dargestellt. Bei dem klassischen Algorithmus gibt es nur drei externe Parameter: G_constant, a_constant, e_constant, die die Eigenschaften der Gravitationswechselwirkung von Objekten bestimmen, und der Rest der Konstanten sind in den Berechnungsgleichungen enthalten, aber ich hielt es für angebracht, diese Konstanten in die externen Parameter des Algorithmus zu verschieben, was eine flexiblere Anpassung der Eigenschaften des Algorithmus als Ganzes ermöglicht. Auf alle Parameter werde ich später noch etwas genauer eingehen, da sie das Verhalten des Algorithmus stark beeinflussen.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GSA
{
  //----------------------------------------------------------------------------
  public: S_Object o       []; //object
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    objectsNumber;     //objects number
  private: double PowerOfdistance;   //power of distance
  private: double GraviPert_Min;     //gravitational perturbation Min
  private: double GraviPert_Max;     //gravitational perturbation Min
  private: double VelocPert_Min;     //velocity perturbation Min
  private: double VelocPert_Max;     //velocity perturbation Max
  private: double G_constant;        //G constant
  private: double a_constant;        //a constant
  private: double e_constant;        //e constant
  private: int    maxIterations;
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Die öffentliche Methode des Algorithmus Init() ist für die Übergabe der externen Parameter des Algorithmus an interne Konstanten zur Initialisierung von Dienstvariablen und zur Zuweisung von Größen an Arrays vorgesehen.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  objectsNumber     = objectsNumberP;
  PowerOfdistance   = PowerOfdistanceP;
  GraviPert_Min     = GraviPert_MinP;
  GraviPert_Max     = GraviPert_MaxP;
  VelocPert_Min     = VelocityPert_MinP;
  VelocPert_Max     = VelocityPert_MaxP;
  G_constant        = G_constantP;
  a_constant        = a_constantP;
  e_constant        = e_constantP;
  maxIterations     = maxIterationsP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);

  ArrayResize (o,  objectsNumber);

  for (int i = 0; i < objectsNumber; i++)
  {
    ArrayResize (o [i].c,  coordinatesNumber);
    ArrayResize (o [i].v,  coordinatesNumber);
    ArrayResize (o [i].R,  objectsNumber);
    ArrayResize (o [i].F,  coordinatesNumber);
    o [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Die erste öffentliche Methode, die bei jeder Iteration der Iteration von Moving() aufgerufen wird. Diese Methode enthält die gesamte Physik und Logik des GSA. Er ist ziemlich umfangreich, also betrachten wir ihn in Teilen. Es ist zu beachten, dass die Methode die aktuelle Iteration als Parameter verwendet, der in die Berechnung der Gravitationskonstante einfließt und das Gleichgewicht zwischen Forschen und Nutzen anpasst.

Bei der ersten Iteration erfolgt die Initialisierung der Objekte. Für alle Koordinaten von Objekten werden zufällige Werte im zulässigen Bereich mit einer gleichmäßigen Verteilung zugewiesen, und es wird geprüft, ob sie außerhalb des zulässigen Bereichs liegen. Zu Beginn des Optimierungsprozesses haben alle Objekte eine Geschwindigkeit von Null, d. h. die Objekte sind im Suchraum in Bezug auf die Koordinaten unbeweglich. Da die Objekte keine Masse haben, müssten sie sich mit Lichtgeschwindigkeit bewegen, aber für die erste Iteration brechen wir die Gesetze der Physik, denn dieser Moment entspricht in gewisser Weise dem Urknall. Die Fitness der Objekte ist zu diesem Zeitpunkt der kleinste der möglichen Werte einer Zahl vom Typ „double“. Beim Debuggen des Algorithmus war es schwierig, Fehler im Zusammenhang mit der Nullmasse zu finden.

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < objectsNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      o [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      o [obj].v [c] = 0.0;
      o [obj].M     = 0.0;
      o [obj].f     = -DBL_MAX;
    }
  }

  revision = true;
}

Der Rest des Codes für die Methode Moving() bezieht sich auf die zweite und die folgenden Iterationen, bei denen die Objekte an Masse, Geschwindigkeit und Beschleunigung gewinnen.

Zunächst einmal müssen wir die Masse berechnen. Wie bereits erwähnt, wird die Masse (per Definition ein positiver skalarer Wert) von Objekten aus den Werten der Fitnessfunktion berechnet, sodass es notwendig ist, die minimalen und maximalen Fitnesswerte zu bestimmen, bevor die Masse auf der Grundlage der erhaltenen Werte berechnet wird. Zu diesem Zeitpunkt ist der Wert der Fitnessfunktion bereits in der vorherigen Iteration ermittelt worden.

//find the minimum and maximum fitness==========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  if (o [obj].f < Fmin) Fmin = o [obj].f;
  if (o [obj].f > Fmax) Fmax = o [obj].f;
}

An dieser Stelle des Codes wird die Masse anhand der Gleichung Mo=(Fo-Fmin)/(Fmax-Fmin) berechnet, wobei

• Mo - Masse des Objekts
• Fo - Objekttauglichkeit
• Fmax - maximaler Fitnesswert unter allen Objekten (bester Wert)
• Fmin - minimaler Fitnesswert unter allen Objekten (schlechtester Wert)
  

Wie aus der Gleichung hervorgeht, kann die Masse nur positive Werte im Bereich von 0 bis einschließlich 1 annehmen. Da wir zuvor besprochen haben, dass die Masse nicht gleich Null sein darf, da sonst die Geschwindigkeit gleich der Lichtgeschwindigkeit ist, beschränken wir die Untergrenze der Masse auf 0,1. Der obere Wert kann durchaus gleich 1 sein. Außerdem ist zu beachten, dass die Masse aller Objekte gleich 1 ist, wenn die Minimal- und Maximalwerte der Fitnessfunktion gleich sind. Dies entspricht dem Fall, dass der Suchraum in dem Bereich, in dem sich die Objekte befinden, homogen ist und alle Objekte in Bezug auf die Qualität der Fitnessfunktion gleich sind sowie die Bewegung in jede Richtung die gleiche Priorität hat. Man sollte meinen, dass sich in diesem Fall alle Objekte allmählich auf einen gemeinsamen Massenschwerpunkt zubewegen und konzentrieren sollten, doch dies geschieht aufgrund der nichtlinearen Wirkung der Gravitationskraft nicht.

//calculating the mass of objects===========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  Fo = o [obj].f;
  if (Fmax == Fmin) Mo = 1.0;
  else Mo = (Fo - Fmin) / (Fmax - Fmin);
  o [obj].M = Scale (Mo, 0.0, 1.0, 0.1, 1.0, false);
}

Nachdem wir die Masse der Objekte berechnet haben, müssen wir nun eine weitere Komponente der R-Gleichung berechnen - den euklidischen Abstand jedes Objekts zu jedem anderen Objekt. Die Berechnung besteht aus zwei Zyklen der Aufzählung von Objekten und einem Zyklus der Berechnung für jede der Koordinaten. Wie wir uns erinnern, ist der euklidische Abstand die Wurzel aus der Summe der Quadrate der Koordinatendifferenzen.

//calculation of Euclidean distances between all objects====================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].R, 0.0);

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      if (o [obj].R [obj2] == 0.0)
      {
        for (int c = 0; c < coordinatesNumber; c++)
        {
          diffDist = o [obj].c [c] - o [obj2].c [c];
          o [obj].R [obj2] += diffDist * diffDist;
        }

        o [obj].R [obj2] = sqrt (o [obj].R [obj2]);
        o [obj2].R [obj] = o [obj].R [obj2];
      }
    }
  }
}

Jetzt können wir Kraftvektoren für Objekte berechnen. Dazu müssen wir auch alle Objekte in zwei Zyklen und einen Zyklus für die Koordinaten durchlaufen, da die Geschwindigkeit für jede Koordinate separat berechnet wird. Wir müssen eine Bedingung hinzufügen, die das Zusammentreffen von Objektindizes ausschließt, damit das Objekt die Berechnung seiner selbst in der Kraftberechnung ausschließt. Hier verwenden wir die bekannte Newtonsche Gleichung zur Berechnung der Gravitationskraft für zwei Objekte (Abbildung 1) und korrigieren den Abstand um das Verhältnis e_constant. Berechnen wir zunächst die Gravitationskonstante G, die sich bei jeder Iteration nach unten verändern sollte, wenn man davon ausgeht, dass sich der Algorithmus am Ende der Optimierung verstärkt.

//calculate the force vector for each object================================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].F, 0.0);

double G = G_constant * exp (-a_constant * (iter / maxIterations));

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      for (int c = 0; c < coordinatesNumber; c++)
      {
        diffDist = o [obj2].c [c] - o [obj].c [c];

        if (o [obj].R [obj2] != 0.0)
        {
          o [obj] .F [c] += G * o [obj].M * o [obj2].M * diffDist / (pow (o [obj].R [obj2], PowerOfdistance) + e_constant);
        }
      }
    }
  }
}

Jetzt müssen wir nur noch die Geschwindigkeit berechnen, mit der sich die Objekte in Bewegung setzen sollen. Aus der Gleichung in Abbildung 1 geht hervor, dass die Berechnung der Geschwindigkeit die Beschleunigung einschließt, wobei die Beschleunigung gleich der auf den Körper wirkenden Kraft geteilt durch die Masse ist. Die Gleichung enthält auch die Zeit V=V0+a*t. In unserem Algorithmus ersetzt die Iteration die Rolle der Zeitabfolge, sodass die Geschwindigkeitsänderung nichts anderes ist als eine Erhöhung der Geschwindigkeit in einer Iteration. Der Geschwindigkeitsvektor ist bereits oben berechnet worden. Es bleibt, durch die Masse zu teilen. Darüber hinaus führen die Autoren Kraft- und Geschwindigkeitsstörung ein. Die Störung ist eine gleichmäßig verteilte Zufallszahl zwischen 0 und 1. Dies fügt der Bewegung von Objekten eine Zufallskomponente hinzu, ohne die die Bewegung streng determiniert wäre und nur von der Ausgangsposition der Körper abhängen würde. Ich hielt es für sinnvoll, die Störungsindikatoren in die externen Parameter des Algorithmus einzubeziehen, wodurch die Bewegung von Objekten von völlig deterministisch bis völlig zufällig reguliert werden kann.

//calculation of acceleration and velocity for all objects==================
double a = 0.0; //acceleration

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int c = 0; c < coordinatesNumber; c++)
  {
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    a = o [obj].F [c] * r / o [obj].M;
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    o [obj].v [c] = o [obj].v [c] * r + a;
    o [obj].c [c] = o [obj].c [c] + o [obj].v [c];

    if (o [obj].c [c] > rangeMax [c]) o [obj].c [c] = rangeMin [c];
    if (o [obj].c [c] < rangeMin [c]) o [obj].c [c] = rangeMax [c];

    o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Die zweite Methode Revision(), die bei jeder Iteration zwingend auszuführen ist. Die Methode ist darauf ausgelegt, den besten Fitnesswert für die aktuelle Iteration zu ermitteln. Gehen Sie in der Schleife alle Objekte durch und ersetzen Sie die global beste Lösung.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Revision ()
{
  for (int s = 0; s < objectsNumber; s++)
  {
    if (o [s].f > fB)
    {
      fB = o [s].f;
      ArrayCopy (cB, o [s].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Testergebnisse

Kommen wir nun zu den Testergebnissen. Im Folgenden sind die Ergebnisse des Prüfstands mit den besten GSA-Parametern, die ich finden konnte, aufgeführt:

2023.02.03 14:12:43.440    Test_AO_GSA (EURUSD,M1)    C_AO_GSA:10;2.0;0.2;0.6;0.0;1.0;2.0;20.0;0.01
2023.02.03 14:12:43.440    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:12:52.198    Test_AO_GSA (EURUSD,M1)    5 Rastrigin's; Funktionsdurchläufe 10000 Ergebnis: 73.64619475145881
2023.02.03 14:12:52.198    Test_AO_GSA (EURUSD,M1)    Score: 0.91252
2023.02.03 14:13:06.105    Test_AO_GSA (EURUSD,M1)    25 Rastrigin's; Funktionsdurchläufe 10000 Ergebnis: 59.4327218024363
2023.02.03 14:13:06.105    Test_AO_GSA (EURUSD,M1)    Score: 0.73640
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    500 Rastrigin's; Funktionsdurchläufe 10000 Ergebnis: 37.550565227034724
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    Score: 0.46527
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD,M1)    5 Forest's; Funktionsdurchläufe 10000 Ergebnis: 0.741456333008312
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD,M1)    Score: 0.41941
2023.02.03 14:14:50.281    Test_AO_GSA (EURUSD,M1)    25 Forest's; Funktionsdurchläufe 10000 Ergebnis: 0.46894018717768426
2023.02.03 14:14:50.282    Test_AO_GSA (EURUSD,M1)    Score: 0.26526
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    500 Forest's; Funktionsdurchläufe 10000 Ergebnis: 0.11382493516764165
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    Score: 0.06439
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:16:18.195    Test_AO_GSA (EURUSD,M1)    5 Megacity's; Funktionsdurchläufe 10000 Ergebnis: 5.279999999999999
2023.02.03 14:16:18.195    Test_AO_GSA (EURUSD,M1)    Score: 0.44000
2023.02.03 14:16:34.536    Test_AO_GSA (EURUSD,M1)    25 Megacity's; Funktionsdurchläufe 10000 Ergebnis: 2.296
2023.02.03 14:16:34.536    Test_AO_GSA (EURUSD,M1)    Score: 0.19133
2023.02.03 14:17:46.887    Test_AO_GSA (EURUSD,M1)    500 Megacity's; Funktionsdurchläufe 10000 Ergebnis: 0.23399999999999999
2023.02.03 14:17:46.887    Test_AO_GSA (EURUSD,M1)    Score: 0.01950

Parameter des Algorithmus:

input double PowerOfdistance_P = 2.0; //Kraft in Relation zum Abstand
input double GraviPert_Min_P = 0.2; //Gravitationsstörung Min
input double GraviPert_Max_P = 0.6; //Gravitationsstörung Max
input double VelocityPert_Min_P = 0.0; //Geschwindigkeitsstörung Min
input double VelocityPert_Max_P = 1.0; //Geschwindigkeitsstörung Max
input double G_Konstante_P = 2.0; //G-Konstante
input double a_constant_P = 20.0; //Konstante a
input double e_constant_P = 0.01; //Konstante e

PowerOfDistance_P - Der Exponent des Abstands zwischen Objekten. Er beeinflusst die Bildung von gravitativ gebundenen Objekten. Je höher der Exponent in der Formel, desto weniger Einfluss haben Objekte auf andere Objekte.

• GraviPert_Min_P - untere Grenze des Bereichs der Gravitationsstörung.
• GraviPert_Max_P - obere Grenze des Bereichs der Gravitationsstörung.
• Im Falle von GraviPert_Min_P = 1,0 und GraviPert_Max_P = 1,0 gibt es keine Gravitationsstörung.
• VelocityPert_Min_P - untere Grenze des Geschwindigkeitsstörungsbereichs.
• VelocityPert_Max_P - obere Grenze des Geschwindigkeitsstörungsbereichs.

Im Falle von VelocityPert_Min_P = 1.0 und VelocityPert_Max_P = 1.0 gibt es keine Geschwindigkeitsstörung.

• G_constant_P - die Gravitationskonstante wirkt als Skalenfaktor: je höher der Wert, desto stärker wirken die Gravitationskräfte und desto schneller ändert sich die Geschwindigkeit von Objekten.
• a_constant_P - Korrekturfaktor für die Gravitationskonstante, der dazu dient, das Suchfeld während der gesamten Optimierung zu verkleinern, um die gefundenen Extrema zu verfeinern.
• e_constant_P - Korrekturfaktor für den Abstand zwischen Objekten.

Werfen wir einen Blick auf die Ergebnisse des Visualisierungstests. Das Verhalten des Algorithmus bei Testfunktionen ist sehr eigenartig und interessant. Tatsächlich zeigt das Experiment die Wirkung der Gravitationskräfte. Die Bewegung der Objekte und die erzielten Optimierungsergebnisse werden stark von den externen Parametern des Algorithmus beeinflusst. Zu Beginn werden Objekte mit einer Geschwindigkeit von Null zufällig über den Suchraum verteilt und setzen sich bei der nächsten Iteration in Bewegung. Die Einstellungen, die beim Testen verwendet wurden (die besten, die ich gefunden habe), bewirken, dass sich die Objekte in Richtung eines gemeinsamen Massenschwerpunkts bewegen.

Vergessen Sie nicht, dass die Schwerkraft jedes Objekts andere Objekte beeinflusst, deren Bewegungsgesetze im Algorithmus mit ausreichend hoher Genauigkeit beschrieben sind. Die Objekte nähern sich dem gemeinsamen Massenschwerpunkt und bewegen sich mit hoher Geschwindigkeit weiter. Es sieht aus wie eine pulsierende Bewegung einer Masse von Teilchen zum gemeinsamen Massenschwerpunkt und zurück. Nach einer bestimmten Anzahl von Iterationen ändert die Bewegung der Objekte ihre Flugbahn unter dem Einfluss des Raumreliefs der Fitnessfunktion, das wie eine Gravitationsinhomogenität wirkt, die die Masse der Objekte beeinflusst. Wie bereits erwähnt, wird die Masse der Objekte anhand des Werts der Fitnessfunktion berechnet. Die achsensymmetrische Rastrigin-Funktion wirkt sich jedoch recht gleichmäßig auf die Bewegung der Objekte aus, und die Aufteilung in Gruppen ist nicht besonders auffällig.

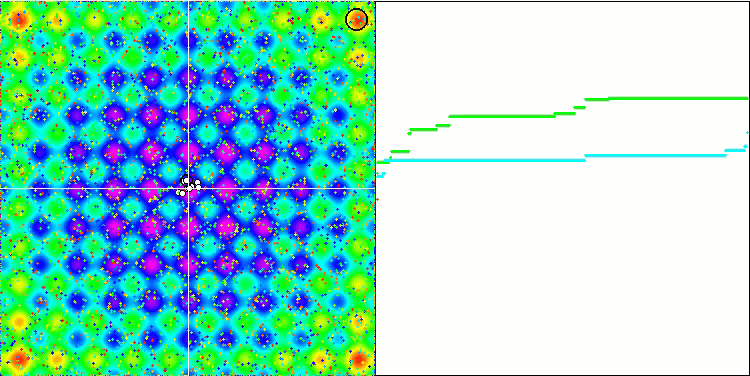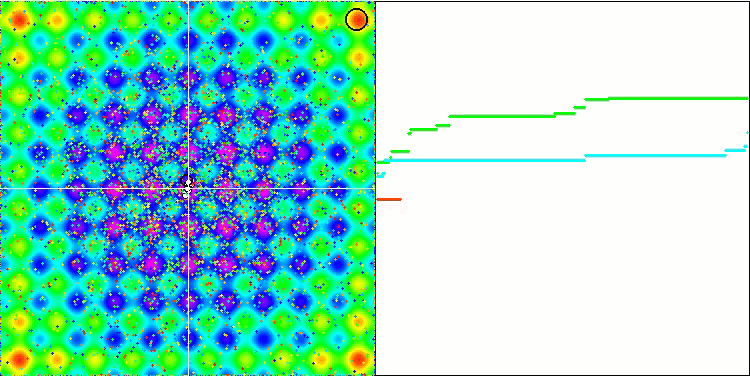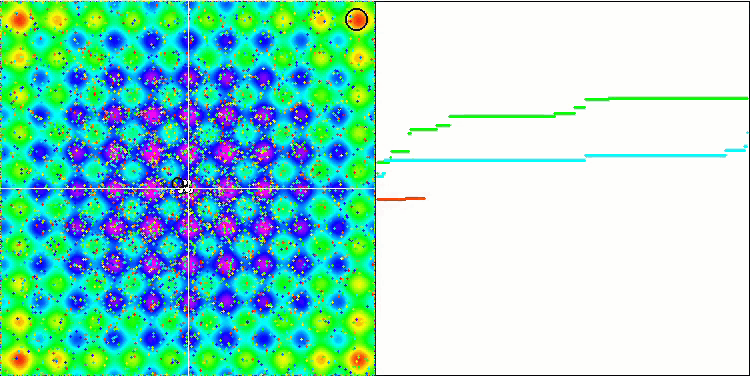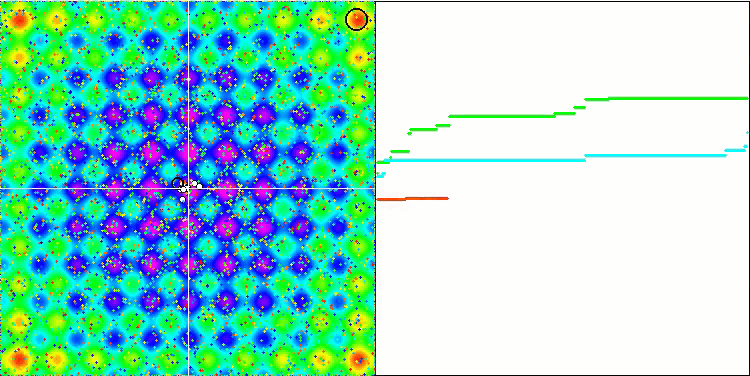
  GSA über die Rastrigin-Testfunktion.

Ein noch interessanteres Verhalten zeigen die Objekte in den Funktionen Forest und Megacity. Diese Funktionen sind nicht symmetrisch und wirken sich daher nicht gleichmäßig auf die gesamte Gruppe von Objekten aus.

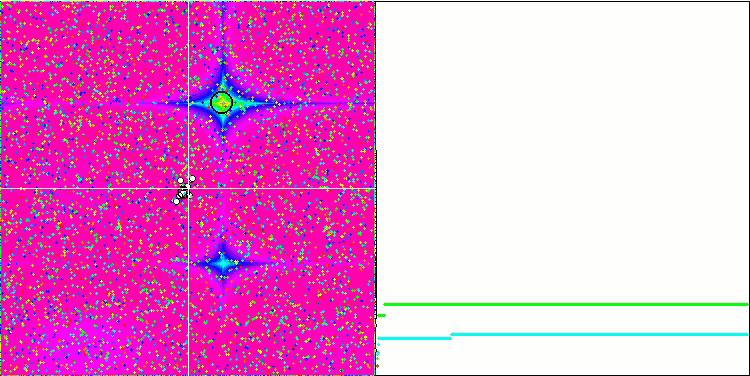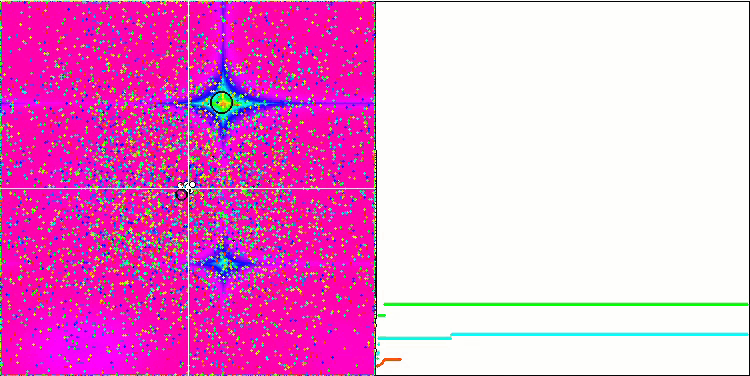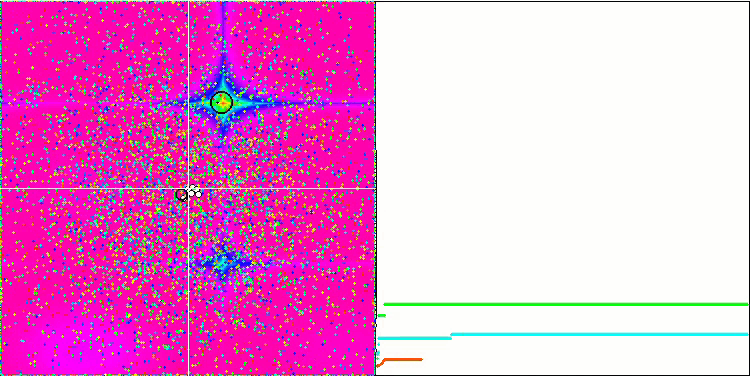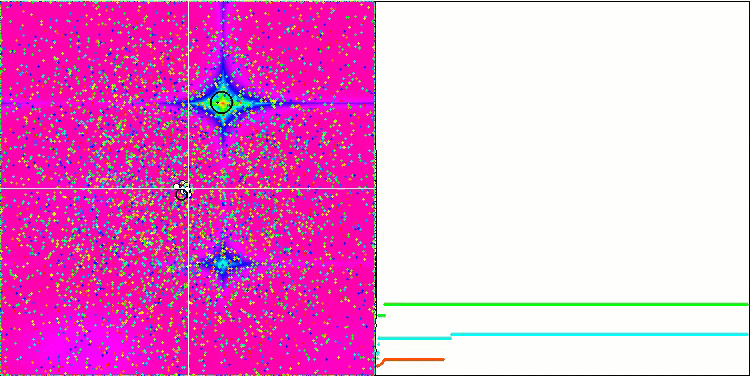
  GSA über die Funktion Forest-Test.

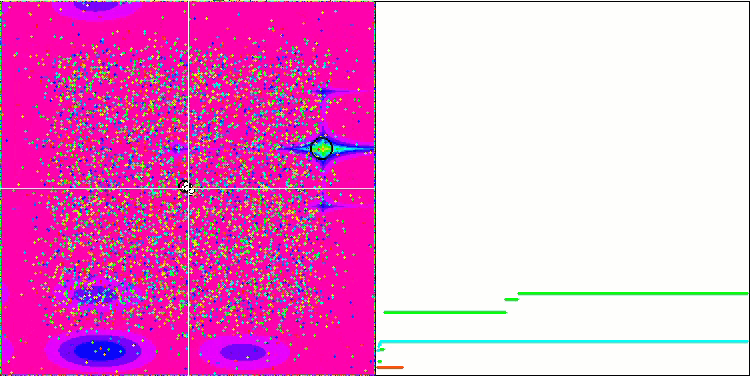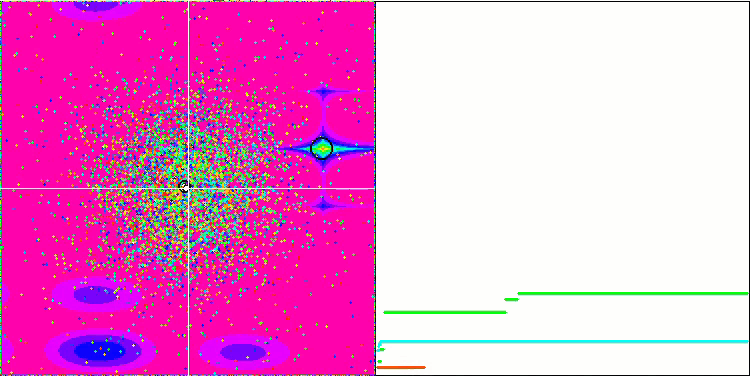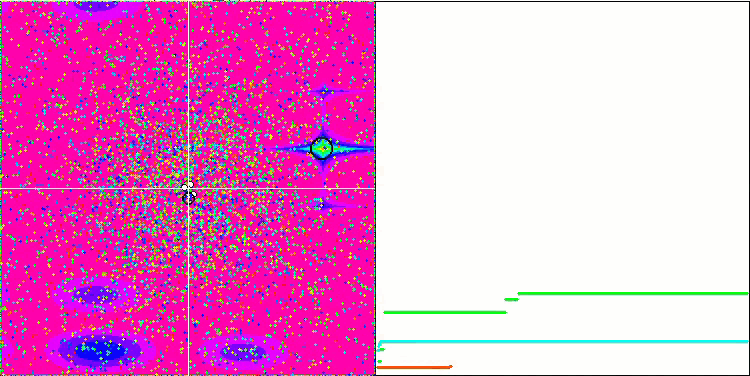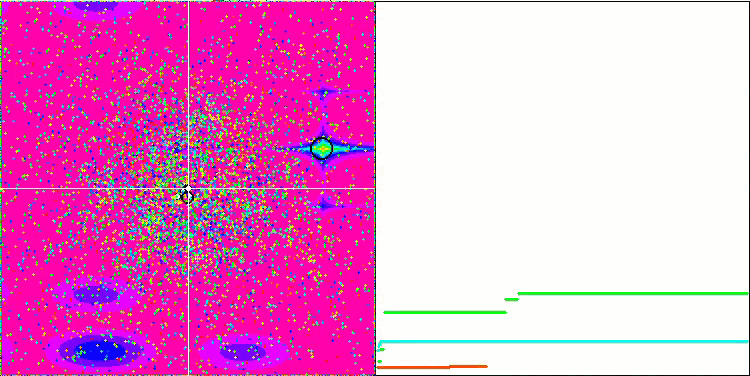
GSA über die Megacity-Testfunktion.

Nach vielen Experimenten mit dem GSA kam ich auf die Idee, einen Simulator für die Bewegung von Weltraumobjekten zu entwickeln. Sie hat keinen praktischen Wert, aber sie vermittelt eine Vorstellung von den physikalischen Gesetzen, die auf Planeten- und Sternsysteme wirken. Der Simulator ist eine Version des GSA mit deaktivierter Zufallsfunktion. Zusätzlich werden drei Objekte vorgestellt, die drei Sterne imitieren (einen blauen Riesen, einen gelben Stern und einen weißen Zwerg). Die Massenparameter werden in den entsprechenden Einstellungen separat angezeigt.

Speziell für den Simulator wurde eine neue Universe-Fitnessfunktion mit einem einheitlichen Raum geschaffen. Der Simulator zeigt deutlich, wie der Gravitationsgrad (Parameter) des Abstands zwischen den Objekten ihre gegenseitige Bewegung beeinflusst. In der folgenden Visualisierung wird eine Potenz von 3 anstelle des Standardwerts des Newtonschen Gesetzes von 2 verwendet. Es wird deutlich, wie sich der Gravitationsgrad auf die Bildung von gravitativ gebundenen Systemen, wie Paar- und Dreifachsternsystemen, auswirkt.

Wäre der Gravitationsgrad in Bezug zum Abstand in unserem Universum größer gewesen, hätten sich die Galaxien viel früher gebildet als in Wirklichkeit. Die Animation zeigt deutlich, dass bei den allerersten Iterationen gepaarte Objekte auftraten, die um einen gemeinsamen Massenschwerpunkt kreisen. Wie erwartet, sammelte der blaue Riese die meisten Objekte um sich herum ein.

Visualisierung des Simulators für die Bewegung von Weltraumobjekten auf der Grundlage des GSA

Kommen wir nun zur Analyse der GSA-Testergebnisse. Die ursprünglichen Merkmale des Algorithmus erlaubten es nicht, in unseren Tests gute Ergebnisse zu erzielen. Zahlreiche Variationen der Parameter, die ich ausprobiert habe, haben die Konvergenz des Algorithmus nicht verbessert. Der Algorithmus zeigte einige positive Ergebnisse im Vergleich zu anderen Testteilnehmern bei der glatten Rastrigin-Funktion mit 10 Variablen und Megacity. In anderen Tests schneidet der GSA unter dem Durchschnitt der Tabelle ab und belegt Platz 8 von 12.

AO	Beschreibung	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (diskret)			Megacity final	Endergebnis
		10 Parameter (5 F)	50 Parameter (25 F)	1000 Parameter (500 F)		10 Parameter (5 F)	50 Parameter (25 F)	1000 Parameter (500 F)		10 Parameter (5 F)	50 Parameter (25 F)	1000 Parameter (500 F)
IWO	Optimierung mit invasiven Unkräutern	1.00000	1.00000	0.35295	2.35295	0.79937	0.46349	0.41071	1.67357	0.75912	0.44903	0.94416	2.15231	100.000
ACOm	Ameisen-Kolonie-Optimierung M	0.36118	0.26810	0.20182	0.83110	1.00000	1.00000	1.00000	3.00000	1.00000	1.00000	0.15901	2.15901	96.805
COAm	Kuckuck-Optimierungsalgorithmus M	0.96423	0.69756	0.30792	1.96971	0.64504	0.34034	0.21362	1.19900	0.67153	0.34273	0.48451	1.49877	74.417
FAm	Firefly-Algorithmus M	0.62430	0.50653	0.20290	1.33373	0.55408	0.42299	0.64360	1.62067	0.21167	0.28416	1.00000	1.49583	70.740
BA	Fledermaus-Algorithmus	0.42290	0.95047	1.00000	2.37337	0.17768	0.17477	0.33595	0.68840	0.15329	0.07158	0.49268	0.71755	59.383
ABC	Künstliches Bienenvolk (Artificial Bee Colony, ABC)	0.81573	0.48767	0.24656	1.54996	0.58850	0.21455	0.17249	0.97554	0.47444	0.26681	0.39496	1.13621	57.393
BFO	Optimierung der bakteriellen Futtersuche	0.70129	0.46155	0.13988	1.30272	0.41251	0.26623	0.26695	0.94569	0.42336	0.34491	0.53694	1.30521	55.563
GSA	Algorithmus für die Schwerkraftsuche	0.73222	0.67404	0.00000	1.40626	0.31238	0.36416	0.42921	1.10575	0.51095	0.36658	0.00000	0.87753	52.786
FSS	Fischschulsuche	0.48850	0.37769	0.13383	1.00002	0.78060	0.05013	0.08423	0.91496	0.00000	0.01084	0.23493	0.24577	20.094
PSO	Partikelschwarmoptimierung	0.21339	0.12224	0.08478	0.42041	0.15345	0.10486	0.28099	0.53930	0.08028	0.02385	0.05550	0.15963	14.358
RND	zufällig	0.17559	0.14524	0.09495	0.41578	0.08623	0.04810	0.06094	0.19527	0.00000	0.00000	0.13960	0.13960	8.117
GWO	Grauer-Wolf-Optimierung	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.04119	0.07252	0.30348	1.000

Im Allgemeinen reagiert der GSA sehr empfindlich auf das Vorhandensein eines Gradienten in der zu optimierenden Funktion. Die geringe Skalierbarkeit erlaubt es nicht, ihn für ernsthafte Aufgaben mit vielen Variablen zu verwenden, daher würde ich den Algorithmus nicht zur Verwendung mit neuronalen Netzen und zur Optimierung von Handelssystemen empfehlen. Ich habe die Möglichkeiten des Algorithmus für die Gravitationssuche nicht vollständig untersucht. Weitere Forschungen könnten neue unbekannte positive Eigenschaften dieses sehr interessanten und ungewöhnlichen Algorithmus aufdecken. Die Hauptvorteile des Algorithmus sind die Unabhängigkeit von der aktuell besten gefundenen globalen Lösung und die Fähigkeit aller Agenten, miteinander zu interagieren. 

Abb. 2 zeigt die Testergebnisse des Algorithmus

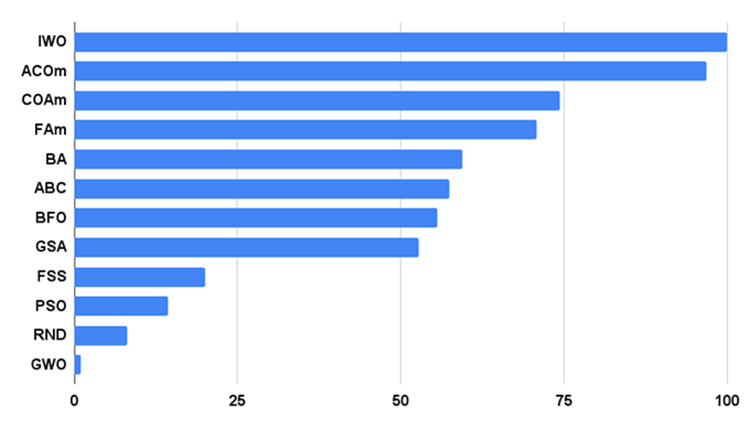
Bild 2. Histogramm der Testergebnisse der Algorithmen

Schlussfolgerungen zu den Eigenschaften des Gravitationssuchalgorithmus (GSA):

Vorteile:
1. Einfache Implementierung.
2. Gute Leistung bei glatten Funktionen mit wenigen Variablen.

Nachteile
1. Hohe rechnerische Komplexität.
2. Schlechte Ergebnisse bei diskreten Funktionen.
3. Schlechte Skalierbarkeit.