
Atmosphere Clouds Model Optimization (ACMO): Die Praxis
Inhalt
Einführung
In der Welt der Wissenschaft, wo sich Technik und Natur überschneiden, ist die einzigartige Idee eines metaheuristischen ACMO-Algorithmus (Atmospheric Cloud Model Optimization) zur Optimierung komplexer Probleme entstanden. Im vorangegangenen Artikel haben wir die Implementierung eines Algorithmus technisch analysiert, der den Prozess der Bildung und Bewegung von Wolken in der Atmosphäre auf der Grundlage verschiedener meteorologischer Parameter modelliert. Im ersten Teil haben wir eine Klasse zur Verwaltung der Wolkensimulation erstellt, die Methoden für die Initialisierung, die Wolkenbewegung, die Aktualisierung der Regionseigenschaften und andere Prozesse enthält.
Wir haben den Suchraum in Regionen unterteilt. Die anfänglichen Feuchtigkeits- und Druckwerte in diesen Regionen wurden bestimmt. Wir legen die Parameter des Modells fest, wie z.B.: Anfangsentropie, Hyperentropie, Schwellenwert der Feuchtigkeit für die Wolkenbildung, und andere. Der nächste Schritt war die Erzeugung von Wolken, indem ein Gebiet mit hoher Luftfeuchtigkeit ausgewählt wurde. Das Wolkenzentrum, die Entropie und die Hyperentropie wurden berechnet. Wir haben die meteorologischen Parameter Feuchtigkeit und Luftdruck in den Regionen nach der Wolkenbildung aktualisiert. Außerdem haben wir die Bewegung von Wolken in Tiefdruckgebiete und die anschließende Aktualisierung der Wolkeneigenschaften in Abhängigkeit von ihrer Bewegung zwischen den Regionen sowie die Ausbreitung von Wolken implementiert.
Was bleibt noch zu tun? Wir müssen Funktionen für die zufällige Platzierung von Tröpfchen und ihre Verteilung auf die Wolken implementieren, den Regenprozess abschließen und die globale Lösung aktualisieren sowie das Modell anhand unserer Testfunktionen mit verschiedenen Parametern testen, um seine Leistung und Genauigkeit zu bewerten. Wir werden Änderungen am Prozess der Regen- und Tröpfchenbildung vornehmen, um einen vollständigeren Austausch von Informationen über vielversprechende Regionen in der Bevölkerung zu ermöglichen.
Implementierung des Algorithmus
Beschreiben wir den gesamten meteorologischen Prozess in Form eines Pseudocodes, der es uns ermöglicht, die endgültige Version des Algorithmus auf dieser Grundlage zusammenzustellen:
1. In der ersten Epoche werden die Wolken zufällig platziert:
EnCk = EnM0;
HeCk = HeM0;
//------------------------------------------------------------------------------
1.1 Bewegung von Wolken in Richtung von Regionen mit niedrigerem Druck:
β = deltaP / normP
d = Tck.x - Cck.c
VC = β * d;
Ck = Ck + VC
Veränderung der Tröpfchenzahl nach der Bewegung:
nk = nk × (1 - γ)
Veränderung der Entropie und Hyperentropie:
α = ΔP / ΔPmax;
EnCk = EnCk * (1 + α)
HeCk = HeCk * (1 - α)
//------------------------------------------------------------------------------
2. Der Vorgang des Regens, das Fallen der Tropfen:
Die Verteilung der Tröpfchen zwischen den Wolken ist proportional zur Luftfeuchtigkeit in der Region.
Erhöhe die Anzahl der Tröpfchen auf die in den Wolken vorhandenen.
//------------------------------------------------------------------------------
3. Berechnung der Fitnessfunktion für Tröpfchen.
//------------------------------------------------------------------------------
4. Aktualisierung der globalen Lösung und des Mindestdrucks in den Regionen, in denen Tropfen gefallen sind.
//------------------------------------------------------------------------------
5. Prüfung, ob die Wolken zerfallen sind und ob neue Wolken entstehen, um die zu ersetzen, die in den Regionen oberhalb des Schwellenwerts zerfallen sind:
Zerfallsregel durch Ausdehnung über den zulässigen Wert hinaus (Wolkenbruch):
En > 5 * EnM0_t
Zerfallsregel bei einem Feuchtigkeitsgehalt unter dem kritischen Wert (Wolkentrocknung):
dCk < dMin
Schwellenwert, oberhalb dessen Regionen Wolken bilden können:
HT = H_min + λ * (H_max - H_min);
//------------------------------------------------------------------------------
6. Berechnung von Entropie und Hyperentropie für neue Wolken:
En = EnM0 / (1 + 2.72 ^ (-(8 - 16 * (t / maxT))))
He = HeM0 / (1 + 2.72 ^ ((8 - 16 * (t / maxT))))
Fahren wir fort. Schauen wir uns die Methode Moving der Klasse C_AO_ACMO an. Die Methode führt zwei Operationen durch: MoveClouds (revision) ist für die Wolkenbewegung zuständig, RainProcess (revision) für den Regen, der vom Zustand der Wolken und dem Parameter revision abhängt. Die Methode Moving führt zwei Hauptaktionen in Bezug auf Wolkendynamik und Regen durch. Sie zeigt die Logik der Wolkenbewegung und der Interaktion mit dem Regenprozess auf. Die Methode Moving wird also verwendet, um den Zustand der Wolken und des Regens als Teil der Wettersimulation zu aktualisieren.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACMO::Moving () { MoveClouds (revision); RainProcess (revision); } //——————————————————————————————————————————————————————————————————————————————
Schauen wir uns die Methode MoveClouds der Klasse C_AO_ACMO genauer an:
1. Der erste Block (wenn rev false ist): Die Methode erzeugt Wolken mit zufälligen Zentren. Für jede Wolke und jede Koordinate:
- Es wird ein Zufallswert des Wolkenmittelpunkts in den angegebenen Bereichen generiert (die Funktion RNDfromCI).
- Der Mittelpunkt wird mit SeInDiSp angepasst, um die Werte zu normalisieren.
- Der Index der Region, in der sich die Wolke befindet, wird mit GetRegionIndex ermittelt.
- Die Werte für Entropie und Anfangsentropie der Wolke werden festgelegt.
- Der Anfangswert der Hyperentropie wird auf hyperEntropie gesetzt.
2. Der zweite Block (wenn rev true ist):
- Wenn rev true ist, beginnt die Methode mit der Suche nach Regionen mit dem niedrigsten Druck.
- Es werden Arrays erstellt, um die Indizes der Regionen mit der niedrigsten Luftfeuchtigkeit lHind zu speichern und den Druck normP zu normalisieren.
3. Schleife, um die Region mit dem niedrigsten Druck zu finden:
- Für jede Koordinate c wird der minimale und maximale Druck in allen Regionen bestimmt.
- Der Index der Region mit dem niedrigsten Druck wird in dem Array lHind gespeichert.
- Der normierte Druck für jede Koordinate wird in normP gespeichert.
4. Wolkenbewegung für jeden von ihnen und jede Koordinate:
- Wenn sich die Wolke bereits in der Region mit dem niedrigsten Druck befindet, wird die Iteration übersprungen.
- Es wird eine zufällige Zielregion mit geringerem Druck ausgewählt.
- Der Druckunterschied zwischen der aktuellen und der Zielregion wird berechnet.
- Der Druckwert wird normalisiert und die Bewegungsgeschwindigkeit der VC-Wolke wird berechnet.
- Das Zentrum der Wolke wird auf der Grundlage der Geschwindigkeit der Bewegung aktualisiert.
- Der Index der Region wird gerade aktualisiert.
- Die Wolkenentropie wird unter Berücksichtigung der Druckveränderung aktualisiert.
- Die Feuchtigkeitsmenge in der Wolke nimmt ab und die Hyperentropie wird aktualisiert, wobei ihr Wert auf maximal 8 begrenzt wird.
Die Methode MoveClouds ist für das Verschieben von Wolken in Regionen mit niedrigerem Druck zuständig, wobei ihre Parameter wie Entropie und Hyperentropie aktualisiert werden. Die Methode implementiert ein dynamisches Modell, das die Veränderungen in der Atmosphäre widerspiegelt.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACMO::MoveClouds (bool &rev) { //---------------------------------------------------------------------------- if (!rev) { //creating clouds with random centers--------------------------------------- for (int i = 0; i < cloudsNumber; i++) { for (int c = 0; c < coords; c++) { clouds [i].center [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); clouds [i].center [c] = u.SeInDiSp (clouds [i].center [c], rangeMin [c], rangeMax [c], rangeStep [c]); clouds [i].regionIndex [c] = GetRegionIndex (clouds [i].center [c], c); clouds [i].entropy [c] = entropy [c] * EnM0; clouds [i].entropyStart [c] = clouds [i].entropy [c]; } clouds [i].hyperEntropy = HeM0; } return; } //search for the region with the lowest pressure------------------------------ int targetRegion = 0; int lHind []; //lowest humidity index ArrayResize (lHind, coords); ArrayInitialize (lHind, 0); double normP []; ArrayResize (normP, coords); double minP; double maxP; for (int c = 0; c < coords; c++) { minP = DBL_MAX; maxP = -DBL_MAX; for (int r = 0; r < regionsNumber; r++) { if (areas [c].regions [r].pressure < areas [c].regions [lHind [c]].pressure) { lHind [c] = r; } if (areas [c].regions [r].pressure < minP) minP = areas [c].regions [r].pressure; if (areas [c].regions [r].pressure > maxP) maxP = areas [c].regions [r].pressure; } normP [c] = maxP - minP; } //moving the cloud to a region with less pressure----------------------------- int clRegIND = 0; double deltaP = 0.0; double α = 0.0; // Entropy factor double β = 0.0; // Atmospheric pressure factor double VC = 0.0; // Cloud velocity double d = 0.0; // Cloud direction for (int i = 0; i < cloudsNumber; i++) { for (int c = 0; c < coords; c++) { //find a region with lower pressure--------------------------------------- if (clouds [i].regionIndex [c] == lHind [c]) continue; clRegIND = clouds [i].regionIndex [c]; do targetRegion = u.RNDminusOne (regionsNumber); while (areas [c].regions [clRegIND].pressure < areas [c].regions [targetRegion].pressure); //------------------------------------------------------------------------ deltaP = areas [c].regions [clRegIND].pressure - areas [c].regions [targetRegion].pressure; β = deltaP / normP [c]; d = areas [c].regions [targetRegion].x - areas [c].regions [clRegIND].centre; VC = β * d; clouds [i].center [c] += VC; clouds [i].center [c] = u.SeInDiSp (clouds [i].center [c], rangeMin [c], rangeMax [c], rangeStep [c]); clouds [i].regionIndex [c] = GetRegionIndex (clouds [i].center [c], c); α = β; clouds [i].entropy [c] *=(1 + α); } clouds [i].droplets *=(1 - γ); clouds [i].hyperEntropy *=(1 + α); if (clouds [i].hyperEntropy > 8) clouds [i].hyperEntropy = 8; } } //——————————————————————————————————————————————————————————————————————————————
Analysieren wir nun die Methode GetRegionIndex der Klasse C_AO_ACMO. Beschreibung der Methode:
1. Berechnung der Position einer Region. Der Regionsindex regPos mit dem angegebenen Punkt wird berechnet und mit der Funktion Floor auf die nächste Ganzzahl abgerundet.
2. Kontrolle der Grenzen. Dieser Block prüft, ob der berechnete Index regPos die zulässigen Werte überschreitet (er darf die zulässige Anzahl der Regionen nicht überschreiten).
3. Die Methode gibt den Index der Region zurück, in der sich der Punkt befindet.
Die Methode GetRegionIndex dient dazu, den Index der Region zu ermitteln, in der sich ein bestimmter Punkt innerhalb eines bestimmten Bereichs befindet. Es berücksichtigt die Anzahl der Regionen und behandelt die Fälle korrekt, in denen der Punkt am Rande des Bereichs liegt.
//—————————————————————————————————————————————————————————————————————————————— int C_AO_ACMO::GetRegionIndex (double point, int ind) { int regPos = (int)floor ((point - rangeMin [ind]) / ((rangeMax [ind] - rangeMin [ind]) / regionsNumber)); if (regPos >= regionsNumber) regPos = regionsNumber - 1; return regPos; } //——————————————————————————————————————————————————————————————————————————————
Beschreiben wir die nächste Methode RainProcess der Klasse C_AO_ACMO:
2. Initialisierung der Arrays:
- Wir erstellen zwei Arrays: cloud zum Speichern der Wolkenwerte und drops zum Speichern der Anzahl der Regentropfen für jede Wolke.
- Beide Felder variieren in ihrer Größe je nach Anzahl der Wolken (cloudsNumber).
3. Initialisierung des Arrays Cloud:
- Wenn rev false ist, werden alle Elemente des Wolkenarrays mit dem Wert 1,0 initialisiert.
- Andernfalls wird das Array cloud mit dem Wert 0,0 initialisiert und dann die Luftfeuchtigkeit für jede Wolke berechnet.
4. Berechnung der Luftfeuchtigkeit:
- Für jede Wolke und jede Koordinate wird die Luftfeuchtigkeit in Abhängigkeit von den Regionen berechnet.
- Ist die Luftfeuchtigkeit ungleich -DBL_MAX, wird sie dem entsprechenden Element des Arrays cloud hinzugefügt. Andernfalls wird der Wert für die kleinsten Tropfen minGp hinzugefügt.
5. Verteilung der Tröpfchen:
- Aufruf der Methode DropletsDistribution zur Verteilung von Tropfen auf der Grundlage von Werten im Array cloud.
6. Die Hauptschleife zur Behandlung von Tröpfchen, für jede Wolke und jedes Tröpfchen:
- Die Werte von dist, center, xMin und xMax werden berechnet.
- Der Wert x wird mit Hilfe der Normalverteilung (Gauß) erzeugt.
- Wenn x außerhalb des Bereichs liegt, wird es mit der Methode RNDfromCI korrigiert.
- Der Wertx wird mit der Methode SeInDiSp normalisiert und in dem Array a gespeichert.
Nachdem alle Tröpfchen für eine Cloud bearbeitet wurden, wird die Gesamtzahl der Tröpfchen in der Cloud aktualisiert. So simuliert die Methode RainProcess einen Regen, der aus den Wolken fällt, wobei die Feuchtigkeit und die Verteilung der Tropfen berücksichtigt werden. Es initialisiert die Arrays, berechnet die Luftfeuchtigkeit für jede Wolke, verteilt die Regentropfen und erzeugt Werte für jeden Tropfen unter der Annahme einer Normalverteilung.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACMO::RainProcess (bool &rev) { //to shed drops from every cloud---------------------------------------------- double cloud []; int drops []; ArrayResize (cloud, cloudsNumber); ArrayResize (drops, cloudsNumber); if (!rev) { ArrayInitialize (cloud, 1.0); } else { ArrayInitialize (cloud, 0.0); double humidity; for (int i = 0; i < cloudsNumber; i++) { for (int c = 0; c < coords; c++) { for (int r = 0; r < regionsNumber; r++) { humidity = areas [c].regions [clouds [i].regionIndex [r]].humidity; if (humidity != -DBL_MAX) cloud [i] += humidity; else cloud [i] += minGp; } } } } DropletsDistribution (cloud, drops); double dist = 0.0; double centre = 0.0; double xMin = 0.0; double xMax = 0.0; double x = 0.0; int dCNT = 0; for (int i = 0; i < cloudsNumber; i++) { for (int dr = 0; dr < drops [i]; dr++) { for (int c = 0; c < coords; c++) { dist = clouds [i].entropy [c]; centre = clouds [i].center [c]; xMin = centre - dist; xMax = centre + dist; x = u.GaussDistribution (centre, xMin, xMax, clouds [i].hyperEntropy); if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], centre); if (x > rangeMax [c]) x = u.RNDfromCI (centre, rangeMax [c]); x = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); a [dCNT].c [c] = x; } dCNT++; } clouds [i].droplets += drops [i]; } } //——————————————————————————————————————————————————————————————————————————————
Die nächste Methode DropletsDistribution der Klasse C_AO_ACMO dient der Verteilung von Regentropfen zwischen den Wolken auf der Grundlage ihrer Feuchtigkeit. Schauen wir uns das einmal genau an.
2. Initialisierung von Variablen:
- minHumidity wird auf den Maximalwert initialisiert, damit die minimale Luftfeuchtigkeit ermittelt werden kann.
- indMinHumidity speichert den Wolkenindex mit minimaler Luftfeuchtigkeit.
- totalHumidity wird verwendet, um die Summe der Luftfeuchtigkeit aller Wolken zu speichern.
3. Die Summierung der Luftfeuchtigkeit summiert die Luftfeuchtigkeit aller Wolken und ermittelt die Wolke mit der niedrigsten Luftfeuchtigkeit.
4. Proportionale Verteilung der Tropfen - für jede Wolke wird die Anzahl der Tropfen proportional zu ihrer Feuchtigkeit im Verhältnis zur Gesamtfeuchtigkeit berechnet. Dieser Wert wird im Array „droplets“ (Tröpfchen) gespeichert.
5. Verteilung der restlichen Tropfen:
- Zunächst wird die Gesamtzahl der verteilten Tröpfchen totalDrops berechnet.
- Anschließend wird die Anzahl der verbleibenden Tropfen (remainingDrops) berechnet.
- Falls noch Tröpfchen übrig sind, werden sie der Wolke mit minimaler Feuchtigkeit hinzugefügt.
Die Methode DropletsDistribution verteilt Regentropfen auf der Grundlage ihres Feuchtigkeitsgehalts effektiv zwischen den Wolken. Sie verteilt die Tröpfchen zunächst proportional und passt dann die Verteilung an, indem es die verbleibenden Tröpfchen der Wolke mit der geringsten Luftfeuchtigkeit hinzufügt. Dies ermöglicht eine realistischere Simulation des Niederschlags, wobei eine konstante Anzahl von Tropfen beibehalten wird, die der Populationsgröße in den externen Parametern des Algorithmus entspricht.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACMO::DropletsDistribution (double &cloud [], int &droplets []) { double minHumidity = DBL_MAX; int indMinHumidity = -1; double totalHumidity = 0; //total amount of humidity in all clouds for (int i = 0; i < ArraySize (cloud); i++) { totalHumidity += cloud [i]; if (cloud [i] < minHumidity) { minHumidity = cloud [i]; indMinHumidity = i; } } // Filling the droplets array in proportion to the value in clouds for (int i = 0; i < ArraySize (clouds); i++) { droplets [i] = int((cloud [i] / totalHumidity)*popSize); //proportional distribution of droplets } // Distribute the remaining drops, if any int totalDrops = 0; for (int i = 0; i < ArraySize (droplets); i++) { totalDrops += droplets [i]; } // If not all drops are distributed, add the remaining drops to the element with the lowest humidity int remainingDrops = popSize - totalDrops; if (remainingDrops > 0) { droplets [indMinHumidity] += remainingDrops; //add the remaining drops to the lightest cloud } } //——————————————————————————————————————————————————————————————————————————————
Die Methode Revision der Klasse C_AO_ACMO führt eine Aktualisierung des Systemzustands durch. Schauen wir uns das genauer an:
1. Die Schleife durch das Array a mit den Elementen (Population von Optimierungsagenten). Diese Schleife durchläuft alle Elemente des Arrays a der Größe popSize:
- Ist der Fitnesswert f des aktuellen Elements größer als der aktuelle maximale Fitnesswert fB, wird fB aktualisiert, während der Index ind auf den aktuellen Index gesetzt wird.
- Die Suche nach dem minimalen Fitnesswert f wird ebenfalls unter allen Elementen des Arrays durchgeführt, und wenn der aktuelle Wert kleiner als minGp ist, wird minGp aktualisiert.
2. Kopieren von Daten: Wenn ein Element mit dem höchsten Fitnesswert f gefunden wurde (ind ist nicht -1), werden die Daten (nämlich a [ind]) aus dem Array c in das Array cB kopiert.
3. Aktualisieren der Regionseigenschaften: Es wird die Methode UpdateRegionProperties aufgerufen. Sie aktualisiert die Parameter für Luftfeuchtigkeit und Luftdruck in verschiedenen Regionen.
4. Wolkenerzeugung: Die Methode GenerateClouds, die für das Verschwinden alter und das Entstehen neuer Wolken verantwortlich ist, wird aufgerufen.
5. Status-Update:
- Das Revisionsflag wird auf true gesetzt, was bedeutet, dass der Anfangszustand des Systems überschritten wurde.
- Der Zähler EpochNow wird erhöht, um die Anzahl der Epochen zu kontrollieren.
Die Methode Revision ist für die Aktualisierung des Systemzustands in Bezug auf Wolken zuständig. Sie findet den maximalen Fitnesswert f, aktualisiert die relevanten Parameter, initialisiert neue Wolken und aktualisiert die Regionseigenschaften. Diese Methode ist der Schlüssel dazu, die Daten im Modell auf dem neuesten Stand zu halten, damit sich das System an Veränderungen anpassen kann.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACMO::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } if (a [i].f < minGp) minGp = a [i].f; } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- UpdateRegionProperties (); //updating humidity and pressure in the regions GenerateClouds (); //disappearance of clouds and the creation of new ones revision = true; epochNow++; } //——————————————————————————————————————————————————————————————————————————————
Die Methode GenerateClouds der Klasse C_AO_ACMO ist für die Erzeugung von Wolken und die Verwaltung ihres Zustands in Abhängigkeit von verschiedenen Faktoren wie Feuchtigkeit und Entropie zuständig. Beschreibung der Methode:
1. Berechnung der Feuchtigkeitsschwelle: Die Funktion CalculateHumidityThreshold wird aufgerufen, die den für die Wolkenbildung erforderlichen Feuchtigkeitsschwellenwert liefert.
2. Struktur zur Speicherung von Regionsindizes:
- Die Struktur S_Areas ist definiert. Die Struktur enthält eine Reihe von Indizes von Regionen, die Wolken bilden können.
- Die Methode ar wird mit einer Größe initialisiert, die der Anzahl der Koordinaten entspricht.
3. Sammlung von Informationen über die Region: Diese Doppelschleife prüft jede Region, um zu sehen, ob sie ihren Feuchtigkeitsschwellenwert erreicht. Ist die Feuchtigkeit einer Region größer als der Schwellenwert, wird der Index dieser Region zum Array regsIND der entsprechenden Struktur S_Areas hinzugefügt.
4. Überprüfung der Bedingungen für den Wolkenzerfall:
- Für jede Wolke wird geprüft, ob ihre Entropie einen bestimmten Grenzwert überschreitet (das Fünffache der ursprünglichen Entropie). Ist dies der Fall, so gilt die Wolke als aufgelöst.
- Dann wird geprüft, ob die Feuchtigkeitsmenge in der Wolke unter dem Mindestwert von dMin liegt, was ebenfalls zur Auflösung der Wolke führen kann.
5. Schaffung einer neuen Wolke in den feuchtesten Regionen:
- Wenn sich die Wolke auflöst, entsteht eine neue Wolke in einer der feuchtesten Regionen. Für jede Koordinate wird ein Regionsindex zufällig ausgewählt, und die Wolke erhält neue Zentralkoordinaten und einen Regionsindex.
- Anschließend wird die Funktion CalculateNewEntropy aufgerufen. Die Funktion berechnet die Entropie für eine neue Wolke in Abhängigkeit von der aktuellen Epoche neu.
Die Methode GenerateClouds verwaltet die Bildung und Auflösung von Wolken auf der Grundlage von Feuchtigkeit und Entropie. Es sammelt Informationen über Regionen, die Wolken bilden können, prüft bestehende Wolken auf Verfall und erzeugt neue Wolken in geeigneten Regionen. Diese Methode ist der Schlüssel zur dynamischen Steuerung des Zustands der Wolken im Modell.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACMO::GenerateClouds () { //Collecting statistics of regions capable of creating clouds----------------- double Ht = CalculateHumidityThreshold (); struct S_Areas { int regsIND []; //index of the potential region }; S_Areas ar []; ArrayResize (ar, coords); int sizePr = 0; for (int i = 0; i < coords; i++) { for (int r = 0; r < regionsNumber; r++) { if (areas [i].regions [r].humidity > Ht) { sizePr = ArraySize (ar [i].regsIND); sizePr++; ArrayResize (ar [i].regsIND, sizePr, coords); ar [i].regsIND [sizePr - 1] = r; } } } //Check the conditions for cloud decay---------------------------------------- bool cloudDecay = false; for (int i = 0; i < cloudsNumber; i++) { cloudDecay = false; //checking the cloud for too much entropy----------------------------------- for (int c = 0; c < coords; c++) { if (clouds [i].entropy [c] > 5.0 * clouds [i].entropyStart [c]) { //Print ("Disintegration of cloud #", i, " - tore at epoch ", epochNow); cloudDecay = true; break; } } //checking the cloud for decay---------------------------------------------- if (!cloudDecay) { if (clouds [i].droplets < dMin) { //Print ("Disintegration of cloud #", i, " - dried up at epoch ", epochNow); cloudDecay = true; } } //if the cloud has decayed-------------------------------------------------- int regIND = 0; if (cloudDecay) { //creating a cloud in a very humid region--------------------------------- for (int c = 0; c < coords; c++) { regIND = u.RNDminusOne (ArraySize (ar [c].regsIND)); regIND = ar [c].regsIND [regIND]; clouds [i].center [c] = areas [c].regions [regIND].x; clouds [i].regionIndex [c] = regIND; } CalculateNewEntropy (clouds [i], epochNow); } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode CalculateHumidityThreshold der Klasse C_AO_ACMO ist für die Berechnung der für die Wolkenbildung erforderlichen Feuchtigkeitsschwelle zuständig. Hier sind die Schritte im Detail:
1. Doppelter Zyklus zur Ermittlung der Mindestfeuchtigkeit. Die äußere Schleife durchläuft alle Koordinaten, während die innere Schleife alle Regionen (regionsNumber) in jeder Koordinate durchläuft. Ist die Luftfeuchtigkeit der Region ungleich -DBL_MAX, wird eine Prüfung durchgeführt: Ist die aktuelle Luftfeuchtigkeit kleiner als der aktuelle H_min, wird H_min aktualisiert.
2. Die Methode liefert H_min, erhöht um das Produkt aus λ und der Differenz von H_max und H_min, was die für die Wolkenbildung erforderliche Feuchtigkeitsschwelle darstellt.
Die Methode CalculateHumidityThreshold berechnet die Feuchtigkeitsschwelle auf der Grundlage der minimalen Luftfeuchtigkeit aller Regionen und passt sie auf der Grundlage der maximalen Luftfeuchtigkeit und des λ-Verhältnisses an. Auf diese Weise lässt sich bestimmen, unter welchen Bedingungen sich Wolken bilden können, je nachdem, wie die Umwelt beschaffen ist.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ACMO::CalculateHumidityThreshold () { double H_max = fB; double H_min = DBL_MAX; for (int c = 0; c < coords; c++) { for (int r = 0; r < regionsNumber; r++) { if (areas [c].regions [r].humidity != -DBL_MAX) { if (areas [c].regions [r].humidity < H_min) { H_min = areas [c].regions [r].humidity; } } } } return H_min + λ * (H_max - H_min); } //——————————————————————————————————————————————————————————————————————————————
Die Methode CalculateNewEntropy der Klasse C_AO_ACMO ist für die Berechnung der neuen Entropie und Hyperentropie für Wolken zuständig, die durch die Struktur S_ACMO_Cloud dargestellt werden. Schauen wir es uns im Detail an:
1. Berechnung der Entropie:
- Der Zyklus durchläuft alle Koordinaten.
- Für jede Koordinate wird ein neuer Entropiewert „cl.entropy [c]“ nach der folgenden Gleichung berechnet: En = (entropy [c] * EnM0) / (1 + e ^ (-(8 - 16 * (t / epochs)))).
- cl.entropyStart [c] und cl.entropy [c] werden mit dem Wert von entropy [c] initialisiert, was dazu dient, den Anfangswert der Entropie zu erhalten.
2. Berechnung der Hyperentropie: He = 1 / (1 + e ^ (8 - 16 * (t / epochs))).
3. Die Hyperentropie wird mit der Scale-Methode des Objekts u skaliert, die es uns ermöglicht, den Hyperentropiewert mit Hilfe der Parameter HeM0 und 8,0 auf einen bestimmten Bereich (von 0 bis 8) zu skalieren.
Die Methode CalculateNewEntropy aktualisiert die Entropie- und Hyperentropiewerte für Wolken auf der Grundlage der aktuellen Zeit t und der angegebenen Parameter.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACMO::CalculateNewEntropy (S_ACMO_Cloud &cl, int t) { //---------------------------------------------------------------------------- //En: 1/(1+2.72^(-(8-16*(t/maxT)))) for (int c = 0; c < coords; c++) { cl.entropy [c] = entropy [c] * EnM0 / (1.0 + pow (M_E, (-(8.0 - 16.0 * (t / epochs))))); cl.entropyStart [c] = cl.entropy [c] = entropy [c]; } //---------------------------------------------------------------------------- //He: 1/(1+2.72^((8-16*(t/maxT)))) cl.hyperEntropy = 1.0 / (1.0 + pow (M_E, ((8.0 - 16.0 * (t / epochs))))); cl.hyperEntropy = u.Scale (cl.hyperEntropy, 0.0, 8.0, HeM0, 8.0); } //——————————————————————————————————————————————————————————————————————————————
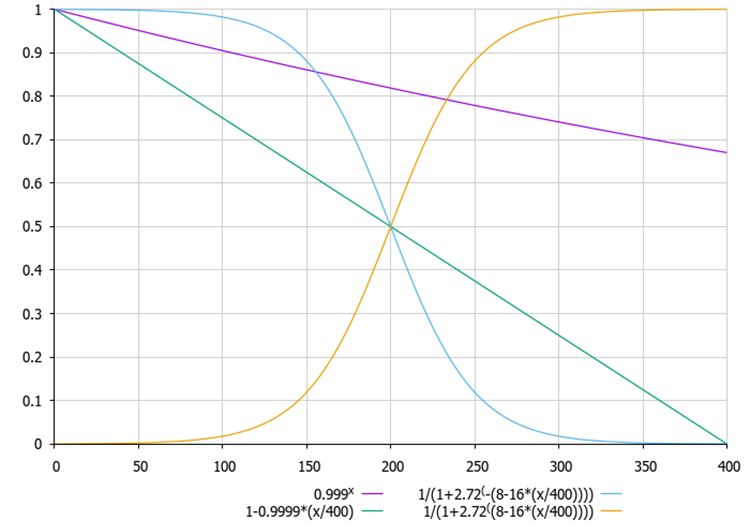
Abbildung 1. Varianten der Gleichungen zur Berechnung des Verhältnisses ζ in Abhängigkeit von der aktuellen Epoche. Wir können eine Gleichung auswählen und den Algorithmus mit jeder dieser Gleichungen ausprobieren (die Codestrings sind auskommentiert)
Testergebnisse
Gehen wir nun zum Testen des Algorithmus über. Das meteorologische Modell der Wolkenbildung, wie es von den Autoren konzipiert wurde, funktioniert wie folgt://Originalfassung
ACMO|Atmospheric Cloud Model Optimization|50.0|5.0|10.0|0.2|5.0|5.0|0.9|0.2|
=============================
5 Hilly's; Func runs: 10000; result: 0.6017884495404766
25 Hilly's; Func runs: 10000; result: 0.3426222382089618
500 Hilly's; Func runs: 10000; result: 0.2526410178225118
=============================
5 Forest's; Func runs: 10000; result: 0.4780554376190664
25 Forest's; Func runs: 10000; result: 0.261057831391174
500 Forest's; Func runs: 10000; result: 0.17318135866144563
=============================
5 Megacity's; Func runs: 10000; result: 0.3507692307692307
25 Megacity's; Func runs: 10000; result: 0.16153846153846158
500 Megacity's; Func runs: 10000; result: 0.09632307692307775
=============================
All score: 2.71798 (30.20%)
Leider sind die Ergebnisse viel niedriger als erwartet. Ich denke, dass die Konvergenz des Algorithmus trotz des schönen Modells des Wolkenbildungsprinzips mit einer großen Anzahl verschiedener Gleichungen und logischer Aktionen, die darauf abzielen, nicht in den Extrema stecken zu bleiben, gering ist. Dem Algorithmus fehlt die direkte Interaktion und der Austausch von Informationen zwischen den Agenten über die besten Lösungen, was in der Regel zu einer Verbesserung der Suchqualitäten eines jeden Algorithmus führt. Daher habe ich beschlossen, den Informationsaustausch durch probabilistische Übertragung von Informationen von den besten zu den schlechtesten Tropfen zu ergänzen. Nun wollen wir sehen, was dabei herausgekommen ist:
ACMOm|Atmospheric Cloud Model Optimization|50.0|4.0|10.0|0.2|0.2|2.0|0.9|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.9032099148349984
25 Hilly's; Func runs: 10000; result: 0.48545807643133143
500 Hilly's; Func runs: 10000; result: 0.30403284557071203
=============================
5 Forest's; Func runs: 10000; result: 0.8026793420899985
25 Forest's; Func runs: 10000; result: 0.3785708322859447
500 Forest's; Func runs: 10000; result: 0.1917777390119122
=============================
5 Megacity's; Func runs: 10000; result: 0.6230769230769231
25 Megacity's; Func runs: 10000; result: 0.244
500 Megacity's; Func runs: 10000; result: 0.10795384615384714
=============================
All score: 4.04076 (44.90%)
Die Ergebnisse haben sich deutlich verbessert. Die Idee war erfolgreich. Die Idee ist, Informationen über die beste Lösung mit einer gewissen Wahrscheinlichkeit zu übertragen, um Tropfen von anderen Tropfen zu trüben, wenn sie eine höhere Feuchtigkeit haben (im Kontext des Algorithmus ist dies die Fitness).
Am Ende wird für jede Wolke die Gesamtzahl der Tropfen (für eine Wolke ein Indikator für die Feuchtigkeit) aktualisiert, indem der entsprechende Wert aus dem Array drops addiert wird. Die Methode RainProcess implementiert einen Mechanismus, der den Regen modelliert und dabei die Luftfeuchtigkeit, die Tröpfchenverteilung und die Interaktion mit der Bevölkerung berücksichtigt. Die Stelle, an der Änderungen am Code vorgenommen wurden, ist grün hervorgehoben.
Für jeden generierten Wert x wird ein zufälliger Index p aus der Grundgesamtheit ausgewählt. Abhängig von der Wahrscheinlichkeit (95%) werden die Werte im Array a aktualisiert. Der Wert steht für eine Grundgesamtheit oder eine Gruppe von Lösungen. Am Ende wird die Gesamtzahl der von der Wolke abgeworfenen Tropfen für jede Wolke aktualisiert, indem der entsprechende Wert aus dem Array drops addiert wird.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACMO::RainProcess (bool &rev) { //to shed drops from every cloud---------------------------------------------- double cloud []; int drops []; ArrayResize (cloud, cloudsNumber); ArrayResize (drops, cloudsNumber); if (!rev) { ArrayInitialize (cloud, 1.0); } else { ArrayInitialize (cloud, 0.0); double humidity; for (int i = 0; i < cloudsNumber; i++) { for (int c = 0; c < coords; c++) { humidity = areas [c].regions [clouds [i].regionIndex [c]].humidity; if (humidity != -DBL_MAX) cloud [i] += humidity; else cloud [i] += minGp; } } } DropletsDistribution (cloud, drops); //ArrayPrint (drops); double dist = 0.0; double centre = 0.0; double xMin = 0.0; double xMax = 0.0; double x = 0.0; int dCNT = 0; for (int i = 0; i < cloudsNumber; i++) { for (int dr = 0; dr < drops [i]; dr++) { for (int c = 0; c < coords; c++) { dist = clouds [i].entropy [c]; centre = clouds [i].center [c]; xMin = centre - dist; xMax = centre + dist; x = u.GaussDistribution (centre, xMin, xMax, clouds [i].hyperEntropy); if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], centre); if (x > rangeMax [c]) x = u.RNDfromCI (centre, rangeMax [c]); x = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); int p = u.RNDminusOne (popSize); if (a [p].f > a [dCNT].f) { if (u.RNDprobab () < 0.95) a [dCNT].c [c] = a [p].c [c]; } else { a [dCNT].c [c] = x; } } dCNT++; } clouds [i].droplets += drops [i]; } } //——————————————————————————————————————————————————————————————————————————————
Die Visualisierung der Funktionsweise des Algorithmus zeigt Folgendes: gute Konvergenz des Algorithmus, lange flache Abschnitte auf dem Konvergenzgraphen mit einer kleinen Anzahl von optimierten Parametern deuten auf eine gewisse Tendenz des Algorithmus hin, in lokalen Extrema stecken zu bleiben, und mit einer Erhöhung der Anzahl der Parameter verschwindet dieser Nachteil.
Die Wolken in der Visualisierung erscheinen als dichte Cluster, aber durch die Wahl verschiedener Einstellungen für externe Parameter (Anzahl der Regionen, Wolken, anfängliche Entropie und Trocknungsschwelle) können sie das Aussehen von schwebenden Wolken am Himmel simulieren, wie in der Natur.
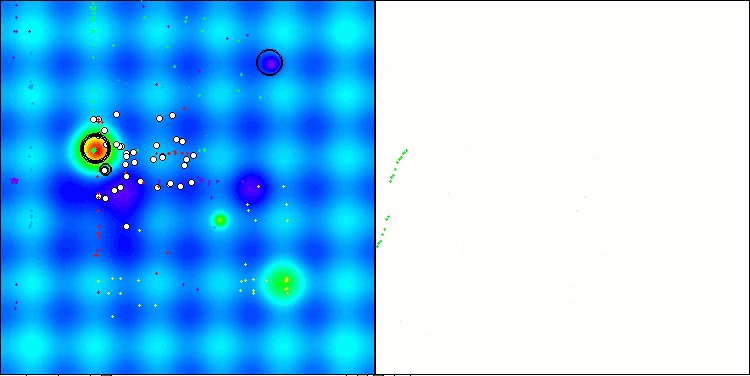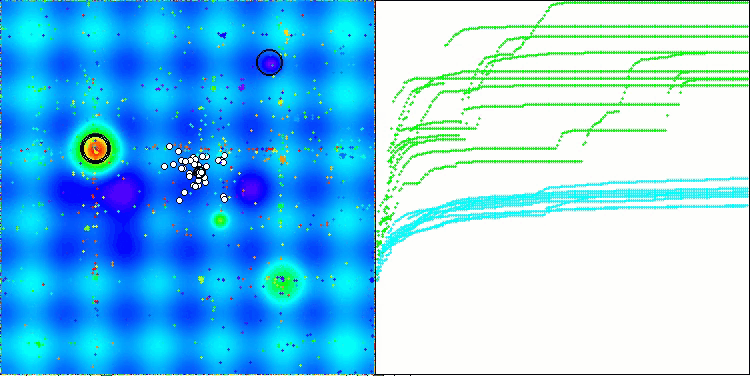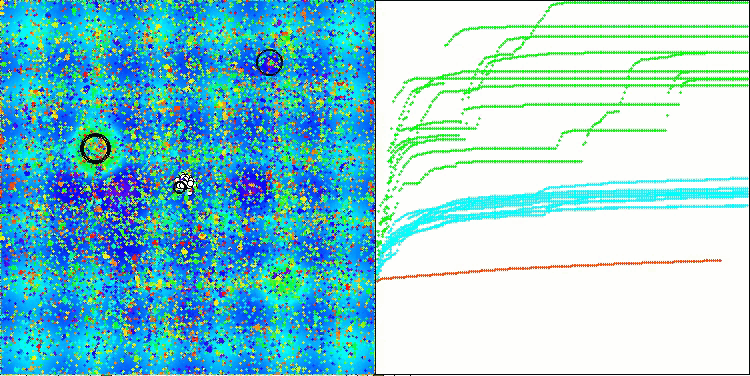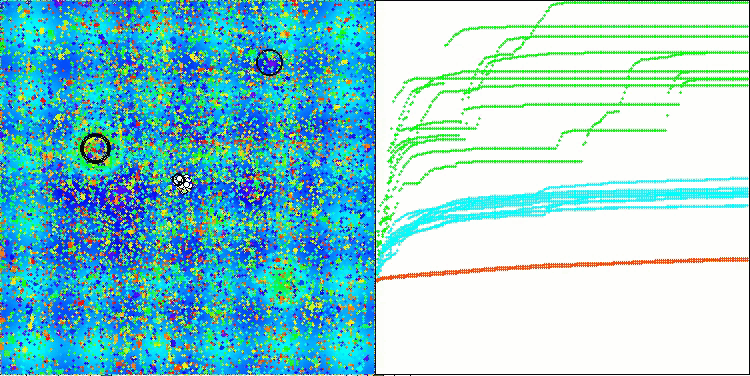
AСMO mit der Testfunktion Hilly
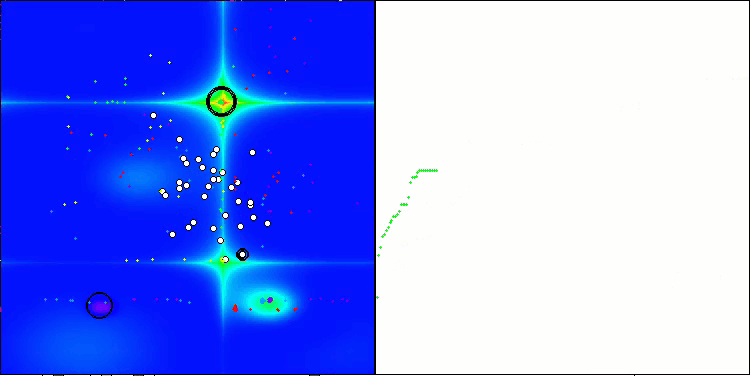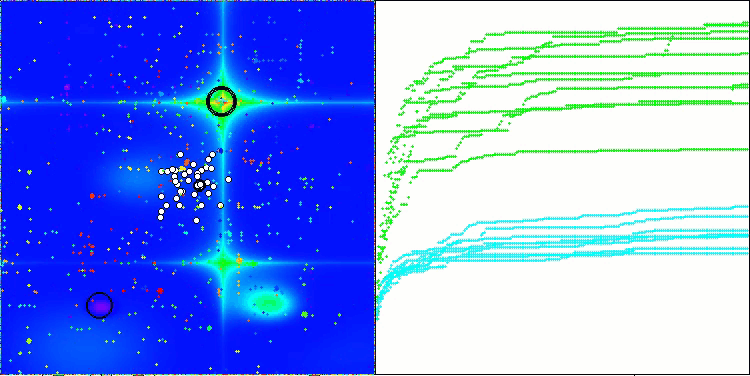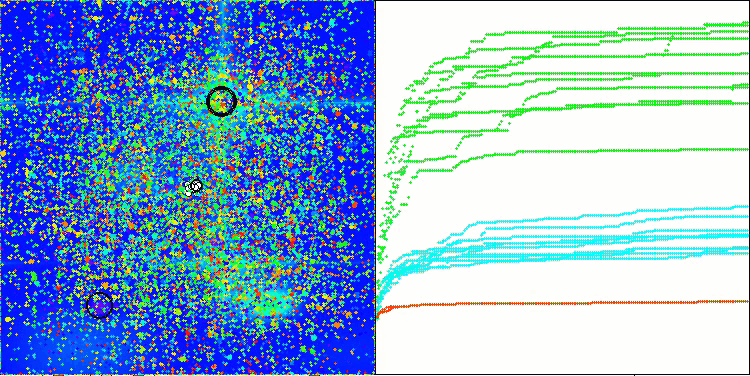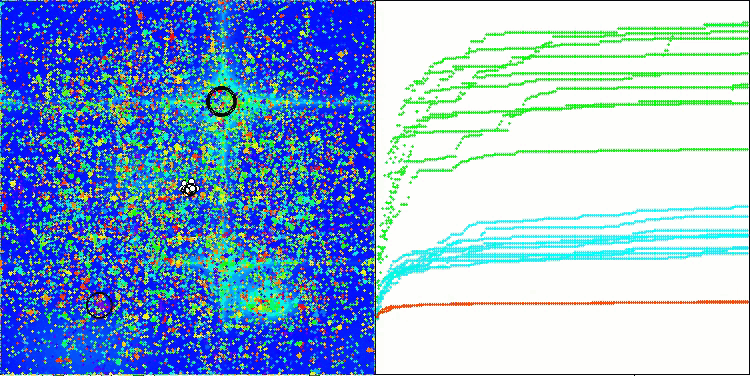
ACMO mit der Testfunktion Forest
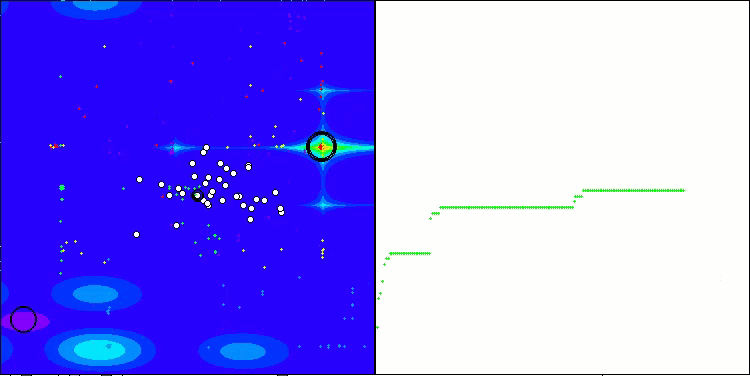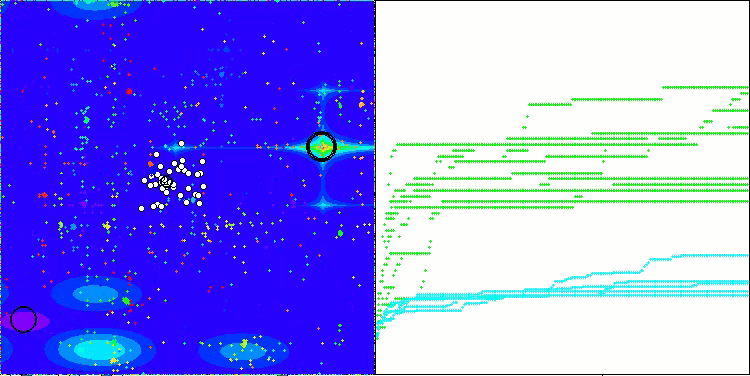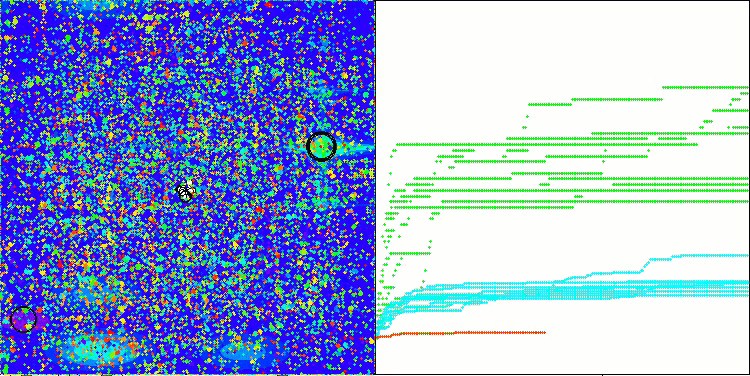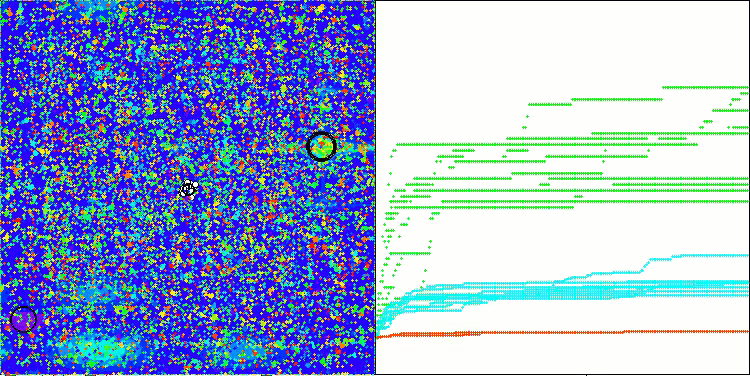
ACMO mit der Testfunktion Megacity
Nach den Ergebnissen des Tests der geänderten Version rangiert der Algorithmus auf Platz 27, was ein recht stabiler Indikator ist. Ich möchte betonen, dass die Tabelle jetzt immer 45 Algorithmen enthält, und dass mit jedem neuen Algorithmus die Differenz zwischen dem vorherigen und dem nachfolgenden Algorithmus allmählich abnimmt, sodass wir sagen können, dass die Tabelle die besten bekannten Algorithmen darstellt.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Сode Lock Algorithmus | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | Entwicklung der sozialen Gruppen | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | Simuliertes isotropes Abkühlen | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 12 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 13 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 14 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 15 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 16 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 17 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 18 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 19 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 20 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 21 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 22 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 23 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 24 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 25 | BFO-GA | Optimierung der bakteriellen Futtersuche - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 26 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 27 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 28 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 29 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 30 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 31 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 32 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 33 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 34 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 35 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 36 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 37 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 38 | ABC | Künstliches Bienenvolk (Artificial Bee Colony, ABC) | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | main0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 39 | BA | Fledermaus-Algorithmus | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 40 | AAA | Künstlicher Algenalgorithmus (AAA) | 0.50007 | 0.32040 | 0.25525 | 1.07572 | 0.37021 | 0.22284 | 0.16785 | 0.76089 | 0.27846 | 0.14800 | 0.09755 | 0.52402 | 2.361 | 26.23 |
| 41 | SA | simuliertes Abkühlen | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 42 | IWDm | intelligente Wassertropfen M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 43 | PSO | Partikelschwarmoptimierung | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 44 | Gebote | Boids-Algorithmus | 0.43340 | 0.30581 | 0.25425 | 0.99346 | 0.35718 | 0.20160 | 0.15708 | 0.71586 | 0.27846 | 0.14277 | 0.09834 | 0.51957 | 2.229 | 24.77 |
| 45 | MA | Affen-Algorithmus | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
Zusammenfassung
Es werden zwei Versionen des Algorithmus vorgestellt: die ursprüngliche und die modifizierte. Letzteres bringt zwar nur kleine Änderungen mit sich, erhöht aber die Leistung durch den Informationsaustausch innerhalb der Population erheblich. Dies zeigt, dass selbst geringfügige Anpassungen der Algorithmuslogik bei einer Vielzahl von Aufgaben zu erheblichen Effizienzsteigerungen führen können.
Die Idee des Algorithmus hat mir sehr gut gefallen, da er darauf abzielt, nicht in den Extrema stecken zu bleiben. Der Algorithmus verwendet eine komplexe mehrstufige Logik, um Wolken von Hochdruckgebieten zu Tiefdruckgebieten und Niederschlägen zu bewegen. Dies war jedoch nicht ausreichend, um eine hohe Konvergenz zu erreichen. Daher habe ich versucht, eine Änderung vorzunehmen, indem ich den Informationsaustausch in der Population einführte, was zu einer besseren Konvergenz beitrug, die einer der Schlüsselaspekte eines jeden Optimierungsalgorithmus ist.
Die Besonderheit des Algorithmus besteht darin, dass keine Wolke zu lange an einem Ort bleibt. Der ständig wachsende Druck in der Region drängt die Wolke unweigerlich in ein neues, unerforschtes Gebiet. Dieser Mechanismus wurde von den Autoren als ein Mittel konzipiert, um dem Steckenbleiben in lokalen Extrema entgegenzuwirken. Der Versuch, die Konvergenz des Algorithmus zu verbessern, erhöhte jedoch die Wahrscheinlichkeit, dass der Algorithmus stecken blieb, was leider die Schlüsseleigenschaft, die mich dazu inspirierte, diesen Ansatz auf andere Optimierungsalgorithmen anzuwenden, teilweise zunichte machte. Bei der Entwicklung von Optimierungsalgorithmen geht es immer darum, einen Kompromiss zwischen der Resistenz gegen das Hängenbleiben und dem Finden einer exakten Lösung zu finden. Falls gewünscht, kann die Wahrscheinlichkeit des Informationsaustauschs im Code reduziert werden. Derzeit sind es 95 %, was die Stabilität erhöhen wird.
Der Algorithmus ist eine wunderbare Grundlage und eine Reihe interessanter Techniken (Regeln für die Bildung von Feuchtigkeit in Regionen und die Verteilung des Drucks zwischen ihnen, und zusätzlich können physikalische Gesetze der Beschleunigung und Trägheit, abhängig von der Masse der Wolken und viele andere Ideen angewendet werden) und ist ein echter Segen für Forscher.
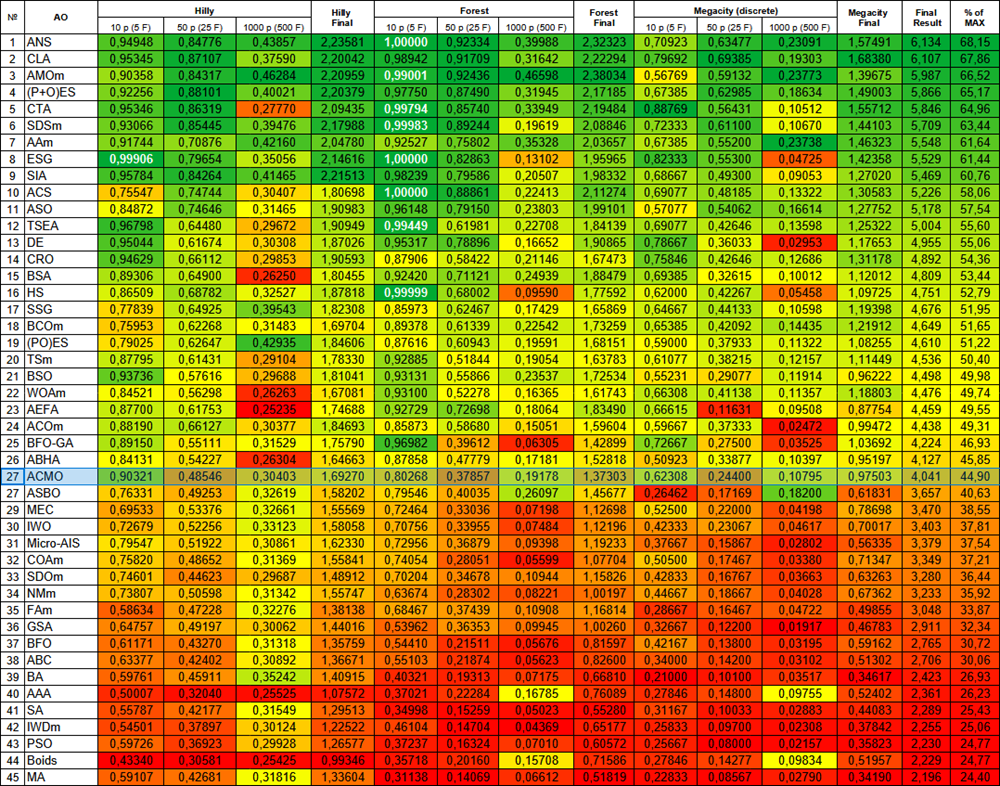
Abbildung 2. Histogramm der Algorithmus-Testergebnisse (Skala von 0 bis 100, je höher, desto besser, wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Bewertungstabelle)
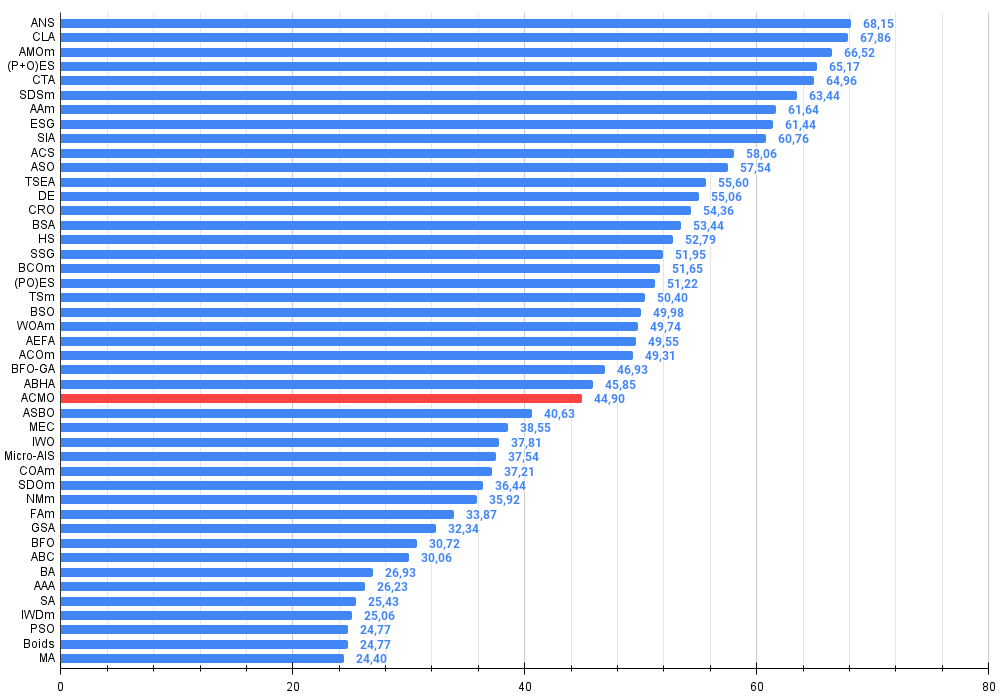
Abbildung 3. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben
Vor- und Nachteile von ACMO:
Vorteile:
- Eingebaute Mechanismen gegen das Hängenbleiben.
- Relativ gute Konvergenz.
- Relativ gute Skalierbarkeit.
Nachteile
- Eine Vielzahl von externen Parametern.
- Komplexe Umsetzung.
- Schwierigkeit, das richtige Gleichgewicht zwischen Festfahren und Konvergenz zu finden.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15921
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Hochfrequenz-Arbitrage-Handelssystem in Python mit MetaTrader 5
Hochfrequenz-Arbitrage-Handelssystem in Python mit MetaTrader 5
 Von der Grundstufe bis zur Mittelstufe: Die Anweisung FOR
Von der Grundstufe bis zur Mittelstufe: Die Anweisung FOR
 Von der Grundstufe bis zur Mittelstufe: Prioritätsfolge der Operatoren
Von der Grundstufe bis zur Mittelstufe: Prioritätsfolge der Operatoren
 Entwicklung eines Handelssystems auf der Grundlage des Orderbuchs (Teil I): Der Indikator
Entwicklung eines Handelssystems auf der Grundlage des Orderbuchs (Teil I): Der Indikator
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wirklich interessantes Thema!
Danke, sehr gerne.